SHAP - 機器學習模型可解釋性工具

github地址：shap/docs/index.rst at master · shap/shap (github.com)

SHAP使用文檔：歡迎使用 SHAP 文檔 — SHAP 最新文檔

SHAP介紹?

????????SHAP（SHapley Additive exPlanations）是一種用于解釋預測結果的方法，它基于Shapley值理論，通過將預測結果分解為每個特征的影響，為模型提供全局和局部的可解釋性。

? ? ? ? SHAP的核心思想是將特征值的的貢獻分配到不同的特征中，計算每個特征的Shapley值，并將其與特征值相乘得到該特征對于預測結果的貢獻，SHAP可以用于機器學習模型，包括分類和回歸模型，可以生成圖像化和定量的解釋結果，幫助用戶解釋模型的決策過程。

????????SHAP的優點包括可解釋性強、精度高、適用于各個模型和特征類型等。它可以幫助用戶更好地理解機器學習模型地預測結果，識別模型地弱點并改進模型，也可以幫助用戶更好地理解機器學習模型地預測結果，識別模型地弱點并改進模型，也可以幫助用戶進行特征工程和數據預處理，提高模型地預測能力。

SHAP安裝

SHAP 可以從?PyPI?或?conda-forge?安裝：

pip install shap
or
conda install -c conda-forge shap

具有 Shapley 值的可解釋 AI 簡介

這是使用 Shapley 值解釋機器學習模型的介紹。Shapley 值是合作博弈論中一種廣泛使用的方法，具有理想的屬性。本教程旨在幫助學生深入了解如何計算和插入基于 Shapley 的機器學習模型解釋。我們將采用實用的動手方法，使用 Python 包來解釋逐漸更復雜的模型。這是一份活生生的文件，服務于作為 Python 包的介紹。因此，如果您有反饋或貢獻，請提出問題或拉取請求，以使本教程更好！shapshap

大綱

解釋線性回歸模型
解釋廣義加性回歸模型
解釋非加性提升樹模型
解釋線性邏輯回歸模型
解釋非加性提升樹邏輯回歸模型
處理相關的輸入要素
解釋 transformers NLP 模型

解釋線性回歸模型

在使用 Shapley 值解釋復雜模型之前，了解它們如何適用于簡單模型會很有幫助。最簡單的模型類型之一是標準線性回歸，因此下面我們在加利福尼亞住房數據集上訓練線性回歸模型。該數據集由 20 年加利福尼亞州的 640,1990 個房屋街區組成，我們的目標是預測 8 個不同房價中位數的自然對數特征：

MedInc - 區塊組的收入中位數
HouseAge - 區塊組的房屋年齡中位數
AveRooms - 每戶平均房間數
AveBedrms - 每戶平均臥室數
population - 區塊組人口
AveOccup - 平均家庭成員人數
Latitude - 塊組緯度
Longitude - 塊組經度

import sklearnimport shap# a classic housing price dataset
X, y = shap.datasets.california(n_points=1000)X100 = shap.utils.sample(X, 100)  # 100 instances for use as the background distribution# a simple linear model
model = sklearn.linear_model.LinearRegression()
model.fit(X, y

?檢查模型系數

理解線性模型的最常見方法是檢查為每個特征學習的系數。這些系數告訴我們，當我們更改每個輸入特征時，模型輸出的變化程度：

print("Model coefficients:\n")
for i in range(X.shape[1]):print(X.columns[i], "=", model.coef_[i].round(5))

雖然系數非常適合告訴我們當我們更改輸入特征的值時會發生什么，但它們本身并不是衡量特征整體重要性的好方法。這是因為每個系數的值取決于輸入要素的比例。例如，如果我們以分鐘而不是年為單位來測量房屋的年齡，則 HouseAge 特征的系數將變為 0.0115 / （365?24?60） = 2.18e-8。顯然是自房子以來的年數構建并不比分鐘數更重要，但它的系數值要大得多。這意味著系數的大小不一定是線性模型中特征重要性的良好度量。

使用部分依賴圖獲得更完整的圖片

要了解特征在模型中的重要性，必須了解更改該特征如何影響模型的輸出，以及該特征值的分布。為了可視化線性模型，我們可以構建一個經典的部分依賴圖，并將特征值的分布顯示為 x 軸上的直方圖：

shap.partial_dependence_plot("MedInc",model.predict,X100,ice=False,model_expected_value=True,feature_expected_value=True,
)

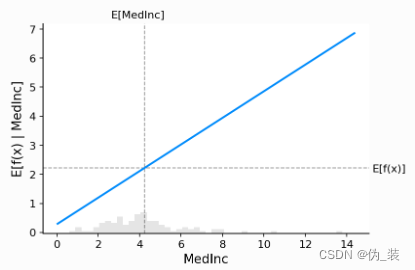?上圖中的灰色水平線表示模型應用于加州住房數據集時的預期值。垂直灰線表示收入中位數要素的平均值。請注意，藍色部分依賴性圖線（當我們將收入中位數特征固定為給定值時，模型輸出的平均值）始終穿過兩條灰色期望值線的交點。我們可以將這個交點視為“中心” 關于數據分布的部分依賴圖。當我們接下來轉向Shapley值時，這種集中的影響將變得清晰。

從部分依賴圖中讀取 SHAP 值

Shapley基于價值的機器學習模型解釋背后的核心思想是使用合作博弈論的公平分配結果，在其輸入特征中分配模型輸出的功勞。為了將博弈論與機器學習模型聯系起來，既要將模型的輸入特征與游戲中的玩家進行匹配，又要將模型函數與游戲規則進行匹配。由于在博弈論中，玩家可以加入或不加入游戲，因此我們需要一種方法用于“連接”或“不連接”模型的特征。定義特征“連接”模型意味著什么的最常見方法是，當我們知道該特征的值時，該特征已“加入模型”，而當我們不知道該特征的值時，它尚未加入模型。為了評估現有模型，當模型中只有一部分特征時，我們使用條件期望值公式將其他特征積分出來。這種配方可以采取兩個形式：

\[E[f(X) \mid X_S = x_S]\]

或

\[E[f(X) \mid do(X_S = x_S)]\]

在第一種形式中，我們知道 S 中特征的值，因為我們觀察它們。在第二種形式中，我們知道 S 中特征的值，因為我們設置了它們。一般來說，第二種形式通常是可取的，因為它告訴我們如果我們要干預和改變其輸入，模型將如何表現，也因為它更容易計算。在本教程中，我們將完全專注于第二種公式。我們還將使用更具體的術語“SHAP 值”來指代應用于機器學習模型的條件期望函數的 Shapley 值。

SHAP 值的計算可能非常復雜（它們通常是 NP 困難的），但線性模型非常簡單，我們可以直接從部分依賴圖中讀取 SHAP 值。當我們解釋預測時，特定特征的 SHAP 值只是預期模型輸出與特征值處的部分依賴圖之間的差值：

# compute the SHAP values for the linear model
explainer = shap.Explainer(model.predict, X100)
shap_values = explainer(X)# make a standard partial dependence plot
sample_ind = 20
shap.partial_dependence_plot("MedInc",model.predict,X100,model_expected_value=True,feature_expected_value=True,ice=False,shap_values=shap_values[sample_ind : sample_ind + 1, :],
)

經典部分依賴圖和 SHAP 值之間的緊密對應關系意味著，如果我們在整個數據集中繪制特定特征的 SHAP 值，我們將精確地跟蹤出該特征的部分依賴圖的均值中心版本：

shap.plots.scatter(shap_values[:, "MedInc"])

Shapley值的累加性

Shapley 值的基本屬性之一是，它們總是匯總所有玩家在場時的游戲結果與沒有玩家在場時的游戲結果之間的差異。對于機器學習模型，這意味著所有輸入特征的 SHAP 值將始終相加為基線（預期）模型輸出與所解釋預測的當前模型輸出之間的差值。最簡單的方法是通過瀑布圖，從我們的背景對房價的先驗預期?，然后一次添加一個特征，直到我們達到當前模型輸出：

# the waterfall_plot shows how we get from shap_values.base_values to model.predict(X)[sample_ind]
shap.plots.waterfall(shap_values[sample_ind], max_display=14)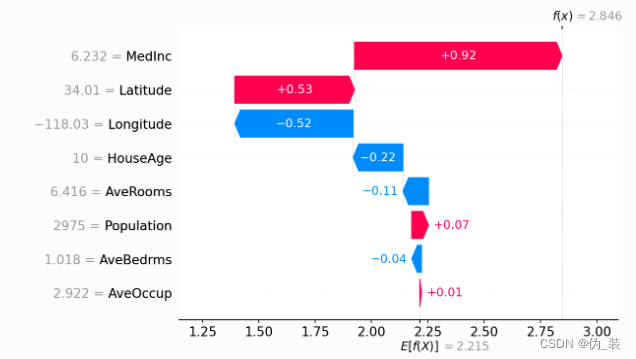

解釋加性回歸模型?

線性模型的偏相關圖與 SHAP 值具有如此緊密的聯系的原因是，模型中的每個特征都獨立于其他所有特征進行處理（效應只是相加而已）。我們可以保持這種累加性，同時放寬直線的線性要求。這導致了眾所周知的一類廣義加法模型（GAM）。雖然有很多方法可以訓練這些類型的模型（例如將 XGBoost 模型設置為 depth-1），但我們將使用專門為此設計的 InterpretML 可解釋的提升機器。

# fit a GAM model to the data
import interpret.glassboxmodel_ebm = interpret.glassbox.ExplainableBoostingRegressor(interactions=0)
model_ebm.fit(X, y)# explain the GAM model with SHAP
explainer_ebm = shap.Explainer(model_ebm.predict, X100)
shap_values_ebm = explainer_ebm(X)# make a standard partial dependence plot with a single SHAP value overlaid
fig, ax = shap.partial_dependence_plot("MedInc",model_ebm.predict,X100,model_expected_value=True,feature_expected_value=True,show=False,ice=False,shap_values=shap_values_ebm[sample_ind : sample_ind + 1, :],
)

shap.plots.scatter(shap_values_ebm[:, "MedInc"])

# the waterfall_plot shows how we get from explainer.expected_value to model.predict(X)[sample_ind]
shap.plots.waterfall(shap_values_ebm[sample_ind])

# the waterfall_plot shows how we get from explainer.expected_value to model.predict(X)[sample_ind]
shap.plots.beeswarm(shap_values_ebm)

?解釋非加性提升樹模型

# train XGBoost model
import xgboostmodel_xgb = xgboost.XGBRegressor(n_estimators=100, max_depth=2).fit(X, y)# explain the GAM model with SHAP
explainer_xgb = shap.Explainer(model_xgb, X100)
shap_values_xgb = explainer_xgb(X)# make a standard partial dependence plot with a single SHAP value overlaid
fig, ax = shap.partial_dependence_plot("MedInc",model_xgb.predict,X100,model_expected_value=True,feature_expected_value=True,show=False,ice=False,shap_values=shap_values_xgb[sample_ind : sample_ind + 1, :],
)

shap.plots.scatter(shap_values_xgb[:, "MedInc"])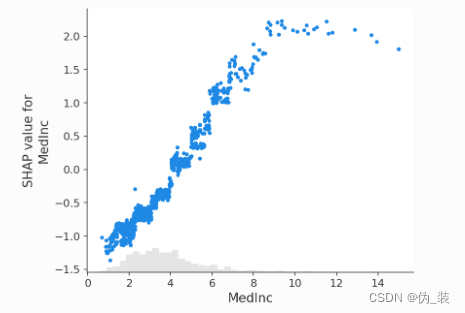

shap.plots.scatter(shap_values_xgb[:, "MedInc"], color=shap_values)

?解釋線性邏輯回歸模型

# a classic adult census dataset price dataset
X_adult, y_adult = shap.datasets.adult()# a simple linear logistic model
model_adult = sklearn.linear_model.LogisticRegression(max_iter=10000)
model_adult.fit(X_adult, y_adult)def model_adult_proba(x):return model_adult.predict_proba(x)[:, 1]def model_adult_log_odds(x):p = model_adult.predict_log_proba(x)return p[:, 1] - p[:, 0]

?請注意，解釋線性邏輯回歸模型的概率在輸入中不是線性的。

# make a standard partial dependence plot
sample_ind = 18
fig, ax = shap.partial_dependence_plot("Capital Gain",model_adult_proba,X_adult,model_expected_value=True,feature_expected_value=True,show=False,ice=False,
)

?如果我們使用 SHAP 來解釋線性邏輯回歸模型的概率，我們會看到很強的交互效應。這是因為線性邏輯回歸模型在概率空間中不是累加的。

# compute the SHAP values for the linear model
background_adult = shap.maskers.Independent(X_adult, max_samples=100)
explainer = shap.Explainer(model_adult_proba, background_adult)
shap_values_adult = explainer(X_adult[:1000])

shap.plots.scatter(shap_values_adult[:, "Age"])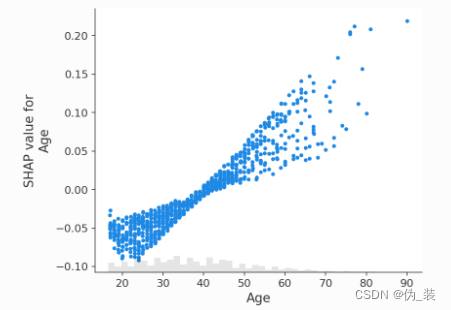

如果我們解釋模型的對數賠率輸出，我們會看到模型輸入和模型輸出之間存在完美的線性關系。重要的是要記住要解釋的模型的單位是什么，解釋不同的模型輸出可能會導致模型行為的非常不同的觀點。

# compute the SHAP values for the linear model
explainer_log_odds = shap.Explainer(model_adult_log_odds, background_adult)
shap_values_adult_log_odds = explainer_log_odds(X_adult[:1000])

shap.plots.scatter(shap_values_adult_log_odds[:, "Age"])

# make a standard partial dependence plot
sample_ind = 18
fig, ax = shap.partial_dependence_plot("Age",model_adult_log_odds,X_adult,model_expected_value=True,feature_expected_value=True,show=False,ice=False,
)

?解釋非加性提升樹邏輯回歸模型

# train XGBoost model
model = xgboost.XGBClassifier(n_estimators=100, max_depth=2).fit(X_adult, y_adult * 1, eval_metric="logloss"
)# compute SHAP values
explainer = shap.Explainer(model, background_adult)
shap_values = explainer(X_adult)# set a display version of the data to use for plotting (has string values)
shap_values.display_data = shap.datasets.adult(display=True)[0].values

默認情況下，SHAP 條形圖將采用數據集所有實例（行）上每個要素的平均絕對值。

shap.plots.bar(shap_values)

但平均絕對值并不是創建特征重要性的全局度量的唯一方法，我們可以使用任意數量的變換。在這里，我們將展示如何使用最大絕對值來突出資本收益和資本損失特征，因為它們具有不常見但高幅度的影響。

shap.plots.bar(shap_values.abs.max(0))

如果我們愿意處理更復雜的問題，我們可以使用蜂群圖來總結每個特征的 SHAP 值的整個分布。

shap.plots.beeswarm(shap_values)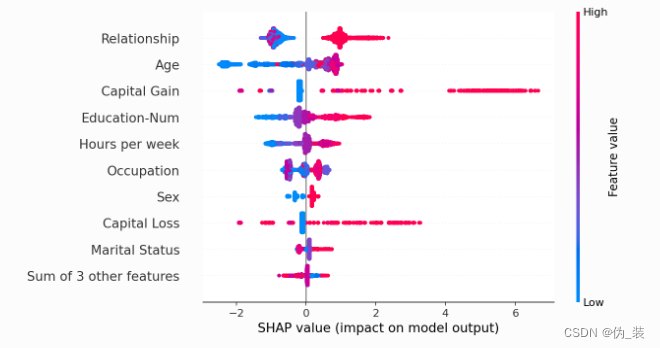

通過取絕對值并使用純色，我們可以在條形圖和完整蜂群圖的復雜性之間達成折衷。請注意，上面的條形圖只是下面蜂群圖中顯示的值的匯總統計數據。

shap.plots.beeswarm(shap_values.abs, color="shap_red")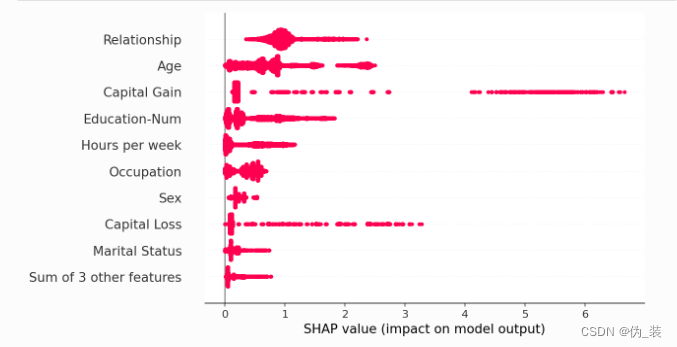

shap.plots.heatmap(shap_values[:1000])

shap.plots.scatter(shap_values[:, "Age"])

shap.plots.scatter(shap_values[:, "Age"], color=shap_values)

shap.plots.scatter(shap_values[:, "Age"], color=shap_values[:, "Capital Gain"])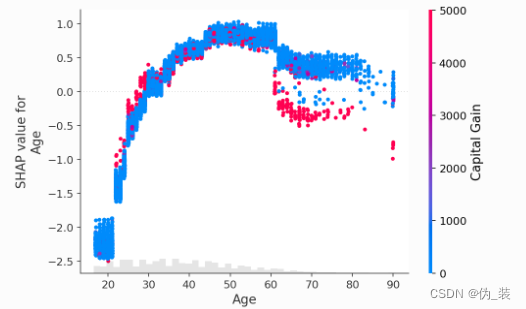

shap.plots.scatter(shap_values[:, "Relationship"], color=shap_values)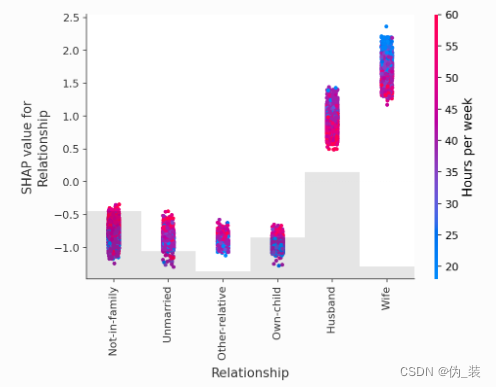

處理相關特征

clustering = shap.utils.hclust(X_adult, y_adult)

shap.plots.bar(shap_values, clustering=clustering)

shap.plots.bar(shap_values, clustering=clustering, clustering_cutoff=0.8)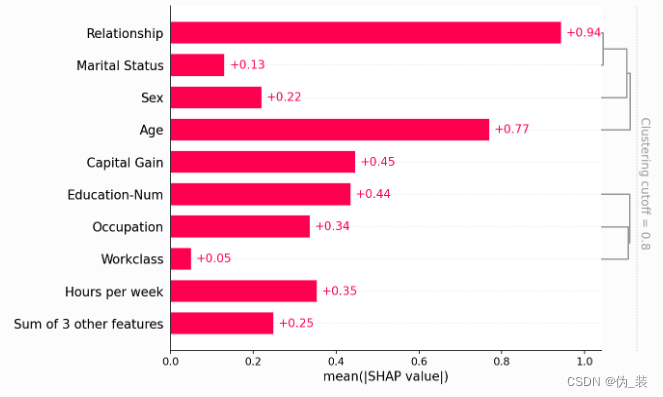

shap.plots.bar(shap_values, clustering=clustering, clustering_cutoff=1.8)

解釋一個 transformers NLP 模型

這演示了如何將 SHAP 應用于具有高度結構化輸入的復雜模型類型。

import datasets
import numpy as np
import scipy as sp
import torch
import transformers# load a BERT sentiment analysis model
tokenizer = transformers.DistilBertTokenizerFast.from_pretrained("distilbert-base-uncased"
)
model = transformers.DistilBertForSequenceClassification.from_pretrained("distilbert-base-uncased-finetuned-sst-2-english"
).cuda()# define a prediction function
def f(x):tv = torch.tensor([tokenizer.encode(v, padding="max_length", max_length=500, truncation=True)for v in x]).cuda()outputs = model(tv)[0].detach().cpu().numpy()scores = (np.exp(outputs).T / np.exp(outputs).sum(-1)).Tval = sp.special.logit(scores[:, 1])  # use one vs rest logit unitsreturn val# build an explainer using a token masker
explainer = shap.Explainer(f, tokenizer)# explain the model's predictions on IMDB reviews
imdb_train = datasets.load_dataset("imdb")["train"]
shap_values = explainer(imdb_train[:10], fixed_context=1, batch_size=2)

# plot a sentence's explanation
shap.plots.text(shap_values[2])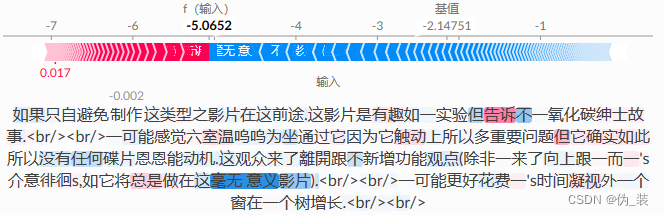

shap.plots.bar(shap_values.abs.mean(0))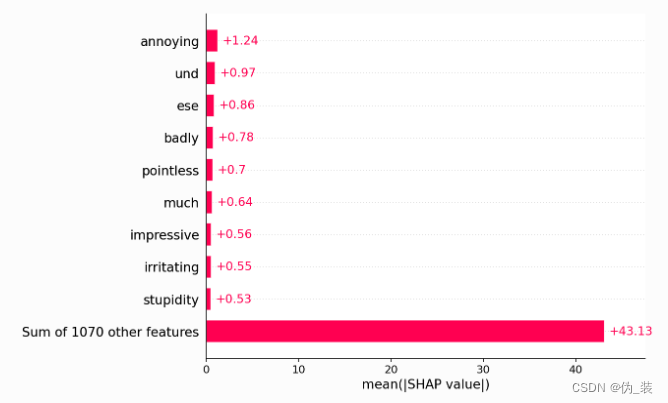

shap.plots.bar(shap_values.abs.sum(0))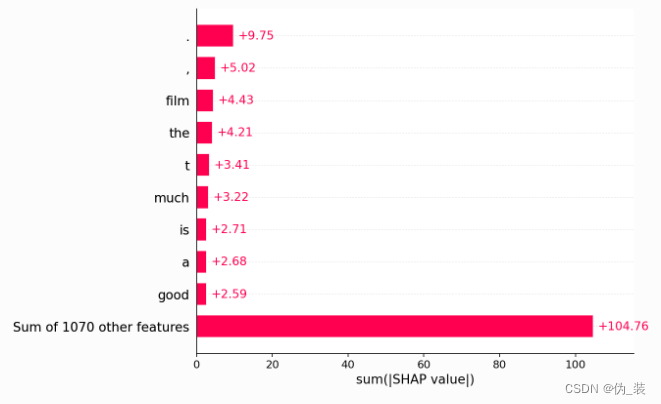