提示：文章寫完后，目錄可以自動生成，如何生成可參考右邊的幫助文檔

---

前言

世上有兩種耀眼的光芒，一種是正在升起的太陽，一種是正在努力學習編程的你!一個愛學編程的人。各位看官，我衷心的希望這篇博客能對你們有所幫助，同時也希望各位看官能對我的文章給與點評，希望我們能夠攜手共同促進進步，在編程的道路上越走越遠!

---

提示：以下是本篇文章正文內容，下面案例可供參考

經典算法OJ題1： 移除元素

給你一個數組 nums?和一個值?val，你需要?原地?移除所有數值等于?val?的元素，并返回移除后數組的新長度。不要使用額外的數組空間，你必須僅使用?O(1)?額外空間并?原地?修改輸入數組。元素的順序可以改變。你不需要考慮數組中超出新長度后面的元素。

首先要想清楚移除的本質并不是真刪除，而是把元素覆蓋即可，覆蓋n個元素后，數組總長度就要-n

解法一、逐個判斷

把數組從頭開始遍歷，找到目標元素val，就執行一次任意位置刪除

注意： 在實際寫代碼時，每刪除一次元素，i 都要回退一次，因為有的測試用例是 3 3 3 3，val = 3，如果不回退，直接覆蓋，會少刪兩個元素。

代碼演示:

void Erase(int* nums, int pos, int len)
{assert(len > 0);while (pos < len){nums[pos] = nums[pos + 1];//數組中后面的數據把前面的數據覆蓋pos++;//向后移動}
}
int removeElement(int* nums, int numsSize, int val)
{assert(nums);  //nums不能為空指針int i = 0;int len = numsSize;//數組的有效元素個數for (i = 0; i < len; i++){if (nums[i] == val){Erase(nums, i, len);i--;//這里i--是因為后面的值把i所在的位置覆蓋，//如果不--，出了這個循環，i++, 就會把再i上賦的值給忽略，少判斷一次len--;}}return len;//返回的是刪除之后的數組長度
}

解法二、雙指針覆蓋

這是一種比較巧妙的解法，用到了雙指針 ，對數組內元素進行覆蓋，具體實現為：存在兩個指針src?、dst?，兩者初始都指向數組起始位置，遍歷 整個數組，對指針 src?和指針 dst?所指向的值進行比較，如果 *src?!= val ，就把 *src?賦給 *dst?，然后 dst?向后移動，當然無論相等還是不相等，src?都需要往后移動，這個解法的目的就是把數組中所有非目標值的元素往前移動，最后返回?dst 的下標（dst的下標就是數組中不等于 val 的值的個數）

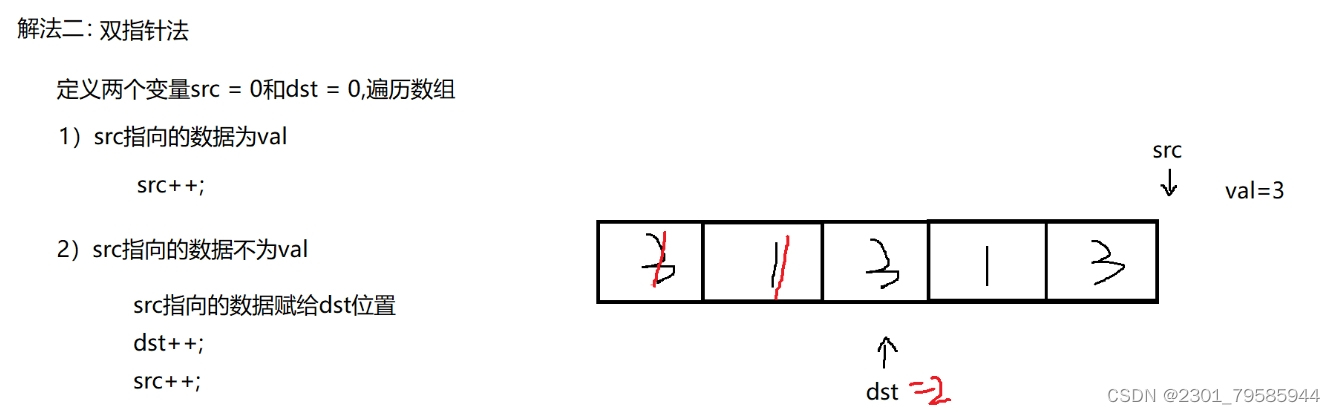
代碼演示：

int removeElement(int* nums, int numsSize, int val) {int src = 0;int dst = 0;while (src < numsSize){if (nums[src] == val){src++;}else{nums[dst] = nums[src];dst++;src++;}}return dst;
}

經典算法OJ題2： 合并兩個有序數組

給你兩個按?非遞減順序?排列的整數數組?nums1?和?nums2，另有兩個整數?m?和?n?，分別表示?nums1?和?nums2?中的元素數目。請你?合并?nums2?到?nums1?中，使合并后的數組同樣按?非遞減順序?排列。

注意：最終，合并后數組不應由函數返回，而是存儲在數組?nums1?中。為了應對這種情況，nums1?的初始長度為?m + n，其中前?m?個元素表示應合并的元素，后?n?個元素為?0?，應忽略。nums2?的長度為?n?。

nums1

數組	1	2	3	0	0	0
下標	0	1	2	3	4	5

nums2

數組	2	5	6
下標	0	1	2

假設比小的思路：設L1為nums1數組的起始位置，L2為nums2數組的起始位置，我們從比小的角度看，L1為1時，L2為2，L2大；L1++，此時L1為2，L2為2，我們假設還是L1的2大；L1++，此時L1為3，L2為2，我們把L2的值賦給L1，那么原來L1位置上的3就沒了，所以這種比小的思路是不行的。

假設比大的思路：設L1為nums1數組實際有效數據的最后一個元素（下標為2），L3為nums1數組初始化的最后一個位置（下標為5）；L2為nums2數組的最后一個元素；L2為6時，L1為3，L2賦值給L3，L2--,L3--，L2不變;L2為5時，L1為3，L2賦值給L3，L2--,L3--，L1不變;L2為2時，L1為3，此時L1賦值給L3，L3--,L1--;L2為2，L1為2，假設L2的2比L1的2要大，L2賦值給L3，L3--,L2--;此時L2已經完成循環，所以比大的思路時正確的。

此外，我們仍需要考慮兩種情況：L2先出循環和L1先出循環。

上面的比大思路就是我們的L2先出循環，沒有是什么好考慮的。

我們來看L1先出循環的情況：

nums1

數組	4	5	6	0	0	0
下標	0	1	2	3	4	5

nums2

數組	1	2	3
下標	0	1	2

仍然是比大的思路：L2為3時，L1為6，L1的值賦給L3，L1--,L3--,L2不變；L2為3時，L1為5，L1的值賦給L3，L3--,L1--,L2不變；L1為4時，L2為3，L1的值賦給L3，L3--,L1--,L2不變；此時L1先完成循環，但是L2的數據還在原位，因為都是遞增的排序，那么只需要把L2數組的元素賦值給L3中。

代碼演示：

void merge(int* nums1, int m, int* nums2, int n) 
{int l1 = m - 1, l2 = n - 1;int l3 = m + n - 1;while (l1 >= 0 && l2 >= 0){if (nums1[l1] > nums2[l2]){nums1[l3] = nums1[l1];l1--;l3--;}else{nums1[l3] = nums2[l2];l3--;l2--;}}while (l2 >= 0){nums1[l3] = nums2[l2];l3--;l2--;}
}

OJ題分為兩個類型：

1：接口型（不需要main()函數，我們把代碼提交之后，后端會自動拼接main()函數）

2：IO型（需要main()函數）

---

總結

好了，本篇博客到這里就結束了，如果有更好的觀點，請及時留言，我會認真觀看并學習。
不積硅步，無以至千里；不積小流，無以成江海。