題目描述

142.環形鏈表II

給定一個鏈表的頭節點 head ，返回鏈表開始入環的第一個節點。 如果鏈表無環，則返回 null。

如果鏈表中有某個節點，可以通過連續跟蹤 next 指針再次到達，則鏈表中存在環。 為了表示給定鏈表中的環，評測系統內部使用整數 pos 來表示鏈表尾連接到鏈表中的位置（索引從 0 開始）。如果 pos 是 -1，則在該鏈表中沒有環。注意：pos 不作為參數進行傳遞，僅僅是為了標識鏈表的實際情況。

不允許修改 鏈表。

示例 1：

輸入：head = [3,2,0,-4], pos = 1
輸出：返回索引為 1 的鏈表節點
解釋：鏈表中有一個環，其尾部連接到第二個節點。

示例 2：

輸入：head = [1,2], pos = 0
輸出：返回索引為 0 的鏈表節點
解釋：鏈表中有一個環，其尾部連接到第一個節點。

示例 3：

輸入：head = [1], pos = -1
輸出：返回 null
解釋：鏈表中沒有環。

提示：

鏈表中節點的數目范圍在范圍 [0, 104] 內
-105 <= Node.val <= 105
pos 的值為 -1 或者鏈表中的一個有效索引

進階：你是否可以使用 O(1) 空間解決此題？

解題思路 & 代碼實現

本題主要解決兩個問題：

• 判斷鏈表是否有環
• 如果有環如何找到環的入口

判斷鏈表是否有環

使用快慢指針法，分別定義fast和slow兩個指針，從頭節點出發，fast指針每次移動兩個節點，slow指針每次移動一個節點，如果兩個指針在途中相遇，說明這個鏈表有環。

強調途中的意思是指兩個指針不是在鏈表末尾相遇的。

因為fast指針移動的快，所以如果兩個指針相遇，一定是fast追上了slow指針，并且一定是在環中相遇，因為假如不在環中相遇，fast是無法從slow的后面追上slow的。

至于fast為什么走兩步，slow為什么走一步，是因為如果存在環，fast相當于是一步一步的追趕slow，也可以想象為slow沒有動，fast一次走一步，這樣就比較好理解了。

之所以slow也要移動，是因為最終要找的是環的入口，slow如果不移動，環的入口就比較難判斷。

如何找到環的入口

假設從頭結點到環形入口節點的節點數為x。 環形入口節點到 fast指針與slow指針相遇節點節點數為y。 從相遇節點再到環形入口節點節點數為z。 如圖所示：

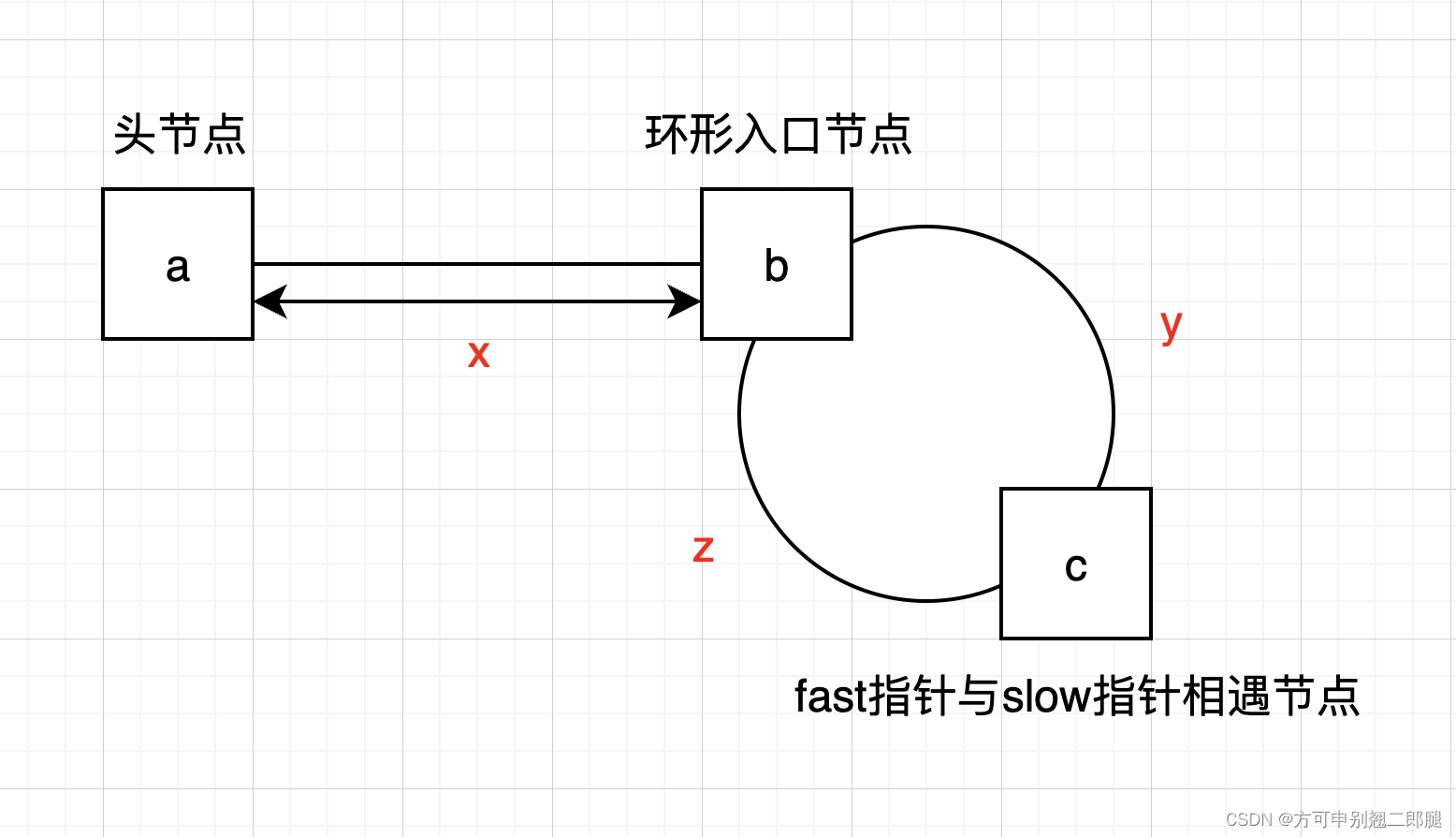
相遇時，slow指針走過的路程為x + y，fast針走過的路程為x + y + n * (y + z)，n表示fast指針在環內走了 n 圈才遇到slow指針。

因為fast指針的速度是slow指針的兩倍，fast指針走的路程是slow指針走的路程的兩倍：

x + y + n * (y + z) = 2 * (x + y)

因為要求的是環形入口節點的位置，因此把 x 放在等式左邊：

x = n * (y + z) - y

再從其中提取出一個 y + z來：

x = (n - 1) (y + z) + z

當 n = 1時，也就是fast指針只走了一圈時，公式可化簡為x = z，這表示如果從頭節點出發一個指針，從相遇節點也出發一個指針，這兩個指針每次只走一個節點， 那么當這兩個指針相遇的時候，那個相遇的節點就是環形入口節點。

當n > 1的時候，由于y + z就是環的長度，這表示fast指針在圈內走了一些圈數，最終還是能得出n = 1時的結論。

class Solution{
public:ListNode* detectCycle(ListNode* head){ListNode* fast = head;ListNode* slow = head;while (fast != NULL && fast -> next != NULL) {slow = slow -> next; // slow移動一步fast = fast -> next -> next; // fast移動兩步if (slow == fast) { // 當 fast 和 slow 相遇時ListNode* curA = head;ListNode* curB = fast;while (curA != curB) {curA = curA -> next;curB = curB -> next;}return curA; // 找到入口節點}}return NULL:}
};