開篇介紹：

Hello 大家，在上一篇博客中，我們一同拆解了「206. 反轉鏈表」和「876. 鏈表的中間結點」這兩道單鏈表經典題目，通過對指針操作的細致打磨，相信大家對單鏈表的特性與算法設計思路有了更深入的理解。而在今天的內容里，我們將邁入單鏈表的一個更具挑戰性的領域 —— 環形鏈表，并聚焦于一道兼具趣味性與實用性的經典問題：「環形鏈表的約瑟夫問題」。

說起約瑟夫問題，它不僅是數據結構領域的經典命題，更蘊含著深刻的數學邏輯與算法智慧。無論是在早期的計算機科學研究中，還是在如今的面試場景里，這道題都以其巧妙的設計考驗著開發者對環形結構的理解、指針操控的熟練度，以及對問題本質的提煉能力。

與我們之前接觸的單鏈表不同，環形鏈表的尾節點不再指向 NULL，而是 “首尾相連”，指向鏈表中的某個節點（通常是頭節點），形成一個閉合的回路。這種特殊的結構，使得遍歷、刪除等操作都與線性鏈表有著顯著差異 —— 比如，在環形鏈表中，你永遠無法通過 “指針指向 NULL” 來判斷遍歷的結束，這就要求我們必須設計更巧妙的邏輯來處理節點的訪問與操作。

在接下來的內容里，我們將從問題的起源與題意分析入手，逐步拆解環形鏈表的構建邏輯、節點遍歷技巧，以及如何在循環淘汰的過程中避免鏈表斷裂。我們會先從最樸素的 “模擬法” 開始 —— 一步步構建環形鏈表，模擬報數與刪除的全過程，讓大家直觀感受環形結構的特性；隨后，我們會深入探討優化思路，分析如何通過數學規律減少不必要的遍歷，提升算法效率。

無論你是剛接觸環形鏈表的新手，還是希望鞏固算法基礎的開發者，相信這道題都能為你帶來新的啟發。它不僅能幫助我們熟練掌握環形鏈表的增刪查改，更能鍛煉我們將實際問題抽象為數據結構模型的能力 —— 而這種能力，在解決復雜工程問題時往往至關重要。

接下來，就讓我們一同走進環形鏈表的世界，揭開約瑟夫問題的神秘面紗。準備好了嗎？讓我們開始吧！

先給出本題鏈接，老規矩，大家先自行練手：環形鏈表的約瑟夫問題_牛客題霸_牛客網https://www.nowcoder.com/practice/41c399fdb6004b31a6cbb047c641ed8a

約瑟夫問題介紹：

約瑟夫問題（Josephus Problem）是一個經典的數學和計算機科學問題，其核心場景可概括為：一群人圍成環形，從某個人開始按固定間隔計數，每數到特定數字時，對應位置的人就被 “淘汰”，之后從下一個人開始重新計數，直到最后只剩下一個人作為幸存者。這個問題的本質是研究在環形結構中，如何通過遞推或模擬等方式找到最后幸存者的位置。

問題的起源與經典描述

約瑟夫問題的名字源于公元 1 世紀的猶太歷史學家弗拉維奧?約瑟夫斯（Flavius Josephus）。傳說在猶太反抗羅馬的戰爭中，約瑟夫斯和其他 40 名反抗者被困在洞穴中，他們約定圍成一圈，從某個人開始每數到 3 就殺死對應之人，直到最后一人自殺。但約瑟夫斯不想自殺，于是他通過數學計算找到最后一個位置，從而幸存下來，這一故事便成為該問題的原型。

經典的數學描述為：設有 n 個人圍成一圈，從第 k 個人開始報數，每次報數到 m 時，該人退出，然后從下一個人重新開始報數，直到剩下最后一個人，求最后幸存者的初始位置。

環形鏈表與約瑟夫問題的關聯

在計算機科學中，約瑟夫問題常與 “環形鏈表” 結合，成為數據結構的經典應用題。原因在于：

• 環形鏈表的 “環形” 結構天然貼合問題中 “圍成一圈” 的場景，每個節點代表一個人，節點間的指針形成閉環，完美模擬了 “首尾相接” 的計數環境；
• 鏈表的節點刪除操作（淘汰某個人）可以直觀地模擬 “退出” 過程，而通過指針移動可以實現 “按順序計數” 的邏輯。

作為經典問題，約瑟夫問題的價值不僅在于其趣味性，更在于它對邏輯思維和算法設計的啟發：

• 它考驗對環形結構的理解和操作（如環形鏈表的構建、指針循環移動）；
• 引導學習者從 “模擬法” 過渡到 “遞推公式法”（通過數學推導直接計算幸存者位置，避免逐次模擬的低效）；
• 在實際場景中，類似的環形計數邏輯可應用于輪詢調度、資源分配、密碼學等領域。

無論是用環形鏈表模擬過程，還是用數學公式推導結果，約瑟夫問題都堪稱環形結構與計數邏輯結合的典范，也是理解 “循環” 與 “淘汰” 問題的基礎。

環形鏈表的約瑟夫問題：
?

我們先看題目：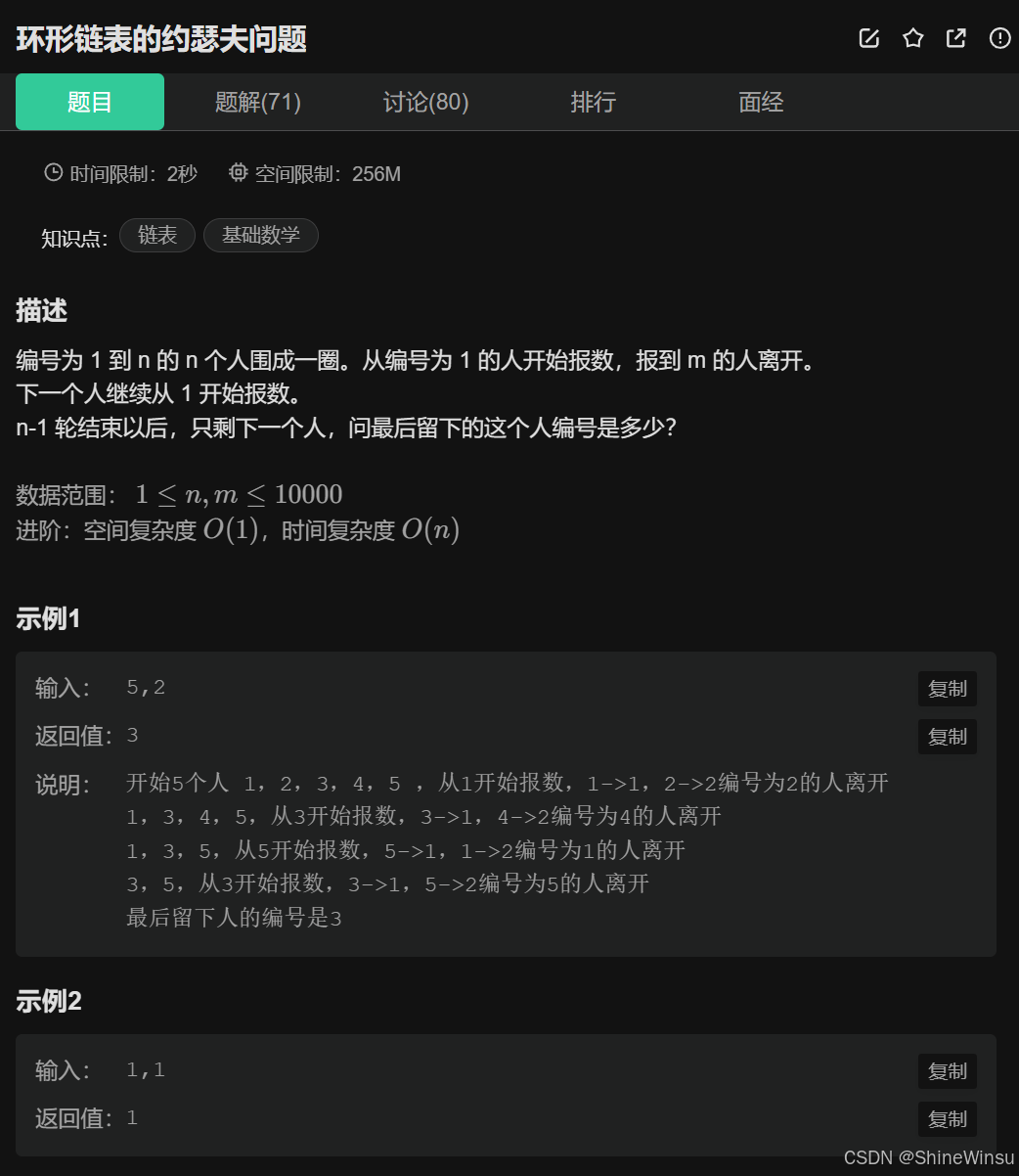

題意分析：

題目核心描述

• 參與人員：編號為?1?到?n?的?n?個人圍成一個圈。
• 報數規則：從編號為?1?的人開始報數，報到?m?的人離開。
• 持續過程：下一個人繼續從?1?開始報數，重復此過程，直到只剩下一個人。
• 目標：求最后留下的人的編號。

數據范圍

• 1≤n,m≤10000，說明數據規模較大，需要考慮算法的時間和空間復雜度。
• 進階要求：空間復雜度?O(1)，時間復雜度?O(n)，這提示我們需要尋找高效的算法，避免使用過多額外空間且保證時間效率。

示例分析

示例 1

• 輸入：n = 5，m = 2
• 過程：
  • 初始人員：1, 2, 3, 4, 5
  • 第一輪報數：報到?2，編號為?2?的人離開，剩余?1, 3, 4, 5。
  • 第二輪報數：從?3?開始，報到?2，編號為?4?的人離開，剩余?1, 3, 5。
  • 第三輪報數：從?5?開始，報到?2，編號為?1?的人離開，剩余?3, 5。
  • 第四輪報數：從?3?開始，報到?2，編號為?5?的人離開，最后剩下?3。
• 返回值：3

示例 2

• 輸入：n = 1，m = 1
• 過程：只有 1 個人，報數到?1?時自己離開，最后留下的就是自己。
• 返回值：1

環形鏈表法：

這道題的最經典解法，就是采用環形鏈表方法去解決，那么在解決題目之前，我們得先創建一個環形鏈表，在之前的一篇關于鏈表的保姆級介紹中，大家已經知道了環形鏈表的概念，如果有不知道的，可以看一下這篇博客：對于數據結構：鏈表的超詳細保姆級解析-CSDN博客https://blog.csdn.net/2503_92929084/article/details/151193278?spm=1001.2014.3001.5502

環形鏈表其實就是一個鏈表中的尾節點的next指針指向該鏈表的頭結點，那么，我們想要創建出環形鏈表其實也很簡單，我們可以先創建一個單向鏈表，隨后再把這個單向鏈表的尾節點的next指針賦值為頭結點的地址即可。

那么針對本題，我們要怎么創建一個單向鏈表呢?與之前的題目不同，之前的題目是有原鏈表的，所以我們可以直接把原鏈表的節點給新鏈表，但是在本題中，是沒有鏈表的，意味著我們只能自己創建節點去接收數據，同時組成鏈表。

除此之外，我們還能看到，在本題中，要生成包含從1到n的數字的鏈表，那么很明顯，這需要借助循環，那么要怎么利用循環呢？其實并不難，大家且看我敘來：

其實與之前的有鏈表的題目很相似，我們依然是要創建新鏈表的頭結點和尾節點，也就是newhead和newtail，而且，既然之前是有原鏈表的節點直接套用，那么雖然在本題中沒有，但是我們可以自力更生，自己創建容納數據的節點去不斷尾插進新鏈表中，那么首先，我們就需要創建新節點的函數，這在對鏈表的保姆級解析中也有所提及，所以我這里也就不贅述，直接上代碼：

//創建新節點
sl* create(int x)
{sl* newsl=malloc(sizeof(sl));newsl->data=x;newsl->next=NULL;return newsl;
}

接下來，我們就得著手使用尾插法去不斷對新鏈表插入數據了，在之前的題目中（對于單鏈表相關經典算法題：203. 移除鏈表元素的解析-CSDN博客），我們是要先判斷是否為空鏈表，然后把原鏈表的節點賦值為新鏈表的頭結點，接下來，我們才能借助newtail去不斷進行尾插。

那么在本題中，我們的新鏈表在剛開始依然也為空，所以很顯然，我們也要對這個新鏈表的插入一個頭結點，而由于本題沒有原鏈表，所以我們就要借助創建節點函數，將第一個節點插入新鏈表中了，具體如下：

sl* head=create(1);//第一個節點存1，后面的節點從1存到n
sl* tail=head;

這一步，就相當于這一步：

sl* newhead = NULL;
sl* newtail = newhead;
sl* temp = head;
while (temp != NULL)
{if (temp->val != val){if (newhead == NULL)  // 當新鏈表為空時，直接插入第一個節點{newhead = temp;newtail = newhead;}// 此處缺少else分支，用于處理非第一個節點的插入邏輯}temp = temp->next;

那么，在處理完了頭結點之后，我們就可以對新鏈表進行尾插了，上面我們有說到，要借助循環，那么其實和之前也很像，同樣是借助newtail移動不斷插入新節點，只不過是由原本的while循環換成了for循環，具體代碼如下：

//創建循環鏈表
sl* createsl(int n)
{sl* newhead=create(1);//第一個節點存1，后面的節點從1存到nsl* newtail=newhead;for(int i=2;i<=n;i++){newtail->next=create(i);newtail=newtail->next;}
}

如此，我們便創建了一個單向鏈表，接下來，我們只需要newtail->next=newhead;就可以實現循環鏈表。

不過，我們要傳回newhead還是newtail呢？答案是newtail，這是為什么呢？且看：

核心原因：環形鏈表刪除節點需要「前驅指針」

在環形鏈表中，刪除一個節點（如報數到?m?的節點）時，必須先找到該節點的前驅節點，才能通過修改前驅節點的?next?指針，將待刪除節點從環中移除（否則會導致鏈表斷裂）。

例如，要刪除節點?prov，需要讓?prov?的前驅節點?pucr?執行?pucr->next = prov->next，才能完成刪除。

為什么返回尾節點更方便？

1. 尾節點是頭節點的前驅
   代碼中?createsl?構建的環形鏈表滿足：尾節點->next = 頭節點（newtail->next = newhead）。
   因此，返回尾節點后，只需通過?尾節點->next?就能直接獲取頭節點（如?pucr->next?即為頭節點），相當于同時掌握了「頭節點」和「頭節點的前驅」。

2. 刪除頭節點時避免特殊處理
   若返回的是頭節點，當需要刪除頭節點時，必須先遍歷整個鏈表找到頭節點的前驅（尾節點），這會增加額外操作。
   而返回尾節點后，無論刪除哪個節點（包括頭節點），都能通過?pucr（前驅）和?prov（當前節點）的配合直接完成刪除，無需特殊判斷。

總結

返回尾節點而非頭節點，是為了在環形鏈表中直接獲取當前節點的前驅指針，從而高效地執行節點刪除操作，避免因尋找前驅而增加額外的遍歷開銷。這一設計讓整個約瑟夫問題的模擬過程（報數、刪除）更加簡潔高效，體現了環形鏈表操作中「前驅指針」的重要性。

因此，完整代碼如下：

//創建循環鏈表
sl* createsl(int n)
{sl* newhead=create(1);//第一個節點存1，后面的節點從1存到nsl* newtail=newhead;for(int i=2;i<=n;i++){newtail->next=create(i);newtail=newtail->next;}newtail->next=newhead;//將尾指針的next指向頭結點，形成循環鏈表return newtail;//將尾指針傳回
}

接下來，我們便要在下一個函數中進行約瑟夫問題的解決了，首先，我們要創建兩個變量pucr和prov分別表示環形鏈表的尾節點和頭節點，然后還要創建一個count變量去進行計數，當count==m的時候，便進行刪除操作，那么，我們要對count初始化為多少呢？很明顯，要初始化為1，因為我們肯定是要從1開始報數的。

下面，我來講一下這個方法的原理：

該函數通過模擬 “報數 - 淘汰” 過程，找到最后剩下的人，具體分為初始化、循環淘汰、返回結果三部分：

1. 初始化指針與計數器

• pucr = createsl(n)：pucr?指向環形鏈表的尾節點（通過?createsl?返回）。
• prov = pucr->next：prov?指向頭節點（因為尾節點的?next?是頭節點），初始代表 “第一個報數的人”（編號 1）。
• count = 1：報數從 1 開始，計數器初始化為 1。

2. 循環淘汰：直到只剩一個節點

循環條件?while(pucr->next != pucr)：當環形鏈表中只剩一個節點時，該節點的?next?會指向自己（pucr->next = pucr），此時循環終止。

每次循環的核心操作：

• 若?count == m（報數到 m，需要淘汰當前節點?prov）：

  • 步驟 1：temp = prov->next：先用?temp?保存?prov?的下一個節點（避免刪除后丟失后續節點）。
  • 步驟 2：pucr->next = prov->next：通過前驅節點?pucr?的?next?直接指向?prov?的下一個節點，將?prov?從環中 “移除”。
  • 步驟 3：free(prov)：釋放被淘汰節點的內存（避免泄漏）。
  • 步驟 4：prov = temp：prov?移動到下一個節點（下一個報數的起點），count?重置為 1（從 1 重新報數）。

• 若?count != m（未報數到 m）：

  • pucr = prov：pucr?移動到當前節點（成為下一個節點的前驅）。
  • prov = prov->next：prov?移動到下一個節點（繼續報數）。
  • count++：報數加 1。

3. 返回結果

當循環終止時，pucr?指向最后剩下的節點，返回其?data（幸存者的編號），并釋放該節點的內存。大家可以結合著這個圖理解：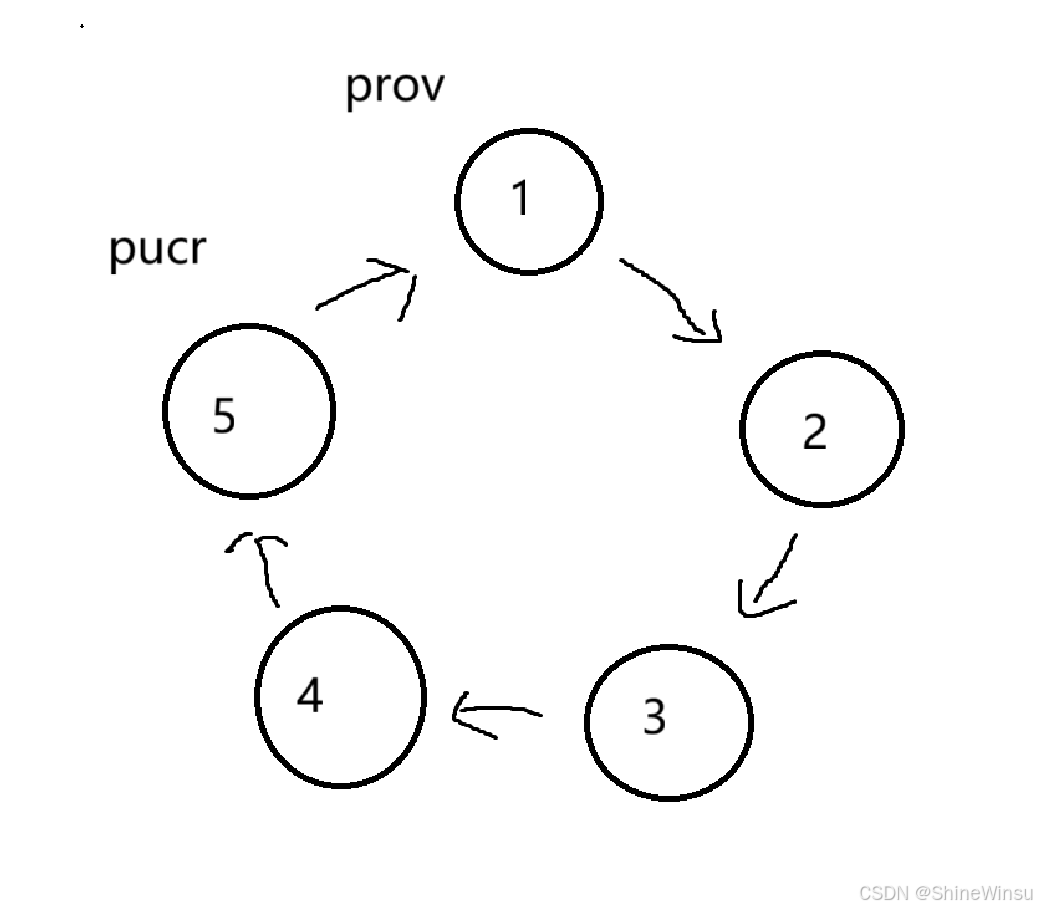

再給大家一個詳細例子進行解釋：

一、初始化階段（以?n=5, m=2?為例）

調用?createsl(5)?后，得到的環形鏈表結構為：
1 → 2 → 3 → 4 → 5 → 1（尾節點?5?的?next?指向頭節點?1）。

• sl* pucr = createsl(n)：pucr?指向尾節點?5（createsl?返回尾節點）。
• sl* prov = pucr->next：pucr->next?是尾節點的?next，即頭節點?1?→?prov?指向?1（第一個報數的人）。
• int count = 1：報數從?1?開始，計數器初始為?1。

二、循環淘汰階段（while (pucr->next != pucr)）

循環條件的含義：當鏈表只剩一個節點時，該節點的?next?會指向自身（如節點?x?的?next = x），此時?pucr->next == pucr，循環終止。

第一次循環（初始狀態：pucr=5，prov=1，count=1）

判斷?count == m？1 == 2?→ 不成立，進入?else?分支：

• pucr = prov：pucr?從?5?移動到?1（現在?pucr?是?1?的前驅，后續要刪除?1?時，pucr?就是操作的關鍵）。
• prov = prov->next：prov?從?1?移動到?2（下一個報數的人）。
• count++：count?變為?2。

此時狀態：pucr=1，prov=2，count=2，鏈表結構仍為?1 → 2 → 3 → 4 → 5 → 1。

第二次循環（pucr=1，prov=2，count=2）

判斷?count == m？2 == 2?→ 成立，進入 “淘汰邏輯”：

• sl* temp = prov->next：prov?是?2，prov->next?是?3?→?temp = 3（保存下一個節點，防止刪除?2?后丟失后續節點）。
• pucr->next = prov->next：pucr?是?1，讓?1?的?next?從?2?改為?3?→ 鏈表結構變為?1 → 3 → 4 → 5 → 1（節點?2?被從環中 “斷開”）。
• free(prov)：釋放節點?2?的內存（模擬 “淘汰”）。
• prov = temp：prov?從?2?移動到?3（下一個報數的起點）。
• count = 1：報數重置為?1，下一輪從?1?開始報。

此時狀態：pucr=1，prov=3，count=1，鏈表結構?1 → 3 → 4 → 5 → 1。

第三次循環（pucr=1，prov=3，count=1）

判斷?count == m？1 == 2?→ 不成立，進入?else?分支：

• pucr = prov：pucr?從?1?移動到?3。
• prov = prov->next：prov?從?3?移動到?4。
• count++：count?變為?2。

此時狀態：pucr=3，prov=4，count=2，鏈表結構?1 → 3 → 4 → 5 → 1。

第四次循環（pucr=3，prov=4，count=2）

判斷?count == m？2 == 2?→ 成立，進入 “淘汰邏輯”：

• temp = prov->next：prov?是?4，prov->next?是?5?→?temp = 5。
• pucr->next = prov->next：pucr?是?3，讓?3?的?next?從?4?改為?5?→ 鏈表結構變為?1 → 3 → 5 → 1（節點?4?被淘汰）。
• free(prov)：釋放節點?4。
• prov = temp：prov?移動到?5。
• count = 1：報數重置為?1。

此時狀態：pucr=3，prov=5，count=1，鏈表結構?1 → 3 → 5 → 1。

第五次循環（pucr=3，prov=5，count=1）

判斷?count == m？1 == 2?→ 不成立，進入?else?分支：

• pucr = prov：pucr?從?3?移動到?5。
• prov = prov->next：prov?從?5?移動到?1（因為是環形鏈表，5?的?next?是?1）。
• count++：count?變為?2。

此時狀態：pucr=5，prov=1，count=2，鏈表結構?1 → 3 → 5 → 1。

第六次循環（pucr=5，prov=1，count=2）

判斷?count == m？2 == 2?→ 成立，進入 “淘汰邏輯”：

• temp = prov->next：prov?是?1，prov->next?是?3?→?temp = 3。
• pucr->next = prov->next：pucr?是?5，讓?5?的?next?從?1?改為?3?→ 鏈表結構變為?3 → 5 → 3（節點?1?被淘汰）。
• free(prov)：釋放節點?1。
• prov = temp：prov?移動到?3。
• count = 1：報數重置為?1。

此時狀態：pucr=5，prov=3，count=1，鏈表結構?3 → 5 → 3。

第七次循環（pucr=5，prov=3，count=1）

判斷?count == m？1 == 2?→ 不成立，進入?else?分支：

• pucr = prov：pucr?從?5?移動到?3。
• prov = prov->next：prov?從?3?移動到?5（3?的?next?是?5）。
• count++：count?變為?2。

此時狀態：pucr=3，prov=5，count=2，鏈表結構?3 → 5 → 3。

第八次循環（pucr=3，prov=5，count=2）

判斷?count == m？2 == 2?→ 成立，進入 “淘汰邏輯”：

• temp = prov->next：prov?是?5，prov->next?是?3?→?temp = 3。
• pucr->next = prov->next：pucr?是?3，讓?3?的?next?從?5?改為?3?→ 鏈表結構變為?3 → 3（節點?5?被淘汰）。
• free(prov)：釋放節點?5。
• prov = temp：prov?移動到?3。
• count = 1：報數重置為?1。

此時狀態：pucr=3，prov=3，count=1，鏈表結構?3 → 3（只剩一個節點）。

三、返回結果階段

循環條件?while (pucr->next != pucr)?判斷：此時?pucr?是?3，pucr->next?也是?3（3->next = 3），條件不成立，循環終止。

• int ret = pucr->data：pucr?指向的節點?data?是?3?→?ret = 3。
• free(pucr)：釋放最后一個節點的內存，防止泄漏。
• pucr = NULL：將指針置空，避免野指針。
• return ret：返回幸存者編號?3，與示例結果一致。

核心邏輯總結

ysf?函數通過以下步驟模擬約瑟夫問題：

1. 初始化：用環形鏈表表示?n?個人，pucr?指向尾節點，prov?指向頭節點，計數器?count=1。
2. 循環淘汰：
   • 報數：prov?移動模擬 “下一個人報數”，count?遞增模擬 “報數計數”。
   • 淘汰：當?count==m?時，通過?pucr->next?修改指針，斷開當前節點?prov，并釋放其內存，同時重置?prov?和?count。
3. 終止與返回：當鏈表只剩一個節點時，循環終止，返回該節點的編號。

以下是詳細注釋版的完整代碼：

// 定義單鏈表節點結構體
// 用于表示環形鏈表中的一個節點（對應約瑟夫問題中的一個人）
typedef struct slistnode
{int data;                  // 數據域：存儲當前節點代表的人的編號（1到n）struct slistnode* next;    // 指針域：指向鏈表中的下一個節點（下一個人）// 注意：此處必須用struct slistnode*而非sl*，因為typedef別名在結構體內部尚未生效
} sl;  // 為結構體起別名sl，簡化后續變量定義// 創建單個鏈表節點的函數
// 參數x：要存儲在節點中的編號（即人的序號）
// 返回值：指向新創建節點的指針（若內存分配失敗可能為NULL，此處簡化處理未判斷）
sl* create(int x)
{// 1. 為新節點分配內存空間// sizeof(sl)計算一個節點所需的字節數，malloc申請對應大小的內存// 強制轉換為sl*類型，因為malloc返回的是void*類型sl* newsl = (sl*)malloc(sizeof(sl));// 2. 初始化節點的數據域// 將參數x存入data成員，代表當前節點對應的人的編號newsl->data = x;// 3. 初始化節點的指針域// 新節點剛創建時還未加入鏈表，暫時指向NULL（空地址）// 后續插入鏈表時會根據位置修改next的指向newsl->next = NULL;// 4. 返回新創建的節點指針return newsl;
}// 創建包含n個節點的環形鏈表
// 功能：模擬n個人圍成一圈的物理結構
// 參數n：參與約瑟夫問題的總人數（n≥1）
// 返回值：指向環形鏈表尾節點的指針（關鍵設計，便于后續刪除節點操作）
sl* createsl(int n)
{// 1. 創建第一個節點（編號為1的人）// 調用create函數生成編號為1的節點，用newhead指針標記這個起始節點sl* newhead = create(1);// 2. 初始化尾指針// 初始狀態下，鏈表只有一個節點（編號1），因此尾節點就是頭節點sl* newtail = newhead;// 3. 循環創建剩余的n-1個節點（編號從2到n）// 從i=2開始是因為編號1已經創建，循環到i=n結束（包含n）for (int i = 2; i <= n; i++){// 3.1 在當前尾節點后面插入新節點// 讓當前尾節點的next指針指向新創建的編號為i的節點// 此時新節點成為鏈表的最后一個節點newtail->next = create(i);// 3.2 更新尾指針的位置// 將尾指針移動到剛插入的新節點，保持尾指針始終指向鏈表最后一個節點newtail = newtail->next;}// 4. 閉合鏈表形成環形結構// 讓最后一個節點（尾節點）的next指針指向頭節點，使整個鏈表首尾相連// 此時鏈表成為"環形"，滿足"圍成一圈"的場景要求newtail->next = newhead;// 5. 返回尾節點指針（而非頭節點）// 核心原因：刪除鏈表節點時必須知道其前驅節點，尾節點是頭節點的天然前驅// 若返回頭節點，刪除頭節點時需要遍歷整個鏈表找前驅（尾節點），效率低return newtail;
}// 約瑟夫問題求解函數
// 功能：模擬"報數-淘汰"過程，計算最后剩下的人的編號
// 參數n：總人數；m：報數到m時淘汰當前人（m≥1）
// 返回值：最后幸存者的編號
int ysf(int n, int m) 
{// 1. 初始化環形鏈表和操作指針// 創建包含n個節點的環形鏈表，pucr指針接收返回的尾節點sl* pucr = createsl(n);// prov指針指向頭節點：因為尾節點的next是頭節點（環形結構的特性）// 初始時prov指向第一個要報數的人（編號1）sl* prov = pucr->next;// 報數計數器：從1開始（符合人類"1,2,...,m"的報數習慣）int count = 1;// 2. 循環執行淘汰過程，直到只剩下一個人// 循環條件：pucr->next != pucr// 解釋：當鏈表中只剩一個節點時，該節點的next會指向自己（pucr->next = pucr），此時循環終止while (pucr->next != pucr){// 2.1 判斷是否報數到m（當前節點需要被淘汰）if (count == m){// 2.1.1 保存當前節點的下一個節點// 原因：刪除prov節點后，需要通過這個臨時指針找到下一個要報數的節點// 若不保存，釋放prov后會丟失后續節點的地址，導致鏈表斷裂sl* temp = prov->next;// 2.1.2 將當前節點從環形鏈表中移除// 讓當前節點的前驅（pucr）直接指向當前節點的后繼（temp）// 此時prov節點不再被任何指針指向，相當于從環中"移除"pucr->next = prov->next;// 2.1.3 釋放被淘汰節點的內存// 調用free函數回收prov指向的內存，避免內存泄漏// 注意：釋放后prov成為野指針，后續不能再使用該指針free(prov);// 2.1.4 更新當前節點指針// 讓prov指向被淘汰節點的下一個節點（temp保存的地址）// 此時prov指向的是下一個要報數的人prov = temp;// 2.1.5 重置報數計數器// 淘汰一個人后，從下一個人開始重新報數"1"count = 1;}// 2.2 未報數到m，繼續移動指針并遞增報數else {// 2.2.1 前驅指針后移// 將pucr移動到當前節點prov的位置，使其成為下一個節點的前驅// 保證pucr始終是prov的前驅節點，為后續刪除操作做準備pucr = prov;// 2.2.2 當前節點指針后移// 將prov移動到下一個節點（pucr的下一個節點，即原prov->next）// 模擬"下一個人準備報數"的過程prov = prov->next;// 2.2.3 報數計數器加1// 模擬報數遞增（如從1→2，2→3，...，m-1→m）count++;}}// 3. 記錄最后幸存者的編號// 循環結束時，pucr指向最后剩下的節點，其data成員就是幸存者的編號int ret = pucr->data;// 4. 釋放最后一個節點的內存// 雖然程序即將結束，但良好的習慣是釋放所有動態分配的內存free(pucr);pucr = NULL;  // 將指針置空，徹底避免野指針（防止后續誤操作）// 5. 返回幸存者的編號return ret;
}

由此，本題的使用環形鏈表的方法，算是大功告成，大家要結合著圖和代碼以及例子仔細體會。

數學解法：

下面，我給大家講一下約瑟夫問題的數學解法，畢竟它是一個數學題，怎么可能少的了數學解法呢？

約瑟夫問題的數學解法，可通過遞推公式結合 “問題規模縮小” 與 “編號映射” 的思想，從基礎情形逐步推導至一般情形，以下是極致詳細的推導與闡釋：

一、問題精準定義

有?n?個人圍成一個環形，從第?1?個人開始按順序報數，當有人報到?m?時，該人出列；隨后從下一個人重新開始報數，重復此過程，直至環形中僅剩余?1?人。我們需要求出最后剩下的那個人的原始編號，記為?f(n,m)。

二、遞推公式的核心邏輯：規模縮小與編號映射

要解決?n?人的問題，我們先假設已經知道?n?1?人時的解?f(n?1,m)，再通過 “第一個人出列后，剩余人員的編號重新映射”，將?n?人的問題轉化為?n?1?人的子問題，最終反向推導出原始編號。

三、遞推公式的分步推導

步驟 1：n=1?的基礎情形

當環形中只有?1?個人時，顯然最后剩下的就是這個人自己，所以：
f(1,m)=1

步驟 2：n>1?的一般情形推導

假設現在有?n?個人（n>1），我們要推導?f(n,m)，需分以下子步驟：

子步驟 2.1：確定第一個出列的人的編號

n?個人依次報數，第一個報到?m?的人的編號?k?可通過取模運算確定：
k=(m?1)%n+1

• 解釋：報數是環形的，取模運算能保證編號落在?1～n?范圍內。例如，若?n=5，m=3，則?k=(3?1)%5+1=3，即第?3?個人第一個出列。

子步驟 2.2：縮小問題規模（剩余?n?1?人）

第一個人（編號?k）出列后，環形中剩余?n?1?個人，新的報數從?k+1?開始（若?k=n，則從?1?開始）。

為了利用?n?1?人的子問題解?f(n?1,m)，我們將剩余?n?1?人的編號重新映射為?1,2,…,n?1（新編號）。

子步驟 2.3：子問題解與原始編號的映射關系

設：

• 子問題（n?1?人）的解為?f(n?1,m)（即重新映射后的新編號）。
• 我們需要把 “新編號” 轉換為 “原始編號”。

映射規律：若重新映射后的新編號為?x，則對應的原始編號為：
原始編號=(x+k?1)%n

• 補充：若上述取模結果為?0，則原始編號為?n（因為環形中編號最大為?n）。

子步驟 2.4：推導遞推公式

結合子問題的解?f(n?1,m)?和映射關系，原始問題的解?f(n,m)?滿足：
f(n,m)=(f(n?1,m)+k?1)%n

將?k=(m?1)%n+1?代入上式，化簡：
f(n,m)?=(f(n?1,m)+[(m?1)%n+1]?1)%n=(f(n?1,m)+(m?1)%n)%n=(f(n?1,m)+m?1)%n(因?(m?1)%n?與?m?1?在取模前等價)?

為了讓結果更直觀（避免取模結果為?0?時的歧義），最終調整遞推公式為：
f(n,m)={1,(f(n?1,m)+m?1)%n+1,?n=1n>1?

• 解釋：若?(f(n?1,m)+m?1)%n=0，則?+1?后結果為?n，恰好對應環形的最大編號。

四、示例深度計算（n=5,m=3）

我們手動計算?5?人報數、每次報?3?出列的情況，驗證遞推公式的正確性：

1. n=1：
   f(1,3)=1

2. n=2：
   f(2,3)?=(f(1,3)+3?1)%2+1=(1+2)%2+1=3%2+1=1+1=2?

3. n=3：
   f(3,3)?=(f(2,3)+3?1)%3+1=(2+2)%3+1=4%3+1=1+1=2?

4. n=4：
   f(4,3)?=(f(3,3)+3?1)%4+1=(2+2)%4+1=4%4+1=0+1=1?

5. n=5：
   f(5,3)?=(f(4,3)+3?1)%5+1=(1+2)%5+1=3%5+1=3+1=4?

實際模擬驗證：

• 第?1?輪：5?人（編號?1～5）報數，報?3?的是?3?號，3?號出列，剩余?1,2,4,5；
• 第?2?輪：從?4?號開始報數，報?3?的是?1?號（4→5→1），1?號出列，剩余?2,4,5；
• 第?3?輪：從?2?號開始報數，報?3?的是?5?號（2→4→5），5?號出列，剩余?2,4；
• 第?4?輪：從?2?號開始報數，報?3?的是?2?號（2→4），2?號出列，最后剩余?4?號。

模擬結果與公式計算結果一致，驗證了遞推公式的有效性。

五、算法復雜度與優化

• 時間復雜度：O(n)。需從?n=1?迭代計算到?n=N（目標人數），共?n?次操作。
• 空間復雜度：O(1)。僅需存儲當前的?f(n,m)，可通過迭代優化，無需遞歸棧空間。

六、總結

約瑟夫問題的數學解法核心是遞推公式，通過 “縮小問題規模” 和 “編號映射”，將?n?人的問題轉化為?n?1?人的子問題，最終反向推導出原始編號。核心公式為：
f(n,m)={1,(f(n?1,m)+m?1)%n+1,?n=1n>1?

該方法高效且直觀，可在?O(n)?時間和?O(1)?空間內解決任意規模的約瑟夫問題。

具體代碼如下：

/*** 求解約瑟夫問題* @param n 總人數* @param m 報數出列的數字* @return 最后剩下的人的編號（從1開始）*/
int josephus(int n, int m) {// 檢查輸入合法性if (n < 1 || m < 1) {printf("錯誤：n和m必須是正整數！\n");return -1; // 返回-1表示錯誤}int result = 1; // 當n=1時，結果為1for (int i = 2; i <= n; i++) {// 應用遞推公式：f(i) = (f(i-1) + m - 1) % i + 1result = (result + m - 1) % i + 1;}return result;
}

到此，約瑟夫問題完美收工。

結語：

在環形鏈表的約瑟夫問題探討中，我們從兩種截然不同的角度找到了問題的答案。

環形鏈表模擬法為我們提供了最直觀的解題路徑。通過構建環形結構、模擬報數與淘汰過程，我們得以親眼見證每一步的變化，深刻理解了環形鏈表中指針操作的精髓 —— 如何利用前驅指針高效刪除節點，如何在循環中保持鏈表的完整性。這種方法雖在時間復雜度上略遜一籌，卻讓我們對問題的本質有了具象化的認知，是理解數據結構與算法邏輯的絕佳實踐。

而數學遞推法則展現了算法優化的魅力。從簡單情形入手，通過規模縮小與編號映射的思想，推導出簡潔而高效的公式，將時間復雜度降至 O (n)，空間復雜度優化到 O (1)。這種從具體到抽象、從復雜到簡單的思維躍遷，正是算法設計的核心智慧所在。

兩種方法各有千秋：模擬法重過程，讓我們知其然；數學法重規律，讓我們知其所以然。在實際解題中，我們既需要模擬法帶來的直觀理解，也需要數學法賦予的高效思路。

約瑟夫問題的探索告一段落，但環形結構與遞推思想的應用遠未結束。無論是輪詢調度、資源分配還是更復雜的算法設計，這些知識都將成為我們解決問題的有力工具。希望這次的學習能為你打開一扇新的思維之門，在未來的算法世界中，繼續保持探索與思考的熱情，發現更多問題背后的規律與美感。

我們下一題再見，諸君共勉！！！