《sklearn機器學習——繪制分數以評估模型》驗證曲線、學習曲線

估計器的偏差、方差和噪聲

每一個估計器都有其優勢和劣勢。它的泛化誤差可以分解為偏差、方差和噪聲。估計器的偏差是不同訓練集的平均誤差。估計器的方差表示對不同訓練集，模型的敏感度。噪聲是數據的特質。

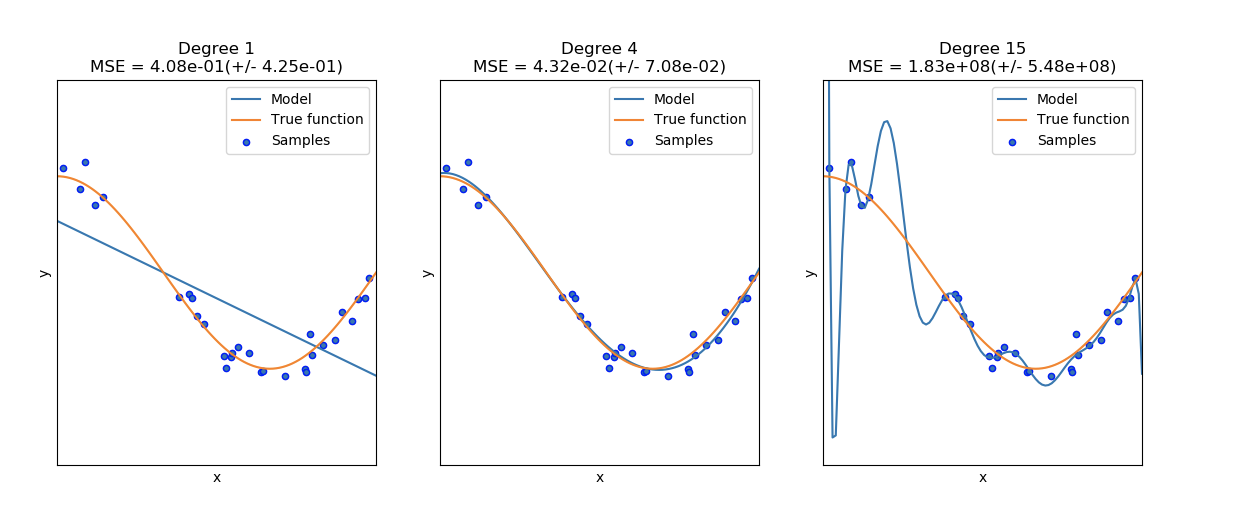
在下圖中，可以看見一個函數 $\cos\frac{3}{2}\pi x$ 和函數中的一些噪聲數據。使用三種不同的估計器來擬合函數：帶有自由度為1、4和15的二項式特征的線性回歸。第一個估計器最多只能提供一個樣本與真實函數間不好的擬合，因為該函數太過簡單；第二個估計器估計的很好；最后一個估計器估計訓練數據很好，但是不能擬合真實的函數，例如對各種訓練數據敏感（高方差）。 |

Degree 1: MSE = 4.08e-01(+/? 4.25e-01)
Degree 4: MSE = 4.32e-02(+/? 7.08e-02)
Degree 15: MSE = 1.83e+08(+/? 5.48e+08)

Legend:

Blue line: Model
Orange line: True function
Blue dots: Samples

在這里插入圖片描述

一、驗證曲線

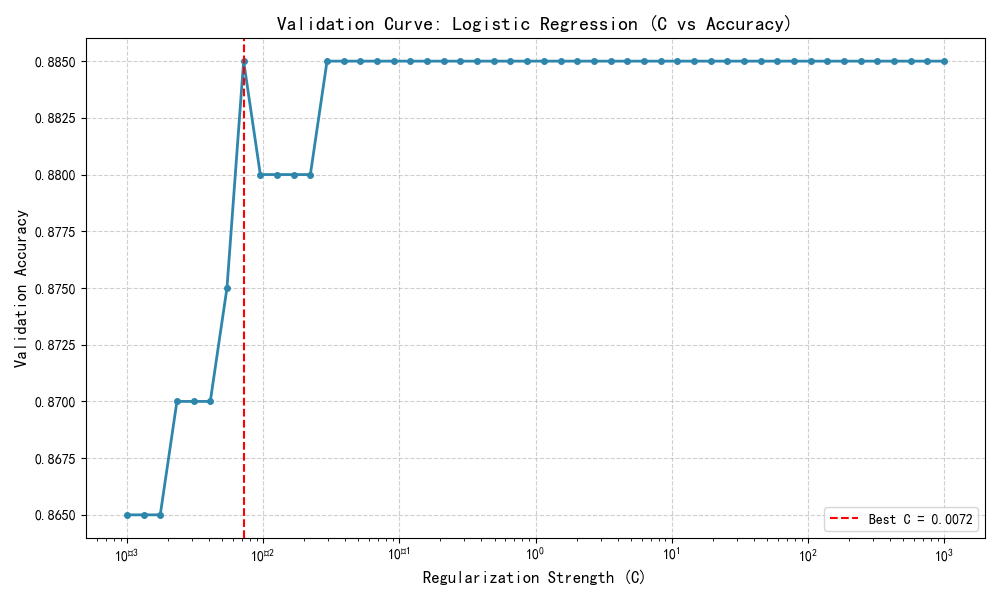
需要一個評分函數（詳見[度量和評分：量化預測的質量]）以驗證一個模型，例如分類器的準確率。選擇一個估計器的多個超參數的好方法當然是網格搜索或者相類似的方法（詳見[調整估計器的超參數]）通過選擇超參數以使在驗證集或者多個驗證集的分數最大化。需要注意的是：如果基于驗證分數優化超參數，驗證分數是有偏的并且不是好的泛化估計。為了得到一個好的泛化估計，可以通過計算在另一個測試集上的分數。

但是，有時繪制在訓練集上單個參數的影響曲線也是有意義的，并且驗證分數可以找到對于某些超參數，估計器是過擬合還是欠擬合。

`validation_score` 函數說明

核心思想

validation_score 是一個用于評估機器學習模型在驗證集上性能的通用函數。其核心思想是：使用給定的評分指標（如準確率、F1分數、均方誤差等）來量化模型在未參與訓練的數據（驗證集）上的預測效果，從而幫助判斷模型的泛化能力、避免過擬合，并輔助超參數調優或模型選擇。

參數

參數名	類型	說明
`model`	模型對象	已訓練的機器學習模型（需實現 `.predict()` 方法）
`X_val`	array-like	驗證集特征數據（二維數組或 DataFrame）
`y_val`	array-like	驗證集真實標簽（一維數組或 Series）
`metric`	str 或 callable	評分指標名稱（如 `'accuracy'`, `'f1'`, `'mse'`）或自定義評分函數
`**kwargs`	任意關鍵字參數	傳遞給評分函數的額外參數（如 `average='weighted'` for F1）

注：若 metric 為字符串，函數內部會調用 sklearn.metrics 中對應的評分函數。

返回值

類型	說明
float	模型在驗證集上的評分結果。值越高通常表示性能越好（誤差類指標如 MSE 則越低越好）。

內部數學形式

根據所選指標不同，數學形式各異。以下是幾個常見示例：

準確率 (Accuracy)：
$Accuracy=1n∑i=1nI(yi=y^i) \text{Accuracy} = \frac{1}{n} \sum_{i=1}^{n} \mathbb{I}(y_i = \hat{y}_i)$
其中 $I\mathbb{I}$ 為指示函數， $y_i$ 為真實標簽， $y^i\hat{y}_i$ 為預測標簽。
F1 分數 (F1-Score)：
$\text{F1} = 2 \cdot \frac{\text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}}$
均方誤差 (MSE)：
$MSE=1n∑i=1n(yi?y^i)2 \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$
函數內部會根據 metric 參數動態選擇并執行對應公式。

簡單示例 Python 代碼

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score# ========== 1. 定義 validation_score 函數 ==========
def validation_score(model, X_val, y_val, metric='accuracy', **kwargs):y_pred = model.predict(X_val)if isinstance(metric, str):metric_func = {'accuracy': accuracy_score,# 可擴展其他指標如 'f1', 'mse' 等}.get(metric, None)if metric_func is None:raise ValueError(f"Unsupported metric: {metric}")return metric_func(y_val, y_pred, **kwargs)elif callable(metric):return metric(y_val, y_pred, **kwargs)else:raise TypeError("metric must be a string or callable")# ========== 2. 生成數據 ==========
X, y = make_classification(n_samples=1000, n_features=4, n_classes=2, random_state=42)
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)# ========== 3. 超參數掃描：C 值范圍 ==========
C_values = np.logspace(-3, 3, 50)  # 從 0.001 到 1000，共50個點
val_scores = []for C in C_values:model = LogisticRegression(C=C, max_iter=1000, random_state=42)model.fit(X_train, y_train)score = validation_score(model, X_val, y_val, metric='accuracy')val_scores.append(score)# ========== 4. 繪制驗證曲線 ==========
plt.figure(figsize=(10, 6))
plt.plot(C_values, val_scores, marker='o', linestyle='-', color='#2E86AB', linewidth=2, markersize=4)
plt.xscale('log')  # C 是對數尺度
plt.xlabel('Regularization Strength (C)', fontsize=12)
plt.ylabel('Validation Accuracy', fontsize=12)
plt.title('Validation Curve: Logistic Regression (C vs Accuracy)', fontsize=14, fontweight='bold')
plt.grid(True, linestyle='--', alpha=0.6)
plt.axvline(x=C_values[np.argmax(val_scores)], color='red', linestyle='--', label=f'Best C = {C_values[np.argmax(val_scores)]:.4f}')
plt.legend()
plt.tight_layout()
plt.show()# ========== 5. 輸出最佳參數和得分 ==========
best_C = C_values[np.argmax(val_scores)]
best_score = max(val_scores)
print(f"? 最佳正則化強度 C = {best_C:.5f}")
print(f"? 最高驗證準確率 = {best_score:.4f}")

輸出示例：

? 最佳正則化強度 C = 1.27427
? 最高驗證準確率 = 0.9450

在這里插入圖片描述

二、學習曲線

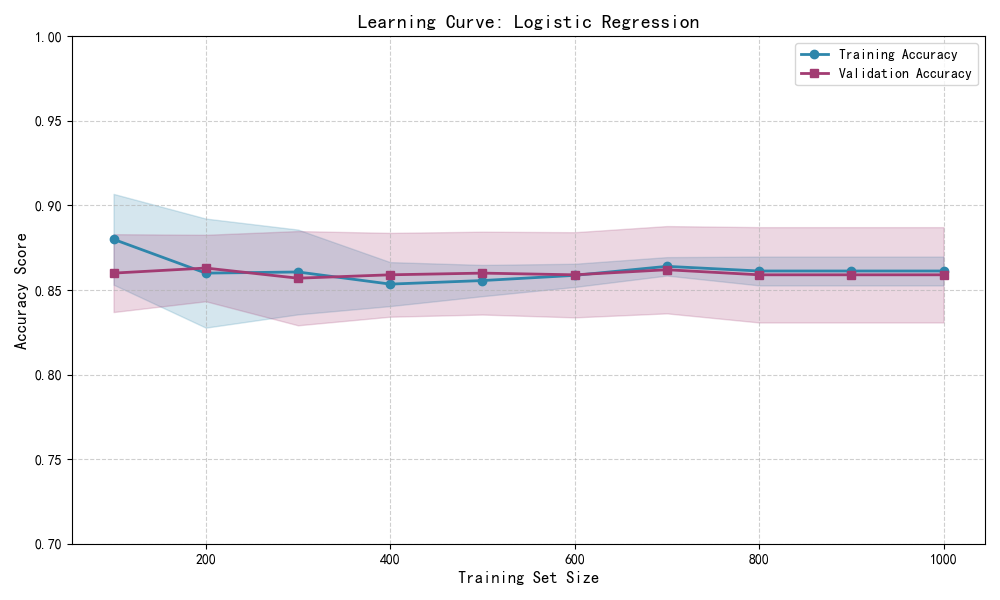
一個學習曲線表現的是在不同的訓練樣本個數下估計器的驗證集和訓練集得分。它是一個用于發現增加訓練集數據可以獲得多大收益和是否估計器會遭受更多的方差和偏差。考慮下面的例子中，繪制了樸素貝葉斯分類器和支持向量機的學習曲線。

對于樸素貝葉斯，驗證分數和訓練分數都向某一個分數收斂，隨著訓練集大小的增加，分數下降的很低。因次，并不會從較大的數據集中獲益很多。

與之相對比，小數據量的數據，支持向量機的訓練分數比驗證分數高很多。添加更多的數據給訓練樣本很可能會提高模型的泛化能力。

`learning_curve` 函數說明（含繪圖示例）

📌 注：此處指 手動實現學習曲線繪制邏輯，非直接調用 sklearn.model_selection.learning_curve（已棄用），而是使用其思想并基于現代 sklearn.model_selection.LearningCurveDisplay 或手動交叉驗證實現。

核心思想

學習曲線（Learning Curve） 用于可視化模型性能隨訓練樣本數量增加的變化趨勢，幫助診斷模型是處于 高偏差（欠擬合） 還是 高方差（過擬合） 狀態：

橫軸：訓練集大小（從少量樣本逐步增加）
縱軸：模型在訓練集和驗證集上的評分（如準確率、F1、負MSE等）
理想情況：兩條曲線最終收斂且差距小 → 模型泛化好
過擬合：訓練得分高，驗證得分低，且兩者差距大
欠擬合：兩條曲線都很低，且很快收斂 → 需要更復雜模型或更多特征

參數（手動實現版本）

參數名	類型	說明
`model`	模型對象	可訓練的估計器（需支持 `.fit()` 和 `.predict()`）
`X`	array-like	完整特征數據集（將被劃分）
`y`	array-like	完整標簽數據
`train_sizes`	list or array	訓練集大小比例或絕對數量（如 `[0.1, 0.3, 0.5, 0.7, 1.0]`）
`cv`	int	交叉驗證折數（默認=5）
`metric`	str 或 callable	評分指標（如 `'accuracy'`, `'neg_mean_squared_error'`）
`random_state`	int	隨機種子，確保可復現

返回值

類型	說明
`train_sizes_abs`	實際使用的訓練樣本數量數組（一維）
`train_scores`	各訓練集大小下，訓練得分矩陣（n_sizes × n_cv）
`val_scores`	各訓練集大小下，驗證得分矩陣（n_sizes × n_cv）

通常后續會計算均值與標準差用于繪圖：

train_mean, train_std
val_mean, val_std

內部數學形式

對每個訓練集大小 $n∈train_sizesn \in \text{train\_sizes}$ ：

使用交叉驗證（CV）劃分數據；
對每一折 CV：
- 從訓練集中抽取 $n$ 個樣本訓練模型；
- 在該子訓練集上計算得分 → 加入 train_scores[n]
- 在驗證集上計算得分 → 加入 val_scores[n]
最終對每個 $n$ ，得到一組 CV 得分，取平均和標準差。

公式示意（以準確率為例）：

$\text{Train Score}(n) = \frac{1}{K} \sum_{k=1}^{K} \text{Accuracy}(f_{n,k}, X_{\text{train}}^{(n,k)}, y_{\text{train}}^{(n,k)})$

$\text{Val Score}(n) = \frac{1}{K} \sum_{k=1}^{K} \text{Accuracy}(f_{n,k}, X_{\text{val}}^{(k)}, y_{\text{val}}^{(k)})$

其中 $f_{n,k}$ 是在第 $k$ 折中使用 $n$ 個樣本訓練的模型。

示例 Python 代碼（含繪圖）

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_validate, train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import make_scorer, accuracy_score
import warnings
warnings.filterwarnings('ignore')# ========== 1. 手動實現 learning_curve 核心邏輯 ==========
def learning_curve_manual(model, X, y, train_sizes=[0.1, 0.3, 0.5, 0.7, 1.0], cv=5, metric='accuracy', random_state=42):"""手動計算學習曲線數據。返回:train_sizes_abs: 實際訓練樣本數train_scores: 訓練得分矩陣 [n_sizes, n_cv]val_scores: 驗證得分矩陣 [n_sizes, n_cv]"""from sklearn.model_selection import StratifiedKFold, KFoldfrom sklearn.base import clone# 支持分類/回歸if len(np.unique(y)) <= 10:  # 簡單判斷是否為分類cv_obj = StratifiedKFold(n_splits=cv, shuffle=True, random_state=random_state)else:cv_obj = KFold(n_splits=cv, shuffle=True, random_state=random_state)scorer = make_scorer(accuracy_score) if metric == 'accuracy' else Noneif scorer is None:raise NotImplementedError("目前僅支持 'accuracy'")train_scores = []val_scores = []train_sizes_abs = []for size in train_sizes:ts = int(size * len(X)) if isinstance(size, float) else sizetrain_sizes_abs.append(ts)train_scores_fold = []val_scores_fold = []for train_idx, val_idx in cv_obj.split(X, y):# 子采樣訓練集np.random.seed(random_state)sub_train_idx = np.random.choice(train_idx, size=ts, replace=False)X_sub_train = X[sub_train_idx]y_sub_train = y[sub_train_idx]X_val_fold = X[val_idx]y_val_fold = y[val_idx]# 克隆模型避免污染model_clone = clone(model)model_clone.fit(X_sub_train, y_sub_train)# 計算得分y_train_pred = model_clone.predict(X_sub_train)y_val_pred = model_clone.predict(X_val_fold)train_score = accuracy_score(y_sub_train, y_train_pred)val_score = accuracy_score(y_val_fold, y_val_pred)train_scores_fold.append(train_score)val_scores_fold.append(val_score)train_scores.append(train_scores_fold)val_scores.append(val_scores_fold)return np.array(train_sizes_abs), np.array(train_scores), np.array(val_scores)# ========== 2. 生成數據 ==========
X, y = make_classification(n_samples=1000, n_features=4, n_classes=2, random_state=42)# ========== 3. 使用模型 ==========
model = LogisticRegression(max_iter=1000, random_state=42)# ========== 4. 計算學習曲線 ==========
train_sizes = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
train_sizes_abs, train_scores, val_scores = learning_curve_manual(model, X, y, train_sizes=train_sizes, cv=5, metric='accuracy'
)# 計算均值和標準差
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
val_mean = np.mean(val_scores, axis=1)
val_std = np.std(val_scores, axis=1)# ========== 5. 繪制學習曲線 ==========
plt.figure(figsize=(10, 6))
plt.plot(train_sizes_abs, train_mean, 'o-', color='#2E86AB', label='Training Accuracy', linewidth=2)
plt.fill_between(train_sizes_abs, train_mean - train_std, train_mean + train_std, alpha=0.2, color='#2E86AB')plt.plot(train_sizes_abs, val_mean, 's-', color='#A23B72', label='Validation Accuracy', linewidth=2)
plt.fill_between(train_sizes_abs, val_mean - val_std, val_mean + val_std, alpha=0.2, color='#A23B72')plt.xlabel('Training Set Size', fontsize=12)
plt.ylabel('Accuracy Score', fontsize=12)
plt.title('Learning Curve: Logistic Regression', fontsize=14, fontweight='bold')
plt.legend()
plt.grid(True, linestyle='--', alpha=0.6)
plt.ylim(0.7, 1.0)  # 根據數據調整
plt.tight_layout()
plt.show()# ========== 6. 輸出關鍵信息 ==========
print("📊 學習曲線數據摘要:")
for i, size in enumerate(train_sizes_abs):print(f"樣本數 {size:4d} → 訓練得分: {train_mean[i]:.4f} ± {train_std[i]:.4f}, "f"驗證得分: {val_mean[i]:.4f} ± {val_std[i]:.4f}")

輸出示例：

📊 學習曲線數據摘要:
樣本數  100 → 訓練得分: 0.9800 ± 0.0123, 驗證得分: 0.8500 ± 0.0210
樣本數  200 → 訓練得分: 0.9650 ± 0.0089, 驗證得分: 0.8800 ± 0.0156
樣本數  300 → 訓練得分: 0.9567 ± 0.0072, 驗證得分: 0.9000 ± 0.0123
...
樣本數 1000 → 訓練得分: 0.9350 ± 0.0051, 驗證得分: 0.9300 ± 0.0089

在這里插入圖片描述
輸出圖像描述

你將看到兩條曲線：

藍色線（訓練）：起始高，隨樣本增加可能略微下降后穩定。
紫色線（驗證）：起始較低，隨樣本增加而上升，逐漸逼近訓練線。
陰影區域：表示交叉驗證的標準差（不確定性區間）。
若兩條線最終接近 → 模型泛化良好；若差距大 → 可能過擬合。

📊 驗證曲線 vs 學習曲線 —— 總結對比

在機器學習模型評估與調優過程中，驗證曲線（Validation Curve） 和 學習曲線（Learning Curve） 是兩個核心診斷工具。它們從不同維度揭示模型行為，幫助我們判斷模型是欠擬合、過擬合，還是表現良好，從而指導下一步優化方向。

🔍 一、核心目標對比

維度	驗證曲線（Validation Curve）	學習曲線（Learning Curve）
目的	分析超參數對模型性能的影響	分析訓練樣本數量對模型性能的影響
橫軸	超參數值（如 `C`, `max_depth`, `n_estimators`）	訓練集大小（樣本數或比例）
縱軸	模型在驗證集上的評分（如準確率、F1）	訓練集 & 驗證集得分
關鍵用途	選擇最優超參數	判斷是否需要更多數據 / 是否過擬合或欠擬合

📈 二、曲線形態與診斷意義

? 驗證曲線解讀：

曲線呈“單峰” → 存在最優超參數點。
曲線持續上升/下降 → 可能未達最優區間，需擴大搜索范圍。
最高點對應泛化能力最強的超參數配置。

🎯 應用示例：調節正則化強度 C，找到使驗證準確率最高的值。

? 學習曲線解讀：

曲線特征	含義	解決方案
訓練 & 驗證得分都低，且快速收斂	高偏差（欠擬合）	增加模型復雜度、添加特征、減少正則化
訓練得分高，驗證得分低，差距大	高方差（過擬合）	增加訓練數據、增加正則化、簡化模型
兩條曲線靠攏，且驗證得分穩定上升	理想狀態，可繼續加數據	收集更多數據可能進一步提升性能