從淘寶推薦到微信搜索：查找算法如何支撐億級用戶—

?本篇技術博文摘要 🌟

本文通過動畫可視化深入解析數據結構中的核心查找算法，從基礎概念到高階應用，全面覆蓋順序查找、折半查找、分塊查找、B樹/B+樹及散列查找的核心原理與實現細節。文章以動態演示為核心工具，直觀展現算法執行過程與數據結構演化，幫助讀者突破抽象理論難點。

內容核心：

基礎算法：

順序查找：從暴力遍歷到哨兵優化，結合判定樹分析ASL（平均查找長度），探討有序表場景下的效率提升策略。

折半查找：通過二分思想與判定樹模型，解析有序數據的高效檢索邏輯，并給出代碼實現與時間復雜度推導。

進階索引結構：

分塊查找：融合順序與折半查找優勢，分析塊劃分對效率的影響。

B樹與B+樹：從多叉查找樹的平衡規則出發，動態演示插入、刪除操作如何維持樹結構穩定；對比B+樹的特性（如葉子節點鏈表），闡釋其在數據庫索引中的核心地位。

散列查找與沖突解決：

詳解哈希函數設計原則（如除留余數法），通過動畫模擬拉鏈法、開放定址法、再散列法的沖突處理過程，揭示哈希表動態擴容與數據分布規律。

引言 📘

在這個變幻莫測、快速發展的技術時代，與時俱進是每個IT工程師的必修課。
我是盛透側視攻城獅，一名什么都會一丟丟的網絡安全工程師，也是眾多技術社區的活躍成員以及多家大廠官方認可人員，希望能夠與各位在此共同成長。

上節回顧

目錄

本篇技術博文摘要 🌟

引言 📘

上節回顧

7.2數據結構與算法之查找算法題目

7.2.1題：

?

代碼算法實現思路：

核心代碼實現：

7.2.2題：?

代碼算法實現思路：

核心代碼實現：

注意:

7.2.3題：?

代碼算法實現思路：

核心代碼實現：

?

?7.3?.數據結構與算法之樹形查找算法題

7.3.1題：?

代碼算法實現思路：

核心代碼實現：

?7.3.2題：?

代碼算法實現思路：

核心代碼實現：

?7.3.3題：?

代碼算法實現思路：

核心代碼實現：

?7.3.4題：?

代碼算法實現思路：

核心代碼實現：

?7.3.5題：?

代碼算法實現思路：

核心代碼實現：

補充：

?7.3.6題：?

代碼算法實現思路：

核心代碼實現：

補充：

歡迎各位彥祖與熱巴暢游本人專欄與技術博客

你的三連是我最大的動力

點擊??指向的專欄名即可閃現

7.2數據結構與算法之查找算法題目

7.2.1題：

?

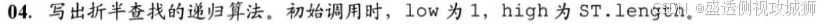?出折半查找的遞歸算法。初始調用時，low為1,high為ST.length。?

代碼算法實現思路：

根據查找的起始位置和終止位置，將查找序列一分為二，判斷所查找的關鍵字在哪一部分，然后用新的序列的起始位置和終止位置遞歸求解。

核心代碼實現：

typedef struct{            //查找表的數據結構  ElemType   *elem;      //存儲空間基址，建表時按實際長度分配，0號留空  int        length;     //表的長度  
} SSTable;  
int BinSearchRec(SSTable ST, ElemType key, int low, int high){  if(low>high)  return 0;  mid=(low+high)/2;              //取中間位置  if(key>ST.elem[mid])           //向后半部分查找  BinSearchRec(ST,key,mid+1,high);  else if(key<ST.elem[mid])  //向前半部分查找  BinSearchRec(ST,key,low,mid-1);  else                         //查找成功  return mid;  
}

7.2.2題：?

?線性表中各結點的檢索概率不等時，可用如下策略提高順序檢索的效率：
若找到指定的結點，則將該結點和其前驅結點(若存在)交換，使得經常被檢索的結點盡量位于表的前端。
試設計在順序結構和鏈式結構的線性表上實現上述策略的順序檢索算法。

代碼算法實現思路：

檢索時可先從表頭開始向后順序掃描，若找到指定的結點，則將該結點和其前趨結點(若存在)交換。

核心代碼實現：

int SeqSrch(RcdType R[], ElemType k) {  //順序查找線性表，找到后和其前面的元素交換  int i=0;  while ((R[i].key !=k) && (i<n))  i++;                          //從前向后順序查找指定結點  if (i<n&&i>0) {                   //若找到，則交換  temp=R[i]; R[i]=R[i-1]; R[i-1]=temp;  return --i;                   //交換成功，返回交換后的位置  }  else return -1;                   //交換失敗  
}

注意:

鏈表方式實現的基本思想與上述思想相似，但要注意用鏈表實現時，在交換兩個結點之前需要保存指向前一結點的指針。

7.2.3題：?

代碼算法實現思路：

從矩陣A的右上角(最右列)開始比較，若當前元素小于目標值，則向下尋找下一個更大的元素；
若當前元素大于目標值，則從右往左依次比較，若目標值存在，則只可能在該行中。

核心代碼實現：

bool findkey(int A[][], int n, int k) {  int i=0, j=n-1;  while (i<n&&j>=0) {                //離開邊界時查找結束  if (A[i][j]==k) return true;  //查找成功  else if (A[i][j]>k) j--;      //向左移動，在該行內尋找目標值  else i++;                      //向下移動，查找下一個更大的元素  }  return false;                      //查找失敗  
}

比較次數不超過2n次，時間復雜度為O(n);空間復雜度為O(1)。

?7.3?.數據結構與算法之樹形查找算法題

7.3.1題：?

試編寫一個算法，判斷給定的二叉樹是否是二叉排序樹。

代碼算法實現思路：

對二叉排序樹來說，其中序遍歷序列為一個遞增有序序列。
因此，對給定的二叉樹進行中序遍歷，若始終能保持前一個值比后一個值小，則說明該二叉樹是一棵二叉排序樹。?

核心代碼實現：

KeyType predt=-32767;              //predt 為全局變量，保存當前結點中序前驅的值，初值為-∞  
int JudgeBST(BiTree bt) {  int b1,b2;  if(bt==NULL)                     //空樹  return 1;  else{  b1=JudgeBST(bt->lchild);     //判斷左子樹是否是二叉排序樹  if(b1==0||predt>=bt->data)  //若左子樹返回值為 0 或前驅大于或等于當前結點  return 0;                //則不是二叉排序樹  predt=bt->data;              //保存當前結點的關鍵字  b2=JudgeBST(bt->rchild);     //判斷右子樹  return b2;                   //返回右子樹的結果  }  
}

?7.3.2題：?

?設計一個算法，求出指定結點在給定二叉排序樹中的層次。

代碼算法實現思路：

設二叉樹采用二叉鏈表存儲結構。
在二叉排序樹中，查找一次就下降一層。
因此，查找該結點所用的次數就是該結點在二叉排序樹中的層次。
采用二叉排序樹非遞歸查找算法，用n保存查找層次，每查找一次，n就加1,直到找到相應的結點。

核心代碼實現：

int level(BiTree bt,BSTNode *p){  int n=0;                          //統計查找次數  BiTree t=bt;  if(bt!=NULL){  n++;  }  while (t->data!=p->data) {  if (p->data<t->data)         //在左子樹中查找  t=t->lchild;  else  t=t->rchild;             //在右子樹中查找  n++;                         //層次加 1  }  return n;  
}

?7.3.3題：?

用二叉樹遍歷的思想編寫一個判斷二叉樹是否是平衡二叉樹的算法。?

代碼算法實現思路：

設置二叉樹的平衡標記balance,以標記返回二叉樹bt是否為平衡二叉樹，若為平衡二叉樹，則返回1,否則返回0;h為二叉樹 bt 的高度。采用后序遍歷的遞歸算法：
1)若 bt為空，則高度為0,balance=1。
2)若 bt僅有根結點，則高度為1,balance=1。
3)否則，對bt的左、右子樹執行遞歸運算，返回左、右子樹的高度和平衡標記，bt 的高度為最高子樹的高度加1。若左、右子樹的高度差大于1,則balance=0;若左、右子樹的高度差小于或等于1,且左、右子樹都平衡時，balance=1,否則 balance=0。

核心代碼實現：

void Judge_AVL(BiTree bt, int &balance, int &h) {  int bl=0, br=0, hl=0, hr=0;             //左、右子樹的平衡標記和高度  if (bt==NULL) {                          //空樹，高度為 0  h=0;  balance=1;  }  else if (bt->lchild==NULL&&bt->rchild==NULL) { //僅有根結點，則高度為 1  h=1;  balance=1;  }  else {  Judge_AVL(bt->lchild, bl, hl);      //遞歸判斷左子樹  Judge_AVL(bt->rchild, br, hr);      //遞歸判斷右子樹  h=(hl>hr?hl:hr)+1;  if (abs(hl-hr)<2)  //若子樹高度差的絕對值<2，則看左、右子樹是否都平衡  balance=bl&&br; //&&為邏輯與，即左、右子樹都平衡時，二叉樹平衡  else  balance=0;  }  
}

?7.3.4題：?

?設計一個算法，求出給定二叉排序樹中最小和最大的關鍵字。

代碼算法實現思路：

一棵二叉排序樹中，最左下結點即為關鍵字最小的結點，最右下結點即為關鍵字最大的結點，本算法只要找出這兩個結點即可，而不需要比較關鍵字。

核心代碼實現：

KeyType MinKey(BSTNode *bt) {  while (bt->lchild!=NULL)  bt=bt->lchild;  return bt->data;  
}  
KeyType MaxKey(BSTNode *bt) {  //求出二叉排序樹中最大關鍵字結點  while (bt->rchild!=NULL)  bt=bt->rchild;  return bt->data;  
}

?7.3.5題：?

?設計一個算法，從大到小輸出二叉排序樹中所有值不小于k的關鍵字。

代碼算法實現思路：

由二叉排序樹的性質可知，右子樹中所有的結點值均大于根結點值，左子樹中所有的結點值均小于根結點值。
為了從大到小輸出，先遍歷右子樹，再訪問根結點，后遍歷左子樹。

核心代碼實現：

void Output(BSTNode *bt, KeyType k) {  //本算法從大到小輸出二叉排序樹中所有值不小于k的關鍵字  if (bt==NULL)  return;  if (bt->rchild!=NULL)  Output(bt->rchild, k);      //遞歸輸出右子樹結點  if (bt->data>=k)  printf("%d", bt->data);     //只輸出大于或等于k的結點值  if (bt->lchild!=NULL)  Output(bt->lchild, k);      //遞歸輸出左子樹的結點  
}

補充：

本題也可采用中序遍歷加輔助棧的方法實現。

?7.3.6題：?

代碼算法實現思路：

所以我們可以對左右子樹的搜索采用相同的規則，

核心代碼實現：

BSTNode *Search_Small(BSTNode*t, int k) {  //在以t為根的子樹上尋找第k小的元素，返回其所在結點的指針。k從1開始計算  //在樹結點中增加一個count數據成員，存儲以該結點為根的子樹的結點個數  if(k<1||k>t->count) return NULL;  if(t->lchild==NULL) {  if(k==1) return t;  else return Search_Small(t->rchild,k-1);  }  else{  if(t->lchild->count==k-1) return t;  if(t->lchild->count>k-1) return Search_Small(t->lchild,k);  if(t->lchild->count<k-1)  return Search_Small(t->rchild, k-(t->lchild->count+1));  }  
}