Smooth L1 Loss

概述

Smooth L1 Loss（平滑 L1 損失），是一個在回歸任務，特別是計算機視覺中的目標檢測領域（如 Faster R-CNN, SSD）非常核心的損失函數。

$x$ 表示模型的預測值，$y$ 表示真實值，$z=x?y$ 表示預測值與真實值之間的差異。常用的 L1 loss、L2 Loss 和 smooth L1 loss 定義分別為
L1 loss（MAE）：
$$L_{L1}(x,y)=|x?y|=|z|$$
L2 loss（MSE）：
$$L_{L2}(x,y)=0.5(x?y{)}^2=0.5z^2$$
Smooth L1 Loss：
$$L_{smoothL1}(x,y)=\{\begin{array}{ll}0.5(x?y{)}^2=0.5z^2,& \text{if?}|x?y|<1\\ |x?y|?0.5=|z|?0.5,& \text{otherwise}\end{array}$$
函數坐標圖如下：橫軸為z，縱坐標為損失loss

• L1 loss 在零點處不可導（梯度不連續），且收斂速度較慢。L1 loss 對 $z$的導數為常數，在訓練后期，誤差值$z$很小時，如果 learning rate 不變，損失函數會在穩定值附近波動，很難收斂到更高的精度。
• L2 loss 當預測值與真實值差距很大時，由于平方項的存在，損失值會變得非常大，梯度也很大，容易導致訓練不穩定（梯度爆炸）
• Smooth L1 Loss 的設計目的就是為了避開了 L1 loss 和 L2 loss 的缺點。它在誤差較小的區域使用像 L2 loss這樣的二次函數，保證梯度平滑且逐漸減小；而在誤差較大的區域使用像 L1 loss這樣的線性函數，限制梯度的大小，從而對異常值不那么敏感。

Smooth L1 Loss 的梯度函數是：
$$\frac{d}{dz}smoothL1=\{\begin{array}{ll}z,& \text{if?}|z|<1\\ +1或?1,& \text{otherwise}\end{array}$$

• 小誤差$|z|<1$時，即當預測值接近真實值時，梯度很小，參數更新幅度小，有利于模型收斂和精細化。且梯度是連續變化的，訓練過程非常穩定。
• 大誤差$|z|\ge 1$時，即使預測結果非常離譜，梯度也不會爆炸（不會像L2 loss那樣變化巨大），避免了因個別異常樣本而導致訓練過程劇烈波動，增強了訓練的魯棒性。

目標檢測中的應用

在目標檢測中，網絡需要預測目標邊界框（Bounding Box）的精確坐標（中心點 x, y，寬 w, 高 h）。這是一個典型的回歸任務。

• 如果使用 L2 Loss，當某個坐標的預測初值離真實值很遠時，會產生巨大的損失和梯度，這會主導整個訓練過程，使得模型難以收斂到好的結果。
• Smooth L1 Loss 對初值不準的預測框更加寬容，提供了穩定且有限的梯度，使得模型能夠逐步修正框的位置，而不是被異常值帶偏。Faster R-CNN 和 SSD 等經典模型都使用了 Smooth L1 Loss 作為邊界框回歸的損失函數。

Smooth L1 Loss 完美地權衡了訓練的穩定性（對抗異常值）和收斂的有效性（小誤差時梯度精細），使其成為需要高精度回歸任務（如目標檢測）的理想選擇。

函數接口

在 PyTorch 中，Smooth L1 Loss 通過 nn.SmoothL1Loss 類實現

torch.nn.SmoothL1Loss(size_average=None,reduce=None,reduction='mean',beta=1.0
)

• reduction (str, optional): 指定損失的聚合方式，可選 ‘none’、‘mean’（默認值）或 ‘sum’。
• beta (float, optional): 一個超參數，指定從二次函數切換到線性函數的閾值。默認值為 1.0，即上面公式中的切換點。修改 beta 可以調整損失函數對“大誤差”和“小誤差”的定義。

import torch
import torch.nn as nn# 創建損失函數
# reduction='mean'：計算所有元素損失的平均值
smooth_l1_loss = nn.SmoothL1Loss(reduction='mean')# 假設預測值和真實值
# 例如：預測了4個邊界框的偏移量
predictions = torch.tensor([1.6, 0.2, -2.0, 0.8])
targets = torch.tensor([1.0, 0.0, -1.0, 1.0])# 計算損失
loss = smooth_l1_loss(predictions, targets)
print(loss)# 手動計算驗證：
# x = predictions - targets = [0.6, 0.2, -1.0, -0.2]
# |x| = [0.6, 0.2, -1.0, 0.2] -> 全部小于beta(1.0)，所以都用 0.5*x^2
# loss = (0.5*0.6^2 + 0.5*0.2^2 + 0.5*(-1.0)^2 + 0.5*(-0.2)^2) / 4
#      = (0.18 + 0.02 + 0.5 + 0.02) / 4
#      = 0.72 / 4 = 0.18

IOU loss

概述

在目標檢測中，最常用的評估模型好壞的指標就是 IOU。它衡量的是預測邊界框（Bounding Box）與真實邊界框之間的重疊程度。

傳統的L1 loss，L2 loss，Smooth L1 loss存在如下問題：

• 通過優化邊界框的坐標（x, y, w, h）來間接優化IOU，但坐標誤差最小并不總是等同于 IOU 最大化，這樣就導致了不一致性。
• 通過4個點回歸坐標框的方式是假設 4個坐標點是相互獨立的，沒有考慮其相關性，而實際上 4個坐標點具有一定的相關性。
• 基于 L1 和 L2 距離的 loss 不具有尺度不變性

IOU Loss 的解決方案：既然最終評估標準是 IOU，那就直接使用 IOU 作為損失函數來指導模型的優化方向。使模型的訓練目標（損失最小化）
和最終的評估目標（IOU 最大化） 實現統一。

IOU loss的計算

對于兩個區域（通常是預測框 B_pred 和真實框 B_gt）
IOU計算如下：
$$\text{IOU}=\frac{\text{Area?of?Overlap}}{\text{Area?of?Union}}=\frac{B_{pred}\cap B_{gt}}{B_{pred}\cup B_{gt}}$$

IOU 的取值范圍是 [0, 1]：1表示兩個框完全重合；0表示兩個框沒有交集

IOU loss 就是將IOU 轉化為損失。損失越低越好，IOU越高越好，所以IOU loss如下計算：
$${\mathcal{L}}_{IOU}=1?IOU$$

IOU = 1（完美預測）時，損失為 0。IOU = 0（毫無交集）時，損失為 1

優點：

• 尺度不變性：IOU 是一個比值，它只關心重疊區域的比例，而不關心框的絕對大小。這意味著它對大小不同的目標物是公平的。
• 與評估指標一致：直接優化 IOU 使得模型訓練過程更直接地對最終的評價指標負責。

缺點：

• 最核心問題是無法處理不相交的情況。如果兩個框沒有交集，則 IOU = 0，損失恒為 1。此時梯度為 0，無法為模型提供如何移動預測框以與真實框相交的梯度信息，導致模型無法學習。
• 無法區分不同方式的重合不良。$IOU$值不能反映兩個框是如何相交的，即使兩個框的 $IOU$值是相同的，其相交方式也可能很不一樣。只要 IOU 相同，損失就是相同的。

def calculate_iou(box1, box2):"""計算兩個框的IoUArgs:box1: (tensor) [x1, y1, x2, y2]box2: (tensor) [x1, y1, x2, y2]Returns:iou: (tensor) scalar"""# 計算交集區域的坐標x1 = torch.max(box1[0], box2[0])y1 = torch.max(box1[1], box2[1])x2 = torch.min(box1[2], box2[2])y2 = torch.min(box1[3], box2[3])# 計算交集面積intersection_area = torch.clamp(x2 - x1, min=0) * torch.clamp(y2 - y1, min=0)# 計算各自面積box1_area = (box1[2] - box1[0]) * (box1[3] - box1[1])box2_area = (box2[2] - box2[0]) * (box2[3] - box2[1])# 計算并集面積union_area = box1_area + box2_area - intersection_area# 避免除零iou = intersection_area / (union_area + 1e-6)return ioudef iou_loss(pred_boxes, target_boxes):"""計算IoU LossArgs:pred_boxes: (tensor) [N, 4] (x1, y1, x2, y2)target_boxes: (tensor) [N, 4] (x1, y1, x2, y2)Returns:loss: (tensor) scalar"""ious = torch.stack([calculate_iou(pred, tgt) for pred, tgt in zip(pred_boxes, target_boxes)])loss = 1 - iousreturn loss.mean() # 使用mean reduction# 使用示例
preds = torch.tensor([[100, 100, 200, 200], [50, 50, 150, 150]], dtype=torch.float32)
targets = torch.tensor([[110, 110, 210, 210], [60, 60, 160, 160]], dtype=torch.float32)loss = iou_loss(preds, targets)
print(f"IoU Loss: {loss}")

IOU loss的變體

為解決IOU loss 的缺陷，在原始IOU 基礎上提出了一系列先進的變體。如GIOU，DIOU，CIOU等等。

通常以IOU為基礎的變體IOU loss可以定義為
$$L=1?IoU+R(B,B_{gt})$$
其中：

• $B$ ： 表示預測框
• $B_{gt}$ ：表示目標框
• $R(B,B_{gt})$ ： 表示預測框 $B$ 和 目標框 $B_{gt}$ 的懲罰項

GIOU loss

即使兩個框不相交，也需要提供一個梯度方向。GIOU 在 IOU 的基礎上引入了一個最小封閉矩形框 C（能夠同時包含預測框和真實框的最小矩形）,它不僅考慮了邊界框之間的重疊程度，還考慮了bboxes 之間的位置和尺寸。
$$GIoU=IoU?\frac{C?(A\cup B)}{|C|}$$ ，其中，C 是 A 和 B 的外接矩形框面積
$$GIoULoss=1?GIoU$$ ，
即 ：
$$L_{GIoU}=1?IoU+\frac{C?(A\cup B)}{|C|}$$

其中：
$0\le =IoU<=1$
$0<=\frac{C?(A\cup B)}{C}<1$

• 當 A 和 B 完全重合時：
  $IoU=1，\frac{C?(A\cup B)}{C}=0$ $\to$ $GIoU=1，GIoU\_Loss=0$
• 當 A，B 完全不重疊時（ A，B 距離無窮遠的時候）：
  $IoU=0，\frac{C?(A\cup B)}{C}趨近于1$ $\to$ $GIoU=?1，GIoU\_Loss=2$

優點：
解決了不相交時梯度為 0 的問題。即使不相交，模型也會學習朝著最小封閉框 C 的中心移動預測框，以減小附加項，從而促使兩個框先發生交集。
GIOU 是 IOU 的一個下界，$\text{GIOU}\le \text{IOU}$。
缺點：
當兩個框包含（如一個框在另一個框內部）時，GIOU 會退化成 IOU，此時提供的移動方向仍然比較模糊。

DIOU loss

DIOU loss 直接最小化兩個框中心點之間的距離。這樣可以為模型的優化提供一個非常明確且高效的方向。
DIOU loss的計算公式如下：
$$L_{DIoU}=1?IoU+\frac{{\rho }^2(b,b_{gt})}{c^2}$$
其中：
$\rho (b,b_{gt})$ 表示預測框與真實框中心點之間的歐式距離。
$b,b_{gt}$ 分別表示預測框的中心點，真實框的中心點。
$c$ 表示真實框與預測框的最小外接矩形框的對角線長度。

優點：

• 具有尺度不變性 : 由于$\frac{{\rho }^2(b,b_{gt})}{c^2}$是一個相對度量，不直接依賴于框的具體寬度和高度，所以在不同尺度下仍能保持一致的度量標準，這種尺度不變性有助于提高檢測的準確性和魯棒性。
• 當兩個框完全重合時，$L_{IoU}=L_{GIoU}=L_{DIoU}=0$
• 當兩個框不相交時，DIoU Loss 可以直接優化 2個框之間的距離，比 GIoU Loss 收斂速度更快
• 對于兩個框包含的情況，DIoU Loss 可以收斂的很快，而 GIoU Loss此時退化為IoU Loss收斂速度較慢

缺點：
DIoU 能夠直接最小化預測框和真實框的中心點距離加速收斂，但是未考慮到高寬比。
如下圖所示：紅色為預測框，藍色為真實框。三個紅框的面積相同，紅框與藍框中心點重合，但是紅框的長寬比不一樣，三種情況下的DIoU相同，但顯然中間的更擬合真實框。

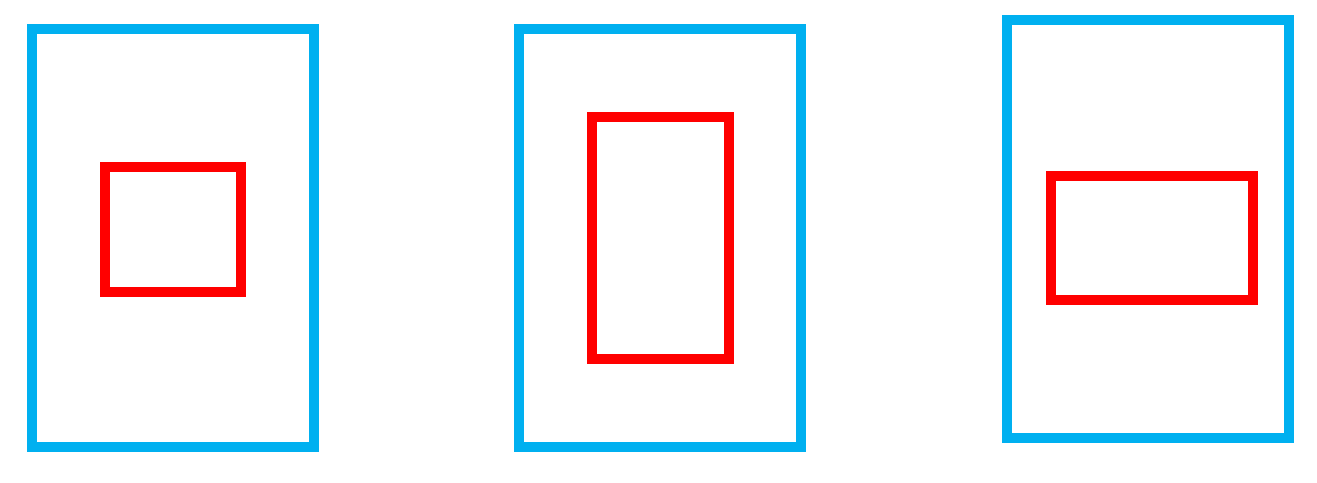
CIOU loss

由于DIOU loss忽略了寬高比的一致性，CIoU 在 DIoU 的基礎上增加了一個懲罰項，同時考慮重疊面積、中心點距離和寬高比。
$$L_{CIoU}=1?IoU+\frac{{\rho }^2(b,b_{gt})}{c^2}+\alpha v$$
其中：
$v$ 衡量長寬比一致性的參數 ： $v=\frac{4}{{\pi }^2}(arctan\frac{w_{gt}}{h_{gt}}?arctan\frac{w}{h}{)}^2$。
$\alpha$ 是權重平衡因子，調整長寬比的影響 ： $\alpha =\frac{v}{(1?IoU)+v}$。

優點：
考慮影響因素相對全面，考慮到了定位損失的三個重要的因素 : 重疊面積、中心點距離、高寬比。

缺點：
$\alpha v$這一項的設計，導致拖累了收斂速度。

• $v$ 僅反映了高寬比的差異性，高寬比一致則$v=0$，這樣的設計存在缺陷。 比如真實框的 $w_{gt}=8,h_{gt}=4，\frac{w_{gt}}{h_{gt}}=2$ ，而預測出的 $w=6,h=3,\frac{w}{h}=2$ ，此時$v=0$
• $v$只反映了高寬比的差異，并沒有分別反映出 $w_{gt}$和 $w$ 之間的關系，以及 $h_{gt}$ 和 $h$ 之間的關系，這導致其收斂方向不夠明確，CIOU損失可能會向不合理的方向優化。
• $v$對 $w$ 和 $h$ 的偏導數分別如下 ：
  $$\frac{?v}{?w}=\frac{8}{{\pi }^2}(arctan\frac{w_{gt}}{h_{gt}}?arctan\frac{w}{h})?\frac{h}{w^2+h^2}$$
  $$\frac{?v}{?h}=?\frac{8}{{\pi }^2}(arctan\frac{w_{gt}}{h_{gt}}?arctan\frac{w}{h})?\frac{w}{w^2+h^2}$$
  由2個偏導數，可以得出 ： $$\frac{?v}{?w}=?\frac{h}{w}?\frac{?v}{?h}$$ ，
  $\frac{?v}{?w}$ 和 $\frac{?v}{?h}$ 的符號是相反的，只要 $w$ 和 $h$ 其中一個的值增加，另一個就會減小，即寬高是相互耦合的。當$w<w^{gt}且h<h^{gt}$時或者 $w>w^{gt}且h>h^{gt}$ 時可能無法快速收斂。

EIOU loss

EIoU Loss 將 CIoU 中的寬高比損失項 $v$ 解耦，直接拆分為分別針對寬度和高度的損失。
$$\begin{array}{rl}{L}_{EIoU}& =L_{IoU}+L_{dis}+L_{asp}\\ & \\ & =1?IoU+\frac{{\rho }^2(b,b_{gt})}{(w_c{)}^2+(h_c{)}^2}+\frac{{\rho }^2(w,w_{gt})}{(w_c{)}^2}+\frac{{\rho }^2(h,h_{gt})}{(h_c{)}^2}\end{array}\text{\hspace{1em}?}$$
其中：

• $b$ 和 $b_{gt}$ ：分別表示預測框的中心點和真實框的中心點
• $\rho (b,b_{gt})$：表示真實框與預測框中心點之間的歐式距離
• $w_c$ 和 $h_c$：分別表示最小外接矩形框的寬度和高度

優點:

• 更直接的收斂目標：直接最小化寬度和高度的差異，為模型提供了更清晰、更直接的優化方向。
• 更快的收斂速度：由于梯度計算更直接，EIoU 通常比 CIoU 收斂得更快。
• 更高的定位精度：在許多基準測試中，EIoU 都展現出了比 CIoU 更優的邊界框回歸精度。

Focal-EIoU loss

Focal-EIoU Loss 的思想源于 Focal Loss（最初用于解決分類中的類別不平衡問題）。在目標檢測中，也存在“樣本不平衡”問題：簡單樣本（IOU 高的樣本）和困難樣本（IOU 低的樣本）的數量不平衡。

問題：在一個訓練批次中，大部分邊界框回歸樣本是“簡單”的（即 IoU 已經較高），只有少數是“困難”的（IoU 低）。標準的 IoU 損失對所有這些樣本一視同仁，導致簡單樣本的損失貢獻主導了總損失，模型難以集中精力去學習那些困難的、回歸得不好的樣本。
思路：借鑒 Focal Loss 的思路，降低簡單樣本的權重，讓損失函數更加關注難以回歸的樣本。
Focal-EIoU Loss 在 EIoU Loss 的基礎上增加了一個聚焦系數
$$L_{Focal?EIoU}=Io{U}^{\gamma }?L_{EIoU}$$

其中：
$L_{EIoU}$：計算的 EIoU 損失。
$\gamma$：聚焦參數（通常 $\gamma >0$），用于調節權重衰減的速率。
$Io{U}^{\gamma }$：聚焦因子，$IoU$ 的值在 [0, 1] 之間。

工作機制

• 對于一個困難樣本（IoU → 0）：$Io{U}^{\gamma }\approx 0$，但 $L_{EIoU}$ 很大（接近 1）。最終的損失 $L_{Focal?EIoU}$ 仍然很大，模型會重點關注這個樣本。
• 對于一個簡單樣本（IoU → 1）：$Io{U}^{\gamma }\approx 1$，但 $L_{EIoU}$ 很小（接近 0）。最終的損失 $L_{Focal?EIOU}$ 會變得更小，從而降低了簡單樣本在總損失中的權重。

優點:

• 解決回歸樣本不平衡：顯著提升模型對困難樣本的回歸能力。
• 進一步提升性能：在 EIOU 的基礎上，通常能獲得更高的檢測精度（mAP）。
• 即插即用：Focal 的思想可以遷移到其他 IOU 變體（如 Focal-CIOU）進行結合使用。