一、分析賽題核心意義
收集近 11 年的賽題并非簡單的 “題目存檔”,而是為了從歷史規律、能力匹配、實戰準備三個維度為參賽者或研究者提供價值。
1.1把握競賽命題趨勢,降低選題盲目性
賽題命題往往緊扣當年社會熱點、科技前沿與行業痛點(如 2024 年 E 題 “交通流量管控” 對應城市旅游擁堵治理,2021 年 A 題 “FAST 主動反射面調節” 關聯國家重大科技工程)。通過縱向梳理,可清晰發現命題從 “純理論建模” 向 “實際問題解決” 傾斜(如近年賽題普遍增加 “數據預處理”“多約束優化” 要求),也能總結高頻命題領域(如交通優化、生產決策、環境分析、科技工程類題目占比超 60%),幫助參賽者提前聚焦優勢領域,避免臨賽時因不熟悉題型而選錯題目。

1.2構建 “問題 - 模型” 對應思維,提升建模效率
數學建模的核心是 “用合適的模型解決特定問題”,而歷史賽題是 “問題與模型匹配” 的最佳案例庫。例如:
遇到 “資源分配 / 成本優化” 類問題(如 2024 年 B 題生產決策、2020 年 C 題信貸決策),可關聯 “線性規劃 / 整數規劃模型”;
遇到 “概率預測 / 風險評估” 類問題(如 2024 年 D 題深彈命中概率、2019 年 E 題薄利多銷分析),可關聯 “概率論 / 馬爾可夫鏈模型”。
收集賽題能幫助使用者建立 “看到問題→聯想對應模型” 的條件反射,減少建模初期的思路混亂。
1.3 積累實戰數據與邊界條件處理經驗
賽題并非 “理想化數學題”,而是包含大量 “實際約束”(如 2023 年 E 題黃河水沙分析需處理 “數據缺失”,2022 年 D 題氣象傳輸需考慮 “誤碼率限制”)。收集賽題時,可同步關注題目中 “隱含的邊界條件”(如時間限制、成本上限、數據誤差范圍),這些細節是建模能否落地的關鍵 —— 而歷史賽題的 “約束設置規律”(如工業類題目常含 “生產周期約束”,環境類題目常含 “自然變量波動約束”),能為后續實戰提供參考,避免因忽略實際約束導致模型 “紙上談兵”。
1.4 為團隊分工與能力補全提供依據
數學建模需 3 人團隊分工(建模、編程、寫作),不同賽題對團隊能力的要求差異顯著:
科技工程類題目(如 2024 年 A 題板凳龍、2014 年 A 題嫦娥三號)需較強的 “物理建模 + 編程實現” 能力(如用 MATLAB 仿真運動軌跡);
數據分析類題目(如 2023 年 C 題蔬菜定價、2018 年 C 題會員畫像)需較強的 “數據處理 + 統計學” 能力(如用 Python 做回歸分析)。
收集賽題后,可根據團隊成員特長(如 “擅長編程者適合工業類題,擅長統計者適合數據分析類題”)提前規劃分工,避免臨賽時因能力不匹配導致效率低下。
| 年份 | 賽題 | 題目 | 簡介 |
|---|---|---|---|
| 2024 年 | A 題 | “板凳龍” 鬧元宵 | 需對動態系統建模,模擬舞龍隊伍在螺旋路徑中的行進過程,求解隊伍每秒的位置、速度,進行碰撞檢測與路徑優化等 |
| 2024 年 | B 題 | 生產過程中的決策問題 | 企業生產電子產品,需購買兩種零配件進行裝配。要為企業設計抽樣檢測零配件的方案,在已知零配件和成品次品率等情況下,對生產各階段(零配件檢測、成品檢測、不合格成品處理、用戶退回不合格品處理)作出決策;還要考慮多工序、多零配件的復雜生產過程的決策 |
| 2024 年 | C 題 | 農作物的中值策略 | 需考慮農作物種植面積、成本、收益、作物間的替代性與互補性,以及價格、氣候等不確定性因素,通過建立動態種植模型研究農作物種植的最優策略 |
| 2024 年 | D 題 | 反潛航空深彈命中概率問題 | 基于反潛戰術中的深彈投射場景,運用軍事知識和概率論原理,對相關情況合理簡化,構建數學模型計算深彈命中潛艇的概率 |
| 2024 年 | E 題 | 交通流量管控 | 以小鎮道路為例,聚焦城市交通擁堵問題,特別是黃金周期間旅游車流的應對,通過數據預處理和條件假設,構建數學模型尋求解決方案 |
| 2023 年 | A 題 | 定日鏡場的優化設計 | 圍繞定日鏡場,從光學、力學等多方面考慮,對定日鏡的布局、角度等進行優化設計,以提高太陽能的收集和利用效率 |
| 2023 年 | B 題 | 多波束測線問題 | 在多波束測量場景下,針對測線的規劃、測量數據的處理和分析等方面展開研究,以實現更高效、準確的海洋測量 |
| 2023 年 | C 題 | 蔬菜類商品的自動定價與補貨決策 | 結合蔬菜市場的需求變化、成本波動等因素,建立數學模型實現蔬菜類商品的自動定價,并制定合理的補貨決策,以平衡收益和庫存成本 |
| 2023 年 | D 題 | 圈養湖羊的空間利用率 | 從圈養湖羊的養殖環境出發,考慮湖羊的生長習性、活動空間需求等,對養殖場地的布局和利用進行優化,提高空間利用率 |
| 2023 年 | E 題 | 黃河水沙監測數據分析 | 對黃河水沙監測所獲得的數據進行深入分析,挖掘數據背后的規律,為黃河的治理、水資源利用和生態保護提供數據支持和決策依據 |
| 2022 年 | A 題 | 波浪能最大輸出功率設計 | 針對波浪能的特點,通過物理建模和數學計算,設計相關裝置或系統,以實現波浪能的高效捕獲和轉化,獲得最大輸出功率 |
| 2022 年 | B 題 | 無人機遂行編隊飛行中的純方位無源定位 | 研究無人機在編隊飛行時,僅依靠方位信息進行無源定位的方法,涉及信號處理、空間幾何計算等多方面知識,以實現無人機的精準定位和編隊控制 |
| 2022 年 | C 題 | 古代玻璃制品的成分分析與鑒別 | 運用化學分析、統計學等方法,對古代玻璃制品的成分數據進行處理和分析,建立鑒別模型,判斷玻璃制品的產地、年代等信息 |
| 2022 年 | D 題 | 氣象報文信息衛星通信傳輸 | 考慮氣象報文信息在衛星通信傳輸過程中的特點和問題,如數據量、傳輸速率、誤碼率等,優化傳輸方案,保障氣象信息的準確、快速傳輸 |
| 2022 年 | E 題 | 小批量物料的生產安排 | 針對小批量物料生產場景,綜合考慮生產流程、成本、交貨期等因素,制定合理的生產計劃和調度方案,提高生產效率和經濟效益 |
| 2021 年 | A 題 | “FAST” 主動反射面的形狀調節 | 基于 “FAST”(中國天眼)主動反射面的工作原理和結構特點,通過建立數學模型,研究如何對反射面的形狀進行精確調節,以實現更好的信號接收效果 |
| 2021 年 | B 題 | 乙醇耦合制備 C4 烯烴 | 圍繞乙醇耦合制備 C4 烯烴的化學工藝過程,考慮反應條件、原料轉化率、產物選擇性等因素,建立數學模型優化反應過程,提高生產效率和產品質量 |
| 2021 年 | C 題 | 生產企業原材料的訂購與運輸 | 生產企業需要對原材料進行訂購和運輸,要綜合考慮原材料價格波動、運輸成本、庫存成本、生產需求等因素,建立模型制定最優的訂購與運輸策略 |
| 2021 年 | D 題 | 連鑄切割的在線優化 | 在連鑄生產過程中,針對鑄坯的切割環節,考慮鑄坯的質量、切割速度、切割損耗等因素,通過數學模型實現切割過程的在線優化,提高生產效益 |
| 2021 年 | E 題 | 中藥材的鑒別 | 利用化學、生物學、統計學等多學科知識,對中藥材的特征數據進行分析處理,建立鑒別模型,實現對中藥材真偽、品質的準確鑒別 |
| 2020 年 | A 題 | 爐溫曲線 | 研究在特定工藝要求下,爐溫隨時間的變化規律,通過建立數學模型優化爐溫控制策略,以滿足生產過程中對爐溫的精確要求 |
| 2020 年 | B 題 | 穿越沙漠 | 給定穿越沙漠的相關條件,如沙漠長度、車輛載油量、加油站位置等,建立數學模型規劃最優的穿越方案,包括行車路線、加油策略等 |
| 2020 年 | C 題 | 中小微企業的信貸決策 | 綜合考慮中小微企業的財務狀況、信用記錄、市場環境等因素,建立數學模型為金融機構提供信貸決策依據,評估貸款風險和收益 |
| 2020 年 | D 題 | 接觸式輪廓儀的自動標注 | 針對接觸式輪廓儀獲取的數據,研究如何通過算法實現自動標注,提高數據處理效率和準確性,涉及圖像處理、模式識別等技術 |
| 2020 年 | E 題 | 校園供水系統智能管理 | 結合校園用水需求的變化規律、供水設備的運行成本等因素,建立數學模型實現校園供水系統的智能管理,優化供水方案,節約水資源和成本 |
| 2019 年 | A 題 | 高壓油管的壓力控制 | 圍繞高壓油管內的壓力變化情況,通過建立物理和數學模型,研究壓力控制方法,確保高壓油管在安全和高效的狀態下工作 |
| 2019 年 | B 題 | “同心協力” 策略研究 | 探索團隊合作中 “同心協力” 的策略問題,可能涉及到博弈論、協同優化等知識,通過建立模型分析不同策略下團隊的表現和收益 |
| 2019 年 | C 題 | 機場的出租車問題 | 針對機場出租車的調度、乘客等待時間、出租車運營效率等問題,綜合考慮機場客流量、出租車數量、交通狀況等因素,建立數學模型優化出租車運營方案 |
| 2019 年 | D 題 | 空氣質量數據的校準 | 對空氣質量監測所獲得的數據,考慮監測設備誤差、環境因素干擾等情況,通過數學方法對數據進行校準處理,提高數據的準確性和可靠性 |
| 2019 年 | E 題 | “薄利多銷” 分析 | 從經濟學角度出發,研究商品價格、銷量、成本和利潤之間的關系,建立數學模型分析 “薄利多銷” 策略在不同市場環境下的可行性和效果 |
| 2018 年 | A 題 | 高溫作業專用服裝設計 | 結合高溫作業環境的特點和人體生理需求,從材料選擇、服裝結構設計等方面建立數學模型,設計出更適合高溫作業人員的專用服裝 |
| 2018 年 | B 題 | 智能 RGV 的動態調度策略 | 針對智能 RGV(軌道式自動導引車)在生產線上的作業情況,考慮任務分配、運行路徑規劃、設備等待時間等因素,建立數學模型制定動態調度策略,提高生產效率 |
| 2018 年 | C 題 | 大型百貨商場會員畫像描繪 | 利用大數據分析技術和數學統計方法,對大型百貨商場會員的消費行為、偏好等數據進行處理和分析,構建會員畫像,為商場精準營銷提供支持 |
| 2018 年 | D 題 | 汽車總裝線的配置問題 | 在汽車總裝生產線上,綜合考慮零部件供應、裝配工藝、生產效率、成本等因素,建立數學模型對總裝線的設備、人員、生產流程等進行優化配置 |
| 2017 年 | A 題 | CT 系統參數標定及成像 | 研究 CT 系統的工作原理,通過建立數學模型對 CT 系統的參數進行標定,并利用標定后的參數實現更準確的成像,提高 CT 檢測的精度 |
| 2017 年 | B 題 | “拍照賺錢” 的任務定價 | 針對 “拍照賺錢” 這種眾包任務平臺的任務定價問題,考慮任務難度、地理位置、市場需求、參與者收益等因素,建立數學模型制定合理的任務定價策略 |
| 2017 年 | C 題 | 顏色與物質濃度辨識 | 運用光學、化學和數學知識,研究顏色與物質濃度之間的關系,通過建立模型實現對物質濃度的準確辨識,可應用于化學分析、質量檢測等領域 |
| 2017 年 | D 題 | 巡檢線路的排班 | 在巡檢工作場景下,考慮巡檢人員數量、工作時間限制、巡檢地點分布、設備重要性等因素,建立數學模型制定合理的巡檢線路排班計劃,提高巡檢效率和質量 |
| 2016 年 | A 題 | 系泊系統的設計 | 圍繞海洋工程中的系泊系統,考慮海洋環境因素(如風浪流)、船舶或海洋結構物的運動特性等,通過建立數學模型設計安全、可靠且經濟的系泊系統 |
| 2016 年 | B 題 | 小區開放對道路通行的影響 | 研究小區開放這一城市規劃措施對周邊道路通行能力、交通流量分布、居民出行時間等方面的影響,通過建立數學模型進行定量分析和評估 |
| 2016 年 | C 題 | 電池剩余放電時間預測 | 利用電池的充放電特性、歷史數據、當前狀態等信息,建立數學模型對電池剩余放電時間進行準確預測,為電池管理和設備使用提供參考 |
| 2016 年 | D 題 | 風電場運行狀況分析及優化 | 針對風電場的運行情況,考慮風力資源的變化、風機的性能、設備維護成本等因素,建立數學模型分析風電場的運行效率,并提出優化策略提高發電效益 |
| 2015 年 | A 題 | 太陽影子定位 | 根據太陽的位置和物體影子的變化規律,通過建立數學模型,利用影子長度和方向等信息確定物體的地理位置或時間等參數 |
| 2015 年 | B 題 | 互聯網 + 時代出租車的資源配置 | 在 “互聯網 +” 背景下,考慮出租車市場的供需關系、乘客出行需求分布、車輛調度成本等因素,建立數學模型優化出租車資源配置,提高運營效率和服務質量 |
| 2015 年 | C 題 | 月上柳梢頭 | 題目可能圍繞月亮與柳樹在特定場景下的光學、幾何關系展開,通過建立數學模型研究相關現象,如月亮在樹梢位置的時間、角度等問題 |
| 2015 年 | D 題 | 眾籌筑屋規劃方案設計 | 結合眾籌的特點和筑屋的需求、成本、收益等因素,建立數學模型制定眾籌筑屋的規劃方案,包括資金籌集、房屋設計、利益分配等方面 |
| 2014 年 | A 題 | 嫦娥三號軟著陸軌道設計與控制策略 | 依據嫦娥三號的任務要求和月球的引力場等環境因素,建立數學模型設計軟著陸軌道,并制定相應的控制策略,確保嫦娥三號安全、準確地軟著陸在月球表面 |
| 2014 年 | B 題 | 創意平板折疊桌 | 從平板折疊桌的功能需求、結構設計、材料選擇等方面出發,建立數學模型進行優化設計,使折疊桌在滿足使用功能的同時,具備更好的便攜性和美觀性 |
| 2014 年 | C 題 | 生豬養殖場的經營管理 | 綜合考慮生豬養殖過程中的飼料成本、市場價格波動、養殖規模、疾病防控等因素,建立數學模型為生豬養殖場制定經營管理策略,實現經濟效益最大化 |
| 2014 年 | D 題 | 儲藥柜的設計 | 根據儲藥的種類、數量、儲存條件、取藥便捷性等要求,建立數學模型對儲藥柜的結構、布局進行優化設計,提高儲藥效率和藥品管理水平 |
二、總結歸納賽題核心事項
總結解決方法需圍繞 “分類歸納→模型拆解→細節優化→實戰復用” 展開,具體可分為 5 個步驟,確保總結內容 “可落地、可遷移”:
2.1 先按 “題目類型” 分類,建立 “問題 - 方法” 對應框架?
第一步需打破 “按年份排序” 的慣性,按 “題目核心需求” 對賽題分類(避免按 “A/B/C/D 題” 標簽分類,因每年標簽對應的題型可能變化),建議分為 6 大類,每類對應典型方法:
| 題目類型 | 典型賽題案例(年份 + 題號) | 核心解決方法(模型 / 工具) | 關鍵注意事項 |
|---|---|---|---|
| 資源優化 / 決策類 | 2024B、2023C、2020C、2014C | 線性規劃 / 整數規劃(Lingo/Excel Solver)、動態規劃 | 需明確 “目標函數”(如 “成本最小”“收益最大”)和 “約束條件”(如產能、預算) |
| 概率預測 / 風險評估類 | 2024D、2019E、2016C、2015A | 概率論、馬爾可夫鏈、蒙特卡洛模擬(Python/MATLAB) | 需驗證 “概率分布假設”(如是否符合正態分布),處理 “小概率事件” |
| 動態系統 / 物理建模類 | 2024A、2023A、2022A、2014A | 微分方程(如牛頓運動方程)、仿真工具(MATLAB/Simulink) | 需簡化 “物理模型”(如忽略次要變量),避免模型過于復雜無法求解 |
| 數據分析 / 模式識別類 | 2023E、2022C、2018C、2017C | 回歸分析、聚類算法(K-Means)、機器學習(如隨機森林) | 需處理 “異常數據”(如用箱線圖剔除 outliers),驗證模型擬合度(R2/MAE) |
| 交通 / 路徑優化類 | 2024E、2023B、2019C、2017D | 圖論(Dijkstra 算法)、遺傳算法(解決復雜路徑問題) | 需考慮 “動態變量”(如交通流量實時變化、巡檢人員工作時長限制) |
| 工業過程 / 流程優化類 | 2022E、2021D、2020A、2018B | 排隊論(處理生產等待問題)、離散事件仿真(AnyLogic) | 需匹配 “工業實際流程”(如連鑄切割需考慮 “生產節拍”,RGV 調度需考慮 “設備切換時間”) |
2.2 對每類題目拆解 “標準解決流程”,明確步驟分工?
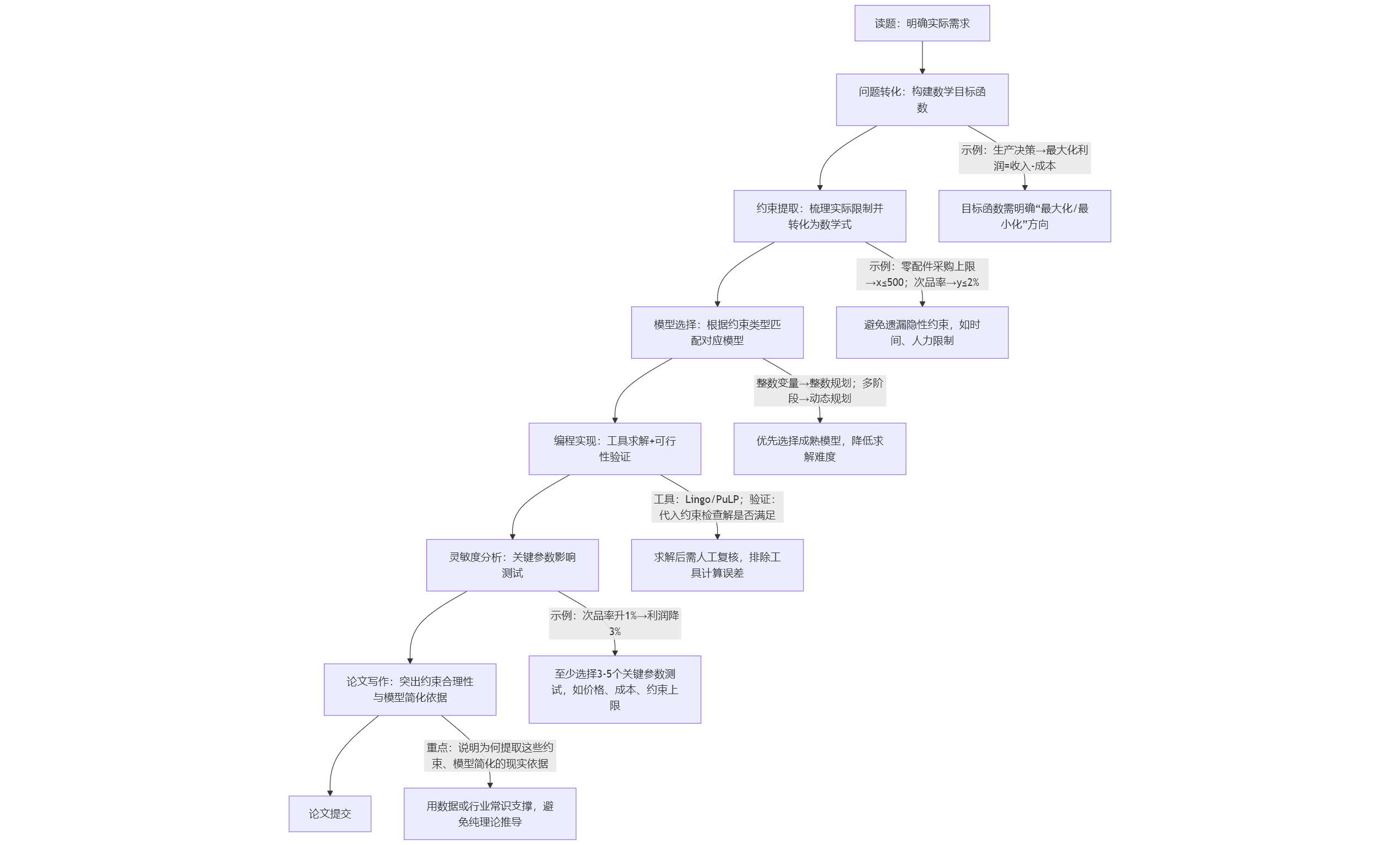
針對每類題目,總結 “從讀題到論文提交” 的標準流程,避免實戰時步驟混亂。以 “資源優化類題目” 為例,標準流程可拆解為:
問題轉化:將題目中的 “實際需求” 轉化為 “數學目標函數”(如 “生產決策”→“最大化利潤 = 收入 - 成本”);
約束提取:列出所有 “實際限制”(如零配件采購量上限、成品次品率限制),轉化為 “數學不等式 / 等式”;
模型選擇:根據約束類型選擇模型(如 “整數變量”→整數規劃,“多階段決策”→動態規劃);
編程實現:用工具求解(如 Lingo 寫規劃方程,Python 用 PuLP 庫求解),驗證解的可行性(如是否滿足所有約束);
靈敏度分析:分析 “關鍵參數變化對結果的影響”(如 “零配件次品率上升 1%,利潤下降多少”),增強模型魯棒性;
論文寫作:重點說明 “約束提取的合理性” 和 “模型簡化的依據”(避免評委認為模型脫離實際)。
2.3 聚焦 “模型細節優化”,總結 “避坑點”?
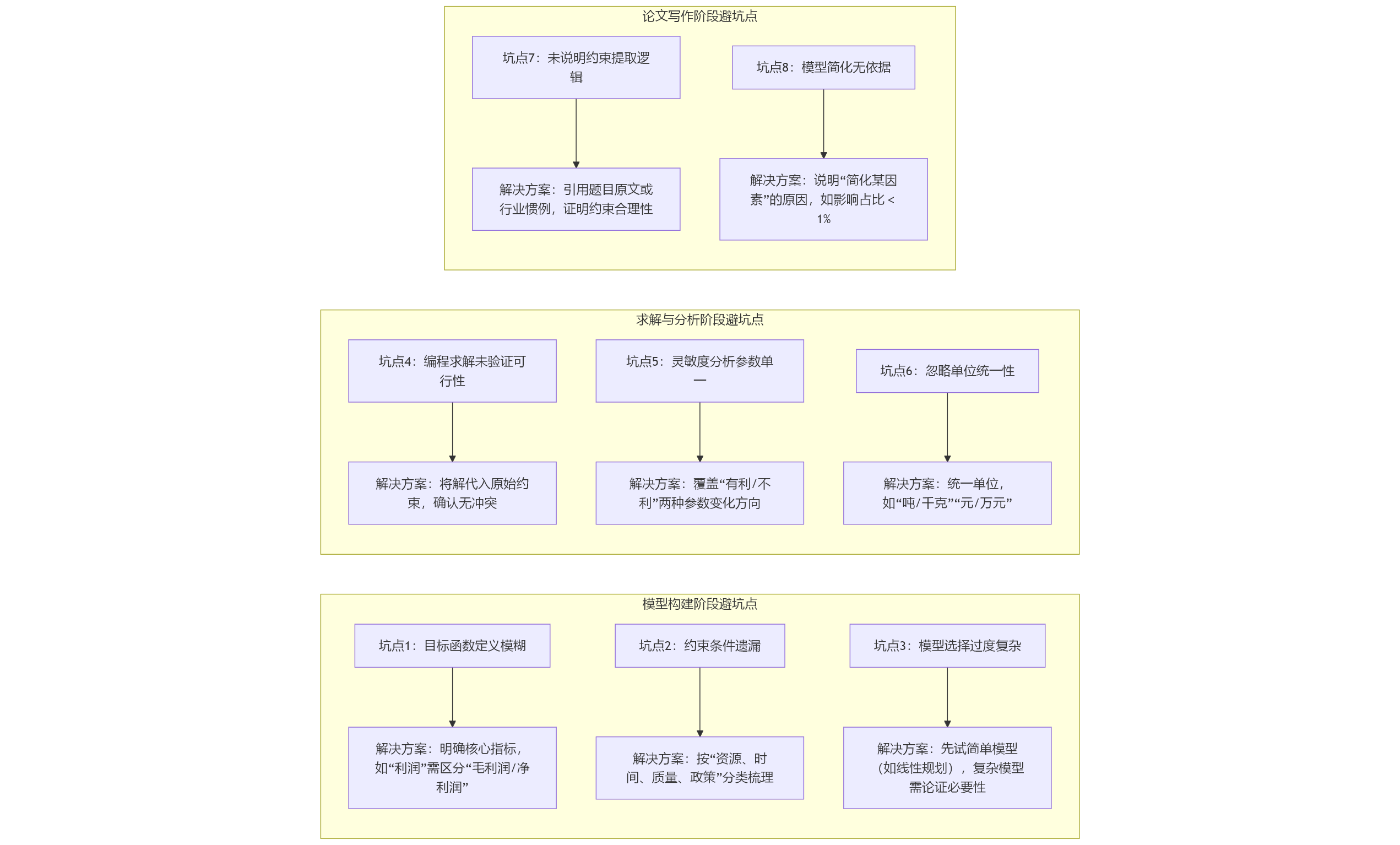
同一模型在不同賽題中的 “細節處理” 差異,是區分建模水平的關鍵。需總結每類模型的 “常見誤區” 和 “優化技巧”,例如:
線性規劃模型:若題目含 “模糊約束”(如 “成本盡可能低”),需補充 “模糊線性規劃” 優化,避免用 “硬約束” 導致解不可行;
蒙特卡洛模擬:需注意 “抽樣次數”(如 2024 年 D 題深彈命中概率,抽樣次數過少會導致結果波動大,建議至少 10000 次);
回歸分析:若數據存在 “多重共線性”(如 2023 年 C 題蔬菜定價中 “銷量與價格高度相關”),需用 “嶺回歸” 替代普通線性回歸,避免系數估計偏差。
整理 “工具與代碼模板”,提升實戰效率?
建模的核心是 “用工具實現思路”,而非重復編寫基礎代碼。總結時可按 “模型類型” 整理工具和模板:
規劃類模型:整理 Lingo/PuLP 的 “線性規劃模板”(含目標函數、約束條件的固定語法);
仿真類模型:整理 MATLAB 的 “動態系統仿真模板”(如運動軌跡仿真的微分方程求解代碼);
數據分析類模型:整理 Python 的 “數據預處理模板”(含缺失值填充、異常值剔除、特征工程的基礎代碼)。
模板需標注 “適用場景”(如 “此回歸模板適用于‘銷量 - 價格’線性關系分析”),避免盲目復用。
2.4. 結合 “優秀論文” 驗證方法有效性,補充 “非模型因素”?
賽題的 “解決方法” 不僅包括模型,還包括 “論文寫作邏輯”“結果可視化” 等非模型因素 —— 這些是拿獎的關鍵。后續總結時,可結合全國一等獎論文(可從競賽官網或高校建模協會獲取)補充:
寫作邏輯:優秀論文如何 “從實際問題切入→引出模型→驗證結果→提出建議”(如 2023 年 E 題黃河水沙分析,優秀論文會先說明 “水沙數據的實際意義”,再講模型,避免純數學推導);
結果可視化:如何用圖表呈現復雜結果(如用熱力圖展示交通流量分布,用折線圖展示利潤隨參數的變化);
模型局限性與改進方向:優秀論文會主動說明 “模型的不足”(如 “未考慮極端天氣對生產的影響”),并提出改進思路 —— 這能體現建模的嚴謹性,需納入總結。
通過以上步驟,總結出的 “解決方法” 將不再是 “零散的模型列表”,而是 “從題目分類到實戰落地” 的完整體系,既能幫助新手快速入門,也能為有經驗的參賽者提供 “優化思路”,真正實現 “以史為鑒,提升實戰能力”。

)






------std::lock_guard)



:Model抽象層 - “馴服”天下AI的“緊箍咒”)



:polygonOffsetFactor工作原理大揭秘)



