樸素貝葉斯分類器就是根據貝葉斯公式計算結果進行分類的模型,“樸素”指事件之間相互獨立無影響. 例 如:有如下數據集:
| Text???????? | Category |
| A great game(一個偉大的比賽) | Sports(體育運動) |
| The election was over(選舉結束 | Not sports(不是體育運動) |
| Very clean match(沒內幕的比賽) | Sports(體育運動) |
| A clean but forgettable game(一場難以忘記的比賽) | Sports(體育運動) |
| It was a close election(這是一場勢均力敵的選舉) | Not sports(不是體育運動) |
求:“A very close game” 是體育運動的概率?數學上表示為 P(Sports | a very close game). 根據貝葉斯 定理,是運動的概率可以表示為:
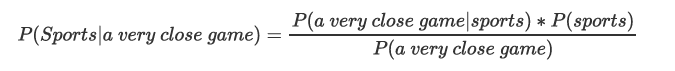
不是運動概率可以表示為:
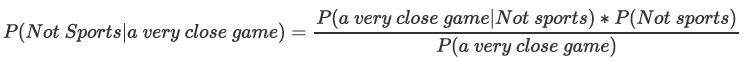
概率更大者即為分類結果. 由于分母相同,即比較分子誰更大即可.
我們只需統計”A very close game“ 多 少次出現在Sports類別中,就可以計算出上述兩個概率. 但是”A very close game“ 并沒有出現在數據集 中,所以這個概率為0,要解決這個問題,就假設每個句子的單詞出現都與其它單詞無關(事件獨立即樸 素的含義),所以,P(a very close game)可以寫成

統計出“a", "very", "close", "game"出現在"Sports"類別中的概率,就能算出其所屬的類別. 具體計算過程 如下:
????????第一步:計算總詞頻:Sports類別詞語總數11,Not Sports類別詞語總數9,詞語總數14(去重之后的單詞數量)
????????第二步:計算每個類別的先驗概率
# Sports和Not Sports概率
P(Sports) = 3 / 5 = 0.6
P(Not Sports) = 2 / 5 = 0.4
# Sports條件下各個詞語概率
P(a | Sports) = (2 + 1) / (11 + 14) = 0.12
P(very | Sports) = (1 + 1) / (11 + 14) = 0.08
P(close | Sports) = (0 + 1) / (11 + 14) = 0.04
P(game | Sports) = (2 + 1) / (11 + 14) = 0.12
# Not Sports條件下各個詞語概率
P(a | Not Sports) = (1 + 1) / (9 + 14) = 0.087
P(very | Not Sports) = (0 + 1) / (9 + 14) = 0.043
P(close | Not Sports) = (1 + 1) / (9 + 14) = ?= 0.087
P(game | Not Sports) = (0 + 1) / (9 + 14) = 0.043
其中,分子部分加1,是為了避免分子為0的情況;分母部分都加了詞語總數14,是為了避免分子增 大的情況下計算結果超過1的可能.
第三步:將先驗概率帶入貝葉斯定理,計算概率: 是體育運動的概率:

不是體育運動的概率:
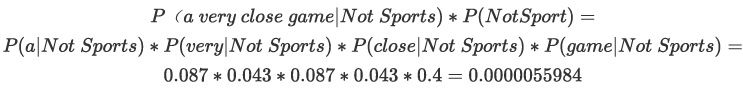
分類結果:P(Sports) = 0.000027648 , P(Not Sports) = 0.0000055984, 是體育運動














)
免安裝中文版)



