強連通分量

基礎概念

強連通：在有向圖 $G$ 中，如果兩個點 $u$ 和 $v$ 是互相可達的，即從 $u$ 出發可以到達 $v$ , 從 $v$ 也可以到達 $u$ , 則稱 $u$ 和 $v$ 是強連通的。如果 $G$ 中任意兩個點都是互相可達的，則稱 $G$ 是強連通圖。

強連通分量：如果一個有向圖 $G$ 不是強連通圖，那么可以把它分成多個子圖， 其中每個子圖的內部是強連通的, 而且這些子圖已經擴展到最大，不能與子圖外的任意點強連通， 稱這樣的一個 “極大強連通” 子圖是 $G$ 的一個強連通分量。

DFS生成樹

SCC(強連通分量) 中的 tarjan 算法主要是靠 DFS生成樹 實現的, 所以接下來介紹DFS生成樹：

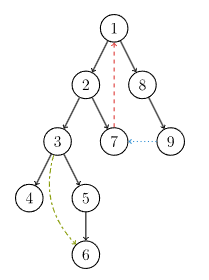
有向圖的 DFS 生成樹主要有 4 種邊：

1. 樹邊 ：示意圖中以黑色邊表示，每次搜索找到一個還沒有訪問過的結點的時候就形成了一條樹邊。
2. 反祖邊 ：示意圖中以紅色邊表示（即 7 → 1），也被叫做回邊，即指向祖先結點的邊。
3. 橫叉邊 ：示意圖中以藍色邊表示（即 9 → 7），它主要是在搜索的時候遇到了一個已經訪問過的結點，但是這個結點 并不是 當前結點的祖先。
4. 前向邊 ：示意圖中以綠色邊表示（即 3 → 6），它是在搜索的時候遇到子樹中的結點的時候形成的。

接下來我們考慮 DFS 生成樹與強連通分量之間的關系。

如果結點 $u$ 是某個強連通分量在搜索樹中遇到的第一個結點，那么這個強連通分量的其余結點肯定是在搜索樹中以 $u$ 為根的子樹中。結點 $u$ 被稱為這個強連通分量的根。

反證法：假設有個結點 $v$ 在該強連通分量中但是不在以 $u$ 為根的子樹中，那么 $u$ 到 $v$ 的路徑中肯定有一條離開子樹的邊。但是這樣的邊只可能是橫叉邊或者反祖邊，然而這兩條邊都要求指向的結點已經被訪問過了，這就和 $v$ 不在以 $u$ 為根的子樹中矛盾了。得證。

為什么這兩種邊都要求“指向的結點已經被訪問過了”？

• 反祖邊：

  • 定義：指向祖先結點的邊。
  • 為什么要求已訪問？ 祖先節點的定義就是在DFS過程中比當前節點更早被訪問的節點。你要指回你的祖先，那個祖先肯定在你之前就被發現了。所以，當DFS走到當前節點，準備沿著反祖邊走去時，它指向的那個祖先節點肯定已經被訪問過了。

• 橫叉邊：

  • 定義：指向一個既不是祖先也不是后代，但已經被訪問過的節點的邊。
  • 為什么要求已訪問？ 這是橫叉邊的核心定義！橫叉邊連接的是DFS樹中兩個不存在祖先-后代關系的分支。當你從一個分支走到另一個分支時，另一個分支的節點必然是在之前某次DFS過程中已經被探索過的。如果那個節點還沒被訪問，DFS就會把它作為當前節點的“后代”（形成一條樹邊），而不是一條橫叉邊。

tarjan相關概念

dfn[u]: 時間戳，DFS遍歷時結點 $u$ 被搜索的次序。
low[u]: $u$ 和 $u$ 的子樹里返祖邊和橫插邊能連到還沒出棧的 $dfn$ 最小的點。

按照DFS遍歷次序對圖中所有的結點進行搜索，維護每個結點的 $dfn$與 $low$ 變量，且讓搜索到的結點入棧。每當找到一個強連通元素，就按照該元素包含結點數目讓棧中元素出棧。在搜索過程中，對于結點 u 和與其相鄰的結點 v（v 不是 u 的父節點）考慮 3 種情況：

1. $v$ 未被訪問：繼續對 $v$ 進行深度搜索。在回溯過程中，用 $lo{w}_v$ 更新 $lo{w}_u$ 。因為存在從 $u$ 到 $v$ 的直接路徑，所以 $v$ 能夠回溯到的已經在棧中的結點，$u$ 也一定能夠回溯到。
2. $v$ 被訪問過，已經在棧中：根據 low 值的定義，用 $df{n}_v$ 更新 $lo{w}_u$。
3. $v$ 被訪問過，已不在棧中：說明 $v$ 已搜索完畢，其所在連通分量已被處理，所以不用對其做操作。

對于一個連通分量圖，我們很容易想到，在該連通圖中有且僅有一個 $u$ 使得 ${\text{dfn}}_u={\text{low}}_u$ 。該結點一定是在深度遍歷的過程中，該連通分量中第一個被訪問過的結點，因為它的 $dfn$ 和 $low$ 值最小，不會被該連通分量中的其他結點所影響。

因此，在回溯的過程中，判定 ${\text{dfn}}_u={\text{low}}_u$ 是否成立，如果成立，則棧中 $u$ 及其上方的結點構成一個 SCC。

void tarjan(int u) {dfn[u] = low[u] = ++tim;stk.push_back(u), in_stk[u] = true;for (auto y : e[u]) {if (dfn[y] == -1) {tarjan(y);low[u] = std::min(low[u], low[y]);} else if (in_stk[y]) {low[u] = std::min(low[u], dfn[y]);}}if (low[u] == dfn[u]) {++scc_cnt;int y;do {y = stk.back();stk.pop_back();in_stk[y] = false;id[y] = scc_cnt;siz[scc_cnt]++;}while(y != u);}}

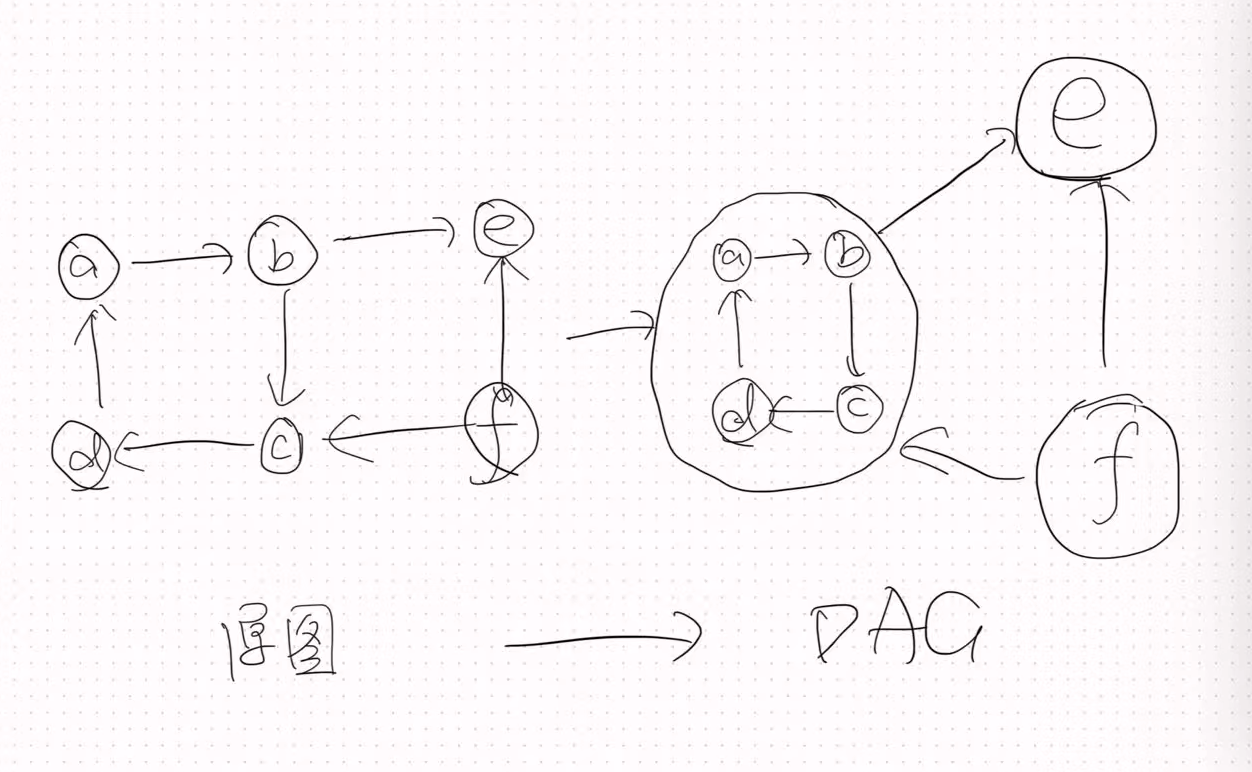
縮點之后，我們的圖就變成了一個DAG(有向無環圖)，我們就可以利用有向無環圖來做很多的事情，比如拓撲排序、DP等。

Template

struct SCC {int n, tim, scc_cnt;std::vector<std::vector<int>> e; std::vector<int> stk;std::vector<int> dfn, low, id;//各個點的時間戳dfn, 各個點能走到的最小的時間戳low, 對應的強連通分量id值std::vector<bool> in_stk;std::vector<int> siz;SCC() {}SCC(int _n) {init(_n);}void init(int _n) {n = _n;e.assign(n, {});dfn.assign(n, -1);in_stk.assign(n, false);low.resize(n);id.assign(n, -1);stk.clear();siz.assign(n, 0);tim = scc_cnt = 0;}void addEdge(int u, int v) { e[u].push_back(v);}void tarjan(int u) {dfn[u] = low[u] = ++tim;stk.push_back(u), in_stk[u] = true;for (auto y : e[u]) {if (dfn[y] == -1) {tarjan(y);low[u] = std::min(low[u], low[y]);} else if (in_stk[y]) {low[u] = std::min(low[u], dfn[y]);}}if (low[u] == dfn[u]) {++scc_cnt;int y;do {y = stk.back();stk.pop_back();in_stk[y] = false;id[y] = scc_cnt;siz[scc_cnt]++;}while(y != u);}}std::vector<int> work() {for (int i = 1;i <= n; i++) {if (dfn[i] == -1) {tarjan(i);}}return id;}};

2-SAT

背景

假設有 $n$ 對夫妻被邀請參加一個聚會，每對夫妻中只有一人可以列席。在 $2\times n$ 個人中，某些人（不包括夫妻）之間有著很大的矛盾，有矛盾的兩個人不會同時出現在聚會上，有沒有可能讓 $n$ 個人同時列席 ？

現在讓我們思考這個問題，如果我們沒有學過相關算法，我們大概會這樣做：每對夫妻都枚舉一個人然后一個一個試，時間復雜度高達 $O\left(2^n\right)$ 。

定義

2-SAT，簡單的說就是給出 $n$ 個集合，每個集合有兩個元素，已知若干個 $?a,b?$ ，表示 $a$ 與 $b$ 矛盾（其中 $a$ 與 $b$ 屬于不同的集合）。然后從每個集合選擇一個元素，判斷能否一共選 $n$ 個兩兩不矛盾的元素。顯然可能有多種選擇方案，一般題中只需要求出一種即可。

解決方法

針對2-SAT問題，我們可以選擇使用SCC + 拓撲排序來解決。

第一步，我們要開始建圖：
我們利用矛盾關系來建圖，比如 $A$ 和 $B$ 矛盾，$\overline{A}$ 和 $\overline{B}$ 矛盾，這就意味著 $A$ 出現的時候， $\overline{B}$ 就一定要出現， 同理，$B$ 出現的時候 $\overline{A}$ 也一定要出現, 這個時候我們就可以用 $A$ 指向 $\overline{B}$ , 然后 $B$ 指向 $\overline{A}$ 。

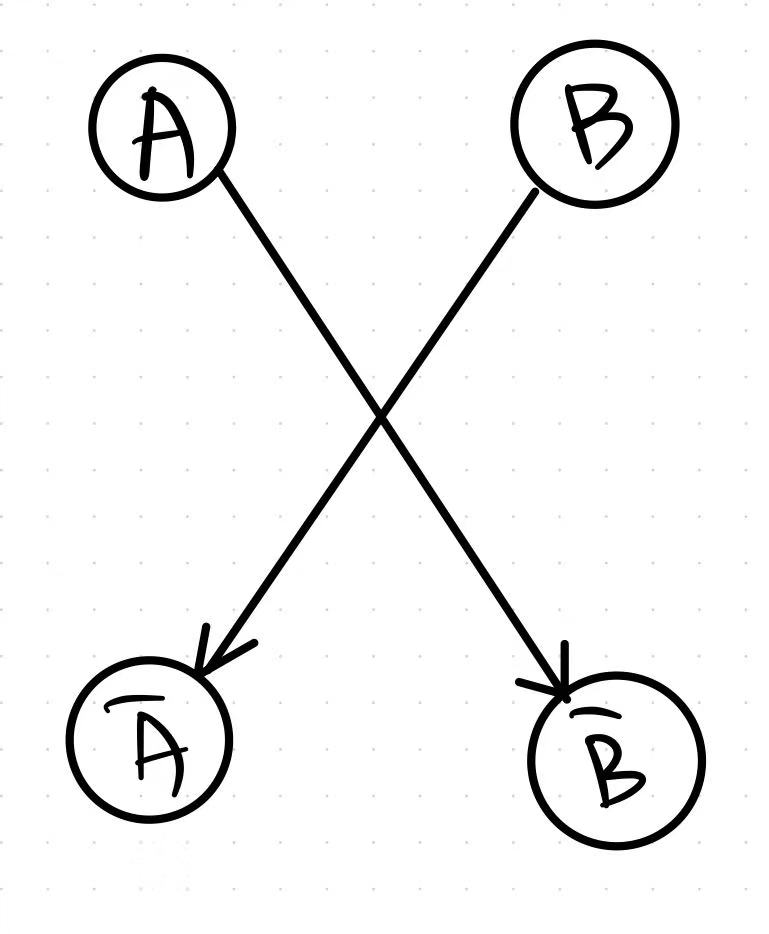
第二步，我們應該如何判斷是否有解呢 ？
當我們建成一個有向圖之后，根據SCC的定義，每個SCC里面各個點都是相互依賴的（一個點出現，其他點都要出現），如果一個人和他的對立面（比如 $A$ 和 $\overline{A}$ ）同時出現在一個SCC，則證明無解。

第三步，證明有解之后我們該怎么辦呢？
我們先縮點，縮完點之后整張圖就變成了一張DAG, 然后我們思考，我們建圖時指向的就是被依賴的，那么我們肯定就是優先選擇被依賴的更多的，那么其實就是一個逆向的拓撲排序, 不過實際上我們并不需要真正的做拓撲排序，因為SCC編號就是逆向的拓撲排序，SCC編號越小，出現優先級越高。

時間復雜度為 $O(n+m)$ 。

例題

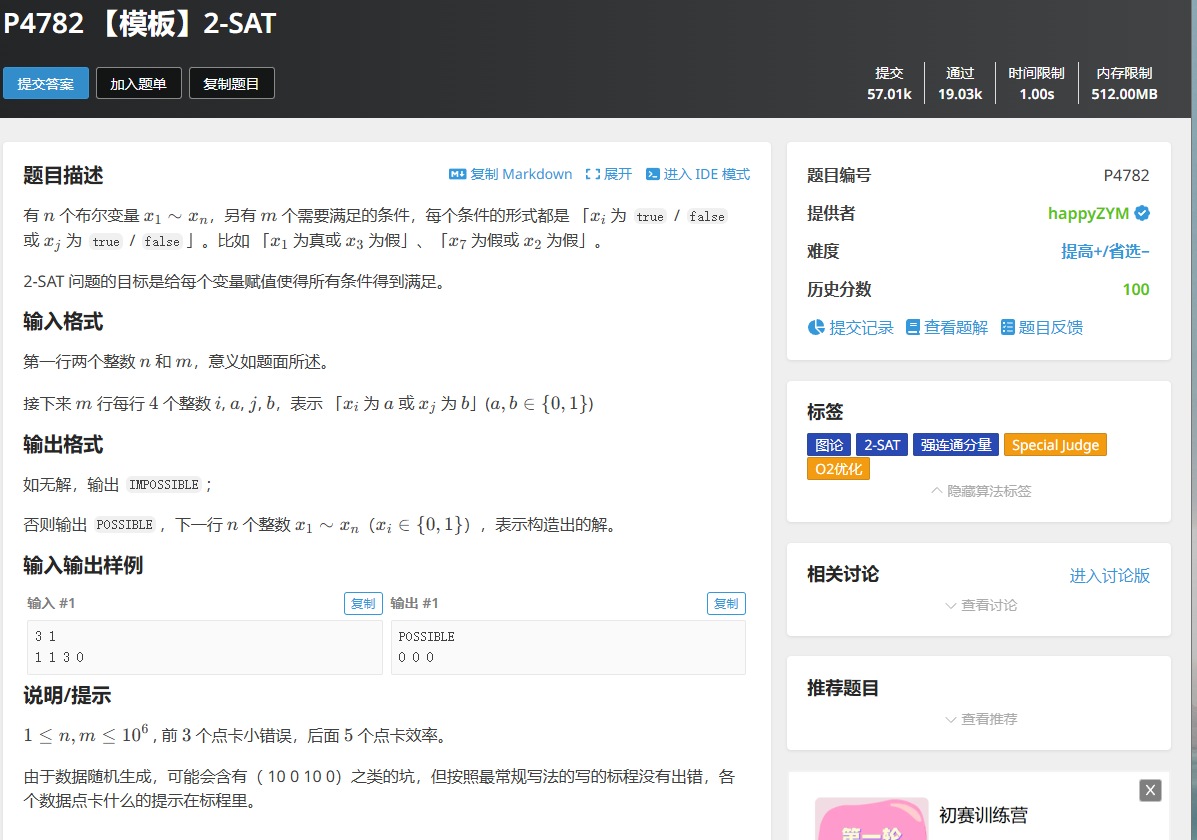
基礎思路

假設 $x$ 為 0， $y$ 為 1 為 一個條件，那么 $x$ 為 1 時，$y$ 就必然需要為 1，$y$ 為 0 時，$x$ 就必然需要為 0，依賴關系已經形成。

代碼模板

#include <bits/stdc++.h>using ll = long long;#ifndef DEBUG
#define debug(x)
#endifstruct TwoSat {int n;std::vector<std::vector<int>> e;std::vector<bool> ans;TwoSat() {}TwoSat(int _n) {init(_n);}void init(int _n) {n = _n;e.resize(2 * n);ans.resize(n);}void addEdge(int u, int a, int v, int b) {int na = (a ^ 1), nb = (b ^ 1);e[u + na * n].push_back(v + b * n);e[v + nb * n].push_back(u + a * n); }bool satisfiable() {std::vector<int> id(2 * n, -1), dfn(2 * n, -1), low(2 * n, -1);std::vector<int> stk;std::vector<bool> in_stk(2 * n, false);int tim = 0, scc_cnt = 0;std::function<void(int)> tarjan = [&](int u) {dfn[u] = low[u] = ++tim;stk.push_back(u), in_stk[u] = true;for (auto v: e[u]) {if (dfn[v] == -1) {tarjan(v);low[u] = std::min(low[u], low[v]);} else if (in_stk[v]) {low[u] = std::min(low[u], dfn[v]);}}if (dfn[u] == low[u]) {scc_cnt++;int y;do {y = stk.back();stk.pop_back();in_stk[y] = false;id[y] = scc_cnt;} while (y != u);}}; for (int i = 0;i < 2 * n; i++) {if (dfn[i] == -1) {tarjan(i);}}for (int i = 0;i < n;i++) {if (id[i] == id[i + n]) {return false;}ans[i] = id[i] > id[i + n];}return true;}std::vector<bool> answer() {return ans;}
};int main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);int n, m;std::cin >> n >> m;TwoSat g(n);for (int i = 1;i <= m; i++) {int x, a, y, b;std::cin >> x >> a >> y >> b;x--;y--;g.addEdge(x, a, y, b);} if (g.satisfiable()) {std::vector<bool> ans = g.answer();std::cout << "POSSIBLE\n";for (int i = 0;i < n; i++) {if (ans[i]) {std::cout << 1 << " ";} else {std::cout << 0 << " ";}}} else {std::cout << "IMPOSSIBLE\n";}return 0;
}

差分約束

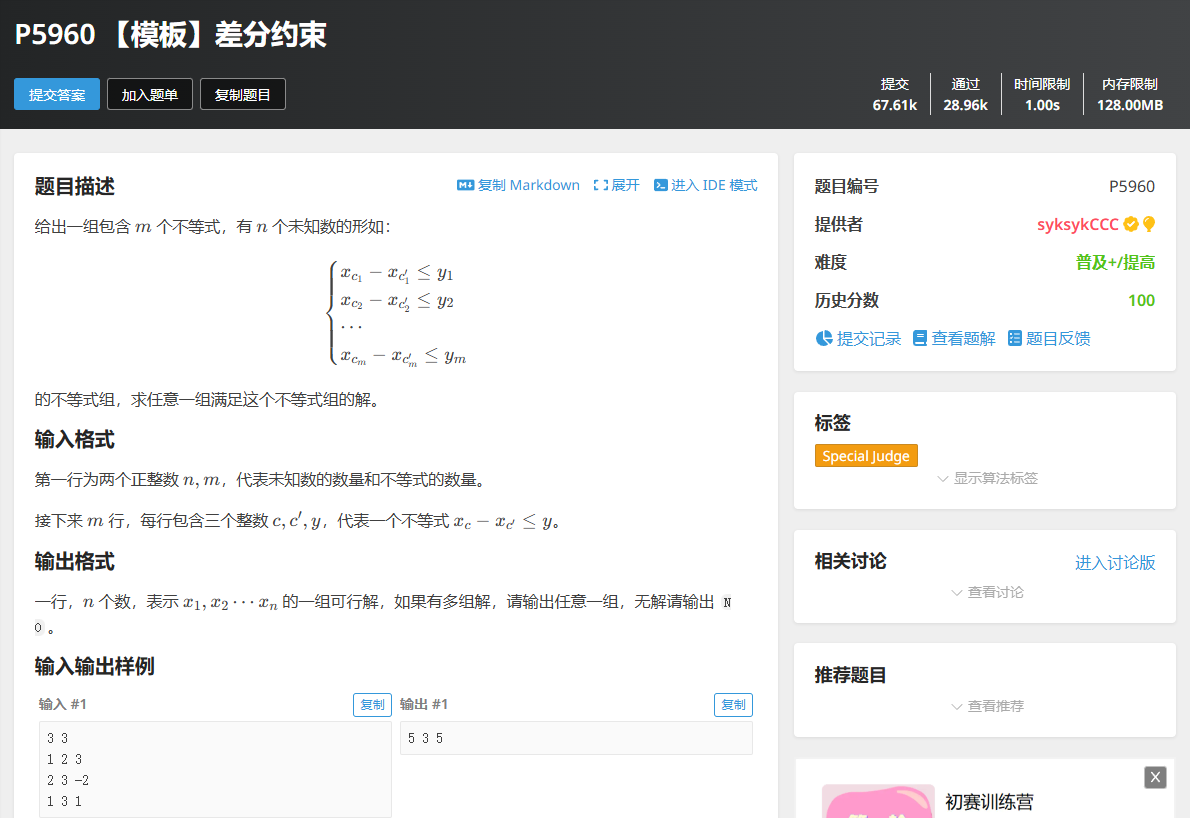
差分約束系統 是一種特殊的 $n$ 元一次不等式組，它包含 $n$ 個變量 $x_1,x_2,\dots ,x_n$ 以及 $m$ 個約束條件，每個約束條件是由兩個其中的變量做差構成的，形如 $x_i?x_j\le c_k$，其中 $1\le i,j\le n,i\ne j,1\le k\le m$ 并且 $c_k$ 是常數（可以是非負數，也可以是負數）。我們要解決的問題是：求一組解 $x_1=a_1,x_2=a_2,\dots ,x_n=a_n$，使得所有的約束條件得到滿足，否則判斷出無解。

差分約束系統中的每個約束條件 $x_i?x_j\le c_k$ 都可以變形成 $x_i\le x_j+c_k$，這與單源最短路中的三角形不等式 $dist[y]\le dist[x]+z$ 非常相似。因此，我們可以把每個變量 $x_i$ 看做圖中的一個結點，對于每個約束條件 $x_i?x_j\le c_k$，從結點 $j$ 向結點 $i$ 連一條長度為 $c_k$ 的有向邊。

注意到，如果 {a1,a2,…,an}\{a_1,a_2,\dots,a_n\}{a1?,a2?,…,an?} 是該差分約束系統的一組解，那么對于任意的常數 $d$，{a1+d,a2+d,…,an+d}\{a_1+d,a_2+d,\dots,a_n+d\}{a1?+d,a2?+d,…,an?+d} 顯然也是該差分約束系統的一組解，因為這樣做差后 $d$ 剛好被消掉。

算法流程

設 $dist[0]=0$ 并向每一個點連一條權重為 $0$ 的邊，跑單源最短路，若圖中存在負環，則給定的差分約束系統無解，否則，$x_i=dist[i]$ 為該差分約束系統的一組解。

例題

#include <bits/stdc++.h>using ll = long long;#ifndef DEBUG
#define debug(x)
#endifconstexpr int inf = 2e9;int main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);int n, m;std::cin >> n >> m;std::vector<std::vector<std::pair<int, int>>> adj(n + 1);for (int i = 0;i < m; i++) {int u, v, c;std::cin >> u >> v >> c;adj[v].push_back({u, c});}for (int i = 1;i <= n; i++) {adj[0].push_back({i, 0});}std::queue<int> q;std::vector<int> cnt(n + 1, 0), w(n + 1, inf);std::vector<bool> st(n + 1, false);q.push(0);w[0] = 0;while (!q.empty()) {auto u = q.front();q.pop();st[u] = false;for (auto [v, c]: adj[u]) {if (w[v] > w[u] + c) {w[v] = w[u] + c;if (!st[v]) {q.push(v);cnt[v]++;if (cnt[v] > n) {std::cout << "NO\n";return 0;}st[v] = true;}}}}for (int i = 1;i <= n; i++) {std::cout << w[i] << " ";}return 0;
}