最短路徑問題（圖論）

1 Floyd

作用：

求圖中所有頂點之間的最短路徑，包括有向圖或者無向圖，權重正負皆可，用來一次性求所有點之間的最短路徑。
思路是通過逐步擴大中間層，使得最短路徑不斷被更新，直到中間層擴大到n位置，最終所求的就是所有節點都有可能經過的最短距離。

原理

遞推公式，F[K][X][Y] 表示頂點x,y中間最多只經過(0,1,2,…k)這些頂點時的最短路徑
三層遍歷，第一層必須為中間層，這樣才會逐步將中間層擴大，如果中間層沒有放在第一層，會導致每個f[x] 實際只會求取一次，結果不正確。
**根據上面實際上需要使用三位數組進行求解，但是可以優化為二維數組，初始狀態時，時候F[X][Y]可能為 “0/實際權重/正無窮”;如果點X，Y直連，則F[X][Y]為實際權重；如果點X==Y,則F[X][Y]=0；如果點X，Y非直連，則F[X][Y] = 正無窮

實際的代碼如下：

for k in range(1, n + 1):for x in range(1, n + 1):for y in range(1, n + 1):f[k][x][y] = min(f[k - 1][x][y], f[k - 1][x][k] + f[k - 1][k][y])

最外層的數組可以省略，優化為如下：

for k in range(1, n + 1):for x in range(1, n + 1):for y in range(1, n + 1):f[x][y] = min(f[x][y], f[x][k] + f[k][y])

詳見 Floyd算法解析

2 Dijsktra算法

作用

是一種單源最短路徑算法，他能找到其中一個點到其他所有點的最短路徑，只支持權重為正的情況，因為Dijkstra算法存在貪心的策略，一旦到某個節點的最短路徑被確定，后續就無法修改。故無法支持權重為負的情，其基本的實現策略為貪心+動態更新，
思路：每一步都是從還未處理的節點當中找到離起點最短的節點，然后嘗試用它來更新其周圍鄰居離起點的最短路徑，這樣一步步擴展，直到找到最短路徑。

實現原理

假設有如下圖結構，求節點A到節點F的最短距離，實現過程如下：

首先準備一個優先隊列，一個最短距離前驅表t1，以及visisted存放是否已經i經訪問過。t1[v] = (d， v1)表示頂點A距離頂點v的最短距離d以及頂點v的前驅節點v1，初始的時候，將頂點A到它自身的距離為0，其他頂點到頂點A的距離為無窮大，前驅節點為空，將（0，A）放到優先隊列中（以第一位距離作為排序的key，小根堆）
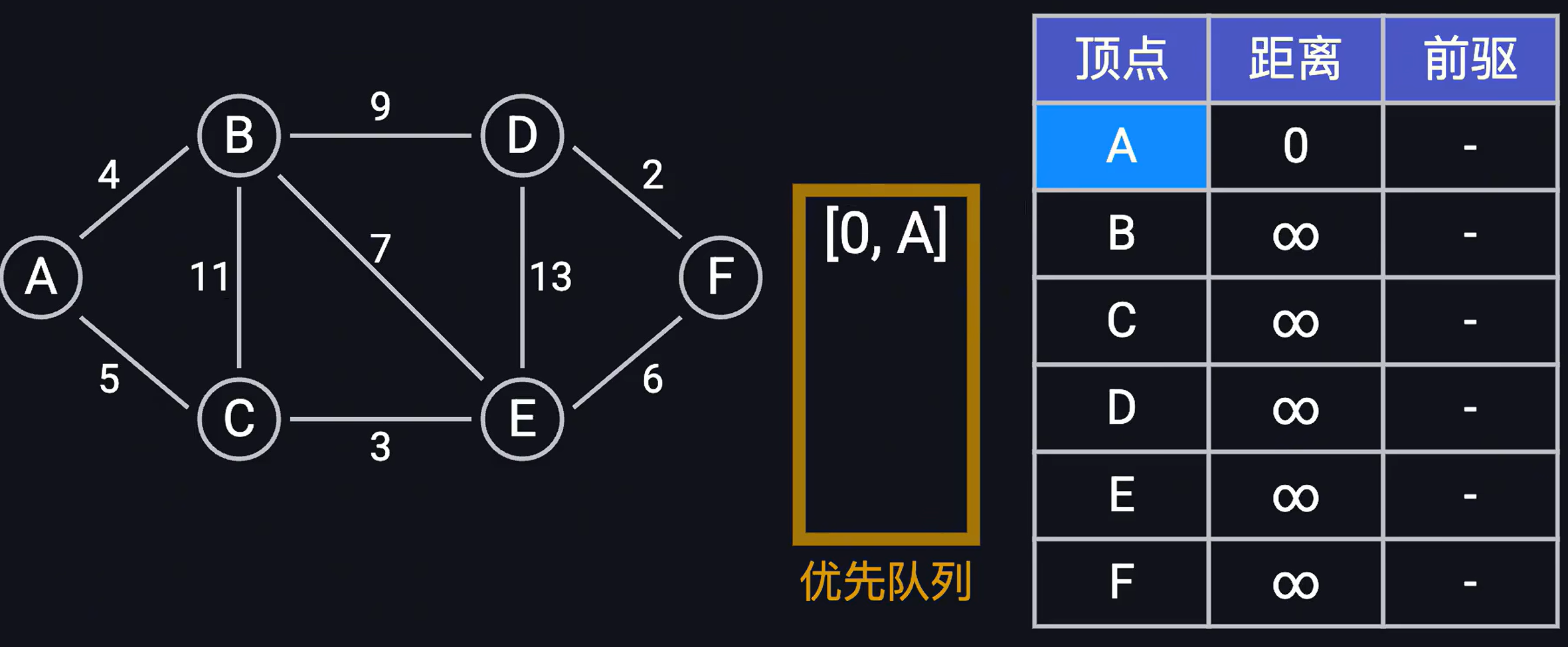
首先從優先隊列中取出首位距離最短的節點信息（0, A），然后依次遍歷頂點A的所有邊（B,C）,將（4, B）,(5,C）放到優先隊列中，同時更新最短距離前驅表，并將頂點A放到visited表，表示下次遍歷到頂點A的時候，直接忽略，具體結果如下:
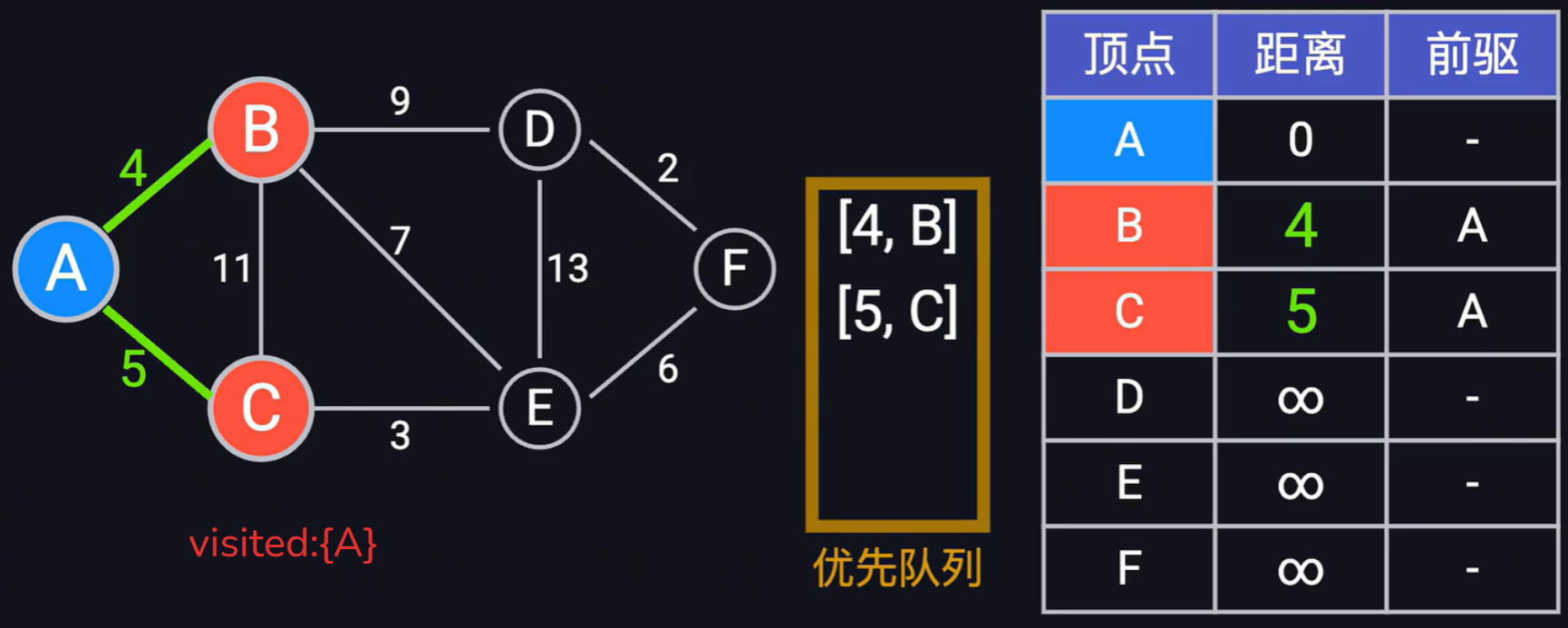
然后再從優先隊列中取出頂點(4, B)信息，依次遍歷B所有的邊（C, D，E）其中A已經被放到visited中，無需再遍歷，遍歷B的邊C的時候，發現權重之和（A->B + B->C =4 + 11 < 5)大于當前表中已經存在的距離，故這里不更新C的距離以及前驅；遍歷邊D的時候，發現(A->B + B-> = 4 + 9 = 13 < 正無窮 )小于當前表中已經存在，更細表中頂點D到A的最短距離為13以及前驅節點為B。
后續的操作與上面一樣，直到優先隊列中的元素被取完在優先隊列中提前碰到目標節點，如果從優先隊列中取出的頂點到A的距離小于表中已經存在的距離或者已經處于visited表中，則直接忽略即可
最后通過得到的最短距離前驅表可以得到頂點A到其他所有節點的最短距離以及對應的路徑
如果只需要求起點到某個終點的最短路徑，則可以在優先隊列中取到目標終點時，可以直接返回，無需再往下處理

備注：最短距離前驅表中前驅信息是用來根據回溯得到目標頂點的最短路徑
代碼實現

def dijkstra(n, source, weights):## weights 列表的每一個元素格式為（n1, n2, w）表示頂點n1->n2的權重為w## n 表示頂點的格式，source表示原頂點## 這里需要將頂點信息都轉化為0,1... n-1的編號# 為求頂點source 到其他頂點的最短距離neighbors = [[] for _ in range(n)]inf = float('inf')edges = [[inf for _ in range(n)] for _ in range(n)]for v1, v2, w in weights:neighbors[v1].append(v2)neighbors[v2].append(v1)edges[v1][v2] = wedges[v2][v1] = wpq = []heapq.heappush(pq, (0, source))visited = set()t1 = {}for i in range(n):t1[i] = (inf, -1)t1[source] = (0, -1)while pq:d, v = heapq.heappop(pq)if d > t1[v][0]:continuevisited.add(v)for p in neighbors[v]:d1 = d + edges[v][p]if p not in visited and (d1 < t1[p][0]):t1[p] = (d1, v)heapq.heappush(pq, (d1, p))return t1if __name__ == '__main__':n = 6source = 0weights = [[0, 1, 4], [0, 2, 5], [1, 2,11], [1, 3, 9], [1, 4, 7], [2, 4, 3], [3, 4, 13], [3, 5, 2], [4, 5, 6]]print(dijkstra(6, 0, weights))

3 Bellman-Ford算法

作用

上面的dijkstra算法只支持權重為正場景，對于有些權值為負的場景需要使用BellmanFord算法，該算法也是求單個頂點到到其余頂點的最短路徑，如果存在負環路徑，則不存在最短路徑
思路：通過不斷的遍歷所有的邊動態的更新到起點的最短距離，不斷地進行松緊操作（迭代），直到n - 1次，確保所有節點到起點均是最短距離。

實現原理

假設有如下圖結構，求節點A到其他節點的最短距離，實現過程如下
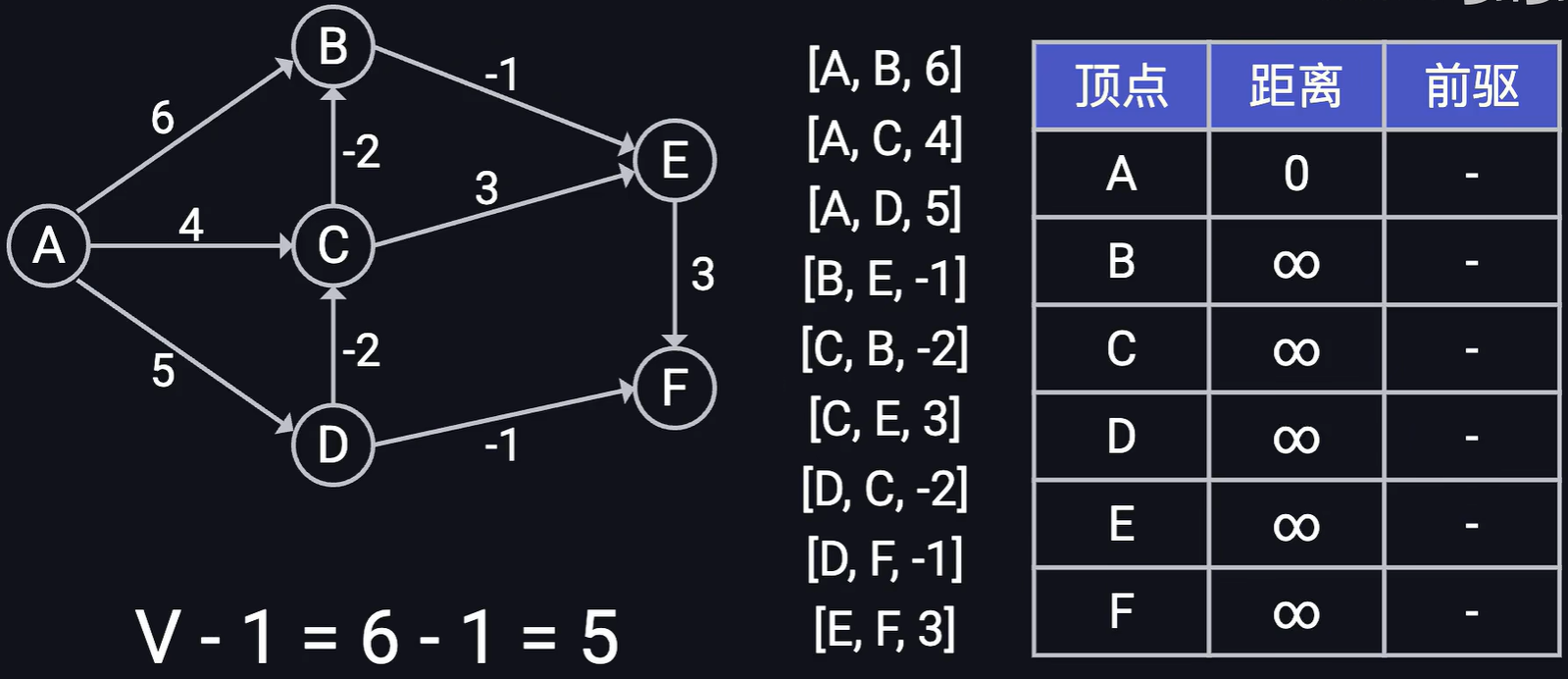
在這里插入圖片描述

首先需要準備一個最短路徑前驅表t1, t1[v] 中包含頂點v到頂點A的最短距離以及頂點v的前驅節點。初始的時候 t1[‘A’] = (0, -1) 其他的t[v] = (正無窮，-1)
然后遍歷所有的邊，每遍歷一個邊(v1, v2)的時候，如果當前節點A到v1的t1[v1][0] + 當前邊的權重w(v1->v2)小于當前t1[v2][0]，則更新v2的最短距離以及前驅節點
t1[v1][0] + w(v1->v2) < t1[v2][0]
上面的步驟最多執行n - 1次，如果中間有一次沒有節點的最短距離需要更新，則說明所有A到所有節點的最短距離已經全部收斂，直接返回。
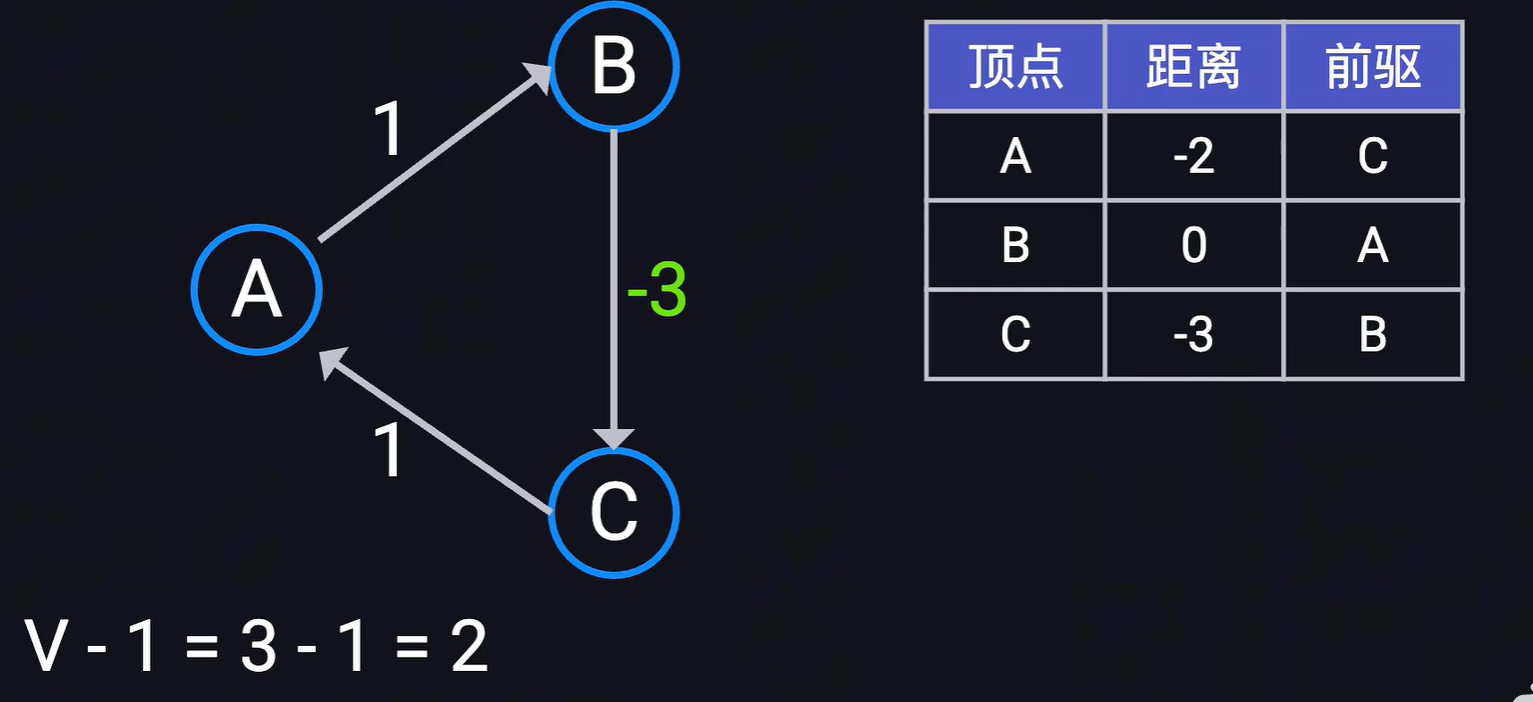
如果上面執行n- 1次，每次均存在節點的最短距離需要更新，則圖中可能存在負權環，所謂負權環就是如下圖所示，隨著遍歷次數的增加，A到C的距離只會越來越小-2， -3， -4等等，此時說明最短路徑，那么只需要再遍歷第n次，看看是否仍存在某個節點的最短路徑被更新，如果被更新，則該節點存在負權環。

def bellmanFord(n, source, weights):## weights 列表的每一個元素格式為（n1, n2, w）表示頂點n1->n2的權重為w## n 表示頂點的格式，source表示原頂點## 這里需要將頂點信息都轉化為0,1... n-1的編號# 為求頂點source 到其他頂點的最短距離t1 = {}inf = float('inf')for i in range(n):t1[i] = (inf, -1)t1[source] = (0, -1)for i in range(n - 1):for v1, v2, w in weights:if (t1[v1][0] + w) < t1[v2][0]:t1[v2] = (t1[v1][0] + w, v1)# make sure weather negative weight loop existflag, v= False, Nonefor v1, v2, w in weights:if (t1[v1][0] + w) < t1[v2][0]:flag, v = True, v2return t1, flag, vif __name__ == '__main__':n = 6source = 0weights = [[0, 1, 6], [0, 2, 4], [0, 3, 5], [1, 4, -1], [2, 1, -2], [2, 4, 3], [3, 2, -2], [3, 5, -1], [4, 5, 3]]print(bellmanFord(6, 0, weights))

4 A* 算法

作用

用來求兩點之間的最短距離，雖然dijkstra算法也能算法圖，但是如果圖中節點的個數非常多，而且邊也很多，dijkstra算法會找到所有的頂點，根據貪心算法進行排除，然找找到最短的距離。
A* 算法與dijkstra算法類似，可以理解為其是基于dijkstra算法優化而來的，不同的是A* 算法則會借助啟發性搜索，避免一些無效節點的搜索。提高計算效率

思路：
對比dijkstra算法，為了因為啟發性搜索，增加一個預估距離與最短距離加在一起，作為優先隊列的key，每次將為

實現原理

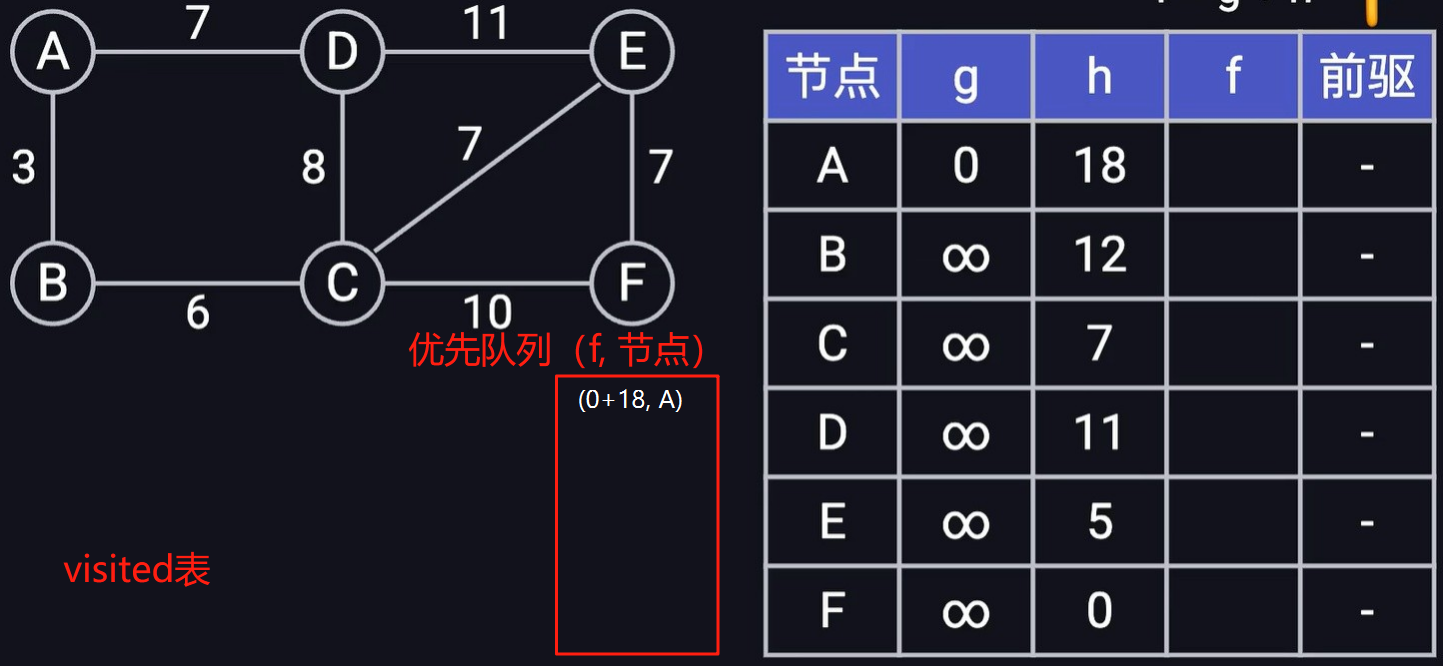
假設有如下圖結構，求節點A到節點F的最短距離，實現過程如下
在這里插入圖片描述

首先準備一個優先隊列，一個最短距離前驅表t1，以及visisted存放是否已經i經訪問過。t1[v] = (g, h ，v2)表示頂點A距離頂點v的最短距離g，頂點A距離頂點v的預估最短距離h，以及頂點v的前驅節點v1，其中(f = g + h)。初始的時候，頂點A到它自身的距離為0，其他頂點到頂點A的距離為無窮大，前驅節點為空，將（d + h，A）放到優先隊列中（以第一位距離d+h 作為排序的key，小根堆）
預估距離，起點到每個頂點都要提前設定一個預估距離，預估距離會作為優先隊列的key的一部分，會影響實際遍歷的順序，預估距離一般由曼哈頓距離或者歐式距離給出，它不作為實際距離，只會影響搜索的方向。可以這樣理解，如果能確認某些節點實際遍歷的時候，大概率是不需要遍歷的，則可以將該節點到起點的預估距離設定的大一些。
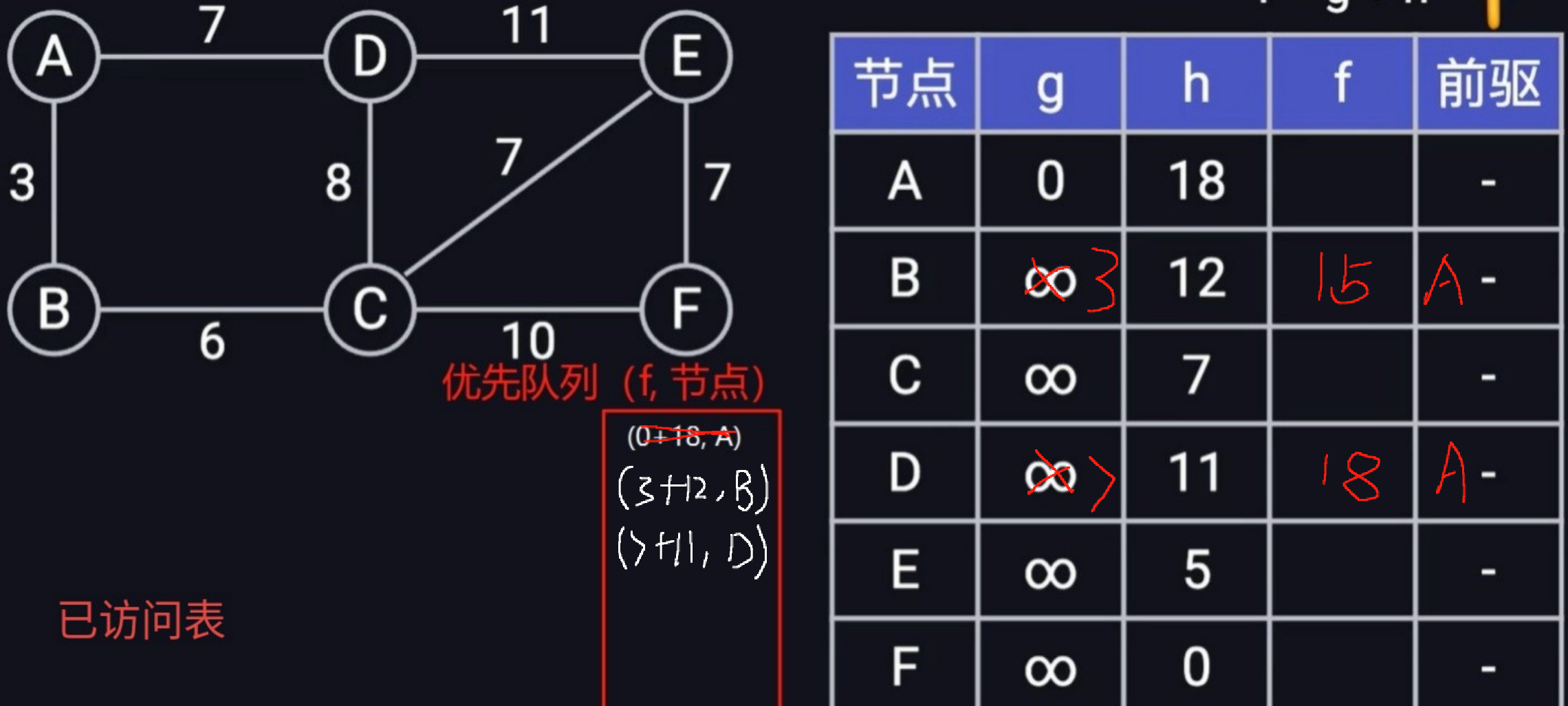
首先從優先隊列中取出首位距離最短的節點信息（18, A），然后依次遍歷頂點A的所有邊（B,D）,將（15, B）,(18,D）放到優先隊列中，同時更新最短距離前驅表中的g項，并將頂點A放到visited表，表示下次遍歷到頂點A的時候，直接忽略，具體結果如下:
然后再從優先隊列中取出頂點(15, B)信息，依次遍歷B所有的邊（C,）其中A已經被放到visited中，無需再遍歷，遍歷B的邊C的時候，發現權重之和（A->B + B->C =3 + 6 < 正無窮)小于當前表中已經存在的距離，故這里需要更新C的距離以及前驅，并將節點（9 + 7, C）放到優先隊列中。
后續的操作與上面一樣，直到優先隊列中的元素被取完在優先隊列中提前碰到目標節點，如果從優先隊列中取出的頂點到A的距離小于表中已經存在的距離或者已經處于visited表中，則直接忽略即可
最后通過得到的最短距離前驅表可以得到頂點A到其他所有節點的最短距離以及對應的路徑
如果只需要求起點到某個終點的最短路徑，則可以在優先隊列中取到目標終點時，可以直接返回，無需再往下處理

def aStar(n, source, weights):## weights 列表的每一個元素格式為（n1, n2, w）表示頂點n1->n2的權重為w## n 表示頂點的格式，source表示原頂點## 這里需要將頂點信息都轉化為0,1... n-1的編號# 為求頂點source 到其他頂點的最短距離neighbors = [[] for _ in range(n)]inf = float('inf')edges = [[inf for _ in range(n)] for _ in range(n)]for v1, v2, w in weights:neighbors[v1].append(v2)neighbors[v2].append(v1)edges[v1][v2] = wedges[v2][v1] = wpq = []g = {0: 18, 1: 12, 2: 7, 3: 11, 4: 5, 5: 0}visited = set()t1 = {}for i in range(n):t1[i] = (inf, g[i], -1)t1[source] = (0, g[source], -1)heapq.heappush(pq, (t1[0][0] + t1[0][0], source))while pq:f, v = heapq.heappop(pq)if f > (t1[v][0] + t1[v][1]) :continuevisited.add(v)for p in neighbors[v]:g1 = t1[v][0] + edges[v][p]if p not in visited and (g1 < t1[p][0]):t1[p] = (g1, t1[p][1], v)heapq.heappush(pq, (g1 + t1[p][1], p))return t1if __name__ == '__main__':n = 6source = 0weights = [[0, 1, 3], [0, 3, 7], [1, 2, 6], [2, 3, 8], [2, 4, 7], [2, 5, 10], [3, 4, 11], [4, 5, 7]]print(aStar(6, 0, weights))