模型選擇與調優：從理論到實戰

1. 引言

在機器學習中，模型選擇與調優是決定模型性能的關鍵步驟。一個好的算法如果參數配置不當，可能表現不如一個簡單模型；而錯誤的評估方法也可能導致“看似很準”，實則泛化能力極差。本文將從模型評估、超參數調優和模型比較三個維度展開，并結合公式、代碼和圖示給出系統性理解。

---

2. 模型評估：為選擇提供依據

2.1 偏差-方差權衡

模型預測誤差可分解為：
$$\mathbb{E}[(y?\hat{f}(x){)}^2]={\text{Bias}}^2+\text{Variance}+{\sigma }^2$$

• Bias（偏差）：模型假設與真實分布的差異。
• Variance（方差）：模型對訓練數據波動的敏感性。
• σ2\sigma^2：不可約誤差。

圖示通常表現為：模型復雜度增加 → 偏差下降、方差上升。最佳點是兩者平衡的位置。

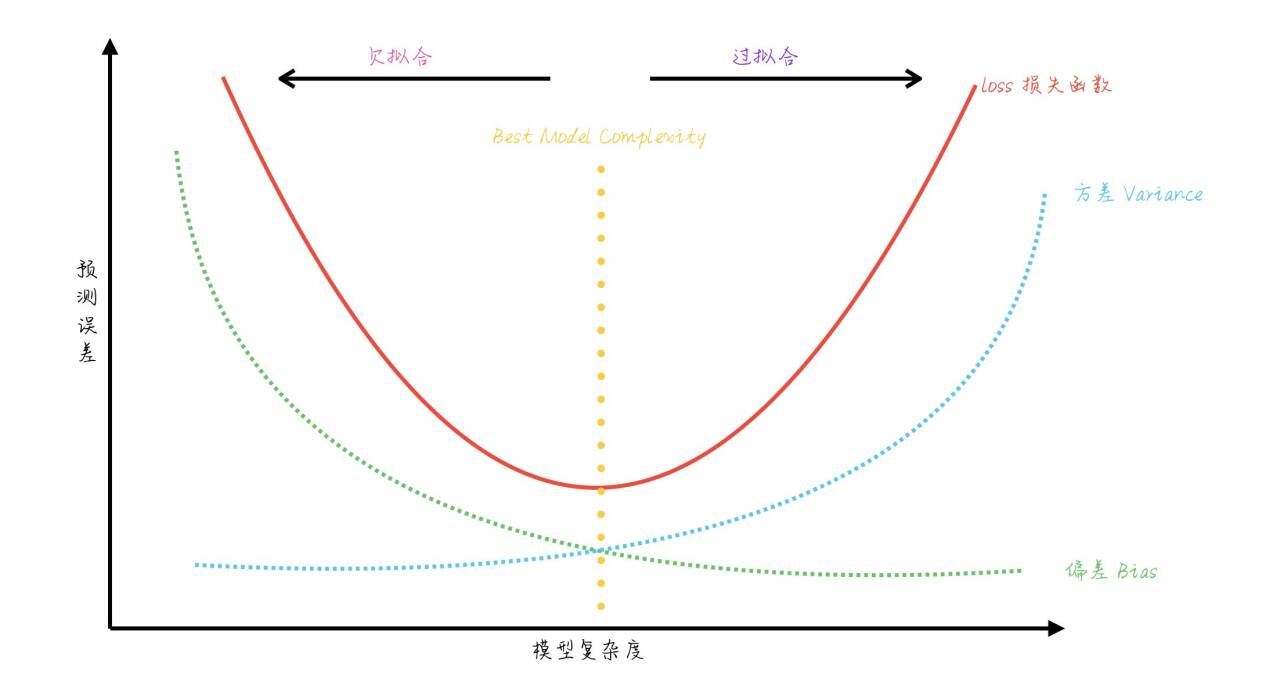
什么是偏差(Bias)? 什么是方差(Variance)?
其實可以套到生活中"準" 跟"確" 這兩個概念，如果用高中軍訓課打靶的經驗來說，那就是：
如果說你打靶打得很精"準"，意味你子彈射中的地方離靶心很近，即Low Bias；
如果說你打靶打得很精"確"，意味你在發射數槍之后這幾槍彼此之間在靶上的距離很近，即Low Variance。
接著下面用一張圖來說明，應該就一目了然了！

---

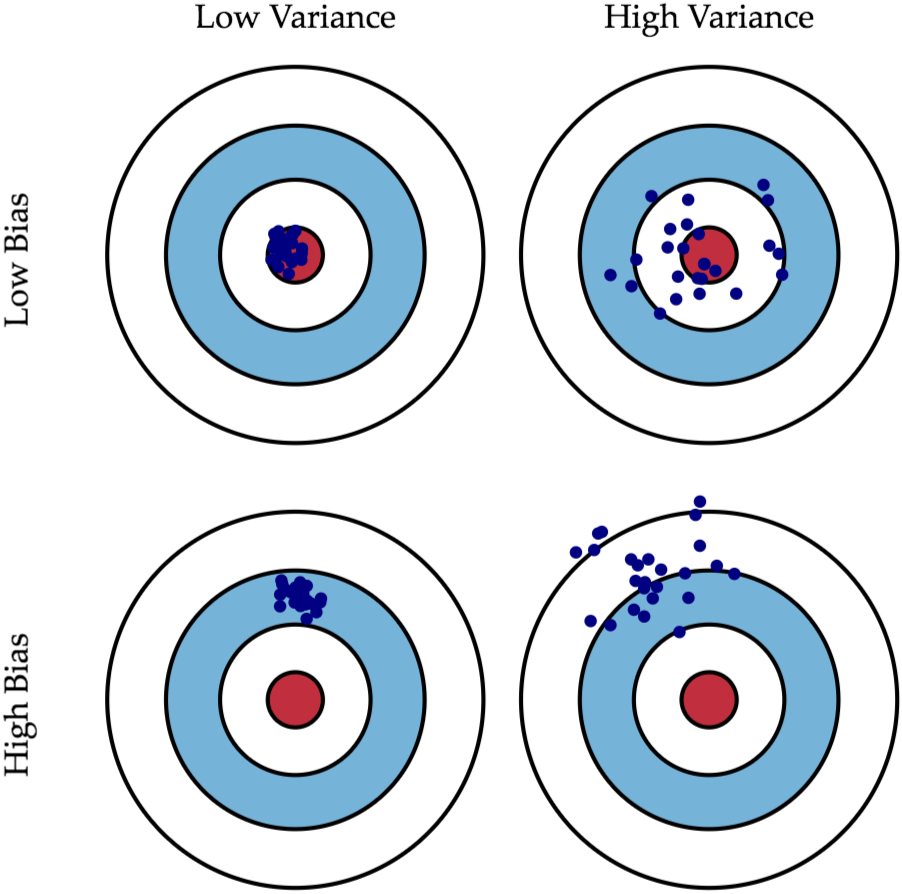
2.2 數據集劃分與分層抽樣

保留交叉驗證Hold-Out（留出法）是最簡單的評估方式：將數據分為訓練集和測試集。但對于類別不平衡問題，普通劃分可能導致訓練或測試集中類別分布偏移。此時應使用 train_test_split 的分層參數：

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, stratify=y, random_state=42
)

• stratify=y：確保分割后各數據集的類別比例與原始數據一致，減少評估偏差。

---

2.3 交叉驗證（Cross-Validation）

不同交叉驗證方法的對比：

1. K-Fold

   • K 折交叉驗證將數據集分割為 K 個互斥的子集（折疊，fold），每次用 K-1 個子集作為訓練集，剩下的 1 個子集作為驗證集，重復 K 次，最終得到 K 個模型的評估結果（如準確率、MSE 等），取平均值作為模型的最終性能指標。

   • 實現：

     from sklearn.model_selection import KFold
     

   • 公式：
     $$\text{CV?Error}=\frac{1}{K}\sum _{i=1}^K{E}_i$$

   • 適用于數據量較大、類別分布均衡的情況。

2. Stratified K-Fold

   • Stratified K-Fold（分層 K 折交叉驗證） 是 K 折交叉驗證的一種改進版本，專門用于分類問題，其核心特點是在劃分數據集時保持每個折中類別比例與原始數據集一致，避免因隨機劃分導致的類別分布失衡，從而更穩健地評估模型性能。

   • 實現：

     from sklearn.model_selection import StratifiedKFold
     

3. Leave-One-Out (LOO)

   • 每次只留一個樣本作為驗證，其余樣本作為訓練。
   • 優點：幾乎無偏估計。
   • 缺點：計算量大、方差高。

4. Hold-Out

   • 單次劃分，計算效率高，但結果波動較大。

K 折交叉驗證的作用不是“提高泛化性”，而是更穩定、無偏地估計泛化誤差。調參過程中，它幫助選擇在新數據上表現最好的模型。

代碼示例：

from sklearn.datasets import load_wine
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import KFold
from sklearn.metrics import accuracy_score
import numpy as np# 1. 加載數據
X, y = load_wine(return_X_y=True)# 2. 標準化數據
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 3. 創建KFold對象
kfold = KFold(n_splits=5, shuffle=True, random_state=42)# 4. 進行交叉驗證
scores = []
for train_idx, test_idx in kfold.split(X_scaled):X_train, X_test = X_scaled[train_idx], X_scaled[test_idx]y_train, y_test = y[train_idx], y[test_idx]# 訓練模型knn = KNeighborsClassifier(n_neighbors=5)knn.fit(X_train, y_train)# 預測并計算準確率y_pred = knn.predict(X_test)score = accuracy_score(y_test, y_pred)scores.append(score)# 5. 輸出結果
print("每折的準確率：", scores)
print("平均準確率：", np.mean(scores))
print("標準差：", np.std(scores))

輸出結果如下：

每折的準確率： [0.9444444444444444, 0.9444444444444444, 0.9722222222222222, 0.9142857142857143, 0.9714285714285714]
平均準確率： 0.9493650793650794
標準差： 0.02139268011280184

---

2.4 信息準則（AIC / BIC）

對于概率模型，可使用信息準則進行模型選擇：

• AIC（Akaike Information Criterion）：
  $$\text{AIC}=2k?2\ln (L)$$

  • $k$：模型參數數量
  • $L$：似然函數最大值
  • 目標：懲罰參數數量，鼓勵較好擬合。

• BIC（Bayesian Information Criterion）：
  $$\text{BIC}=k\ln (n)?2\ln (L)$$

  • $n$：樣本數量
  • 與 AIC 區別：BIC 對模型復雜度懲罰更強，更傾向選擇簡單模型。

功能總結：

• AIC 偏好泛化能力強的模型。
• BIC 偏好更簡單、更保守的模型。
• 二者都基于最大似然估計，適用于概率模型（如回歸、時間序列）。

---

3. 超參數調優：讓模型更好

3.1 網格搜索 (Grid Search)

窮舉所有組合，計算成本高但適合小搜索空間：

from sklearn.model_selection import GridSearchCV
param_grid = {'n_neighbors': [3,5,7], 'weights': ['uniform','distance']}
grid = GridSearchCV(KNeighborsClassifier(), param_grid, cv=5)
grid.fit(X_train, y_train)
print(grid.best_params_, grid.best_score_)

weights='uniform'（默認值）：等權重

• 含義：所有 K 個鄰居的投票權重相同，預測結果由 “多數鄰居的類別” 決定（簡單多數投票）。

weights='distance'：距離加權

• 含義：鄰居的權重與其到待預測樣本的距離成反比 ——距離越近的鄰居，權重越大，對預測結果的影響越強。

3.2 隨機搜索 (Randomized Search)

隨機采樣部分參數組合：
$$P(\text{找到最優解})=1?(1?p{)}^n$$
（其中$p$ 為采樣一次命中最優區域的概率，$n$ 為采樣次數。）

3.3 貝葉斯優化 (Bayesian Optimization)

利用高斯過程或樹模型擬合“超參數 → 評分”的函數，通過采集函數（如期望改進 EI）智能選擇下一步采樣位置。

---

4. 模型選擇：如何最終定奪

4.1 集成學習的思路

• Bagging：降低方差（隨機森林）。
• Boosting：降低偏差（XGBoost）。
• Stacking：綜合多模型優勢。

4.2 評估指標（詳細公式）

分類任務：

• 準確率：
  $$\text{Accuracy}=\frac{TP+TN}{TP+FP+TN+FN}$$

• 精確率（Precision）：
  $$\text{Precision}=\frac{TP}{TP+FP}$$

• 召回率（Recall）：
  $$\text{Recall}=\frac{TP}{TP+FN}$$

• F1 分數：
  $$F1=2?\frac{\text{Precision}?\text{Recall}}{\text{Precision}+\text{Recall}}$$

• AUC（ROC 曲線下面積）：衡量分類器對正負樣本排序能力。

  這個鏈接有個在線實驗可以幫助理解：
  Google實驗案例
  

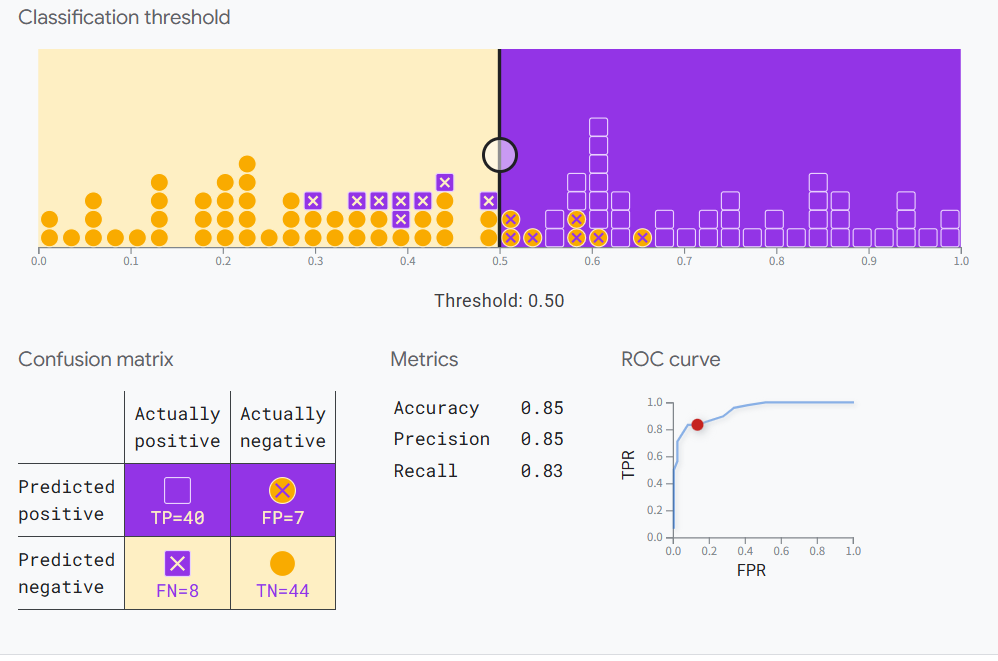
回歸任務：

• 均方誤差 (MSE)：
  $$\text{MSE}=\frac{1}{n}\sum _{i=1}^n(y_i?{\hat{y}}_i{)}^2$$

• 平均絕對誤差 (MAE)：
  $$\text{MAE}=\frac{1}{n}\sum _{i=1}^n|y_i?{\hat{y}}_i|$$

• 決定系數 (R2)：
  $$R^2=1?\frac{\sum (y_i?{\hat{y}}_i{)}^2}{\sum (y_i?\bar{y}{)}^2}$$

---

5. 實戰案例：以 KNN 和隨機森林為例

1. 劃分數據集并進行標準化

2. 使用 Stratified K-Fold 進行評估

3. 分別通過 Grid Search 和 Random Search 調參

4. 對比最佳模型性能（表格+曲線）

   import numpy as np
   import pandas as pd
   import matplotlib.pyplot as plt
   from sklearn.datasets import make_classification
   from sklearn.model_selection import train_test_split, StratifiedKFold, GridSearchCV, RandomizedSearchCV
   from sklearn.preprocessing import StandardScaler
   from sklearn.neighbors import KNeighborsClassifier
   from sklearn.ensemble import RandomForestClassifier
   from sklearn.pipeline import Pipeline
   from scipy.stats import randint# 1. 加載數據
   data = make_classification(n_samples=1000, n_features=20, n_informative=10, n_redundant=5,n_classes=3, n_clusters_per_class=1, random_state=42
   )
   X, y = data
   print(f"數據集特征數: {X.shape[1]}, 樣本數: {X.shape[0]}, 類別數: {len(np.unique(y))}")# 2. 分層劃分訓練集和測試集（保持類別比例）
   X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, stratify=y, random_state=42
   )# 3. 定義分層K折交叉驗證（適合分類問題）
   cv = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)# 4. KNN - 網格搜索（KNN需要標準化）
   knn_pipe = Pipeline([('scaler', StandardScaler()),  # KNN對特征尺度敏感，必須標準化('knn', KNeighborsClassifier())
   ])
   param_knn = {'knn__n_neighbors': [3, 5, 7, 9],  # 增加參數范圍'knn__weights': ['uniform', 'distance']
   }
   grid_knn = GridSearchCV(estimator=knn_pipe,param_grid=param_knn,cv=cv,scoring='accuracy',n_jobs=-1,  # 使用所有可用CPUverbose=1  # 顯示調參過程
   )
   grid_knn.fit(X_train, y_train)# 5. 隨機森林 - 隨機搜索（隨機森林不需要標準化）
   rf_pipe = Pipeline([# 移除StandardScaler，隨機森林對特征尺度不敏感('rf', RandomForestClassifier(random_state=42))
   ])
   param_rf = {'rf__n_estimators': randint(50, 200),  # 增加參數范圍'rf__max_depth': randint(3, 15),'rf__min_samples_split': randint(2, 10),'rf__min_samples_leaf': randint(1, 5)  # 增加葉子節點參數
   }
   random_rf = RandomizedSearchCV(estimator=rf_pipe,param_distributions=param_rf,n_iter=20,  # 增加搜索迭代次數cv=cv,scoring='accuracy',n_jobs=-1,random_state=42,verbose=1
   )
   random_rf.fit(X_train, y_train)# 6. 性能對比表格
   results = pd.DataFrame({'模型': ['KNN(網格搜索)', '隨機森林(隨機搜索)'],'最佳參數': [grid_knn.best_params_, random_rf.best_params_],'交叉驗證準確率': [f"{grid_knn.best_score_:.4f}", f"{random_rf.best_score_:.4f}"],'測試集準確率': [f"{grid_knn.score(X_test, y_test):.4f}", f"{random_rf.score(X_test, y_test):.4f}"]
   })
   print("\n模型性能對比:")
   print(results)# 7. 可視化 - KNN超參數(n_neighbors)與準確率關系
   plt.rcParams['font.sans-serif'] = ['SimHei']  # 顯示中文
   plt.rcParams['axes.unicode_minus'] = False    # 顯示負號
   plt.figure(figsize=(10, 6))# 提取網格搜索結果
   mean_scores = grid_knn.cv_results_['mean_test_score']
   params = grid_knn.cv_results_['params']# 按權重分組繪制
   for weight in ['uniform', 'distance']:# 篩選當前權重的結果scores = [mean_scores[i] for i, p in enumerate(params) if p['knn__weights'] == weight]n_neighbors = [p['knn__n_neighbors'] for i, p in enumerate(params) if p['knn__weights'] == weight]plt.plot(n_neighbors, scores, marker='o', label=f'權重={weight}')plt.xlabel('近鄰數量(n_neighbors)')
   plt.ylabel('交叉驗證準確率')
   plt.title('KNN不同近鄰數量與權重的性能對比')
   plt.legend()
   plt.grid(alpha=0.3)
   plt.tight_layout()
   plt.show()# 8. 輸出最佳模型在測試集上的表現
   print("\nKNN最佳模型測試集準確率:", grid_knn.score(X_test, y_test))
   print("隨機森林最佳模型測試集準確率:", random_rf.score(X_test, y_test))

   數據集特征數: 20, 樣本數: 1000, 類別數: 3
   Fitting 5 folds for each of 8 candidates, totalling 40 fits
   Fitting 5 folds for each of 20 candidates, totalling 100 fits模型性能對比:模型                                               最佳參數 交叉驗證準確率  \
   0   KNN(網格搜索)  {'knn__n_neighbors': 7, 'knn__weights': 'dista...  0.9262   
   1  隨機森林(隨機搜索)  {'rf__max_depth': 9, 'rf__min_samples_leaf': 1...  0.9287   測試集準確率  
   0  0.9450  
   1  0.9200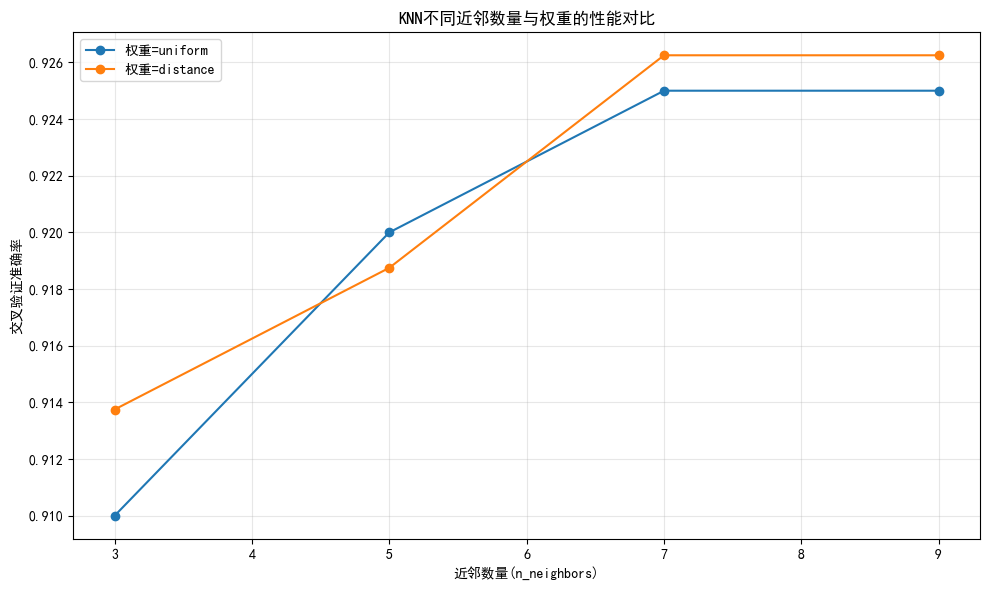
   

   

---

6. 總結與建議

• 分層抽樣在類別不平衡下必不可少。
• K 折交叉驗證是為了更穩定地估計泛化誤差，而非直接“提高泛化性”。
• AIC/BIC更適用于概率模型；交叉驗證適合通用機器學習場景。
• 實戰中可結合隨機搜索 + 貝葉斯優化以降低計算成本。
• 評估指標需根據業務目標選取，而非盲目追求單一指標。

---