目錄
一、空域濾波基礎
一、空域濾波的基本概念
二、空域濾波的數學原理
三、空域濾波器的分類與典型示例
(一)線性濾波器(Linear Filter)
(二)非線性濾波器(Non-linear Filter)
中值濾波(Median Filter)
最大值 / 最小值濾波
四、空域濾波的應用場景
五、空域濾波的關鍵參數與影響
濾波器大小
權重分布
六、空域與頻域濾波的對比
七、總結
二、平滑空間濾波器
平滑空間濾波器:去噪與模糊的核心工具
1. 定義與本質
2. 典型濾波器及原理
3. 應用場景
三、銳化空間濾波器
銳化空間濾波器:邊緣增強與細節提取
1. 定義與本質
2. 典型濾波器及原理
3. 應用場景
四、平滑與銳化的核心區別對比?編輯
選擇策略:何時用平滑?何時用銳化?
五、技術深層解析:為什么這些濾波器能實現對應效果?
六、總結:平滑與銳化的辯證關系
五、題目
1、下面的濾波器哪些可作為圖像平滑濾波器,哪些可作為圖像銳化濾波器?為什么?
?平滑濾波器(低通濾波)特點
銳化濾波器(高通濾波)特點
解:?
2、問題1+問題2
問題1:以下兩個濾波器屬于平滑濾波器還是銳化濾波器?為什么?
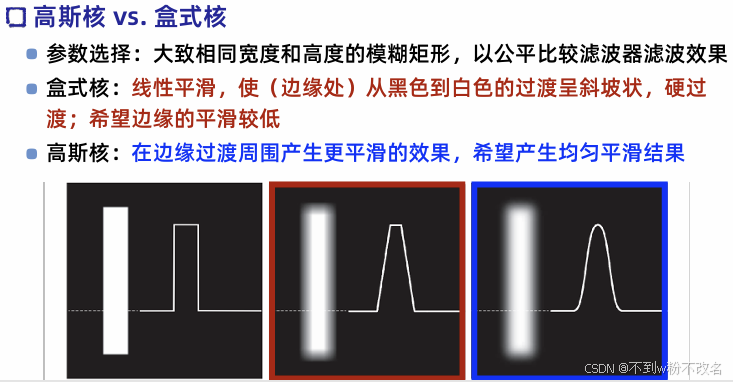
問題2:下面2個高斯濾波器對圖像平滑,哪個濾波器使圖像平滑后更模糊?為什么?
觀察法(定性分析)
計算法(定量分析):通過離散統計方差估算標準差??
一、空域濾波基礎
一、空域濾波的基本概念
空域濾波(Spatial Filtering)?是圖像處理中最基礎的操作之一,其核心思想是通過對圖像像素及其鄰域進行局部運算來修改圖像的像素值。與頻域濾波(基于傅里葉變換處理頻率成分)不同,空域濾波直接在圖像的空間域上進行操作,主要通過濾波器(Filter)?或模板(Kernel)?實現。
二、空域濾波的數學原理
-
核心操作:卷積(Convolution)
空域濾波的本質是濾波器與圖像的卷積運算。對于一幅圖像?f(x,y)?和一個大小為?m×n?的濾波器?h(x,y),輸出圖像?g(x,y)?的計算方式為: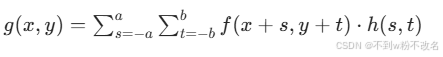
其中?(a,b)?為濾波器中心坐標,通常取?m=2a+1,n=2b+1(奇數大小便于定位中心)。
-
濾波器滑動過程
- 濾波器從圖像左上角開始,以像素為步長逐行滑動。
- 每個位置上,濾波器中心與當前像素對齊,計算鄰域像素與濾波器權重的乘積和,作為輸出像素值。
三、空域濾波器的分類與典型示例
(一)線性濾波器(Linear Filter)
基于線性加權求和,滿足疊加原理,主要用于平滑去噪或模糊處理。
| 濾波器類型 | 核心特點 | 典型模板(3×3) | 應用場景 |
|---|---|---|---|
| 均值濾波 | 簡單平均鄰域像素值,降低噪聲但模糊邊緣。 | ?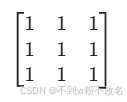 | 去除高斯噪聲、圖像模糊 |
| 高斯濾波 | 基于高斯分布加權,中心像素權重高,邊緣權重低,平滑效果更自然。 | ?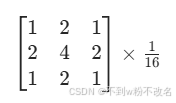 | 圖像去噪、高斯模糊、邊緣檢測前預處理 |
| 加權平均濾波 | 自定義權重,可針對特定方向或特征增強,如邊緣保持濾波(EPF)。 | 自定義權重矩陣,如邊緣方向加權 | 保留細節的同時去噪 |
(二)非線性濾波器(Non-linear Filter)
不滿足線性疊加原理,通過排序、取極值等操作處理像素,更適合去除脈沖噪聲(如椒鹽噪聲)。
-
中值濾波(Median Filter)
- 原理:將鄰域像素值排序后取中值,替換中心像素。
- 模板示例(3×3):將 9 個像素值排序,取第 5 大的值。
- 特點:有效去除椒鹽噪聲,同時保留邊緣(相比均值濾波)。
-
最大值 / 最小值濾波
- 最大值濾波:取鄰域最大值,增強亮區域,適用于突出亮點(如檢測光斑)。
- 最小值濾波:取鄰域最小值,增強暗區域,適用于去除亮噪聲(如鹽噪聲)。
四、空域濾波的應用場景
圖像去噪
- 線性濾波(如高斯濾波)適合處理高斯噪聲(連續分布噪聲)。
- 非線性濾波(如中值濾波)適合處理脈沖噪聲(離散噪聲點)。
邊緣檢測預處理
高斯濾波常用于模糊圖像,減少噪聲對邊緣檢測的干擾(如 Canny 算子前的高斯平滑)。特征增強與抑制
- 銳化濾波(如拉普拉斯算子)通過增強像素梯度突出邊緣,公式為:
其中??2f?為拉普拉斯算子,典型模板:圖像模糊與降采樣
均值濾波或高斯濾波常用于圖像縮放前的預處理,減少鋸齒效應。
五、空域濾波的關鍵參數與影響
-
濾波器大小
- 小尺寸(3×3、5×5):保留細節,去噪能力弱。
- 大尺寸(7×7 及以上):去噪能力強,但過度模糊圖像,丟失細節。
-
權重分布
- 線性濾波器的權重決定了對不同位置像素的敏感度(如高斯濾波的中心權重更高)。
- 非線性濾波器的操作邏輯(如排序取中值)決定了對異常值的魯棒性。
六、空域與頻域濾波的對比
| 維度 | 空域濾波 | 頻域濾波 |
|---|---|---|
| 處理空間 | 直接在像素空間操作,直觀易理解。 | 基于傅里葉變換,處理頻率成分。 |
| 計算復雜度 | 復雜度低,適合實時處理(尤其小模板)。 | 需進行傅里葉變換,計算開銷大。 |
| 典型應用 | 去噪、邊緣檢測、局部特征增強。 | 全局頻率成分調整(如高通 / 低通濾波)。 |

七、總結
空域濾波是圖像處理的基石,通過設計不同的濾波器模板,可實現去噪、模糊、銳化等多種效果。理解其數學原理(如卷積運算)和濾波器特性(線性 / 非線性),有助于根據實際需求(如圖像噪聲類型、處理目標)選擇合適的濾波方法。實際應用中,常需結合濾波器大小、權重設計與多次實驗,平衡去噪效果與細節保留。
二、平滑空間濾波器
平滑空間濾波器:去噪與模糊的核心工具
1. 定義與本質
平滑濾波通過鄰域像素加權平均減少局部像素值波動,本質是低通濾波(抑制高頻,保留低頻)。
作用效果:去除圖像中的噪聲(如高斯噪聲、椒鹽噪聲),模糊細節(如平滑紋理、弱化邊緣)。
2. 典型濾波器及原理
| 濾波器類型 | 原理描述 | 公式 / 模板示例 | 特點與應用場景 |
|---|---|---|---|
| 均值濾波 | 鄰域像素值算術平均,權重均勻分布。 | 3×3?模板: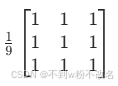 | 簡單高效,但易模糊邊緣,適合輕度高斯噪聲。 |
| 高斯濾波 | 基于高斯函數加權,中心像素權重最大,離中心越遠權重越小。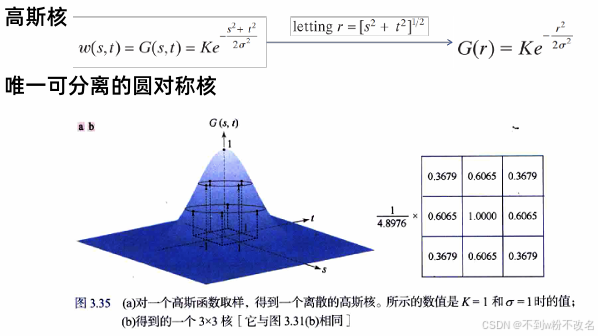 | 二維高斯核: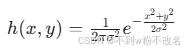 | 平滑效果更自然,可通過調整 σ 控制模糊程度,常用于圖像預處理(如 CNN 前的降采樣)。 |
| 中值濾波 | 取鄰域像素值的中值替代中心像素,屬于非線性濾波。 | 操作:排序鄰域像素,取中間值。 | 對椒鹽噪聲(脈沖噪聲)效果極佳,能保護邊緣(因不依賴加權平均)。 |
| 雙邊濾波 | 同時考慮像素空間距離和灰度差異的加權平均,屬于保邊平滑。 | 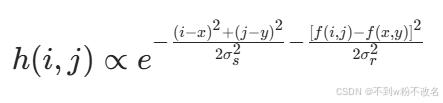 ? ? | 保留邊緣的同時去除噪聲,常用于人像磨皮(保留輪廓,平滑皮膚)。 |
3. 應用場景
- 噪聲去除:醫學影像(CT/MRI)去噪、衛星圖像去云霧干擾。
- 圖像預處理:降低圖像分辨率前的平滑,避免鋸齒效應(如雙線性插值前的高斯濾波)。
- 風格化處理:油畫效果、卡通化中的背景模糊。
三、銳化空間濾波器
銳化空間濾波器:邊緣增強與細節提取
1. 定義與本質
銳化濾波通過增強像素梯度變化突出邊緣和細節,本質是高通濾波(抑制低頻,保留高頻)。
作用效果:使模糊圖像變清晰,強化物體輪廓(如文字邊緣、細胞邊界),提升圖像對比度。
2. 典型濾波器及原理
| 濾波器類型 | 原理描述 | 公式 / 模板示例 | 特點與應用場景 |
|---|---|---|---|
| 梯度算子(一階導數) | 通過計算像素灰度梯度值增強邊緣,常用算子包括 Sobel、Prewitt、Roberts。 | Sobel 算子(x 方向): | 對水平 / 垂直邊緣敏感,輸出為梯度幅值,常用于邊緣檢測(如 Canny 算法前處理)。 |
| 拉普拉斯算子(二階導數) | 計算像素鄰域的二階導數,邊緣處二階導數值為零(過零點),用于定位邊緣位置。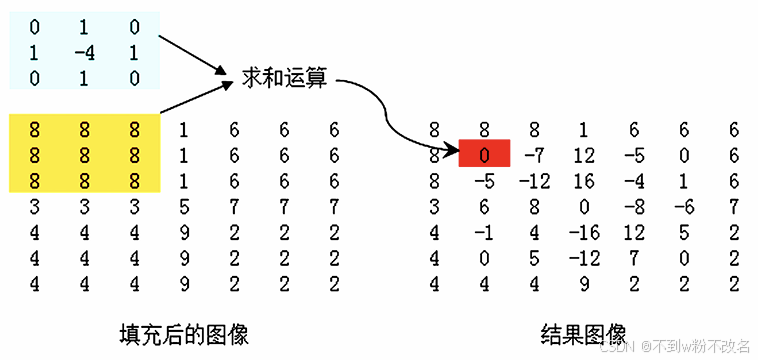 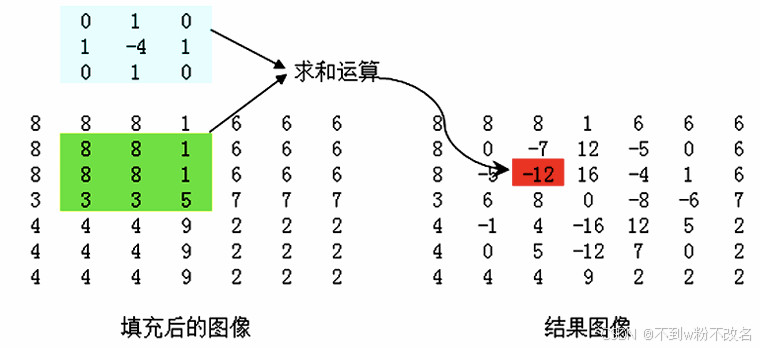 | 4×4?拉普拉斯模板: | 對噪聲敏感(因強化高頻),常與原圖疊加使用(銳化 = 原圖 + 拉普拉斯結果)。 |
| 非銳化掩模(Unsharp Mask) | 先模糊圖像,再用原圖減去模糊圖,得到高頻細節增強的結果。 | 流程: 1. 高斯模糊? 2. 掩模 3. 銳化結果?fsharp?=f+k?mask | 效果自然,廣泛用于攝影后期(如風光片增強巖石紋理)。 |
| 高提升濾波(High Boost Filter) | 非銳化掩模的增強版,通過調整權重突出特定頻率成分。 | 公式: | 可自定義增強強度,適合需要突出微小細節的場景(如顯微圖像)。 |
3. 應用場景
- 邊緣檢測:醫學圖像中的器官輪廓提取、文檔掃描中的文字邊緣強化。
- 圖像增強:老照片修復(銳化模糊的人像邊緣)、遙感圖像中的地形輪廓突出。
- 特征提取:計算機視覺中預處理步驟(如車牌識別前的邊緣增強)。
四、平滑與銳化的核心區別對比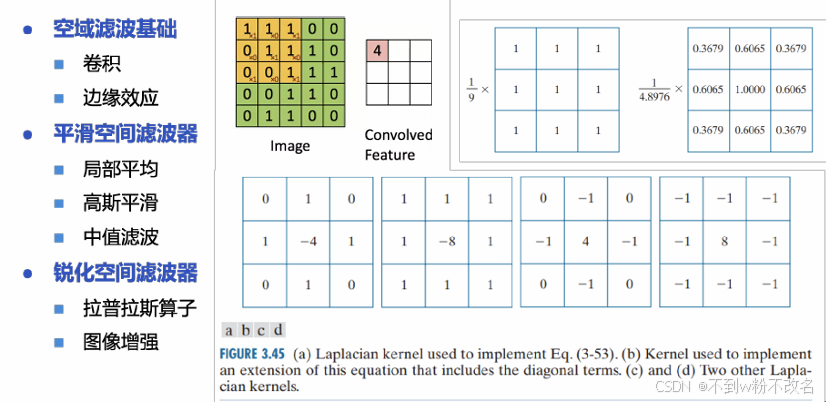
| 維度 | 平滑濾波 | 銳化濾波 |
|---|---|---|
| 數學本質 | 鄰域加權平均(積分操作) | 梯度計算(微分操作) |
| 頻域特性 | 低通濾波器(抑制高頻,保留低頻) | 高通濾波器(抑制低頻,保留高頻) |
| 對噪聲的影響 | 減少噪聲(但可能模糊細節) | 放大噪聲(因噪聲多為高頻成分) |
| 邊緣處理 | 弱化邊緣,使邊緣過渡平滑 | 強化邊緣,使邊緣更陡峭 |
| 典型算子示例 | 均值、高斯、中值 | 拉普拉斯、Sobel、非銳化掩模 |
| 視覺效果 | 圖像變模糊,噪聲減少 | 圖像變清晰,細節更突出 |
選擇策略:何時用平滑?何時用銳化?
1. 優先使用平滑濾波的場景
- 圖像存在明顯噪聲(如拍攝時的 ISO 過高導致的噪點)。
- 需要去除小尺度紋理(如背景虛化),突出主體。
- 預處理步驟中需要降低圖像分辨率(先平滑再縮放可減少鋸齒)。
2. 優先使用銳化濾波的場景
- 圖像因對焦不準或運動模糊導致細節模糊。
- 需要從圖像中提取邊緣特征(如物體識別、OCR 文字識別)。
- 增強圖像的視覺沖擊力(如廣告圖片中的產品細節強化)。
3. 組合使用案例
- 去噪 + 銳化流程:先中值濾波去除椒鹽噪聲,再用非銳化掩模恢復細節(如天文圖像處理)。
- 保邊處理:雙邊濾波(平滑噪聲)+ 拉普拉斯銳化(增強保留的邊緣),用于醫學圖像的器官分割前處理。
五、技術深層解析:為什么這些濾波器能實現對應效果?
1. 平滑濾波的數學原理
- 均值濾波:通過鄰域平均降低像素值方差,公式表達為:
鄰域噪聲通常是隨機高頻信號,平均后被弱化。
- 高斯濾波:權重符合高斯分布,離中心越近的像素影響越大,等效于對不同頻率成分按高斯函數衰減,數學上可證明高斯濾波是唯一的 “各向同性” 平滑操作(無方向偏好)。
2. 銳化濾波的數學原理
- 一階導數(梯度):邊緣處灰度值突變,梯度幅值大,因此梯度算子可定位邊緣位置,如 Sobel 算子通過橫向和縱向模板分別計算梯度:
- 二階導數(拉普拉斯):邊緣處二階導數為零,通過檢測過零點可更精確地定位邊緣,同時拉普拉斯算子的輸出與原圖疊加時,會在邊緣處產生 “過沖” 和 “下沖”,增強視覺對比度:
六、總結:平滑與銳化的辯證關系
- 互補性:平滑和銳化是圖像處理中的 “對立統一”—— 平滑去除不必要的高頻(噪聲),銳化增強需要的高頻(邊緣)。
- 應用關鍵:根據噪聲類型和目標特征選擇濾波器,例如:
- 高斯噪聲→高斯濾波(線性平滑);
- 椒鹽噪聲→中值濾波(非線性平滑);
- 弱邊緣目標→拉普拉斯銳化(二階導數增強);
- 強邊緣目標→Sobel 梯度(一階導數定位)。
實際應用中常結合兩者,如 “先平滑去噪,再適度銳化恢復細節”,或通過參數調整(如高斯濾波的 σ、銳化的權重 k)平衡去噪與細節保留。
五、題目
1、下面的濾波器哪些可作為圖像平滑濾波器,哪些可作為圖像銳化濾波器?為什么?
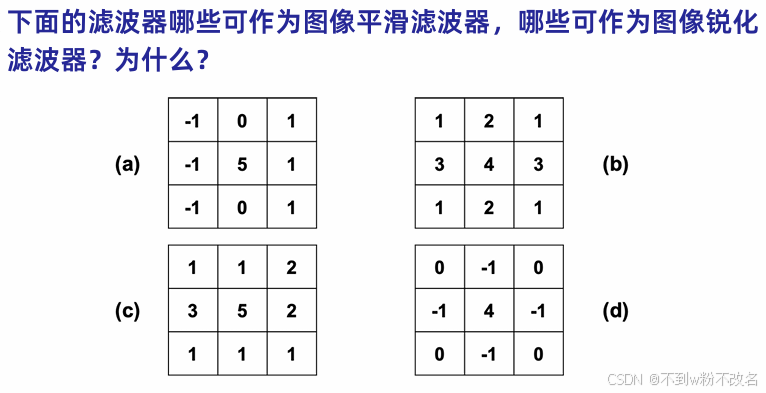
?平滑濾波器(低通濾波)特點
數值均勻:所有值相近(如均值濾波器);
無正負交替:通常全為正數,中心值一般較大,鄰近值較小且正。正數為平滑的必要條件。
銳化濾波器(高通濾波)特點
正負交替:通過正負值相乘增強邊緣對比(例如,邊緣像素與背景的差異被放大);
中心權重高:突出當前像素與鄰域的差異,鄰域像素為負或較小正數。
解:?
 ?
?
 ?
?
2、問題1+問題2
問題1:以下兩個濾波器屬于平滑濾波器還是銳化濾波器?為什么?
都是平滑,都是正數,總和>9,模糊效果明顯
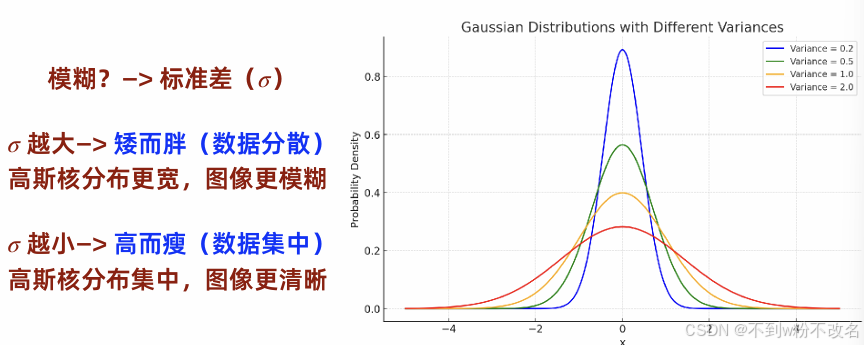
問題2:下面2個高斯濾波器對圖像平滑,哪個濾波器使圖像平滑后更模糊?為什么?
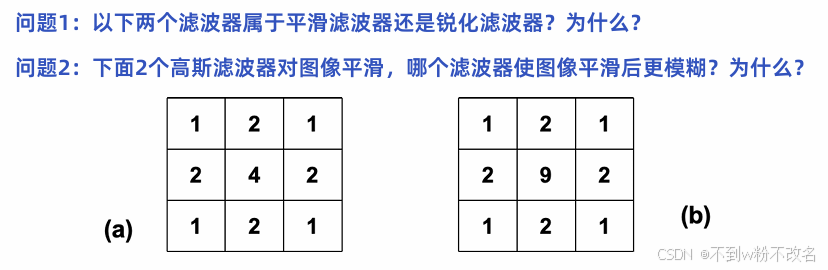
σ越大->高斯核分布更寬,圖像模糊+
σ越小->高斯核分布集中,圖像模糊 -
觀察法(定性分析)
(a)中央元素為4,整體權重之和為:1+2+1+2+4+2+1+2+1=16
(b)中央元素為9,整體權重之和為:1+2+1+2+9+2+1+2+1=21
【中央值9相對于周圍值占比更大,意味著它更傾向于保留當前像素本身的信息,對鄰域的平滑作用較弱。?】
計算法(定量分析):通過離散統計方差估算標準差
?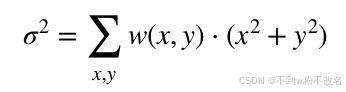
![]()
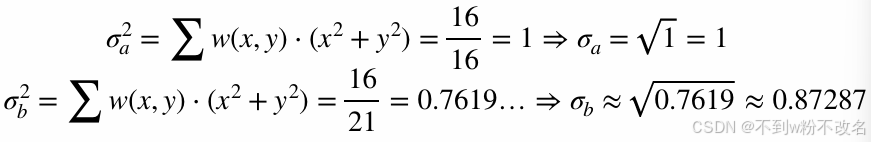
a更模糊,原因見上分析


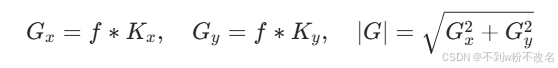
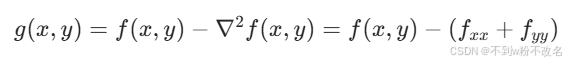












)






 ls2k1000 openwrt)