堅持用 清晰易懂的圖解 + 多語言代碼，讓每道題變得簡單！
呆頭個人主頁詳情
呆頭個人Gitee代碼倉庫
呆頭詳細專欄系列
座右銘： “不患無位，患所以立。”

---

前言

🚀 你好，歡迎來到《編程闖關記》！
這里是算法與數據結構的實戰基地，也是你從“暴力解法”到“最優解”的進化場。

🔍 專欄初衷：

• 用清晰的圖解 + 多語言代碼（Python/Java/C++/C），拆解每道題背后的邏輯。
• 不只講“怎么做”，更講“為什么”——從題目分析、邊界條件到復雜度優化。
• 適合想夯實基礎或突擊面試的你，尤其針對LeetCode/牛客高頻題！

💡 如何使用本專欄：
1?? 先獨立思考：嘗試自己寫出第一版代碼（哪怕很爛）。
2?? 對比解法：看看我的思路和你的差異，吸收優化技巧。
3?? 舉一反三：每篇末尾會附相似題目鏈接，趁熱打鐵。

📌 堅持打卡：
算法沒有捷徑，但正確的方法能讓你少走彎路。每天15分鐘，和我一起用代碼雕刻思維！

（正文開始👇）

---

目錄

1.移除元素

力扣鏈接直達<請點擊

int removeElement(int* nums, int numsSize, int val) 
{int count = 0;for(int i=0;i<numsSize;i++){if(nums[i]!=val){nums[count] = nums[i];count++;}}return count;
}

代碼說明：

• 初始化計數count： count從0開始，用于記錄不等于val的元素數量，并作為新數組的索引。

• **遍歷數組：**使用i遍歷整個數組，檢查每個元素是否等于val。

• 如果nums[i]不等于val，則將其復制到nums[k]的位置，并遞增k。

• 如果等于val，則跳過該元素。

• 返回結果：最終k即為新數組的長度，且數組的前k個元素均為不等于val的元素。

這種方法高效且滿足題目要求的原地修改條件。

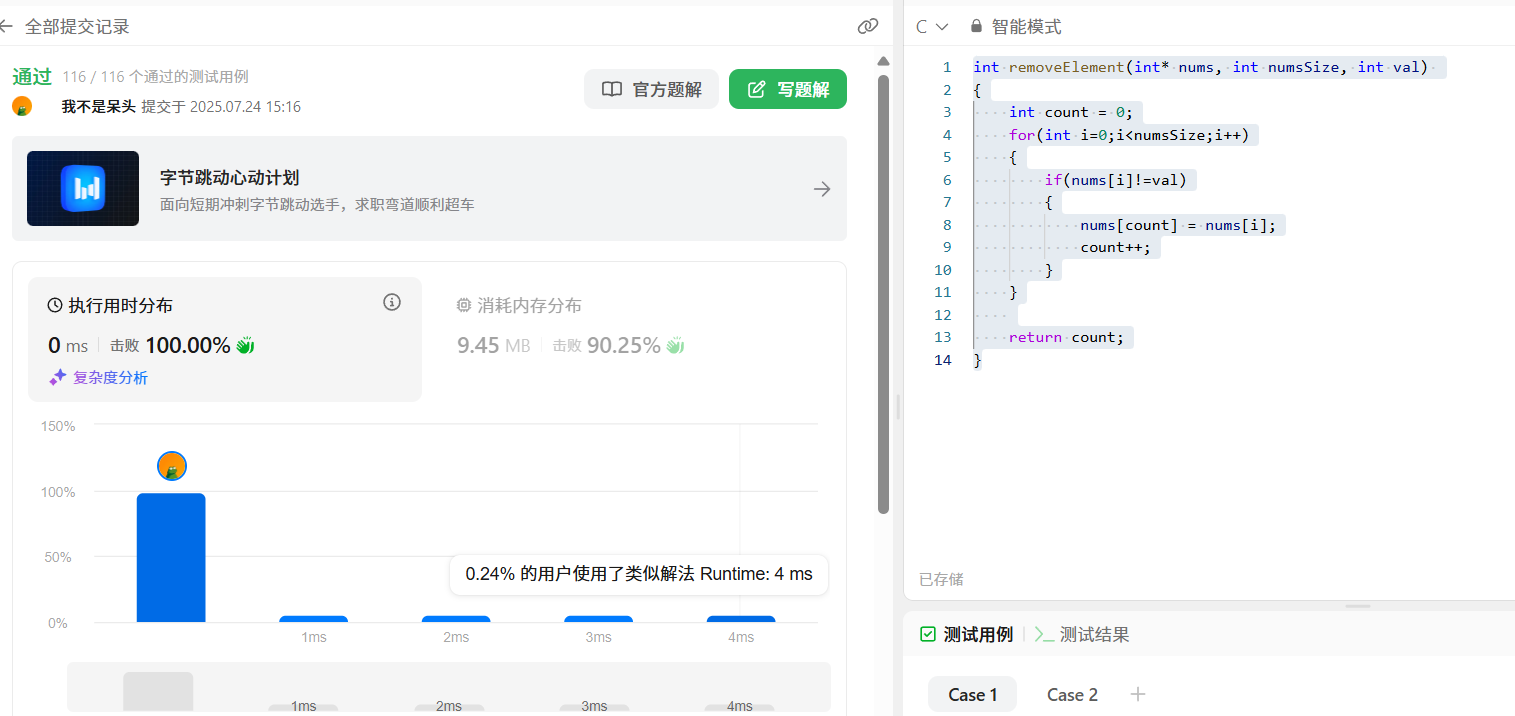
2.刪除有序數組中的重復項

力扣鏈接直達<請點擊

int removeDuplicates(int* nums, int numsSize) {if (numsSize == 0) return 0; // 空數組直接返回 0int k = 0; // 慢指針，初始指向第一個元素for (int i = 1; i < numsSize; i++) {if (nums[i] != nums[k]) { // 發現新元素k++; // 移動慢指針nums[k] = nums[i]; // 存入新元素}// 如果 nums[i] == nums[k]，跳過（i 繼續前進）}return k + 1; // 返回去重后的長度
}

在 “原地移除重復元素” 的算法中，當遇到重復元素時，并不是真的刪除它，而是通過 覆蓋（跳過） 的方式，讓后面的非重復元素占據前面的位置，最終只保留不重復的部分。

關鍵點

1. 不真正刪除元素：數組在內存中是連續的，不能直接刪除某個元素，只能覆蓋。
2. 雙指針策略：
   • 慢指針 k：記錄 不重復元素應該存放的位置。
   • 快指針 i：遍歷數組，檢查是否有新元素。
3. 覆蓋重復元素：
   • 如果 nums[i] 是新元素（即 nums[i] != nums[k]），就把它存到 nums[k+1]，然后 k++。
   • 如果 nums[i] 是重復的（即 nums[i] == nums[k]），就 跳過它（i 繼續前進，k 不動）。

---

詳細步驟（以 nums = [1, 1, 2, 2, 3] 為例）

i	k	nums[i]	nums[k]	操作	nums 變化
1	0	1	1	nums[i] == nums[k]，跳過	[1, 1, 2, 2, 3]（不變）
2	0	2	1	nums[i] != nums[k]，存入 nums[1] = 2，k++	[1, 2, 2, 2, 3]
3	1	2	2	nums[i] == nums[k]，跳過	[1, 2, 2, 2, 3]（不變）
4	1	3	2	nums[i] != nums[k]，存入 nums[2] = 3，k++	[1, 2, 3, 2, 3]

最終結果：

• 前 k+1 = 3 個元素是去重后的：[1, 2, 3]（后面的 2, 3 可以忽略）。
• 返回 k + 1 = 3（去重后的長度）。

---

為什么 nums[i] == nums[k] 時，k 不移動？

• k 指向的是當前不重復部分的最后一個元素。
• 如果 nums[i] 和 nums[k] 相同，說明 nums[i] 是重復的，直接跳過（不存入數組）。
• 只有遇到新元素時，才存入 nums[k+1] 并移動 k。

---

總結

• 移除重復元素 實際上是 用后面的不重復元素覆蓋前面的重復位置。
• k 的作用：
  • 記錄 去重后的數組末尾位置。
  • 只有遇到新元素時才移動 k，否則跳過。
• 時間復雜度 O(n)，空間復雜度 O(1)（原地修改）。

這樣，最終 nums 的前 k+1 個元素就是去重后的結果，而后面部分可以忽略。

3.合并兩個有序數組

力扣鏈接直達<請點擊

解決思路

由于 nums1 有足夠的空間容納 nums2 的元素，我們可以利用 雙指針 的方法從后向前合并，以避免覆蓋 nums1 中還未處理的元素。具體步驟如下：

1. 初始化指針：

   • i 指向 nums1 的最后一個有效元素（即 m - 1）。
   • j 指向 nums2 的最后一個元素（即 n - 1）。
   • k 指向 nums1 的最后一個位置（即 m + n - 1）。

2. 從后向前比較并合并：

   • 比較 nums1[i] 和 nums2[j]，將較大的元素放到 nums1[k]。
   • 移動相應的指針（i 或 j）和 k。

3. 處理剩余元素：

   • 如果 nums2 中還有剩余元素（即 j >= 0），直接復制到 nums1 的前面。

解決代碼

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {int i = m - 1;      // nums1 的最后一個有效元素int j = n - 1;      // nums2 的最后一個元素int k = m + n - 1;  // nums1 的最后一個位置// 從后向前合并while (i >= 0 && j >= 0) {if (nums1[i] > nums2[j]) {nums1[k--] = nums1[i--];} else {nums1[k--] = nums2[j--];}}// 如果 nums2 還有剩余元素，直接復制到 nums1 的前面while (j >= 0) {nums1[k--] = nums2[j--];}
}

代碼解釋

1. 初始化指針：

   • i 從 nums1 的有效末尾開始。
   • j 從 nums2 的末尾開始。
   • k 從 nums1 的最后一個位置開始。

2. 比較并合并：

   • 比較 nums1[i] 和 nums2[j]，將較大的元素放入 nums1[k]，并移動相應的指針。
   • 這樣確保 nums1 的后半部分不會被覆蓋，直到所有元素正確歸位。

3. 處理剩余元素：

   • 如果 nums2 中還有元素未合并（即 j >= 0），直接復制到 nums1 的前面，因為 nums1 的前面部分已經處理完畢。

示例

輸入：

nums1 = [1, 2, 3, 0, 0, 0], m = 3
nums2 = [2, 5, 6], n = 3

執行過程：

1. i = 2, j = 2, k = 5：
   • nums1[2] = 3 < nums2[2] = 6 → nums1[5] = 6, j--, k--
2. i = 2, j = 1, k = 4：
   • nums1[2] = 3 < nums2[1] = 5 → nums1[4] = 5, j--, k--
3. i = 2, j = 0, k = 3：
   • nums1[2] = 3 > nums2[0] = 2 → nums1[3] = 3, i--, k--
4. i = 1, j = 0, k = 2：
   • nums1[1] = 2 == nums2[0] = 2 → nums1[2] = 2, j--, k--
5. j = -1，循環結束。
6. nums2 已無剩余元素，合并完成。

最終結果：

nums1 = [1, 2, 2, 3, 5, 6]

復雜度分析

• 時間復雜度：O(m + n)，每個元素最多被比較一次。
• 空間復雜度：O(1)，沒有使用額外空間，原地修改 nums1。

這種方法高效且避免了不必要的元素移動，是最優解。