1、題干

給定一個 n × n 的二維矩陣 matrix 表示一個圖像。請你將圖像順時針旋轉 90 度。
你必須在 原地 旋轉圖像，這意味著你需要直接修改輸入的二維矩陣。請不要 使用另一個矩陣來旋轉圖像。

示例 1：

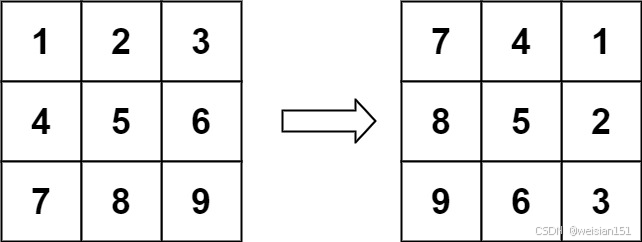
輸入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
輸出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

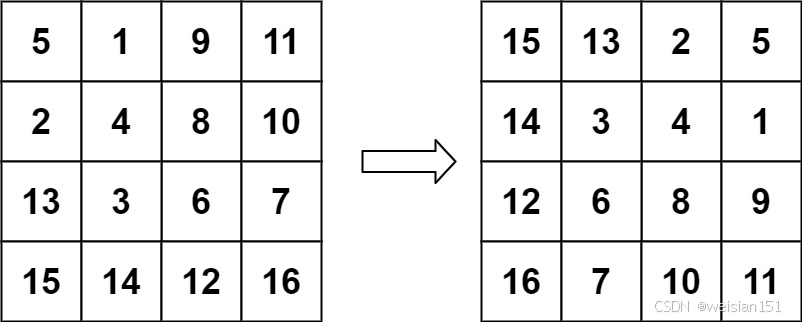
輸入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
輸出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：
n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

2、解題

旋轉數組，我們根據示例可以發現：原本的第一行數據旋轉變成了最后一列；第二行的數據變成了倒數第二列；依次類推。
結合具體的數組找規律可以發現：
假設n=4，規律：3,0–>0,0 2,0–>0,1 1,0–>0,2 0,0–>0,3
從索引的角度可以發現：前元素的行=新元素的列； 新元素的列+前元素的行=n-1

方法一：（輔助數組法）

使用輔助數組，保持和原數組相同的數據。可以借助輔助數組對原始數組快速賦值。
規律：
旋轉后元素的行為之前的列；旋轉后元素的列+之前的行=n-1

技巧：
需要結合當n=3和n=4的簡單場景下，自己找規律，不能懶。

代碼示例：

import java.util.Arrays;public class Test47 {// 使用輔助數組public static void rotate(int[][] matrix) {int n = matrix.length;int[][] matrixN = new int[n][n];for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {matrixN[i][j] = matrix[i][j];  // 輔助數組保持相同的數據}}// 假設=4，規律：3,0-0,0  2,0-0,1  1,0-0,2  0,0-0,3// 前元素的行=新元素的列；  新元素的列+前元素的行=n-1for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {matrix[i][j] = matrixN[n-j-1][i];    // 旋轉后元素的行為之前的列；旋轉后元素的列+之前的行=n-1}}}public static void main(String[] args) {int[][] matrix = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};rotate(matrix);System.out.println(Arrays.deepToString(matrix));}
}

方法二：（原地旋轉法）

相對輔助數組法，原地選擇法進需要一次遍歷原始數據，且輔助空間為O(1)，性能更好，但是相對難度也高一點。

注意點：
（1）、一次旋轉的規律
結合簡單數據可以看出。下標位置變化如：（0,0）–>(0,5)–>(5,5)–>(5,0)–>(0,0)
可以發現相鄰的兩個數之間的內部一定相等，外部相加一定=n-1。

（2）、旋轉的次數
同一個元素會攜帶者對應的其他三個元素在一次過程中完成選擇。所以不能完全遍歷數據，會造成同一個元素多次旋轉，最終回到原始數據。
如原始為一個55的二維數組，我們只需要對如下的23的區域進行旋轉即可（或3*2的區域也一樣）。如果旋轉多了就會造成問題。

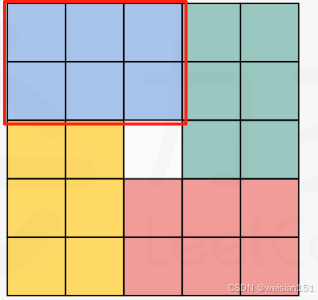
代碼示例：

import java.util.Arrays;public class Test47 {public static void rotate(int[][] matrix) {int n = matrix.length;// 假設=4，規律：3,0-0,0  2,0-0,1  1,0-0,2  0,0-0,3// 前元素的行=新元素的列；  新元素的列+前元素的行=n-1for (int i = 0; i < (n + 1) / 2; i++) {    // 防止重復旋轉（旋轉一半，只能+1一次，橫+1則縱不能+1）for (int j = 0; j < n / 2; j++) {      // 防止重復旋轉int temp = matrix[i][j];matrix[i][j] = matrix[n - j - 1][i];     // 規律：外部相等，內部相加=n-1matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];matrix[j][n - i - 1] = temp;}}}public static void main(String[] args) {int[][] matrix = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};rotate(matrix);System.out.println(Arrays.deepToString(matrix));}
}

向陽前行，Dare To Be！！！