來自上傳文件中的文章《[Causal Machine Learning for Growth: Loyalty Programs, LTV, and What to Do When You Can’t Experiment | by Torty Sivill | Towards AI]》
本文探討了當 A/B 測試不可行時，如何利用因果推斷從歷史數據中獲取洞察。技術亮點在于通過構建反事實世界來估計處理效應，并強調了混雜變量的重要性。文章介紹了在已知因果結構下使用線性回歸進行因果效應估計，以及在未知結構下利用 NOTEARS 等因果發現算法推斷因果圖。該方法適用于無法進行隨機實驗的場景，例如評估忠誠度計劃對客戶生命周期價值的影響，或處理混雜因素復雜的龐大數據集。

---

---

這是一個關于用反事實推理取代 A/B 測試的實踐指南。

圖片來自 Mathieu LESNIAK, Unsplash

很明顯，因果推斷正變得越來越重要。那些嚴重依賴實驗的公司現在面臨著 A/B 測試不可行、不切實際甚至適得其反的情況。他們正在尋找替代方法，從現有數據中獲取因果洞察。

讓我們以一家假日預訂公司為例，這是一種實驗深度嵌入的業務。增長或留存團隊可能會問一個關鍵問題：

我們的忠誠度計劃對客戶生命周期價值 (LTV) 有何影響？

這是一個經典的“處理效應”場景：一些用戶加入了忠誠度計劃，我們想知道這如何影響他們未來的消費。

為何我們無法對忠誠度計劃進行 A/B 測試？

1. 公平性和風險：隨機地對一半客戶不提供忠誠度計劃，尤其是包含折扣或福利的計劃，這感覺很不道德。聲譽成本太高。
2. 時間跨度：LTV 是按月或按年衡量的。等到測試結束時，產品、用戶行為或市場條件可能已經發生變化，導致結果過時。
3. 自愿加入性質：忠誠度計劃不是用戶可以被強制分配的。實際上，用戶是自愿選擇加入該計劃的，而選擇加入的用戶很可能是常旅客、更富有且參與度更高。這意味著他們更高的 LTV 可能歸因于他們本身的特質，而非計劃本身。

所以現在我們陷入困境。我們無法運行實驗，但我們確實有一個裝滿歷史數據的儀表板……

因果推斷作為替代方案

這就是因果推斷發揮作用的地方。我們不進行實時實驗，而是使用歷史數據來估計如果用戶沒有加入忠誠度計劃會發生什么。

在 A/B 測試中，隨機化確保混雜變量（例如財富、旅行頻率）在處理組和對照組之間均勻分布。這樣，結果的任何差異都可以歸因于處理。

但對于觀測數據，這種平衡并不存在。因此，因果推斷背后的思想是重建一個反事實世界，一個通過使用來自相似用戶的合成對照，將忠誠度計劃用戶與他們如果沒有加入該計劃的 LTV 進行比較的世界。

構建模擬數據集

為了演示其工作原理，我們創建了一個合成數據集，該數據集捕獲了我們的假日預訂示例。

import pandas as pd  
import numpy as np  
from sklearn.preprocessing import StandardScaler  
from linear import notears_linear  n = 1000  
np.random.seed(42)  
past_bookings = np.random.poisson(lam=3, size=n)  
average_booking_value = np.random.normal(loc=400, scale=100, size=n)  
is_high_income = np.random.binomial(1, p=0.3, size=n)  
channel = np.random.choice(["email", "ads", "organic"], size=n)  
channel_encoded = pd.get_dummies(channel, prefix="channel")loyalty_score = (  0.4 * past_bookings +  0.003 * average_booking_value +  1.0 * is_high_income +  0.5 * (channel == "email").astype(int)  
)  
p_loyalty = 1 / (1 + np.exp(-loyalty_score / 5))  
loyalty_enrolled = np.random.binomial(1, p_loyalty)lifetime_spend = (  100 * past_bookings +  0.8 * average_booking_value +  300 * loyalty_enrolled +  500 * is_high_income +  np.random.normal(0, 200, n)  
)df = pd.DataFrame({  "past_bookings": past_bookings,  "average_booking_value": average_booking_value,  "is_high_income": is_high_income,  "loyalty_enrolled": loyalty_enrolled,  "lifetime_spend": lifetime_spend  
})  
df = pd.concat([df, channel_encoded], axis=1)  
df

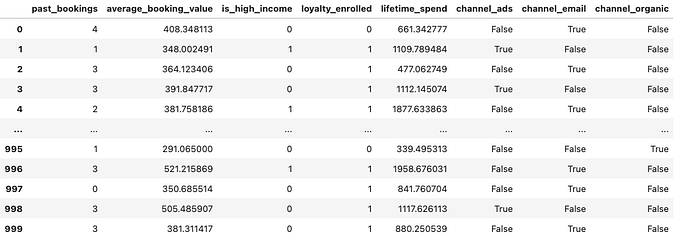
作者生成圖片。表格顯示了假日預訂公司示例的生成數據集。

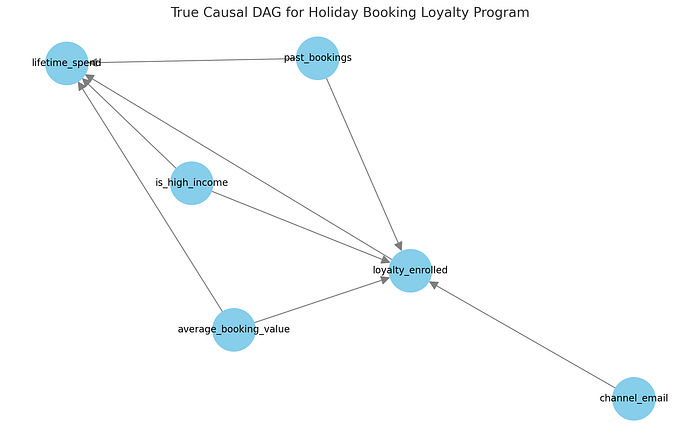
預訂公司示例的真實因果圖。

在我們的數據生成過程中：

• past_bookings（過去預訂量）、average_booking_value（平均預訂價值）和 is_high_income（是否高收入）等變量會影響加入忠誠度計劃的可能性以及總客戶消費。這些是我們的混雜因素。
• 忠誠度計劃本身對客戶生命周期消費有因果效應，這是我們想要估計的。
• 營銷渠道（例如 channel_email）可能會影響計劃注冊，但不一定會影響未來消費。

我們使用這種結構來模擬數據，模擬真實業務中可能出現的歷史客戶行為。這為我們提供了一個清晰的環境來探討兩個問題：

1. 如果我們知道真實的因果結構，將如何估計忠誠度注冊的因果效應？
2. 如果我們不知道，并且必須使用 NOTEARS 等技術從數據中推斷結構，又該如何？

使用已知因果圖確定因果效應

在這里，我們很幸運地自己生成了數據，因此可以輕松提取真實的因果結構。然而，對于描述真實世界系統的真實數據，我們需要嘗試自己構建因果圖。

因此，大量精力投入到首先理解問題的因果結構上。目標是得到一個因果圖——一個變量如何相互影響的模型——它決定了必須調整哪些變量才能無偏估計因果效應。

一旦你有了這個圖（或一個合理的近似），你就可以使用標準統計工具來估計因果效應。例如：

adjustment_vars = ["past_bookings", "average_booking_value", "is_high_income", "channel_email"]  
X = df[adjustment_vars + ["loyalty_enrolled"]]  
y = df["lifetime_spend"]model = LinearRegression().fit(X, y)  
print("Estimated effect of loyalty program (NOTEARS-adjusted):", model.coef_[-1])

乍一看，線性回歸可能看起來像一個預測工具，確實如此。但當與因果圖結合使用時，它也可以為我們提供處理效應的因果估計，在本例中是忠誠度計劃注冊對客戶生命周期消費的影響。

關鍵在于混雜。混雜變量是同時影響處理（加入忠誠度計劃）和結果（某人消費多少）的變量。如果我們不考慮混雜變量，我們就無法判斷觀察到的效應是由于處理還是僅僅是相關的背景因素。

在因果推斷中，我們旨在通過調整混雜變量來阻斷所有后門路徑：處理和結果之間間接的、非因果的路徑。這被稱為后門調整準則。

在我們的回歸模型中，我們根據因果圖包含了所有已知的混雜變量。這意味著我們正在比較那些在過去預訂量、收入和獲取渠道方面相似，但僅在是否加入忠誠度計劃方面不同的用戶。然后，回歸估計了那些加入計劃的用戶平均多花了多少錢，同時控制了所有其他因素。

這就是為什么 loyalty_enrolled 上的系數是一個因果效應估計，而不僅僅是相關性。

當然，這僅在以下情況下成立：

• 我們正確識別并包含了所有相關的混雜變量。
• 背景中沒有主要的未測量混雜變量。

如果這些假設成立，線性回歸就成為一個強大的、可解釋的工具，用于估計因果效應，即使在沒有 A/B 測試的情況下也是如此。

飛行員注冊對 LTV 的因果效應估計。

平均而言，在控制了混雜因素后，加入忠誠度計劃的用戶在 12 個月內比未加入的用戶多花費了約 ￡315.81。

如果你甚至不知道哪些變量是混雜變量怎么辦？

也許你的數據量巨大、雜亂，并且充滿了客戶特征：你不確定哪些是混雜變量，哪些不是。

因果發現來救援

這就是因果發現工具的用武之地。因果發現是機器學習中一個相對較新（且令人興奮）的分支，它試圖根據一組數據找到最佳的因果圖。其中一種方法是 NOTEARS，這是 Zheng 等人于 2018 年在卡內基梅隆大學提出的一種因果發現算法。

NOTEARS 學習一種特殊類型的因果圖，即 DAG（有向無環圖），這意味著該圖中的每條邊都有一個方向，并且沒有循環（這在因果關系中非常重要，因為事物不能既是原因又是結果！）。

學習 DAG 是非常困難的，因為符合數據的可能圖空間是組合爆炸的（非常非常大）。這意味著測試所有可能的圖是不可能的。更糟糕的是，檢查圖中的循環是不可微分的（因此不能使用基于梯度的常規機器學習方法）。

由于我們無法遍歷所有可能的因果圖，因此因果發現方法必須采用更具計算優雅性的方式來發現最符合數據的因果圖。許多方法使用基于啟發式的搜索。

NOTEARS 根本不搜索 DAG 空間，它通過一個巧妙的技巧學習因果圖，該技巧將離散搜索轉換為連續優化問題。這意味著可以使用基于梯度的求解器。

使用 NOTEARS 進行因果效應估計

對我們來說幸運的是，我們不必自己實現 NOTEARS，我們可以克隆原始倉庫，然后簡單地像這樣導入：

from linear import notears_linear    features = df[[  "past_bookings", "average_booking_value", "is_high_income",  "channel_ads", "channel_email", "channel_organic",  "loyalty_enrolled", "lifetime_spend"  
]]  
X = StandardScaler().fit_transform(features)  
W_est = notears_linear(X, lambda1=0.01, loss_type='l2')

然后我們可以使用這個鄰接矩陣來可視化 NOTEARS 推斷出的因果圖。

import matplotlib.pyplot as plt  
import networkx as nxadj_matrix = pd.DataFrame(W_est, index=features.columns, columns=features.columns)  
G = nx.DiGraph()  
threshold = 0.3  
for i, src in enumerate(adj_matrix.index):  for j, tgt in enumerate(adj_matrix.columns):  if abs(W_est[i, j]) > threshold:  G.add_edge(tgt, src, weight=W_est[i, j])plt.figure(figsize=(12, 7))  
pos = nx.spring_layout(G, seed=42)  
nx.draw(G, pos, with_labels=True, node_color='skyblue', node_size=2000,  edge_color='gray', font_size=10, arrowsize=20)  
plt.title("Inferred Causal DAG (NOTEARS)", fontsize=14)  
plt.tight_layout()  
plt.show()

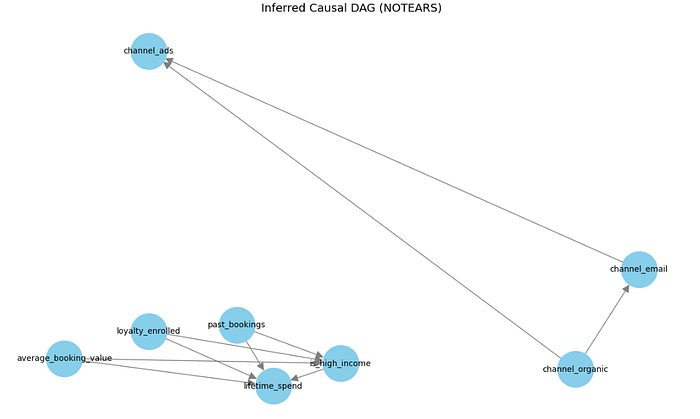
NOTEARS 在預訂公司示例上學習到的因果圖。

有趣的是，在 NOTEARS 推斷出的因果圖中，loyalty_enrolled 似乎是一個根節點，沒有來自任何其他變量的入邊。這表明，在該圖下，處理和結果之間沒有混雜因素。

如果這是真的，我們就不需要調整任何東西：忠誠度注冊和客戶生命周期消費之間觀察到的關系可以被解釋為因果關系，而無需任何控制。

然而，這與已知的數據生成過程相矛盾。在我們的模擬中，past_bookings 和 is_high_income 等變量顯然影響注冊和消費，使它們成為混雜因素。

如果我們使用這個因果圖來確定忠誠度計劃注冊對 LTV 的因果效應，我們將得到一個被高估的估計，雖然方向正確，但被混雜因素嚴重夸大。

treated_mean = df[df["loyalty_enrolled"] == 1]["lifetime_spend"].mean()  
control_mean = df[df["loyalty_enrolled"] == 0]["lifetime_spend"].mean()  
unadjusted_effect = treated_mean - control_meanprint(unadjusted_effect)

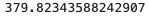
因果發現的局限性

因果發現的強大程度取決于其背后數據的質量。噪聲、有限的樣本或模型偏差可能導致遺漏依賴關系和不完整的圖。這就是為什么在選擇調整集時，將算法與領域知識結合起來至關重要。

這種局限性或許是因果發現尚未廣泛應用的原因。許多團隊缺乏手動定義因果結構的時間或工具。更好的自動化發現將使因果推斷更易于訪問，而這正是 AI 可以提供幫助的地方。

在 Decima2，我們開發了強大而準確的基于 AI 的因果發現算法。