遞歸的理解與限制條件

? ? ? ? 所謂函數遞歸就是遞推加回歸的過程，就是函數自己調用自己。遞歸的思想就是把復雜的問題拆分成與原來那個大問題相似的子問題來求解，大事化小，像剝洋蔥一樣，最終把問題解決。

? ? ? ? 遞歸的限制條件：

? ? ? ? 一個遞歸程序，除了處理問題的遞歸主體之外，肯定是有遞歸的出口的(也就是遞歸的限制條件)，每一次遞歸都是在棧區上給函數開辟一塊空間，沒有出口也就意味著棧沒有銷毀，最終會導致棧溢出的問題。所以每一次遞歸都要更加的接近這個限制條件才行。

遞歸舉例

????????問題1：求n的階乘。

? ? ? ? 問題分析：首先要知道什么是階乘，就比如 5！= 5 * 4 * 3 * 2 * 1 ，就是一個數從自己本身，一直累乘到1。那么這個就可以用遞歸來解決，假設我們就求5的階乘。

5! = 5 * 4 * 3 * 2 * 1

可以看成 5! = 5 * 4!

而4! = 4 * 3!

...................

從上邊的分析就可以得出一個遞歸的公式

n! = n * (n - 1)! (由這個公式，我們就可以設計出一個計算 n! 的函數)

又因為 0! = 1，所以可以把這個設置成遞歸的出口。

? ? ? ? 代碼實現：

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>//Fact函數用于計算n的階乘
int Fact(int n)
{if (n == 0)return 1;elsereturn n * Fact(n - 1);
}int main()
{int number = 0;scanf("%d", &number);int res = Fact(number);printf("%d\n", res);return 0;
}

? ? ? ? 畫圖理解：

?

---

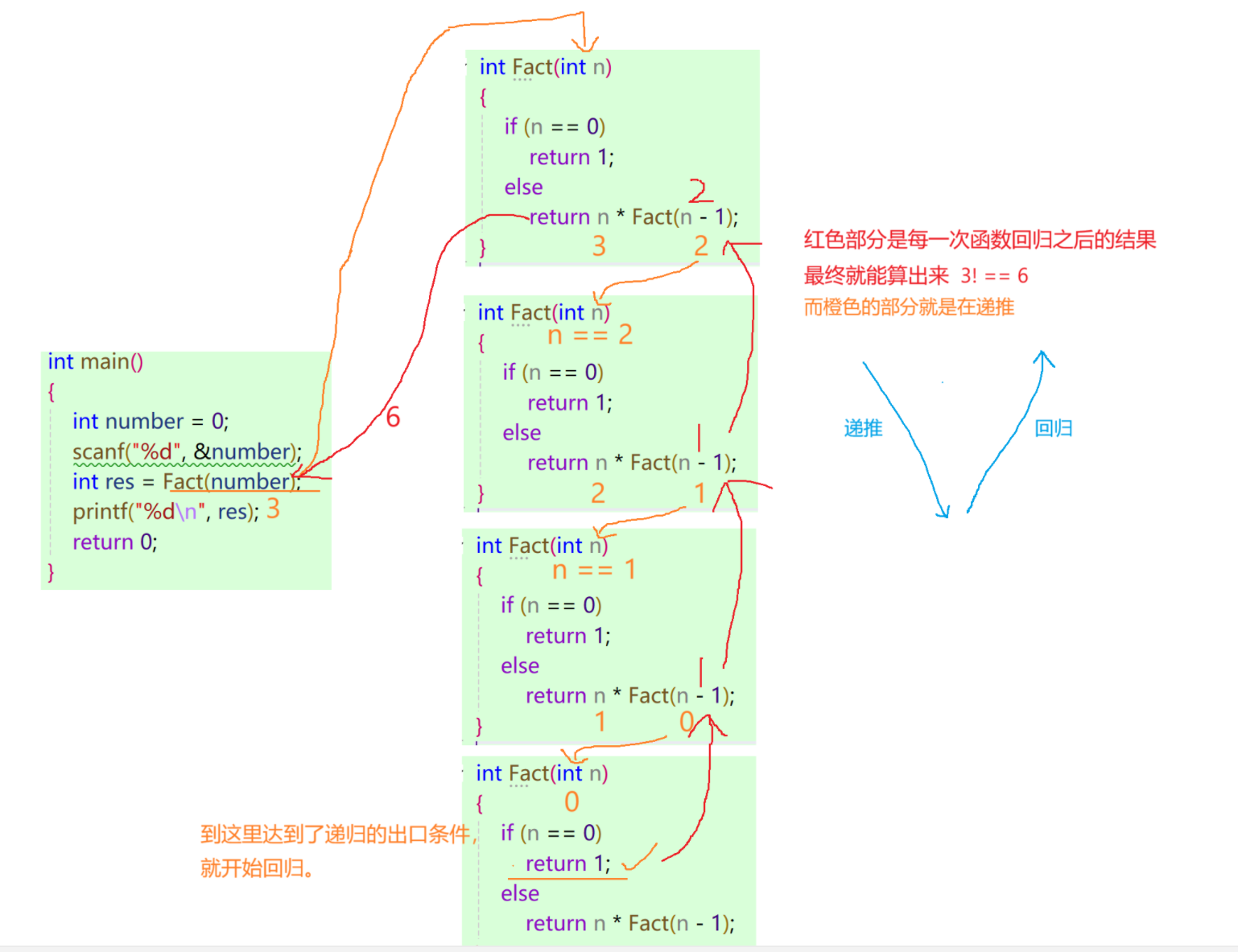????????問題2：順序打印一個整數的每一位。

? ? ? ? 問題分析：假設現在有一個數字為1234，我想要順序打印它的每一位，就是依次打印 1 2 3 4。我們如果想要直接獲取到1，然后打印，這是非常困難的，但是，獲取到最后一位的4很容易，只需要 1234 % 10 就可以了，又由于我現在想要順序打印，所以4是要最后打印的，那就可以先打印前邊的123，再打印4，而打印123，又可以拆分為先打印12，再打印3.............就是一個遞歸

假設Print是我們自己設計的一個函數，專門用來順序打印數字的

那么上邊的思路就轉化如下：

--> Print(1234) --> Print(123) + 4;

--> Print(123) --> Print(12) + 3;?

--> Print(12) --> Print(1) + 2;

--> Print(1) --> 1(直接打印)

并且123，12......都是由原來的數字 num / 10 得到的

而由上邊的分析就可以知道遞歸的出口就是當打印的數字為一位數的時候，就直接打印。

如果打印的數字是兩位數，就先打印前邊的數字，再打印最后一位的數字。

? ? ? ? 代碼實現：

#include<stdio.h>
void Print(int n)
{if (n > 9)//大于9就說明是超過一位的，需要遞歸處理{Print(n / 10);printf("%d ", n % 10);//獲取n的最后一位，并且是最后打印}elseprintf("%d ", n);//如果只有一位，直接打印
}int main()
{int num = 0;scanf("%d", &num);Print(num);return 0;
}

????????畫圖理解：

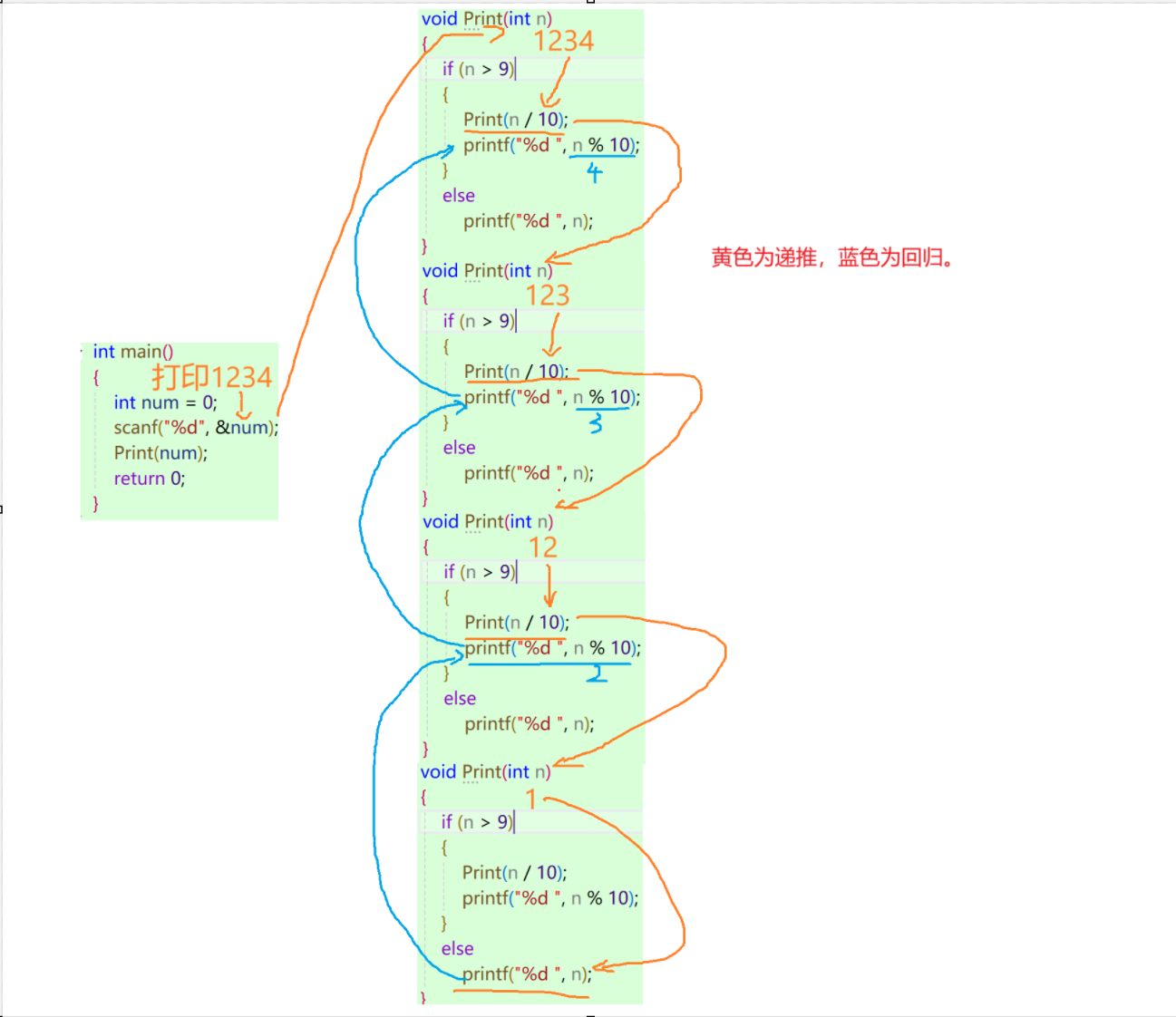
????????再注意一個點，就是這里的Print函數是沒有返回值的其實，但是得先Print函數調用結束之后才會執行下邊的代碼，這也叫回歸。

---

????????問題3：求第n個斐波那契數

? ? ? ? 問題分析：所謂斐波那契數就是 1 1 2 3 5 8 13 21 34............其實這里的規律很容易被發現，就是從第三個數字開始，后一個數字是由前兩個數字加起來。而第一個和第二個斐波那契數，我們就可以把它看做是函數的遞歸出口。

? ? ? ? 代碼實現：

#include<stdio.h>
//Fib(n)就表示的是第n個斐波那契數
int Fib(int n)
{if (n == 1 || n == 2)return 1;elsereturn Fib(n - 1) + Fib(n - 2);
}int main()
{int num = 0;scanf("%d", &num);printf("%d\n", Fib(num));return 0;
}

---

????????附加：

????????還有兩個問題之前已經寫過了，是青蛙跳臺階和漢諾塔問題。鏈接如下。

????????用C語言函數遞歸實現青蛙跳臺階和漢諾塔問題-CSDN博客

---

遞歸與迭代

? ? ? ? 在上邊就提到過函數遞歸如果從來沒有遞歸出口的話就會導致棧溢出的問題，同樣的，就算有遞歸出口，如果遞歸的層次太深，也會導致棧溢出。

? ? ? ? 如果不用遞歸的方式，迭代也是很好的解決方式，迭代通常就是由循環來實現的。它們倆是相輔相成的，不過迭代相對來說消耗的棧空間較少。效率要高一點。

迭代舉例

????????問題1：用迭代的方式實現n的階乘。

? ? ? ? 問題分析：剛才已經說了，迭代其實就是用循環來實現的，求n的階乘可以先循環產生1~n之間的每一個數字，然后再累乘起來。

? ? ? ? 代碼實現：

#include<stdio.h>
int main()
{int res = 1;//res用來存最后的結果，初始化為1是因為便于下邊直接累乘int num = 0;scanf("%d", &num);//for循環產生1~num的數字for (int i = 1; i <= num; i++){res *= i;}printf("%d\n", res);return 0;
}

---

????????問題2：用迭代的方式求第n個斐波那契數

? ? ? ? 問題分析：關于斐波那契數的定義已經在上邊的遞歸里邊講到了。但是如果用遞歸求第50個斐波那契數的話，我們就會明顯的發現，遞歸的結果遲遲沒有出現，這就是上邊提到的遞歸的層次太深了，會影響效率。

用迭代的方式：

為了計算第n個斐波那契數，我們可以先定義三個變量。

int a = 1;

int b = 1;

int c = 1;//這是第三個數字，用來最后返回的結果

根據斐波那契數列的規律，c可以通過a + b來實現，然后再把a的值改為b原來的值，b的值改為c的值，而現在的c就又可以由a+b來計算了，以此迭代下去，效果如下。

下邊紅色代表斐波那契數，而黑色就代表該數是第幾個斐波那契數。

1 1 2 3 5 8 13 21.......

1 2 3 4 5 6? 7? 8.........

a b c..........................

? ?a b c.......................

最后解釋一下為什么c為1，因為如果要求的是第1或者第2個斐波那契數，就不會進入循環，所以直接初始化為1，具體大家可以看下邊的代碼。

????????代碼實現：

#include<stdio.h>
int Fib(int n)
{int a = 1;int b = 1;int c = 1;//計算第三個斐波那契數及之后的數才進入循環//另外，找規律可以發現// 計算第3個斐波那契數只要計算一次// 計算第4個斐波那契數要計算兩次.............while(n>=3){c = a + b;a = b;b = c;n--;}return c;
}int main()
{int num = 0;scanf("%d", &num);printf("%d\n", Fib(num));return 0;
}