計算圖

• 計算圖（Computation Graph）是一種用于描述計算過程的圖形化表示方法。

• 在深度學習中，計算圖通常用于描述 網絡結構、運算過程 和數據流向。

• 計算圖是一種有向無環圖，用圖形方式來表示算子與變量之間的關系，直觀高效。

• 它由節點（Node）和邊（Edge）組成，如下圖Netron庫可視化的例子，其中節點表示操作或函數，邊表示數據流向。

前向傳播 與 反向傳播

• 在Pytorch中，計算圖的構建是通過神經網絡的 前向傳播 (forward) 過程完成的。

• 反向傳播 根據計算圖來計算梯度，從而進行參數更新。它為自動微分（automatic differentiation）提供了基礎，使得深度學習框架能夠自動計算梯度并進行反向傳播。

靜態計算圖、動態計算圖

計算圖可以分為兩種類型：靜態計算圖 和 動態計算圖

• 靜態計算圖： 在靜態計算圖中，計算圖在模型定義階段就被固定下來，不會發生變化。典型的例子是 TensorFlow 1.x 中的計算圖。在這種情況下，首先定義計算圖，然后運行會話（session）來執行圖中的操作。

• 動態計算圖： 在動態計算圖中，計算圖在運行時根據輸入數據的形狀和大小動態構建。PyTorch 和 TensorFlow 2.x 采用了動態計算圖的方式。在這種情況下，每次前向傳播都會重新構建計算圖，使得模型更加靈活。

在整個前向計算過程中，PyTorch采用 動態計算圖 的形式進行組織，且在每次 前向傳播時重新構建。
其他深度學習架構，如TensorFlow、Keras 一般為靜態圖。

葉子節點、非葉子節點、根節點

• 上面的計算圖中，圓形表示變量，矩形表示算子，這些變量和算子構成了一個完整的前向傳播過程
• 葉子節點 ： $x、w、b$ 為葉子節點，它們是用戶創建的變量，不依賴于其他變量
• 非葉子節點 ： $y、z$為非葉子節點，它們是通過計算得到的變量
• 根節點 ： $z$ 為根節點，它之后不會再有后續的運算，我們一般讓根節點來執行 反向傳播方法 z.backward()

torch.tensor()的requires_grad參數

• 對于葉子節點（Leaf Node）的 張量Tensor，需要用 requires_grad 指明是否記錄對其的操作運算，以便之后通過 反向傳播求梯度。

• 一般僅對 葉子節點 設置 requires_grad， 這些葉子節點，一般就是網絡中層的參數，他們一般都是 torch.nn.Parameter 對象，requires_grad 屬性 默認為 True

• 葉子結點如果需要求導，requires_grad 需設置為 True，那么由這些葉子節點計算得出的非葉子節點，requires_grad 會自動置為True

import torchx = torch.tensor([2.0], requires_grad=True)   # 葉子節點
w = torch.tensor([3.0], requires_grad=True)   # 葉子節點
b = torch.tensor([1.0], requires_grad=True)   # 葉子節點y = w * x  # 非葉子節點
z = y + b  # 非葉子節點# 查看葉子節點和非葉子節點的 requires_grad 屬性
print('x 的 requires_grad 屬性:', x.requires_grad)
print('w 的 requires_grad 屬性:', w.requires_grad)
print('b 的 requires_grad 屬性:', b.requires_grad)
print('y 的 requires_grad 屬性:', y.requires_grad)
print('z 的 requires_grad 屬性:', z.requires_grad) 

grad_fn屬性

• 通過運算創建的非葉子節點 tensor，會自動被賦予 grad_fn 屬性，用于表明生成這個張量的操作
• 葉子節點的 grad_fn 為 None，因為它們不是通過其他操作計算得來的，而是網絡的參數或輸入數據

一些常見的 grad_fn 類型包括：

• <CatBackward>：表示這個張量是通過 torch.cat 操作得到的。
• <MatMulBackward>：表示這個張量是通過矩陣乘法操作得到的。
• <AddBackward>：表示這個張量是通過加法操作得到的。
• <AddmmBackward>：表示一個張量是通過 torch.addmm 操作得到的。
• <DivBackward>：表示這個張量是通過除法操作得到的。
• <ReLUBackward>：表示這個張量是通過 ReLU 激活函數得到的。

**import torch# 創建葉子節點張量
x = torch.tensor([2.0], requires_grad=True)
y = torch.tensor([3.0], requires_grad=True)# 創建非葉子節點張量，通過運算生成
z = x * y# 查看葉子節點和非葉子節點的 grad_fn 屬性
print('x 的 grad_fn:', x.grad_fn) 
print('y 的 grad_fn:', y.grad_fn)
print('z 的 grad_fn:', z.grad_fn) **

反向傳播

在反向傳播中，以 loss（根節點 tensor ）為核心，步驟為：

1. 用 optimizer.zero_grad() 清空葉子節點梯度，避免多次 optimizer.step() 時梯度累加。
2. 調用 loss.backward() 反向傳播，計算葉子節點梯度并存入 .grad 屬性。
3. 執行 optimizer.step() ，依優化器算法和學習率，用 .grad 梯度更新葉子節點（即模型參數 ） 。

for epoch in range(epochs):model.train()for imgs, labels in train_loader        :# trainoptimizer.zero_grad()loss.backward()optimizer.step()

完整舉例：

import torch# 輸入張量 x， require_grad 屬性默認為 False
x = torch.Tensor([2])# 初始化 權重參數w, 偏移量b，并設置 require_grad 屬性為 True, 為自動求導
w = torch.randn(1, requires_grad=True)
b = torch.randn(1, requires_grad=True)# 實現向前傳播
y = torch.mul(w, x)
z = torch.add(y, b)# 分別查看葉子節點 x, w, b 和 非葉子節點 y、z 的require_grad屬性
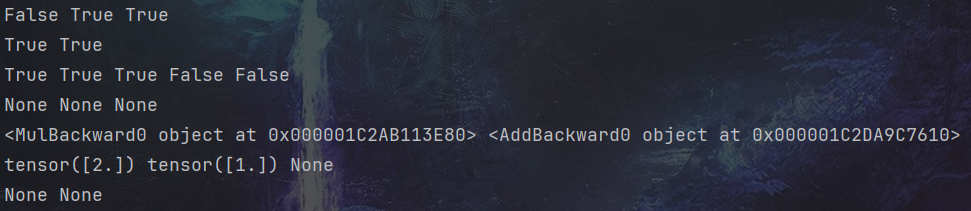
print(x.requires_grad, w.requires_grad, b.requires_grad)  # False True True
print(y.requires_grad, z.requires_grad )  # True True# 查看各節點是否為葉子節點
print(x.is_leaf, w.is_leaf, b.is_leaf, y.is_leaf, z.is_leaf)  # True True True False False# 分別查看 葉子節點 和 非葉子節點 的 grad_fn 屬性
print(x.grad_fn, w.grad_fn, b.grad_fn)   # None None None
print(y.grad_fn, z.grad_fn)   # <MulBackward0 object at 0x7f8ac1303910> <AddBackward0 object at 0x7f8ac1303070># 反向傳播計算梯度
z.backward()  # 查看葉子節點的梯度，x是葉子節點但它無須求導，故其梯度為None 
print(w.grad,b.grad,x.grad)  # tensor([2.]) tensor([1.]) None# 非葉子節點的梯度，執行backward之后，會自動清空 
print(y.grad,z.grad)  # None None

自動求導 Autograd

• 在神經網絡中，一個重要內容就是進行參數學習，而參數學習的反向傳播離不開求導。
• 現在大部分深度學習架構都有自動求導的功能，torch.autograd包 就是用來自動求導的。
• torch.autograd 包為張量上所有的操作提供了自動求導功能

實驗：backward()反向傳播自動求導

以下代碼實現 ： 機器學習 回歸問題舉例，使用 backward() 反向傳播自動求導，并手動更新參數

1. 先來造一批數據，作為樣本數據 x 和 標簽值y

import torch
import matplotlib.pyplot as plttorch.manual_seed(100)# 生成 x坐標數據，形狀為 100 x 1
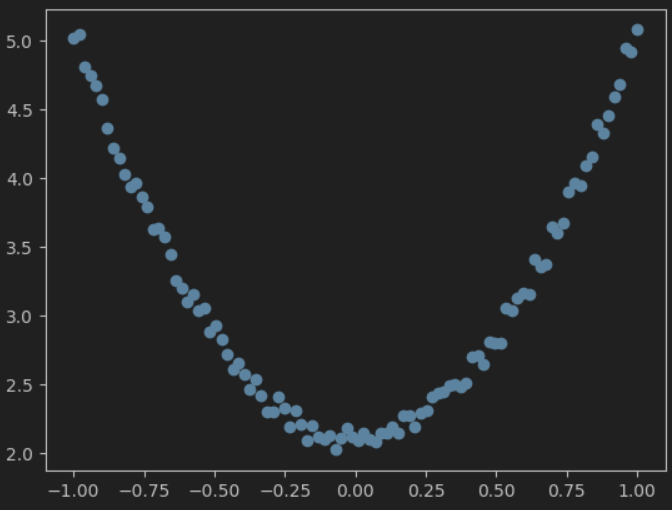
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)# 生成 y坐標數據，，形狀為 100 x 1，加上一些噪聲
y = 3 * x.pow(2) + 2 + 0.2 * torch.rand(x.size())# 把tensor數據轉換為numpy數據，并可視化
plt.scatter(x.numpy(), y.numpy())
plt.show()

2. 定義一個模型 y = wx +b, 我們要學習出 w 和 b 的值，用來擬合 x 和 y

# 初始化權重參數，參數 w、b 為需要學習的，故需要設置參數 requires_grad=True
w = torch.randn(1, 1, dtype=torch.float, requires_grad=True)
b = torch.zeros(1, 1, dtype=torch.float, requires_grad=True)
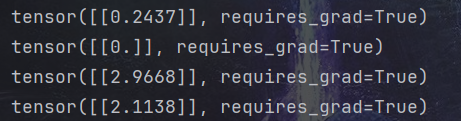
print(w)  # tensor([[1.1046]], requires_grad=True)
print(b)  # tensor([[0.]], requires_grad=True)lr = 0.001 # 學習率for i in range(800):# 向前傳播，得到預測的y值，記為 y_predy_pred = w * x.pow(2) + b# 定義損失函數loss = (y - y_pred) ** 2loss = loss.sum()# 反向傳播，自動計算梯度，存放在 grad 屬性中loss.backward()# 手動更新參數，需要用torch.no_grad(), 使上下文環境中切斷自動求導的計算with torch.no_grad():# 更新參數w -= lr * w.gradb -= lr * b.grad# 梯度清零w.grad.zero_()b.grad.zero_()print(w)  # tensor([[2.9668]], requires_grad=True)
print(b)  # tensor([[2.1138]], requires_grad=True)

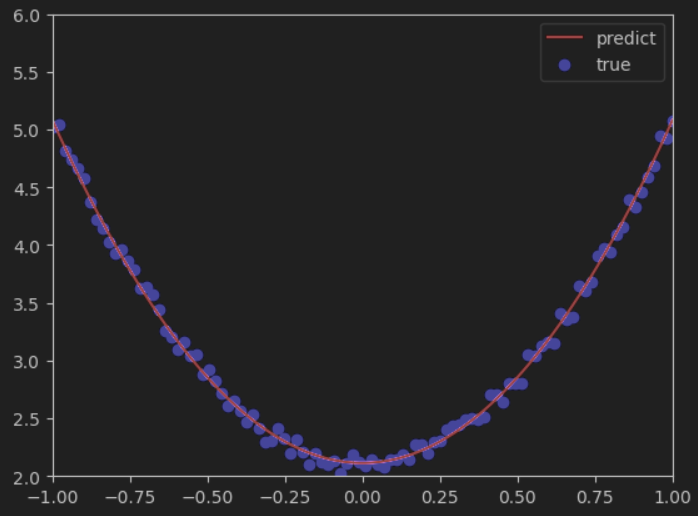
3. 可視化一下結果，紅色曲線是預測結果 ，藍色點是真實標簽值