一·介紹

邏輯回歸是處理二分類問題的線性模型，通過sigmoid函數將線性輸出映射到[0,1]，輸出事件發生概率，廣泛用于預測與分類。

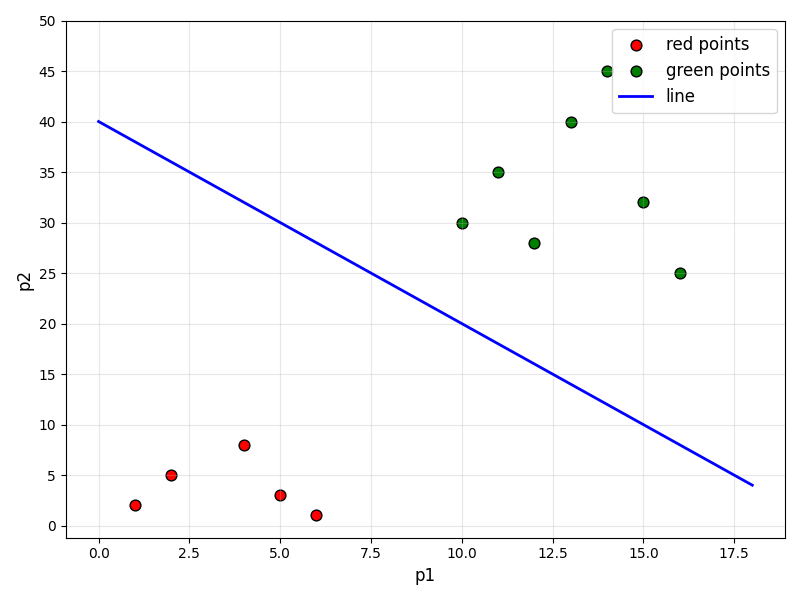
如果做坐標的話，特征就是p1和p2，結果就是y紅的與綠的?

二·Sigma函數

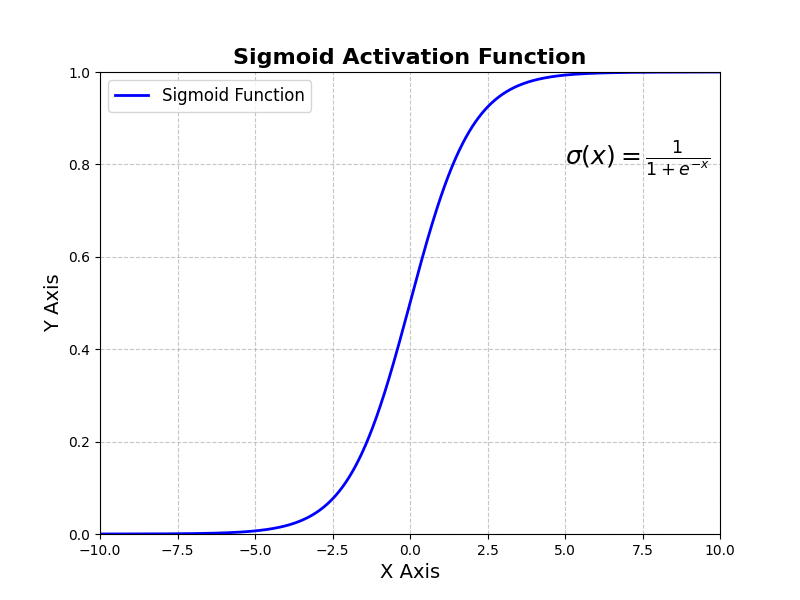
代碼說明

1. Sigmoid 函數定義：

   • sigmoid(x)?實現了 Sigmoid 公式：
2. 

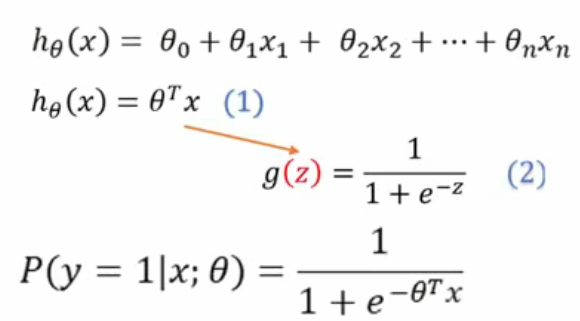
-x可以看成y

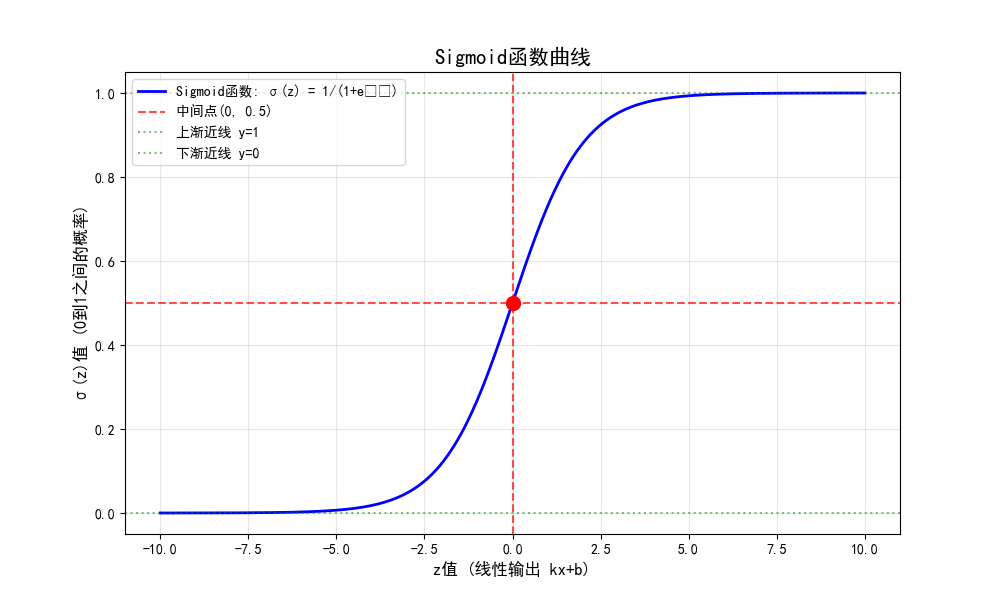
邏輯回歸模型原理示意：先由線性函數 (y = kx + b) 輸出結果,的Sigmoid函數轉換，將線性輸出映射到0 - 1區間,把線性可分數據的分類問題，轉化為用概率判斷0或1類別的問題，簡化分類求解 。

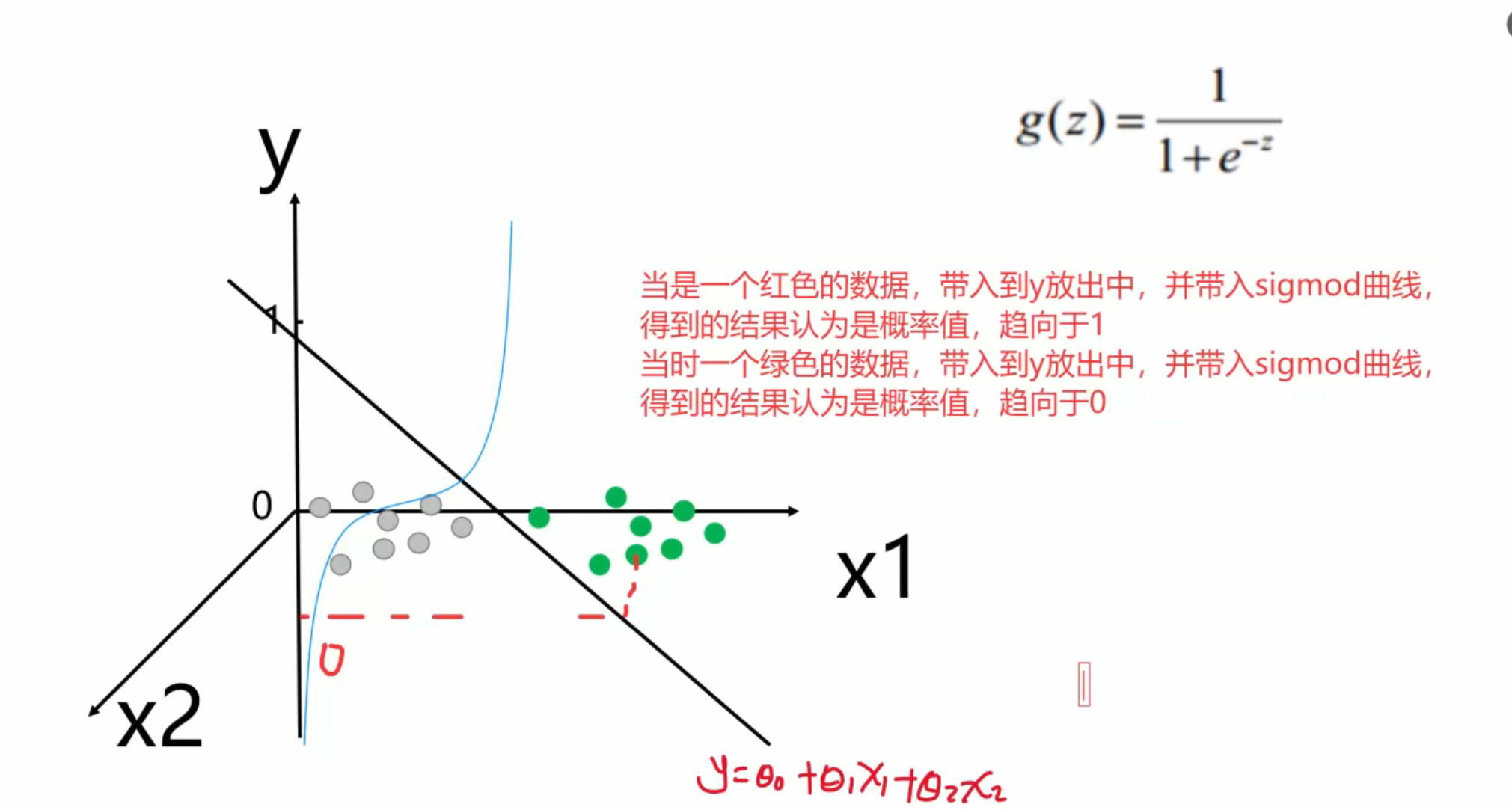
放出為方程，筆誤抱歉改的時間成本很高，見諒?

最終是為了求h（x）中的012

二·數學

邏輯回歸

1·線性回歸結果：

2·帶入 sigmoid 函數：

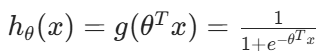
3·對于二分類任務：?

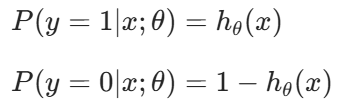
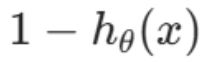?就表示sigmoid函數的另一個分類

4·整合?

4這里的?y如果是紅色的話應該是1那么右邊的式子就是0消失了，反之如果是0綠色左邊是1不影響結果所以是這樣的原理

邏輯回歸 - 求解

1·似然函數：

2·對數似然

3·轉換為梯度下降任務（損失函數）

?（1·最小二乘法求解極值2梯度下降也可以求極值）

4·目標函數這是邏輯回歸（Logistic Regression）中的代價函數（Cost Function），也叫交叉熵損失函數（Cross - Entropy Loss） ，公式為：

?

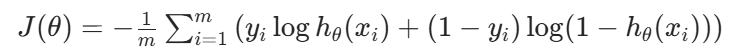
這是關于 ** 梯度（Gradient）** 的數學定義：

• 實體信息為 “梯度” 的概念闡述，即梯度是函數全部偏導數構成的向量，其方向是函數值增長最快的方向 ，常用于機器學習、微積分等領域，指導函數優化（如梯度下降法找極值） 。

?