環境:PyCharm + python3.8
👉【循環神經網絡】(recurrent neural network,RNN)
RNN通過
- 引入狀態變量存儲過去的信息和當前的輸入,從而可以確定當前的輸出。
- 狀態變量捕捉序列的時序依賴,是處理文本、時間序列等數據的基石,
- 但其梯度問題推動了更先進的架構(如LSTM、Transformer)的發展。
數據類型的差異與模型適配
- 表格數據:結構化數據,傳統機器學習模型(如線性回歸、決策樹)可直接處理。
- 圖像數據:具有空間局部性(像素位置敏感),需通過卷積神經網絡(CNN)利用局部特征(如邊緣、紋理)和層級抽象(從低級到高級特征)。
- 序列數據(如文本、視頻、音頻、時間序列):
- 順序依賴性:數據元素間存在時序或邏輯關聯(如單詞順序決定句子含義)。
- 非獨立同分布(independently and identically distributed,i.i.d.):樣本間存在依賴關系,傳統模型(如MLP)無法捕捉。
- 需求:需模型能記憶歷史信息并理解上下文。
CNN vs RNN的核心差異:
| 特性 | CNN | RNN |
|---|---|---|
| 數據類型 | 圖像(空間數據) | 序列(時序/邏輯數據) |
| 核心操作 | 卷積(局部連接+權重共享) | 循環(狀態傳遞+權重共享) |
| 信息利用 | 局部特征→全局特征 | 歷史狀態→當前輸出 |
| 典型任務 | 分類、檢測、分割 | 預測、生成、翻譯 |
| 訓練挑戰 | 參數多、過擬合 | 梯度消失/爆炸、長期依賴 |
1.?序列模型
序列數據的動態性與模型挑戰
1. 電影評分的時間依賴性
- 評分非靜態:用戶對電影的評價隨時間、外部事件及個人體驗變化,典型現象包括:
- 錨定效應:受他人評價或外部事件(如奧斯卡獲獎)影響,導致評分系統性偏差(如評分提升0.5分以上)。
- 享樂適應:用戶對連續優質內容產生適應性,導致對后續普通內容的評價降低(如“由奢入儉難”)。
- 季節性:內容與時間背景的匹配度影響評價(如圣誕電影在8月評分低)。
- 外部事件沖擊:導演/演員丑聞或內容爭議導致評分突變(如道德因素覆蓋質量評價)。
- 小眾效應:極端質量(如極差)導致電影被特定群體關注,形成非典型評分分布(如“爛片”文化)。
- 模型啟示:需引入時間動力學(如時間衰減因子、事件嵌入)捕捉評分漂移,而非依賴靜態用戶-物品矩陣。
2. 用戶行為的時空模式
- 習慣驅動的序列性:
- 周期性行為:用戶活動與日常/周期事件強相關(如學生放學后使用社交媒體、股市開盤時交易軟件活躍)。
- 場景化需求:工具類應用(如地圖、外賣)使用頻率受地理位置、時間(如工作日/周末)影響。
- 模型啟示:需結合時間特征(小時/日/周粒度)與上下文特征(位置、事件)構建混合模型(如時序+圖神經網絡)。
3. 預測任務的難度差異
- 外推法(Extrapolation) vs 內插法(Interpolation):
- 外推法:預測未來或未知范圍數據(如明日股價),需模型理解長期趨勢與突變(如政策、黑天鵝事件)。
- 內插法:在已知范圍內估計(如填充缺失評分),可依賴局部模式(如用戶偏好相似性)。
- 挑戰:外推法需處理不確定性與非平穩性(如數據分布隨時間變化),傳統模型(如ARIMA)易失效。
4. 序列的連續性與語義敏感性
- 順序決定意義:
- 文本/語音:詞序顛倒導致語義完全改變(如“狗咬人” vs “人咬狗”)。
- 視頻/音樂:幀/音符順序破壞敘事或旋律(如電影剪輯錯亂)。
- 模型要求:需捕捉局部依賴(如N-gram)與全局結構(如注意力機制),避免獨立假設(如詞袋模型失效)。
5. 自然現象的時空相關性
- 地震序列:
- 余震模式:大地震后余震強度更高、時間/空間更集中(如“主震-余震”序列符合冪律分布)。
- 預測難點:需聯合建模時間衰減與空間傳播(如ETAS模型)。
- 模型啟示:需引入時空圖神經網絡(STGNN)或點過程模型(如霍克斯過程)捕捉事件間依賴。
6. 人類互動的連續性
- 社交媒體動態:
- 爭吵/辯論演化:用戶回復形成樹狀結構,情緒隨時間累積(如憤怒升級、冷靜消退)。
- 信息傳播:謠言與事實的擴散速度差異體現序列影響力(如轉發鏈分析)。
- 模型要求:需結合文本內容與交互時序(如RNN處理對話歷史)或圖結構(如傳播路徑建模)。
7. 序列數據的共性挑戰與模型方向
挑戰 典型場景 模型需求 非平穩性 電影評分、股價 時間自適應權重、在線學習 長程依賴 文本生成、用戶行為鏈 注意力機制、記憶網絡 高維稀疏性 用戶-物品交互矩陣 嵌入降維、圖嵌入 多模態融合 視頻評論、社交媒體帖子 跨模態注意力、聯合編碼 實時性要求 金融交易、地震預警 流式計算、輕量化模型(如TinyML) 8. 關鍵結論
- 序列數據是動態系統:其統計特性(如均值、方差)隨時間變化,需放棄i.i.d.假設。
- 上下文即特征:時間、空間、社交關系等元數據是序列建模的核心輸入。
- 從預測到解釋:現代模型(如Transformer)需平衡預測性能與可解釋性(如注意力權重分析)。
1.1.?統計工具
處理序列數據需要統計工具和新的深度神經網絡架構。 為了簡單起見,以?圖8.1.1所示的股票價格(富時100指數)為例。
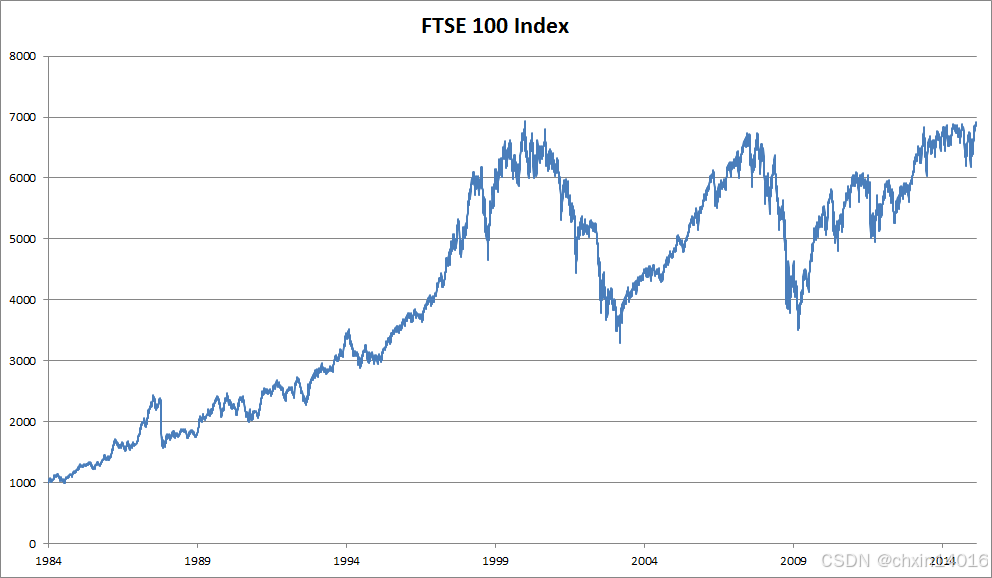
- 其中,
?表示價格,即在時間步(time step)
?時,觀察到的價格
?。
- 注意,
?對于本文中的序列通常是離散的,并在整數或其子集上變化。
- 假設一個交易員想在?
?日的股市中表現良好,于是通過以下途徑預測
?:(序列數據生成過程的數學表達)
![]()
?:在時間步?t?觀測到的價格
- P(A∣B):條件概率分布,表示“在給定某些條件B下,某事件A發生的概率”
- 條件分布【B已發生的條件下,A發生的概率】
:
當前數據點???是從以歷史序列?
??為條件的概率分布中采樣得到的。即:
“當前狀態依賴于過去所有狀態的聯合作用”
1.1.1.?自回歸模型
核心問題:輸入數據的動態性?
要實現這個預測,交易員可以使用回歸模型, 例如在(線性回歸實現 & softmax回歸實現—— 動手學深度學習3.2~3.7_自己動手寫線性回歸-CSDN博客中的 線性回歸的簡潔實現)中訓練的模型。
但序列預測任務中,有個主要問題:(輸入數據的動態性)
- 輸入數據的數量,輸入
?本身因
?而異。
- 即 輸入數據的長度(歷史觀測窗口)會隨著遇到的數據量的增加而增加 (隨時間動態變化)。
- 計算不可行性:直接使用全歷史序列(如所有歷史股價)作為輸入,參數數量隨數據量指數增長。
- 模型訓練困難:深度網絡需要固定尺寸的輸入,而動態長度破壞這一前提。
- 因此需要一個近似方法來使這個計算變得容易處理。
兩種主流解決策略?
本章后面的大部分內容將圍繞著如何有效估計??展開。 簡單地說,它歸結為以下兩種主流解決策略:
策略一:自回歸模型(autoregressive models)
- 假設在現實情況下長序列?
?不必要, 只需滿足某個長度為
?的時間跨度即可, 即 使用觀測序列
。當下獲得的最直接的好處就是參數數量恒定, 至少在
?時如此,這樣即可訓練深度網絡。 這種模型是對自己執行回歸。
- 核心思想:假設長序列依賴不必要,僅使用固定長度的歷史窗口(如最近?k?個時間步)作為輸入。
- 關鍵優勢:
- 參數恒定:輸入尺寸固定為?k,模型復雜度不隨數據增長。
- 可訓練性:可直接應用深度網絡(如RNN、Transformer)處理定長輸入。
- 典型應用:
- 股價預測:用過去30天的價格預測下一天價格。
- 語言模型:用前?n?個詞預測下一個詞(如GPT的滑動窗口)。
- 局限性:
- 信息丟失:若長程依賴關鍵(如經濟周期對股價的影響),固定窗口會截斷有用信號。
策略二:隱變量自回歸模型(latent autoregressive models)。
- 如?圖8.1.2所示, 是保留一些對過去觀測的總結
?, 并同時更新預測
?和總結
?。 這就產生了基于
?估計
?, 以及公式
?更新的模型。 由于
?從未被觀測到,這類模型也被稱為 隱變量自回歸模型。
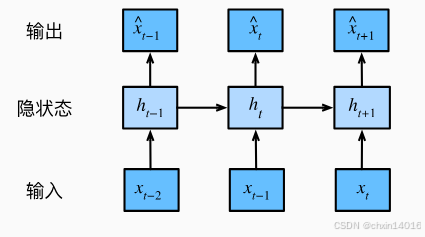
- 核心思想:
引入隱狀態(latent state)??壓縮歷史信息,同時更新預測和隱狀態(如圖8.1.2)。
- 數學表達:
- 預測更新:
- 隱狀態更新:
(其中?f?和?g?為可學習函數,如LSTM的細胞狀態更新)
- 預測更新:
- 關鍵優勢:
- 動態信息壓縮:隱狀態?
??高效編碼歷史,無需固定窗口長度。
- 處理長程依賴:通過隱狀態的遞歸更新傳遞長期信息(如RNN的隱藏層)。
- 動態信息壓縮:隱狀態?
- 典型應用:
- 時間序列:LSTM/GRU預測氣溫、交易量。
- 強化學習:狀態-動作值函數依賴隱歷史(如DQN)。
- 挑戰:
- 隱狀態可解釋性:黑盒更新可能導致調試困難。
- 訓練復雜性:需通過BPTT(隨時間反向傳播)優化,計算成本高。
訓練數據生成方法
以上兩種情況都有一個顯而易見的問題:如何生成訓練數據?
- 一個經典方法是使用歷史觀測來預測下一個未來觀測。
- (通用范式****:歷史觀測 → 預測未來觀測)
- 滑動窗口法:用?
?預測?
,滾動生成訓練樣本(如時間序列交叉驗證)。
假設基礎:
- 序列動力學靜止性(Stationarity):
- 雖然特定值可能會改變, 但是序列本身的動力學不會改變。
- 即 數據生成機制(如市場規律)不變,僅具體值變化。
- 合理性:新動力學需新數據,無法從歷史中預測(如政策突變影響股價)。
統計學家稱不變的動力學為靜止的(stationary)。 因此,整個序列的估計值都將通過以下的方式獲得:
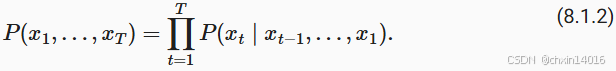
注意:(離散數據適配)
- 若
?為離散對象(如單詞),而不是連續的數字,則上述的考慮仍然有效。
- 差別在于,離散對象 需替換回歸模型為分類器(如Softmax輸出概率分布)來估計
?。
策略對比與選擇指南
| 維度 | 自回歸模型 | 隱變量自回歸模型 |
|---|---|---|
| 輸入長度 | 固定窗口?k | 動態壓縮至隱狀態?ht? |
| 信息保留 | 依賴窗口選擇,可能丟失長程信號 | 通過遞歸更新保留長期依賴 |
| 計算效率 | 高(矩陣運算固定尺寸) | 低(需BPTT,隱狀態更新復雜) |
| 適用場景 | 短程依賴任務(如語音識別片段) | 長程依賴任務(如視頻劇情預測) |
| 典型模型 | CNN、Transformer(局部注意力) | RNN、LSTM、GRU、Transformer-XL |
1.1.2.?馬爾可夫模型
回想一下,在自回歸模型的近似法中, 使用? 而不是
?來估計
?。 只要這種是近似精確的,就說序列滿足馬爾可夫條件(Markov condition)。 特別是,如果
,得到一個?一階馬爾可夫模型(first-order Markov model),?
?由下式給出:
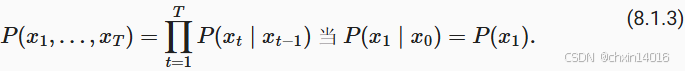
當假設 ?僅是離散值時,這樣的模型特別棒, 因為在這種情況下,使用動態規劃可以沿著馬爾可夫鏈精確地計算結果。 例如,我們可以高效地計算
?:
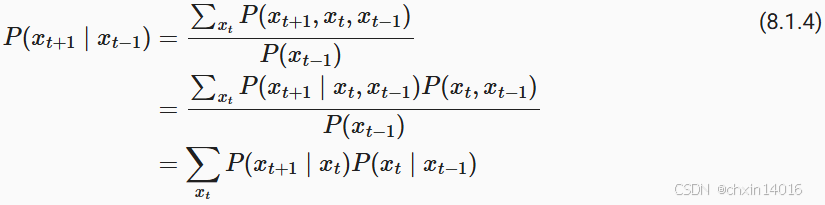
利用這一事實,我們只需要考慮過去觀察中的一個非常短的歷史:?。 隱馬爾可夫模型中的動態規劃超出了本節的范圍 (我們將在?9.4節雙向循環神經網絡再次遇到), 而動態規劃這些計算工具已經在控制算法和強化學習算法廣泛使用。
1.1.3.?因果關系
原則上,將 ?倒序展開也沒什么問題。畢竟,基于條件概率公式,總是可以寫出:
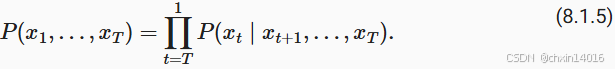
- 基于馬爾可夫模型,可得到 反向條件概率分布。
- 然而,許多情況下,數據存在時間上的前進方向。未來的事件不能影響過去。
- 因此,若改變
?,則可能會影響未來發生的事情
,但不能反過來。也就是說,若改變
?,基于過去事件得到的分布不會改變。
- 因此,解釋
?應該比解釋
?更容易。
- 例如,在某些情況下,對于某些可加性噪聲
?,顯然可以找到
?(能找到順著時間方向的因果關系), 而反之則不行?(Hoyer?et al., 2009)。而這個向前推進的方向恰好也是我們通常感興趣的方向。
- 彼得斯等人?(Peters?et al., 2017)?對該主題的更多內容做了詳盡的解釋,而上述討論只是其中的冰山一角。
1.2.?訓練
開始實踐:
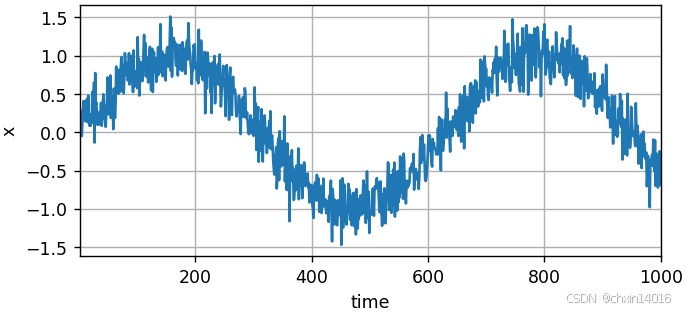
1)首先生成一些數據,并可視化:
- 使用正弦函數和一些可加性噪聲來生成序列數據,時間步為 1,2, ...,1000 。
import torch
from torch import nn
import common# 1. 數據生成及可視化
# 生成含噪聲的周期性時間序列數據(正弦波+噪聲)
T = 1000 # 總共產生1000個點
time = torch.arange(1, T + 1, dtype=torch.float32) # 時間步 [1, 2, ..., 1000]
# (T,) 是表示張量形狀(shape)的元組,用于指定生成的高斯噪聲(正態分布)的維度(指定生成一維張量,長度為T)
x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,)) # 生成正弦信號 + 高斯噪聲
print(f"x的形狀:{x.shape}")
common.plot(time, [x], 'time', 'x', xlim=[1, 1000], figsize=(6, 3)) # 繪制時間序列![]()
2)將序列轉換為 模型的特征-標簽(feature-label)對(構造特征與標簽)。
- 基于嵌入維度,將數據映射為數據對?
和
。
- 這比我們提供的數據樣本少了
?個,因為沒有足夠的歷史記錄來描述前
?個數據樣本。
- 解決辦法1:若擁有足夠長的序列就丟棄這幾項;
- 解決辦法2:用零填充序列。
用過去4個時間步預測下一個時間步,即:
- 標簽為當前的值,其對應有4個特征,分別是他往前4個時間步的值。
- 最開始的4個時間步的值由于缺少特征或沒有特征,則被丟棄或用0填充確實特征。
這里的代碼選擇將前τ項丟棄,即 前4項丟棄。
# 2. 構造特征與標簽
# 將時間序列轉換為監督學習問題(用前4個點預測第5個點
tau = 4 # 用過去4個時間步預測下一個時間步
features = torch.zeros((T - tau, tau)) # 特征矩陣形狀: (996, 4)(總共996個有效樣本,每個樣本對應4個特征)
for i in range(tau):features[:, i] = x[i: T - tau + i] # 滑動窗口填充特征
labels = x[tau:].reshape((-1, 1)) # 標簽形狀: (996, 1) (前4項丟棄)3)創建數據迭代器,支持批量訓練
這里僅使用前600個“特征-標簽”對進行訓練:
# 3. 數據加載器
# 創建數據迭代器,支持批量訓練
batch_size, n_train = 16, 600 # 批量大小16,訓練集600樣本
# 將前n_train個樣本用于訓練
train_iter = common.load_array((features[:n_train], labels[:n_train]),batch_size, is_train=True) # 創建數據迭代器,支持批量訓練4)網絡初始化:
這里訓練模型使用的架構相當簡單:
- 一個擁有兩個全連接層的多層感知機,
- ReLU激活函數和平方損失。
# 4. 網絡初始化
# 初始化網絡權重的函數
def init_weights(m):if type(m) == nn.Linear:nn.init.xavier_uniform_(m.weight) # Xavier初始化權重# 定義一個簡單的多層感知機(MLP)
def get_net():net = nn.Sequential(nn.Linear(4, 10), # 輸入層(4) → 隱藏層(10)nn.ReLU(), # 激活函數nn.Linear(10, 1)) # 隱藏層(10) → 輸出層(1)net.apply(init_weights) # 應用初始化return net# 平方損失。注意:MSELoss計算平方誤差時不帶系數1/2
# reduction='none' 返回每個樣本的損失,后續需手動 .sum() 或 .mean()
loss = nn.MSELoss(reduction='none') # 均方誤差損失,不自動求和/平均現在準備訓練模型。實現下面的訓練代碼的方式與前面幾節?(如線性回歸實現 & softmax回歸實現—— 動手學深度學習3.2~3.7_自己動手寫線性回歸-CSDN博客中的 線性回歸的簡潔實現) 中的循環訓練基本相同。
# 對模型進行訓練和測試
def evaluate_loss(net, data_iter, loss): #@save"""評估給定數據集上模型的損失"""metric = common.Accumulator(2) # 損失的總和,樣本數量for X, y in data_iter:out = net(X) # 模型預測輸出結果y = y.reshape(out.shape) # 將實際標簽y的形狀調整為與模型輸出out一致l = loss(out, y) # 模型輸出out與實際標簽y之間的損失metric.add(l.sum(), l.numel()) # 將損失總和 和 樣本總數 累加到metric中return metric[0] / metric[1] # 損失總和/預測總數,即平均損失def train(net, train_iter, loss, epochs, lr):trainer = torch.optim.Adam(net.parameters(), lr) # Adam優化器for epoch in range(epochs):for X, y in train_iter:trainer.zero_grad() # 梯度清零l = loss(net(X), y) # 計算損失(形狀[batch_size, 1])l.sum().backward() # 反向傳播(對所有樣本損失求和)trainer.step() # 更新參數# 打印訓練損失(假設evaluate_loss是自定義函數)print(f'epoch {epoch + 1}, 'f'loss: {evaluate_loss(net, train_iter, loss):f}')net = get_net() # 初始化網絡
train(net, train_iter, loss, 5, 0.01) # 訓練5個epoch,學習率0.01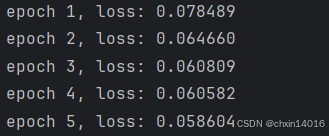
1.3.?預測
由于訓練損失很小,因此期望模型能有很好的工作效果。讓我們看看這在實踐中意味著什么。
首先檢查模型預測下一個時間步的能力,也就是?單步預測(one-step-ahead prediction)。
- 單步預測:模型預測下一個時間步的能力。
# 單步預測:模型預測下一時間步的能力
onestep_preds = net(features)
common.plot([time, time[tau:]],[x.detach().numpy(), onestep_preds.detach().numpy()], 'time','x', legend=['data', '1-step preds'], xlim=[1, 1000],figsize=(6, 3))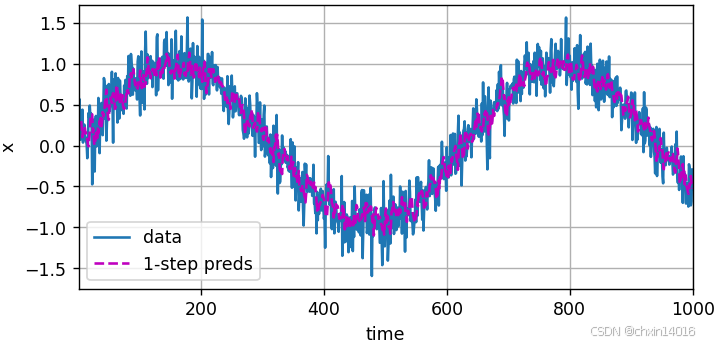
如圖所示,單步預測效果不錯?即使這些預測的時間步超過了 600+4(n_train + tau), 其結果看起來仍然是可信的。然而有一個小問題:若數據觀察序列的時間步只到604,我們需要一步一步地向前邁進:

通常,對于直到 ?的觀測序列,其在時間步
?處的預測輸出?
?稱為 k步預測(k-step-ahead-prediction)。由于觀察已經到了
?,它的步預測是
。 換句話說,我們必須使用我們自己的預測(而不是原始數據)來進行多步預測。 下面看看效果:
- 簡單的 K步預測:使用預測 來進行后面的K步預測。(遞歸預測)
- 是嚴格的遞歸預測,每個新預測都基于之前的預測。
- 潛在問題:遞歸預測的誤差會累積,因為每個預測都基于之前的預測。
# 簡單的K步預測:使用預測 來進行K步預測(遞歸預測)
# 是嚴格的遞歸預測,每個新預測都基于之前的預測
# 潛在問題:遞歸預測的誤差會累積,因為每個預測都基于之前的預測
multistep_preds = torch.zeros(T) # 初始化預測結果張量
multistep_preds[: n_train + tau] = x[: n_train + tau] # 用真實值填充前面已知的真實值
for i in range(n_train + tau, T): # 遞歸預測# 使用前tau個預測值作為輸入,預測下一個值multistep_preds[i] = net(multistep_preds[i - tau:i].reshape((1, -1)))common.plot([time, time[tau:], time[n_train + tau:]],[x.detach().numpy(), onestep_preds.detach().numpy(),multistep_preds[n_train + tau:].detach().numpy()], 'time','x', legend=['data', '1-step preds', 'multistep preds'],xlim=[1, 1000], figsize=(6, 3))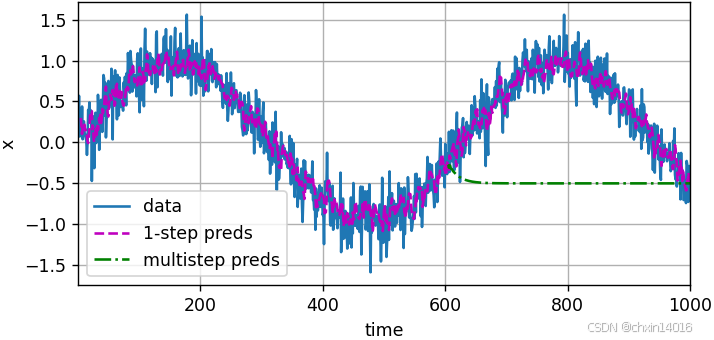
如上面的例子所示,綠線的預測顯然并不理想。 經過幾個預測步驟之后,預測的結果很快就會衰減到一個常數。算法效果這么差是由于錯誤的累積:
- 假設在步驟1之后,我們積累了一些錯誤
?。
- 于是,步驟2的輸入被擾動了
?,結果積累的誤差是依照次序的?
?,其中c為某個常數,后面的預測誤差依此類推。
- 因此誤差可能會相當快地偏離真實的觀測結果。
例如,未來24小時的天氣預報往往相當準確, 但超過這一點,精度就會迅速下降。本章及后續章節中會討論如何改進這一點。
基于 k=? 1, 4, 16, 64,通過對整個序列預測的計算,讓我們更仔細地看一下k步預測的困難:
- 多步預測:同時獲得多個未來時間步的預測(序列預測)
- 是序列預測,可以同時獲得多個未來時間步的預測(雖然這些中間預測也基于之前的預測)。
- 潛在問題:雖然能一次預測多個步長,但長期預測仍然依賴中間預測結果。
# 多步預測(序列預測)
# 是序列預測,可以同時獲得多個未來時間步的預測(雖然這些中間預測也基于之前的預測)
# 潛在問題:雖然能一次預測多個步長,但長期預測仍然依賴中間預測結果
max_steps = 64 # 最大預測步數# 初始化特征張量,(要預測的樣本數,特征數),其中
# 前 tau 列:存儲真實歷史數據(作為輸入)
# 后 max_steps 列:存儲模型預測的未來值
# T-tau-max_steps+1是可計算的時間窗口數量,特征數(tau列真實數據 + max_steps列預測數據)
features = torch.zeros((T - tau - max_steps + 1, tau + max_steps))# 前tau列用真實值填充
# 列i(i<tau)是來自x的觀測(實際真實值),其時間步從(i)到(i+T-tau-max_steps+1)
print(f"真實值填充:{x[i: i + T - tau - max_steps + 1].shape}") # torch.Size([1])
for i in range(tau):features[:, i] = x[i: i + T - tau - max_steps + 1]# 對于 i=0,features[:, 0] = x[0 : 0 + 927](即 x[0] 到 x[926])# 對于 i=1,features[:, 1] = x[1 : 1 + 927](即 x[1] 到 x[927])# ...# 對于 i=9,features[:, 9] = x[9 : 9 + 927](即 x[9] 到 x[935])# 后max_steps列用模型預測填充
# 列i(i>=tau)是來自(i-tau+1)步的預測,其時間步從(i)到(i+T-tau-max_steps+1)
for i in range(tau, tau + max_steps):features[:, i] = net(features[:, i - tau:i]).reshape(-1) # .reshape(-1)展平為一維向量steps = (1, 4, 16, 64) # 要展示的預測步數
common.plot([time[tau + i - 1: T - max_steps + i] for i in steps],[features[:, (tau + i - 1)].detach().numpy() for i in steps], 'time', 'x',legend=[f'{i}-step preds' for i in steps], xlim=[5, 1000],figsize=(6, 3))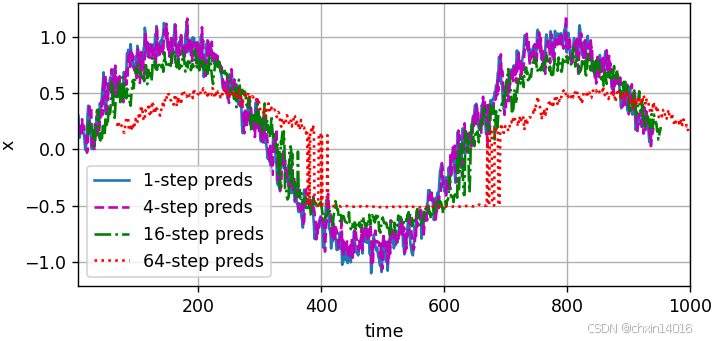
- 上例清楚地說明了當試圖預測更遠的未來時,預測的質量會急速下降。
- 雖然“步預測”看起來仍然不錯,但超過這個跨度的任何預測幾乎都是無用的
1.4.?小結
內插法和外推法在實踐的難度上差別很大。因此,對于所擁有的序列數據,訓練時要尊重其時間順序,即最好不要基于未來的數據進行訓練。
內插法:在現有觀測值之間進行估計
外推法:對超出已知觀測范圍進行預測
序列模型的估計需要專門的統計工具,兩種較流行的選擇是
自回歸模型 和
隱變量自回歸模型。
對于時間是向前推進的因果模型,正向估計通常比反向估計更容易。
對于直到時間步的觀測序列,其在時間步的預測輸出是“步預測”。隨著對預測時間值的增加,會造成誤差的快速累積和預測質量的極速下降。
2.?文本預處理
- 對于序列數據處理問題,數據存在多種形式,文本是最常見例子之一。
- 例如,一篇文章可以被簡單地看作一串單詞序列,甚至是一串字符序列。
文本的常見預處理步驟 通常包括:
- 將文本作為字符串加載到內存中。
- 將字符串拆分為詞元(如單詞和字符)。
- 建立一個詞表,將拆分的詞元映射到數字索引。
- 將文本轉換為數字索引序列,方便模型操作。
import common
import collections # 提供高性能的容器數據類型,替代Python的通用容器(如 dict, list, set, tuple)
import re # 供正則表達式支持,用于字符串匹配、搜索和替換'''
假設原始文本前兩行為:
The Time Machine, by H. G. Wells [1898]
I
預處理后:['the time machine by h g wells', 'i']
詞元化結果:[['the', 'time', 'machine', 'by', 'h', 'g', 'wells'], ['i']]
'''2.1.?讀取數據集
首先,從H.G.Well的時光機器中加載文本。
- 這是一個 只有30000多個單詞 的語料庫,足夠我們小試牛刀。
- 現實中的文檔集合可能會包含數十億個單詞。
下面的函數:
- 將數據集讀取到 由多條文本行組成的 列表中,
- 其中 每條文本行都是一個字符串。
- 這里忽略了標點符號和字母大寫。
# 下載器與數據集配置
# 為 time_machine 數據集注冊下載信息,包括文件路徑和校驗哈希值(用于驗證文件完整性)
downloader = common.C_Downloader()
DATA_HUB = downloader.DATA_HUB # 字典,存儲數據集名稱與下載信息
DATA_URL = downloader.DATA_URL # 基礎URL,指向數據集的存儲位置DATA_HUB['time_machine'] = (DATA_URL + 'timemachine.txt','090b5e7e70c295757f55df93cb0a180b9691891a')
# 加載文本數據
def read_time_machine(): #@save"""將時間機器數據集加載到文本行的列表中"""# 通過 downloader.download('time_machine') 獲取文件路徑with open(downloader.download('time_machine'), 'r') as f:lines = f.readlines() # 逐行讀取文本文件# 用正則表達式 [^A-Za-z]+ 替換所有非字母字符為空格# 調用 strip() 去除首尾空格,lower() 轉換為小寫# 返回值:處理后的文本行列表(每行是純字母組成的字符串)return [re.sub('[^A-Za-z]+', ' ', line).strip().lower() for line in lines]lines = read_time_machine()
print(f'# 文本總行數: {len(lines)}')
print(lines[0]) # 第1行內容
print(lines[10]) # 第11行內容
正則表達式替換:
re.sub('[^A-Za-z]+', ' ', line)
- 將字符串?
line?中所有非字母字符替換為空格。
[^A-Za-z]+:
[^...]:匹配不在括號內的任意字符(補集)A-Za-z:匹配所有大小寫字母(ASCII)+:匹配前面的模式1次或多次(連續的非字母字符會被替換為單個空格)- 局限性:
- 僅匹配ASCII字母,無法處理其他語言(如中文、帶重音的拉丁字母)。
- 可能需要調整為?
[^\w]+(匹配非單詞字符,包括下劃線)或更復雜的模式。
2.2.?詞元化
tokenize函數:
- 輸入:(預處理后的)文本行列表(
lines),- 列表中的每個元素是一個文本序列(如一條文本行)。
- 每個文本序列又被拆分成一個詞元列表,詞元(token)是文本的基本單位。
- 返回:一個由詞元列表組成的列表,其中的每個詞元都是一個字符串(string)。
# 詞元化函數:支持按單詞或字符拆分文本
# lines:預處理后的文本行列表
# token:詞元類型,可選 'word'(默認)或 'char
# 返回值:嵌套列表,每行對應一個詞元列表
def tokenize(lines, token='word'): #@save"""將文本行拆分為單詞或字符詞元"""if token == 'word':return [line.split() for line in lines] # 按空格分詞elif token == 'char':return [list(line) for line in lines] # 按字符拆分else:print('錯誤:未知詞元類型:' + token)tokens = tokenize(lines)
for i in range(11):print(f"第{i}行:{tokens[i]}")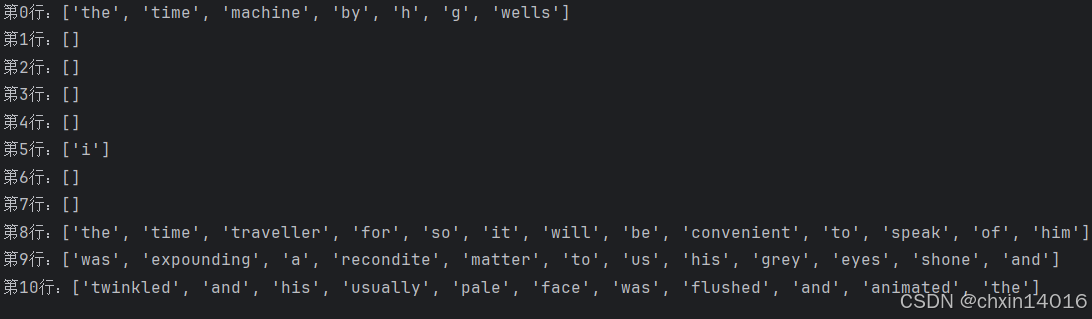
2.3.?詞表
- 詞元的類型 是 字符串,
- 而 模型需要的輸入 是 數字,
- 因此這種類型不方便模型使用。
詞表(vocabulary):字典類型,用來將字符串類型的詞元映射到數字索引中(從0開始)。
- 先將訓練集中的所有文檔合并在一起,對它們的唯一詞元進行統計,得到的統計結果稱之為語料(corpus)。
- 然后根據每個唯一詞元的出現頻率,為其分配一個數字索引。
- 很少出現的詞元則被移除,以降低復雜性。
- 將語料庫中不存在或已刪除的任何詞元都映射到一個特定的未知詞元“<unk>”。
可以選擇增加一個列表,用于保存那些被保留的詞元, 例如:
- 填充詞元(“<pad>”)
- 序列開始詞元(“<bos>”)
- 序列結束詞元(“<eos>”)
'''
Vocab類:構建文本詞表(Vocabulary),管理詞元與索引的映射關系
功能:
構建詞表,管理詞元與索引的映射關系,支持:
詞元 → 索引(token_to_idx)
索引 → 詞元(idx_to_token)
過濾低頻詞
保留特殊詞元(如 <unk>, <pad>填充符, <bos>起始符, <eos>結束符)
'''
class Vocab: #@save"""文本詞表"""# tokens:原始詞元列表(一維或二維)# min_freq:最低詞頻閾值,低于此值的詞會被過濾# reserved_tokens:預定義的特殊詞元(如 ["<pad>", "<bos>"])def __init__(self, tokens=None, min_freq=0, reserved_tokens=None):if tokens is None:tokens = []if reserved_tokens is None:reserved_tokens = []# 統計詞頻,按出現頻率排序counter = count_corpus(tokens) # 統計詞頻self._token_freqs = sorted(counter.items(), key=lambda x: x[1],reverse=True) # 按頻率降序排序(self._token_freqs)# 初始化詞表,索引0留給未知詞元(<unk>)# 未知詞元的索引為0# idx_to_token:索引 → 詞元,索引0 默認是 <unk>(未知詞元),后面是reserved_tokens# token_to_idx:詞元 → 索引,是 idx_to_token 的反向映射self.idx_to_token = ['<unk>'] + reserved_tokensself.token_to_idx = {token: idxfor idx, token in enumerate(self.idx_to_token)}# 按詞頻從高到低添加詞元,過濾低頻詞for token, freq in self._token_freqs: # 跳過低頻詞if freq < min_freq: # 跳過低頻詞breakif token not in self.token_to_idx: # 若詞元不在token_to_idx中,則添加到詞表self.idx_to_token.append(token)self.token_to_idx[token] = len(self.idx_to_token) - 1def __len__(self): # 詞表大小(包括 <unk> 和 reserved_tokens)return len(self.idx_to_token) # 返回詞表大小# 詞表查詢# 支持單個詞元或詞元列表查詢:# vocab["hello"] → 返回索引(如 1)# vocab[["hello", "world"]] → 返回索引列表 [1, 2]# 若詞元不存在,返回 unk 的索引(默認 0)def __getitem__(self, tokens):if not isinstance(tokens, (list, tuple)):return self.token_to_idx.get(tokens, self.unk) # 單個詞元返回索引,未知詞返回0return [self.__getitem__(token) for token in tokens] # 遞歸處理列表# 索引轉詞元# 支持單個索引或索引列表轉換:# vocab.to_tokens(1) → 返回詞元(如 "hello")# vocab.to_tokens([1, 2]) → 返回詞元列表 ["hello", "world"]def to_tokens(self, indices):if not isinstance(indices, (list, tuple)):return self.idx_to_token[indices] # 單個索引返回詞元return [self.idx_to_token[index] for index in indices] # 遞歸處理列表@propertydef unk(self): # 未知詞元的索引為(默認0)return 0@propertydef token_freqs(self): # 原始詞頻統計結果(降序排列)return self._token_freqs # 返回詞頻統計結果# 輔助函數:統計詞元(tokens)的頻率,返回一個 Counter對象
def count_corpus(tokens): #@save"""統計詞元的頻率"""# 這里的tokens是1D列表或2D列表# 如果tokens是空列表或二維列表(如句子列表),則展平為一維列表if len(tokens) == 0 or isinstance(tokens[0], list):# 將詞元列表展平成一個列表tokens = [token for line in tokens for token in line]# collections.Counter統計每個詞元的出現次數,返回類似{"hello":2, "world":1}的字典return collections.Counter(tokens)首先使用時光機器數據集作為語料庫來構建詞表,然后打印前幾個高頻詞元及其索引:
vocab = common.Vocab(tokens)
print(f"前幾個高頻詞及其索引:\n{list(vocab.token_to_idx.items())[:10]}")
現在將每一條文本行轉換成一個數字索引列表:
for i in [0, 10]: # 將每一條文本行轉換成一個數字索引列表print('文本:', tokens[i])print('索引:', vocab[tokens[i]])
2.4.?整合所有功能
在使用上述函數時,將所有功能打包到load_corpus_time_machine函數中, 該函數返回corpus(詞元索引列表)和vocab(時光機器語料庫的詞表)。 這樣做的目的:
- 為了簡化后續的訓練,使用字符(而非單詞)實現文本詞元化;
- 時光機器數據集中的每個文本行不一定是一個句子或一個段落,還可能是一個單詞,因此返回的
corpus僅處理為單個列表,而不是使用多詞元列表構成的一個列表。
- 原始文本數據:通過?
read_time_machine()?加載。- 處理流程:
- 按行讀取文本。
- 按字符拆分為詞元。
- 構建詞表并統計詞頻。
- 將詞元轉換為索引序列。
- (可選)截斷序列長度。
- 輸出:詞元索引列表 + 詞表對象,可直接用于訓練或推理。
# 獲取《時光機器》的 詞元索引序列和詞表對象
# max_tokens:限制返回的詞元索引序列的最大長度(默認 -1 表示不限制)
def load_corpus_time_machine(max_tokens=-1): #@save"""返回時光機器數據集的詞元索引列表和詞表"""lines = read_time_machine() # 加載文本數據,得到文本行列表tokens = tokenize(lines, 'char') # 詞元化:文本行列表→詞元列表,按字符級拆分vocab = common.Vocab(tokens) # 構建詞表# 因為時光機器數據集中的每個文本行不一定是一個句子或一個段落,# 所以將所有文本行展平到一個列表中# vocab[token] 查詢詞元的索引(如果詞元不存在,返回0,即未知詞索引)corpus = [vocab[token] for line in tokens for token in line] # 展平詞元并轉換為索引if max_tokens > 0: # 限制詞元序列長度corpus = corpus[:max_tokens] # 截斷 corpus 到前 max_tokens 個詞元# corpus:詞元索引列表(如 [1, 2, 3, ...])# vocab:Vocab 對象,用于管理詞元與索引的映射return corpus, vocabcorpus, vocab = load_corpus_time_machine() # 加載數據
print(f"corpus詞元索引列表的長度:{len(corpus)}")
print(f"詞表大小:{len(vocab)}")![]()
print(f"詞頻統計(降序):\n{vocab.token_freqs}")
# 索引 ? 詞元轉換
print(f"前10個索引對應的詞元:\n{vocab.to_tokens(corpus[:10])}")
print(f":\n{[vocab[token] for token in corpus[:10]]}") # 等價于直接取corpus[:10]
小結
文本 是序列數據的一種最常見的形式之一。
為了對文本進行預處理,通常:
將文本拆分為詞元,
構建詞表將詞元字符串映射為數字索引,
將文本數據轉換為詞元索引以供模型操作。
3.?語言模型和數據集
在前面(2.文本預處理)中,已解了如何將文本數據映射為詞元,以及將這些詞元可以視為一系列離散的觀測,例如單詞或字符。
- 假設 長度為T的文本序列中的詞元依次為
?。
- 于是,
(
) 可以被認為是文本序列在時間步處的觀測或標簽。
- 在給定這樣的文本序列時,語言模型(language model)的目標是估計序列的聯合概率:
![]()
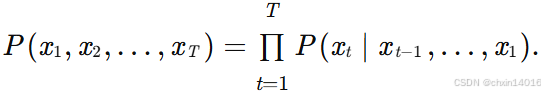
應用場景:
- 生成文本:通過采樣逐詞生成自然語言(如GPT系列模型)。?
- 例如,只需一次抽取一個詞元
,一個理想的語言模型就能夠基于模型本身生成自然文本。
- 從這樣的模型中提取的文本 都將作為自然語言(例如,英語文本)來傳遞。
- 只需要基于前面的對話片斷中的文本,就足以生成一個有意義的對話。
- 但這個需要“理解”文本,而不僅僅是生成語法合理的內容。
- 例如,只需一次抽取一個詞元
- 解決歧義:在語音識別、機器翻譯等任務中,利用語言模型選擇更合理的輸出(如區分“to recognize speech”和“to wreck a nice beach”)。
- 評估文本合理性:判斷句子是否符合語言習慣(如“狗咬人”比“人咬狗”更常見)。
3.1.?學習語言模型
要面對的問題:如何對一個文檔, 甚至是一個詞元序列進行建模。假設在單詞級別對文本數據進行詞元化,則可以依靠在前面(1.序列模型)中對序列模型的分析。從基本概率規則開始:
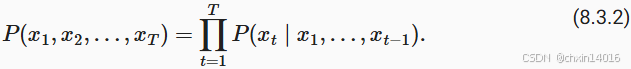
例如,包含了四個單詞的一個文本序列的概率是:
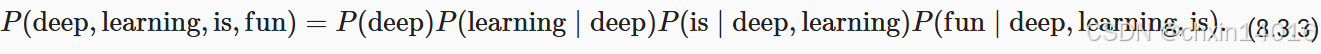
訓練語言模型 需要計算單詞的概率(單字概率),以及給定前面幾個單詞后出現某個單詞的條件概率(條件概率)。這些概率本質上就是語言模型的參數。
- 基于詞頻的統計方法:
-
單字概率:統計語料庫中單詞?w?的出現次數?count(w),除以總單詞數?N:
-
-
條件概率(n-gram模型):統計連續詞元對的出現次數,計算條件概率(如二元語法Bigram):
-
-
假設訓練數據集是一個大型的文本語料庫。
- 訓練數據集中詞的概率可以根據給定詞的相對詞頻來計算。 例如,將估計值?
?計算為任何以單詞“deep”開頭的句子的概率。
- 一種(稍稍不太精確的)方法是統計單詞“deep”在數據集中的出現次數,然后將其除以整個語料庫中的單詞總數(如上面的單字概率)。這種方法效果不錯,特別是對于頻繁出現的單詞。
條件概率如下:
![]()
其中
?:單個單詞 的 出現次數
?:連續單詞對 的 出現次數
局限性:
- 數據稀疏性:長序列(如三元語法Trigram)在語料庫中可能未出現,導致概率為0。
- 語義忽略:無法捕捉“貓”和“貓科動物”的語義關聯。
由于連續單詞對“deep learning”的出現頻率要低得多,所以估計這類單詞正確的概率要困難得多。 特別是對于一些不常見的單詞組合,要想找到足夠的出現次數來獲得準確的估計可能都不容易。 而對于三個或者更多的單詞組合,情況會變得更糟。許多合理的三個單詞組合可能是存在的,但是在數據集中卻找不到。 除非我們提供某種解決方案,來將這些單詞組合指定為非零計數,否則將無法在語言模型中使用它們。如果數據集很小,或者單詞非常罕見,那么這類單詞出現一次的機會可能都找不到。(數據稀疏性)
統計語言模型的改進:拉普拉斯平滑(Laplace smoothing)。
- 具體方法:在所有計數中添加一個小常數?α,避免零概率問題。(m是唯一詞元數)
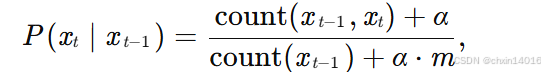
超參數調整:
α=0? :退化為原始計數? ? ? ? ? ? ??
α→∞:概率趨近于均勻分布?1/m
此解決方案有助于處理單元素問題,例如通過:
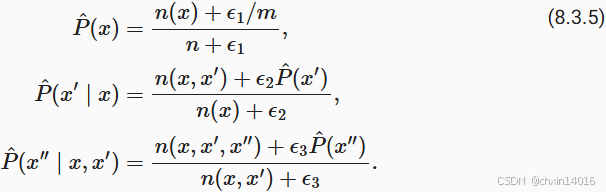
- n:訓練集中的單詞總數,
- m:唯一單詞的數量。
?和
是超參數。以為
?例:
- 當
?時,不應用平滑;
- 當
?接近正無窮大時,
?接近均勻概率分布 1/m。
- 當
上面的公式是?(Wood?et al., 2011)?的一個相當原始的變形。
但這樣的模型很容易變得無效,原因如下:(語義忽略)
- 需要存儲所有計數,內存消耗大。
- 其次,完全忽略了單詞的意思。例如,“貓”(cat)和“貓科動物”(feline)可能出現在相關的上下文中,但是想根據上下文調整這類模型其實是相當困難的。即?無法建模長距離依賴(如跨句子的上下文)。
- 最后,長單詞序列大部分是沒出現過的,因此一個模型如果只是簡單地統計先前“看到”的單詞序列頻率, 那么模型面對這種問題肯定是表現不佳的。
3.2.?馬爾可夫模型與元語法
在討論包含深度學習的解決方案之前,我們需要了解更多的概念和術語。 回想一下在前面(1.序列模型)中對馬爾可夫模型的討論, 并且將其應用于語言建模。
- 如果
, 則序列上的分布滿足一階馬爾可夫性質。
- 階數越高,對應的依賴關系就越長。
- 這種性質推導出了許多可以應用于序列建模的近似公式:
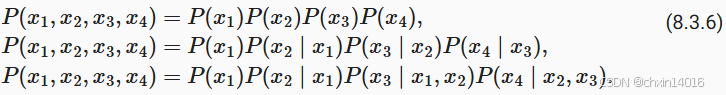
通常,涉及一個、兩個和三個變量的概率公式分別被稱為?一元語法(unigram)、二元語法(bigram)和三元語法(trigram)模型。
馬爾可夫模型與n-gram
- 馬爾可夫性質:假設當前詞元僅依賴前?n?1?個詞元,推導出:
- 一元語法(Unigram):
,忽略上下文。
- 二元語法(Bigram)??:
。
- 三元語法(Trigram)??:
。
- 局限性:
- 高階n-gram稀疏性:三元及以上語法數據更稀疏,性能提升有限。
- 固定窗口大小:無法靈活捕捉不同長度的依賴關系。
【此處開始往后未整理】3.3.?自然語言統計
下面看看在真實數據上如果進行自然語言統計。
根據前面(2.文本預處理)中介紹的時光機器數據集構建詞表,并打印前個最常用的(頻率最高的)單詞:
import random
from mxnet import np, npx
from d2l import mxnet as d2lnpx.set_np()tokens = d2l.tokenize(d2l.read_time_machine())
# 因為每個文本行不一定是一個句子或一個段落,因此我們把所有文本行拼接到一起
corpus = [token for line in tokens for token in line]
vocab = d2l.Vocab(corpus)
vocab.token_freqs[:10]正如我們所看到的,最流行的詞看起來很無聊, 這些詞通常被稱為停用詞(stop words),因此可以被過濾掉。 盡管如此,它們本身仍然是有意義的,我們仍然會在模型中使用它們。 此外,還有個明顯的問題是詞頻衰減的速度相當地快。 例如,最常用單詞的詞頻對比,第10個還不到第1個的1/5。 為了更好地理解,我們可以畫出的詞頻圖:
freqs = [freq for token, freq in vocab.token_freqs]
d2l.plot(freqs, xlabel='token: x', ylabel='frequency: n(x)',xscale='log', yscale='log')通過此圖我們可以發現:詞頻以一種明確的方式迅速衰減。 將前幾個單詞作為例外消除后,剩余的所有單詞大致遵循雙對數坐標圖上的一條直線。 這意味著單詞的頻率滿足齊普夫定律(Zipf’s law), 即第個最常用單詞的頻率為:
![]()
等價于:
![]()
其中α是刻畫分布的指數,c是常數。 這告訴我們想要通過計數統計和平滑來建模單詞是不可行的, 因為這樣建模的結果會大大高估尾部單詞的頻率,也就是所謂的不常用單詞。 那么其他的詞元組合,比如二元語法、三元語法等等,又會如何呢? 我們來看看二元語法的頻率是否與一元語法的頻率表現出相同的行為方式。
bigram_tokens = [pair for pair in zip(corpus[:-1], corpus[1:])]
bigram_vocab = d2l.Vocab(bigram_tokens)
bigram_vocab.token_freqs[:10]這里值得注意:在十個最頻繁的詞對中,有九個是由兩個停用詞組成的, 只有一個與“the time”有關。 我們再進一步看看三元語法的頻率是否表現出相同的行為方式。
trigram_tokens = [triple for triple in zip(corpus[:-2], corpus[1:-1], corpus[2:])]
trigram_vocab = d2l.Vocab(trigram_tokens)
trigram_vocab.token_freqs[:10]最后,我們直觀地對比三種模型中的詞元頻率:一元語法、二元語法和三元語法。
bigram_freqs = [freq for token, freq in bigram_vocab.token_freqs]
trigram_freqs = [freq for token, freq in trigram_vocab.token_freqs]
d2l.plot([freqs, bigram_freqs, trigram_freqs], xlabel='token: x',ylabel='frequency: n(x)', xscale='log', yscale='log',legend=['unigram', 'bigram', 'trigram'])這張圖非常令人振奮!原因有很多:
- 除了一元語法詞,單詞序列似乎也遵循齊普夫定律, 盡管公式?(8.3.7)中的指數更小 (指數的大小受序列長度的影響);
- 詞表中元組的數量并沒有那么大,這說明語言中存在相當多的結構, 這些結構給了我們應用模型的希望;
- 很多元組很少出現,這使得拉普拉斯平滑非常不適合語言建模。 作為代替,我們將使用基于深度學習的模型。
3.4.?讀取長序列數據
由于序列數據本質上是連續的,因此我們在處理數據時需要解決這個問題。 在?8.1節中我們以一種相當特別的方式做到了這一點: 當序列變得太長而不能被模型一次性全部處理時, 我們可能希望拆分這樣的序列方便模型讀取。
在介紹該模型之前,我們看一下總體策略。 假設我們將使用神經網絡來訓練語言模型, 模型中的網絡一次處理具有預定義長度 (例如個時間步)的一個小批量序列。 現在的問題是如何隨機生成一個小批量數據的特征和標簽以供讀取。
首先,由于文本序列可以是任意長的, 例如整本《時光機器》(The Time Machine), 于是任意長的序列可以被我們劃分為具有相同時間步數的子序列。 當訓練我們的神經網絡時,這樣的小批量子序列將被輸入到模型中。 假設網絡一次只處理具有個時間步的子序列。?圖8.3.1畫出了 從原始文本序列獲得子序列的所有不同的方式, 其中,并且每個時間步的詞元對應于一個字符。 請注意,因為我們可以選擇任意偏移量來指示初始位置,所以我們有相當大的自由度。

因此,我們應該從?圖8.3.1中選擇哪一個呢? 事實上,他們都一樣的好。 然而,如果我們只選擇一個偏移量, 那么用于訓練網絡的、所有可能的子序列的覆蓋范圍將是有限的。 因此,我們可以從隨機偏移量開始劃分序列, 以同時獲得覆蓋性(coverage)和隨機性(randomness)。 下面,我們將描述如何實現隨機采樣(random sampling)和?順序分區(sequential partitioning)策略。
3.4.1.?隨機采樣
在隨機采樣中,每個樣本都是在原始的長序列上任意捕獲的子序列。 在迭代過程中,來自兩個相鄰的、隨機的、小批量中的子序列不一定在原始序列上相鄰。 對于語言建模,目標是基于到目前為止我們看到的詞元來預測下一個詞元, 因此標簽是移位了一個詞元的原始序列。
下面的代碼每次可以從數據中隨機生成一個小批量。 在這里,參數batch_size指定了每個小批量中子序列樣本的數目, 參數num_steps是每個子序列中預定義的時間步數。
def seq_data_iter_random(corpus, batch_size, num_steps): #@save"""使用隨機抽樣生成一個小批量子序列"""# 從隨機偏移量開始對序列進行分區,隨機范圍包括num_steps-1corpus = corpus[random.randint(0, num_steps - 1):]# 減去1,是因為我們需要考慮標簽num_subseqs = (len(corpus) - 1) // num_steps# 長度為num_steps的子序列的起始索引initial_indices = list(range(0, num_subseqs * num_steps, num_steps))# 在隨機抽樣的迭代過程中,# 來自兩個相鄰的、隨機的、小批量中的子序列不一定在原始序列上相鄰random.shuffle(initial_indices)def data(pos):# 返回從pos位置開始的長度為num_steps的序列return corpus[pos: pos + num_steps]num_batches = num_subseqs // batch_sizefor i in range(0, batch_size * num_batches, batch_size):# 在這里,initial_indices包含子序列的隨機起始索引initial_indices_per_batch = initial_indices[i: i + batch_size]X = [data(j) for j in initial_indices_per_batch]Y = [data(j + 1) for j in initial_indices_per_batch]yield torch.tensor(X), torch.tensor(Y)下面我們生成一個從0到34的序列。 假設批量大小為2,時間步數為5,這意味著可以生成? 個“特征-標簽”子序列對。 如果設置小批量大小為2,我們只能得到3個小批量。
my_seq = list(range(35))
for X, Y in seq_data_iter_random(my_seq, batch_size=2, num_steps=5):print('X: ', X, '\nY:', Y)3.4.2.?順序分區
在迭代過程中,除了對原始序列可以隨機抽樣外, 我們還可以保證兩個相鄰的小批量中的子序列在原始序列上也是相鄰的。 這種策略在基于小批量的迭代過程中保留了拆分的子序列的順序,因此稱為順序分區。
def seq_data_iter_sequential(corpus, batch_size, num_steps): #@save"""使用順序分區生成一個小批量子序列"""# 從隨機偏移量開始劃分序列offset = random.randint(0, num_steps)num_tokens = ((len(corpus) - offset - 1) // batch_size) * batch_sizeXs = torch.tensor(corpus[offset: offset + num_tokens])Ys = torch.tensor(corpus[offset + 1: offset + 1 + num_tokens])Xs, Ys = Xs.reshape(batch_size, -1), Ys.reshape(batch_size, -1)num_batches = Xs.shape[1] // num_stepsfor i in range(0, num_steps * num_batches, num_steps):X = Xs[:, i: i + num_steps]Y = Ys[:, i: i + num_steps]yield X, Y基于相同的設置,通過順序分區讀取每個小批量的子序列的特征X和標簽Y。 通過將它們打印出來可以發現: 迭代期間來自兩個相鄰的小批量中的子序列在原始序列中確實是相鄰的。
for X, Y in seq_data_iter_sequential(my_seq, batch_size=2, num_steps=5):print('X: ', X, '\nY:', Y)現在,我們將上面的兩個采樣函數包裝到一個類中, 以便稍后可以將其用作數據迭代器。
class SeqDataLoader: #@save"""加載序列數據的迭代器"""def __init__(self, batch_size, num_steps, use_random_iter, max_tokens):if use_random_iter:self.data_iter_fn = d2l.seq_data_iter_randomelse:self.data_iter_fn = d2l.seq_data_iter_sequentialself.corpus, self.vocab = d2l.load_corpus_time_machine(max_tokens)self.batch_size, self.num_steps = batch_size, num_stepsdef __iter__(self):return self.data_iter_fn(self.corpus, self.batch_size, self.num_steps)最后,我們定義了一個函數load_data_time_machine, 它同時返回數據迭代器和詞表, 因此可以與其他帶有load_data前綴的函數 (如?3.5節中定義的?d2l.load_data_fashion_mnist)類似地使用。
?
def load_data_time_machine(batch_size, num_steps, #@saveuse_random_iter=False, max_tokens=10000):"""返回時光機器數據集的迭代器和詞表"""data_iter = SeqDataLoader(batch_size, num_steps, use_random_iter, max_tokens)return data_iter, data_iter.vocab3.5.?小結
語言模型是自然語言處理的關鍵。
n元語法通過截斷相關性,為處理長序列提供了一種實用的模型。
長序列存在一個問題:它們很少出現或者從不出現。
齊普夫定律支配著單詞的分布,這個分布不僅適用于一元語法,還適用于其他n元語法。
通過拉普拉斯平滑法可以有效地處理結構豐富而頻率不足的低頻詞詞組。
讀取長序列的主要方式是隨機采樣和順序分區。在迭代過程中,后者可以保證來自兩個相鄰的小批量中的子序列在原始序列上也是相鄰的。
4.?循環神經網絡
在?8.3節中, 我們介紹了n元語法模型, 其中單詞 ?在時間步t的條件概率僅取決于前面 n-1個單詞。 對于時間步 t-(n-1)之前的單詞, 如果我們想將其可能產生的影響合并到
?上, 需要增加n,然而模型參數的數量也會隨之呈指數增長, 因為詞表
?需要存儲
?個數字, 因此與其將
?模型化, 不如使用隱變量模型:
![]()
其中 ?是隱狀態(hidden state), 也稱為隱藏變量(hidden variable), 它存儲了到時間步 t-1 的序列信息。 通常,我們可以基于當前輸入
?和先前隱狀態?
?來計算時間步t處的任何時間的隱狀態:
![]()
對于?(8.4.2)中的函數,隱變量模型不是近似值。 畢竟
?是可以僅僅存儲到目前為止觀察到的所有數據, 然而這樣的操作可能會使計算和存儲的代價都變得昂貴。
回想一下,我們在?4節中 討論過的具有隱藏單元的隱藏層。 值得注意的是,隱藏層和隱狀態指的是兩個截然不同的概念。 如上所述,隱藏層是在從輸入到輸出的路徑上(以觀測角度來理解)的隱藏的層, 而隱狀態則是在給定步驟所做的任何事情(以技術角度來定義)的輸入, 并且這些狀態只能通過先前時間步的數據來計算。
循環神經網絡(recurrent neural networks,RNNs) 是具有隱狀態的神經網絡。 在介紹循環神經網絡模型之前, 我們首先回顧?4.1節中介紹的多層感知機模型。
4.1.?無隱狀態的神經網絡
讓我們來看一看只有單隱藏層的多層感知機。 設隱藏層的激活函數為Φ, 給定一個小批量樣本 , 其中批量大小為n,輸入維度為d, 則隱藏層的輸出
?通過下式計算:
![]()
![]()
4.2.?有隱狀態的循環神經網絡
4.3.?基于循環神經網絡的字符級語言模型
4.4.?困惑度(Perplexity)
4.5.?小結
對隱狀態使用循環計算的神經網絡稱為循環神經網絡(RNN)。
循環神經網絡的隱狀態可以捕獲直到當前時間步序列的歷史信息。
循環神經網絡模型的參數數量不會隨著時間步的增加而增加。
我們可以使用循環神經網絡創建字符級語言模型。
我們可以使用困惑度來評價語言模型的質量。
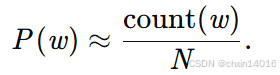
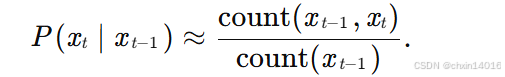

html基礎和開發工具)




 ——在職考研 199 管綜 + 英語二 30 周「順水行舟」上岸指南)
)


![ndk { setAbiFilters([‘armeabi-v7a‘, “arm64-v8a“]) }](http://pic.xiahunao.cn/ndk { setAbiFilters([‘armeabi-v7a‘, “arm64-v8a“]) })





進程地址空間)


