數據結構
1.緒論

1.1.1數據結構的基本概念
- 數據
- 數據元素:數據的基本單位,一個數據元素由多個數據項組成,數據項是組成數據元素不可分割的最小單位
- 數據對象:具有相同性質的數據元素的集合,是數據的一個子集
- 數據類型:是一個值的集合和定義在此集合上的一組操作的總稱
- 原子類型:值不可再分
- 結構類型:值可以再分解為若干成分
- 抽象數據類型(ADT):一個數學模型及定義在該數學模型上的一組操作,通常包括數據的某種抽象,定義了數據的取值范圍及其結構形式,以及對數據操作的集合
- 數據結構:相互之間寸止一種或多種特定關系的數據元素的集合,包括三方面:邏輯結構、存儲結構、數據的運算
1.1.2數據結構三要素
邏輯結構
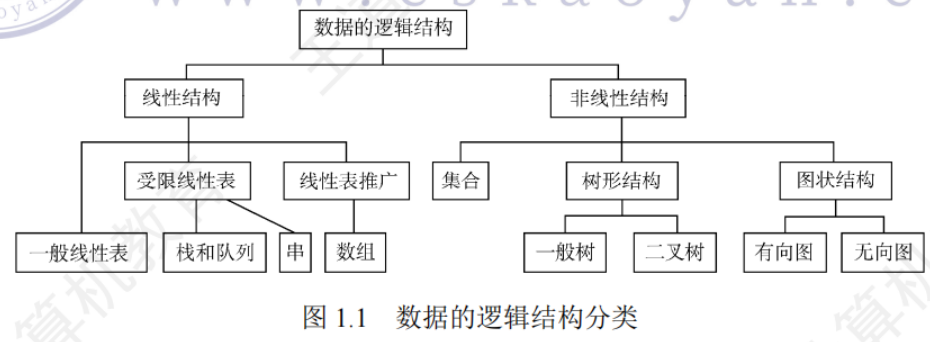
集合、線性結構、樹形結構、圖狀結構、網狀結構
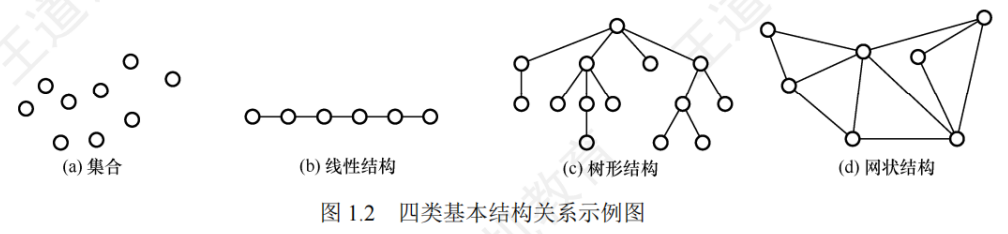
存儲結構
順序存儲:邏輯上相鄰的元素存儲在物理位置上也相鄰的存儲單元中,元素之間的關系由存儲單元之間的鄰接關系來體現
優點:隨機存取 元素占用的存儲空間最少
缺點:只能使用相鄰的存儲單元 外部碎片多
鏈式存儲:不要求邏輯上相鄰的元素在物理位置上也相鄰,借助指示元素存儲地址的指針來指示元素之間的邏輯關系
優點:不產生碎片
缺點:存儲指針占用額外的存儲空間 只能順序存取
索引存儲:存儲元素信息同時建立索引表,索引表中的每一項稱為索引項,索引項的一般形式(關鍵字、地址)
有點:檢索速度快
缺點:索引表占用額外存儲空間 增加和刪除數據時也要修改索引表
散列存儲:根據元素的關鍵字直接計算其存儲地址(哈希存儲)
優點:計算,增加、刪除節點快
缺點:散列函數的性能造成哈希沖突,解決沖突造成時間和空間開銷
1.2算法及其評價
1.2.1算法
五大特性
- 有窮性:算法必須在有限步之后結束,每一步在有限時間內完成
- 確定性:每條指令有明確的含義,相同的輸入只能有相同的輸出
- 可行性:算法描述操作都可以通過已實現的基本運算執行有限次實現
- 輸入:零個或多個輸入
- 輸出:一個或多個輸出
目標
確定性:正確的解決求解問題
可讀性:便于理解
健壯性:對非法輸入做出反應/處理,不會產生莫名其妙的輸出
高效率與低存儲量要求
1.2.2算法效率
時間復雜度

最壞時間復雜度(一般考慮最壞時間復雜度)
平均時間復雜度
最好時間復雜度
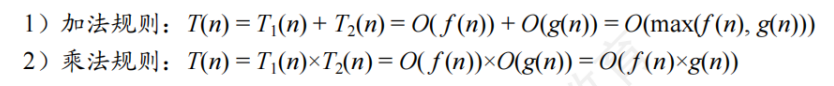
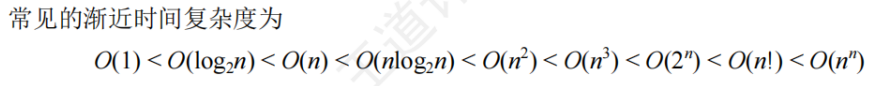
空間復雜度

2.線性表

2.1.1定義與基本操作

特點:
- 元素個數有限
- 元素具有邏輯上的順序性,表中元素有其先后次序
- 元素都是數據元素,每個元素單個
- 元素數據類型相同,每個元素占用相同大小的存儲空間
- 元素具有抽象性
2.1.2線性表的基本操作

2.2.1順序表的定義
線性表的順序存儲也稱順序表,用一組地址連續的存儲單元一次存儲線性表中的數據元素,從而使邏輯上相鄰的兩個元素在物理位置上也相鄰
特點:邏輯順序與其存儲的物理順序相同

注意:線性表中的元素位序是從1開始的,而數組中的元素下標從0開始
優缺點
優點:
隨機訪問,可通過首地址和元素序號在O(1)時間復雜度內查找元素
存儲密度高
缺點:
元素的插入和刪除需要移動大量元素,插入平均移動n/2,刪除平均移動(n-1)/2
需要連續的存儲空間
靜態分配
#define MaxSize 50
typedef struct{ElemType data{MaxSize};int length;
}SqList;
動態分配
#define InitSize 50
typedef struct{ElemType *data;int Maxsize,length;
}SeqList; L.data = (ElemType*)malloc(sizeof(ElemType) * InitSize)
2.2.2順序表基本操作實現
初始化
//靜態
void InitList(SqList &L){L.length = 0 ;
}
//動態
void InitList(SeqList &L){L.data = (ElemType*)malloc(sizeof(ElemType) * InitSize);L.length = 0 ;L.MaxSize = InitSize;
}插入
在順序表的第i個位置插入元素
- 判斷i是否合法
- 將第i個元素及其后所有元素一次向后移動一個位置
- 插入新元素e
- 順序表長度加1
bool ListInsert(SqList &L,int i,ElemType e){if(i < 1 || i > L.length+1)return false;if(L.length >= MaxSize)return false;for(int j = L.length;j>=i;j--)L.data[j] = L.data[j-1];L.data[i-1] = e;L.length++;return true;
}
最好情況:在表尾插入,O(1)
最壞情況:表首插入,O(n)
平均:O(n)
刪除操作
刪除表中第i個位置的元素,用引用變量e返回
- 判斷i是否合法
- 將被刪除元素賦值給e
- 將第i+1個元素及其后所有元素依次向前移動一個位置
bool ListDelete(SqList &L,int i, ElemType &e){if(i<1||i>L.length)return false;e=L.data[i-1];for(int j = i;j<L.length;j++){L.data[j-1] = L.data[j];}L.length--;return true;
}
最好情況:刪除表尾元素,O(1)
最壞情況:刪除表頭元素,O(n)
平均:O(n)
順序表的插入和刪除操作時間耗費主要在元素移動上
按值查找
查找第一個元素值等于e的元素,并返回其位序
int LocateElem(SqList L,ElemType e){int i;for(int j = 0;j<L.length;j++){if(L.data[j]==e){return i+1;}return 0;}
}
最好:查找元素在表頭,O(1)
最壞:查找元素在表尾,O(n)
平均:O(n)
2.3.1單鏈表的定義
線性表的鏈式存儲也稱單鏈表,通過任意一組存儲單元來存儲線性表中數據元素,對于每個鏈表節點,出存放其自身信息外,還需要存放一個指向其后繼的指針

typedef struct LNode{ElemType data;struct LNode *next;
}LNode,*LinkList;
優點:不再需要大量連續存儲單元
缺點:增加了指針域,資源占用多 非隨機存取,不能直接找到表中某個特定節點,查找節點需要從頭遍歷
通常使用一個頭指針來標識一個單鏈表,指出鏈表的起始地址,頭指針為NULL表示一個空表
另外,為了操作方便,也會在第一個數據節點之前附加一個頭節點,數據域可以不設任何信息,也可以記錄表長等信息
單鏈表帶頭節點時,頭指針指向頭節點,不帶頭結點時,頭指針指向第一個數據節點

頭節點與頭指針的關系:不管帶不帶頭節點,頭指針始終指向鏈表的第一個節點,而頭節點時帶頭結點的鏈表中的第一個節點,通常不保存信息
引入頭節點的好處:
- 第一個數據節點的位置與被存放在頭節點的指針域中,因此鏈表的第一個外置上的操作和在表其他位置上的操作一致,無須特殊處理
- 無論鏈表是否為空,頭指針都是指向頭節點的非空指針,因此空表和非空表的處理也統一
2.3.2單鏈表基本操作實現
單鏈表初始化
帶頭結點
bool InitList(LinkList &L){L = (LNode*)malloc(sizeof(LNode));L->next = NULL;return true
}
不帶頭節點
bool InitList(LinkList &L){L=NULL;return true;
}
求表長
從第一個節點開始依次訪問每一個節點,計數值加1
//求表的長度
int Length(LinkList L){int len = 0; //統計表長 LNode *p = L;while(p->next != NULL){p = p->next;len++;}return len;
}
O(n)
按序號查找節點
//按位查找,返回第i個元素(帶頭結點)
LNode * GetElem(LinkList L, int i){if(i<0)return NULL;LNode *p; //指針p指向當前掃描到的結點 int j=0; //當前p指向的是第幾個結點 p = L; //L指向頭結點,頭結點是第0個結點(不存數據) while(p!=NULL && j<i){ //循環找到第i個結點 p = p->next;j++;}return p;
}
O(n)
按值查找節點
//按值查找,找到數據域==e的結點
LNode *LocateElem(LinkList L, ElemType e){LNode *p = L->next;//從第1個結點開始查找數據域為e的結點while(p!=NULL && p->data!=e)p = p->next;return p; //找到后返回該結點指針,否則返回NULL
}
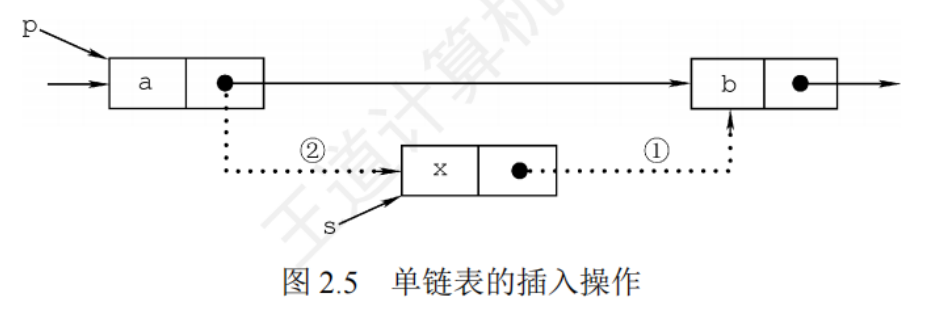
插入節點
需要先找到待插入位置的前驅,即第i-1個節點
注意順序
//在第i個位置插入元素e(帶頭結點)
bool ListInsert(LinkList &L,int i, ElemType e){if(i<1)return false;LNode *p; //指針p指向當前掃描到的結點 int j=0; //當前p指向的是第幾個結點 p = L; //L指向頭結點,頭結點是第0個結點(不存數據) while(p!=NULL && j<i-1){ //循環找到第 i-1 個結點 p=p->next;j++;}if(p==NULL) //i值不合法 return false;LNode *s = (LNode *)malloc(sizeof(LNode));s->data = e;s->next = p->next;p->next = s; //將結點s連到p之后 return true; //插入成功
}

O(n)
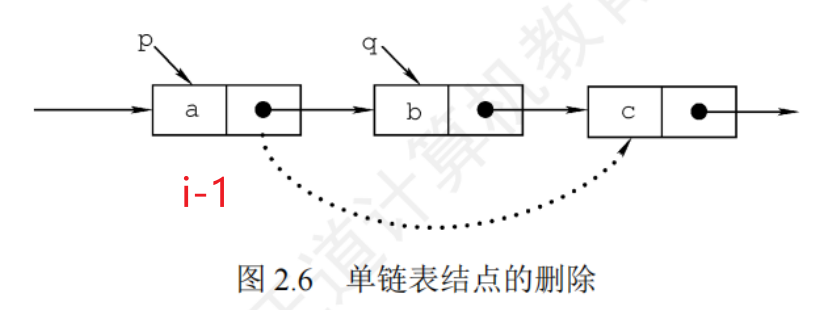
刪除節點
- 檢查合法性
- 找到第 i-1 個節點
- 再刪除第 i 個節點
//刪除指定結點p
bool DeleteNode (LNode *p){if(p==NULL)return false;LNode *q = p->next; //令q指向*p的后繼結點 p->data = p->next->data;//和后繼結點交換數據域 p->next = q->next; //將*q結點從鏈中“斷開” free(q); //釋放后繼結點的存儲空間 return true;
}
O(n)
插入時,若鏈表不帶頭節點,需要判斷插入位置是否為1,若是,需要修改頭指針:若帶頭節點則不修改
刪除時,若鏈表不帶頭節點,需要判斷刪除節點是否為第一個數據節點,若是,則需要修改頭指針;若帶頭節點則不修改
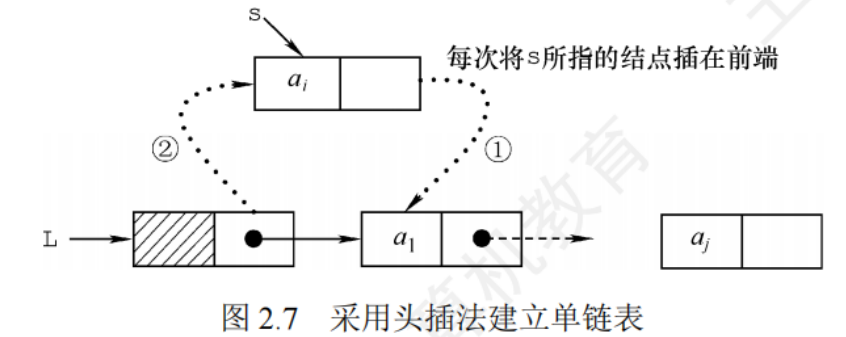
頭插法建立單鏈表(重點)
生成鏈表中節點的次序與輸入數據的次序不一致
LinkList List_HeadInsert(LinkList &L){ //逆向建立單鏈表 LNode *s;int x;L = (LinkList)malloc(sizeof(LNode));//創建頭結點 L->nest = NULL; //初始為空鏈表 scanf("%d",&x); //輸入結點的值 while(x!=9999){ //輸入9999表示結束 s=(LNode*)malloc(sizeof(LNode));//創建新結點 s->data = x;s->next = L->next;L->next = s; //將新結點插入表中,L為頭指針 scanf("%d",&x);}return L;
}
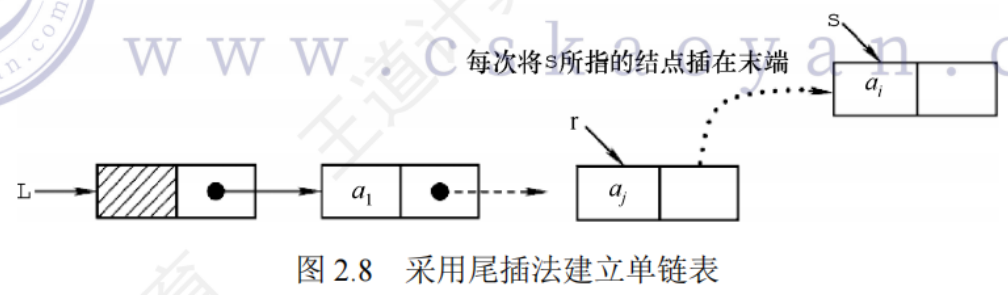
尾插法建立單鏈表(重點)
鏈表中節點的順序與輸入順序一致
增加一個尾指針,指向鏈表尾部
LinkList List_TailInsert(LinkList &L){ //正向建立單鏈表 int x; //設ElemType為整型 L = (LinkList)malloc(sizeof(LNode));//建立頭結點 LNode *s, *r=L; //r為表尾指針 scanf("%d",&x); //輸入結點的值 while(x!=9999){ //輸入9999表示結束 s = (LNode*)malloc(sizeof(LNode));s->data = x;r->next = s;r=s; //r指向新的表尾結點 scanf("%d",&x);} r->next->NULL; //尾結點指針置空 return L;
}
2.3.3雙鏈表
單鏈表局限:只有一個指向其后繼的指針,只能從前向后遍歷,要訪問某個節點的前驅,只能從頭開始遍歷
prior和next分別指向某節點的直接前驅和直接后繼

typedef struct DNode{ //定義雙鏈表結點類型ElemType data; //數據域 struct DNode *prior,*next; //前驅和后繼指針
}DNode, *DLinklist; //初始化雙鏈表(帶頭結點)
bool InitDLinklist(DLinklist &L){L = (DNode *)malloc(sizeof(DNode));if(L == NULL)return false;L->prior = NULL;L->next = NULL;return true;
} void testDLinkList(){//初始化雙鏈表DLinklist L;InitDLinkList(L);......
}
雙鏈表的插入和刪除操作時間復雜度只有O(1)
插入
被插入節點先連后繼再連前驅
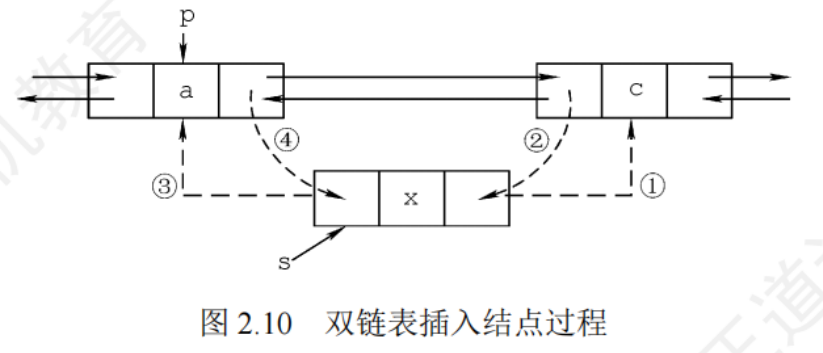

//在p結點之后插入s結點
bool InsertNextDNode (DNode *p, DNode *s){if(p==NULL || s==NULL) //非法參數 return false;s->next = p->next;if(p-next != NULL)p->next->prior=s; //如果p結點后有后繼節點 s->prior = p;p->next = s;return true;
}
刪除
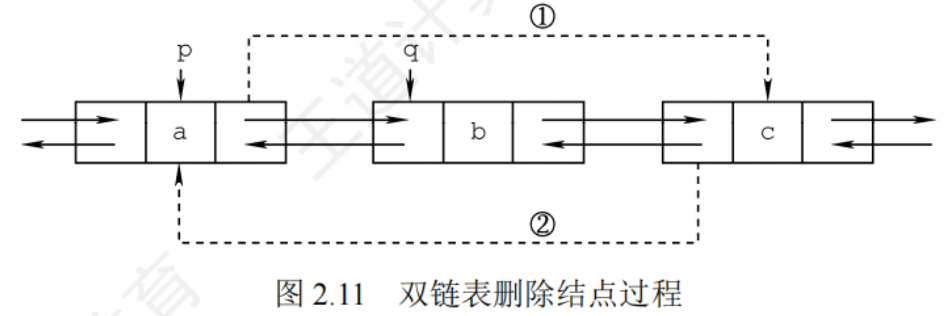
//刪除p結點的后繼結點
bool DeleteNextDNode(DNode *p){if(p == NULL) return false;DNode *q = p->next; //找到p的后繼結點qif(q == NULL) return false; //p沒有后繼 p->next = q->next;if(q->next != NULL)q->next->prior = p;free(q); //釋放結點空間 return true;
} void DestoryList(DLinklist &L){//循環釋放各個數據節點while (L->next != NULL)DeleteNextDNode(L);free(L); //釋放頭結點 L = NULL; //頭指針指向NULL
}
2.3.4循環鏈表
循環鏈表與單鏈表的區別:表中最后一個節點的指針不是指向NULL,而是指向頭節點,從而整個鏈表形成一個環
單鏈表只能從頭節點開始遍歷,循環單鏈表可以從任意節點開始遍歷
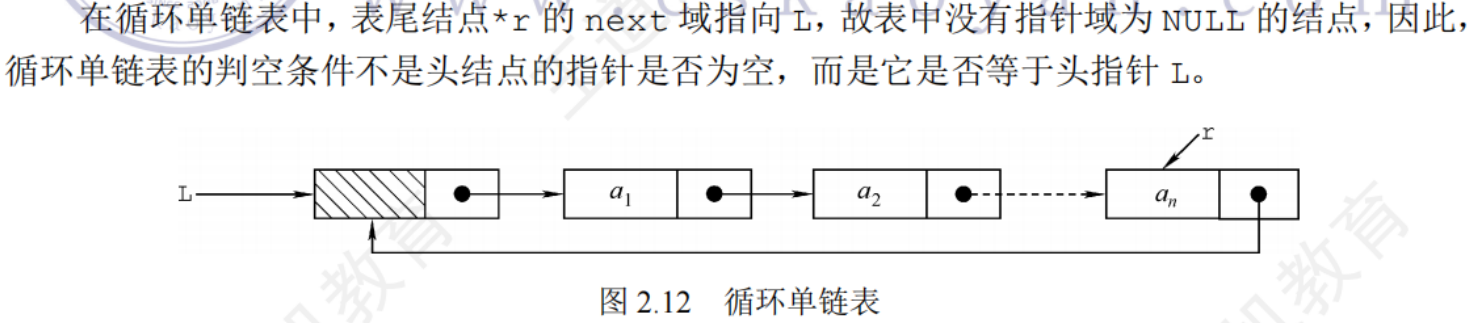
typedef struct LNode{ //定義單鏈表結點類型 ElemType data; //每個結點存放一個數據元素 struct LNode *next; //指針指向下一個結點
}LNode, *LinkList;//初始化一個循環單鏈表
bool InitList(LinkList &L){L = (LNode *)malloc(sizeof(LNode)); //分配一個頭結點 if(L==NULL) //內存不足,分配失敗 return false;L->next = L; //頭結點next指向頭結點 return true;
}//判斷循環單鏈表是否為空
bool Empty(LinkList L){if(L->next == L)return true;elsereturn false;
} //判斷結點p是否為循環單鏈表的表尾結點
bool isTail(LinkList L, LNode *p){if(p->next == L)return true;elsereturn false;
}
2.3.4循環雙鏈表
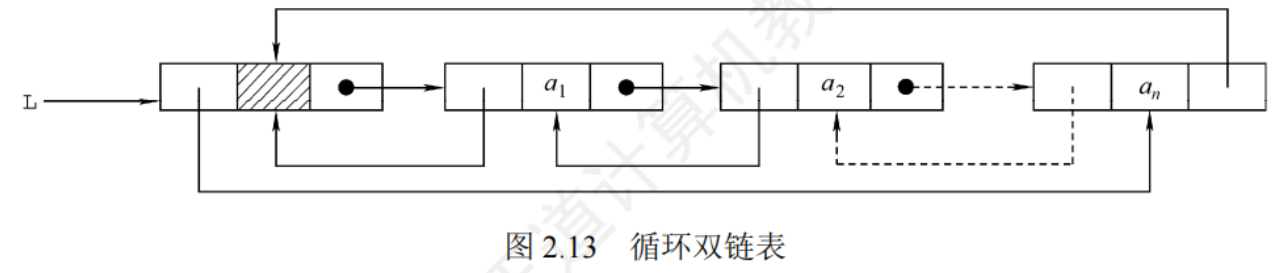
typedef struct DNode{ElemType data;struct DNode *prior,*next;
}DNode,*DLinklist;//初始化空的循環雙鏈表
bool InitDLinkList(DLinklist &L){L = (DNode *)malloc(sizeof(DNode)); //分配一個頭結點 if(L==NULL) //內存不足,分配失敗 return false;L->prior = L; //頭結點的 prior 指向頭結點 L->next = L; //頭結點的 next 指向頭結點 return true;
} void testDLinkList(){//初始化循環雙鏈表DLinklist L;InitDLinkList(L);......
}//判斷循環雙鏈表是否為空
bool Empty(DLinklist L){if(L->next == L)return true;elsereturn false;
} //判斷結點p是否為循環雙鏈表的表尾結點
bool isTail(DLinklist L, DNode *p){if(p->next == L)return true;elsereturn false;
}
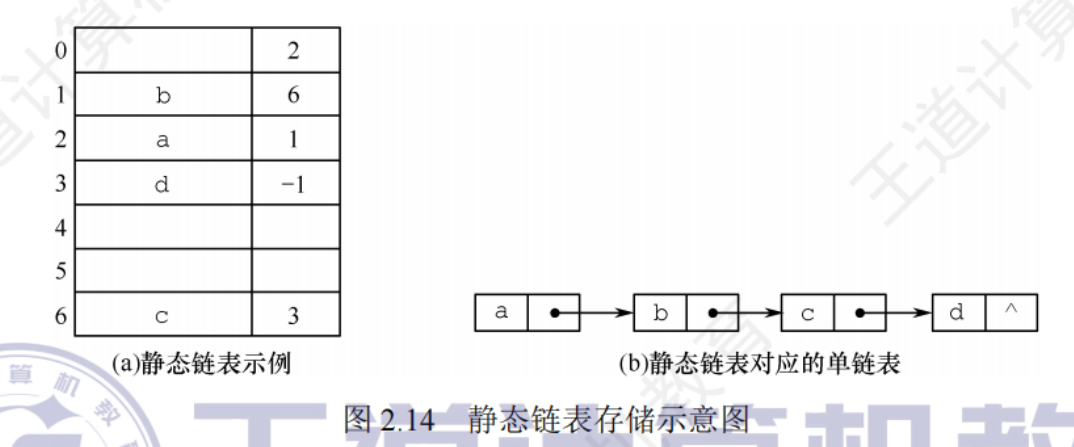
2.3.5靜態鏈表
使用數組來描述鏈表的鏈式存儲結構,節點也有數據域和指針域,但是指針是節點在數組中的相對地址(數組下標),也稱游標,和順序表一樣,靜態鏈表也需要預先分配一塊連續的內存空間
#define MaxSize 10 //靜態鏈表的最大長度
struct Node{ //靜態鏈表結構類型的定義 ElemType data; //存儲數據元素 int next; //下一個元素的數組下標
};
typeof struct Node SLinkList [MaxSize];
2.3.6順序表和鏈表的比較(重點)
存取方式
順序表既可以順序存取,又可以隨機存取,鏈表只能從表頭開始依次順序存取
邏輯結構和物理結構
采用順序存儲時,邏輯上相鄰的元素,對應物理位置也相鄰
采用鏈式存儲時,邏輯上相鄰的元素,物理存儲位置不一定相鄰,對應邏輯關系是通過指針鏈接實現的
查找、插入、刪除
按值查找,順序表無序時,時間復雜度均為O(n),順序表有序時,可采用折半查找,此時時間復雜度為O(longn)
按序號查找,順序表支持隨機訪問,時間復雜度只有O(1),而鏈表的時間復雜度為O(n),
順序表的插入和刪除平均需要移動半個表長元素,鏈表的插入刪除只需修改相關節點的指針域
空間分配
順序存儲在靜態存儲分配情形下,一旦存儲空間裝滿就不能擴充,若再加入新元素,則會出現內存溢出,因此需要預先分配足夠大的存儲空間。預先分配過大,可能會導致順序表后部大量閑置;預先分配過小,又會造成溢出。動態存儲分配雖然存儲空間可以擴充,但需要移動大量元素,導致操作效率降低,而且若內存中沒有更大塊的連續存儲空間,則會導致分配失敗。鏈式存儲的結點空間只在需要時申請分配,只要內存有空間就可以分配,操作靈活、高效。此外,鏈表的每個結點都帶有指針域,因此存儲密度不夠大。
3.棧、隊列、數組

3.1.1棧的基本概念
棧是只允許在一端進行插入或刪除操作的線性表
棧頂:線性表允許進行插入和刪除操作的一端
棧底:固定的,不允許進行插入或刪除操作的一端
空棧:不含任何元素的空表
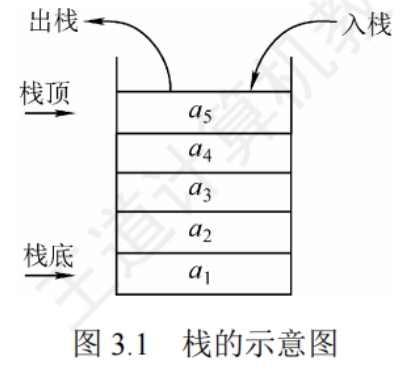
后進先出 LIFO
基本操作

棧的數學性質:卡特蘭數公式,當有n個不同的元素入棧時,出棧元素不同排列個數為
1n+1C2nn
\frac{1}{n+1}C_{2n}^n
n+11?C2nn?
3.1.2棧的順序存儲結構
采用順序存儲的棧稱為順序棧,使用一組地址連續的存儲單元存放自棧底到棧頂的數據元素,同時增加一個指示當前棧頂元素位置的指針
//初始化棧
void InitStack(SqStack &S){S.top = -1; //初始化棧頂指針
} void testStack(){SqStack S; //聲明一個順序棧(分配空間)InitStack(S);......
} //判斷棧空
bool StackEmpty(SqStack S){if(S.top == -1) //棧空return true;elsereturn false; //不空
}
順序棧的入棧操作手數組上界的約束,入棧時可能會發生棧上溢
順序棧基本操作
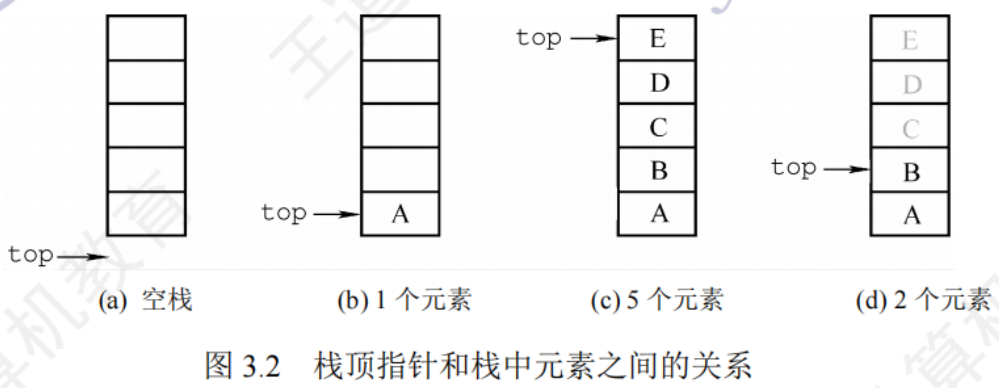
入棧
- 判斷棧滿
- 棧頂指針加1
- 元素入棧
//新元素入棧
bool Push(SqStack &S,ElemType x){if(S.top == MaxSize-1) //棧滿,報錯return false;S.top = S.top+1; //指針先+1 S.data[S.top] = x; //新元素入棧 return true;
}
出棧
- 判斷棧空
- 元素出棧
- 棧頂指針減1
//出棧操作
bool Pop(SqStack &S,ElemType &x){if(S.top == -1) //棧空,報錯return false;x = S.data[S.top]; //棧頂元素先出棧 S.top = S.top-1; //指針再-1 return true;
}
讀棧頂元素
//讀棧頂元素操作
bool Pop(SqStack &S,ElemType &x){if(S.top == -1) //棧空,報錯return false;x = S.data[S.top]; //x記錄棧頂元素 return true;
}
共享棧
將兩個棧底分別設置在共享空間的兩端,兩個棧頂向共享空間中間延伸
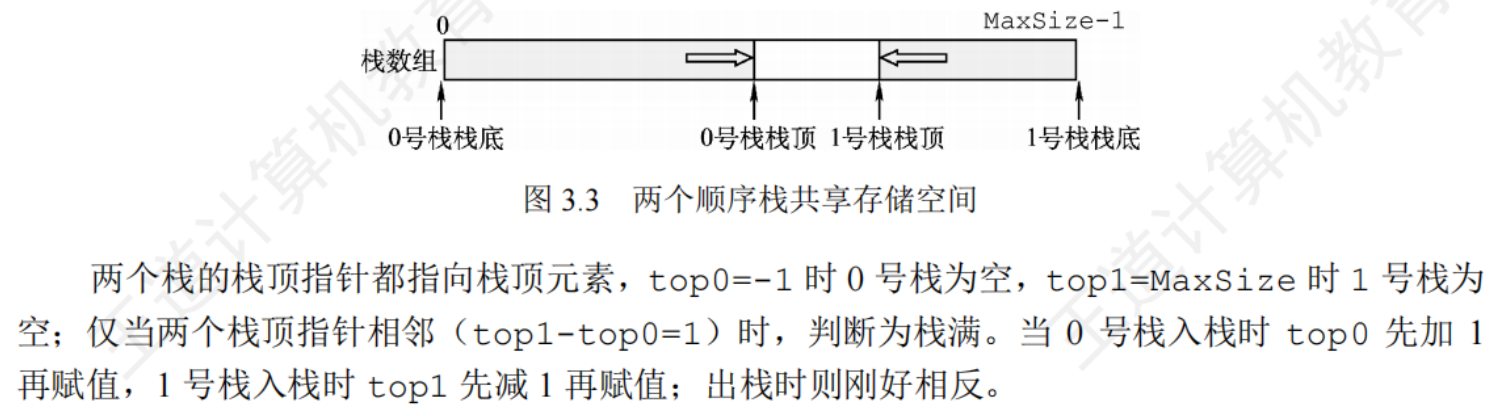
3.1.3棧的鏈式存儲結構
采用鏈式存儲結構的棧稱為鏈棧,其優點是便于多個棧共享存儲空間提高效率,且不存在棧上溢

typedef struct Linknode{ElemType data; //數據域 struct Linknode *next; //指針域
}*LiStack; //棧類型定義
3.2.1隊列的定義
隊列簡稱隊,也是一種操作受限的線性表,只允許在表的一端進行插入,在表的另一端進行刪除
先進先出 FIFO

隊頭:只允許刪除的一端,也稱隊首
隊尾:允許插入的一端
空隊列:不含任何元素的空表
基本操作
棧和隊列都不可以直接讀取中間元素

3.2.2隊列的順序存儲結構
兩個指針:隊首指針front指向隊首元素,隊尾指針rear指向隊尾元素的下一個位置
#define MaxSize 10 //定義隊列中元素的最大個數
typedef struct{ElemType data[MaxSize]; //用靜態數組存放隊列元素int front,rear; //隊頭指針和隊尾指針
}SqQueue;//初始化隊列
void InitQueue(SqQueue &Q){//初始時 隊頭、隊尾指針指向0Q.rear = Q.front = 0;
} void testQueue(){//聲明一個隊列(順序存儲)SqQueue Q;InitQueue(Q);......
}//判斷隊列是否為空
bool QueueEmpty(SqQueue Q) {if(Q.rear == Q.front) //隊空條件return true;else return false;
}
入隊
- 判斷隊滿
- 元素隊尾入隊
- 隊尾指針加1
//入隊操作
bool EnQueue(SqQueue &Q,ElemType x){if(隊列已滿)return false; //隊滿則報錯Q.data[Q.rear] = x;Q.rear = Q.rear+1;return true;
}
出隊
- 判斷對空
- 隊首元素出隊
- 對數指針加1
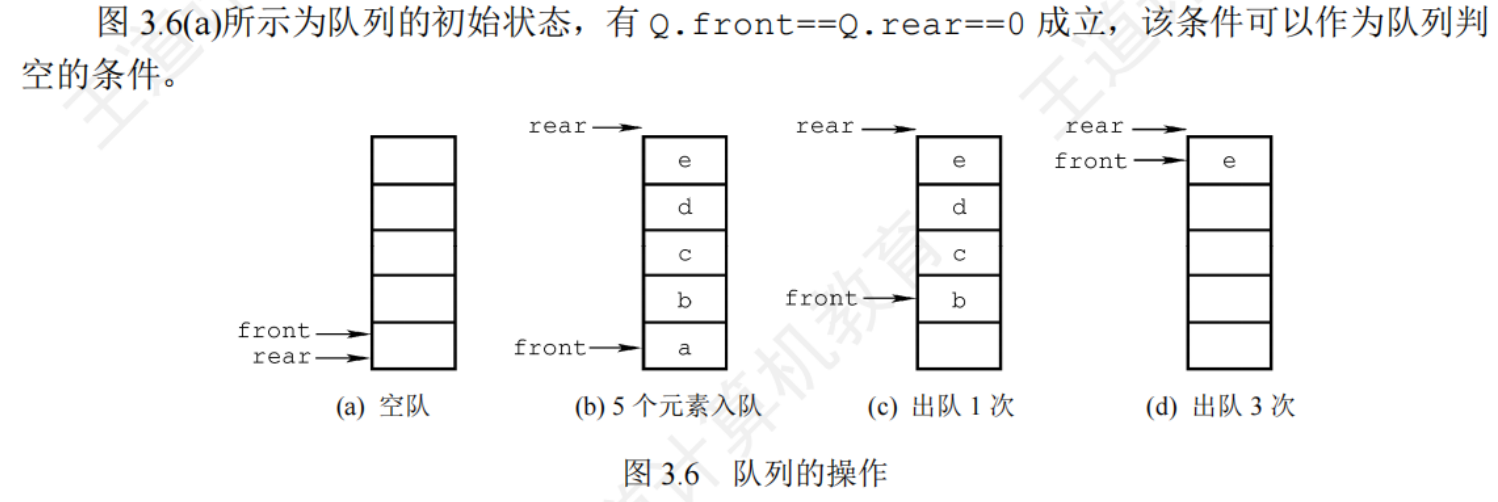
循環隊列(模運算)
把存儲隊列元素的表在邏輯上視為一個環,稱為循環隊列
初始時:Q.front == (Q.front + 1) %MaxSize
隊首指針進1:Q.front = (Q.rear + 1)%MaxSize
隊尾指針進1:Q.rear = (Q.rear + 1)%MaxSize
隊列長度:(Q.rear + MaxSize - Q.front)%MaxSize
出入隊時,指針都按順時針方向進1
隊空條件:Q.front == Q.rear
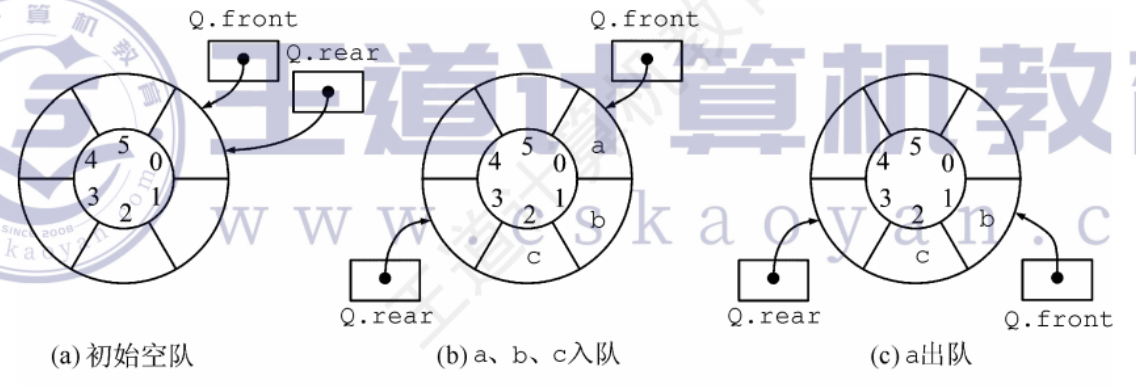
區分隊滿隊空:
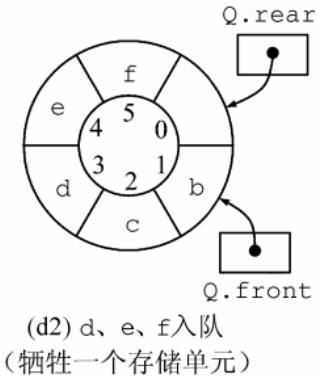
-
犧牲一個存儲單元來區分隊空和隊滿,入隊時少用一個隊列單元
約定——隊首指針在隊尾指針的下一個位置作為隊滿標志
隊滿條件:(Q.rear+1)%MaxSize == Q.front
隊空條件:Q.front == Q.rear
隊列中元素個數:(Q.rear - Q.front + MaxSize)%MaxSize
-
增設size數據成員,表示元素個數,若刪除成功,size–,若插入成功,size++
隊空:Q.size == 0
隊滿:Q.size == MaxSize
都會使Q.front == Q.rear
-
增設tag數據成員,以區分隊滿隊空
刪除成功 tag = 0 若Q.front == Q.rear ,則隊空
插入成功 tag = 1 若Q.front == Q.rear ,則隊滿
//判斷隊列是否為空
bool QueueEmpty(SqQueue Q){if(Q.rear == Q.front) //隊空條件return true;elsereturn false;
} //入隊
bool EnQueue(SqQueue &Q,ElemType x){if((Q.rear+1)%MaxSize == Q.front)return false; //隊滿則報錯Q.data[Q.rear] = x; //新元素插入隊尾 Q.rear = (Q.rear+1)%MaxSize; //隊尾指針+1取模return true;
} //出隊(刪除一個隊頭元素,并用x返回)
bool DeQueue(SqQueue &Q,ElemType &x){if(Q.rear == Q.front)return false; //隊空則報錯 x = Q.data[Q.front];Q.front = (Q.front+1)%MaxSize;return true;
} //獲得隊頭元素的值,用x返回
bool GetHead(SqQueue Q,ElemType &x){if(Q.rear == Q.front)return false; //隊空則報錯x = Q.data[Q.front]return true;
}
3.2.3隊列的鏈式存儲結構
隊列的鏈式表示稱為鏈式隊列,實際上是一個同時具有隊首指針和隊尾指針的單鏈表
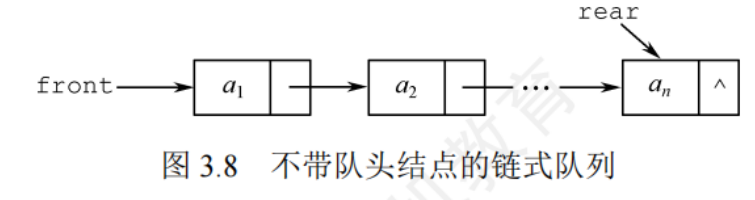
typedef struct LinkNode { //鏈式隊列結點ElemType data;struct LinkNode *next;
}LinkNode;typedef struct{ //鏈式隊列 LinkNode *fron,*rear; //隊列的隊頭和隊尾指針
}LinkQueue;
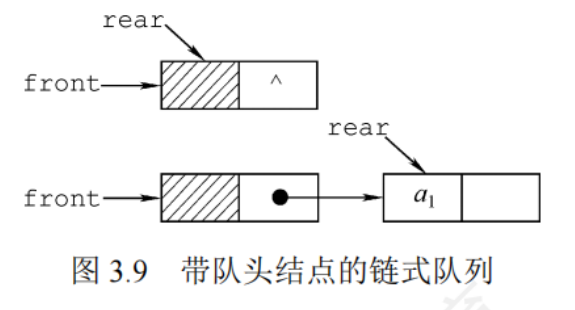
初始化
//初始化隊列(帶頭結點)
void InitQueue (LinkQueue &Q){//初始時 front、rear 都指向頭結點Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));Q.front->next = NULL;
}
//判斷隊列是否為空(帶頭結點)
bool IsEmpty(LinkQueue Q){if(Q.front == Q.rear)return true;elsereturn false;
}
----------------------------------------
//初始化隊列(不帶頭結點)
void InitQueue(LinkQueue &Q){//初始時 front、rear 都指向NULLQ.front= NULL;Q.rear = NULL;
}
//判斷隊列是否為空(不帶頭結點)
bool IsEmpty(LinkQueue Q){if(Q.front == NULL)return true;elsereturn false;
} void testLinkQueue(){LinkQueue Q; //聲明一個隊列InitQueue(Q); //初始化隊列......
}
入隊
//新元素入隊(帶頭結點)
void EnQueue(LinkQueue &Q,ElemType x){LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));s->data = x;s->next = NULL;Q.rear->next = s; //新結點插入到rear之后 Q.rear = s; //修改表尾指針
}
-------------------------------------------------------
//新元素入隊(不帶頭結點)
void EnQueue(LinkQueue &Q,ElemType x){LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));s->data = x;s->next = NULL;if(Q.front == NULL){ //在空隊列中插入第一個元素 Q.front= s; //修改隊頭隊尾指針 Q.reat= s;}else{Q.rear->next = s; //新結點插入到 rear 之后 Q.rear = s; //修改rear指針 }
}
出隊
//隊頭元素出隊(帶頭結點)
bool DeQueue(LinkQueue &Q,ElemType &x){if(Q.front == Q.rear)return false; //空隊LinkNode *p = Q.front->next;//p指針指向要刪除的結點(隊頭元素出隊)x = p->data; //用變量x返回隊頭元素Q.front->next = p->next; //修改頭結點的next指針if(Q.rear == p) //此次是最后一個結點出隊 Q.rear = Q.front; //修改 rear 指針 free(p); //釋放結點空間 return true;
}
3.2.4雙端隊列
兩端都可以進行插入和刪除的線性表,兩端地位平等,左前右后

輸出受限的雙端隊列:允許在一端進行插入和刪除,但在另一端只允許插入的雙端隊列

輸入受限的雙端隊列:允許一端進行插入和刪除,但在另一端只允許刪除的雙端隊列
若限定從某個端點插入元素只能從該端點刪除,則雙端隊列==兩個棧底相連的棧

重要例題:各種雙端隊列序列輸出序列

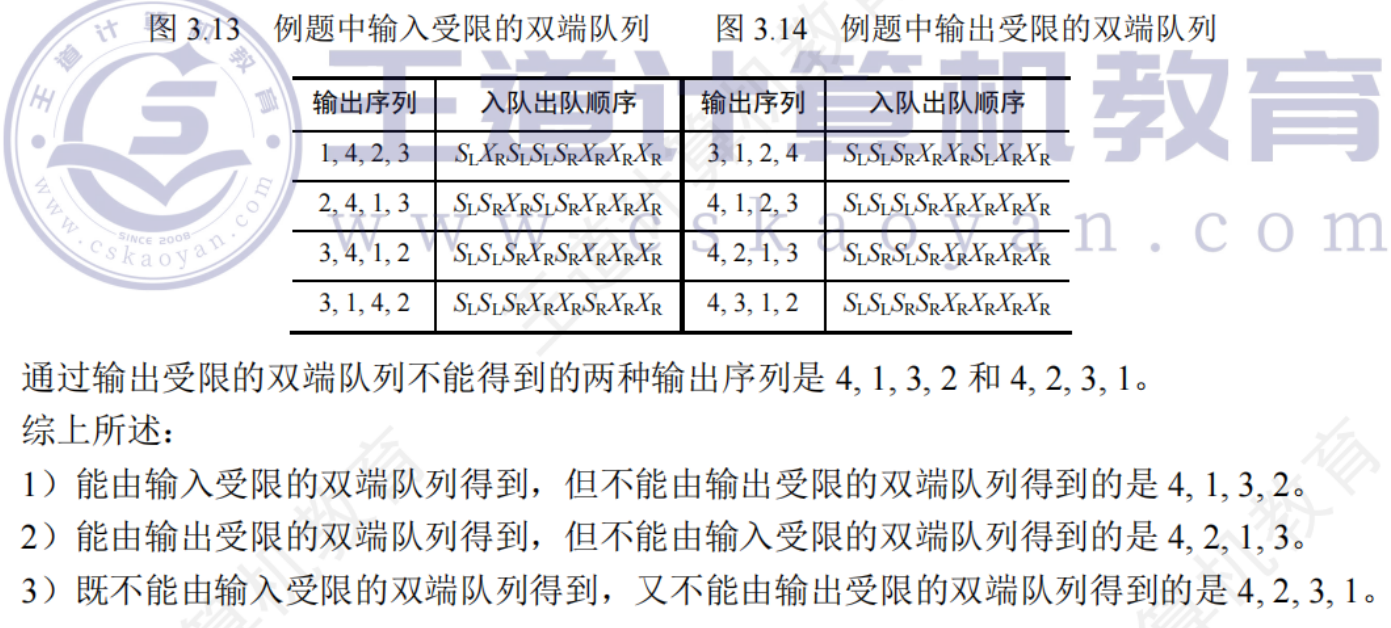
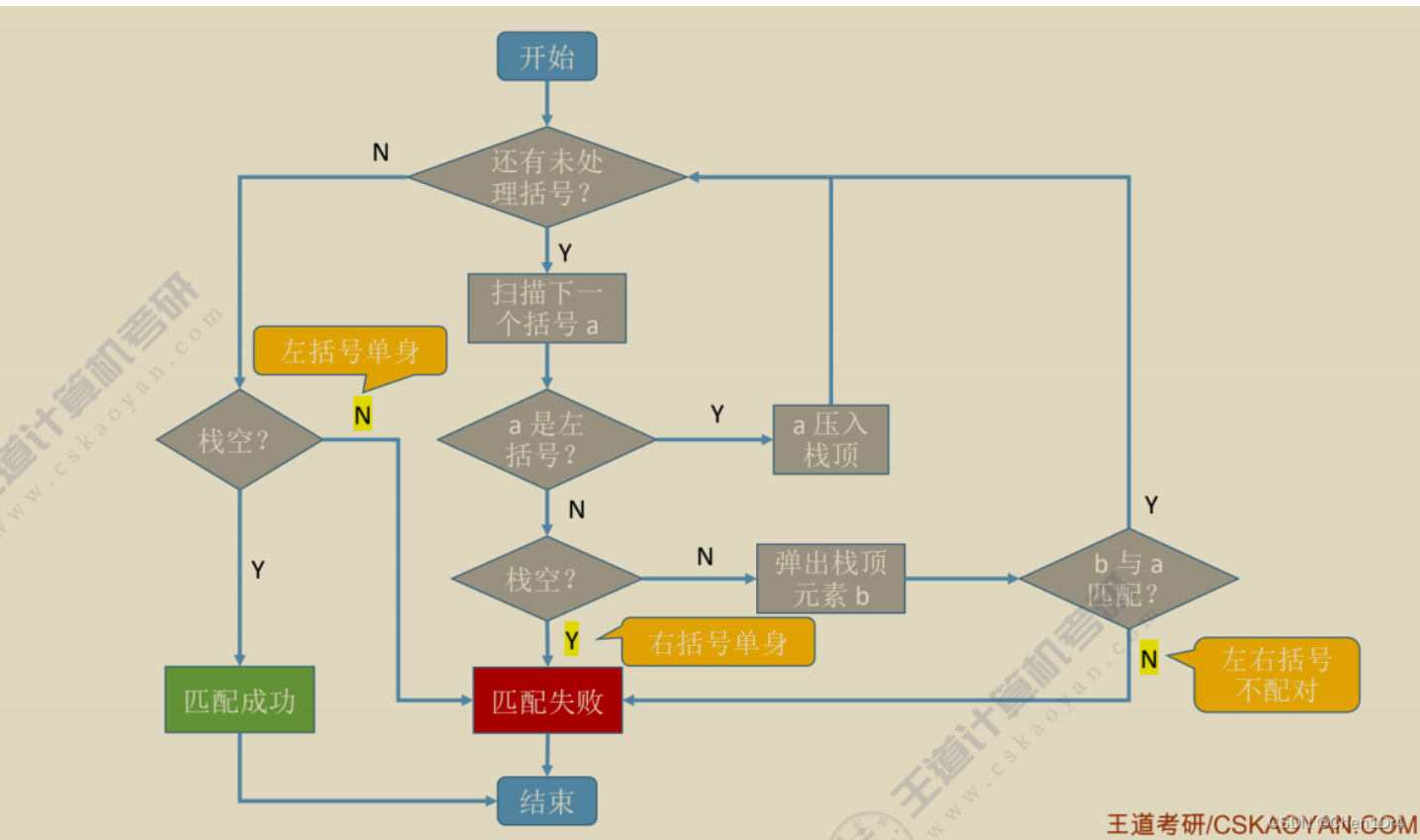
3.3.1棧在括號匹配中的應用(重點)
題目描述

bool bracketCheck(char str[],int length){SqStack S;InitStack(S); //初始化一個棧for(int i=0; i<length; i++){if(str[i] == '(' || str[i] == '[' || str[i] == '{')Push(S,str[i]); //掃描到左括號,壓入棧 }else{if(StackEmpty(S)) //掃描到右括號,且當前棧空 return false; //掃描失敗char topElem;Pop(S,topElem); //棧頂元素出棧 if(str[i] == ')' && topElem != '(')return false;if(str[i] == ']' && topElem != '[')return false;if(str[i] == '}' && topElem != '{')return false;} return StackEmpty(S); //檢索完全部括號后,棧空說明匹配成功
}
3.3.2棧在表達式求值中的應用

中綴表達式與前綴、后綴表達式有何不同:中綴表達式中括號是必須的
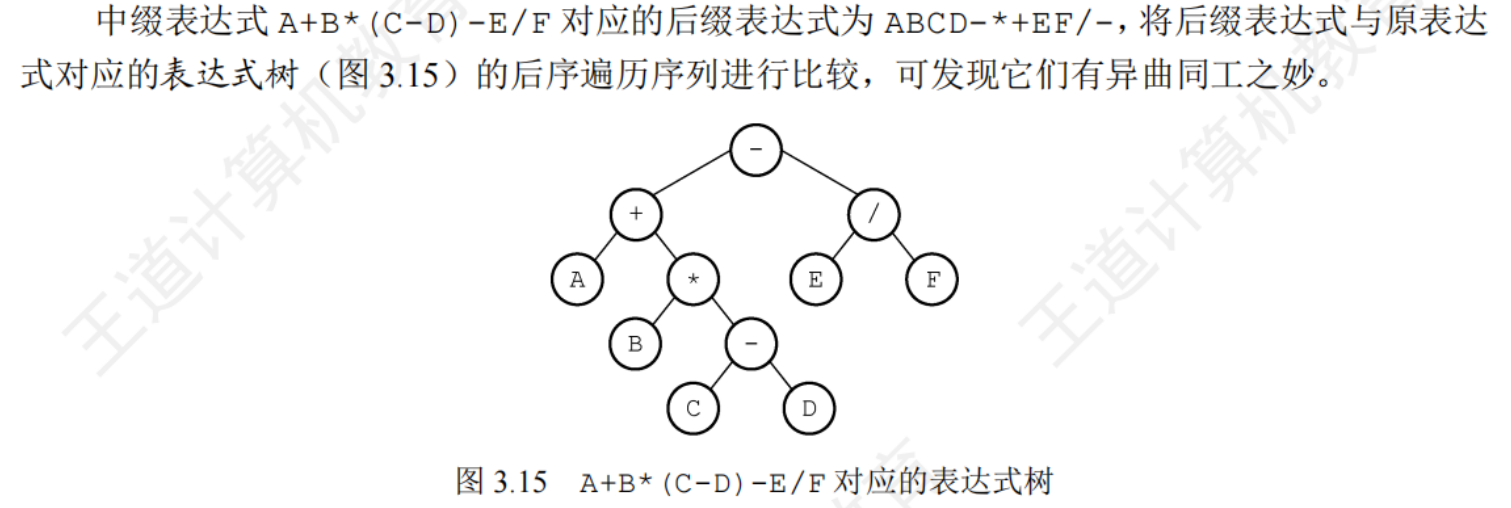
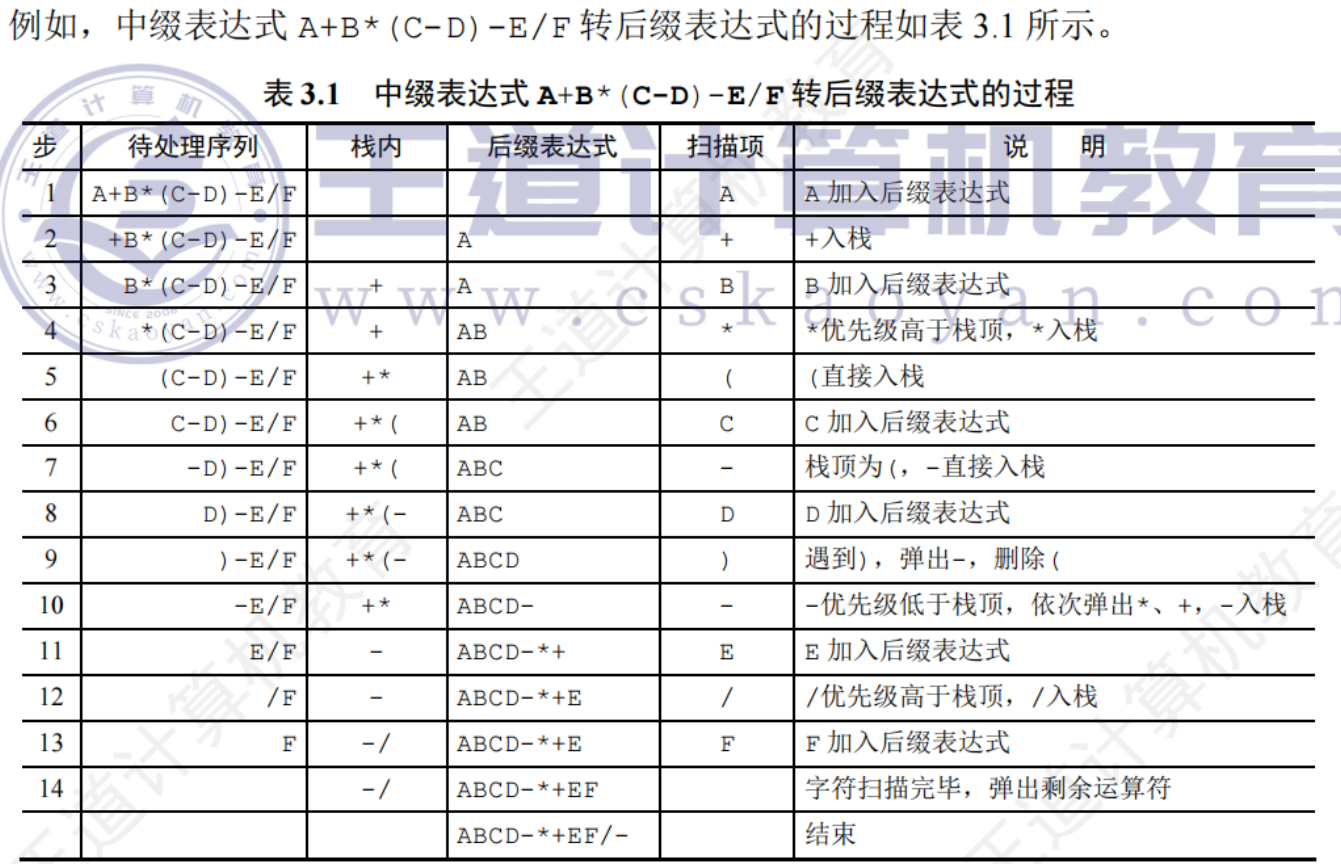
中綴表達式轉后綴表達式
- 按照運算符的運算順序隊所有運算單位加括號
- 將運算符移至對應括號的后面,相當于 左操作數 右操作數 運算符 重新組合
- 去除所有括號

使用棧實現中綴表達式轉后綴表達式:
- 遇到操作數,直接加入后綴表達式
- 遇到界限符,若為( 則直接入棧,若為 )則不入棧,且依次彈出棧中的運算符并加入后綴表達式,直到遇到 ( 為止,并直接刪除(
- 遇到運算符
- 若其優先級高于棧頂運算符或遇到棧頂為( ,則直接入棧
- 若其優先級低于或等于棧頂運算符,則依次彈出棧中的運算符并加入后綴表達式,直到遇到一個優先級低于他的運算符或( 棧空為止,之后將當前運算符入棧
棧的深度:棧中元素個數,通常是給出入棧和出棧序列,求最大深度(棧的容量應大于或等于最大深度)
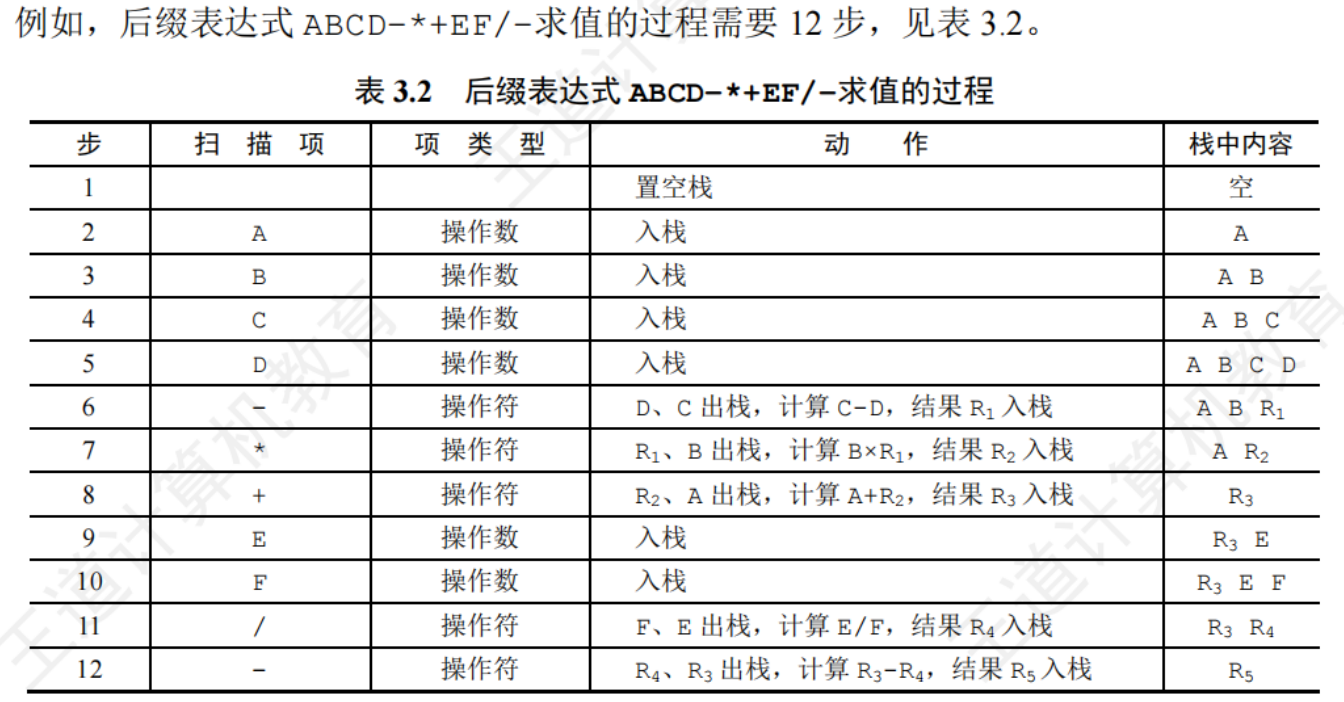
后綴表達式求值
從左往右掃描表達式每一項,若是操作數,將其壓入棧中
若是操作符,則從棧中退出兩個操作數X、Y形成運算指令 X (運算符)Y,并將結果入棧
所有項都掃描之后,棧頂存放的就是最后的計算結果
3.3.3棧在遞歸中的應用
遞歸:若在一個函數、過程或數據結構的定義中有應用到了它自身
遞歸通常把一個大型的復雜問題轉化為一個與原問題相似的規模較小的問題來求解
遞歸組成:
- 遞歸表達式(遞歸體)
- 邊界條件(遞歸出口)

在遞歸調用的過程中,系統為每一層的返回點,局部遍歷,傳入實參等開辟了遞歸工作棧來進行數據存儲,遞歸次數過多容易造成棧溢出
效率不高的原因——包含許多重復的過程
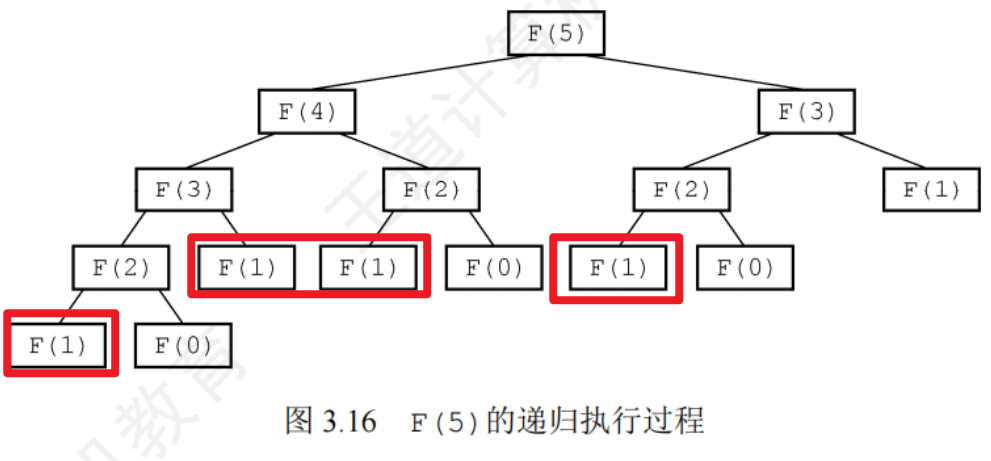
3.3.4隊列在層次遍歷中的應用
如果問題需要 逐層或逐行處理,解決方法通常是在處理當前層或當前行之前就對下一層或下一行進行預處理
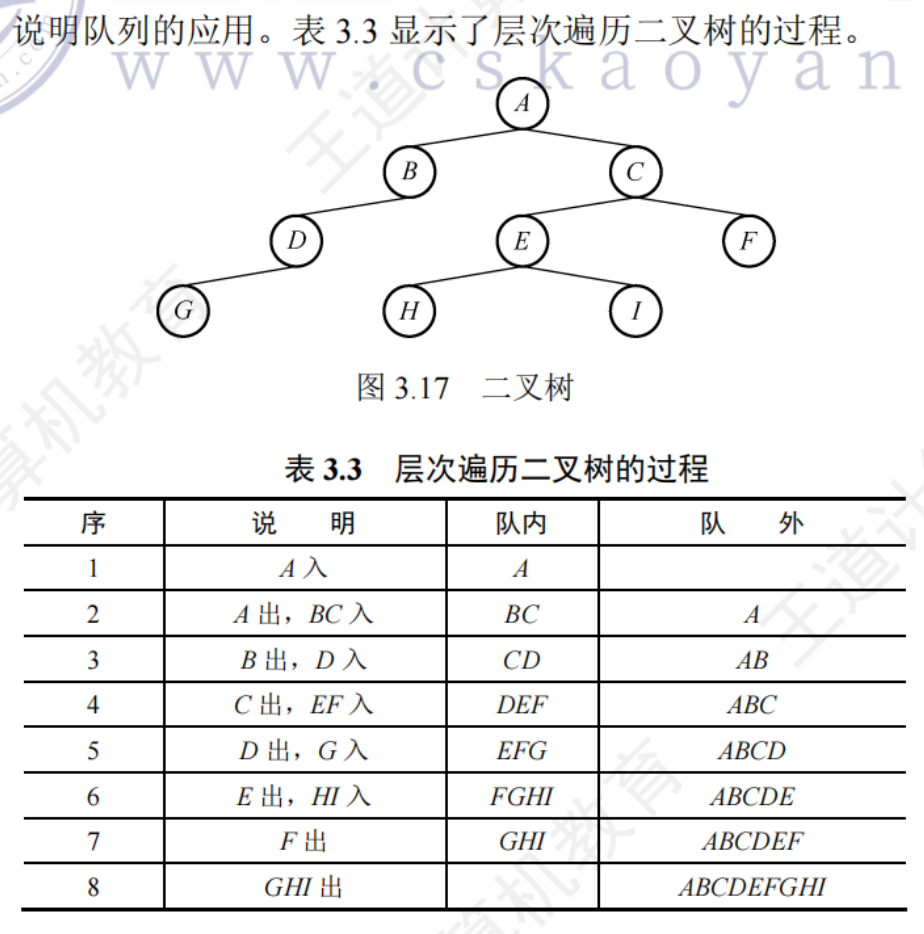
隊列實現二叉樹的層序遍歷
描述:
- 根節點入隊
- 若隊空,則結束遍歷,否則重復操作3
- 隊列中的隊首節點出隊,并訪問之,若其有左孩子,左孩子入隊,若其有右孩子,右孩子入隊,返回2
3.3.5隊列在計算機系統中的應用

3.4.1數組的定義
數組是由n個相同類型的數據元素構成的有限序列,每個元素稱為一個數組元素,每個元素在n個線性關系中的序號稱為該元素的下標,下標的取值范圍稱為數組的維界
數組與線性表的關系:數組是線性表的推廣,一位數組可視為一個線性表,二維數組可視為其元素是定長數組的線性表
數組一旦定義,其維數和維界就不再改變
3.4.2數組的存儲結構
一個數組的所有元素在內存中占用一段連續的存儲空間

多維數組映射:
? 按行優先:先行后列,先存儲行號較小的元素,行號相等先存儲列號較小的元素

? 按列存儲

3.4.3特殊矩陣的壓縮存儲
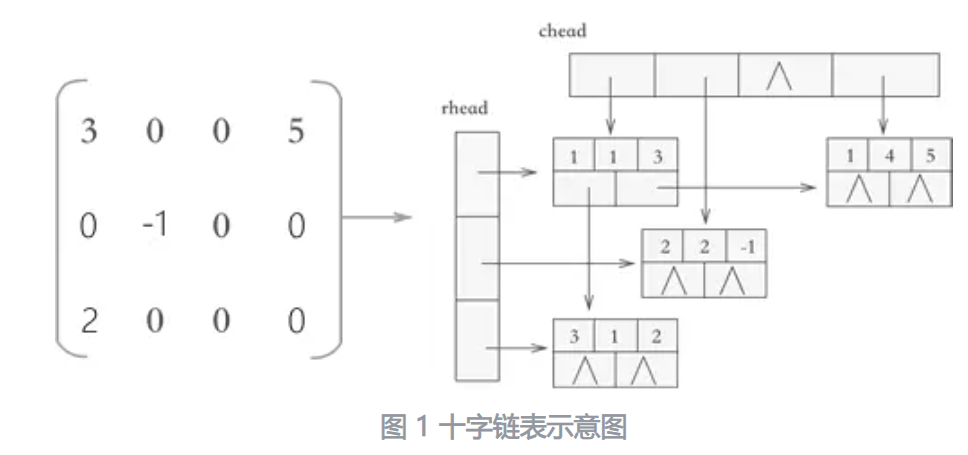
壓縮存儲:為多個值相同的元素只分配一個存儲空間,對零元素不分配空間
特殊矩陣:具有許多相同矩陣元素或零元素,并且這些相同矩陣元素或零元素的分布有一定規律的矩陣
對稱矩陣


三角矩陣

下三角矩陣

上三角矩陣

三對角矩陣


稀疏矩陣
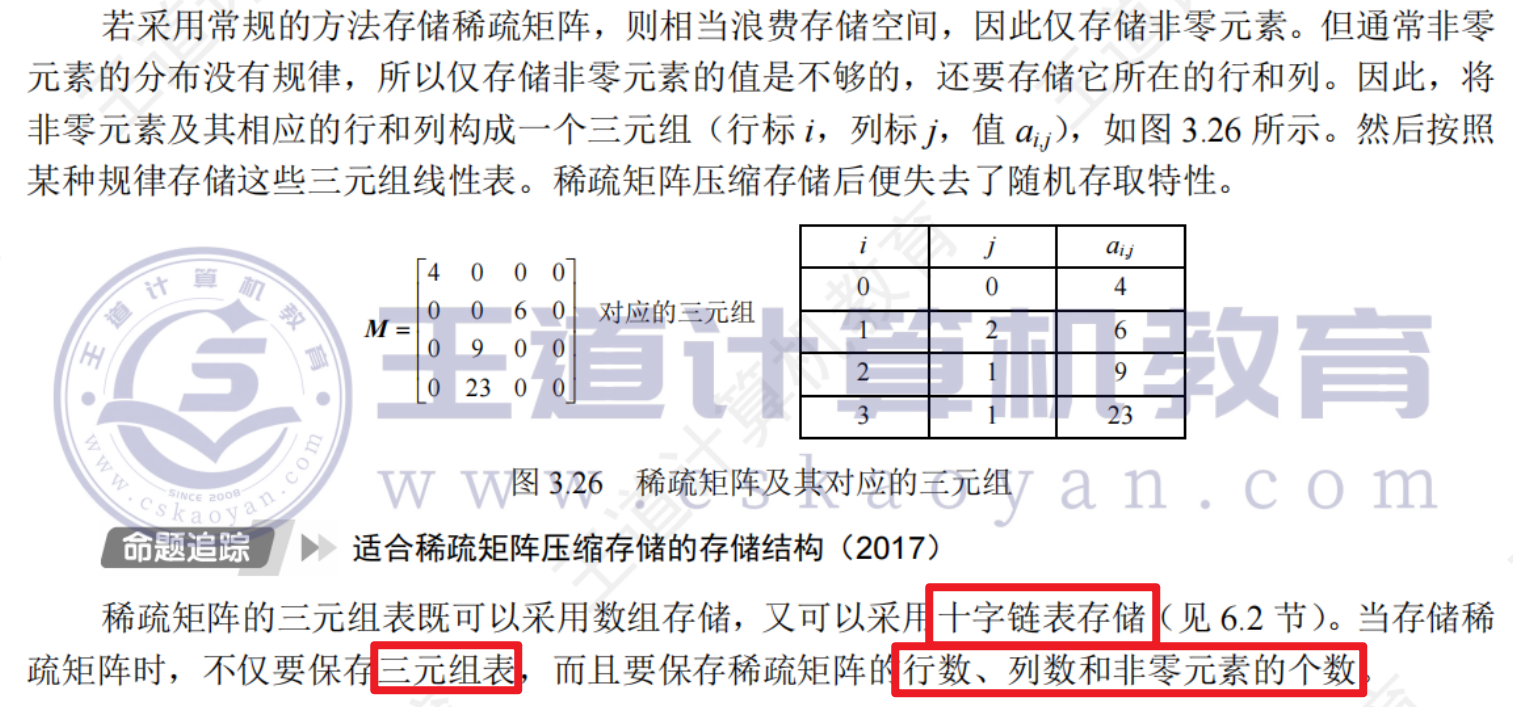
十字鏈表存儲稀疏矩陣

4.串

4.2.1簡單的模式匹配算法
模式匹配:在主串中找到與模式串相同的子串,并返回其所在的位置,串采用定長順序存儲結構
//樸素模式匹配算法
int Index(SSring S,SString T){int i=1,j=1;while(i<=s.length && j<=T.length){if(S.ch[i] == S.ch[j]){++i; ++j; //繼續比較后續字符 }else{i=i-j+2; //i=(i-(j-1))+1 j=1; //指針后退重新開始匹配 } }if(j>T.length)return i-T.length;elsereturn 0;
}
算法思想:從主串S的第一個字符起,與模式串T的第一個字符比較,若相等,則繼續逐個比較后續字符,否則從主串的下一個字符起,再重新和模式串T的字符比較

設主串和模式串長度分別為n和m,則最多需要n-m+1趟匹配,每趟最多進行m次比較,最壞時間復雜度O(mn)
4.2.2KMP算法
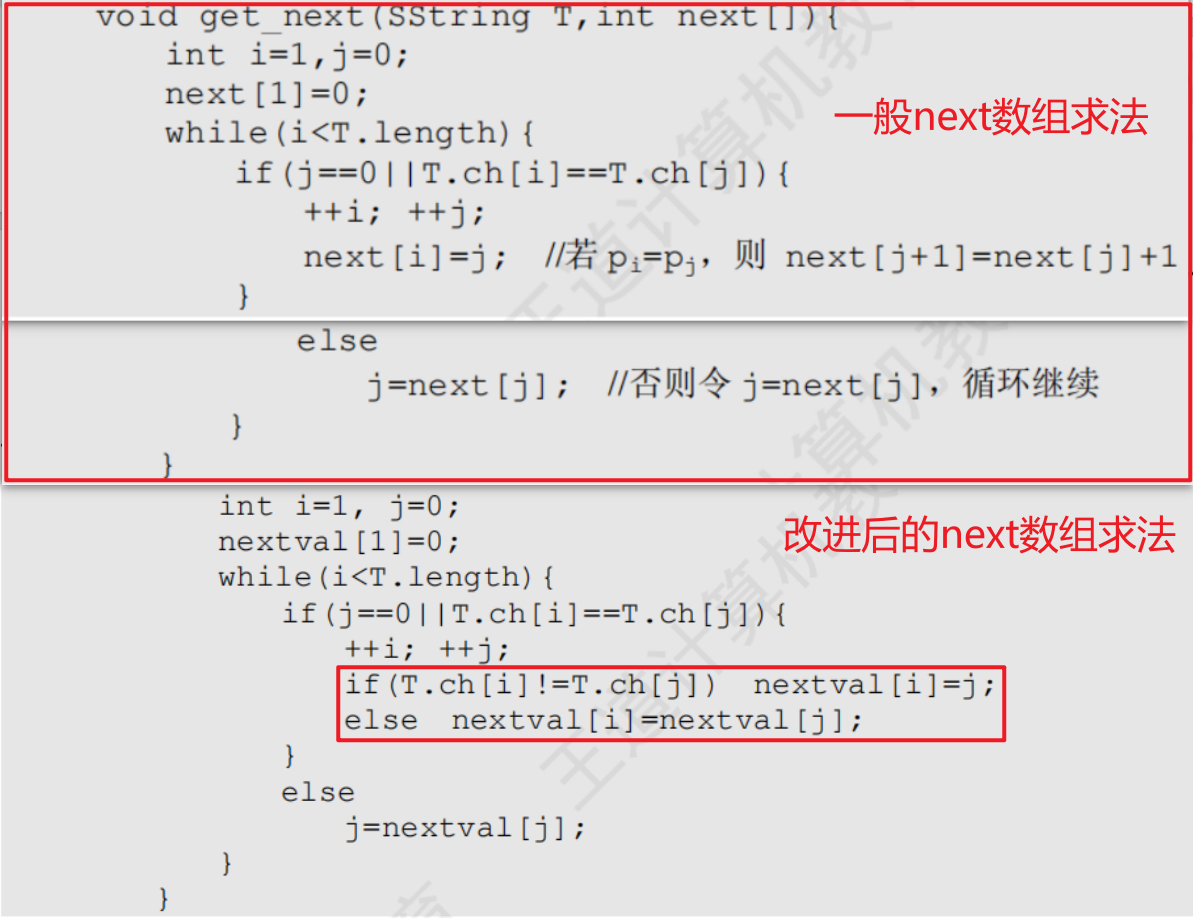
kmp算法的PM表 next數組都是對模式串來說的
算法思想:若已匹配相等的前綴序列中有某個后綴正好是模式串的前綴,則可將模式串向右滑動到與這些相等字符對齊的位置,主串指針 i 無須回溯
kmp算法原理
前綴:除最后一個字符外,字符串中所有頭部子串
后綴:除第一個字符外,字符串的所有尾部子串
部分匹配值:字符串的前綴和后綴的最長相等前后綴的長度
ababa:

主串 S=ababcabcacbab
模式串 T=abcac
PM表——對模式串求部分匹配值

利用PM表進行模式匹配



next數組手算方法
每趟匹配失敗時,只有模式串指針j在變化,主串指針i不會回溯,為此可以定義一個next數組
next[j]的含義是每當模式串的第j個字符失配時,跳到next[j]的位置進行比較
next數組與PM表的關系
編號從1開始,PM表右移一位并整體加1

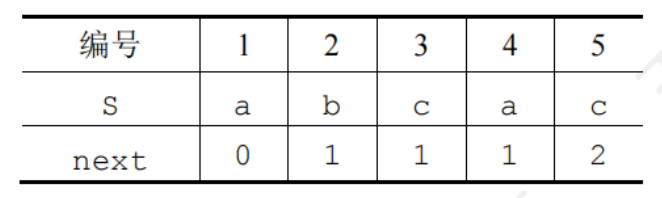
- 第一個元素右滑后的空缺用0來填充,因為若是第一個元素匹配失效,則需要將主串指針與模式串同步向右移動一位,從而不需要計算模式串指針移動位數
- 最后一個元素在右滑過程中溢出,因為原來的模式串中,最后一個元素的部分匹配值是下一個元素使用的,但已經沒有下一個元素了,所以舍去
- PM表右移一位并整體加1,編號從0開始,不加1,從1開始加1
4.2.3KMP算法的進一步優化
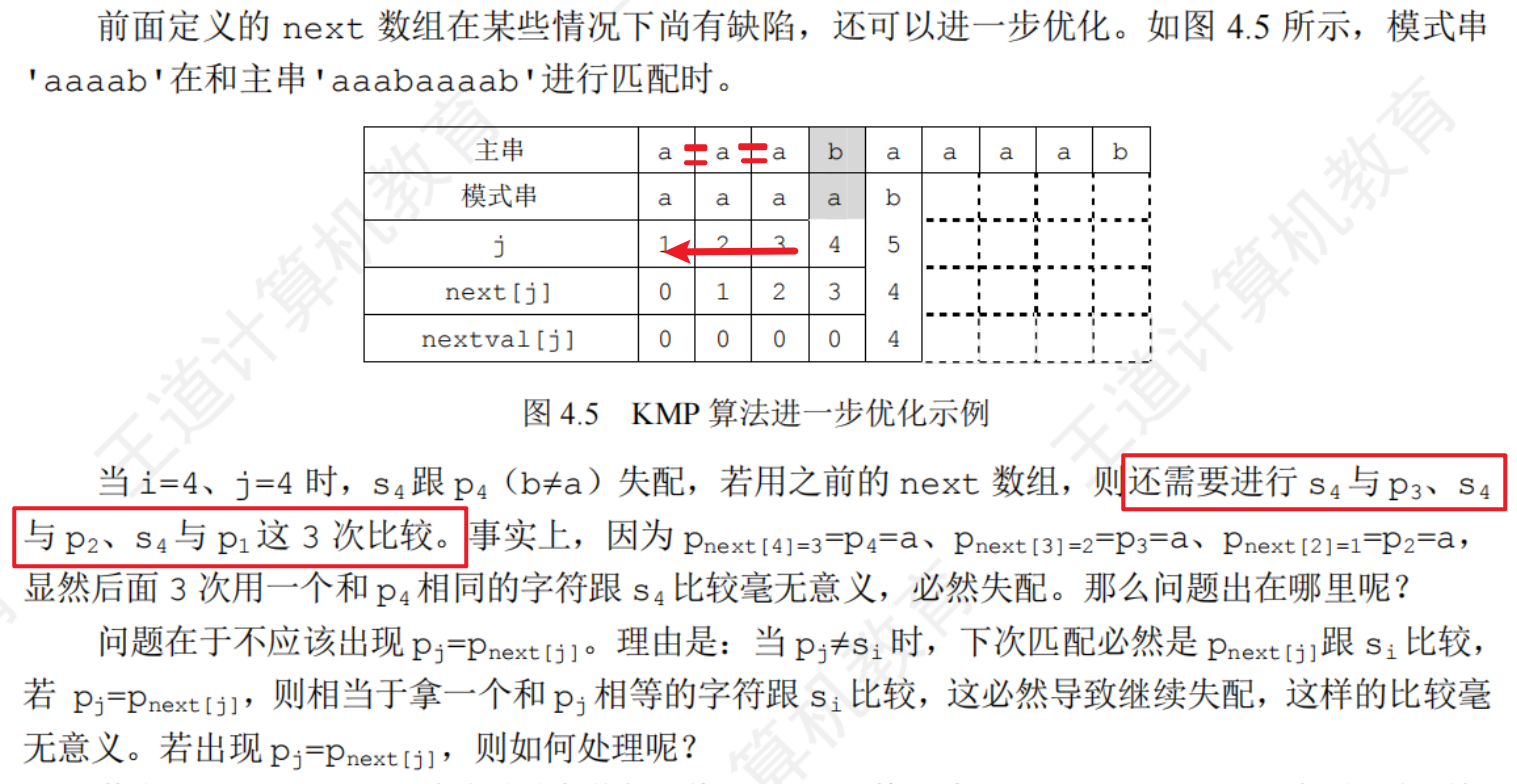

5.樹與二叉樹

5.1.1樹的定義
樹是n個節點的有限集,n=0時為空樹
任何一顆非空樹都需要滿足:
- 有且只有一個特定的根節點
- n>1時其余節點可以分為m個互不相交的有限集T1,T2…Tm,其中每個集合本身又是一棵樹,并且稱為根的子樹
樹的定義是 遞歸定義 的
樹的特點:
- 樹的根節點沒有前驅,除根節點外的所有節點有且只有一個前驅
- 樹中所有節點都可以有零個或多個后繼
n個節點的樹有n-1條邊
5.1.2基本術語
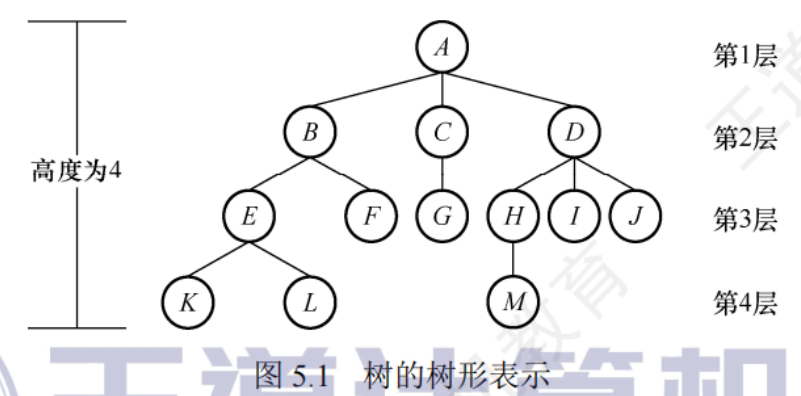
-
祖先、子孫、雙親、孩子、兄弟、堂兄弟
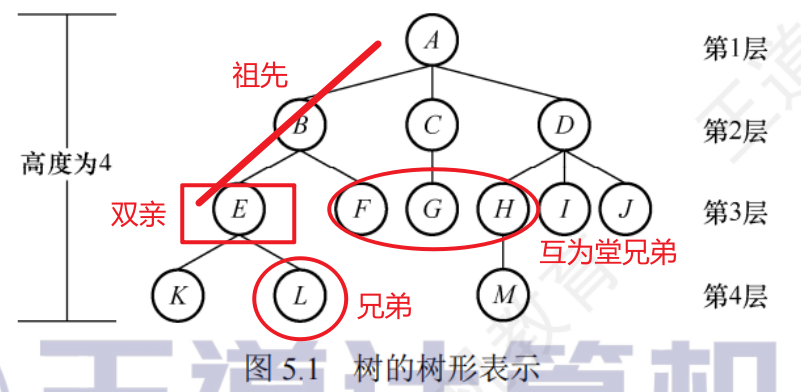
-
層次、深度、高度
- 節點的層次:從根節點開始為第一層,其孩子為第二層
- 樹的高度/深度:樹中節點的最大層數
- 節點的高度:以該節點為根的子樹的高度
-
節點的度和樹的度
- 節點的度:一個節點孩子的個數
- 樹的度:樹中節點的最大度數
-
分支節點和葉節點
- 分支節點:度大于0的節點
- 葉節點:度為0(沒有孩子節點)的節點
-
有序樹和無序樹
- 有序樹:樹中節點的各子樹從左到右是有次序的,不能互換
- 無序樹:不滿足以上條件
-
路徑和路徑長度
- 路徑:兩個節點之間經過的節點序列
- 路徑長度:路徑上所經過的邊的個數
-
森林
- m棵互不相交的樹的集合
5.1.3樹的性質
- 樹的節點數n等于 = 節點的度數之和 + 1 = 邊數 + 1

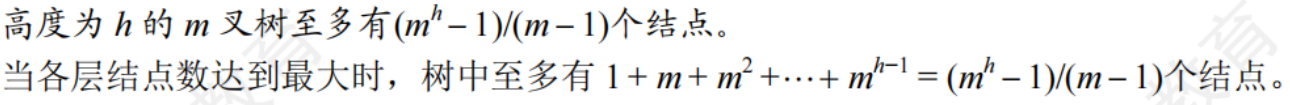


常用于求解樹節點與度之間的關系

5.2.1二叉樹的定義及其主要特性
每個節點至多只有兩棵子樹(二叉樹不存在度大于二的節點),并且子樹有左右之分,次序不能隨意顛倒
二叉樹與度為2的有序樹的區別:
- 度為2的樹至少有3個節點,而二叉樹可以為空
- 度為2的有序樹的孩子的左右次序是相對于另一個孩子而言的,若某個節點只有一個孩子,則這個孩子無須七分左右次序,而二叉樹無論其孩子個數是否為2,均需確定其左右次序
特殊的二叉樹
滿二叉樹
一棵樹高為h,節點個數等于 2^h-1
每一層都含有最多的節點
葉節點只位于二叉樹的最底層
分支節點度為2
若對按二叉樹層序編號,對于一個編號為 i 的節點,若有雙親則其編號為 i/2 ,左孩子為 2i ,右孩子為 2i+1
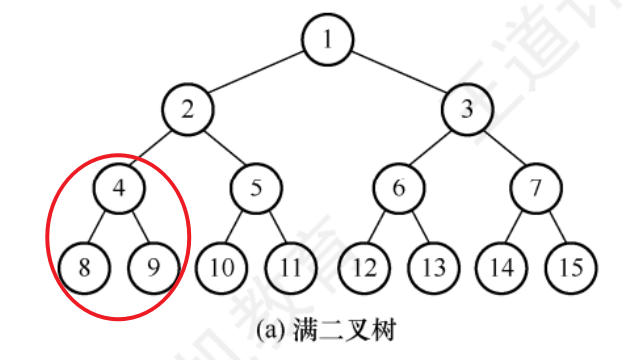
完全二叉樹
高為h的完全二叉樹,當且僅當每個節點與高為h的滿二叉樹中的節點編號一一對應
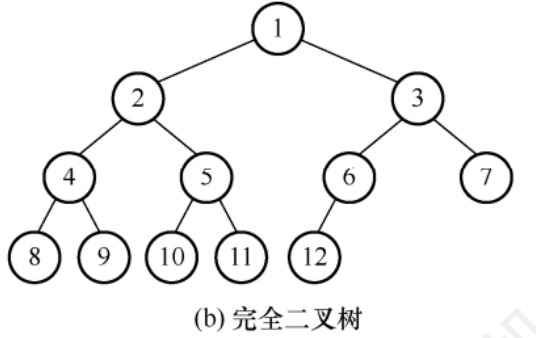
完全二叉樹 = 滿二叉樹去掉部分大編號節點
分支節點數 = 最大葉子節點數 / 2
性質
完全二叉樹從上到下,從左到右編號有以下性質:
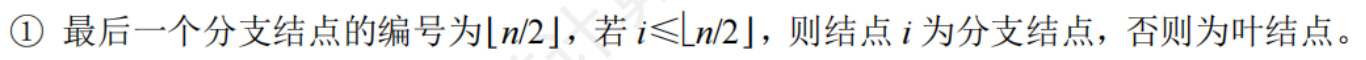
- 葉節點只能在最后兩層上出現(相當于在相同高度的滿二叉樹的最底層,最右邊減少一些連續的葉節點,當減少2個或以上的葉節點時,次底層出現葉節點)
- 若有度為1的節點,則至多有一個,且該節點只有左孩子沒有右孩子(度為1的分支節點只可能是最后一個分支節點,編號為 n/2)
- 按層序編號后,一旦出現某節點為葉節點或只有做孩子的情況,則編號大于該節點的節點均為葉節點
- 若n為奇數,每個分支節點都有左右孩子,若n為偶數,則編號最大的分支節點只有左孩子沒有右孩子,其余分支節點都有左右孩子
- 節點i所在的層次(深度)為 long2i + 1

二叉排序樹
左子樹上所有節點的關鍵字小于根節點的關鍵字,右子樹上所有節點的關鍵字均大于根節點的關鍵字
左右子樹仍為二叉排序樹
平衡二叉樹
樹中任意一個節點的左子樹和右子樹的高度只差絕對值不超過1
正則二叉樹
樹中每個分支節點都有2個孩子
樹只有度為0或2的節點
二叉樹的性質
-
葉節點數等于度為2的節點數加1 n0 = n2 + 1
-
非空二叉樹的第k層最多有 2^(k-1)個節點
-
高度為h的二叉樹至多有 2^h -1個節點
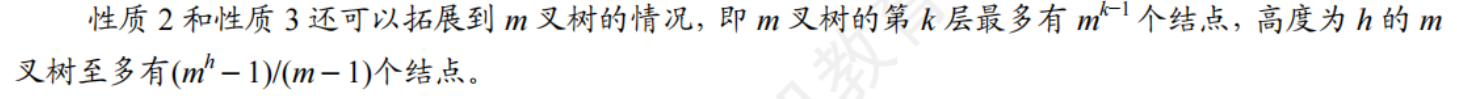
5.2.2二叉樹的存儲結構
順序存儲結構
用一組連續的存儲單元依次從上到下,從左到右存儲完全二叉樹上的節點元素
完全二叉樹和滿二叉樹適用于順序存儲,因為樹中的節點序號可以唯一的反映節點之間的邏輯關系
對于一般的二叉樹,需要添加一些不存在的空節點,每個節點需要與完全二叉樹上的節點對應
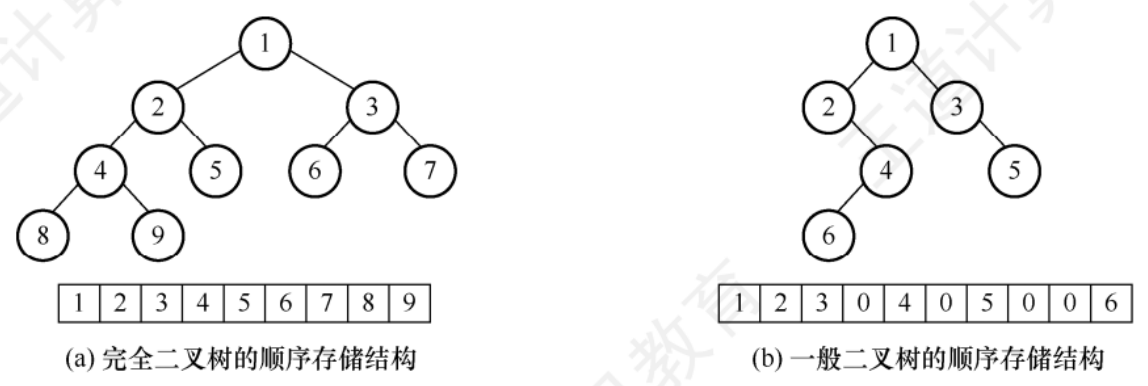
鏈式存儲結構
順序存儲結構空間利用率低

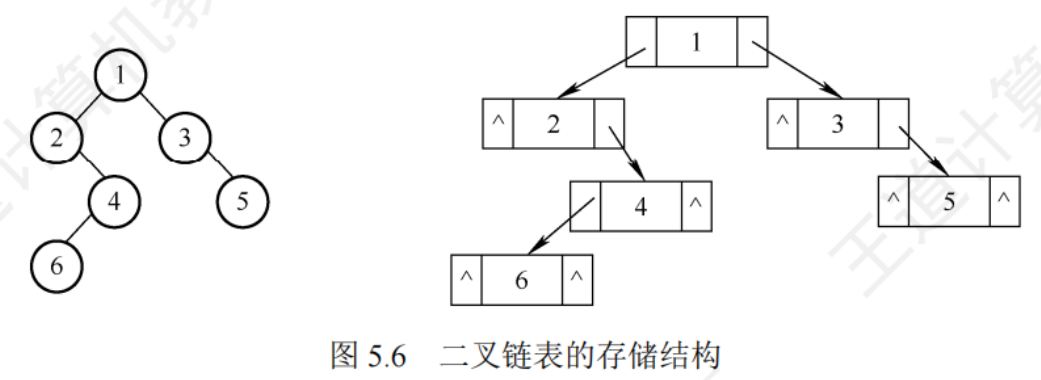
//二叉樹的結點(鏈式存儲)
struct ElemType{int value;
};typedef struct BiTNode{ElemType data; //數據域struct BiTNode *lchild,*rchild; //左、右孩子指針 (sruct BiTNode *parent;) //父結點指針
}BiTNode,*BiTNode; //定義一棵空樹
BiTree root = NULL;//插入根節點
root = (BiTree) malloc(sizeof(BiTNode));
root->data = {1};
root->lchild = NULL;
root->rchild = NULL;//插入新結點
BiTree *p = (BiTNode *) malloc(sizeof(BiTNode));
p->data = {2};
p->lchild = NULL;
p->rchild = NULL;
root->lchild = p; //作為根節點的左孩子
在含有n個節點的二叉鏈表中,含有n+1個空鏈域
5.3.1二叉樹的遍歷
先序遍歷
中左右
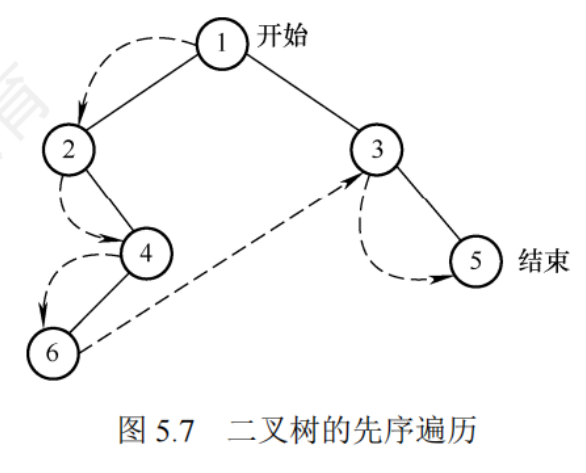
//先序遍歷
void PreOrder(BiTree T){if(T != NULL){visit(T); //訪問根節點PreOrder(T->lchild);//遞歸遍歷左子樹 PreOrder(T->rchild);//遞歸遍歷右子樹 }
}
中序遍歷
左中右
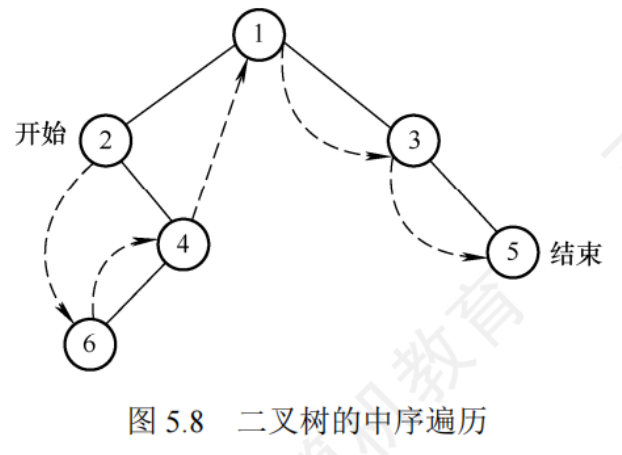
//中序遍歷
void InOrder(BiTree T) {if(T != NULL){InOrder(T->lchild);//遞歸遍歷左子樹 visit(T); //訪問根節點InOrder(T->rchild);//遞歸遍歷右子樹 }
}
后序遍歷
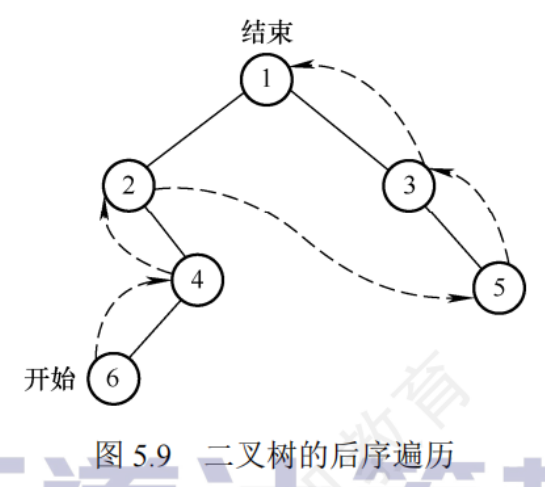
//后序遍歷
void PostOrder(BiTree T){if(T != NULL){PostOrder(T->lchild);//遞歸遍歷左子樹 PostOrder(T->rchild);//遞歸遍歷右子樹visit(T); //訪問根節點}
}
層序遍歷
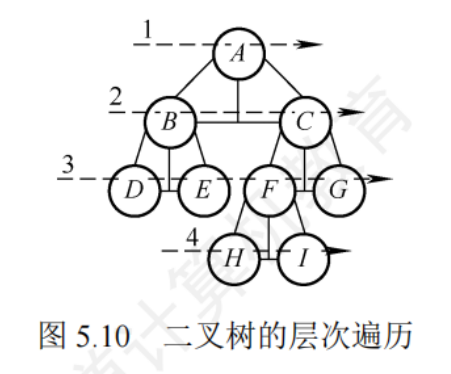
- 引入一個隊列
- 首先將根節點入隊
- 若隊列非空,從隊首頭節點出隊,若其有左孩子,左孩子入隊,若其有右孩子,右孩子入隊
//層序遍歷
void LevelOrder(BiTree T){LinkQueue Q; InitQueue(Q); //初始化輔助隊列 BiTree p;EnQueue(Q,T); //將根節點入隊while(!IsEmpty(Q)){ //隊列不空則循環 DeQueue(Q,p); //對頭結點出隊visit(p); //訪問出隊結點if(p->lchild!=NULL)EnQueue(Q,p->lchild); //左孩子入隊 if(p->rchild!=NULL)EnQueue(Q,p->rchild); //右孩子入隊 }
} typedef struct BiTNode{ElemType data; struct BiTNode *lchild,*rchild;
}BiTNode,*BiTNode; //鏈式隊列結點
typedef struct LinkNode{BiTNode * data;struct LinkNode *next;
}LinkNode;typedef struct{LinkNode *front,*rear; //隊頭隊尾
}LinkQueue;
遍歷序列構造二叉樹
中序序列+其他三種序列中的任意一種 = 一顆二叉樹
一、中序序列 + 前序序列構造二叉樹
- 確定根節點
- 前序序列的第一個元素是整棵樹的根節點。
- 例如,前序序列為
ABDECF,中序序列為DBEAFC。那么A就是整棵樹的根節點。
- 劃分左右子樹
- 在中序序列中找到根節點的位置,根節點左邊的序列是左子樹的中序序列,右邊的序列是右子樹的中序序列。
- 根節點
A在中序序列DBEAFC中的位置是第4個。那么DBE就是左子樹的中序序列,FC是右子樹的中序序列。 - 同時,根據左子樹和右子樹的節點數量,可以確定前序序列中左子樹和右子樹對應的序列。左子樹有3個節點(
D、B、E),所以前序序列ABDECF中,ABDE是左子樹的前序序列,CF是右子樹的前序序列。
- 遞歸構造左右子樹
- 對左子樹的前序序列
ABDE和中序序列DBE重復上述步驟,確定左子樹的根節點B,劃分左子樹的左右子樹,繼續遞歸。 - 對右子樹的前序序列
CF和中序序列FC也重復上述步驟,確定右子樹的根節點C,劃分右子樹的左右子樹,繼續遞歸。 - 遞歸的終止條件是序列為空,即沒有子樹可以劃分。
- 對左子樹的前序序列
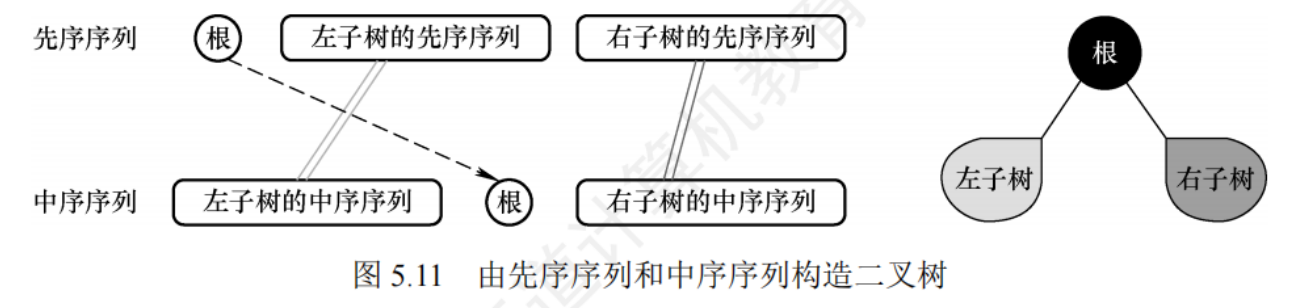
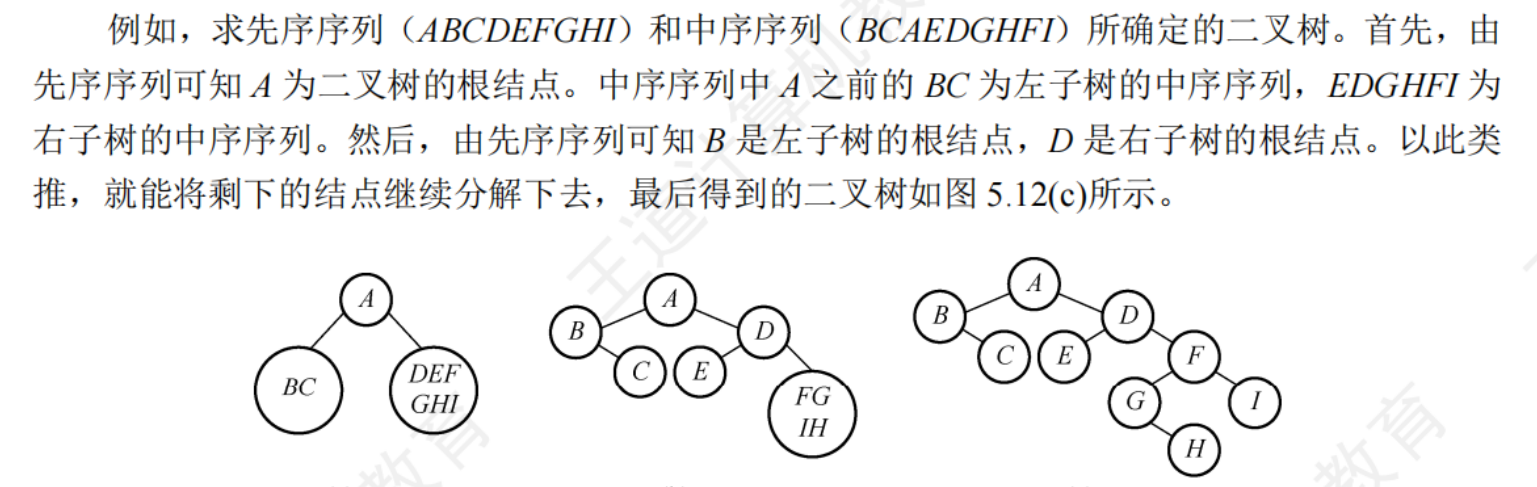
二、中序序列 + 后序序列構造二叉樹
- 確定根節點
- 后序序列的最后一個元素是整棵樹的根節點。
- 例如,后序序列為
DEBFCA,中序序列為DBEAFC。那么A就是整棵樹的根節點。
- 劃分左右子樹
- 在中序序列中找到根節點的位置,根節點左邊的序列是左子樹的中序序列,右邊的序列是右子樹的中序序列。
- 根節點
A在中序序列DBEAFC中的位置是第4個。那么DBE就是左子樹的中序序列,FC是右子樹的中序序列。 - 同時,根據左子樹和右子樹的節點數量,可以確定后序序列中左子樹和右子樹對應的序列。左子樹有3個節點(
D、B、E),所以后序序列DEBFCA中,DEB是左子樹的后序序列,FC是右子樹的后序序列。
- 遞歸構造左右子樹
- 對左子樹的后序序列
DEB和中序序列DBE重復上述步驟,確定左子樹的根節點B,劃分左子樹的左右子樹,繼續遞歸。 - 對右子樹的后序序列
FC和中序序列FC也重復上述步驟,確定右子樹的根節點C,劃分右子樹的左右子樹,繼續遞歸。 - 遞歸的終止條件是序列為空,即沒有子樹可以劃分。
- 對左子樹的后序序列
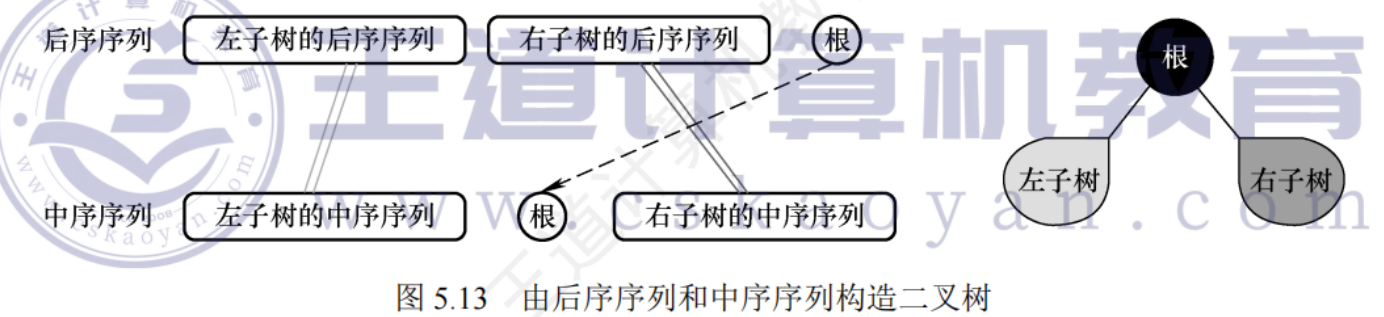
三、中序序列 + 層序序列構造二叉樹
- 確定根節點:
- 層序遍歷的第一個節點是整棵樹的根節點。
- 在上面的例子中,根節點是
A。
- 劃分左右子樹:
- 在中序序列中找到根節點的位置,根節點左邊的序列是左子樹的中序序列,右邊的序列是右子樹的中序序列。
- 在上面的例子中,
A在中序序列D B E A F C中的位置是第4個。那么D B E是左子樹的中序序列,F C是右子樹的中序序列。
- 確定左右子樹的層序序列:
- 從層序序列中去掉根節點后,剩下的節點需要根據中序序列的劃分來分配到左右子樹。
- 在上面的例子中,去掉
A后,層序序列剩下B C D E F。 - 左子樹的中序序列是
D B E,右子樹的中序序列是F C。 - 我們可以假設左子樹的層序序列是
B D E,右子樹的層序序列是C F(但這只是一個假設,實際上可能有多種分配方式)。
- 遞歸構造左右子樹:
- 對左子樹的層序序列
B D E和中序序列D B E重復上述步驟。 - 對右子樹的層序序列
C F和中序序列F C重復上述步驟。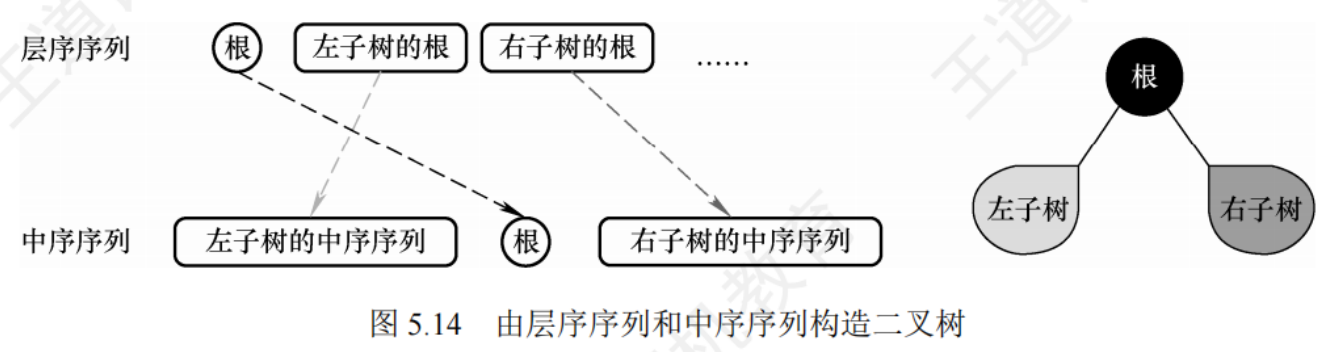
- 對左子樹的層序序列
5.3.2線索二叉樹
若無左子樹,令lchild指向其前驅節點,若無右子樹,rchild指向其后繼節點

- Ltag = 0 :lchild指示節點左孩子
- Ltag = 1 :lchild指示節點的前驅
- Rtag = 0 :rchild指示節點的右孩子
- Rtaag = 1 :rchild指示節點的后繼
//線索二叉樹結點
typedef struct ThreadNode{ElemType data;struct ThreaDNode *lchild,*rchild;int ltag,rtag; //左、右線索標志 //ltag == 1,表示lchild指向前驅;ltag == 0,表示lchild指向左孩子//rtag == 1,表示rchild指向前驅;rtag == 0,表示rchild指向右孩子
}ThreadNode,*ThreadTree;
中序線索二叉樹構造
- 快慢指針:pre指示剛剛訪問過的節點,p指示正在訪問的節點,即pre指向p的前驅
- 檢查p的左指針是否為空(p節點是否有左孩子),若為空就將它指向pre
- 檢查pre的右指針是否為空(pre是否有右孩子),若為空就將它指向p
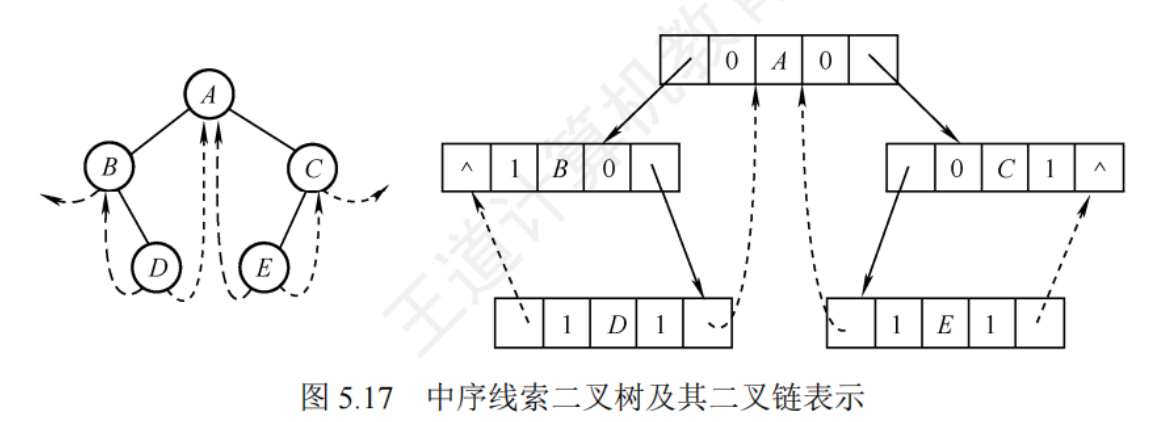
void InThread(ThreadTree &p, ThreadTree &pre) {if (p != NULL) {InThread(p->lchild, pre); // 遞歸,線索化左子樹if (p->lchild == NULL) { // 當前結點的左子樹為空p->lchild = pre; // 建立當前結點的前驅線索p->ltag = 1;}if (pre != NULL && pre->rchild == NULL) { // 前驅結點非空且其右子樹為空pre->rchild = p; // 建立前驅結點的后繼線索pre->rtag = 1;}pre = p; // 標記當前結點成為剛剛訪問過的結點InThread(p->rchild, pre); // 遞歸,線索化右子樹}
}void CreateInThread(ThreadTree T) {ThreadTree pre = NULL;if (T != NULL) { // 非空二叉樹,線索化二叉樹InThread(T, pre); // 線索化二叉樹pre->rchild = NULL; // 處理遍歷的最后一個結點pre->rtag = 1;}
}
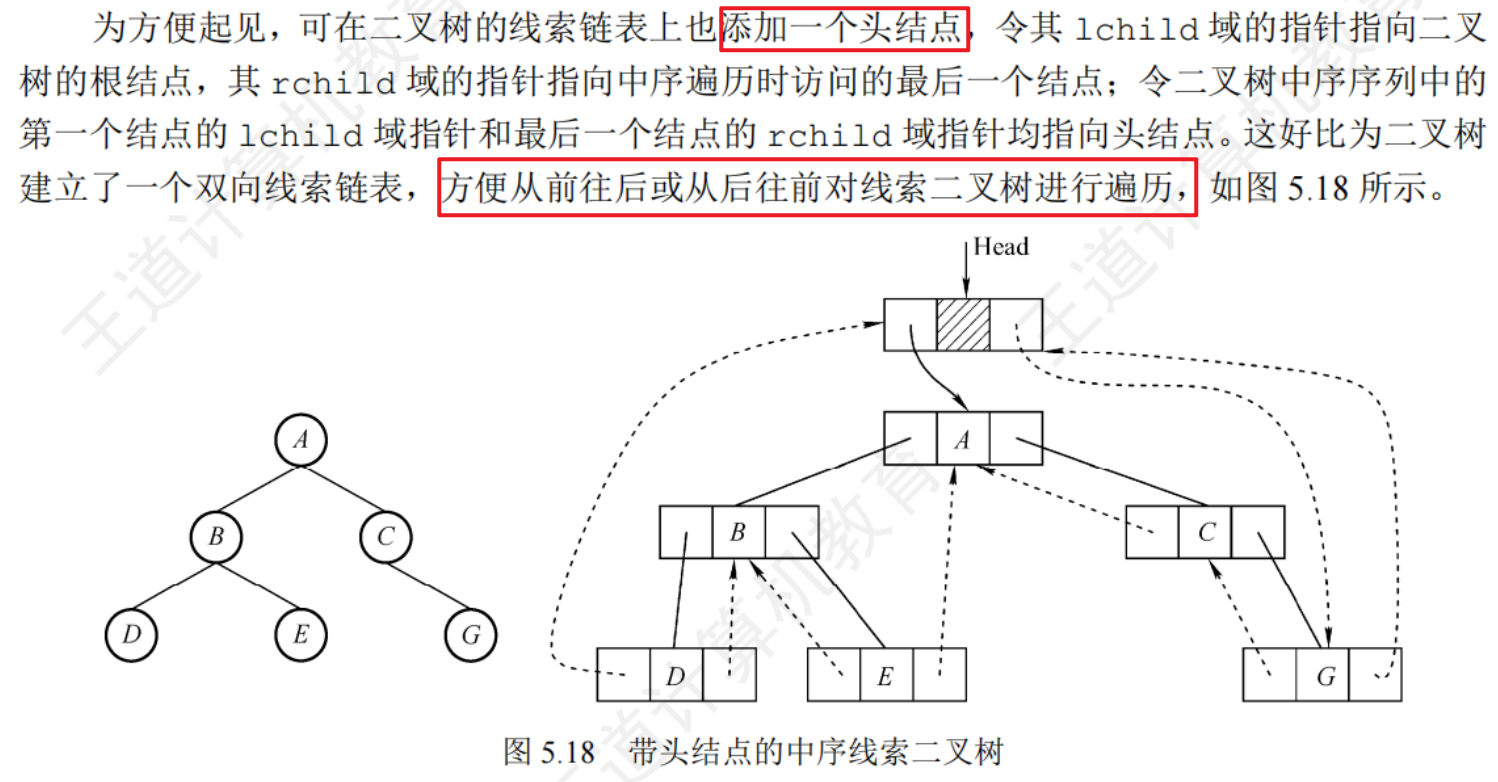
中序線索二叉樹的遍歷
思路:線索二叉樹包含節點的前驅后繼信息,遍歷時需要先找到第一個節點(最左下節點),然后依次找后繼節點:若右標志(Rtag = 1)為線索,則其指示后繼,否則指示右子樹,繼續找右子樹最左下節點
//中序線索二叉樹找中序后繼//找到以P為根的子樹中,第一個被中序遍歷的結點
ThreadNode *Firstnode(ThreadNode *p){//循環找到最左下結點(不一定是葉結點)while(p->ltag == 0)p=p->lchild;return p;
}
//在中序線索二叉樹中找到結點p的后繼結點
ThreadNode *Nextnode(ThreadNode *p){//右子樹中最左下結點if(p->rtag == 0)return Firstnode(p->rchild);else return p->rchild; //rtag==1直接返回后繼線索
}
//對中序線索二叉樹進行中序遍歷(利用線索實現的非遞歸算法)
void Inorder(ThreadNode *T){for(ThreadNode *p=Firstnode(T); p!=NULL; p=Nextnode(p))visit(p);
}
線序線索二叉樹和后序線索二叉樹
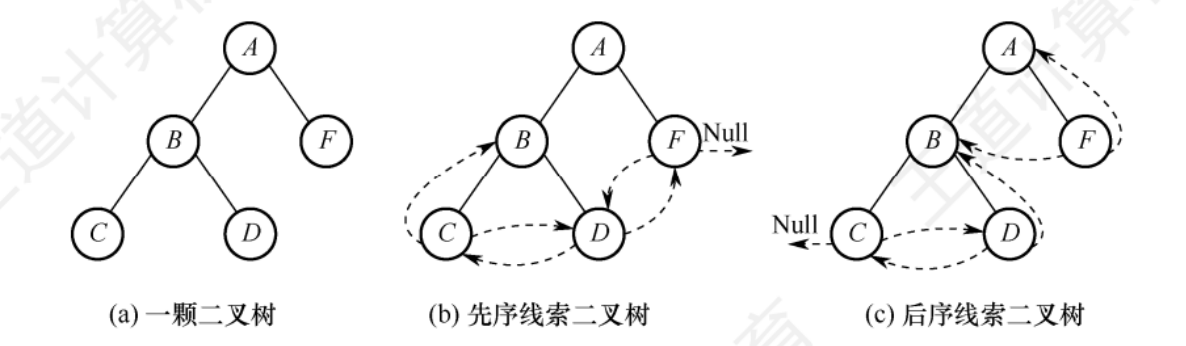
線序線索二叉樹找后繼:若有左孩子,左孩子是后繼,若無左孩子有右孩子,右孩子是后繼,若為葉節點,右鏈域為后繼
后序二叉樹找后繼:
- 若節點x是二叉樹的根,則其后繼為空
- 若節點x是其雙親的右孩子,或是其雙親的左孩子且其雙親沒有右子樹,則其后繼即為雙親
- 若節點x是其雙親的左孩子,且其雙親有右子樹,則其后繼為雙親的右子樹上按后序遍歷的第一個節點
5.4.1樹的存儲結構(注意與二叉樹的區分)
樹會有多個孩子節點
雙親表示法
采用一組連續的存儲空間存儲每個節點,同時增設一組偽指針,指示其雙親節點在數組中的位置
//雙親表示法(順序存儲)
#define MAX_TREE_SIZE 100 //樹中最多結點數
typedef struct{ //樹中的結點定義ElemType data; //數據元素 int parent; //雙親位置域
}PTNode;
typedef struct{ //樹的類型定義 PTNode nodes[MAX_TREE_SIZE];//雙親表示 int n; //結點數
}PTree;
利用了每個節點只有唯一雙親的特性,很快就能找到每個節點的雙親節點,但求孩子節點時需要遍歷整個數組 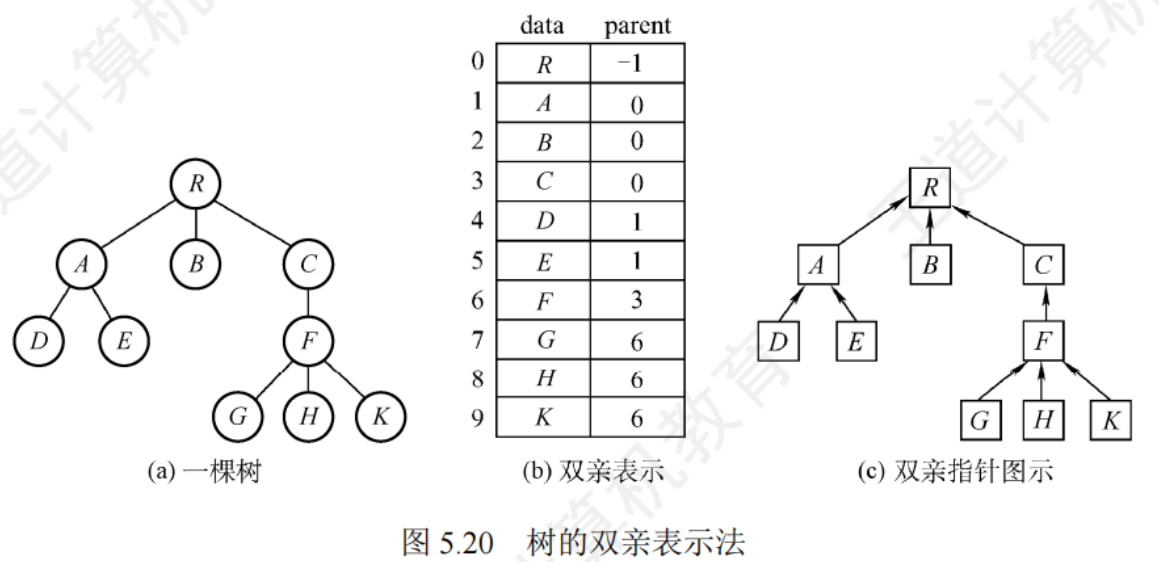
孩子表示法
將每個節點的孩子視為一個線性表,且以單鏈表作為存儲結構,則n個節點就有n個孩子鏈表
n個頭指針又組成一個線性表,可采用順序存儲結構
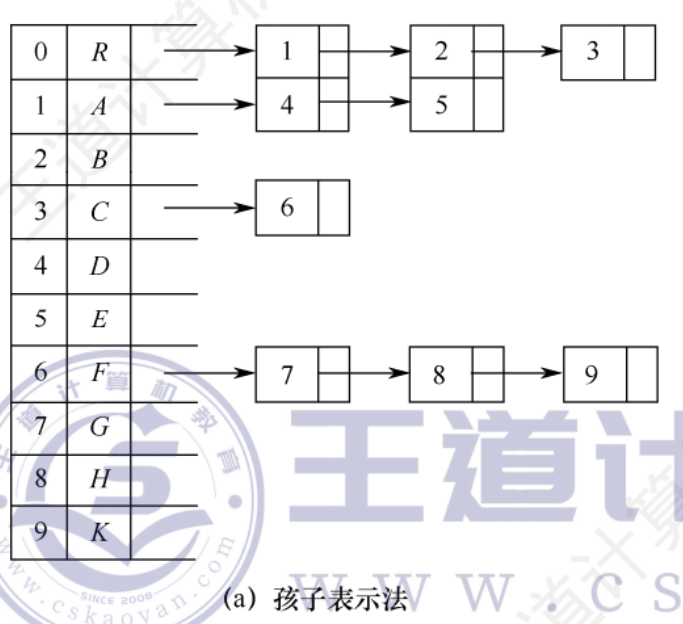
孩子表示法尋找孩子操作簡單,尋找雙親操作則需要遍歷
孩子兄弟表示法
二叉樹表示法,使用二叉鏈表作為樹的存儲結構,每個節點包括:節點值、指向節點第一個孩子節點的指針,指向節點下一個兄弟節點的指針
優點:可以方便的實現樹轉二叉樹的操作
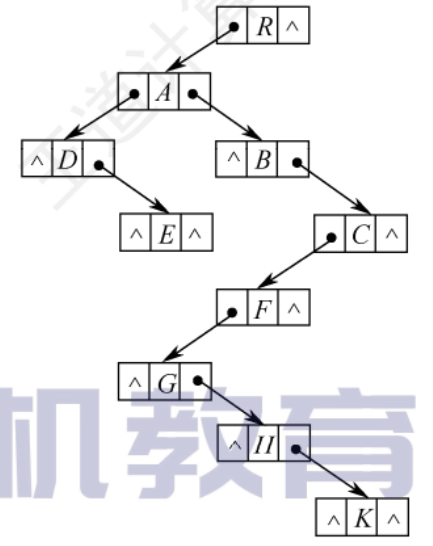
5.4.2樹、森林、二叉樹的轉換
樹轉二叉樹
每個節點的左指針指向它的第一個孩子,右指針指向它在樹中的相鄰右兄弟
根沒有兄弟,所以樹轉換為二叉樹時沒有右子樹
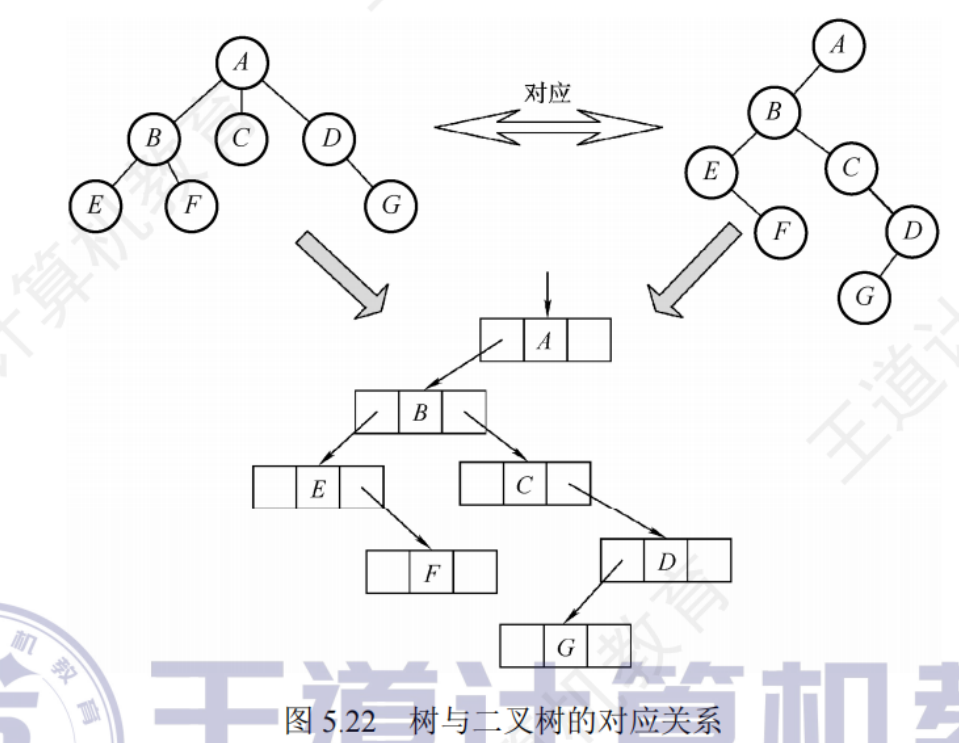
- 在兄弟節點之間加一條線
- 對每個節點,只保留它與左邊第一個孩子的連線,與其他孩子的連線刪除
- 以樹根為中心,旋轉
森林轉二叉樹
先將森林中的每一棵樹轉二叉樹,森林中的各棵樹視為兄弟關系,后一棵樹作為前一棵樹的右子樹
- 森林中的每一棵樹都轉換成相應的二叉樹
- 每棵樹的根視為兄弟,每棵樹的跟之間增加一條連線
- 以一顆樹的根為中心旋轉
二叉樹轉森林
若二叉樹非空,二叉樹的根及其左子樹作為第一棵樹的二叉樹形式,將根的右連接斷開。二叉樹根的右子樹視為一個由除第一棵樹外的森林轉換后的二叉樹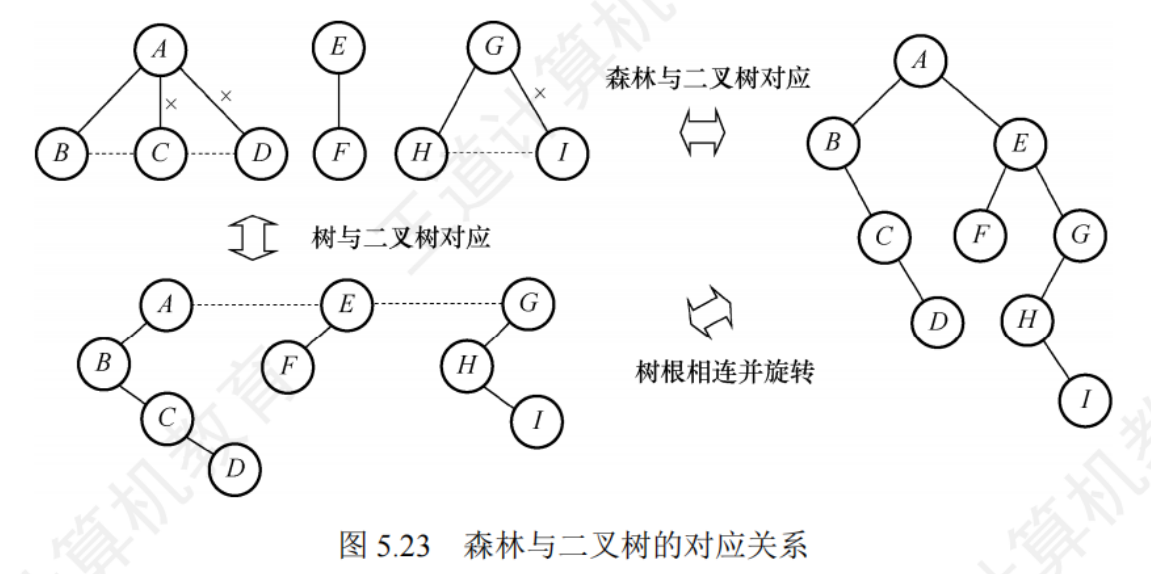
5.4.3樹和森林的遍歷
樹的遍歷
- 先根遍歷
- 先訪問根節點
- 再依次訪問根節點的每一棵子樹,遍歷子樹時仍遵循先根后子樹
- 后根遍歷
- 先依次遍歷根節點的每棵子樹,子樹遍歷時仍遵循先子樹后根
- 訪問根節點
二叉樹的后根遍歷 = 中序遍歷
森林的遍歷
- 先序遍歷森林
- 訪問森林中每一棵樹的根節點
- 先序遍歷第一棵樹中根節點的子樹森林
- 先序遍歷除去第一棵樹之后剩余的樹構成的森林
- 中序遍歷森林
- 中序遍歷森林中第一棵樹的根節點的子樹森林
- 訪問第一棵樹的根節點
- 中序遍歷除去第一棵樹之后剩余的樹構成的森林

5.5.1哈夫曼樹與哈夫曼編碼
帶權路徑長度:從樹的根到一個節點的路徑長度與該節點上權值的乘積
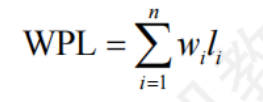
哈夫曼樹:n個節點的二叉樹中,其中帶權路徑長度 WPL最小的二叉樹
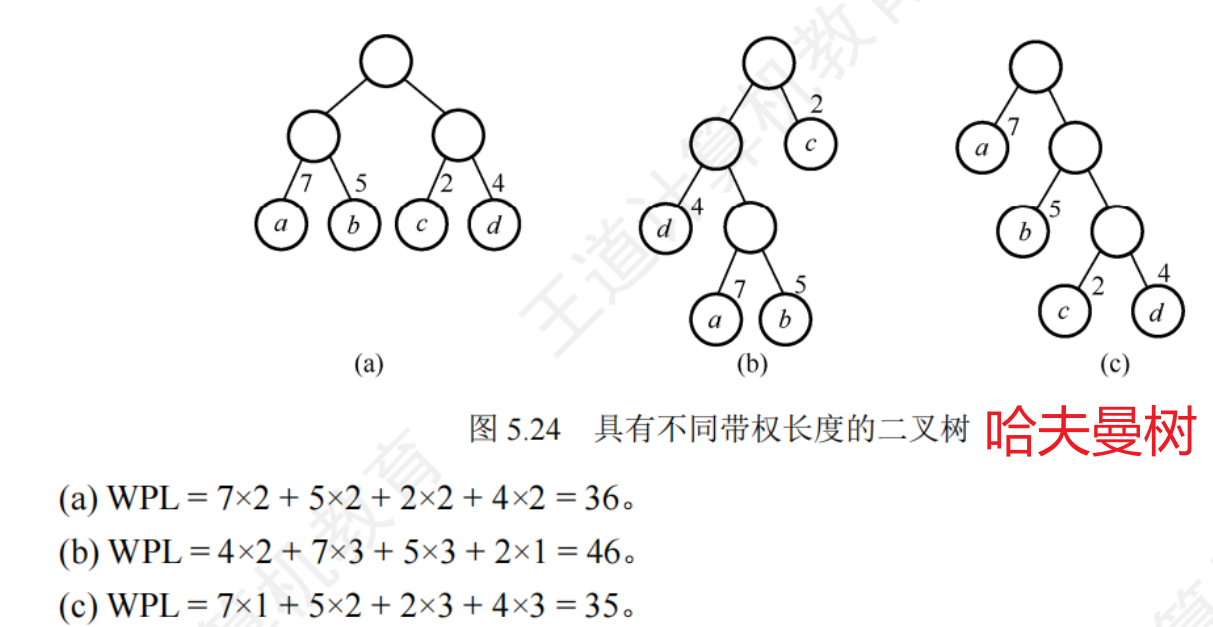
哈夫曼樹的構造
- 將n個節點分別作為n棵僅含一個節點的二叉樹,構成森林F
- 構造一個新節點,從F中選出兩棵根節點權值最小的樹作為新節點的左右子樹,并且新節點的權值置為左右子樹上根節點的權值之和
- 從F中刪除剛才選出的兩棵樹,同時加入新樹
- 重復
特點:
- 每個初始節點最終都成為葉節點,權值越小的節點到根節點的路徑長度越大
- 構造過程共創建了n-1個新節點,因此節點總數為2n-1
- 每次構造選取2棵子樹作為新節點的孩子,因此哈夫曼樹不存在度為1的節點
哈夫曼編碼
固定長度編碼:對每個字符使用相等長度的二進制位表示
可變長度編碼:允許對不同字符使用不等長的二進制位編碼
前綴編碼:沒有一個編碼是另一個編碼的前綴

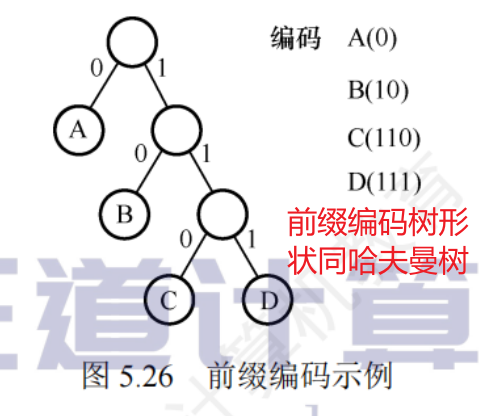
哈夫曼編碼:
將每個字符作為一個獨立的節點,其權值為它出現的頻度(次數),構造出對應的哈夫曼樹,從根到葉節點的路徑上的分支標記字符串作為該字符編碼
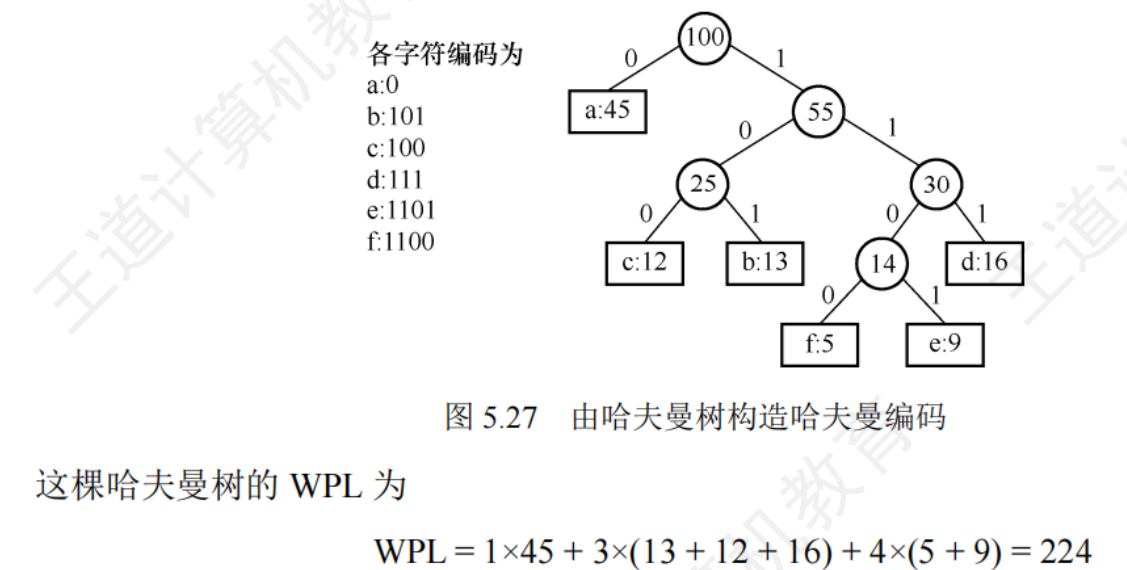
左分支、右分支表示0或者1不確定,得出的哈夫曼樹不一定
5.5.2并查集
樹的雙親表示作為并查集的存儲結構,每個子集合使用一棵樹表示,所有表示集合的樹構成表示全集合的森林,存放在雙親表示數組內,通常使用數組元素下標表示元素名,用根節點的下標代表子集合名,根節點的雙親域為負數(可設置為該子集合元素數量的相反數)
并查集初始化
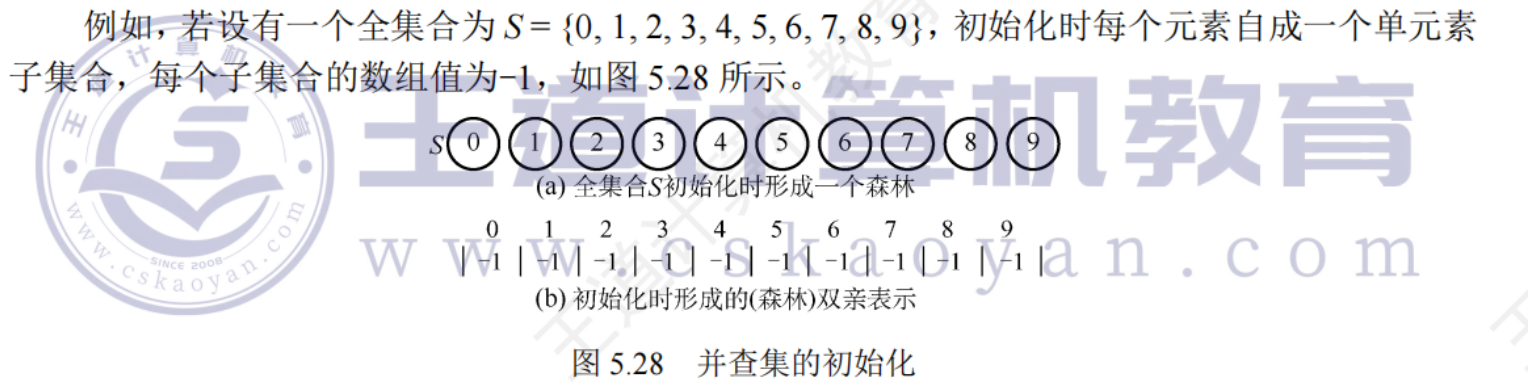
樹表示并查集
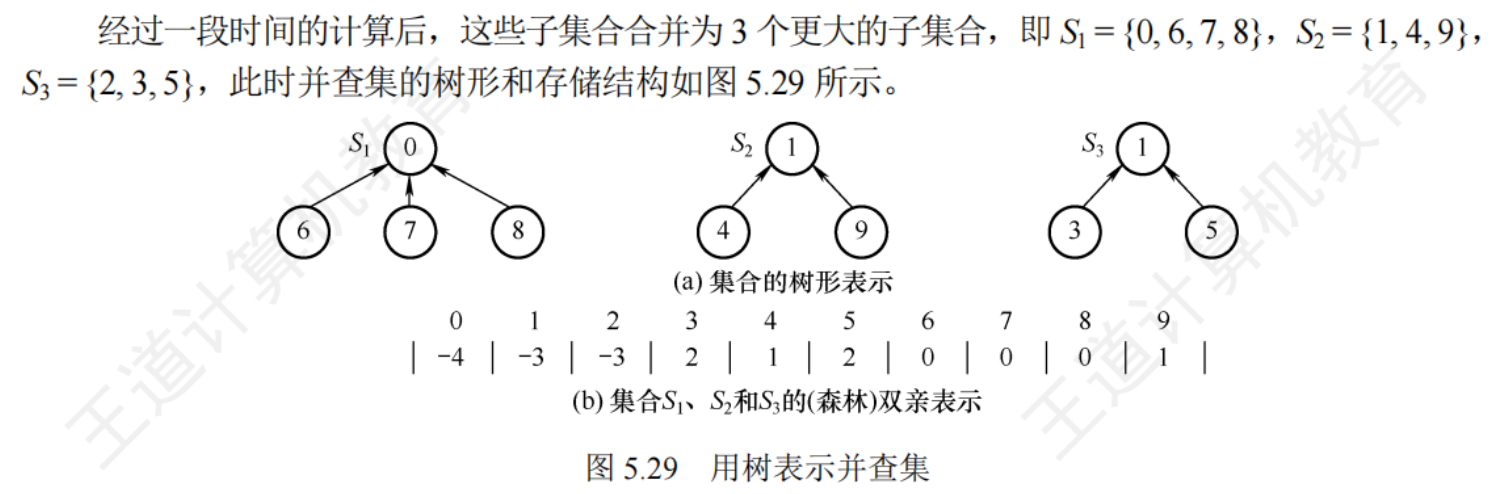
兩個集合的并

基本實現
//并查集的基本操作
#define SIZE 13
int UFSets[SIZE]; //集合元素數組//初始化并查集
void Initial(int S[]){for(int i=0; i<SIZE; i++)S[i] = -1;
} //Find “查”操作,找x所屬集合(返回x所屬根節點)
int Find(int S[],int x){while(S[x]>=0) //循環尋找x的根x = S[x];return x; //根的S[]小于0
}
//Union “并”操作,將兩個集合合并為一個
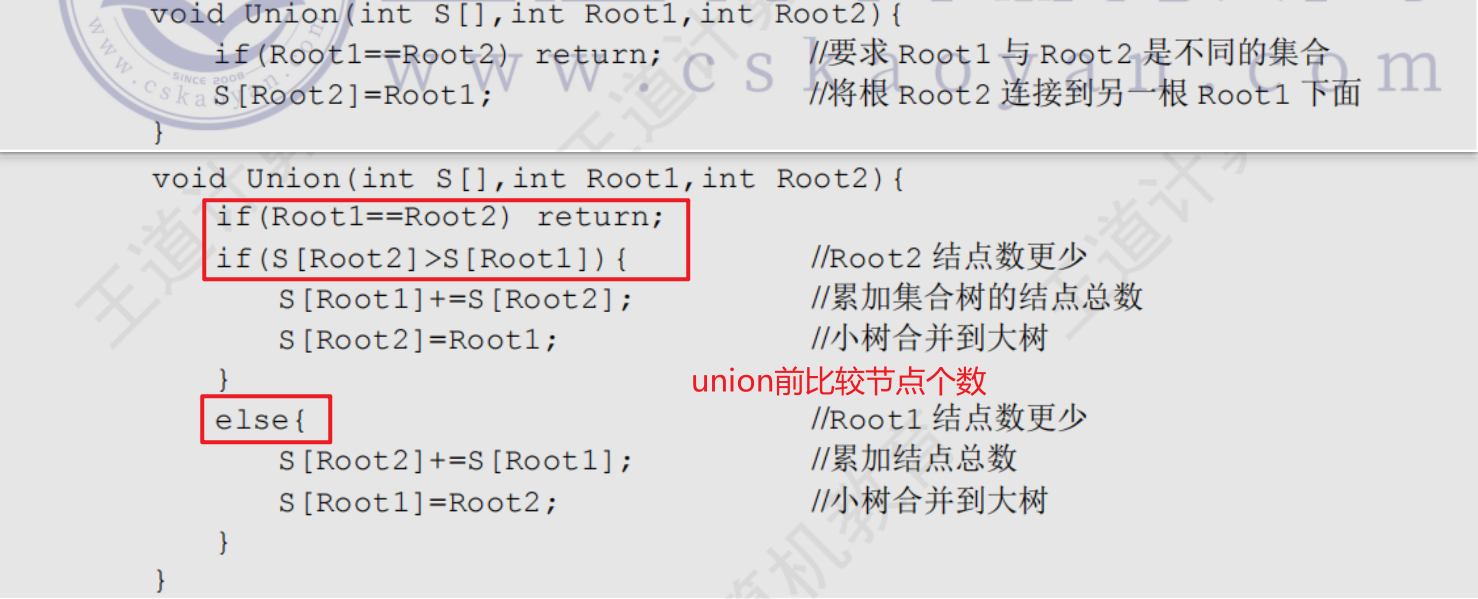
void Union(int S[],int Root1,int Root2){//要求Root1與Root2是不同的集合if(Root1 == Root2) return;//將根Root2連接到另一根Root1下面S[Root2] = Root1;
}
并查集優化



6.圖

6.1.1圖的定義
圖G由頂點集V和邊集E組成,記為 G = (V,E),其中V(G)表示圖的有限非空集,E(G)表示圖G中頂點之間的關系
線性表可以是空表,樹可以是空樹,但圖不能是空圖
圖中不能一個頂點也沒有,即頂點集V一定非空,但邊集E可以為空
有向圖
E是有向邊(弧)的有限集合,弧是頂點的有序對,記為<v,w>,其中v,w是頂點,v稱為弧尾,w稱為弧頭
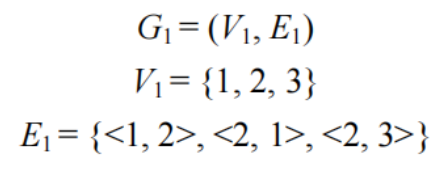
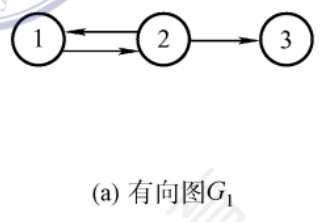
無向圖
邊是頂點的無序對,記為(v,w)
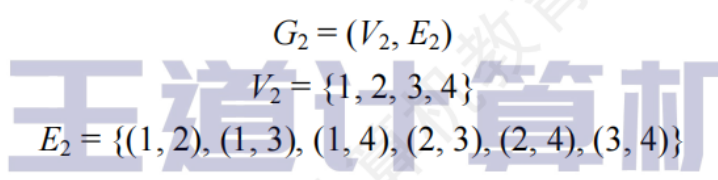
簡單圖
不存在重復邊
不存在頂點到自身的邊
多重圖
某兩個頂點之間的邊數大于1條,又允許頂點通過一條邊和自身關聯
頂點的度
頂點的度:依附于頂點v的邊的條數,TD(v)
無向圖的全部頂點的度之和等于邊數的2倍
入度:有向圖中,以頂點為終點的有向邊的數目,ID(v)
出度:有向圖中,以頂點為起點的有向邊的數目,OD(v)
路徑
指從頂點 vp 到 vq 之間的頂點序列
路徑長度:路徑上邊的數目
回路/環:第一個頂點和最后一個頂點相同的路徑
若一個圖有n個頂點,且有大于n-1條邊,則圖一定有環
簡單路徑:頂點不重復出現的路徑
簡單回路:除第一個頂點和最后一個頂點外,其余頂點不重復出現的回路
距離
兩頂點之間最短路徑長度
子圖
設有兩個圖 G = (V,E) 和 G’ = (V’,E’),若 V‘ 是 V 的子集,E’ 是 E 的子集,則稱 G‘ 是 G 的子圖
并非V E的任何子集都可以構成子圖——有可能不是圖,即E的子集中的某些邊關聯的頂點不在 V的子集中
連通
無向圖中,從頂點v到頂點w有路徑存在
連通圖
圖G中任意兩個頂點都是連通的,否則為非連通圖
連通分量
無向圖的極大連通子圖
一個圖有n個頂點,若邊數小于n-1,必為非連通圖
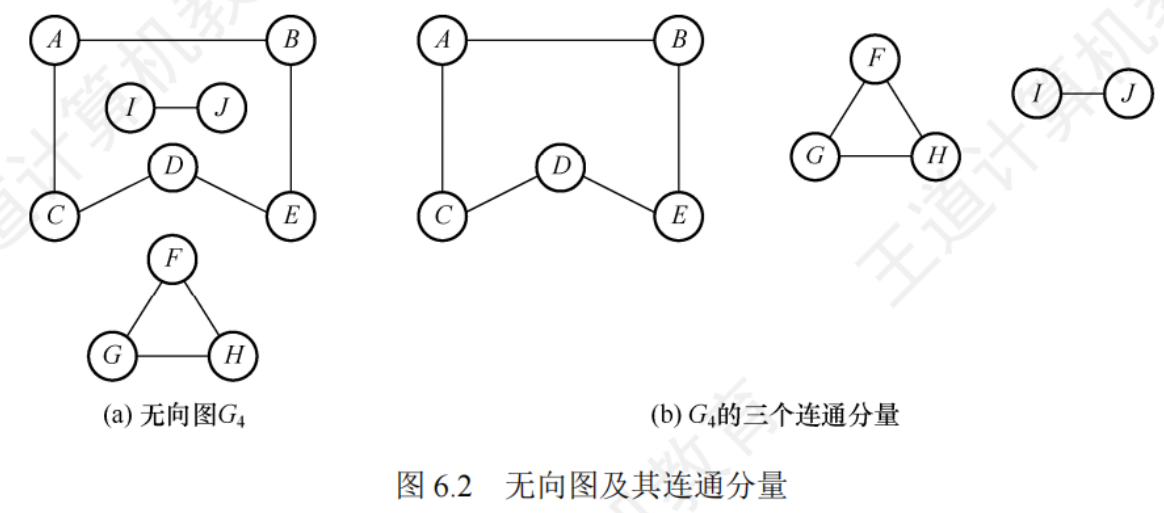
強連通圖
強連通:有向圖中,一對頂點 v 和 w 之間,既有 v 到 w 的路徑,又有 w 到 v 的路徑
若任意一對頂點都是強連通的,則稱之為強連通圖
強連通分量
有向圖中的極大強連通子圖
生成樹
連通圖的生成樹是包含圖中全部頂點的一個極小連通子圖,若圖中頂點數為n,則它的生成樹含有n-1條邊
生成樹若刪除一條邊就會變成非連通圖,若加上一條邊就是形成回路

邊的權重
一個圖中,每條邊都可以標上含有某種含義的數值,該數值稱為權值
帶權圖:邊上帶有權值的圖
帶權路徑長度:路徑上所有邊的權值之和
完全圖
對于無向圖,|E|的取值范圍從 0 到 n(n-1)/2,有 n(n-1)/2的圖稱為完全圖
完全圖任意兩個頂點之間存在邊
有向完全圖
對于有向圖,|E|的取值范圍為 0 到 n(n-1) ,有 n(n-1)條弧的有向圖稱為有向完全圖
有向完全圖兩頂點之間存在方向相反的兩條弧
稠密圖
邊數很少的圖,一般 |E| < |V|log2|V|
又向樹
一個頂點的入度為0,其余頂點的入度均為1的有向圖
6.2.1圖的存儲——鄰接矩陣法
用一個一維數組存儲圖中頂點的信息,用一個二維數組存儲圖中邊的信息(各頂點之間的鄰接關系),存儲頂點之間的鄰接關系的二維數組稱為鄰接矩陣


出入度計算:
第i個節點的出度 = 第 i 行非0元素
第i個節點的入度 = 第 i 列非0元素
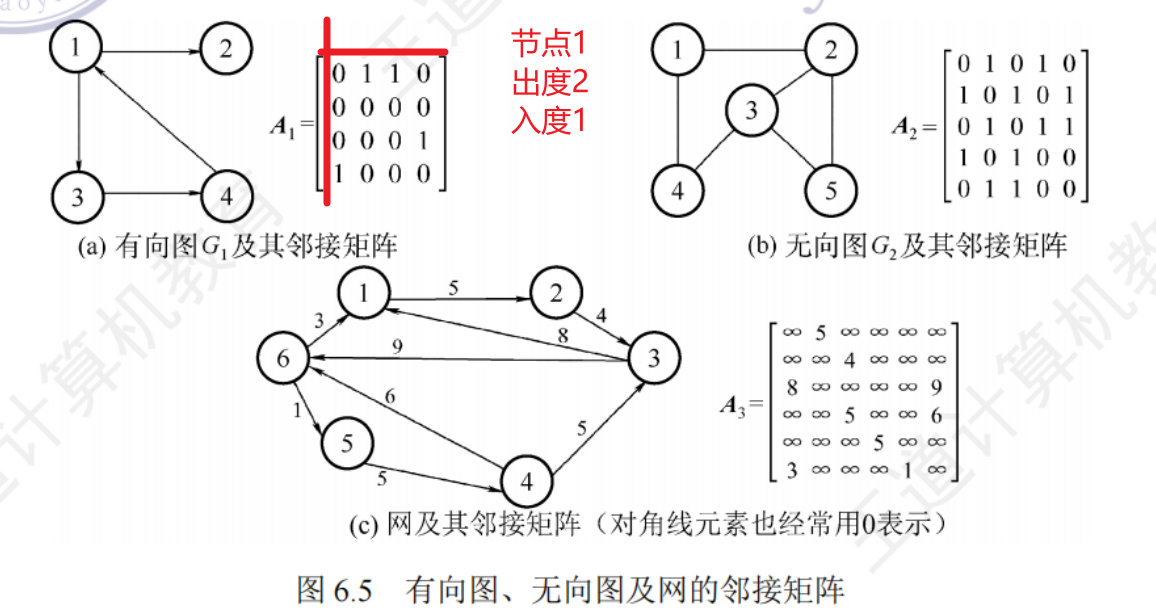
//鄰接矩陣法
#define MaxVertexNum 100 //頂點數目的最大值
typedef struct{char Ver[MaxVertexNum]; //頂點表 int Edge[MaxVertexNum][MaxVertexNum]; //鄰接矩陣、邊表int vexnum,arcnum; //圖的當前頂點數和邊數/弧數
}MGraph;
//鄰接矩陣法存儲帶權圖
#define MaxVertexNum 100 //頂點數目的最大值
#define INFINITY 最大的int值 //宏定義常量“無窮”
typedef char VertexType; //頂點的數據類型
typedef int EdgeType; //帶權圖中邊上權值的數據類型
typedef struct{VertexType Vex[MaxVertexNum]; //頂點 EdgeType Edge[MaxVertexNum][MaxVertexNum]; //邊的權 int vexnum,arcnum; //圖的當前頂點數和弧數
}MGraph;
無向圖的鄰接矩陣是對稱矩陣,規模大時可使用壓縮存儲
鄰接矩陣表示法的空間復雜度 O(n^2),n為頂點數 |V|
特點
- 無向圖的鄰接矩陣一定是一個唯一的對稱矩陣,因此,實際存儲鄰接矩陣時只需要存儲上(下)三角矩陣
- 對于無向圖,鄰接矩陣的第 i 行非零元素的個數正好是頂點 i 的出度,第 i 列非零元素的個數正好是頂點 i 的入度
- 鄰接矩陣存儲很容易確定兩個頂點之間是否有邊相連
- 稠密圖適合鄰接矩陣存儲

6.2.2圖的存儲——鄰接表法
對圖G中的每個頂點建立單鏈表,第 i 個單鏈表中的節點表示依附于頂點 v 的邊(有向圖表示以頂點 v 為尾的弧),這個單鏈表稱為頂點 v 的邊表(對于有向圖稱為出邊表)
邊表的頭指針和頂點的數據信息采用順序存儲,稱為頂點表
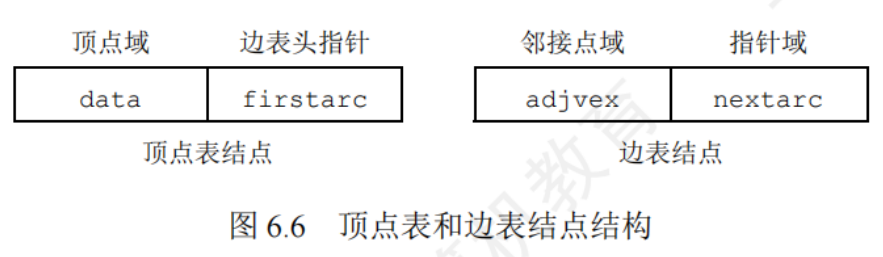
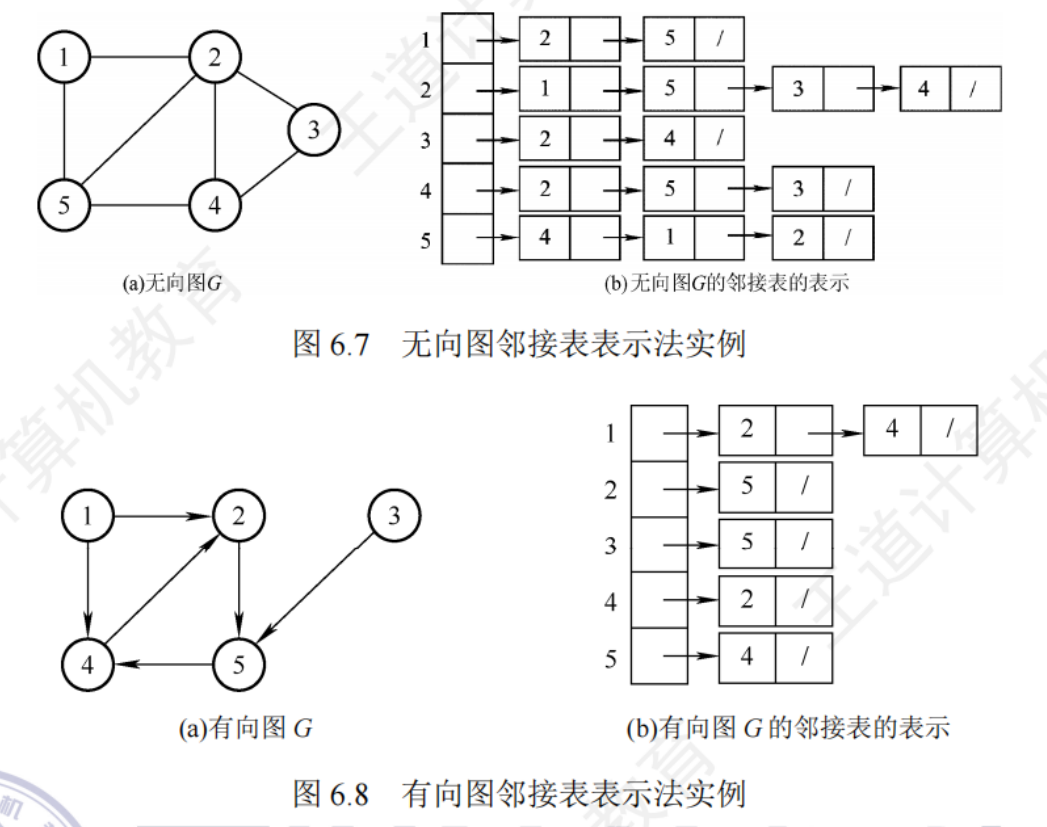
//用鄰接表存儲的圖
typedef struct{AdjList vertices;int vexnum,arcnum;
}ALGRaph;
//“邊/弧”
typedef struct ArcNode{int adjvex; //邊/弧指向哪個結點 struct ArcNode *next; //指向下一條弧的指針 //InfoType info; //邊權值
}ArcNode;
//頂點
typedef struct VNode{VertexType data; //頂點信息 ArcNode *first; //第一條邊/弧
}VNode,AdjList[MaxvertexNum];
特點
- 若G為無向圖,所需存儲空間 O(|V| + 2|E|),若G是有向圖,所需存儲空間O(|V| + |E|)
- 對于稀疏圖,適合采用鄰接表存儲
- 給定一個頂點很容易找到它所有的鄰邊,O(n)
- 無向圖鄰接表中,某個頂點的度只需計算其鄰接表中邊表節點的個數,在有向圖的鄰接表中,求某個頂點的出度只需計算其鄰接表中的邊表節點的個數,但求某個頂點的入度則需要遍歷全部鄰接表
- 圖的鄰接表表示不唯一
6.2.3圖的存儲——十字鏈表
十字鏈表是有向圖的一種鏈式存儲結構,有向圖的每一條弧用一個節點來表示,每個頂點也用一個節點來表示

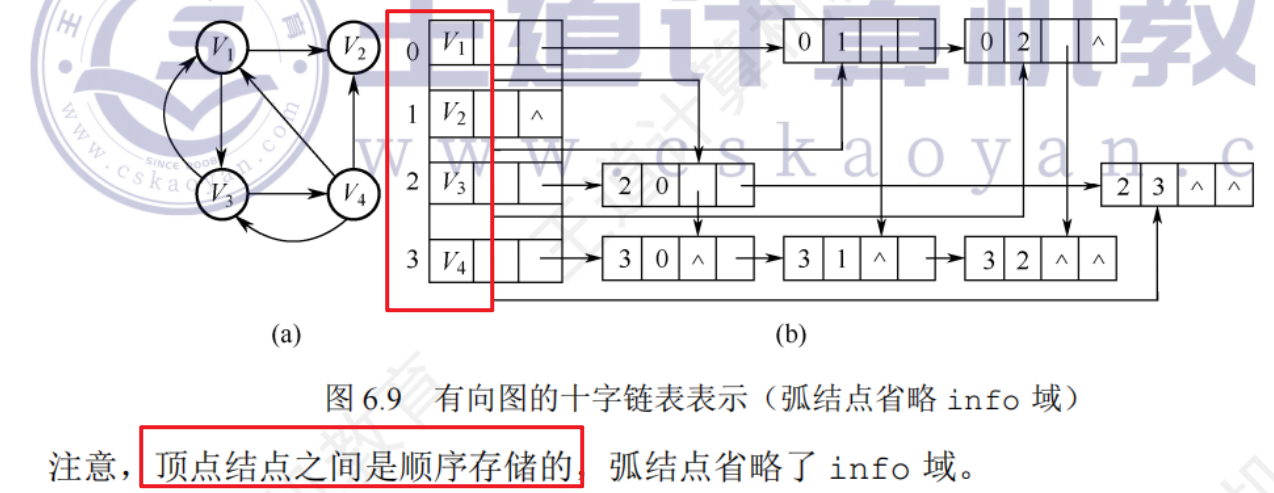
很容易找到頂點的入度和出度,圖的十字鏈表示不唯一,但十字鏈表示唯一確定一個圖
6.2.4鄰接多重表
鄰接多重表是無向圖的一種鏈式存儲結構
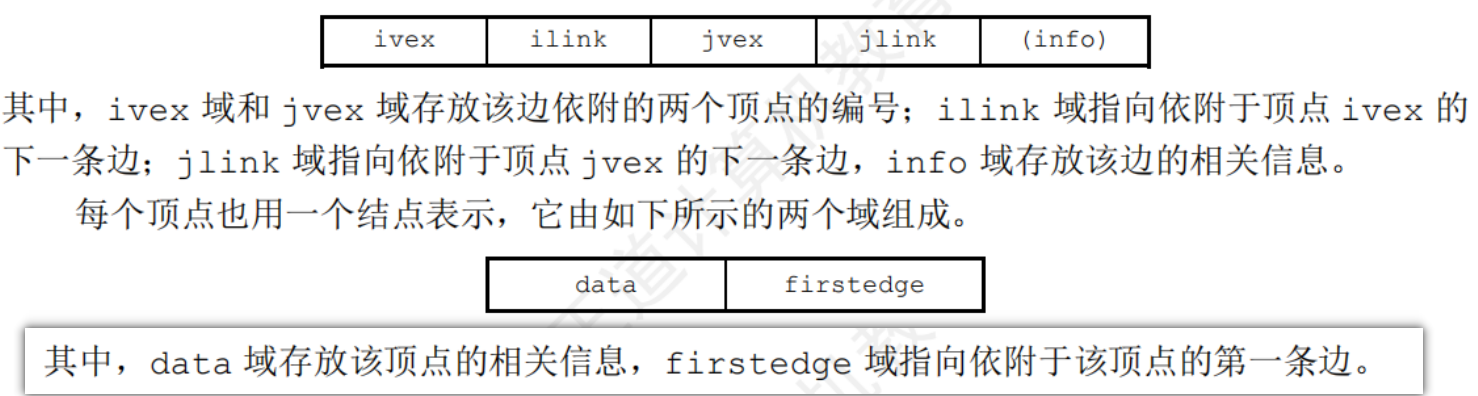
鄰接多重表中,所有依附于同一頂點的邊串聯在同一鏈表中,因為每條邊依附于兩個頂點,所以每個邊節點同時連接在兩個鏈表中
對比
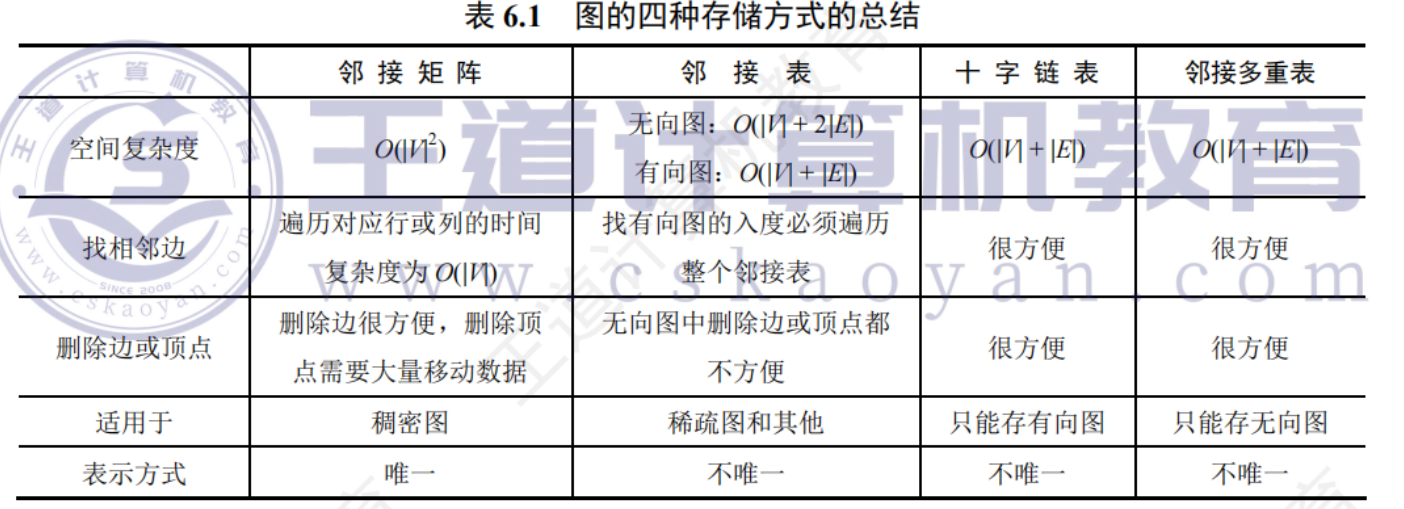
6.2.5圖的基本操作

6.3.1廣度優先搜索
類似于樹的層次遍歷,首先訪問起點v,接著由v出發,依次訪問v的各個未訪問過的鄰接頂點 w1,w2,w3…,然后依次訪問w1,w2,w3…的所有未被訪問過的鄰接頂點,再從這些訪問過的頂點出發,訪問他們所有未被訪問過的鄰接頂點,直至所有節點都被訪問
算法必須借助一個輔助隊列
廣度優先搜索地偽碼
bool visited[MAX_VERTEX_NUM]
void BFSTraverse(Graps G){for(i = 0 ; i < G.vexnum; i++){visited[i] = FALSE;}IniQueue(Q);for(i = 0 ; i < G.vernum ; i++){if(!visited[i])BFS(G,i);}
}
鄰接表實現廣度優先搜索
void BFS(ALGraph G,int i){//訪問初始節點visit(i); //對 i 做已訪問標記visited[i] = TRUE;//頂點i入隊EnQueue(Q,i);while(!IsEmpty(Q)){//隊首v出隊DeQueue(Q,v);//檢測v的所有鄰接點for(p = G.vertices[v].firstarc;p;p=p->nextarc){w = p->adjvex;if(visited[w] == FALSE){//w為v的尚未訪問的鄰接點,訪問wvisit(w);//對 w 做已訪問標記visited[w] = TRUE;//頂點 w 入隊EnQueue(Q,w);}}}
}
鄰接矩陣實現廣度優先搜索
//廣度優先遍歷
bool visited[MAX_VERTEX_NUM]; //訪問標記數組
void BFSTraverse(Graph G){ //對圖G進行廣度優先遍歷 for(i=0; i<G.vexnum; ++i) visited[i] = FALSE; //訪問標記數組初始化 InitQueue(Q); //初始化輔助隊列Q for(i=0; i<G.vexnum; ++i) //從0號頂點開始遍歷 if(!visited[i]) //對每個連通分量調用一次BFS BFS(G,i); //vi未訪問過,從vi開始BFS
}
void BFS(Graph G,int v){ //從頂點v出發,廣度優先遍歷圖G visit(v); //訪問初始頂點v visited[i] = TRUE; //對v做已訪問標記 Enqueue(Q,v); //頂點v入隊列Q while(!isEmpty(Q)){DeQueue(Q,v); //頂點v出隊列 for(w=FirstNeighbor(G,v); w>=0; w=NextNeighbor(G,v,w))//檢測v所有鄰接點if(!visited[w]){ //w為v的尚未訪問的鄰接頂點 visit(w); //訪問頂點w visited[w]=TRUE;//對w做已訪問標記 EnQueue(Q,w); //頂點w入隊列 }//if}//while
}
廣度優先遍歷的過程
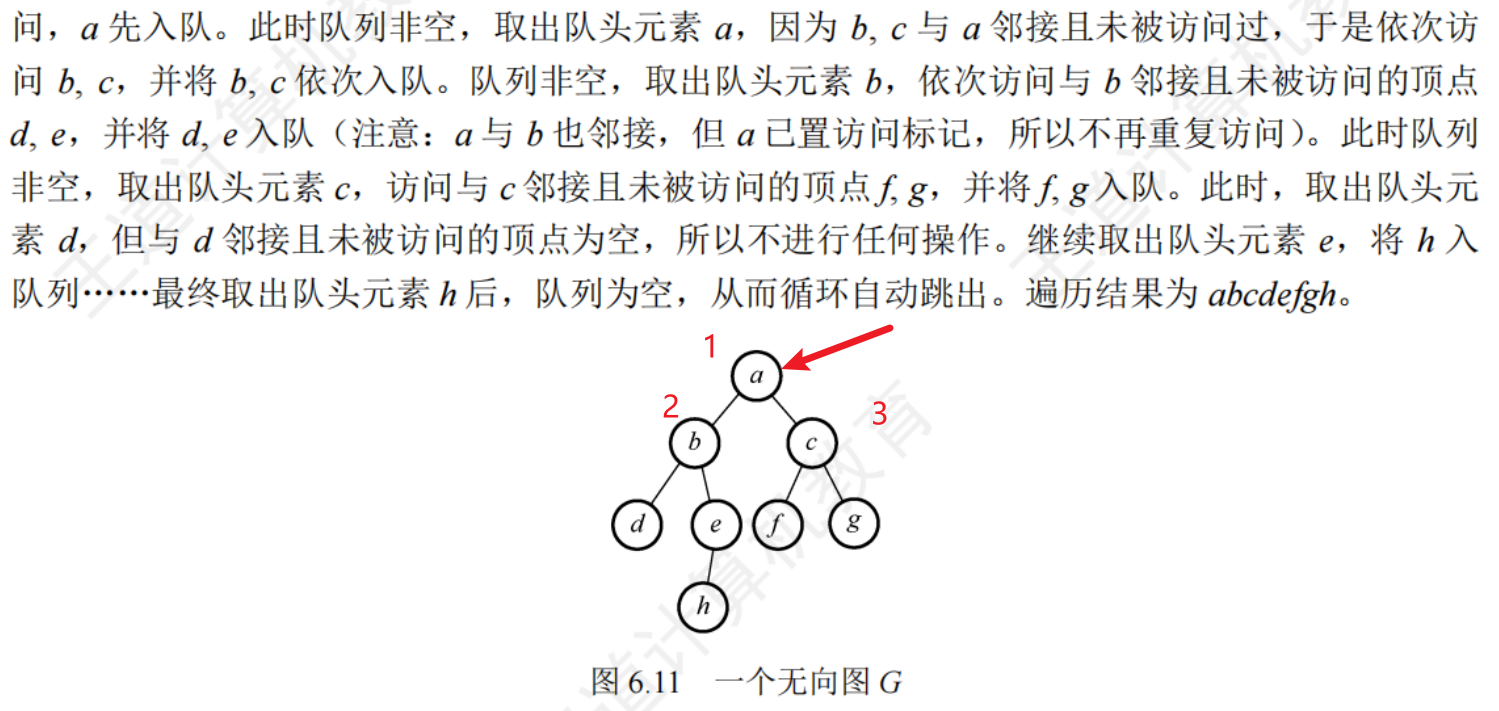
性能分析
需要借助一個輔助隊列Q,n個頂點均需入隊一次,最壞空間復雜度為O(|V|)
時間復雜度 鄰接矩陣 O(|V| + |V|^2) 鄰接表 O(|V|+|E|)
BFS求解單源最短路徑問題
非帶權圖的單源最短路徑:從頂點u到頂點v的最短路徑為從u到v的任何路徑中邊數最少
//求頂點u到其他頂點的最短路徑
void BFS_MIN_Distance(Graph G,int u){//d[i]表示u到i結點最短路徑 for(i=0; i<G.vexnum; ++i){d[i] = ∞; //初始化路徑長度 path[i] = -1; //最短路徑從哪個頂點過來 } d[u] = 0;visited[u] = TRUE;EnQueue(Q,u);while(!isEmpty(Q)){while(!isEmpty(Q)){ //BFS算法主過程 DeQueue(Q,u); //隊頭元素u出隊 for(w=FirstNeighbor(G,u); w>=0; w=NextNeighbor(G,u,w))if(!visited[w]){ //w為u的尚未訪問的鄰接頂點 d[w] = d[u]+1; //路徑長度加1 path[w] = u; //最短路徑應從u到w visited[w] = TRUE; //設已訪問標記 EnQueue(Q,w); //頂點w入隊 }//if}//while}
}
廣度優先生成樹
廣度優先搜索的遍歷樹為一棵廣度優先生成樹
圖的鄰接矩陣存儲表示是唯一的,所以其廣度優先生成樹唯一
圖的鄰接表存儲表示不唯一,所以其廣度優先生成樹不唯一
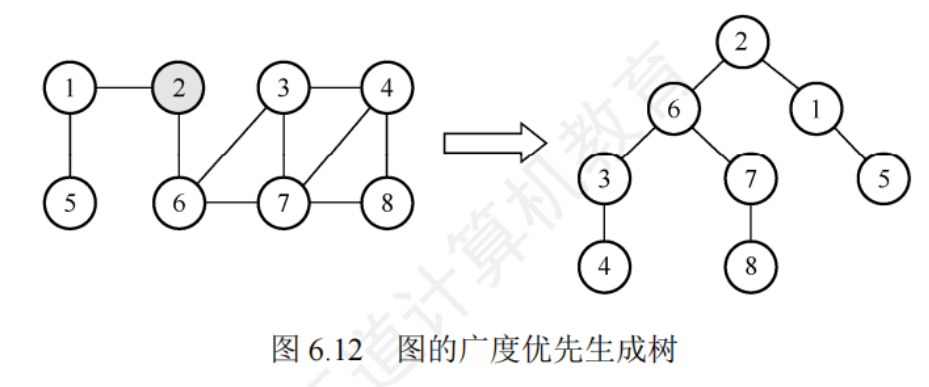
6.3.2深度優先搜索
它的基本思想如下:首先訪問圖中某一起始頂點v,然后由ν出發,訪問與ν鄰接且未被訪問的任意一個頂點w1,再訪問與w1鄰接且未被訪問的任意一個頂點w2··重復上述過程。當不能再繼續向下訪問時,依次退回到最近被訪問的頂點,若它還有鄰接頂點未被訪問過,則從該點開始繼續上述搜索過程,直至圖中所有頂點均被訪問過為止。
//深度優先遍歷
bool visited[MAX_VERTEX_NUM]; //訪問標記數組
void DFSTraverse(Graph G){ //對圖G進行深度優先遍歷 for(v=0; v<G.vexnum; ++v)visited[v] = FALSE; //初始化已訪問標記數據 for(v=0; v<G.vexnum; ++v) //從v = 0開始遍歷 if(!visited[w])DFS(G,v);
}
void DFS(Graph G,int v){ //從頂點v出發,深度優先遍歷G visit(v); //訪問頂點v visited[v] = TRUE; //設已訪問標記 for(w=FirstNeighbor(G,v); w>=0; w=NextNeighor(G,v,w))if(!visited[w]){ //w為u的尚未訪問的鄰接頂點 DFS(G,w);} //if
}void DFS(MGraph G,int i){visit(i);visited[i] = TRUE;for(j = 0 ; j < G.vexnum ; j++){if(visited[j] == FALSE && G.edge[i][j] == 1){DFS(G,j);}}
}
圖的鄰接矩陣遍歷得到的DFS和BFS序列唯一
圖的鄰接表遍歷得到的DFS和BFS序列不唯一
性能分析
空間復雜度 DFS是一個遞歸算法,需要一個遞歸工作棧,空間復雜度為 O(|V|)
時間復雜度 鄰接矩陣 O(|V|^2) 鄰接表 O(|V|+|E|)
深度優先生成樹與生成森林
只有連通圖調用DFS時才能生成深度優先生成樹,否則產生的是深度優先生成森林,且鄰接表產生的結果不唯一
6.3.3圖的遍歷與圖的連通性

6.4.1最小生成樹
一個連通圖的最小生成樹包含圖中所有頂點,且含有盡可能少的邊
權值之和最小的那棵生成樹稱為G的最小生成樹
性質
- 若圖G中存在權值相同的邊,則G的最小生成樹可能不唯一,即最小生成樹的樹形不唯一,當圖G中各邊的權值互不相等時,G的最小生成樹唯一;若無向連通圖G的邊數比定點數少1,即G本身是一棵樹時,G的最小生成樹就是它本身
- 雖然最小生成樹不唯一,但其對應邊的權值之和是唯一的,而且是最小的
- 最小生成樹的邊數為頂點數減1
最小生成樹中所有邊的權值之和最小,但是不能保證任意兩個頂點之間的路徑是最短路徑
Prim算法
初始時從圖中任取一頂點,加入樹T,此時樹中只包含一個頂點,之后選擇一個與當前T中頂點集合距離最近的頂點,并將該頂點和相應的邊加入T,每次操作后T的頂點數和邊數加1
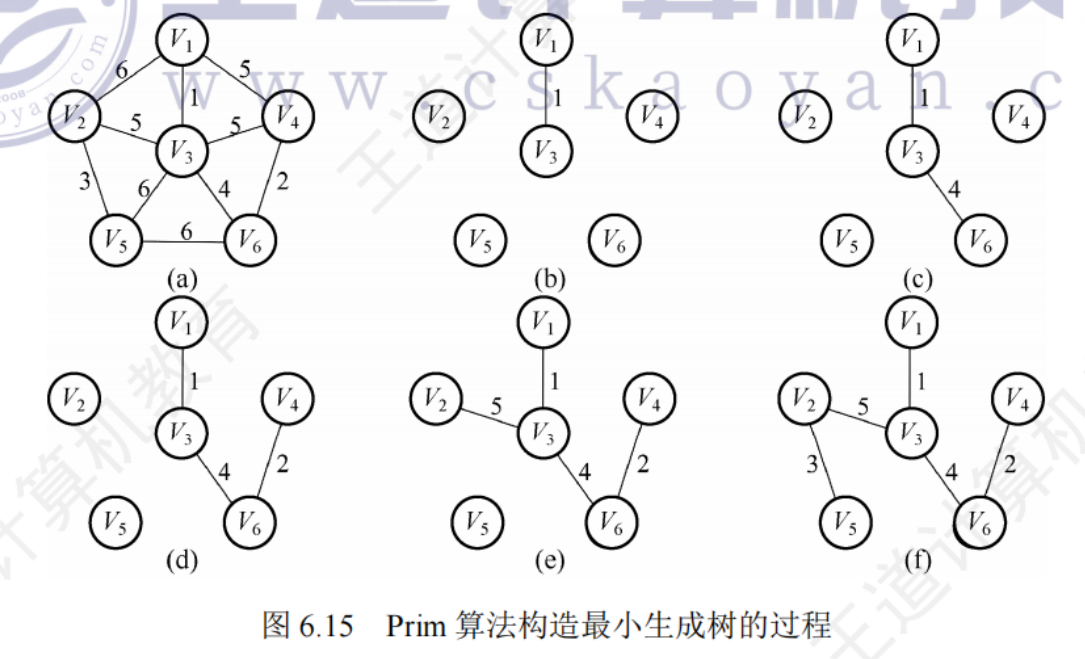

時間復雜度 O(|V|^2)
不依賴于|E|,適用于求邊稠密圖的最小生成樹
Kruskal算法
初始時只有n個頂點而無邊的非連通圖T{V,{}},每個頂點自成一個連通分量,然后按照邊的權值大小排序,不斷選取當前未被選取過的權值最小的邊,,若該邊依附的頂點落在T中不同的連通分類上(使用并查集判斷這兩個頂點是否屬于一棵集合樹),則將邊加入T,否則舍棄此邊而選擇下一條權值最小的邊
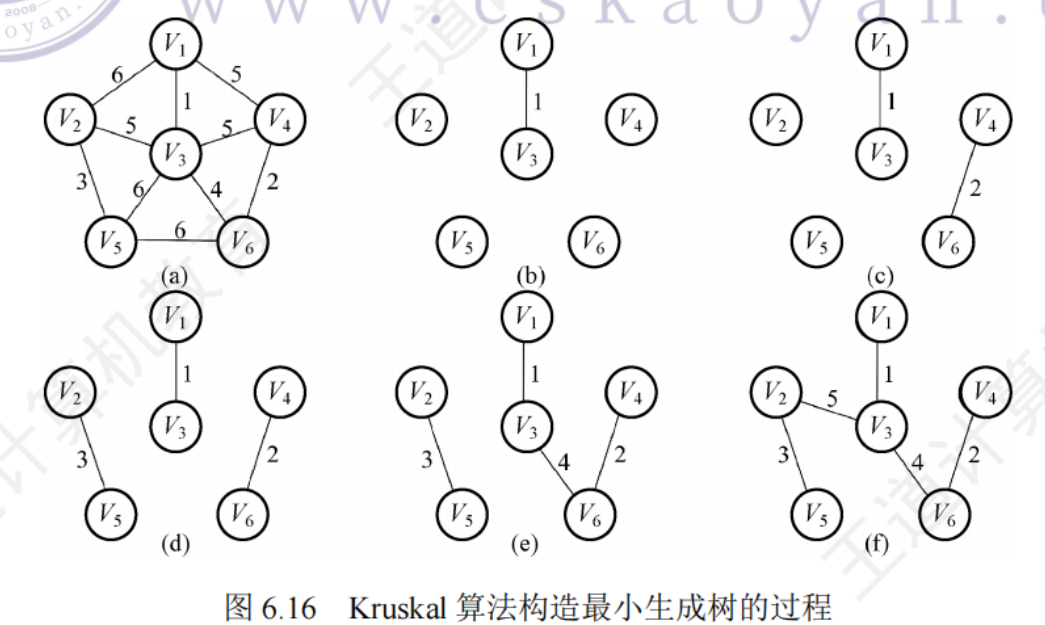


時間復雜度 O(|E|log2|E|)
不依賴于|V|適用于邊稀疏而頂點數多的圖
6.4.2最短路徑
廣度優先搜索查找最短路徑——無向圖
帶權有向圖的最短路徑問題可以分為兩類:
- 單源最短路徑:求圖中某一頂點到其他各點的最短路徑——Dijkstra算法
- 求每對頂點的最短路徑——Floyed算法
Dijkstra求解單源最短路徑問題
構造過程設置3個輔助數組:
- final[]:標記各頂點是否已找到最短路徑,即是否加入S集合
- dist[]:記錄從源點v到其他各點的最短路徑長度,初始值為:若v到頂點有弧,則dist[i]為弧長,否則置∞
- path[]:path[i]表示從源點到頂點i之間的最短路徑的前驅節點,算法結束時可通過它追溯最短路徑

實例
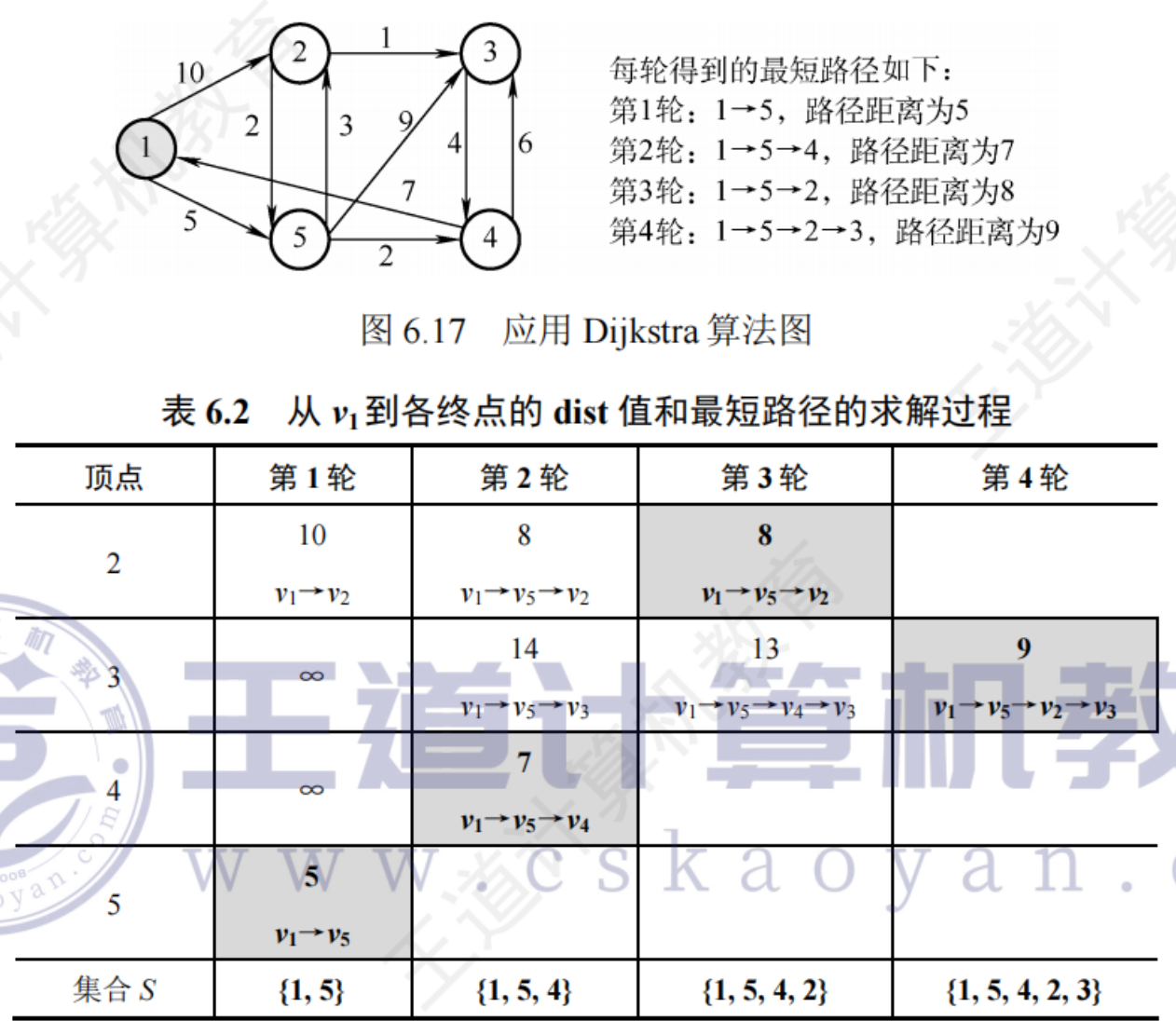

時間復雜度 鄰接表和鄰接矩陣表示 O(|V|^2)
邊上帶有負權值時,Dijkstra算法并不適用
Floyd算法求各頂點之間最短路徑問題
Floyd算法的基本思想是:遞推產生一個 n 階方陣序列 A—1 A0.,A0.,AF1,其中AP國歷表示從頂點v到頂點 v的路徑長度,k表示繞行第 k個頂點的運算步驟。初始時,對于任意兩個頂點v,和v,若它們之間存在邊,則以此邊上的權值作為它們之間的最短路徑長度;若它們之間不存在有向邊,則以。作為它們之間的最短路徑長度。以后逐步嘗試在原路徑中加入頂點k作為中間頂點。若增加中間頂點后,得到的路徑比原來的路徑長度減少了,則以此新路徑代替原路徑
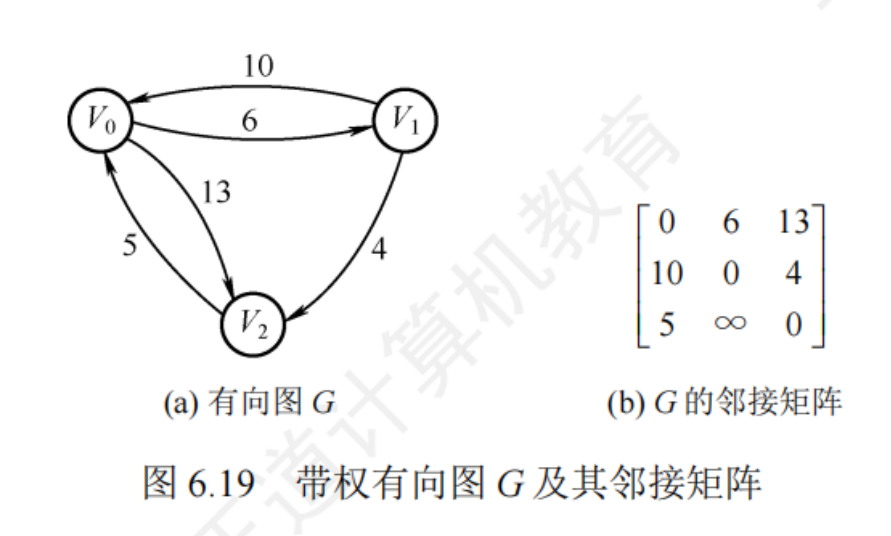
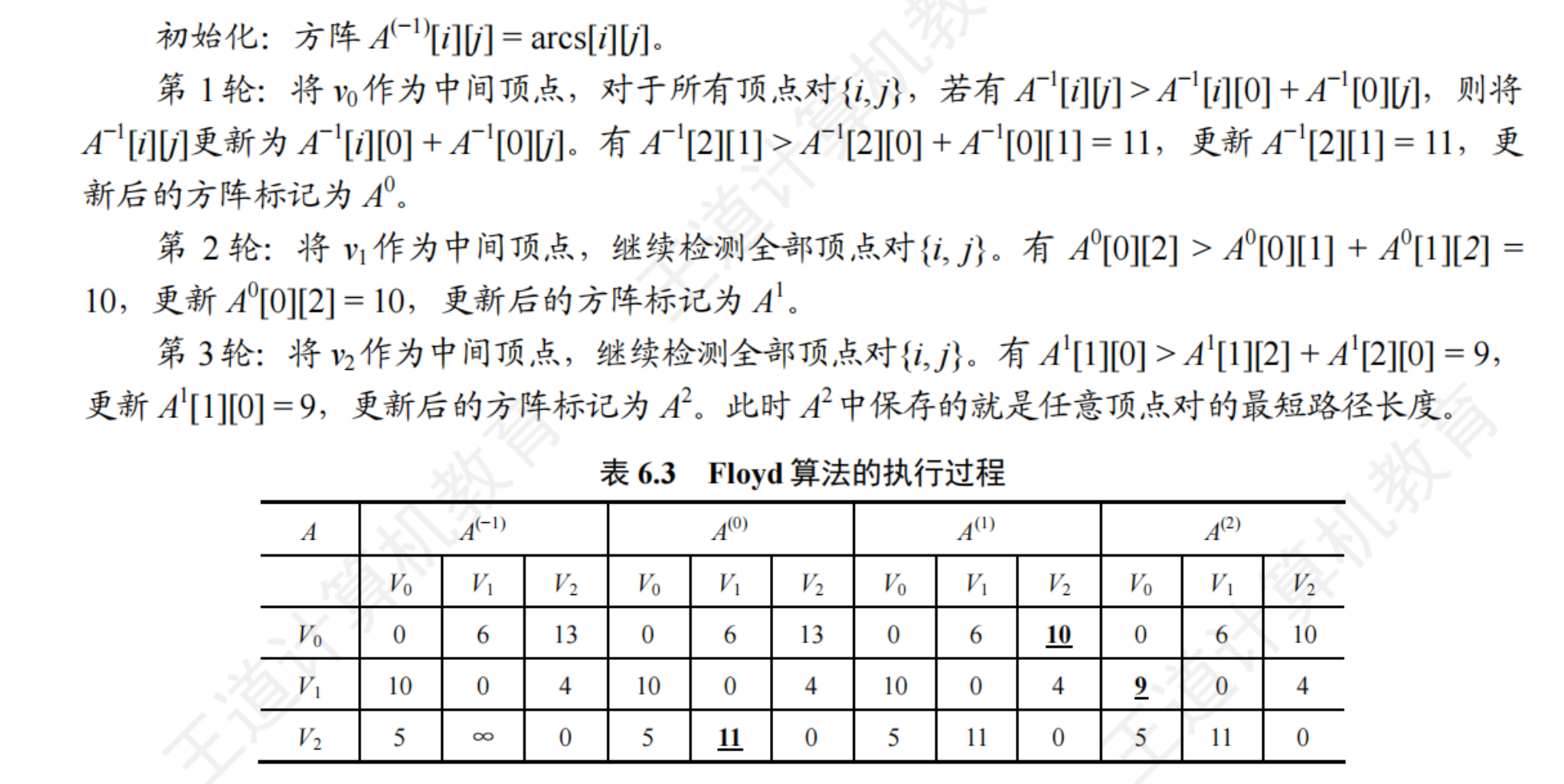
時間復雜度 O(|V|^3)
允許帶有負權值的邊,但不允許總權值為負的回路
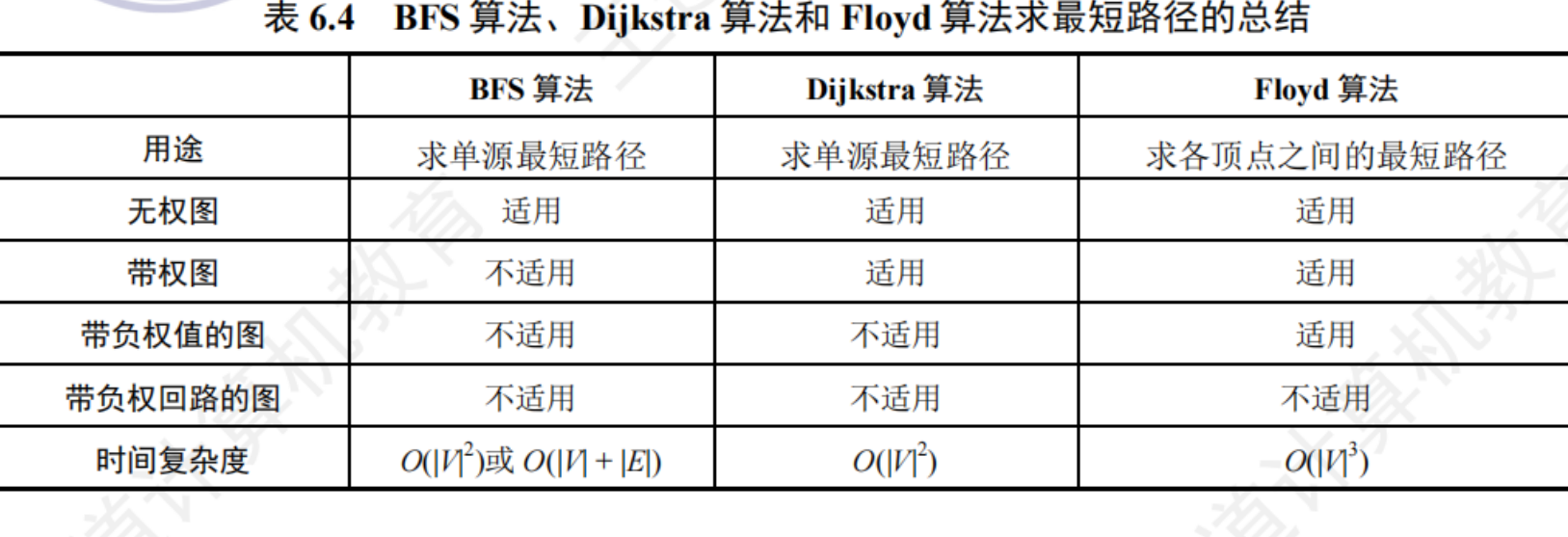
6.4.3有向無環圖描述表達式
有向無環圖:若一個有向圖中不存在環,則稱有向無環圖,簡稱DAG圖
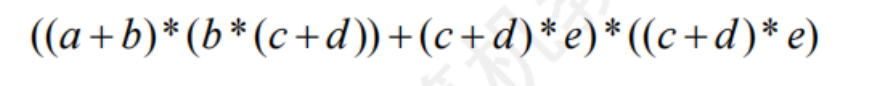
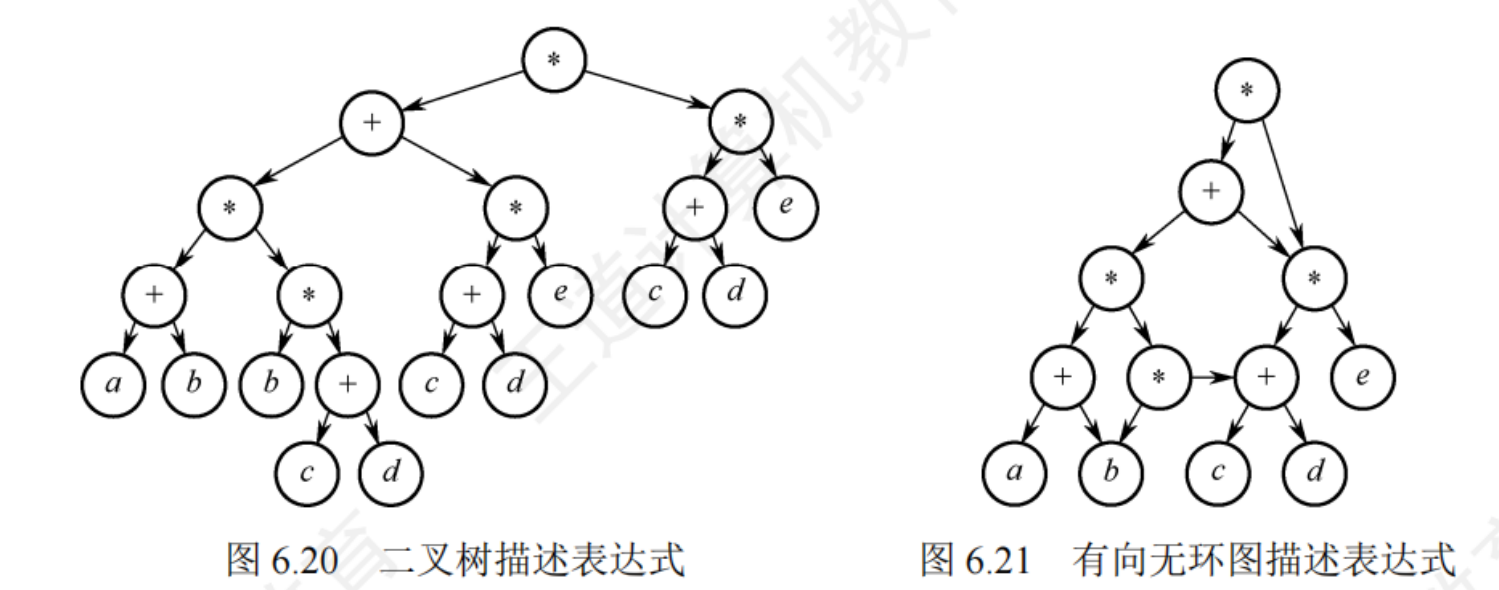
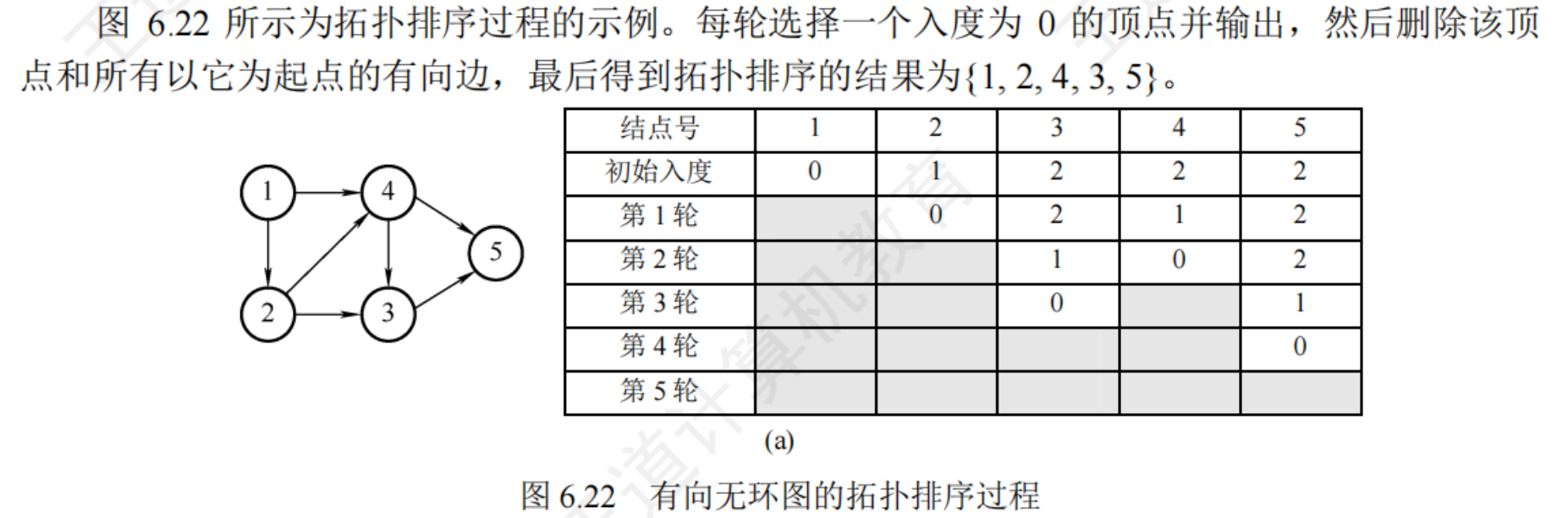
6.4.4拓撲排序
AOV網:若用有向無環圖表示一個工程,其頂點表示活動,用有向邊<Vi,Vj>表示活動Vi必須經過活動Vj進行的這樣一種關系,則這種有向圖稱為頂點表示活動的網絡
拓撲排序:由一個有向無環圖的頂點組成的序列,當且僅當滿足:
- 每個頂點只出現一次
- 若頂點A在序列中排在頂點B的前面,則在圖中不存在B到A的路徑
稱為一個拓撲圖
對一個AOV網進行拓撲排序:
- 從AOV網中選擇一個沒有前驅(入度為0)的頂點并輸出
- 從網中刪除該頂點和所有以它為起點的有向邊
- 重復1和2,直到當前AOV網為空所當前網中不存在無前驅的頂點為止
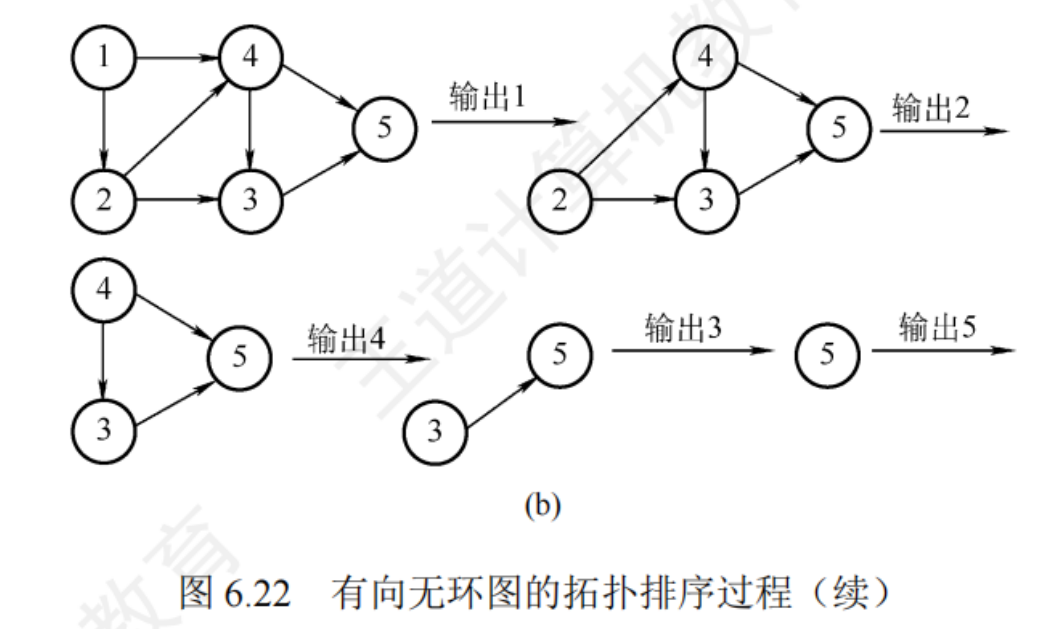
//拓補排序
#define MaxVertexNum 100 //圖中頂點數目的最大值
typedef struct ArcNode{ //邊表結點 int adjvex; //該弧所指向的頂點的位置 struce ArcNode *nextarc;//指向下一條弧的指針 //InfoType info; //網的邊權值
}ArcNode;
typedef struct VNode{ //頂點表結點 VertexType data; //頂點信息 ArcNode * firstare; //指向第一條依附該頂點的弧的指針
}VNode,AdjList[MaxvertexNum];
typedef struct{AdjList vertices; //鄰接表 int vexnm,arcnum; //圖的頂點數和弧數
}Graph; //Graph是以鄰接表存儲的圖類型 bool TopologicalSort(Graph G){InitStack(S);for(int i=0 ;i<G.vexnum; i++)if(indegree[i] == 0)Push(S,i);int count=0;while(!IsEmpty(S)){Pop(S,i);print[count++]=i;for(P=G.vertices[i].firstarc; p; p->nextarc){//將所有i指向的頂點的入度減1,并且講入度減為0的頂點壓入棧Sv=p->adjvex;if(!(--indegree[v])) Push(S,v); }}//while
if(count<G.vexnum)return false;
elsereturn true;
}
因為輸出每個頂點的同時還要刪除以它為起點的邊,所以采用鄰接表存儲時時間都咋讀為O(|V|+|E|),采用鄰接矩陣存儲時時間復雜度為O(|V|^2)
對于有向無環圖G中的任意節點u,v,他們之間的關系必然如下:
- 若u是v的祖先,則在調用dfs訪問u之前,必然已經對v進行了dfs訪問,即v的dfs結束時間先于u的dfs結束時間,從而可以考慮在dfs函數中設置一個時間標記,在DFS調用結束時,對各頂點計時,因此祖先的結束時間必然大于子孫的結束時間
- 若u和v沒有路徑關系,則在u和v拓撲序列的關系任意
于是,按結束時間從大到小排列,就可以得到一個拓撲序列
逆拓撲序列
- 從AOV網中選擇一個沒有后繼的頂點并輸出
- 從網中刪除該頂點和所有以它為終點的有向邊
- 重復
拓撲排序處理AOV網時的問題:
- 入度為0的頂點,即沒有前驅活動或前驅活動都已經完成的頂點,工程可以從這個頂點代表的活動開始或繼續
- 拓撲排序的結果可能不唯一:拓撲序列唯一的條件是在每次輸出頂點時,檢測入度為0的頂點是否唯一,若每次都是唯一,則拓撲序列唯一
- AOV網中各頂點地位相等,每個頂點的編號是人為的
6.4.5關鍵路徑
用邊表示活動的網絡——AOE網:帶權有向圖中,以頂點表示事件,以有向邊表示活動,以邊上的權值表示完成該活動的開銷
AOE網與AOV網對比:AOE網和AOV網都是有向無環圖,不同之處在于它們的邊和頂點所代表的含義是不同的,AOE網的邊有權值,AOV網的邊無權值
AOE網的性質:
- 只有在某頂點所代表的事件發生后,從該頂點出發的各有向邊所代表的活動才能開始
- 只有在進入某頂點的各有向邊所代表的活動都已經結束時,該頂點所代表的事件才能發生
AOE網中僅有一個入度為0的頂點,稱為開始頂點,表示整個工程的開始,也僅有一個出度為0的頂點,稱為結束頂點,表示整個工程的結束
關鍵路徑:從源點到匯點的所有路徑中,具有最大路徑長度的路徑稱為關鍵路徑,關鍵路徑上的活動稱為關鍵活動
完成整個工程的最短時間就是關鍵路徑的長度,即關鍵路徑上各項活動花費開銷的總和
事件的最早發生時間
從源點到事件頂點的最長路徑長度

事件的最遲發生時間


活動最早開始時間
該活動的弧的起點所表示的事件的最早發生時間
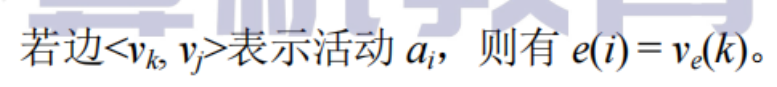
活動的最遲開始時間

一個活動的最遲開始時間和最早開始時間的差
指該活動完成的時間余量,即在不增加整個工程完成所需時間的情況下,活動可以拖延的時間
若一個活動的時間余量為0,則說明該活動必須要如期完成,否則會拖延整個工程進度,所以這樣的活動為關鍵活動
求關鍵路徑

實例

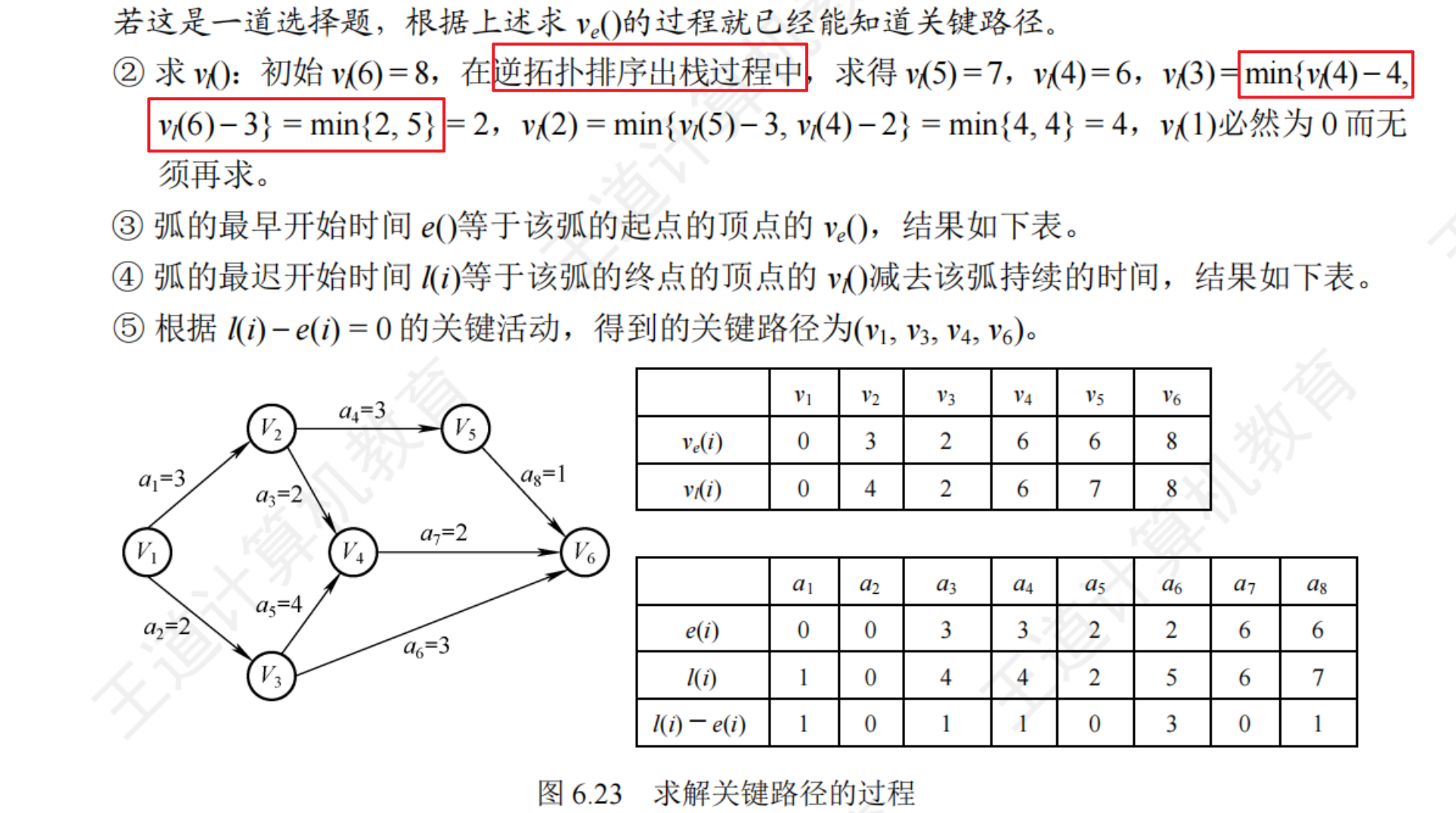
- 關鍵路徑上的所有活動都是關鍵活動,決定整個工期的關鍵因素,可以通過加快關鍵路徑來縮短整個工程的工期,但也不能任意縮短關鍵轟動,因為一旦縮短到一定程度,該關鍵活動就可能會變成非關鍵活動
- 網中的關鍵路徑并不唯一,對于有多條關鍵路徑的網,僅縮短一條關鍵路徑上的關鍵活動并不能縮短整個工程的工期,只有縮短包含在所有關鍵路徑上的關鍵活動的才能縮短工期
7.查找

7.1.1查找的基本概念
查找:在數據結構中尋找滿足某種條件的數據元素的過程
查找表:用于查找的數據集合,由同一類的數據元素組成
靜態查找表:靜態查找表。若一個查找表的操作只涉及查找操作,則無須動態地修改查找表,此類查找表稱為靜態查找表。與此對應,需要動態地插入或刪除的查找表稱為動態查找表。適合靜態查找表的查找方法有順序查找、折半查找、散列查找等;適合動態查找表的查找方法有二叉排序樹的查找、散列查找等。
關鍵字:數據元素中唯一標識該元素的某個數據項的值,使用基于關鍵字的查找,查找結果應該是唯一的
平均查找長度:一次查找的長度是指需要比較的關鍵字的次數,平均查找長度是指所有查找過程進行關鍵字比較次數的平均值

7.2.1順序查找
順序查找也稱線性查找,對順序表和鏈表都適用
一般線性表的順序查找
- 從線性表的一端開始,逐個檢查關鍵字是否滿足給定條件
- 若查找到某個元素的關鍵字滿足給定條件,則查找成功,返回該元素在線性表中的位置
- 若已經查找到表的另一端,但還沒查找到符合給定條件的元素,則返回查找失敗信息
typedef struct{ //查找表的數據結構(順序表) ElemType *elem; //動態數組基址 int TableLen; //表的長度
}SSTable;
//順序查找
int Search_Seq(SSTable ST,ElemType key){int i;for(i=0; i<ST.TableLen && ST.elem[i] != key; ++i);//查找成功,則返回元素下標;查找失敗,則返回-1return i==ST.TableLen? -1:i;
} //順序查找(哨兵)
int Search_Seq(SSTable ST,ElemType key){(ST.elem[0] = key;) //哨兵 int i;for(i=ST.TableLen; ST.elem[i] != key; --i); //引入哨兵時 //查找成功,則返回元素下標;查找失敗,則返回0 return i;
}

查找成功時的平均查找次數
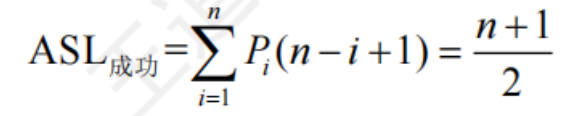
查找失敗時的平均查找次數

優點:對數據元素的存儲沒有要求
缺點:n比較大時,平均查找長度大,效率低
鏈表只能進行順序查找
有序線性表的順序查找
若在查找之前就已經知道表中所有關鍵字是有序的,則查找失敗時可以不用比較到表的另一端就能返回查找失敗的信息,從而降低查找失敗的平均查找長度
判定樹
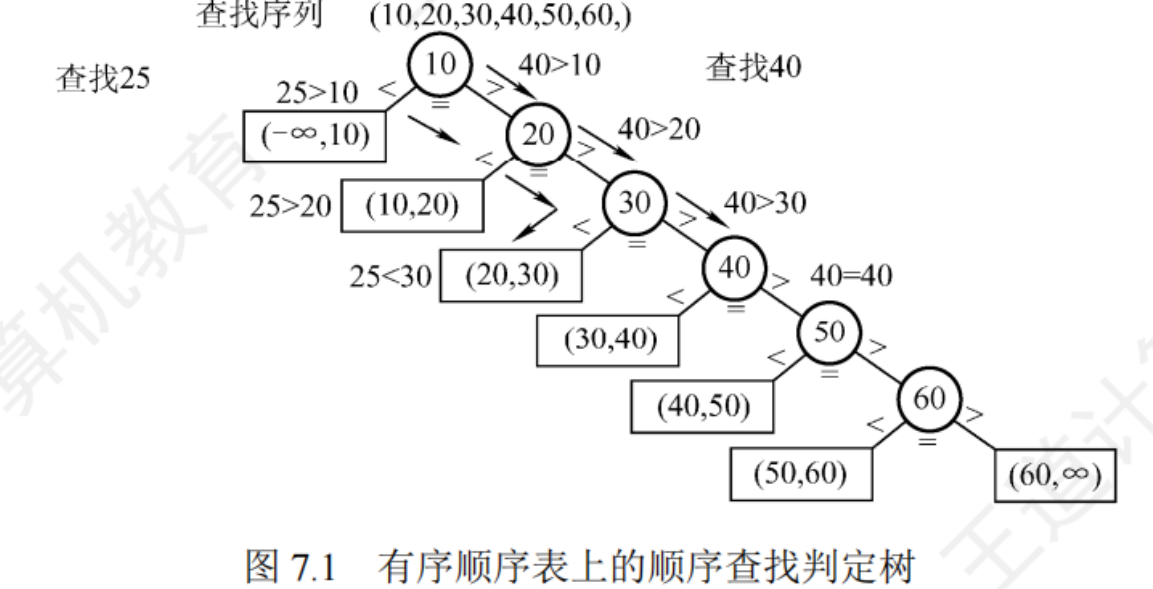
查找成功的平均查找長度和一般線性表的順序查找一樣
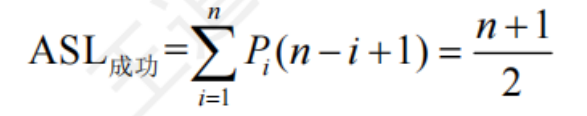
查找失敗時的平均查找長度
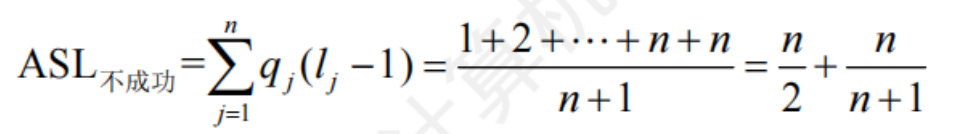
優于一般的順序查找
注意有序順序表的順序查找的數據結構可以是鏈式存儲結構,但折半查找只能是順序存儲結構
7.2.2折半查找
- 首先將給定值key與表中間位置的元素進行比較,若相等,則查找成功,返回該元素的存儲位置
- 若不等,則所需查找的元素只能在中間元素以外的前半部分或后半部分
- 在縮小的范圍內繼續查找
//折半查找
int Binary_Search(SSTable L, ElemType key){int low = 0, high = L.TableLen-1, mid;while(low <= high){mid = (low + high)/2; //取中間位置 if(L.elem[mid] == key)return mid; //查找成功則返回所在位置 else if(L.elem[mid] > key)high = mid - 1; //從前半部分繼續查找 elselow = mid + 1; //從后半部分繼續查找 }return -1; //查找失敗,返回-1
}
折半查找下標從零開始

折半查找判定樹
每個圓形節點表示一個記錄,節點中的值為該記錄的關鍵字值,樹中最下面的葉節點都是方形的,表示查找失敗的區間
特點
每個節點值均大于左子節點值,均小于右子節點值
若有序序列有n各元素,則對應判定樹有n個圓形的非葉節點和n+1個方形的葉節點
折半查找的判定樹是一棵平衡二叉樹
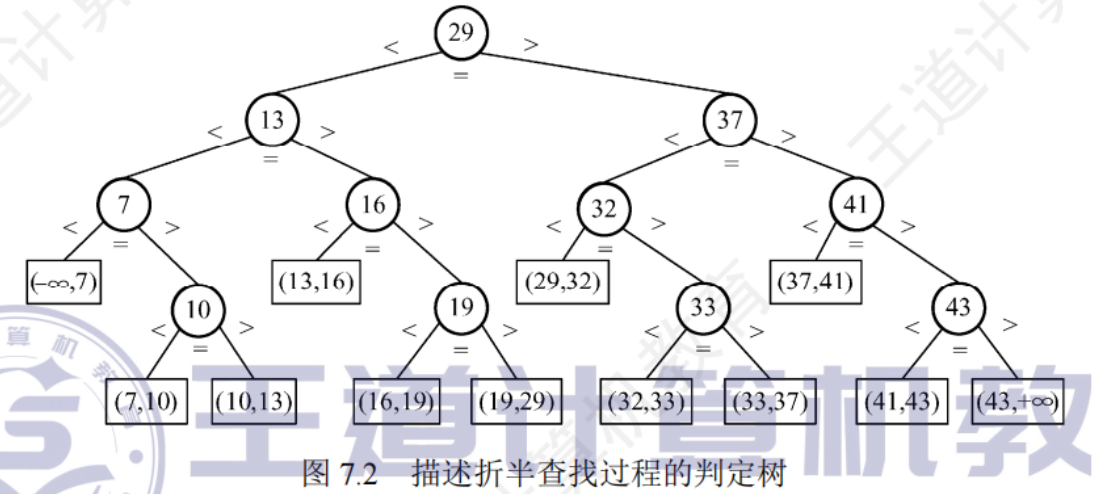
查找成功時的平均查找長度

判定樹求查找成功與失敗的查找長度
查找成功時的查找長度是從根節點到目的節點的路徑上的節點數
查找失敗時的查找長度是從根節點到對應失敗節點的父節點的路徑上的節點數

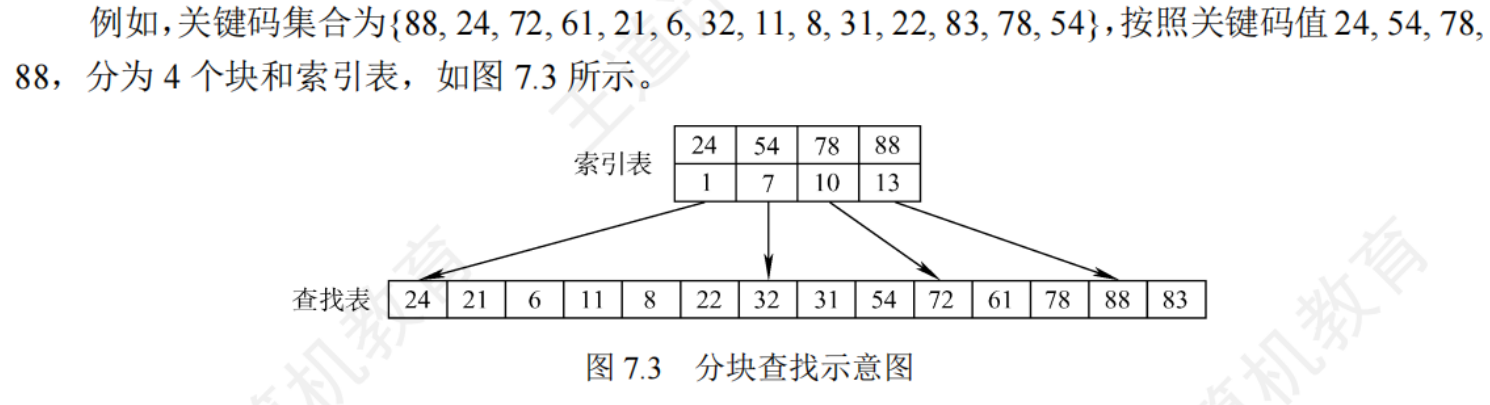
7.3.2分塊查找
分塊查找也稱索引順序查找
基本思想:
- 將查找表分為若干個小塊,塊內元素可以無須,但塊間元素是有序的,即第一塊的最大關鍵字小于第二塊中所有記錄的關鍵字
- 建立一個索引表,索引表中每個元素含有各塊的最大關鍵字和各塊中第一個元素的地址,索引表按關鍵字有序排列
- 查找時,在索引表中確定待查找記錄所在的塊,可以順序查找或折半查找索引表
- 在塊內順序查找

7.3.1二叉排序樹
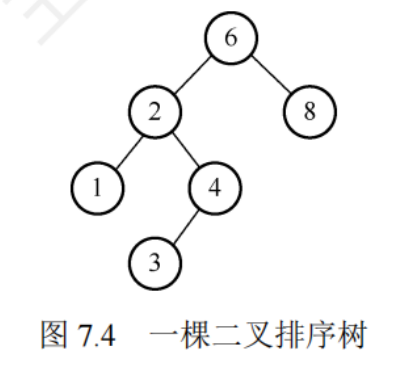
特性:
- 若左子樹非空,則左子樹上所有節點的值均小于根節點的值
- 若右子樹非空,則右子樹上所有節點的值均大于根節點的值
- 左右子樹也是一棵二叉排序樹
對二叉排序樹進行中序遍歷可以得到一個遞增有序序列
二叉排序樹的查找
若二叉排序樹非空,先將給定值與根節點關鍵字比較,若相等,則查找成功,若不等,當小于根節點的關鍵字,則在根節點的左子樹上查找,否則在根節點的右子樹上查找
這是一個遞歸的過程
//二叉排序樹結點
typedef struct BSTNode{int key;struct BSTNode *lchild,*rchild;
}BSTNode,*BSTree;
//在二叉排序樹中查找值為key的結點
BSTNode *BST_Search(BSTree T,int key){while(T!=NULL && key!=T->key){ //若樹空或等于根結點值,則結束循環 if(key<T->key)T=T->lchild; //小于,則在左子樹上查找 elseT=T->rchild; //大于,則在右子樹上查找 }return T;
} //在二叉排序樹中查找值為key的結點(遞歸實現)
BSTNode *BSTSearch(BSTree T, int key){if(T == NULL)return NULL; //查找失敗if(key == T->key)return T; //查找成功else if(key < T->key)return BSTSearch(T->lchild,key); //在左子樹中找elsereturn BSTSearch(T->rchild,key); //在右子樹中找
}
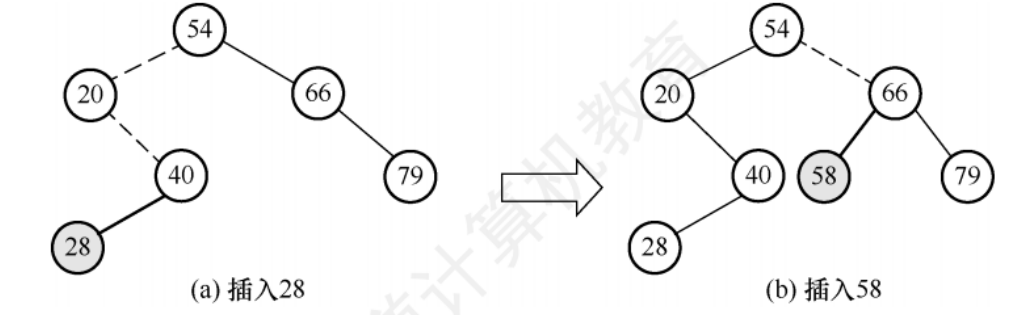
二叉排序樹的插入
若二叉排序樹為空,則直接插入,否則,若關鍵字k小于根節點值,則插入到左子樹,若關鍵字k大于根節點值,則插入到右子樹
新插入節點一定是一個葉節點,且是查找失敗時查找路徑上訪問的最后一個節點的左孩子或右孩子
//在二叉排序樹插入關鍵字為k的新結點(遞歸實現)
int BST_Insert(BSTree &T, int k){if(T==NULL){ //原樹為空,新插入結點為根結點 T=(BSTree)malloc(sizeof(BSTNode));T->key = k;T->lchild = T->rchild = NULL;return 1; //返回1.插入成功 }else if(k == T->key) //樹中存在相同關鍵字的結點,插入失敗 return 0; else if(k<T->key) //插入到T的左子樹 return BST_Insert(T->lchild,k);else //插入到T的右子樹 return BST_Insert(T->rchild,k);
}
二叉排序樹的構造
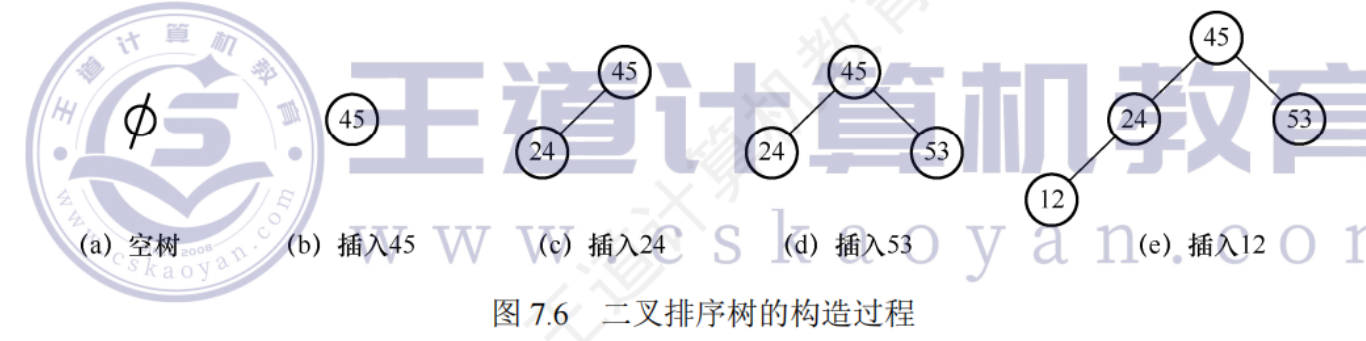
//按照 str[] 中的關鍵字序列建立二叉排序樹
void Creat_BST(BSTree &T,int str[],int n){T=NULL; //初始時T為空樹 int i=0;while(i<n){ //依次將每個關鍵字插入到二叉排序樹中 BST_Insert(T,str[i]);i++;}
}
二叉排序樹的刪除
三種情況:
- 若被刪除節點z是葉節點,則直接刪除,不會破壞二叉排序樹的性質
- 若節點z只有一棵左子樹或右子樹,則讓z的子樹成為z父節點的子樹,替代z的位置
- 若節點z有左右兩棵子樹,則令z的直接后繼(或直接前驅)代替,然后從二叉排序樹中刪除這個最直接后序(直接前驅),轉化為第一二中情況
二叉樹中序序列找前驅、后繼:
前驅:左子樹最右下節點
后繼:右子樹最左下節點
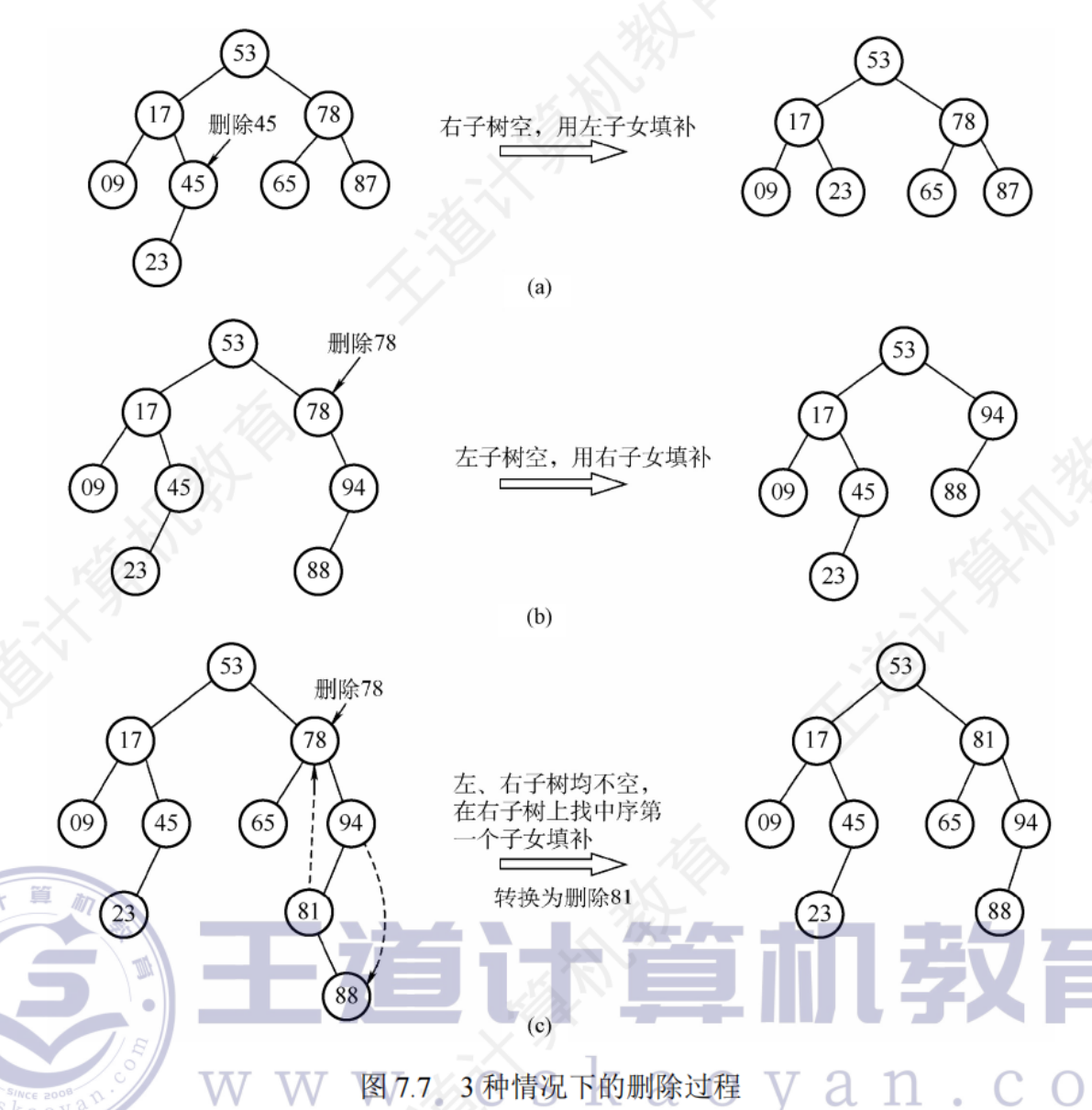
查找效率分析
主要取決于樹的高度
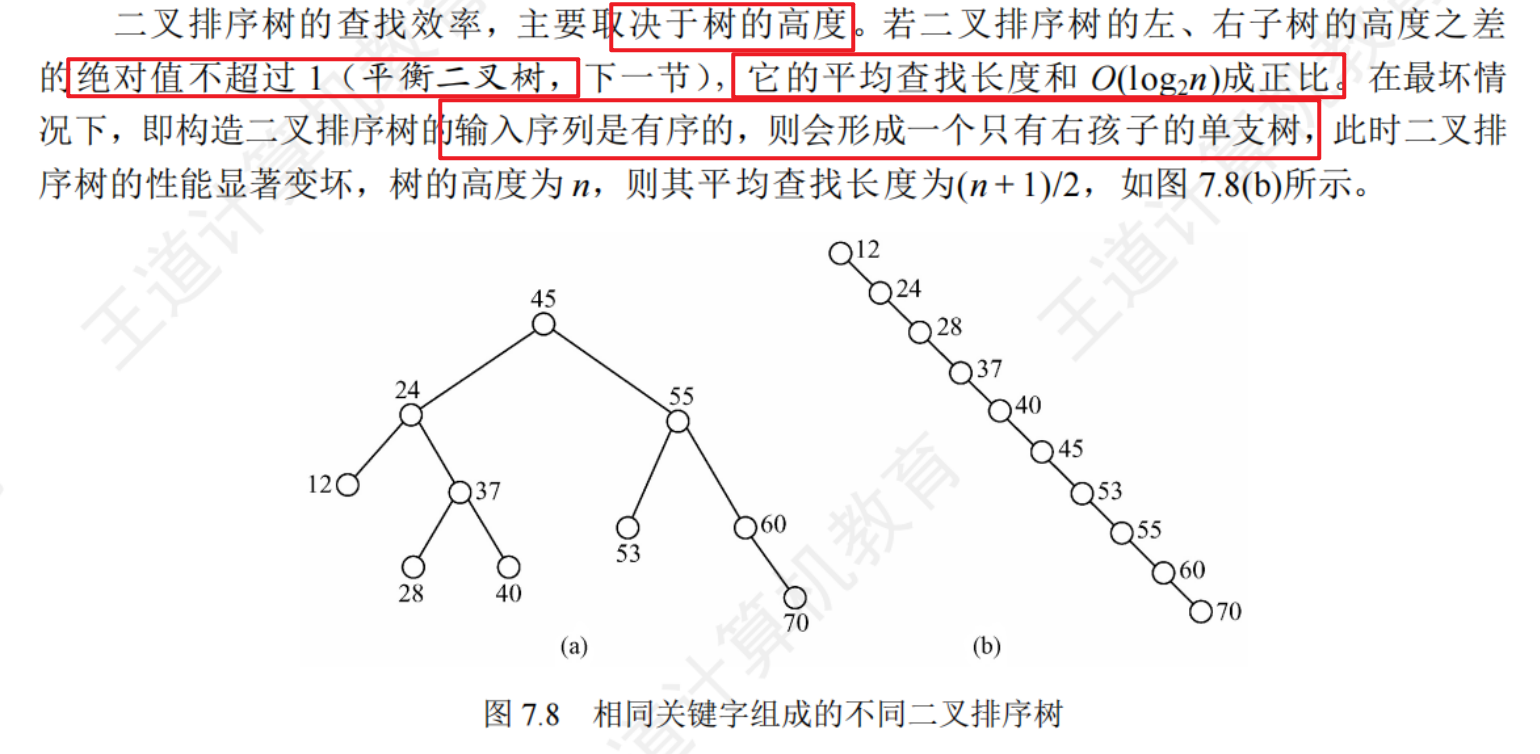
二叉排序樹與折半查找對比:

7.3.2平衡二叉樹(AVL樹)
規定在插入和刪除節點時,要保證任意節點的左右子樹高度差的絕對值不超過1
平衡因子:節點左右子樹的高度差,取值 -1 0 1
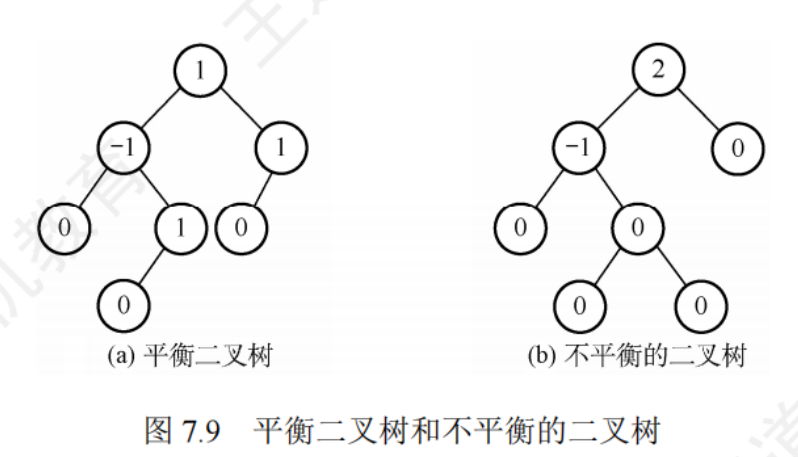
平衡二叉樹的插入
每當在二叉排序樹中插入(刪除)一個節點時,首先檢查其插入路徑上的節點是否因為此次操作導致了不平衡,,若導致了不平衡,則先找到插入路徑上李插入節點最近的平很因子大于1的節點A,在對以A為根的子樹(最小不平衡子樹),進行調整
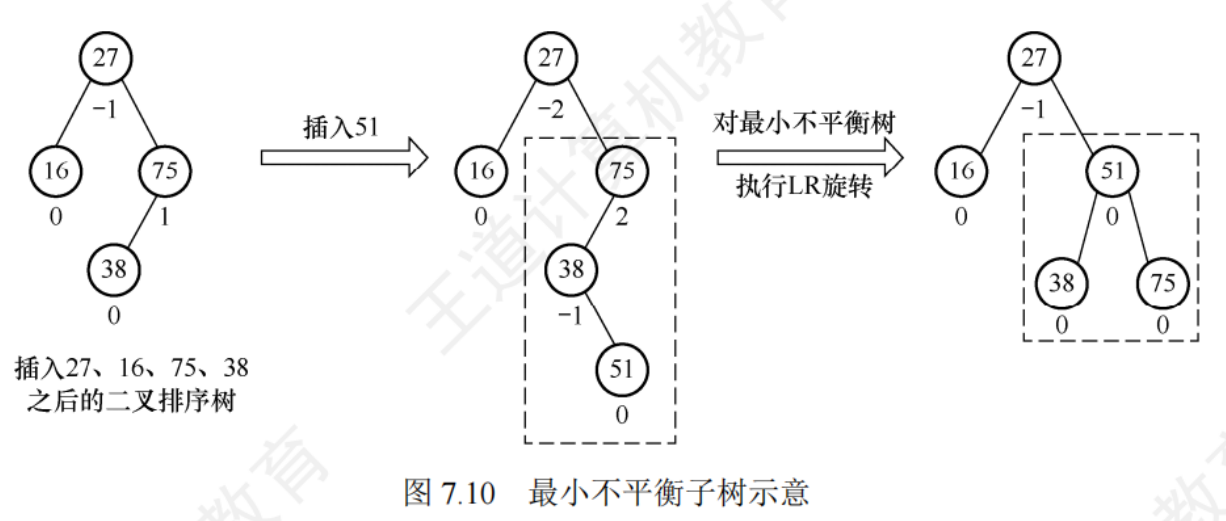
-
LL平衡旋轉(右單旋轉):在節點A的左孩子(L)的左子樹(L)上插入了新節點
A的左孩子B向右上旋轉代替A成為根節點,將A向右下旋轉成為B的右孩子,而B的原右子樹作為A的左子樹
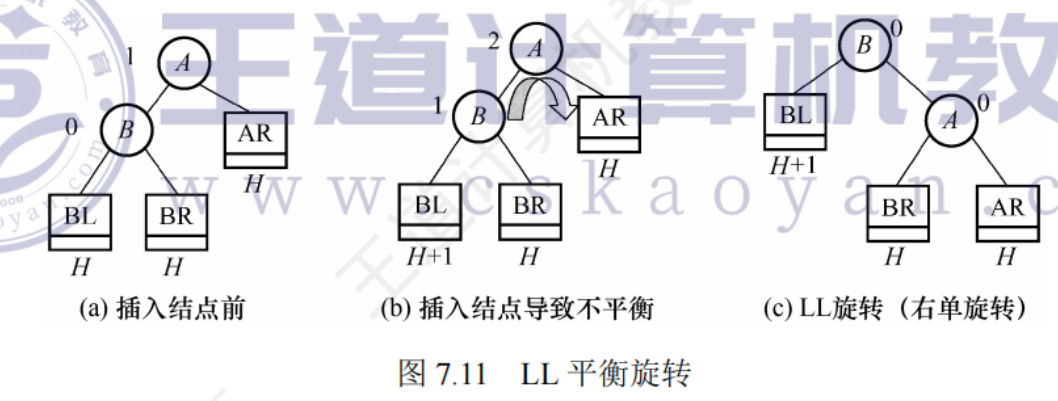
-
RR平衡旋轉(左單旋轉):在節點A的右孩子(R)的右子樹(R)上插入了新節點
將A的右孩子B向左上旋轉代替A成為根節點,將A向坐下旋轉成為B的左孩子,而B的原左子樹作為A的右子樹
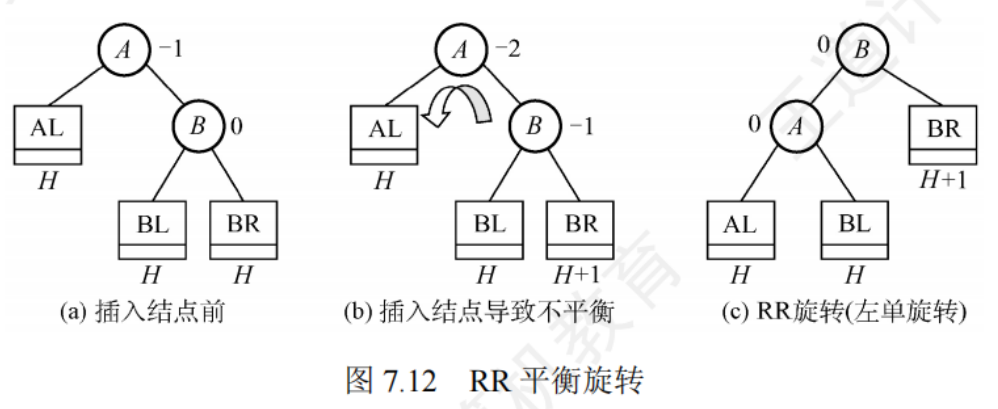
-
LR平衡旋轉(先左后右雙旋轉):在節點A的左孩子(L)的右子樹(R)上插入了新節點
先將A的左孩子B的右子樹根節點C向左上旋轉提升到B的位置,然后把C向右下旋轉提升到A的位置
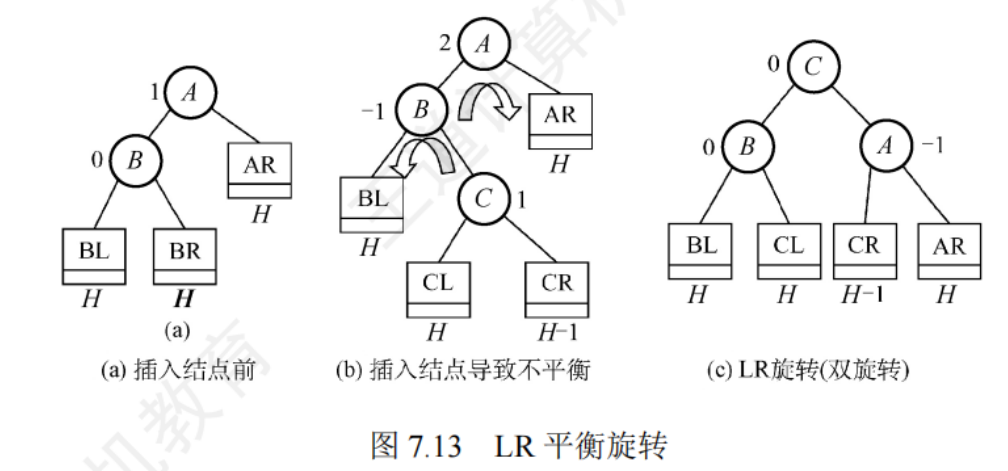
-
RL平衡旋轉(先右后左雙旋轉):在節點A的右孩子(R)的左子樹(L)上插入新節點
先將A的右孩子B的左子樹的根節點C向右上旋轉提升到B的位置,然后把C向左上旋轉提升到A的位置
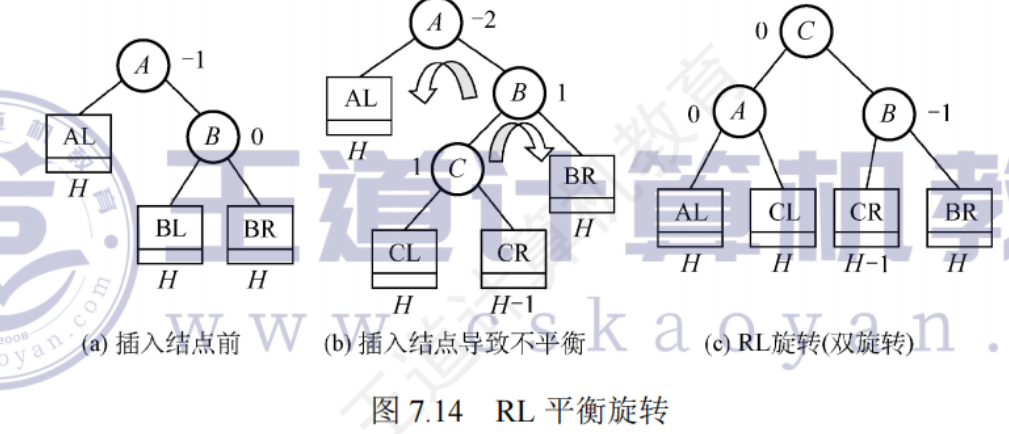
平衡二叉樹的構造
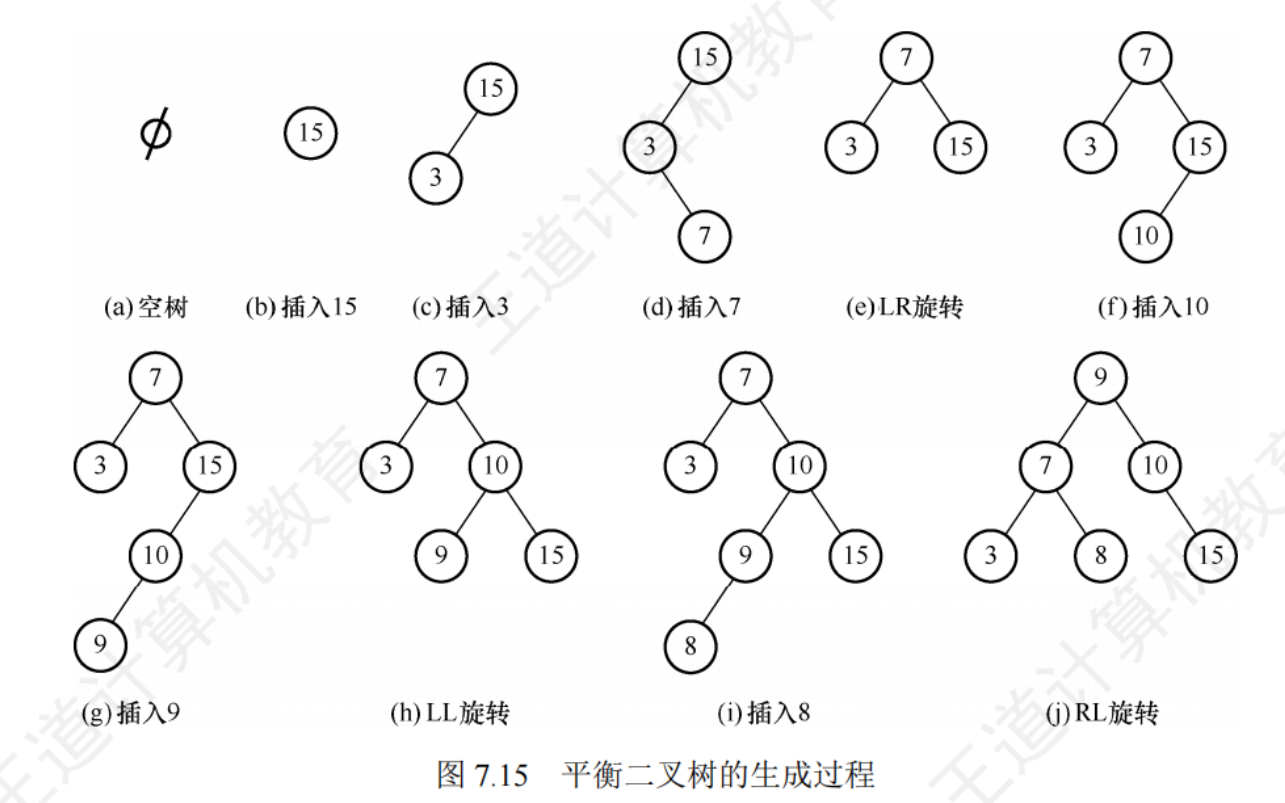
平衡二叉樹的刪除
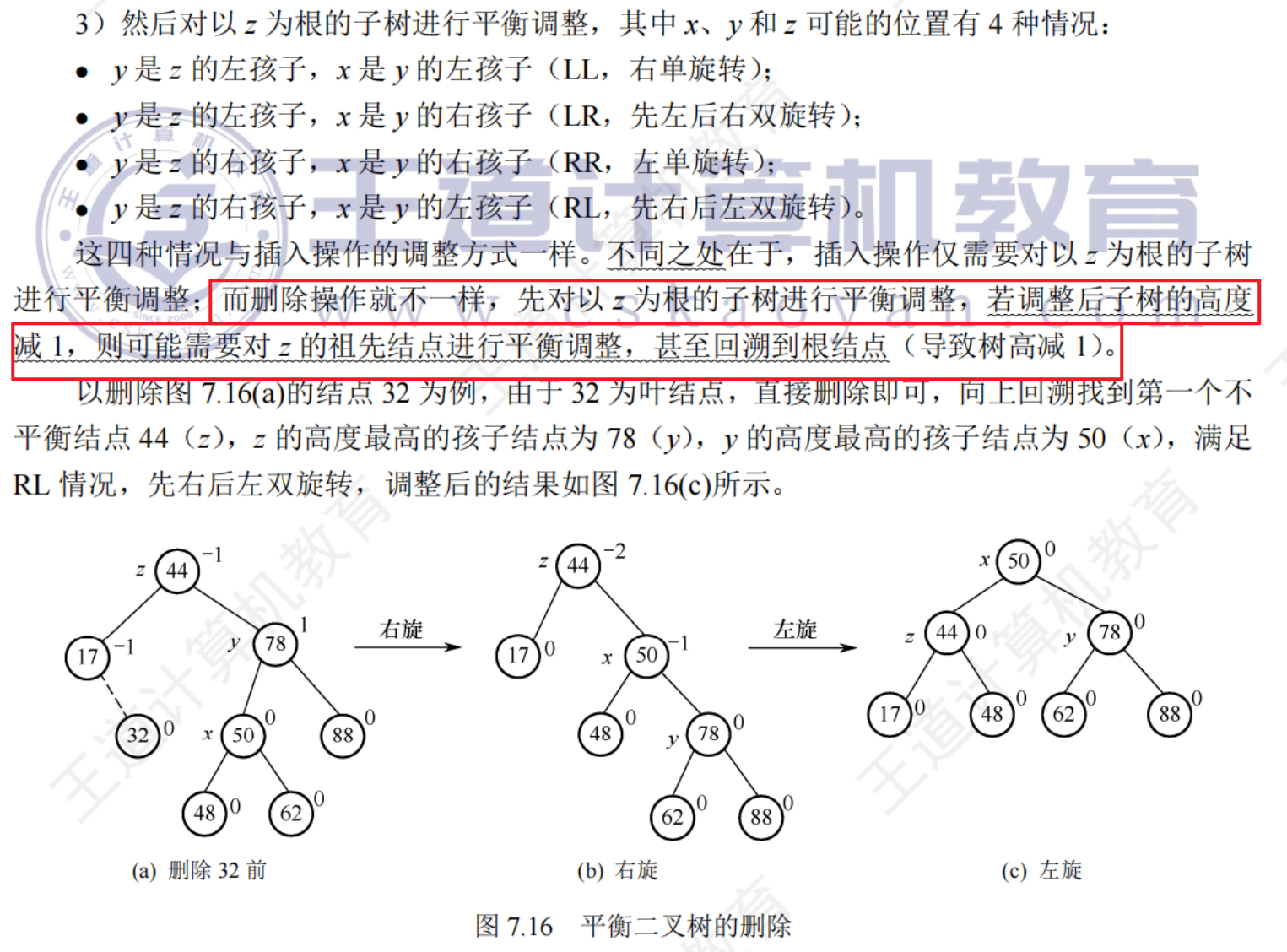
平衡二叉樹的查找
進行關鍵字比較的次數不超過樹的深度
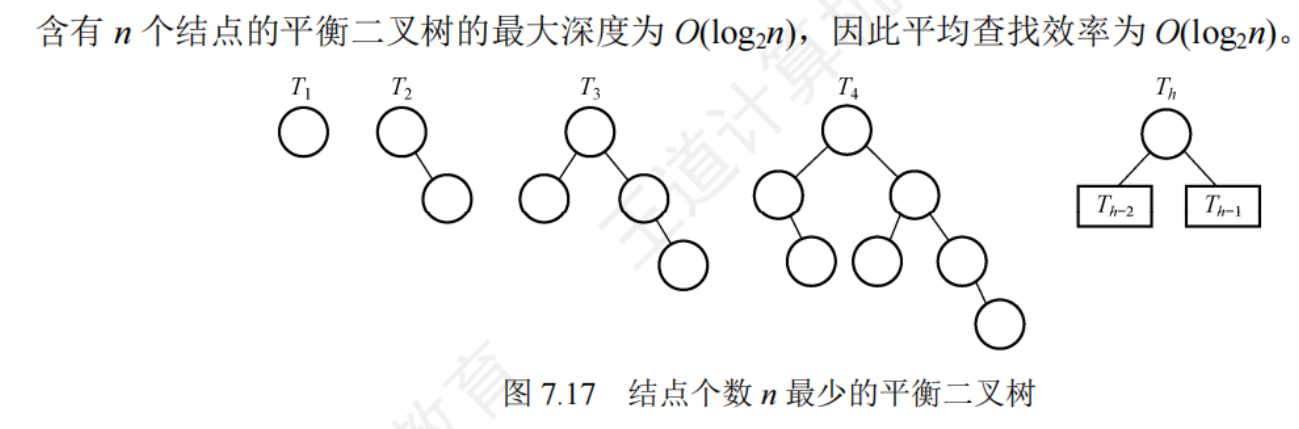
7.3.3紅黑樹
- 每個節點是紅色或者黑色的
- 根節點是黑色的
- 葉節點(虛構的外部節點,NULL節點)都是黑色的
- 不存在兩個相鄰的紅節點(紅節點的父節點和孩子節點都是黑色的)
- 對每個節點,從該節點到任意一個節葉節點的簡單路徑上,所含黑節點的數量相同
左根右 根葉黑
不紅紅 黑路同
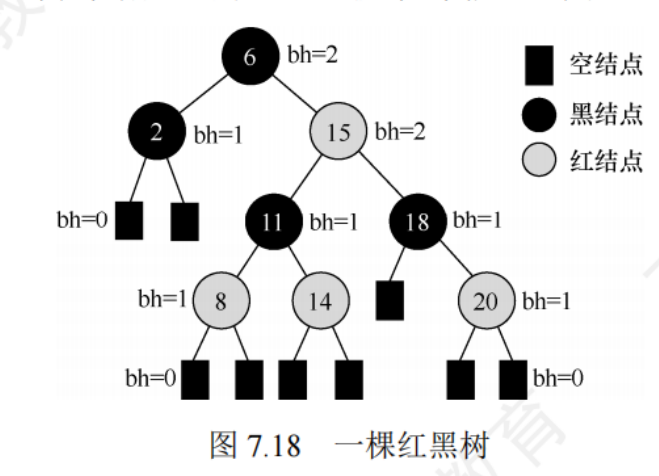
黑高:從某節點出發(不含該節點)到達一個葉節點的任意一個簡單路徑上的黑節點總數稱為黑高,根節點的黑高為紅黑樹的黑高
- 從根節點到葉節點的最長路徑不能大于最短路徑的2倍:從根節點到任意一個葉節點的簡單路徑最短時,這條路徑必然全由黑節點構成,某條路徑最長時,必然由黑節點和紅節點相間構成,黑紅節點數量相同
- 有n個內部節點的紅黑樹的高度
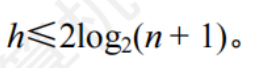
- 新插入紅黑樹中的節點初始為紅色——只需要關注是否滿足條件:不紅紅
平衡二叉樹——任意一個節點的左右子樹高度差不超過1
紅黑樹——任意一個節點的左右子樹的高度,相差不超過2倍
紅黑樹的插入
- 二叉排序樹插入法插入,并將新插入節點z著色為紅色,若節點z的父節點為黑色,無須做任何調整,此時就是一個標準的紅黑樹,結束
- 若節點z是根節點,則將z著色為黑色(樹的黑高增加1),結束
- 若節點z不是根節點,且z的父節點z.p不是紅色的,則按照z的叔父系欸但的顏色不同,分為三種情況:
- z的叔節點y是黑色的,且z是一個右孩子:(LR,先左旋,后右旋)即z是其爺節點的左孩子的右孩子——先做一次左旋,轉化為情況2(變為情況2 后再做一次右旋),左旋后z和父節點z.p交換位置
- z的叔節點y是黑色的,且z是一個左孩子:(LL,右單選)即z是其爺節點的左孩子的左孩子,做一次右旋,并交換z的原父節點和原爺節點的顏色
- z的叔節點是紅色的,z的父節點z.p和叔節點都是紅色的,因為爺節點z.p.p是黑色的,將z.p和y都著為黑色,z.p.p著為紅色
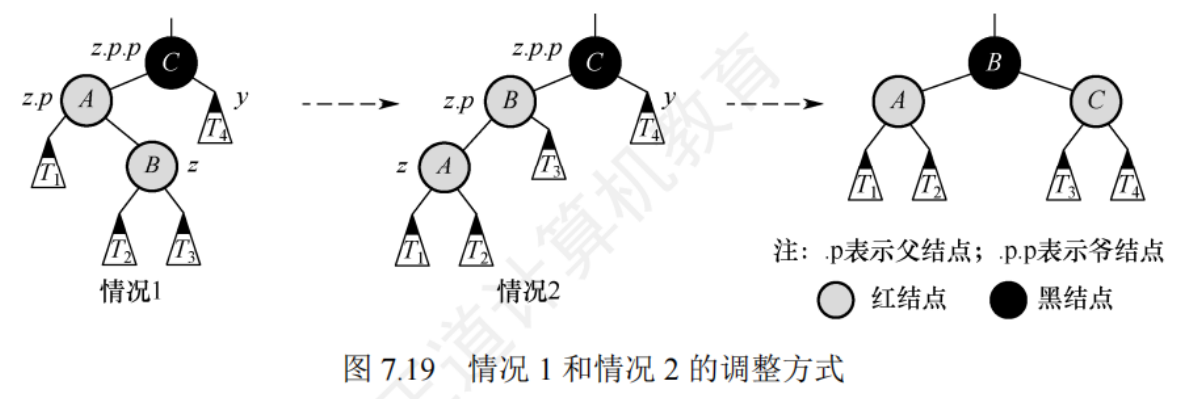
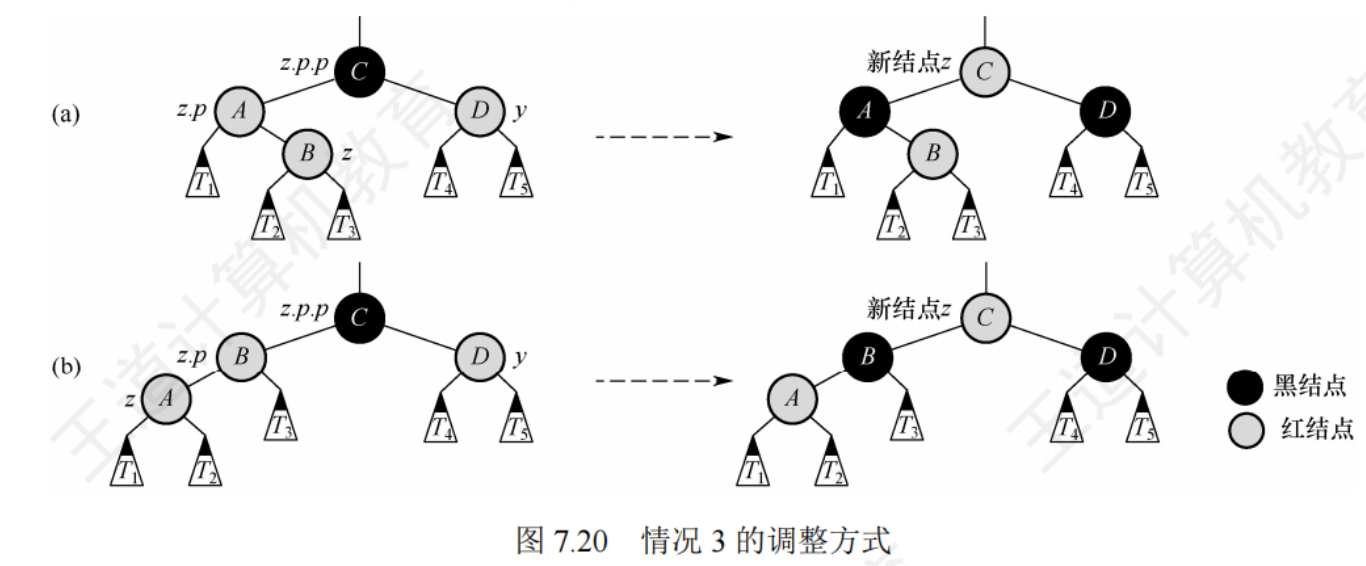
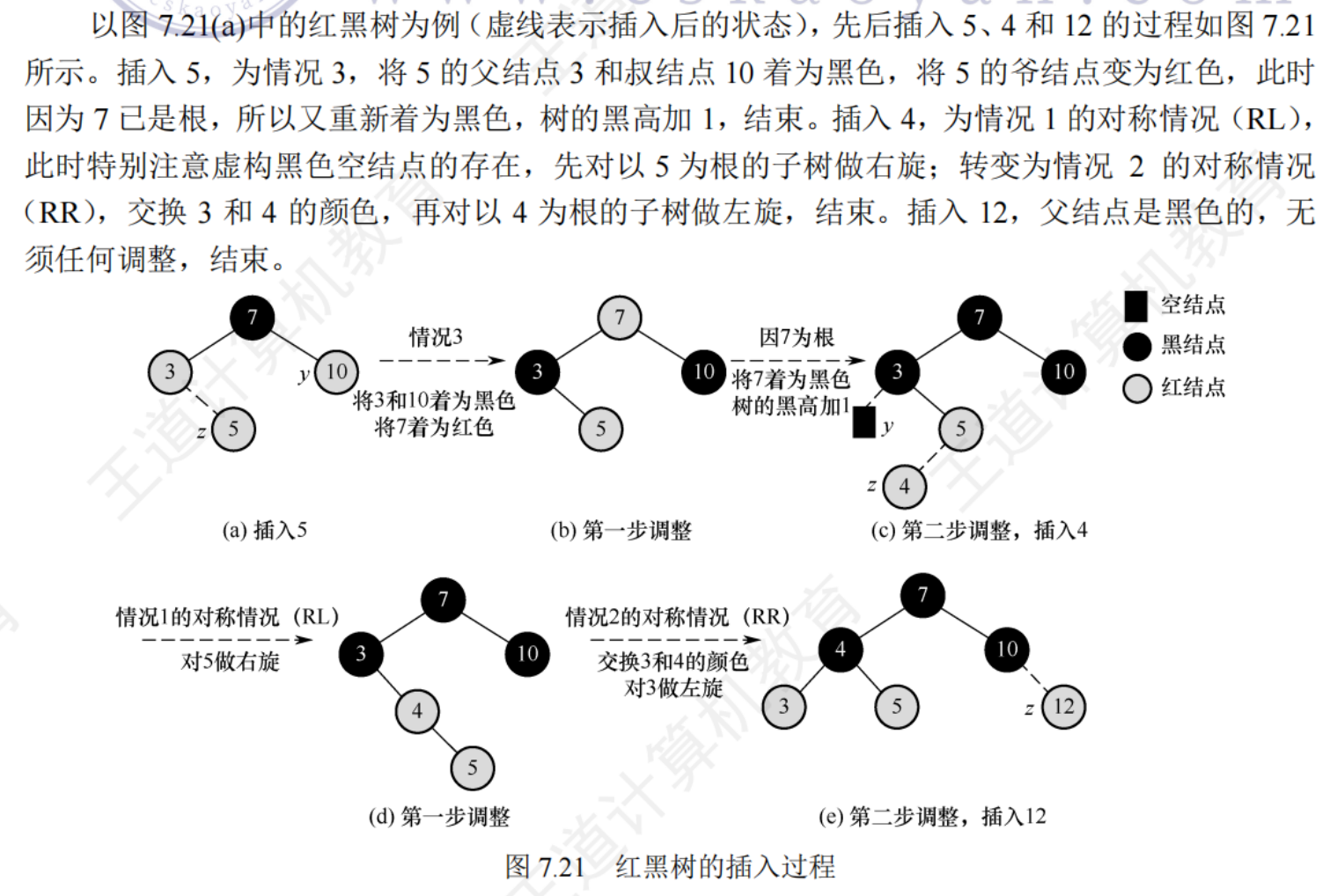
7.4.1B樹及其基本操作
m階B樹是所有節點的平衡因子均小于等于0的m路平衡查找樹
m階B樹:
- 樹中每一節點至多有m棵子樹,即至多m-1個關鍵字
- 若根節點不是葉結點,則至少有2棵子樹,即至少1個關鍵字
- 除根節點之外的所有非葉節點至少有 m/2 向上取整棵子樹,即至少有 m/2向上取整-1 個關鍵字
- 所有非葉節點結構如下:

- 所有的葉結點都出現在同一層次上,并且不帶信息(可以視為外部節點或類似于折半查找判定樹的失敗節點,實際上這些節點并不存在,指向這些節點的指針為空)
一顆 5 階B樹
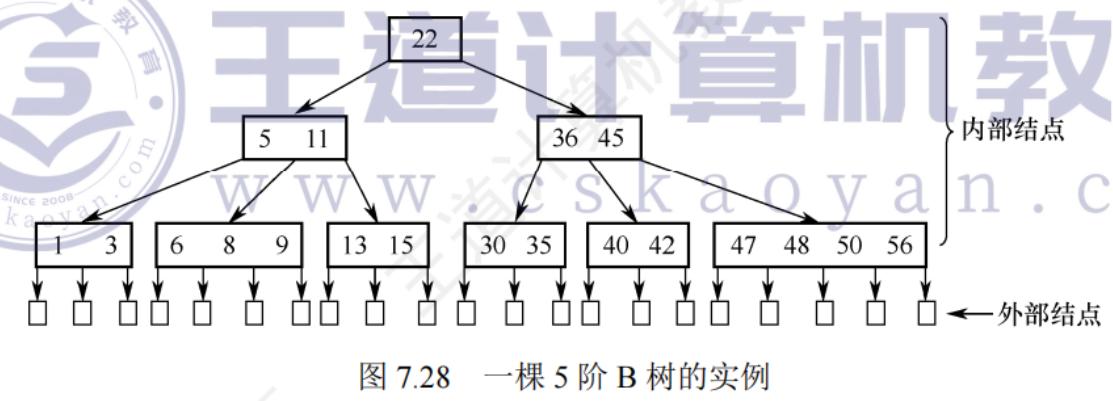
- 節點的孩子個數等于該節點的關鍵字個數加1
- 若根節點沒有關鍵字就沒有子樹,則此時B樹為空,若根節點有關鍵字,則其子樹個數必然大于等于2,因為子樹個數等于關鍵字個數加1
- 除根節點之外,所有非葉節點至少有 3 棵子樹,至多有5棵子樹
- 結點中的關鍵字從左到右遞增有序,關鍵字兩側均有指向子樹的指針,左側指針所指子樹的所有關鍵字均小于該關鍵字,右側指針所指子樹的所有關鍵字均大于該關鍵字。或者看成下層結點的關鍵字總是落在由上層結點的關鍵字所劃分的區間內,如第二層最左結點的關鍵字劃分成了3個區間:(—∞,5),(5,11),(11,+∞),該結點中的3個指針所指子樹的關鍵字均分別落在這3個區間內。
- 所有葉結點君主第4層,代表查找失敗位置
B樹的查找
B樹的查找包含兩個基本操作:0在B樹中找結點; 2在結點內找關鍵字。B樹常存儲在磁盤上,因此前一查找操作是在磁盤上進行的,而后一查找操作是在內存中進行的,即在磁盤上找到目標結點后,先將結點信息讀入內存,然后再采用順序查找法或折半查找法。因此,在磁盤上進行查找的次數即目標結點在B樹上的層次數,決定了B樹的查找效率。
B樹的高度
B樹中大部分操作所需的磁盤存取次數與B樹高度成正比

B樹的插入
- 定位:利用B樹的查找算法,找出插入該關鍵字的終端節點(在B樹中查找key時會找到表示查找失敗的葉結點,因此插入位置一定是最底層的葉結點)
- 插入:每個非根節點的關鍵字個數都在 [ m/2 向上取整 -1 , m -1],若節點插入后的關鍵字個數小于m,可以直接插入,若節點插入后的關鍵字個數大于m-1,必須對節點進行分裂
- 分裂的方法:取一個新節點,在插入key后的源節點,從中間位置(m/2 向上取整)將其中的關鍵字分為兩部分,做部分放在源節點中,有部分包含的關鍵字放到新系欸但中,中間位置 ( m/2 向上取整) 的節點插入源節點的父節點
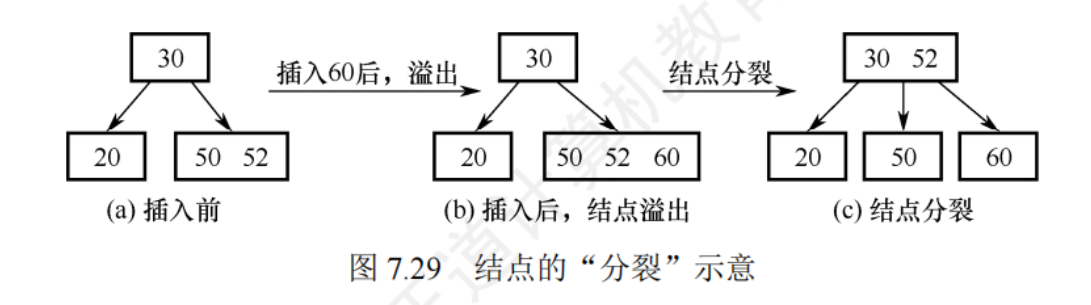
B樹的刪除
要保證刪除后的節點中的關鍵詞個數 >= m/2 向上取整 -1 ——需要進行節點合并操作
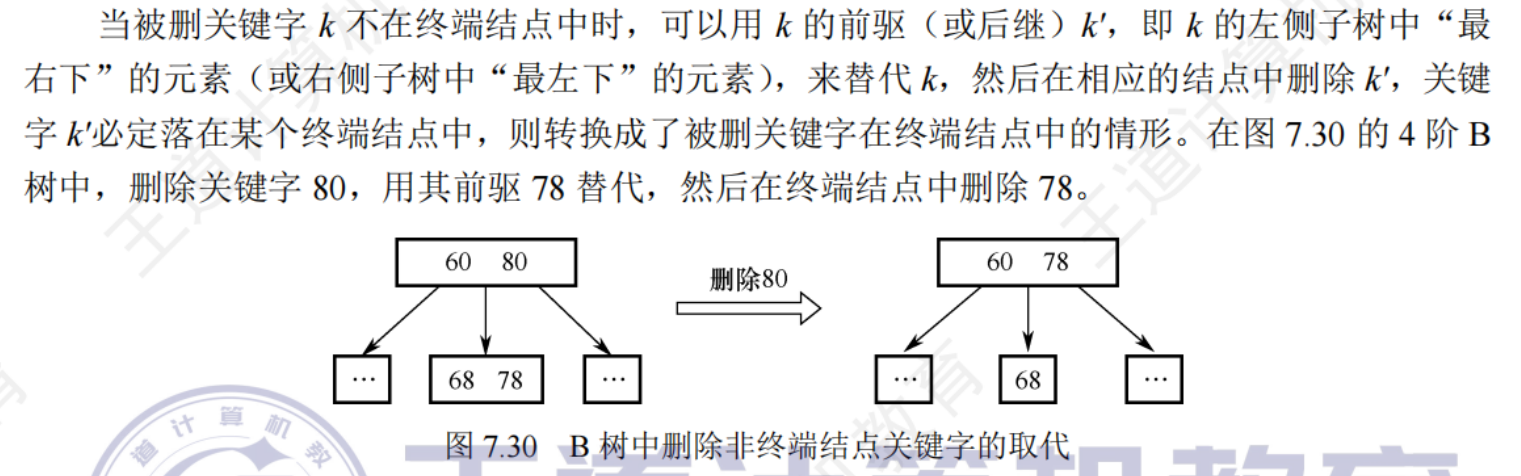
- 直接刪除關鍵字:若被刪關鍵字所在的節點刪除前的關鍵字個數 >= m/2 向上取整 ,表明刪除該關鍵字后仍滿足B樹的定義,則直接刪除
- 兄弟夠借:若被刪關鍵字所在節點刪除前的關鍵字個數 = m/2向上取整 - 1 ,且與該節點相鄰的右(左)兄弟節點的關鍵字個數 >= m/2 向上取整 ,則需要調整該節點、右兄弟節點及其雙親節點
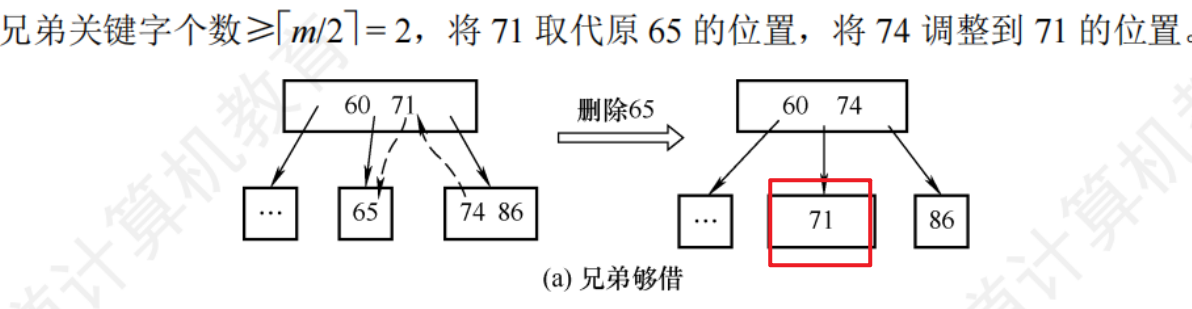
- 兄弟不夠借:若被刪關鍵字所在節點刪除前的關鍵字個數 = m/2 向上取整 - 1,且此時與該節點相鄰的左右兄弟節點的關鍵字個數都 = m/2向上取整 - 1 ,則將關鍵字刪除后與左右兄弟節點及雙親節點中的關鍵字進行合并
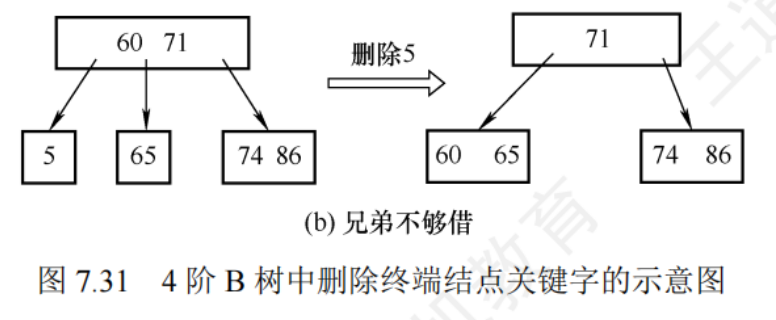

7.4.2B+樹的基本概念
一棵m階B+樹應滿足:
- 每個分支節點最多m棵子樹
- 非葉根節點至少有兩棵子樹,其他分支節點至少有 m/2 向上取整棵子樹
- 節點的子樹個數與關鍵字個數相等
- 所有葉結點包含全部的關鍵字及指向相應記錄的指針,葉結點中將關鍵字按大小順序排列,并且相鄰葉結點按大小順序鏈接起來(支持順序查找)
- 所有分支節點(可視為索引的索引)中僅包含它的各個子節點(下一級索引塊)中關鍵字的最大值及指向其子節點的指針
B+樹與B樹的差異:
- 在B+樹中,具有n個關鍵字的節點只含有 n 棵子樹,,即每個關鍵字對應一顆子樹:而在B樹中,具有n個關鍵字的節點含有n+1棵子樹

- 在B+樹中,葉結點包含了全部的關鍵字,非葉節點出現的關鍵字也會出現在葉結點中;而在B+樹中最外層的終端節點包含的關鍵字和其他節點包含的關鍵字是不重復的
- 在B+樹中,葉結點包含信息,所有非葉節點僅起索引作用,非葉節點的每個索引項只含有對應子樹的最大關鍵字和指向該樹的指針,不含有對應記錄得存儲地址,這樣能使一顆磁盤塊存儲更多的關鍵字,使得磁盤存讀寫次數更少,查找速度更快
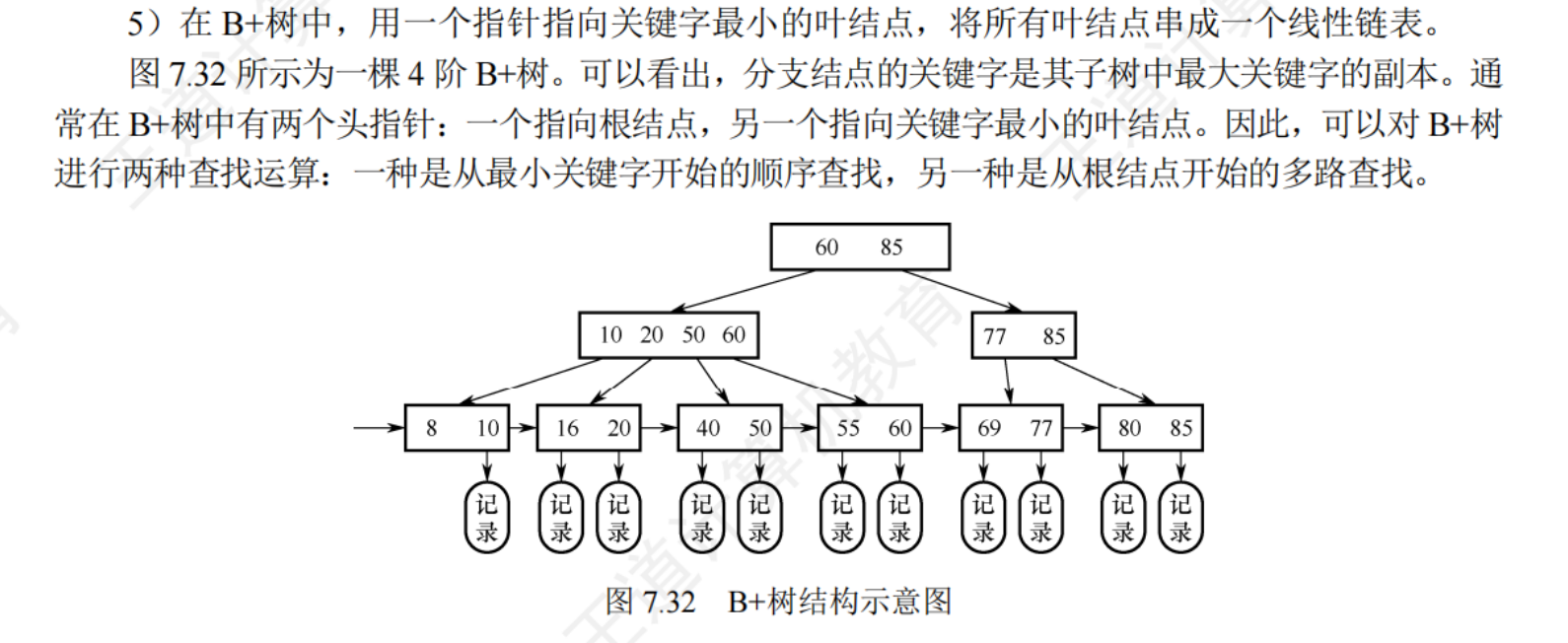
7.5.1散列表的基本概念
散列函數(也稱哈希函數):一個把查找表中的關鍵字映射成該關鍵字對應的地址的函數,記為Hash(key)=Addr(這里的地址可以是數組下標、索引或內存地址等)。
散列函數可能會把兩個或兩個以上的不同關鍵字映射到同一地址,稱這種情況為沖突,這些發生沖突的不同關鍵字稱為同義詞。一方面,設計得好的散列函數應盡量減少這樣的沖突;另一方面,因為這樣的沖突總是不可避免的,所以還要設計好處理沖突的方法。
散列表:根據關鍵字至今進行訪問的數據結構,時間復雜度O(1)
7.5.2散列函數構造方法
在構造散列函數時,必須注意以下幾點:
1)散列函數的定義域必須包含全部關鍵字,而值域的范圍則依賴于散列表的大小。
2)散列函數計算出的地址應盡可能均勻地分布在整個地址空間,盡可能地減少沖突。
3)散列函數應盡量簡單,能在較短的時間內計算出任意一個關鍵字對應的散列地址。
下面介紹常用的散列函數。
直接定址法

除留取余法

數字分析法

平方取中法

7.5.3處理沖突的方法
開放定址法
表中可存放新表項的空閑地址既向它的同義詞表項開放,又向它的非同義詞表項開放


拉鏈法
可以把所有的同義詞存儲在一個線性鏈表中,這個線性鏈表由其他散列地址唯一標識
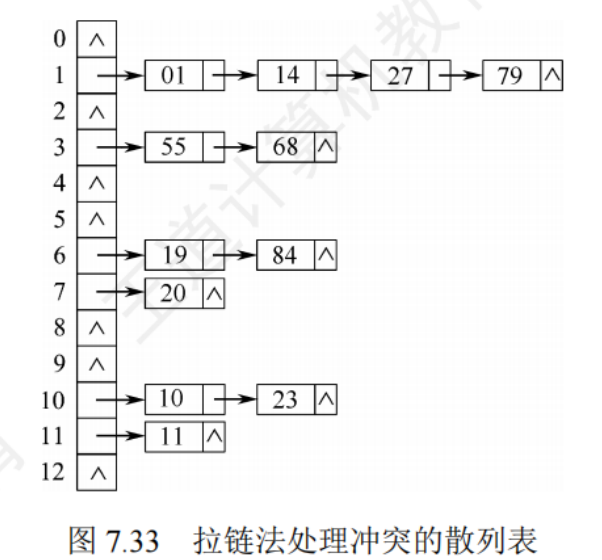
7.5.4散列查找及性能分析


8.排序

8.1.1排序的定義
排序:重新排列表中元素,使表中元素滿足關鍵字有序的過程
算法的穩定性:關鍵字相同的元素在表中的相對位置排序后是否發生改變
內部排序:排序期間元素全部放在內存中
外部排序:排序期間元素無法全部同時放在內存中,必須在排序過程中根據要求不斷地在內外存中移動
8.2.1直接插入排序
插入排序基本思想
每次將一個待排序的記錄按其關鍵字大小插入到前面已經排好序的子序列中,直到全部記錄插入完成
直接插入排序

- 查找L(i)在L(1 … i-1)中插入的位置k
- 將L(k … i-1)中所有元素依次后移一個位置
- 將L(i)復制到L(k)
//直接插入排序
void InsertSort(int A[], int n){int i,j,temp;for(i=1; i<n; i++) //將各元素插入已排好序的序列中 if(A[i]<A[i-1]){ //若A[i]關鍵字小于前驅 temp = A[i]; //用temp暫存A[i] for(j=i-1; j>=0&&A[j]>temp; --j) //檢查所有前面已排好序的元素 A[j+1] = A[j]; //所有大于temp的元素都向后挪位 A[j+1] = temp; //復制到插入位置 }
}
//直接插入排序(帶哨兵)
void InsertSort(int A[], int n){int i,j;for(i=2; i<=n; i++) //依次將A[2]~A[n]插入到前面已排序序列 if(A[i]<A[i-1]){ //若A[i]關鍵字小于前驅,將A[i]插入有序表 A[0] = A[i]; //復制為哨兵,A[0]不存元素 for(j=i-1; A[0]<A[j]; --j) //向后往前查找待插入位置 A[j+1] = A[j]; //向后挪位 A[j+1] = A[0]; //復制到插入位置 }
}


8.2.2折半插入排序
直接插入排序過程:
①從前面的有序子表中查找出待插入元素應該被插入的位置;
②給插入位置騰出空間,將待插入元素復制到表中的插入位置。注意到在該算法中,總是邊比較邊移動元素。
當待排序表是順序存儲的線性表時,查找有序子表時可以使用折半查找來實現
//折半插入排序
void InsertSort(int A[], int n){int j,i,low,high,mid;for(i=2; i<=n; i++){ //依次將A[2]~A[n]插入前面的已排序序列 A[0]=A[i]; //將A[i]暫存到A[0] low = 1; high = i-1; //設置折半查找的范圍 while(low<=high){ //折半查找(默認遞增有序) mid=(low+high)/2; //取中間點 if(A[mid]>A[0]) high = mid-1;//查找左半子表 else low = mid+1; //查找右半子表 }for(j=i-1; j>=high+1; --j)A[j+1] = A[j]; //統一后移元素,空出插入位置 A[high+1] = A[0]; //插入操作 }
}

8.2.3希爾排序
基本思想:先將待排序表分割成若干個形如 L[i,i+d,i+2d…i+kd]的特殊子表,即把相隔某個增量的記錄組成一個子表,對各個子表分別進行直接插入排序,當整個表中元素已成基本有序時,再對全體記錄進行一次直接插入排序
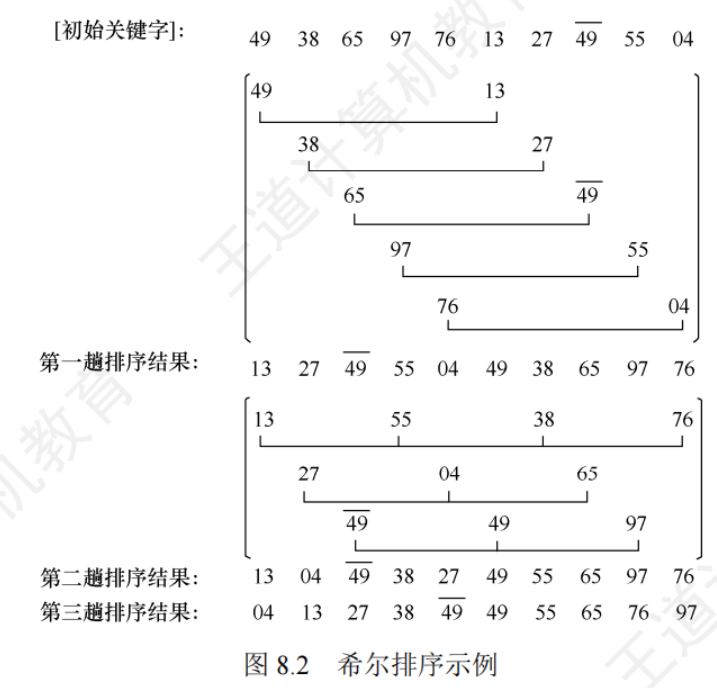
//希爾排序
void ShellSort(int A[],int n){int d,i,j;//A[0]只是暫存單元,不是哨兵,當j<=0時,插入位置已到for(d=n/2; d>=1; d=d/2) //步長變化for(i=d+1; i<=n; ++i)if(A[i]<A[i-d]){ //需要將A[i]插入有序增量子表 A[0]=A[i]; //暫存在A[0] for(j=i-d; j>0 && A[0]<A[j]; j-=d) A[j+d]=A[j]; //記錄后移,查找插入位置 A[j+d]=A[0]; //插入 }
}

8.3.1冒泡排序
交換排序
根據序列中兩個關鍵字的比較結果來對換這兩個記錄在序列中的位置
冒泡排序
基本思想:從后往前(從前往后)兩兩比較相鄰元素的值,若為逆序,則交換他們,直到序列比較完。稱為——第一趟冒泡,結果是將最小的元素交換到第一個位置…
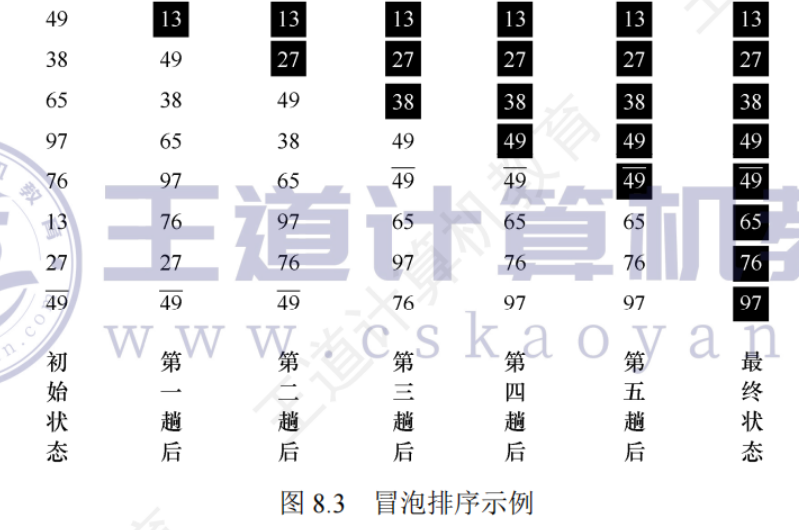
//交換
void swap(int &a,int &b){int temp = a;a = b;b = temp;
}
//冒泡排序
void BubbleSort(int A[], int n){for(int i=0; i<n-1; i++){bool flag = false; //表示本趟冒泡是否發生交換的標志 for(int j=n-1; j>i; j--) //一趟冒泡過程 if(A[j-1] > A[j]){ //若為逆序 swap(A[j-1],A[j]); //交換 flag = true;}if(flag == false)return //本趟遍歷后沒有發生交換,說明表已經有序 }
}

8.3.2快速排序
基本思想:在待排序表L[1…n]中,任取一個元素piovt作為樞軸(基準,通常取首元素),通過一趟排序將待排序表劃分為兩個獨立部分L[1…k-1]和L[k+2…n],使得L[1…k-1]中的所有元素小于piovt,L[k+1…n]中的所有元素大于或等于piovt,則piovt放在了最終位置L[k],這是一次劃分,遞歸重復


//用第一個元素將待排序序列劃分成左右兩個部分
int Partition(int A[], int low, int high){int pivot = A[low]; //第一個元素作為樞軸 while(low<high){ //用low、high搜索樞軸的最終位置 while(low<high&&A[high]>=pivot) --high;A[low] = A[high]; //比樞軸小的元素移動到左端 while(low<high&&A[low]<=pivot) ++low;A[high] = A[low]; //比樞軸大的元素移動到右端 }A[low] = pivot; //樞軸元素存放到最終位置 return low; //返回存放樞軸的最終位置
}
//快速排序
void QuickSort(int A[], int low, int high){if(low<high){ //遞歸跳出的條件 int pivotpos = Partition(A,low,high); //劃分 QuickSort(A,low,pivotpos-1); //劃分左子表 QuickSort(A,pivotpos+1,high); //劃分右子表 }
}


8.4.1簡單選擇排序
選擇排序
每一趟(第 i 趟)在后面n-i+1個待排序元素中選取關鍵字最小的元素,作為有序序列的第 i 個元素,直至 n-1 趟做完,待排序元素只剩一個
簡單選擇排序
基本思想:假設排序表為L[1…n],第 i 趟排序即從 L[i…n]中選擇關鍵字最小的元素與L(i)交換,每一趟排序可以確定一個元素的最終位置,這樣經過n-1趟排序可使排序表有序
//簡單選擇排序
void SelectSort (int A[],int n){for(int i=0; i<n-1;i++){ //一共進行n-1躺 int min=i; //記錄最小元素位置 for(int j=i+1; j<n; j++) //在A[i...n-1]中選擇最小的元素 if(A[j]<A[min]) min=j; //更新最小元素位置 if(min!=i) swap(A[i],A[min]);//封裝的swap()函數共移動元素3次 }
}
//交換
void swap(int &a,int &b){int temp = a;a = b;b = temp;
}

8.4.2堆排序
堆
大根堆: 父結點的值 大于或等于 其子結點的值
小根堆: 父結點的值 小于或等于 其子結點的值
堆 = 一棵完全二叉樹
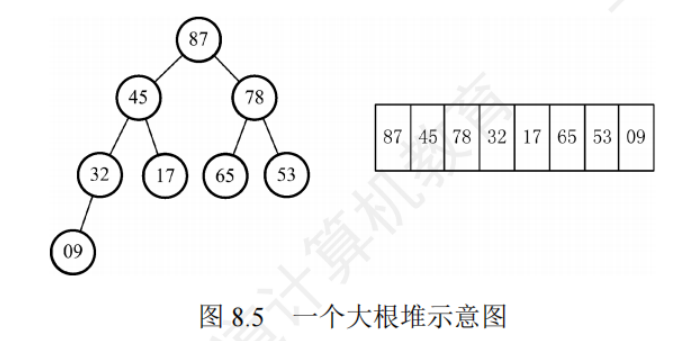
堆排序思路:首先將存放在L[1…n]中的n個元素構建初始堆,因為堆本身的特點,所以堆頂元素就是最大值,輸出堆頂元素之后,通常將堆底元素送入堆頂,此時根節點已不再滿足大根堆的性質,堆被破壞,將堆頂元素向下調整使其繼續保持大根堆的性質,再輸出堆頂元素
初始堆

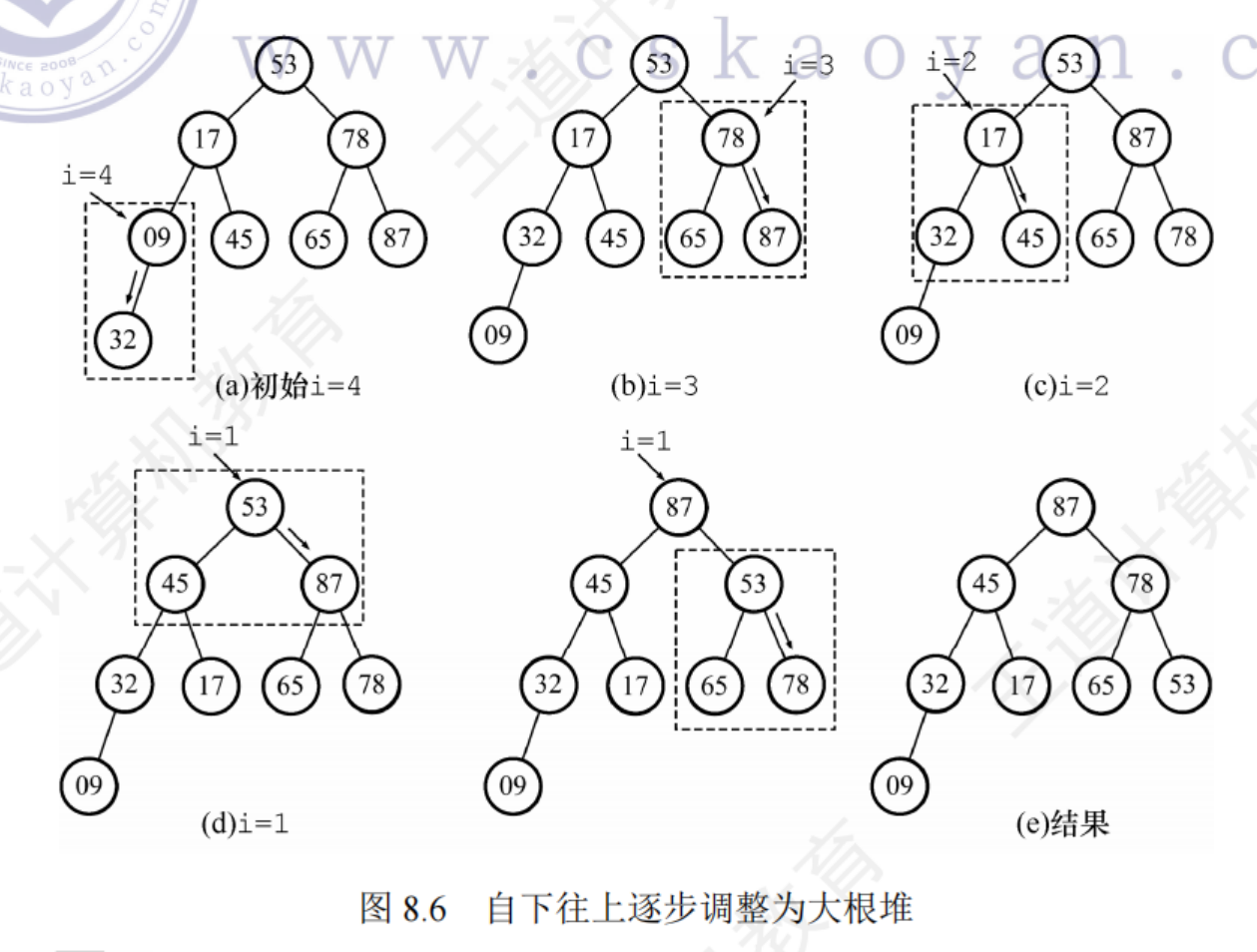
堆刪除與調整
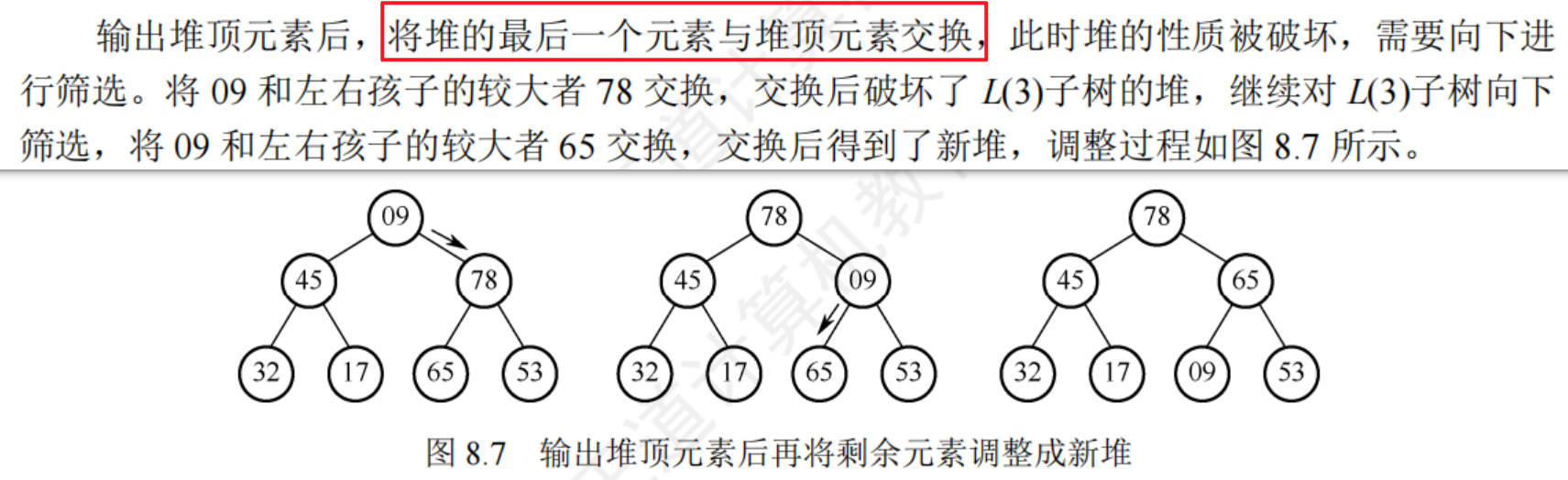
//建立大根堆
void BuildMaxHeap(int A[], int len){for(int i=len/2; i>0; i--) //從后往前調整所有非終端結點HeadAdjust(A,i,len);
}
//將以k為根的子樹調整為大根堆
void HeadAdjust(int A[],int k, int len){A[0]=A[k]; //A[0]暫存子樹的根結點 for(int i=2*k; i<=len; i*=2){ //沿key較大的子結點向下篩選 if(i<len&&A[i]<A[i+1])i++; //取key較大的字結點的下標 if(A[0]>=A[i]) break; //篩選結束 else{ A[k] = A[i]; //將A[i]調整到雙親結點下 k = i; //修改k值,以便向下繼續篩選 } }A[k] = A[0]; //被篩選結點的值放入最終位置
}
//完整邏輯
void HeapSort(int A[], int len){BuildMaxHeap(A,len); //初始建堆 for(int i=len; i>1; i--){ //n-1躺的交換和建堆過程 swap(A[i],A[1]); //把堆頂元素和堆底元素交換 HeadAjdust(A,1,i-1); //把剩余的待排序元素整理成堆 }
}

堆的插入及調整
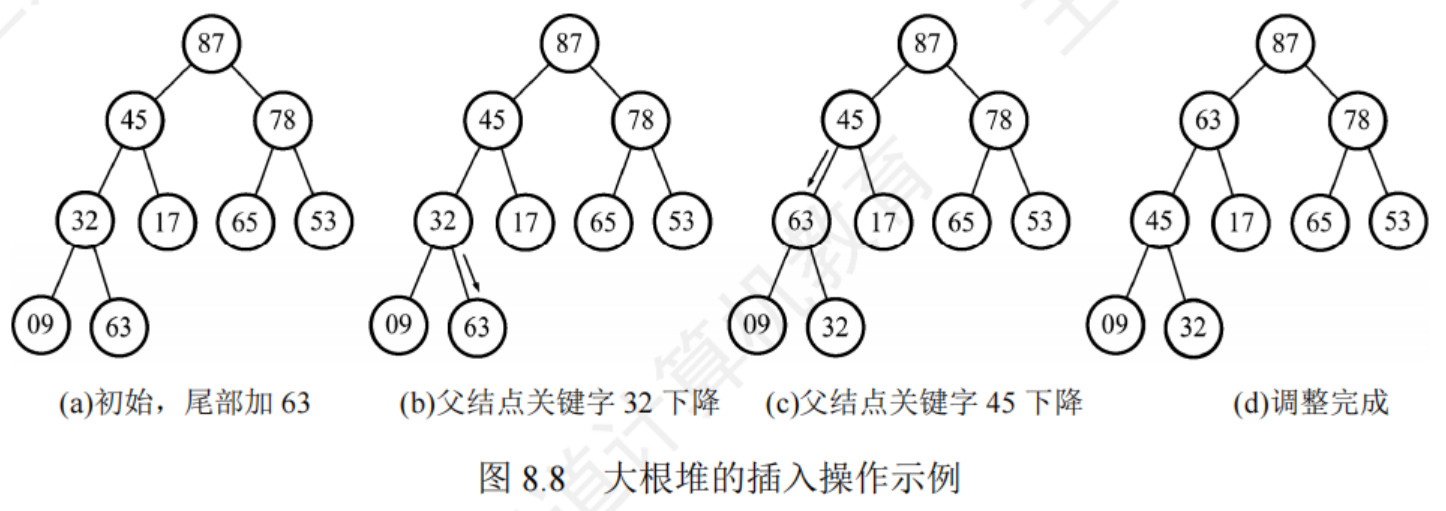
性能分析

8.5.1歸并排序
歸并:將兩個或兩個以上的有序表合并成一個新的有序表

//歸并排序
int *B = (int *)malloc(n*sizeof(int)); //輔助數組B//A[low...mid]和A[mid+1...high]各自排序,將兩個部分歸并
void Merge(int A[], int low, int mid, int high){int i,j,k;for(k=low; k<=high; k++)B[k] = A[k]; //將A中所有元素復制到B中for(i=low,j=mid+1,k=i; i<=mid&&j<=high; k++){if(B[i] <= B[j])A[k] = B[i++]; //將較小值復制到A中elseA[k] = B[j++]; }//if while(j<=mid) A[k++] = B[i++];while(j<=high) A[k++] = B[j++];
} void MergeSort(int A[], int low, int high){if(low<high){int mid = (low+high)/2; //從中間劃分 MergeSort(A,low,mid); //對左半部分歸并排序 MergeSort(A,mid+1,high); //對右半部分歸并排序Merge(A,low,mid,high); //歸并 }//if
}
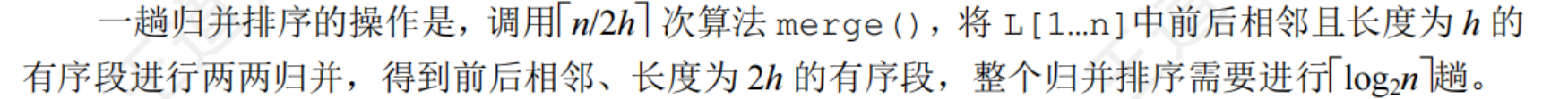

8.5.2基數排序

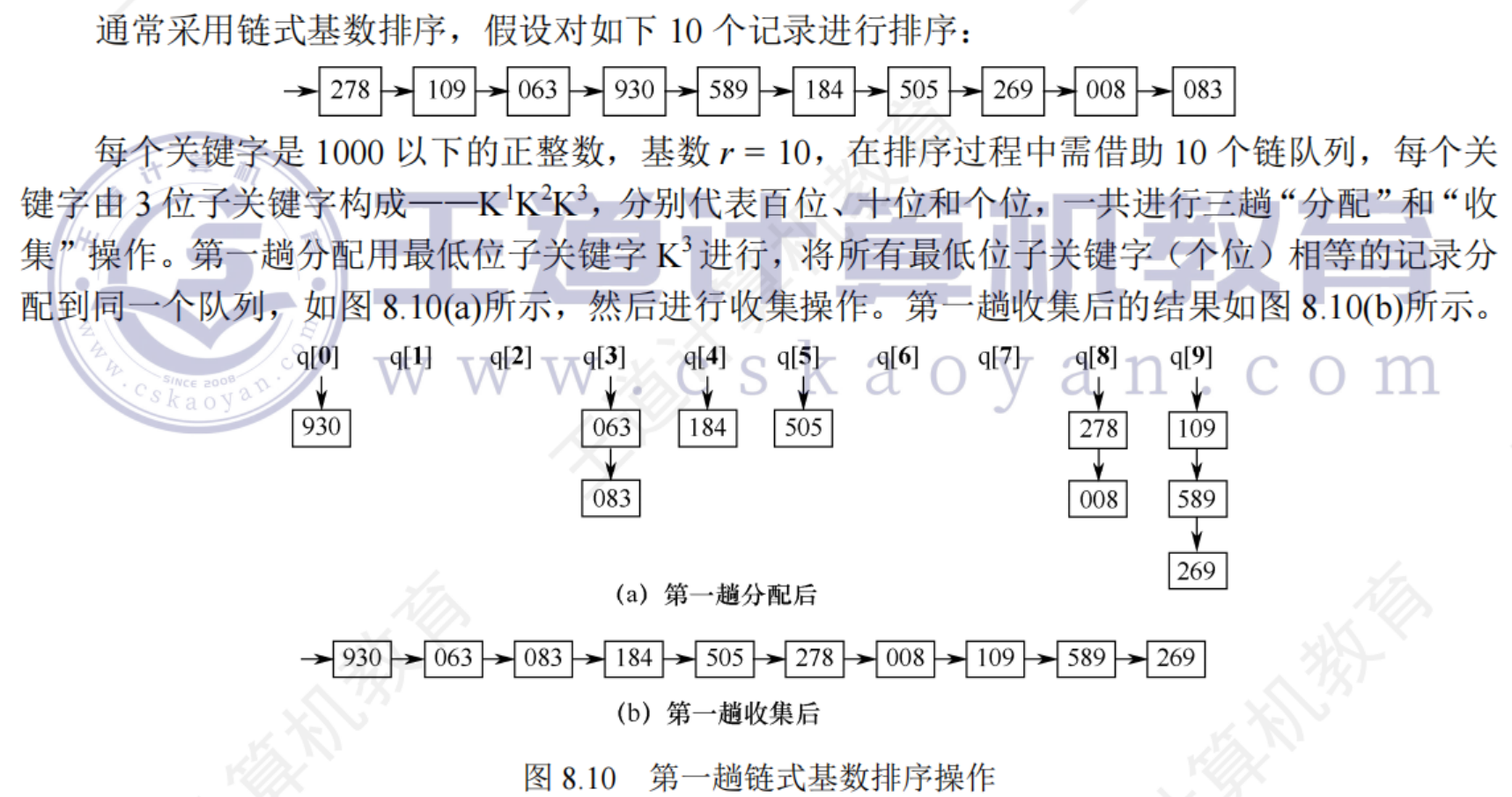
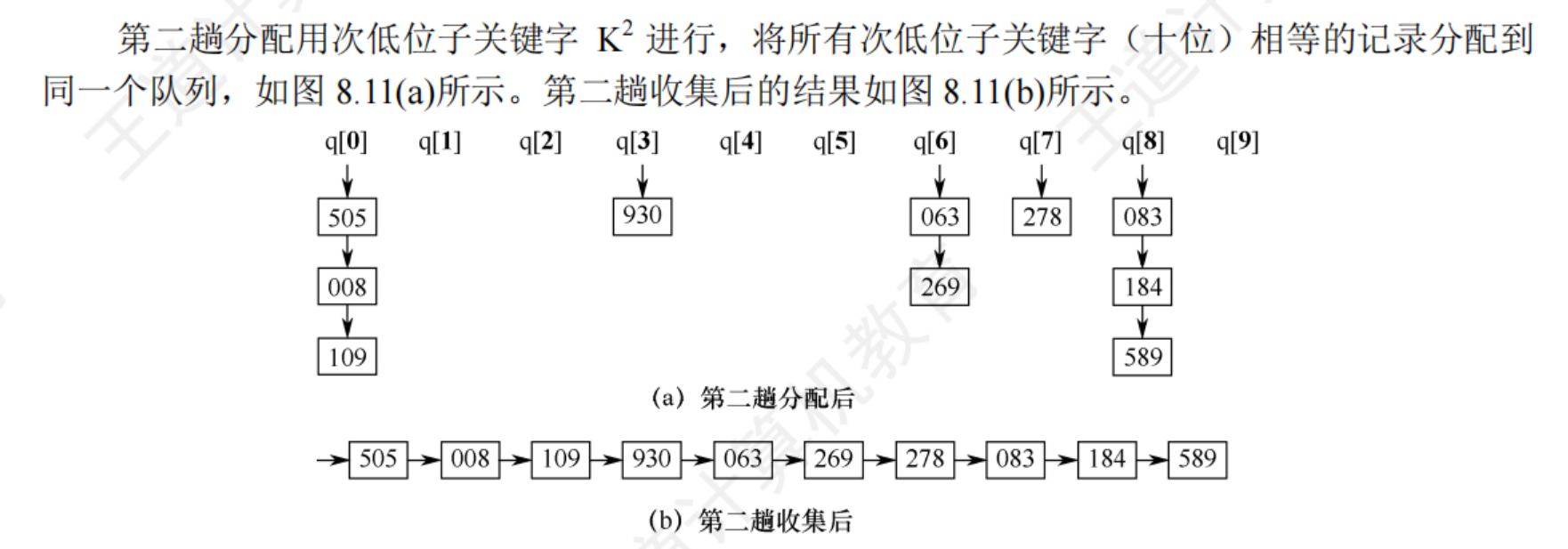


8.6.1內部排序算法比較
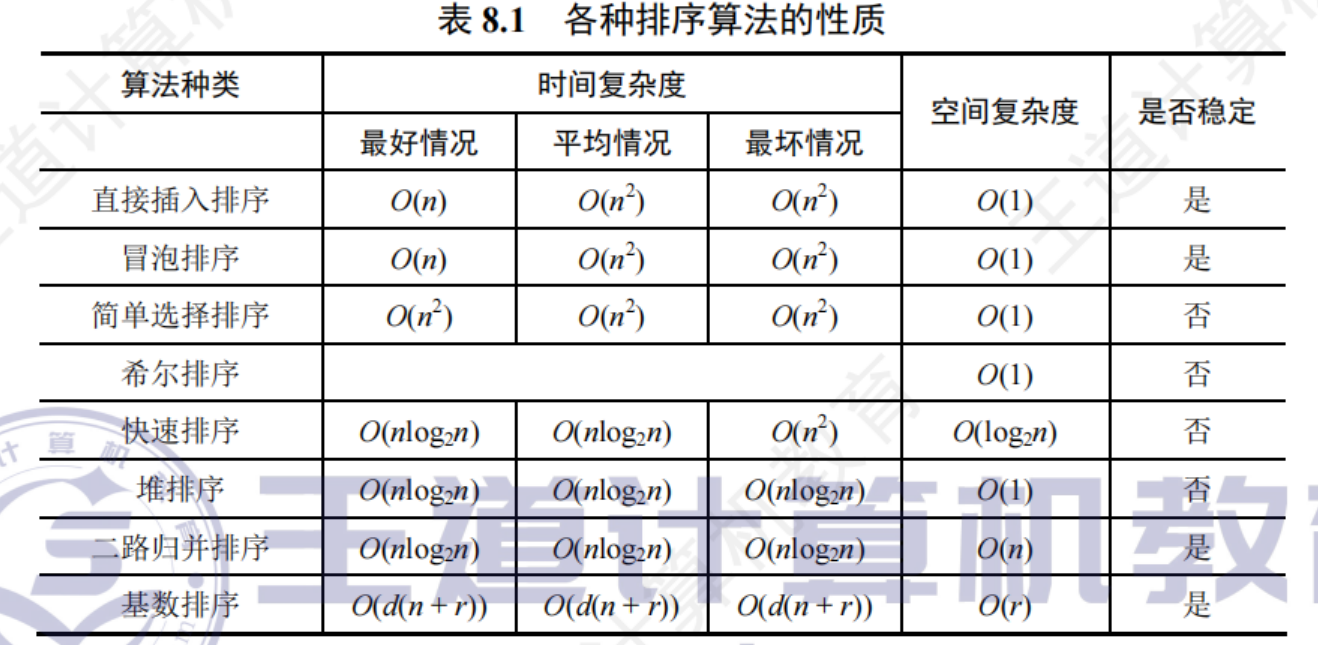
8.7.1外部排序基本概念
- 外部排序指的是大文件的排序,即待排序的記錄存儲在外存中,待排序的元素無法依次性裝入內存,需要在內存和外存之間進行多次數據交換,達到排序整個文件的目的
- 減少平衡歸并中外存堆笑次數的方法:增大歸并路數和減少歸并段個數
- 利用敗者樹增大歸并路數
- 利用置換—選擇算法進行多路平衡歸并,需要構造最佳歸并樹
外部排序:對大文件進行排序,因為文件中的記錄很多,無法將整個文件復制進內存中進行排序。因此,需要將待排序的記錄存儲在外存上,排序時再把數據一部分一部分地調入內存進行排序,在排序過程中需要多次進行內存和外存之間的交換。這種排序算法就稱為外部排序。
8.7.2外部排序方法
外部排序通常采用歸并排序算法,包括兩個階段:
- 根據內存緩沖區的大小,將外存上的文件分成若干長度為 l 的子文件,依次讀入內存并利用內部排序算法對他們進行排序,并將排序后得到的額有序子文件重新寫回萬村,稱這些有序子文件為歸并段或串
- 對這些歸并段進行逐趟歸并,使歸并段由小到大排列,直至得到整個有序文件
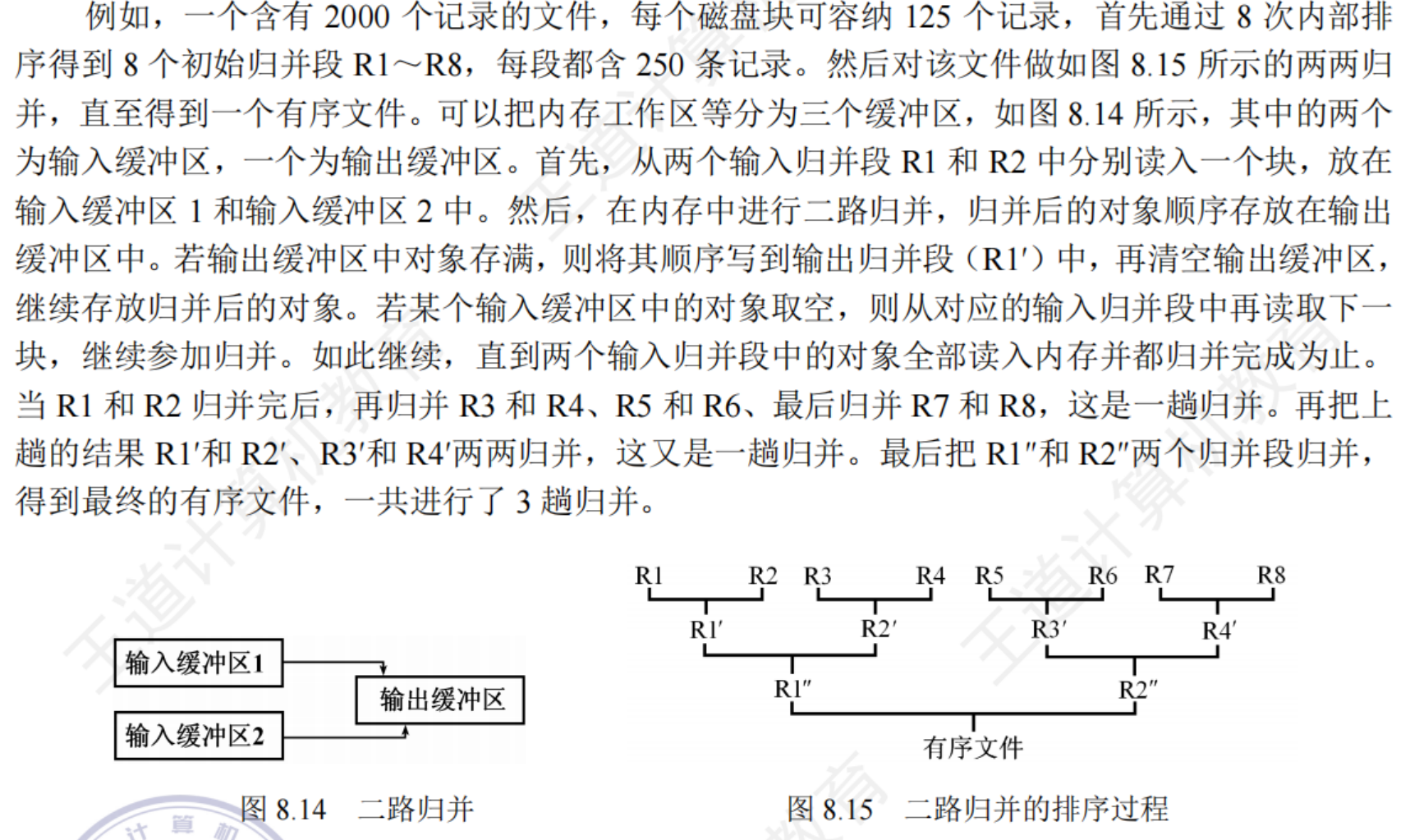
外部排序總時間 = 內部排序時間 + 外存信息度/寫時間 + 內部歸并時間
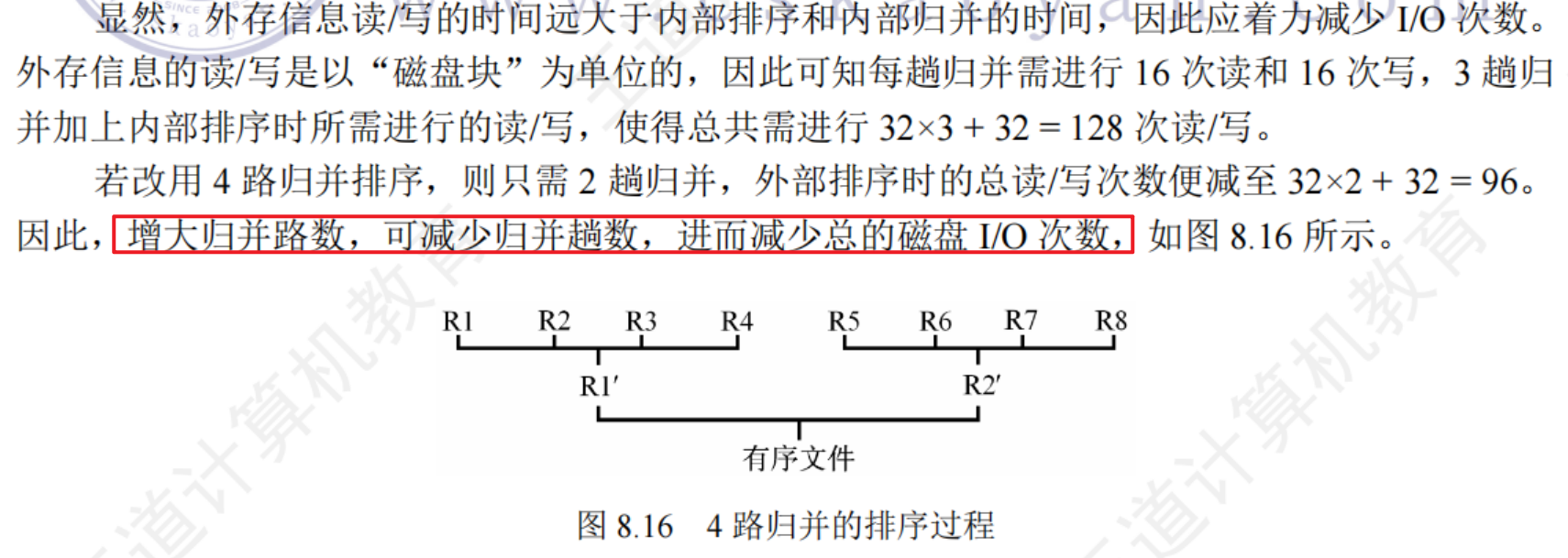

8.7.3多路平衡歸并與敗者樹

為了使內部排序不受k的增大的影響:引入敗者樹
敗者樹:是樹形選擇排序的一種變體,可視為一棵完全二叉樹,k個葉結點分別存放k個歸并段唉歸并過程中當前參加比較的元素,內部節點用來記憶左右子樹中的失敗者,而讓勝利者繼續向上比較,一直到根節點
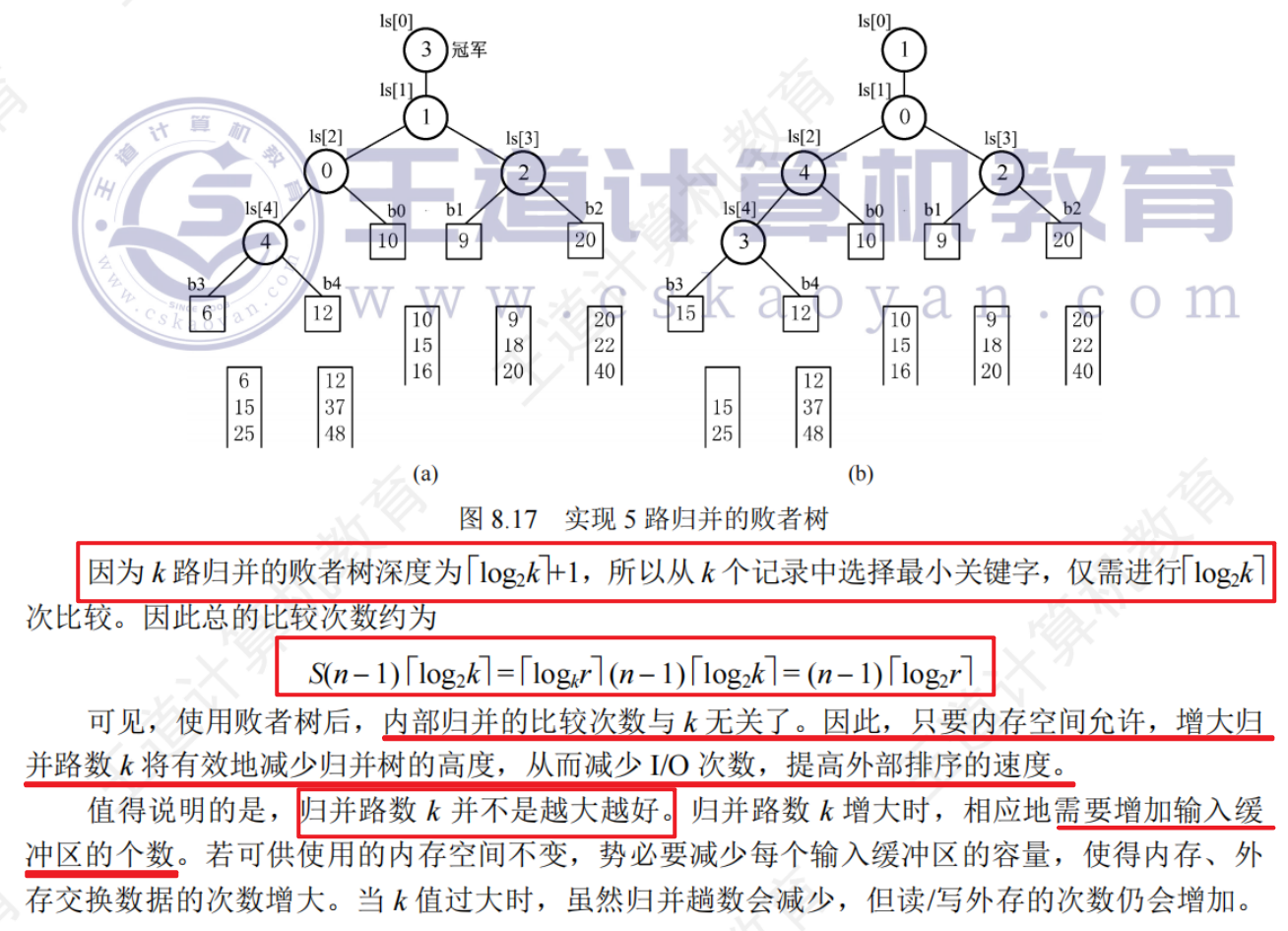
8.7.4置換—選擇算法

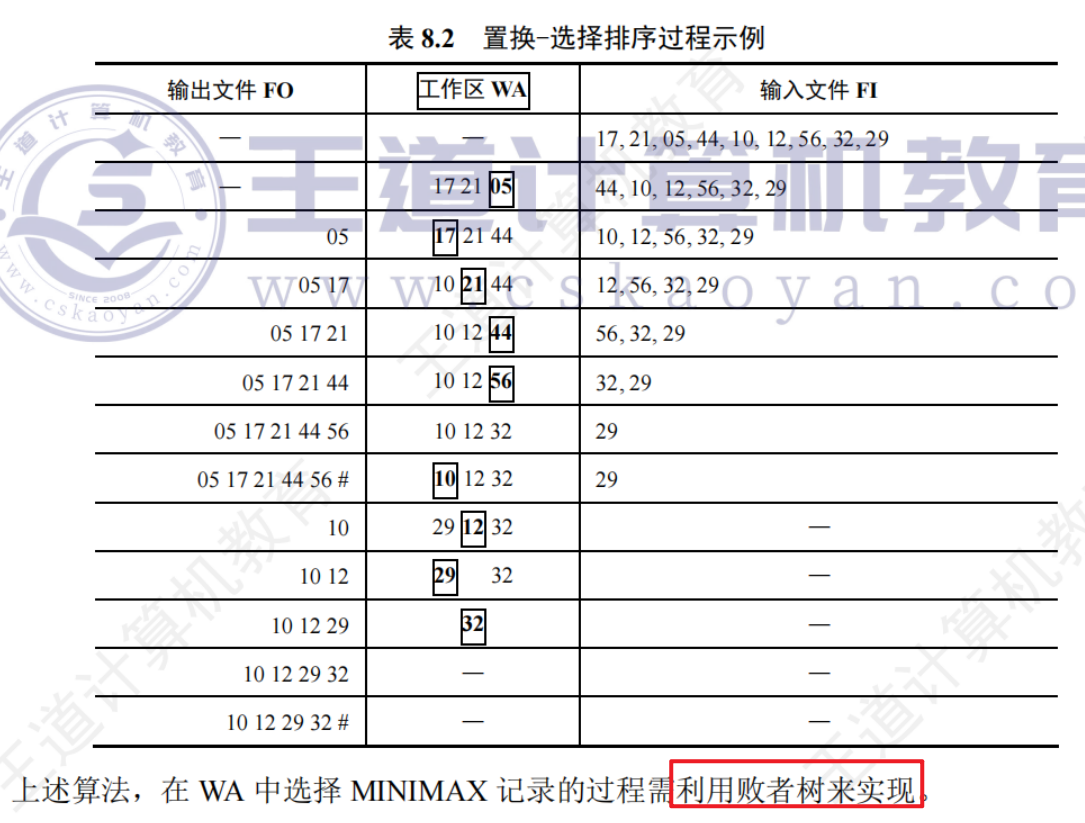
8.7.5最佳歸并樹
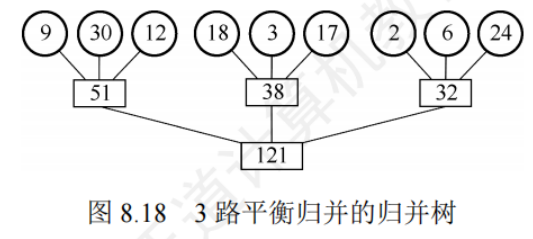
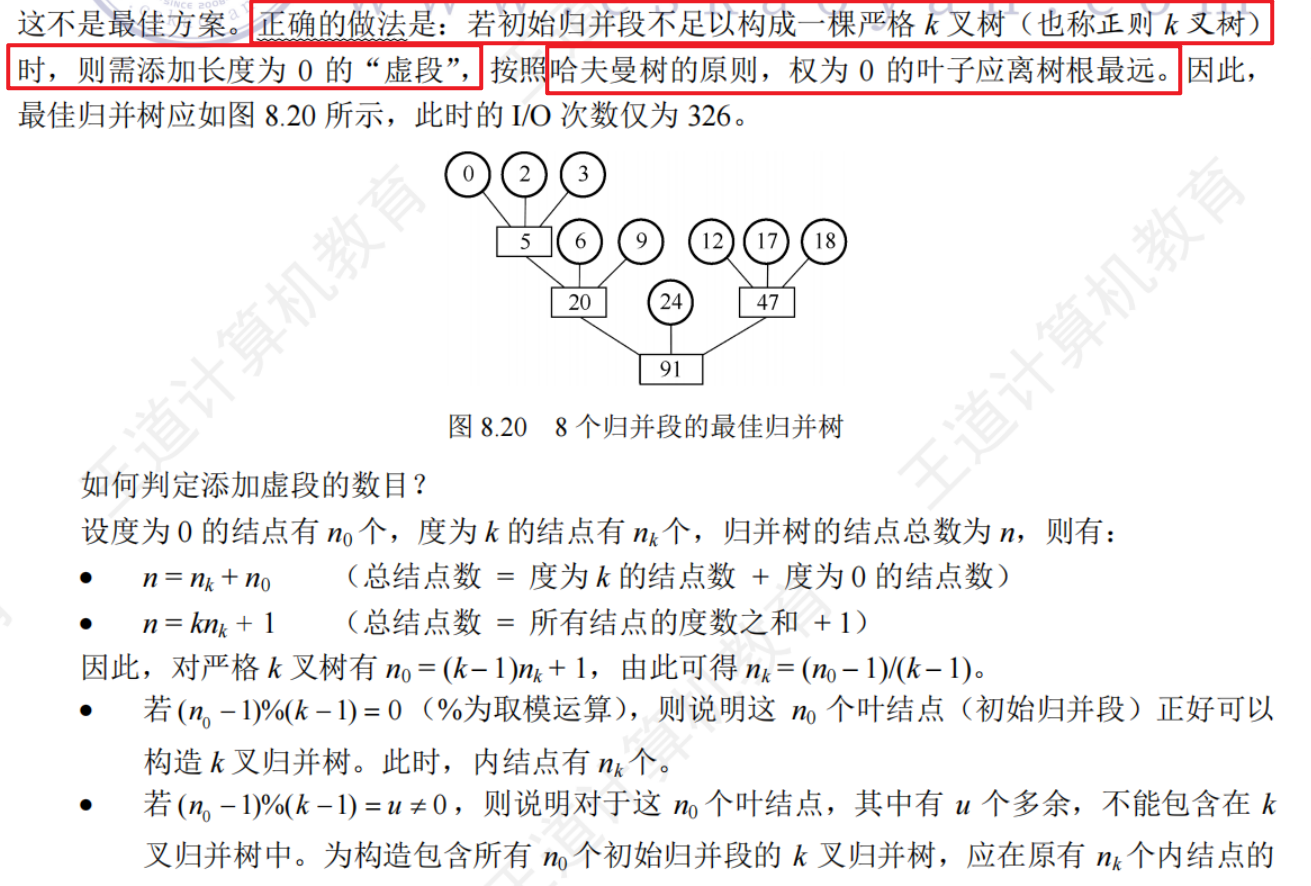
文件經過置換選擇排序后,得到的是長度不等的初始歸并段
如何組織長度不等的初始歸并段的歸并順序使得I/O次數最少

特點,所以堆頂元素就是最大值,輸出堆頂元素之后,通常將堆底元素送入堆頂,此時根節點已不再滿足大根堆的性質,堆被破壞,將堆頂元素向下調整使其繼續保持大根堆的性質,再輸出堆頂元素
初始堆
[外鏈圖片轉存中…(img-FiVCZU10-1753781638178)]
[外鏈圖片轉存中…(img-YeeQ02y1-1753781638179)]
堆刪除與調整
[外鏈圖片轉存中…(img-GUWtKPdk-1753781638179)]
//建立大根堆
void BuildMaxHeap(int A[], int len){for(int i=len/2; i>0; i--) //從后往前調整所有非終端結點HeadAdjust(A,i,len);
}
//將以k為根的子樹調整為大根堆
void HeadAdjust(int A[],int k, int len){A[0]=A[k]; //A[0]暫存子樹的根結點 for(int i=2*k; i<=len; i*=2){ //沿key較大的子結點向下篩選 if(i<len&&A[i]<A[i+1])i++; //取key較大的字結點的下標 if(A[0]>=A[i]) break; //篩選結束 else{ A[k] = A[i]; //將A[i]調整到雙親結點下 k = i; //修改k值,以便向下繼續篩選 } }A[k] = A[0]; //被篩選結點的值放入最終位置
}
//完整邏輯
void HeapSort(int A[], int len){BuildMaxHeap(A,len); //初始建堆 for(int i=len; i>1; i--){ //n-1躺的交換和建堆過程 swap(A[i],A[1]); //把堆頂元素和堆底元素交換 HeadAjdust(A,1,i-1); //把剩余的待排序元素整理成堆 }
}
[外鏈圖片轉存中…(img-3irwjcCI-1753781638179)]
堆的插入及調整
[外鏈圖片轉存中…(img-PWlceYcR-1753781638179)]
性能分析
[外鏈圖片轉存中…(img-sc3YrpRF-1753781638179)]
8.5.1歸并排序
歸并:將兩個或兩個以上的有序表合并成一個新的有序表
[外鏈圖片轉存中…(img-g3AKwHp5-1753781638179)]
//歸并排序
int *B = (int *)malloc(n*sizeof(int)); //輔助數組B//A[low...mid]和A[mid+1...high]各自排序,將兩個部分歸并
void Merge(int A[], int low, int mid, int high){int i,j,k;for(k=low; k<=high; k++)B[k] = A[k]; //將A中所有元素復制到B中for(i=low,j=mid+1,k=i; i<=mid&&j<=high; k++){if(B[i] <= B[j])A[k] = B[i++]; //將較小值復制到A中elseA[k] = B[j++]; }//if while(j<=mid) A[k++] = B[i++];while(j<=high) A[k++] = B[j++];
} void MergeSort(int A[], int low, int high){if(low<high){int mid = (low+high)/2; //從中間劃分 MergeSort(A,low,mid); //對左半部分歸并排序 MergeSort(A,mid+1,high); //對右半部分歸并排序Merge(A,low,mid,high); //歸并 }//if
}
[外鏈圖片轉存中…(img-0KVVToUT-1753781638179)]
[外鏈圖片轉存中…(img-I32d98hn-1753781638180)]
[外鏈圖片轉存中…(img-R2LprRAR-1753781638180)]
8.5.2基數排序
[外鏈圖片轉存中…(img-DUaTPhHO-1753781638180)]
[外鏈圖片轉存中…(img-ds7cd8Vq-1753781638180)]
[外鏈圖片轉存中…(img-vRq3gEtw-1753781638180)]
[外鏈圖片轉存中…(img-8Iw00Gbq-1753781638181)]
[外鏈圖片轉存中…(img-JmlDGCOU-1753781638181)]
8.6.1內部排序算法比較
[外鏈圖片轉存中…(img-NwvJRKuS-1753781638181)]
8.7.1外部排序基本概念
- 外部排序指的是大文件的排序,即待排序的記錄存儲在外存中,待排序的元素無法依次性裝入內存,需要在內存和外存之間進行多次數據交換,達到排序整個文件的目的
- 減少平衡歸并中外存堆笑次數的方法:增大歸并路數和減少歸并段個數
- 利用敗者樹增大歸并路數
- 利用置換—選擇算法進行多路平衡歸并,需要構造最佳歸并樹
外部排序:對大文件進行排序,因為文件中的記錄很多,無法將整個文件復制進內存中進行排序。因此,需要將待排序的記錄存儲在外存上,排序時再把數據一部分一部分地調入內存進行排序,在排序過程中需要多次進行內存和外存之間的交換。這種排序算法就稱為外部排序。
8.7.2外部排序方法
外部排序通常采用歸并排序算法,包括兩個階段:
- 根據內存緩沖區的大小,將外存上的文件分成若干長度為 l 的子文件,依次讀入內存并利用內部排序算法對他們進行排序,并將排序后得到的額有序子文件重新寫回萬村,稱這些有序子文件為歸并段或串
- 對這些歸并段進行逐趟歸并,使歸并段由小到大排列,直至得到整個有序文件
[外鏈圖片轉存中…(img-LwRSVQ3Z-1753781638181)]
外部排序總時間 = 內部排序時間 + 外存信息度/寫時間 + 內部歸并時間
[外鏈圖片轉存中…(img-nWeQubar-1753781638181)]
[外鏈圖片轉存中…(img-JVDjzsDy-1753781638181)]
8.7.3多路平衡歸并與敗者樹
[外鏈圖片轉存中…(img-sWSutVhX-1753781638182)]
為了使內部排序不受k的增大的影響:引入敗者樹
敗者樹:是樹形選擇排序的一種變體,可視為一棵完全二叉樹,k個葉結點分別存放k個歸并段唉歸并過程中當前參加比較的元素,內部節點用來記憶左右子樹中的失敗者,而讓勝利者繼續向上比較,一直到根節點
[外鏈圖片轉存中…(img-XIa5J7Eg-1753781638182)]
8.7.4置換—選擇算法
[外鏈圖片轉存中…(img-FcHiQCPM-1753781638182)]
[外鏈圖片轉存中…(img-1WgULkTj-1753781638182)]
8.7.5最佳歸并樹
文件經過置換選擇排序后,得到的是長度不等的初始歸并段
如何組織長度不等的初始歸并段的歸并順序使得I/O次數最少
[外鏈圖片轉存中…(img-zO0UL4oX-1753781638182)]
[外鏈圖片轉存中…(img-PajMykKD-1753781638182)]
[外鏈圖片轉存中…(img-sNgjz06s-1753781638182)]


——攻擊者使用什么漏洞獲取了服務器的配置文件?)

)



結構型:橋接模式詳解)
)
)




)



![[機緣參悟-235]:通過AI人工升級網絡的工作方式和特征理解人的思維方式](http://pic.xiahunao.cn/[機緣參悟-235]:通過AI人工升級網絡的工作方式和特征理解人的思維方式)
—— 重寫虛方法】)
