還記得第一次見該題根本無從下手。其實，我們不妨把問題拆解，簡單化。不要怕自己寫的是暴力算法，有很多算法技巧其實就是在暴力算法的基礎上優化得來。
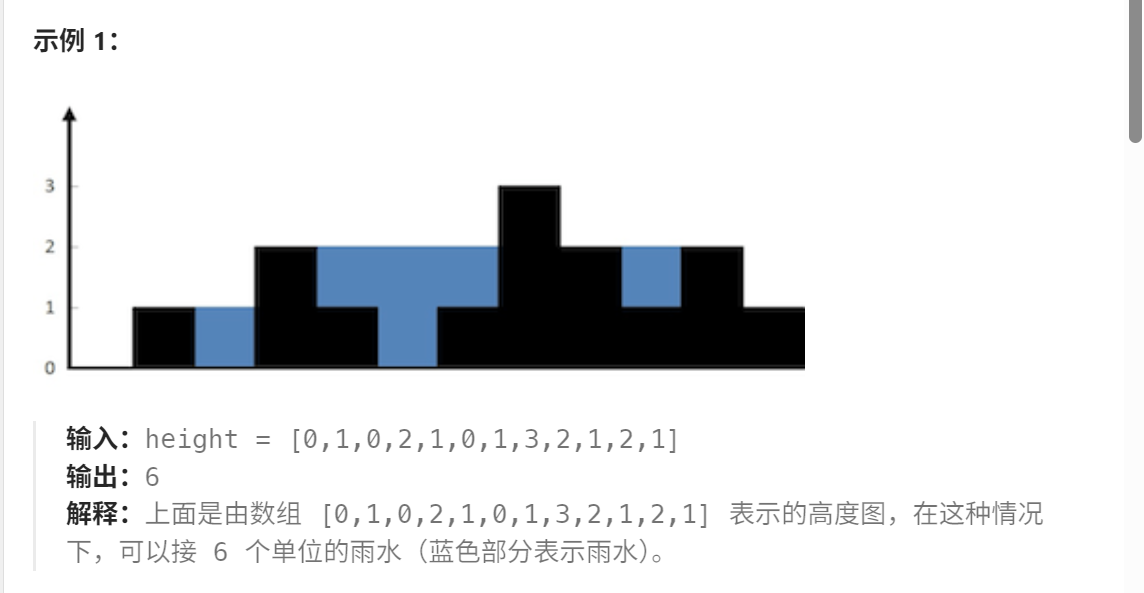
題目目的是求所有可接雨水數量，我們可以求出每一個位置可接雨水數量，最后加起來即可。
就是如下流程：
int trap(vector<int>& height) {int n = height.size();vector<int> water(n, -1);for(int i = 0; i < n; ++i){// 求height[i]能存多少水water[i] = getWater(height, i);}int ans = 0;for(int x : water){ans += x;}return ans;}那么現在問題只有一個，如何求單個位置的可接雨水量，根據題目，不難想到，只需要找左右兩邊可以“望”到的最高值，選取二者最小值，減去該位置高度即可。
完整代碼：
class Solution {
public:int trap(vector<int>& height) {int n = height.size();vector<int> water(n, -1);for(int i = 0; i < n; ++i){// 求height[i]能存多少水water[i] = getWater(height, i);}int ans = 0;for(int x : water){ans += x;}return ans;}int getWater(vector<int>& height, int k){int n = height.size();// 計算左高點int lmax = height[k];for(int i = k - 1; i >= 0; --i){if(height[i] > lmax){lmax = height[i];}}// 計算右高點int rmax = height[k];for(int i = k + 1; i < n; ++i){if(height[i] > rmax){rmax = height[i];}}// 返回結果return min(lmax, rmax) - height[k];}
};不過這肯定是超時的。
在此基礎上，分析算法中重復計算的部分，我們在每一個位置得到?lmax?和?rmax?時都從零開始計算，這樣很浪費算力。由于求 lmax 和 rmax 本質就是簡單的求單調最大值，所以我們可以一遍遍歷求出每個位置的 lmax 或?rmax ，因為我們只需要向對應方向“望”到的最大值即可。
class Solution {
public:int trap(vector<int>& height) {int n = height.size();vector<int> lmax(n, 0);vector<int> rmax(n, 0);lmax[0] = height[0];for(int i = 1; i < n; ++i){lmax[i] = max(lmax[i - 1], height[i]);}rmax[n - 1] = height[n - 1];for(int i = n - 2; i >= 0; --i){rmax[i] = max(rmax[i + 1], height[i]);}int ans = 0;for(int i = 0; i < n; i++){ans += min(lmax[i], rmax[i]) - height[i];}return ans;}
};最后，考慮是否可以繼續優化時間和空間。
我們假設只有兩個變量，分別記錄 1 位置的 lmax 和 n - 2 位置的 rmax ，考慮現在誰的雨水量是可求的。
思考分析后得出，當兩個變量進行比較，較小的一方所指位置的雨水量是可求的。
以 lmax 指向 1 位置，值為100， rmax 指向 n - 2 為位置，值為70為例，即使當前 lmax 對于? ? ??n - 2位置來說并不是真正的 lmax ，但其真正值只會比100大，而接雨水量是由小的一方決定的。
class Solution {
public:int trap(vector<int>& height) {int lidx = 1;int lmax = height[0];int ridx = height.size() - 2;int rmax = height[ridx + 1];int ans = 0;while(lidx <= ridx){if(lmax > rmax){ans += max(0, rmax - height[ridx]);rmax = max(rmax, height[ridx--]);}else{ans += max(0, lmax - height[lidx]);lmax = max(lmax, height[lidx++]);}}return ans;}
};
)
