本文的內容通下面這篇文章有著緊密的聯系，讀者可以選擇性閱讀?

C語言————二、八、十、十六進制的相互轉換-CSDN博客

目錄

基本概念

原碼?反碼 補碼 轉換

數據的存儲方式

基本存儲單位

數據的計算方式

補碼的模運算原理?

移位操作符

左移操作符

右移操作符

位操作符：&、|、^、~

&的運算規則

|的運算規則

^的運算規則

~的運算規則

---

基本概念

我們知道不同進制的數字，歸根結底都是一個個不同的表現形式?。

原碼、補碼和反碼是整數類型在計算機內部以二進制存儲時的三種不同表現形式，雖然整數具有這三種類型的存儲方式，但是在內存中以補碼的形式進行存儲。

有符號整數在這三種方法中均由符號位和數值位兩部分組成，在二進制序列中，最高的一位被視為符號位，其余都是數值位。

下面我們對這三種方式進行逐一介紹：

原碼：直接將數字按照二進制轉換方法得到的就是原碼

反碼：符號位不變，其余位依次取反得到的就是反碼

補碼：反碼+1得到的就是補碼

注：知道一個負整數的補碼或者反碼，想求這個負整數的值，那么應該將補碼或者反碼逆推回去得到原碼，再由原碼進行計算得到的值才是正確的，在計算中，符號位不參與權重，僅用以判斷正負。

正整數的原碼、反碼、補碼都相同；

原碼?反碼 補碼 轉換

負整數的原碼、反碼、補碼有如下的轉換形式（轉換中符號位不變）：

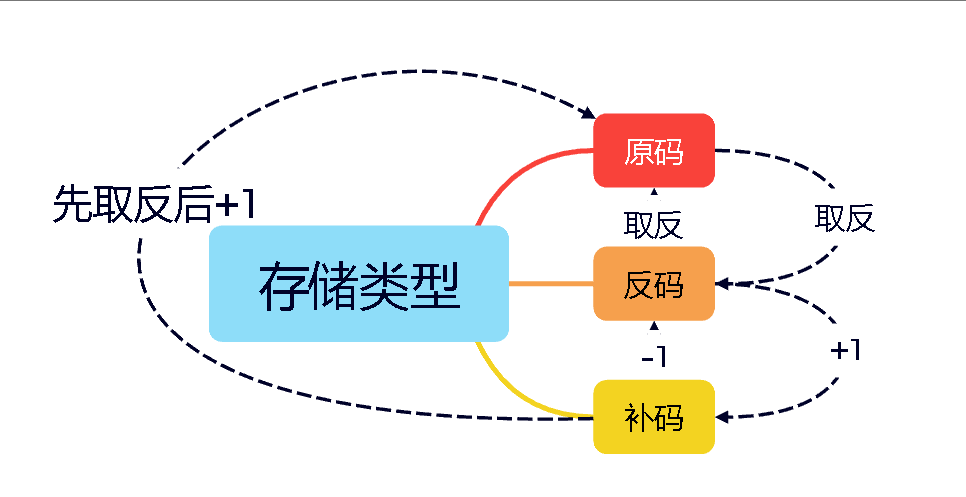
在對這三種形式運用的深入之前，我們先進行一個前置的知識儲備。?

數據的存儲方式

我們知道，計算機內部采用二進制存儲所有數據，原因是電子元件（如晶體管）的 “導通” 與 “截止” 兩種狀態可直接對應二進制的 “1” 和 “0”，物理實現簡單且穩定。

基本存儲單位

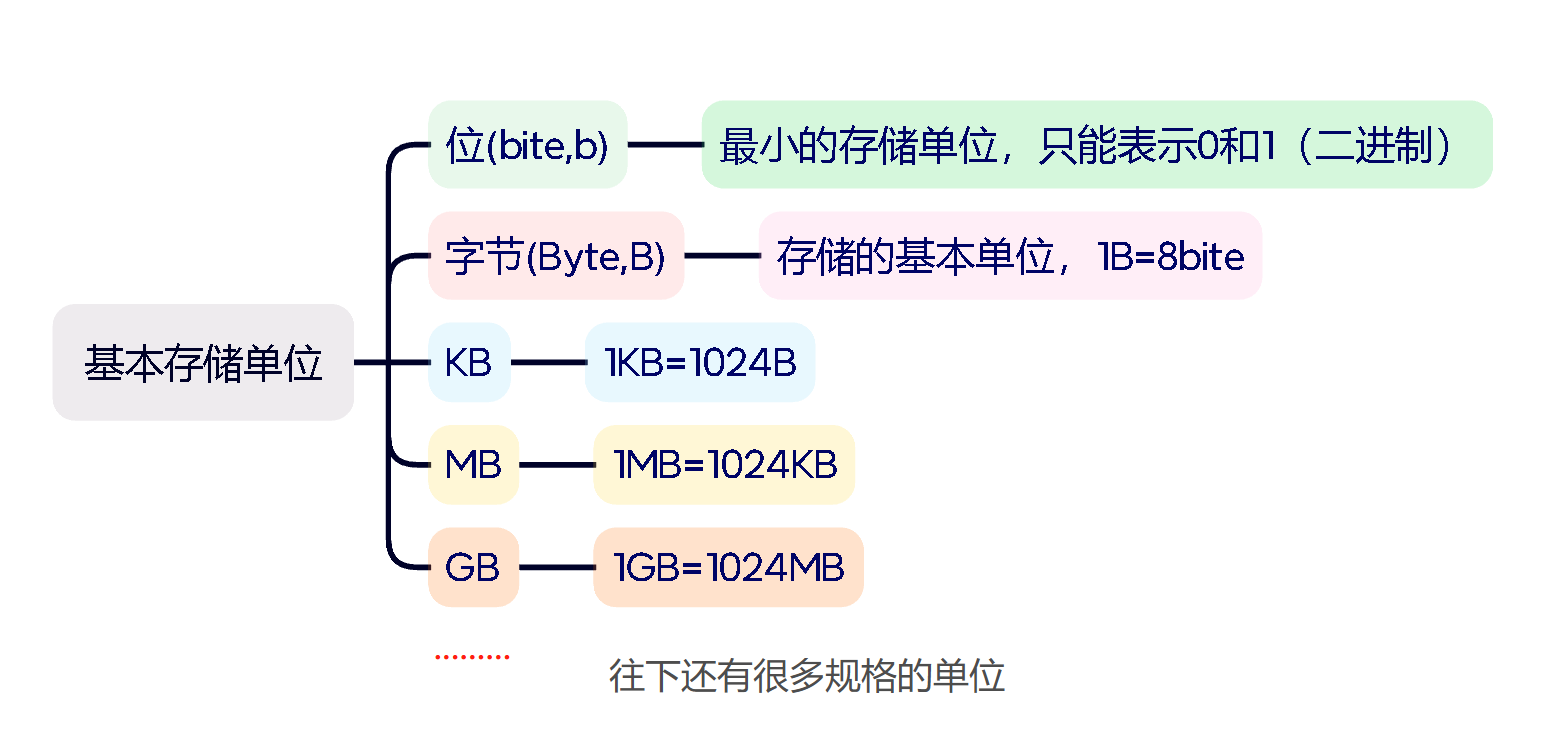
我們知道一個int的字節大小為4，那么他的二進制位數為32位，接下來我們會用int來介紹三種碼之間的運用方式。

數據的計算方式

在計算機中，數據的計算和存儲都是通過補碼來完成的。這是因為使用補碼可以對符號位和數值域進行統一的處理，同時加減法也可以進行統一處理（CPU處理器只有加法器），此外，原碼和補碼的相互轉換，二者的方式是相同的，也不需要額外的電子元件。

那為什么使用補碼而不是原碼呢？

原碼是利用最高位表示符號（0 代表正數，1 代表負數），其余位表示數值的絕對值。不過，原碼在進行加減法運算時會碰到一些難題：

• 符號位處理復雜：在進行加減法運算時，需要先判斷操作數的符號，然后再決定是進行加法還是減法運算。
• 存在正負零：原碼中存在兩種零的表示方式，即+0（0000）和-0（1000），這會使比較操作變得復雜。
• 減法運算困難：當進行減法運算時，需要設計專門的電路來執行減法操作，這增加了硬件的復雜度。

補碼是通過對原碼取反后加 1 得到的，它成功解決了原碼存在的上述問題。

• 統一加減法運算：在補碼系統中，減法可以轉換為加法來進行計算，比如A - B可以表示為A + (-B)。這樣一來，計算機就不需要設計專門的減法電路，只需一個加法器就能完成加減法運算。
• 消除正負零：在補碼表示中，零只有一種表示形式，即0000。而1000則被用來表示-8，這使得數值的表示范圍得到了擴展。（+0和-0的補碼結果時一致的，所以只有一種表示形式）
• 簡化硬件設計：由于加減法運算可以統一用加法器來實現，硬件設計變得更加簡單，同時還能減少出錯的概率。

  int main()
  {//1 - 1//1 + (-1)//00000000000000000000000000000001 ---- 1的原碼//00000000000000000000000000000001 ---- 1的補碼//00000000000000000000000000000001 ---- 1的反碼//10000000000000000000000000000001 ---- -1的原碼//11111111111111111111111111111110 ---- -1的反碼//11111111111111111111111111111111 ---- -1的補碼//那么我們用原碼進行計算時我們可以得到值為10000000000000000000000000000010  即-2，與結果不符//我們使用補碼進行計算時可以得到00000000000000000000000000000000    即0，數值相符return 0;
  }

  通過上述代碼，我們發現，使用原碼進行計算時（相當于沒有考慮正負符號直接求和），得到的結果與值不符，而補碼計算時完美的彌補了他的不足。

補碼的模運算原理?

補碼其實是一種模運算系統。對于 n 位二進制數，其模為 2?。例如，4 位二進制數的模就是 16。在模運算中，減去一個數就相當于加上這個數的補數，即x - y ≡ x + (2? - y) (mod 2?)。

以 4 位二進制數計算5 - 3為例：

• 可以轉化為5 + (-3)

• -3的補碼為1101（也就是16 - 3 = 13）

• 計算5 + 13 = 18，由于模為 16，18 mod 16 = 2，結果正確。

另，整數值和其補碼對應的值由如下對應關系：

• 正數：直接表示為二進制，范圍是?0?到?2^(n-1)-1。

• 負數：-N?表示為?2^n - N，范圍是?-2^(n-1)?到?-1。

  例如，4 位補碼的模是?16：

• -5?表示為?16 - 5 = 11（二進制?1011）。{取反+1得到1101即-5}

• -8?表示為?16 - 8 = 8（二進制?1000）。{取反+1得到0000，這是錯誤的示范，8在4位二進制無法用原碼表示，進一步體現了原碼的局限性}

移位操作符

<< 為左移位操作符

>> 為右移位操作符

注：他們的操作數都只能是整數，有且僅有兩個操作數，只能移動非負數位

左移操作符

移動規則：左邊拋棄，右邊補0

對于 10 << 1 ,他的具體變化如下：

#include <stdio.h>
int main()
{int num = 10;int n = num<<1;printf("n= %d\n", n);//變成20printf("num= %d\n", num);//num不變，即不改變num自身的值return 0;
}

右移操作符

右移操作符具有兩種不同的移動規則：

1.算術右移：左邊用原該值的符號位填充，右邊丟棄

2.邏輯右移：左邊用0填充，右邊丟棄

對于-10 >> 1,采用算術右移變化如下：

對于-10 >> 1,采用邏輯右移變化如下：

#include <stdio.h>
int main()
{int num = -10;int n = num>>1;printf("n= %d\n", n);//變成-5printf("num= %d\n", num);//num不變，即不改變num自身的值return 0;
}

在實際運算中，>>右移操作符采用算術右移還是邏輯右移，取決于編輯器規則；但一般情況下采用的是算術右移。?

位操作符：&、|、^、~

位操作符有：?

&的運算規則

|的運算規則

以兩個整數的補碼進行計算，對應的二進制位上，有1就為1，同時為0才為0。

^的運算規則

以兩個整數的補碼進行計算，對應的二進制位上，相同為0，相異為1。

~的運算規則

根據取反的規則，對整數的補碼進行取反運算。

———————————————————————————————————————————

后續會更新針對于二進制數的相關操作符

有表述不當的地方辛苦大家指出，三克油。

打怪升級中................................................................................................................................................