一 算法介紹
????????K近鄰(K-Nearest Neighbors, KNN)是一種基于實例的監督學習算法,適用于分類和回歸任務。其核心思想是通過計算待預測樣本與訓練集中樣本的距離,選取距離最近的K個鄰居,根據這些鄰居的標簽進行投票(分類)或均值計算(回歸)來預測結果。
二 原理
-
距離度量:常用歐氏距離(Euclidean Distance)計算樣本間的相似性,公式為:
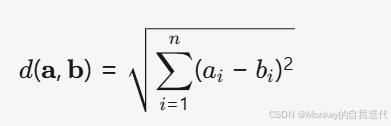
,這里表示a,b兩點間的距離。其他可選距離包括曼哈頓距離、余弦相似度等。 -
K值選擇:K是用戶定義的超參數,影響模型復雜度。較小的K容易過擬合,較大的K可能忽略局部特征。通常通過交叉驗證確定最優K值。
-
決策規則:
- 分類:統計K個鄰居中最多數的類別作為預測結果。
- 回歸:取K個鄰居目標值的平均值作為預測輸出。
三 具象化
根據上面原理我們知道主要是依據距離來判斷的,可能會有點模糊,下面我來舉例說明:
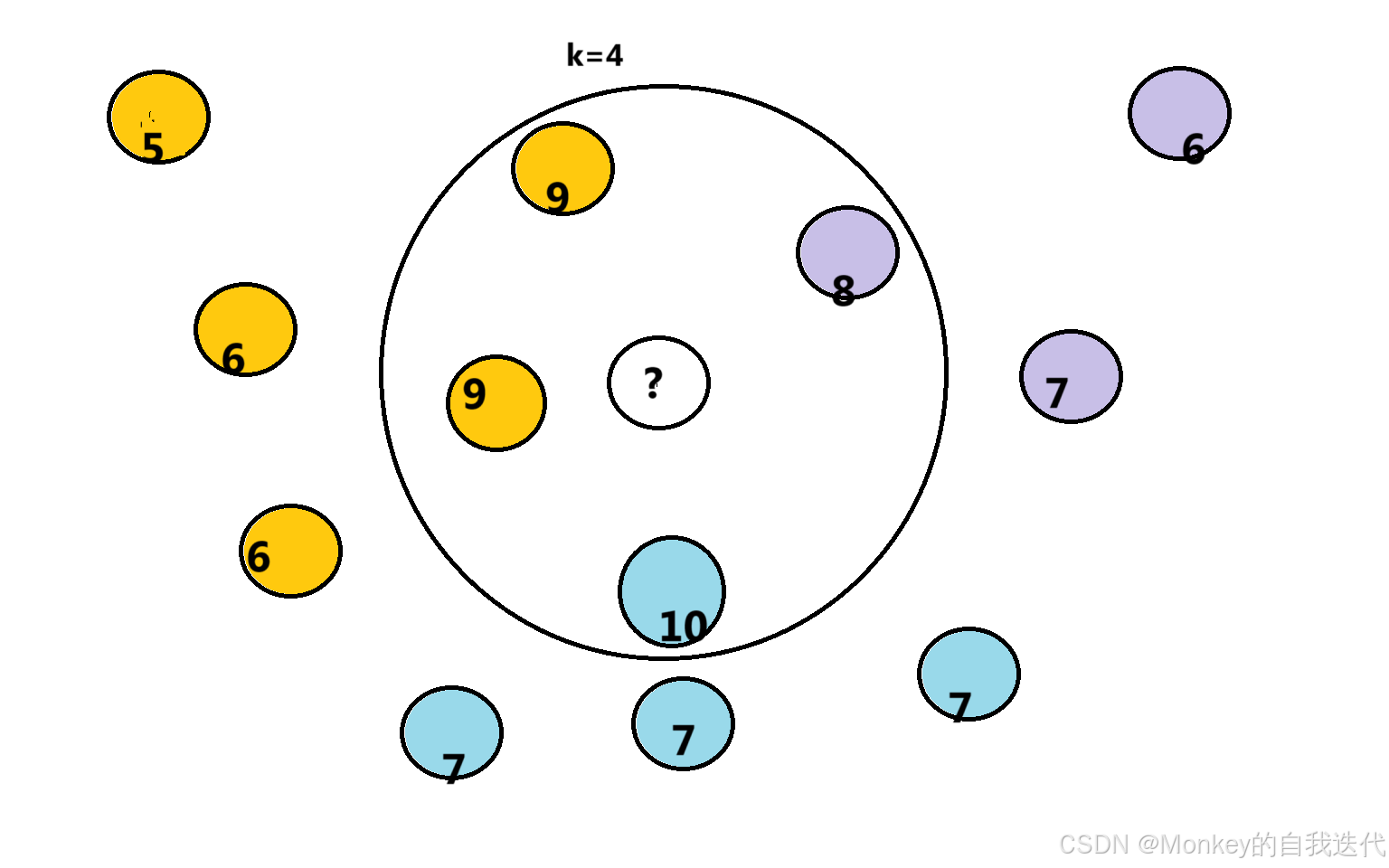
在圖中表示有多個圈圈,每個圈圈都有各自的價格和顏色。
1 分類
????????在這個中,這里我們k=4,意思就是找具體他們最近的四個元素,如何找其中一個顏色最多的那個就把我們這個未知的歸為那一類,這里我們距離是按坐標算的。我們可以想一下,這里每個圈圈的坐標就是它的特征,如果是其他類型的數據,我們也可以用他們的特征之間的差距,去找臨近的一個,如何去分類
2 回歸?
????????這個和上面差不多,在找到最近的幾個,如何依據他們的值,如何去求平均,就可以得到他們的具體值了。
四 代碼實現
1 分類
# 導入庫
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score# 加載數據
iris = load_iris()
X, y = iris.data, iris.target# 劃分訓練集和測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 創建KNN分類器(K=5)
knn_classifier = KNeighborsClassifier(n_neighbors=5)# 訓練模型
knn_classifier.fit(X_train, y_train)# 預測并評估
y_pred = knn_classifier.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"分類準確率: {accuracy:.2f}") # 示例輸出:分類準確率: 0.98[4,11](@ref)- 使用
sklearn.neighbors.KNeighborsClassifier實現分類。 - 通過
n_neighbors參數控制鄰居數量(K值),默認K=5。
2 回歸
# 導入庫
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error# 生成模擬數據
np.random.seed(0)
X = np.sort(5 * np.random.rand(100, 1), axis=0)
y = np.sin(X).ravel() + np.random.normal(0, 0.1, X.shape[0])# 劃分訓練集和測試集
X_train, X_test = X[:80], X[80:]
y_train, y_test = y[:80], y[80:]# 創建KNN回歸器(K=3)
knn_regressor = KNeighborsRegressor(n_neighbors=3, weights='distance')# 訓練模型
knn_regressor.fit(X_train, y_train)# 預測并評估
y_pred = knn_regressor.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print(f"均方誤差(MSE): {mse:.4f}") # 示例輸出:均方誤差(MSE): 0.0123[6,7](@ref)?我們會發現,python的sklearn包封裝的特別好,我們幾乎可以不用了解內部計算過程,只需要他是解決什么問題,有個大致了解就可以使用了。
擴展
我們從sklearn的官網上查看這個,有很多參數,下面我們拓展的講幾項。
KNeighborsClassifier(n_neighbors=5,?*,?weights='uniform',?algorithm='auto',?leaf_size=30,?p=2,?metric='minkowski',?metric_params=無,?n_jobs=無)[來源]
1 weights權重
這個就是,在我們計算的過程中,某些東西可能影響比較大,那么就會對最終結果印象較大。
用于預測的權重函數。可能的值:
-
'uniform' :統一的權重。每個鄰域中的所有點 權重相等。
-
'distance' :按距離的倒數加權點。 在這種情況下,查詢點的更近鄰居將有一個 比距離較遠的鄰居具有更大的影響力。
-
[callable] :一個用戶定義的函數,它接受 距離數組,并返回相同形狀的數組 包含權重。
在統計學中,k-最近鄰算法(k-NN)是一種非參數監督學習方法。它最初由?Evelyn Fix?和?Joseph Hodges?于 1951 年開發,[1]后來由?Thomas Cover?擴展。[2]大多數情況下,它用于分類,作為?k-NN?分類器,其輸出是類成員資格。對象通過其鄰居的多個投票進行分類,該對象被分配給其?k 個最近鄰中最常見的類(k?是正整數,通常很小)。如果?k?= 1,則對象被簡單地分配給該單個最近鄰的類。
k-NN?算法也可以推廣用于回歸。在?k-NN?回歸(也稱為最近鄰平滑)中,輸出是對象的屬性值。該值是?k?個最近鄰值的平均值。如果?k?= 1,則輸出將簡單地分配給該單個最近鄰的值,也稱為最近鄰插值。
對于分類和回歸,一種有用的技術是為鄰居的貢獻分配權重,以便較近的鄰居比遠鄰對平均值的貢獻更大。例如,常見的加權方案包括為每個鄰居提供 1/d?的權重,其中?d?是到鄰居的距離。[3]
輸入由數據集中最接近的?k?個訓練示例組成。 鄰居取自一組對象,其類(用于 k-NN 分類)或對象屬性值(用于?k-NN?回歸)已知。這可以被認為是算法的訓練集,盡管不需要顯式訓練步驟。
k-NN 算法的一個特點(有時甚至是一個缺點)是它對數據的局部結構敏感。 在?k-NN?分類中,函數僅在局部近似,所有計算都推遲到函數評估。由于該算法依賴于距離,如果特征代表不同的物理單位或尺度差異很大,那么對訓練數據進行特征歸一化可以大大提高其準確性。[4]
參數選擇
k?的最佳選擇取決于數據;通常,較大的 k?值會降低噪聲對分類的影響,[8]但使類之間的邊界不那么明顯。可以通過各種啟發式技術選擇一個好的?k(參見超參數優化)。該類被預測為最接近訓練樣本的類(即當?k?= 1 時)的特殊情況稱為最近鄰算法。
k-NN 算法的準確性可能會因存在嘈雜或不相關的特征,或者如果特征尺度與其重要性不一致而嚴重下降。在選擇或縮放特征以改進分類方面投入了大量研究工作。一種特別流行的[需要引用]方法是使用進化算法來優化特征縮放。[9]另一種流行的方法是通過訓練數據與訓練類的互信息來縮放特征。[需要引用]
在二元(兩類)分類問題中,選擇?k?作為奇數是有幫助的,因為這可以避免平局投票。在此設置中選擇經驗最優?k?的一種流行方法是通過引導方法。[10]
?距離計算方法
1.?歐氏距離(Euclidean Distance)
2.?曼哈頓距離(Manhattan Distance)
3.?閔可夫斯基距離(Minkowski Distance)
4.?切比雪夫距離(Chebyshev Distance)
5.?馬氏距離(Mahalanobis Distance)
6.?余弦相似度(Cosine Similarity)
7.?漢明距離(Hamming Distance)
8.?杰卡德距離(Jaccard Distance)
9.?布雷葉距離(Bray-Curtis Distance)
10.?馬氏重合距離(Mahalanobis–Ovchinnikov Distance)









)



)
)
)

)

