前言
這是我數據結構系列的第一篇,其余C語言模擬的數據結構均會在開學之后跟隨老師上課而更新(雖然我已經寫完了),更新這塊主要是因為要由二叉搜索樹講到AVL樹再講到紅黑樹,因為map和set的底層是紅黑樹,就需要知道紅黑樹的原理等等來封裝實現map和set。
二叉搜索樹的部分一定要掌握,avl樹和紅黑樹的基礎就是二叉搜索樹,也更容易理解map和set的特性。
一、什么是二叉搜索樹
binary-search-tree,簡稱BST(不要叫成SBTree),可以是空樹,如果是非空樹,滿足下列規則:
1.如果根結點的左子樹存在,那么左子樹上的所有結點的鍵值都比根節點上的鍵值小。
2.如果根結點的右子樹存在,那么右子樹上的所有結點的鍵值都比根節點上的鍵值大。
3.左右子樹也滿足二叉搜索樹的規則。
二叉搜索樹又稱二叉排序樹,因為它走一個中序遍歷拿到的就是升序。
二、二叉搜索樹的模擬
一些重要的操作
要知道模擬,就需要了解重要的操作了,對于這樣一棵樹,操作當然是增刪查了。不支持改是因為不能單獨動某個點,否則會導致不再是一顆二叉搜索樹,后面的set和map也均不支持改key,后面提到應用會涉及到key-value可以進行value的修改,或者修改可以進行erase這個點 + insert新點來達到類似改的效果(但實際上并不是直接修改)。
我們模擬的增刪查均可以實現遞歸和非遞歸版本,其中遞歸版本不好理解但是代碼量較少,非遞歸版本好理解但是細節問題很多且很容易出錯,代碼量很長。
1.增加 -bool insert(const T& key)
增加相對好寫,因為有這樣的特性在,大致思路就是比當前結點大就往右走,小于就往左走,如果相等直接返回false,走到空進行連接即可。
2.查找- bool find(const T& key)
也比較好寫,和insert的過程類似,就是比當前結點大就往右走,小于就往左走,如果相等直接返回true,走到空返回false。
3.刪除-bool erase(const T& key)
這個是相對麻煩的場景,要考慮的東西很多。
1.先找到要刪的結點,過程和find類似,如果找到了,進行下一步,如果沒找到,直接返回false就可以。
2.找到要刪的結點之后,分為四種情況。
2.1 如果既沒有左孩子也沒有右孩子,直接刪除即可
2.2 如果有左孩子沒有右孩子,父節點與其左孩子節點鏈接即可,考慮情況:
1.父節點為空。
2.父結點的左邊是要刪除結點還是右邊是要刪除結點
2.3 如果有右孩子沒有左孩子,父節點與其右孩子節點鏈接即可,考慮情況:
1.父節點為空。
2.父結點的左邊是要刪除結點還是右邊是要刪除結點。
2.4 如果既有左孩子又有右孩子呢?這時要用替換法,步驟:
1.找左子樹的最大結點或者右子樹的最小結點。
2.將被刪結點的值與其交換。
3.如果左子樹的最大結點有左孩子,轉化為第二種情況,右子樹的最小結點有右孩子。
4.刪除左子樹的最大結點 / 右子樹的最小結點。
這就是刪除的步驟了,注意:一個孩子和沒有孩子的情況可以歸為一類,因為直接指向左邊/右邊就可以,如果有結點就鏈接上了,沒有就鏈接上nullptr也符合。
下圖演示刪除一些結點的過程:

接著就是一些比較簡單的,結點啊啥的,先寫個結點,這里的結點只需要維護左右孩子,可以搞成三叉鏈(還有父親)但是沒必要,會更加麻煩
template<class T>
class BSTreeNode
{
public:BSTreeNode<T>* _left;BSTreeNode<T>* _right;T _key;
public:BSTreeNode(const T& val = T()):_key(val),_left(nullptr), _right(nullptr){}
};
二叉樹:
template<class T>
class BSTree
{typedef BSTreeNode<T> Node;public:BSTree():_root(nullptr){}private:Node* _root;
}
三、非遞歸代碼
非遞歸除了刪除還是比較好寫的。
直接上代碼就行
insert
bool insert(const T& x){if (_root == nullptr){Node* newnode = new Node(x);_root = newnode;return true;}else{//找到位置Node* cur = _root;Node* _parent = nullptr;while (cur != nullptr){if (cur->_key < x){_parent = cur;cur = cur->_right;}else if (cur->_key > x){_parent = cur;cur = cur->_left;}else{cout << "插入失敗" << endl;return false;}}Node* newnode = new Node(x);//鏈接起來if (_parent->_key > x){_parent->_left = newnode;}else{_parent->_right = newnode;}return true;}}
find
bool find(const T& val)
{Node* cur = _root;while (cur){if (cur->_key > val){cur = cur->_left;}else if (cur->_key < val){cur = cur->_right;}else{return true;}}return false;
}
erase
erase像我上面一樣把握住細節就行。
像我上面一步一步思考就行:
首先先找到要刪除結點—
分為三種情況,左為空,右為空,左右都不為空,其中左為空和右為空代碼類似----
左為空,先看父親是不是空,如果父親是空,說明cur是根,改一下根就可以,如果不是空,看父親是左鏈接的cur還是右,將父親和cur的右邊鏈接起來就可以—
右為空情況類似–
看都不為空,要找左子樹的最大結點,也要記錄最大結點的父親,因為還要鏈接,找到最大結點,判斷最大結點的父親是左鏈接還是右,與lmax的左相連即可,因為lmax一定沒有右結點,他是最大,因為最后要刪cur,再把lmax給cur即可。注意:代碼里寫了不可遞歸去刪,因為此時已經不是二叉搜索樹。
完整代碼:
bool erase(const T& val){Node* cur = _root;Node* _parent = nullptr;while (cur != nullptr){if (cur->_key < val){_parent = cur;cur = cur->_right;}else if (cur->_key > val){_parent = cur;cur = cur->_left;}else{if (cur->_left == nullptr){if (_parent == nullptr){_root = cur->_right;}else{if (_parent->_left == cur){_parent->_left = cur->_right;}else{_parent->_right = cur->_right;}}}else if (cur->_right == nullptr){if (_parent == nullptr){_root = cur->_left;}else{if (_parent->_left == cur){_parent->_left = cur->_left;}else{_parent->_right = cur->_left;}}}else{//左邊樹的最大結點Node* lmaxp = cur;Node* lmax = cur->_left;while (lmax->_right){lmaxp = lmax;lmax = lmax->_right;}//lmax為最大結點swap(lmax->_key, cur->_key);//這里不能遞歸去刪,因為此時已經不是搜索二叉樹,比如要刪的結點是8,swap的結點是7,//去遞歸找8,最開始就會去右邊發現找不到,所以不能遞歸if (lmaxp->_left == lmax){lmaxp->_left = lmax->_left;}else{lmaxp->_right = lmax->_left;}cur = lmax;}delete cur;return true;}}return false;}
正確性
驗證正不正確,首先先嘗試插入和走一個中序遍歷,這沒問題就去檢查find,find沒問題,就去erase,如果程序不會崩潰一般是沒問題,建議把所有結點從上往下刪并且每次中序跑一遍,這樣都沒問題基本就沒問題了。
四、遞歸代碼
循環一般都是可以改遞歸的,有遞歸和非遞歸還是優先寫非遞歸,因為遞歸畢竟要建立一層一層的棧幀。
遞歸最簡單的就是find了,輕輕松松寫下來
因為樹里的遞歸一般都需要拿結點來玩,而外面無法傳根節點,所以需要寫一個子函數把根節點傳過去即可。
冷知識:遞歸單詞是recursion
find:
bool _find(const T& val, Node* node)
{if (node == nullptr) return false;if (node->_val > val) return _find(val, node->_left);else if (node->_val < val) return _find(val, node->_right);else return true;
}bool find(const T& val)
{return _find(val, _root);
}
insert
insert的遞歸還是很牛的,先看代碼再解釋。
bool insert(const T& x)
{return _insert(x, _root);
}
bool _insert(const T& val, Node*& node)
{if (node == nullptr){node = new Node(val);return true;}if (val < node->_val) return _insert(val, node->_left);else if (val > node->_val) return _insert(val, node->_right);else return false;
}
這里一個引用直接無敵,這里一層一層取別名只有走到空的時候起了作用,通過引用傳遞來修改上層的指針,比如到最后一層的左邊,node是node->_left的別名,node走到nullptr,搞了一個結點,相當于node->_left = new Node(val);不僅不用額外搞父節點,代碼也簡潔很多。
不用引用的遞歸–非常不推薦
bool _insert(const T& val, Node* node, Node* parent)
{if (_root == nullptr){_root = new Node(val);return true;}if (node == nullptr){Node* newnode = new Node(val);if (parent->_val > val){parent->_left = newnode;}else{parent->_right = newnode;}return true;}if (node->_val > val){return _insert(val, node->_left, node);}else if (node->_val < val){return _insert(val, node->_right, node);}else{return false;}
}
erase
同樣使用遞歸,先看代碼再解釋,其實能搞明白insert還是很好寫的
bool erase(const T& val)
{return _erase(val, _root);
}
bool _erase(const T& val, Node* & node)
{if (node == nullptr) return false;if (node->_val < val) return _erase(val, node->_right);else if (node->_val > val) return _erase(val, node->_left);else{Node* del = node;if (node->_left == nullptr) {node = node->_right;}else if (node->_right == nullptr) {node = node->_left;}else {Node* lmax = node->_left;while (lmax->_right) lmax = lmax->_right;swap(lmax->_val, node->_val);return _erase(val,node->_left);}delete del;return true;}
}
前面都是正常邏輯,主要看else里的,簡單畫個圖理解

并且這個可以最后交換完遞歸去刪,為什么?為什么非遞歸不能遞歸去刪?
來看:
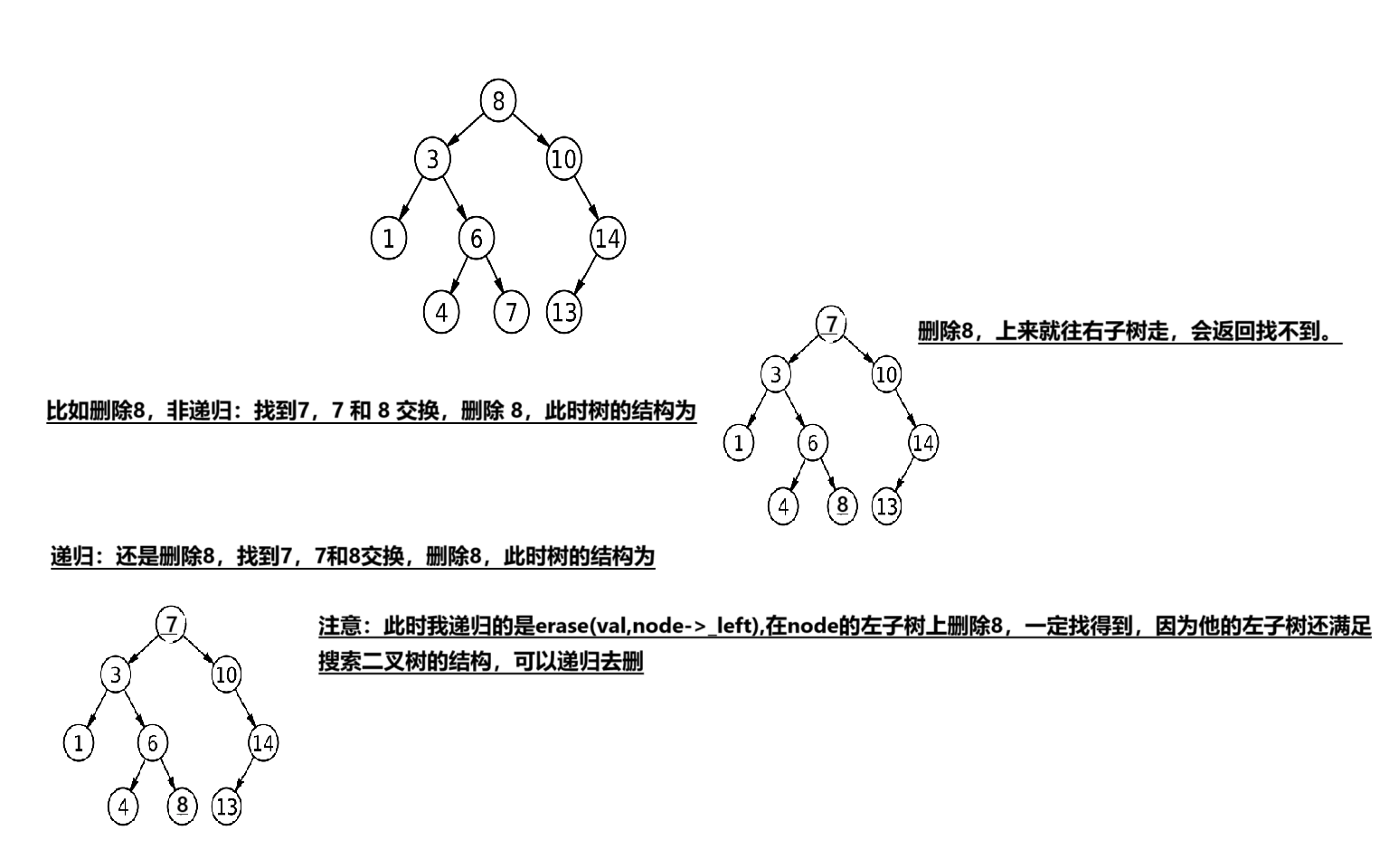
所以遞歸寫起來還是很爽的。
五、完善代碼
1.拷貝構造
這里當然不能淺拷貝,需要拷貝出一顆樹,返回根結點,所以需要再寫一個函數,按結點拷貝就可以。走一個前序比較舒服,因為中序和后序代碼還得多寫兩句,析構也是后序來析構。
BSTree(const BSTree<T>& t)
{t._root = Copy(_root);
}
Node* Copy(Node* node)
{if (node == nullptr) return nullptr;Node* newnode = new Node(node->_key,node->_val);newnode->_left = Copy(node->_left);newnode->_right = Copy(node->_right);return newnode;
}
2.賦值運算符重載
有了拷貝構造直接現代寫法
BSTree<T>& operator=(BSTree<T>&& t)
{swap(_root, t._root);return *this;
}
BSTree<T>& operator=(const BSTree<T>& t)
{BSTreeT> tmp(t);swap(tmp._root, _root);return *this;
}
3.析構函數
同樣也需要一個額外的函數,后序來刪除,也比較簡單
~BSTree()
{Destroy(_root);
}
void Destroy(Node*& node)
{if (node == nullptr) return;Destroy(node->_left);Destroy(node->_right);delete node;node = nullptr;
}
六、應用
1.K模型:K模型即只有key作為關鍵碼,結構中只需要存儲Key即可,關鍵碼即為需要搜索到的值。
比如:給一個單詞word,判斷該單詞是否拼寫正確,具體方式如下:
以詞庫中所有單詞集合中的每個單詞作為key,構建一棵二叉搜索樹
在二叉搜索樹中檢索該單詞是否存在,存在則拼寫正確,不存在則拼寫錯誤。
2. KV模型:每一個關鍵碼key,都有與之對應的值Value,即<Key, Value>的鍵值對。該種方式在現實生活中非常常見:
比如英漢詞典就是英文與中文的對應關系,通過英文可以快速找到與其對應的中文,英文單詞與其對應的中文<word, chinese>就構成一種鍵值對;
再比如統計單詞次數,統計成功后,給定單詞就可快速找到其出現的次數,單詞與其出現次數就是<word, count>就構成一種鍵值對。
set是key模型,map是KV模型,學到底層會發現set也使用的key-value模型。
將搜索二叉樹改為key和key-value模型,其實很簡單,key模型就是模板參數是key,key-value模型模板參數就是K,V,然后插入的是pair<K,V> p;結點里存儲的也是KV結構。
這里就不放代碼了,比較簡單,完整代碼在:
個人gitee
七、時間復雜度和缺陷
插入的時間復雜度是多少,高度次,不是logN,最優情況下logN,滿二叉樹的情況下,最壞情況O(N),退化成一條鏈,比如:
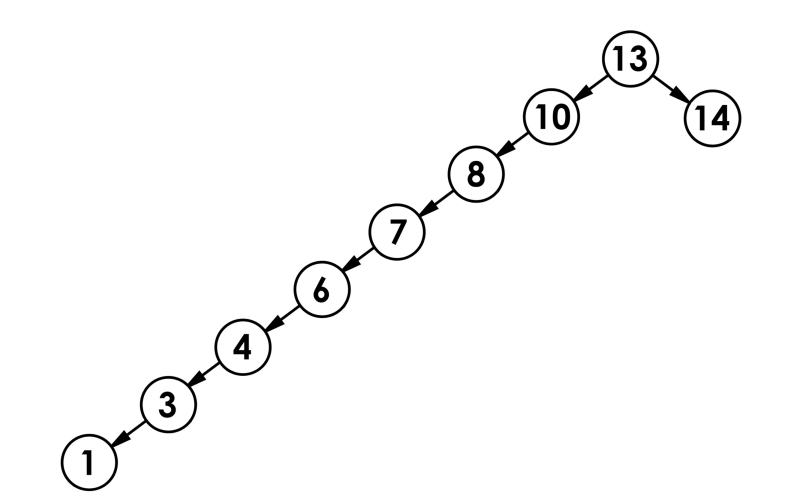
這個的性能就非常差了,所以后面要引入AVL和紅黑樹,AVL樹通過平衡因子來控制,紅黑樹通過規則來控制。
總結
這個還是建議要掌握牢的,因為后面的學習建立在這個的基礎上。


![[3-02-02].第04節:開發應用 - RequestMapping注解的屬性2](http://pic.xiahunao.cn/[3-02-02].第04節:開發應用 - RequestMapping注解的屬性2)







)



- 數據結構】緒論)
-day25)



)