Python機器學習：從零基礎到項目實戰

5.1 邏輯回歸：看似回歸，實為分類的智慧
5.2 K-近鄰（KNN）：“物以類聚，人以群分”的樸素哲學
5.3 支撐向量機（SVM）：“一劃開天”的數學之美
5.4 決策樹與隨機森林：“集思廣益”的集成智慧
5.5 樸素貝葉斯：“執果索因”的概率思維

第6章：監督學習之“預測”——回歸算法

6.1 線性回歸：從簡單到多元，探尋變量間的線性關系
6.2 嶺回歸與Lasso回歸：正則化下的“中庸之道”
6.3 多項式回歸：用曲線擬合復雜世界
6.4 回歸樹與集成回歸模型（例如 GBDT, XGBoost）

第7章：無監督學習之“歸納”——聚類與降維

7.1 K-均值聚類（K-Means）：尋找數據中的“引力中心”
7.2 層次聚類：構建數據的“家族譜系”
7.3 DBSCAN：基于密度的“社區發現”
7.4 主成分分析（PCA）：在紛繁中見本質的降維之道

第8章：集成學習——從“三個臭皮匠”到“諸葛亮”

8.1 Bagging思想：隨機森林的再思考
8.2 Boosting思想：從AdaBoost到梯度提升樹（GBDT）
8.3 Stacking/Blending：模型的“圓桌會議”
8.4 XGBoost與LightGBM：工業界的“大殺器”詳解

第9章：神經網絡入門——通往深度學習的橋梁

9.1 從生物神經元到感知機模型
9.2 多層感知機（MLP）與反向傳播算法
9.3 激活函數：為神經網絡注入“靈魂”
9.4 使用Scikit-Learn與Keras/TensorFlow構建你的第一個神經網絡

第三部分：登堂入室——高級專題與實戰演練

第10章：實戰項目一：金融風控——信用卡欺詐檢測

10.1 問題定義與數據探索：理解不平衡數據
10.2 特征工程與采樣技術（SMOTE）
10.3 模型選擇、訓練與評估
10.4 解釋性分析：模型為何做出這樣的決策？ (SHAP/LIME)

第11章：實戰項目二：自然語言處理——文本情感分析

11.1 文本數據的預處理：分詞、停用詞與向量化（TF-IDF, Word2Vec）
11.2 從傳統模型到簡單神經網絡的情感分類
11.3 主題模型（LDA）：挖掘文本背后的隱藏主題

第12章：模型部署與工程化——讓模型“活”起來

12.1 模型持久化：序列化與保存
12.2 使用Flask/FastAPI構建API服務
12.3 Docker容器化：為模型打造一個“家”
12.4 MLOps初探：自動化、監控與再訓練

第13章：超越經典——未來展望與進階路徑

13.1 深度學習概覽：CNN、RNN的世界
13.2 強化學習：與環境交互的智能體
13.3 圖神經網絡、聯邦學習等前沿簡介
13.4 “知行合一”：如何持續學習與成長

附錄

A. 數學基礎回顧（線性代數、微積分、概率論核心概念）
B. 常用工具與庫速查手冊
C. 術語表（中英對照）
D. 推薦閱讀與資源列表

第一部分：思想與基石——萬法歸宗，筑基問道

核心目標： 建立學習者的宏觀認知，不僅知其然，更要知其所以然。將機器學習置于科學、哲學乃至東方智慧的廣闊背景下，培養學習者的“數據直覺”與“模型思維”。

第一章：初探智慧之境——機器學習世界觀

1.1 何為學習？從人類學習到機器智能
1.2 機器學習的“前世今生”：一部思想與技術的演進史
1.3 為何是Python？——數據科學的“通用語”
1.4 破除迷思：AI是“神”還是“器”？

歡迎您，未來的數據探索者。在您正式踏入這個由數據、算法與代碼構成的迷人世界之前，我們希望與您一同稍作停留，登高望遠。本章并非一本技術手冊的常規開篇，它不急于展示紛繁的代碼或深奧的公式。相反，它是一張地圖，一幅星圖，旨在為您建立一個宏大的時空坐標，讓您清晰地看到“機器學習”這片新大陸在人類智慧版圖中的位置。

我們將從最本源的問題開始：何為“學習”？我們將借助嬰兒認知世界的過程，以及自然界演化的宏偉篇章，來類比機器學習的三種基本范式。隨后，我們將穿越時空，回顧這段波瀾壯闊的技術思想史，從圖靈的深邃構想，到今日深度學習的璀璨成就，并向那些推動時代前行的巨匠們致敬。我們還將探討為何Python能夠成為這門“新學問”的通用語言，并深入其設計哲學與強大的生態系統。

最后，也是至關重要的一點，我們將共同思辨：人工智能究竟是無所不能的“神”，還是我們手中強大的“器”？我們將直面其能力邊界與深刻的倫理挑戰，并提出一種“以出世之心，做入世之事”的從業心法。

這不僅是知識的鋪陳，更是一場思想的洗禮。當您建立起這樣的世界觀后，未來學習道路上的每一個技術細節，都將不再是孤立的碎片，而是這幅宏大畫卷中和諧的一部分。

現在，讓我們一同啟程！

1.1 何為學習？從人類學習到機器智能

“學習”一詞，于我們而言再熟悉不過。從呱呱墜地到白發蒼蒼，我們的一生便是學習的一生。我們學習語言、學習騎車、學習一門手藝、學習與人相處。但我們是否曾靜心深思，這個過程的本質是什么？

從信息論的角度看，學習是一個系統（如人類大腦）通過與環境的交互，獲取信息并優化自身內部模型，以期在未來更好地完成特定任務或適應環境的過程。 這個定義中包含幾個關鍵要素：系統、環境、交互、信息、模型優化、未來任務。這恰恰構成了機器學習的核心框架。機器，作為我們創造的“系統”，通過我們提供的“數據”（源于環境的信息），進行“訓練”（交互與模型優化），最終目的是為了在新的、未見過的數據上做出精準的“預測”或“決策”（完成未來任務）。

因此，理解機器學習的最佳途徑，便是回溯我們自身最熟悉、最本源的學習過程。

1.1.1 嬰兒如何認識世界？——類比監督、無監督、強化學習

想象一個嬰兒，她/他認識世界的過程，正是機器學習三大范式最生動、最本源的體現。

1. 監督學習（Supervised Learning）：有“標簽”的教導

當父母指著一個紅色的、圓圓的物體，對嬰兒說：“寶寶，這是‘蘋果’。”然后又指著一個黃色的、彎彎的物體說：“這是‘香蕉’。”這個過程在不斷重復。每一次，嬰兒都接收到兩樣東西：一個感官輸入（物體的形狀、顏色、氣味）和一個明確的標簽（它的名字叫“蘋果”）。

感官輸入，在機器學習中被稱為“特征（Features）”。
明確的標簽，被稱為“標簽（Label）”或“目標（Target）”。

嬰兒的大腦在做什么？它在努力尋找“特征”與“標簽”之間的關聯。它會逐漸歸納出：“哦，紅色的、圓形的、有特定香味的，很可能就是‘蘋果’。”當父母下次拿出一個新的、她從未見過的蘋果時，她能夠根據已經建立的內部模型，正確地識別出：“蘋果！”

這就是監督學習的本質。我們為機器提供一大批已經“標注好”的數據（例如，一堆郵件，每封都標好了“是垃圾郵件”或“不是垃圾郵件”；一堆房產數據，每套都標好了“最終成交價格”），然后讓算法去尋找特征和標簽之間的映射關系。算法學成之后，我們給它一封新的郵件，它就能判斷是否為垃圾郵件；給它一套新的房產特征，它就能預測其可能的價格。

監督學習的核心在于“有答案的輸入”。 它主要解決兩類問題：
分類（Classification）：預測一個離散的標簽。例如，判斷圖片是貓還是狗，判斷郵件是否為垃圾郵件。嬰兒認識水果，就是一個分類任務。
回歸（Regression）：預測一個連續的數值。例如，預測明天的氣溫，預測房屋的價格。

2. 無監督學習（Unsupervised Learning）：無言的探索

現在，想象一下，沒有人明確告訴嬰兒每樣東西的名字。桌上放著一堆玩具：一些是積木（方的、硬的、彩色的），一些是毛絨娃娃（軟的、形狀不規則的），還有一些是塑料小球（圓的、光滑的）。

嬰兒會做什么？她會自己去探索。她會發現，這些東西可以分成幾堆。她可能會把所有硬邦邦、有棱有角的東西放在一起，把所有軟綿綿的東西放在另一邊，把所有能滾來滾去的東西歸為一類。她并不知道這些類別叫“積木”、“娃娃”或“球”，但她通過觀察物體自身的特性，自發地完成了“聚類（Clustering）”。

這就是無監督學習的精髓。我們只給機器一堆數據，沒有任何標簽，然后讓算法自己去發現數據中隱藏的結構、模式或關系。

無監督學習的核心在于“發現內在結構”。 它的典型應用包括：
聚類（Clustering）：將相似的數據點分組。例如，根據用戶的購買行為，將他們劃分為不同的客戶群體，以便進行精準營銷。
降維（Dimensionality Reduction）：在保留大部分信息的前提下，減少數據的特征數量。好比我們描述一個人，與其羅列上百個細節，不如抓住“高、瘦、戴眼鏡”這幾個核心特征，這便是降維的思想。
關聯規則挖掘（Association Rule Mining）：發現數據項之間的有趣關系。經典的“啤酒與尿布”的故事，就是通過挖掘購物籃數據發現，購買尿布的顧客很可能同時購買啤酒。

3. 強化學習（Reinforcement Learning）：試錯與獎懲

再來看嬰兒學習走路的過程。這個過程沒有人能給她一個明確的“標簽”。沒有一個“正確”的姿勢可以一步到位地教會她。

她只能自己嘗試。她試著晃晃悠悠地站起來，邁出一步，然后“啪”地摔倒了。這次嘗試的結果是“摔倒”，這是一個負向的反饋（懲罰）。她的大腦接收到這個信號：“剛才那樣做，結果不好。” 于是，她下次會微調自己的策略，可能身體更前傾一點，或者腿邁得小一點。某一次，她成功地走了兩步而沒有摔倒，內心充滿了喜悅和成就感。這是一個正向的反饋（獎勵）。她的大腦會記住：“這樣做，結果是好的！”

通過無數次的“嘗試-反饋-調整策略”循環，她最終學會了如何平穩地行走。在這個過程中，她不是被動地接收知識，而是作為一個意識體/智能體，在與環境的互動中，通過試錯，來學習一套能讓自己獲得最大累積獎勵的策略。

這就是強化學習。它與監督學習的關鍵區別在于，反饋信號不是一個正確的“標簽”，而是一個評價性的“獎勵”或“懲罰”信號，并且這個信號往往是延遲的（摔倒是邁出那一步之后的結果）。

強化學習的核心在于“通過與環境交互學習最優策略”。 它的應用場景極具魅力：
游戲AI：AlphaGo擊敗人類頂尖棋手，其核心就是強化學習。它通過自我對弈，不斷探索能贏得棋局的策略。
機器人控制：控制機械臂抓取物體，讓無人機自主飛行。
資源調度：優化數據中心的能源消耗，智能調度城市交通信號燈。

小結：三種學習范式的關系

學習范式	數據形式	學習目標	核心思想	人類類比
監督學習	(特征, 標簽)	學習從特征到標簽的映射	有師指導，模仿范例	父母教嬰兒識物
無監督學習	只有特征	發現數據內在的結構與模式	無師自通，歸納總結	嬰兒自己給玩具分類
強化學習	(狀態, 動作, 獎勵)	學習在環境中最大化獎勵的策略	實踐出真知，趨利避害	嬰兒學走路

這三種范式并非涇渭分明，現實世界的問題往往需要融合多種思想。例如，半監督學習（Semi-supervised Learning）就結合了監督和無監督學習，利用少量有標簽數據和大量無標簽數據進行學習。但理解這三大支柱，是理解整個機器學習大廈的基石。

1.1.2 道法自然：從自然界的演化看學習的本質

如果說嬰兒學步是“個體學習”的縮影，那么地球生命長達數十億年的演化史，則是“群體學習”最宏偉、最深刻的篇章。《道德經》有云：“人法地，地法天，天法道，道法自然。” 機器學習的許多深刻思想，尤其是那些被稱為“遺傳算法”、“進化策略”的分支，其靈感正是源于對自然演化這一“終極學習過程”的模擬。

1. 適應度函數（Fitness Function）：環境的選擇壓力

在自然界，不存在一個絕對的“最優”生物。在冰河世紀，長毛象的厚皮毛是巨大的生存優勢；而當氣候變暖，這身皮毛反而成了累贅。環境，就是那個最終的“裁判”，它通過生存和繁衍的壓力，來“評估”每一個生物體對其的適應程度。這種適應程度，在進化計算中被稱為適應度（Fitness）。一個物種能否將基因傳遞下去，取決于其適應度的高低。

這與機器學習中的損失函數（Loss Function）或目標函數（Objective Function）異曲同工。我們定義一個函數來評估我們的模型“好不好”。例如，在預測房價時，損失函數可能就是“預測價與真實價的差距”，差距越小，模型的“適應度”就越高。整個模型訓練的過程，就是不斷調整參數，以期在損失函數上取得最優值的過程，正如生物演化是在環境的適應度函數下，不斷“優化”自身基因的過程。

2. 遺傳與變異（Inheritance and Mutation）：探索與利用的平衡

演化有兩個核心驅動力：

遺傳（Inheritance）：父母的優秀性狀（高適應度的基因）通過繁殖傳遞給后代。這保證了已經獲得的成功經驗不會輕易丟失。在機器學習中，這類似于一種“利用（Exploitation）”策略——我們傾向于在當前已知效果好的模型參數附近進行微調，希望能獲得更好的結果。
變異（Mutation）：基因在復制過程中會發生隨機的、微小的錯誤，即基因突變。絕大多數突變是有害或無意義的，但極少數突變可能會帶來意想不到的生存優勢（例如，某種蛾子產生了更接近樹皮的保護色）。這種不確定性，為物種提供了跳出局部最優、適應全新環境的可能性。這正是一種“探索（Exploration）”策略。

機器學習算法，尤其是強化學習和優化算法，也必須精妙地平衡“利用”與“探索”。如果一個算法只懂得“利用”，它可能會很快陷入一個“局部最優解”（比如一個只會在家附近找食物的原始人，他可能永遠發現不了遠處食物更豐富的山谷）。如果一個算法只懂得“探索”，它將永遠在隨機嘗試，無法收斂到一個有效的解決方案。遺傳算法通過模擬交叉、變異等操作，在解空間中進行高效的探索和利用，尋找問題的最優解。

3. 物競天擇（Natural Selection）：迭代優化的過程

“物競天擇，適者生存。”這八個字精準地描述了演化的核心機制。每一代生物中，適應環境的個體有更大的概率存活下來并繁殖后代，不適應的個體則被淘汰。經過一代又一代的篩選，整個種群的基因庫會朝著越來越適應環境的方向“進化”。

這不就是機器學習中迭代優化（Iterative Optimization）的過程嗎？以梯度下降算法為例，我們從一組隨機的初始參數開始，計算當前參數下的“損失”（不適應度），然后沿著能讓損失下降最快的方向（梯度方向）微調參數。然后，在新的參數位置上，重復這個過程。一步一步，一次一次迭代，模型參數就像生物種群的基因一樣，被不斷“選擇”和“優化”，最終達到一個損失極小（適應度極高）的狀態。

因此，當我們思考機器學習時，不妨將視野拉遠。我們所做的，無非是借鑒了宇宙間最古老、最強大的學習法則——演化。我們創造的算法，是我們對“道法自然”的一次次笨拙而又充滿敬意的模仿。理解了這一點，我們便能以更謙卑、更宏大的視角，看待我們即將學習的每一個模型和技術。

1.2 機器學習的“前世今生”：一部思想與技術的演進史

任何一門學科的誕生，都不是一蹴而就的，它必然是思想的河流長期沖刷、積淀的結果。機器學習的發展史，更是一部交織著數學、計算機科學、神經科學、哲學乃至運籌學等多個領域的英雄史詩。了解這段歷史，能讓我們明白今日的技術從何而來，為何如此，以及未來可能走向何方。

1.2.1 從圖靈的構想到今天的深度學習：關鍵里程碑

這段歷史猶如一條奔騰的河流，有涓涓細流的源頭，有波瀾壯闊的轉折，也有過冰封潛行的低谷。

源頭與古典時期（20世紀40-60年代）：思想的播種

1943年，麥卡洛克-皮茨神經元（MCP Neuron）：神經生理學家沃倫·麥卡洛克和邏輯學家沃爾特·皮茨，首次提出了一個形式化的神經元數學模型。它接收多個二進制輸入，通過一個閾值函數，產生一個二進制輸出。這雖然是一個極其簡化的模型，但它第一次從計算的角度，建立了連接生物大腦與機器智能的橋梁。它是神經網絡大廈的第一塊磚。
1950年，圖靈測試與《計算機器與智能》：艾倫·圖靈，這位計算機科學的奠基人，在他劃時代的論文中，沒有直接定義“機器能否思考”，而是提出了一個可操作的測試——“模仿游戲”，即后人所稱的“圖靈測試”。他將焦點從哲學的思辨轉向了行為的判斷，并預言了“學習機器”的可能性。這篇文章，是人工智能領域的思想“開山之作”。
1952年，亞瑟·薩繆爾的跳棋程序：IBM的工程師亞瑟·薩繆爾編寫了一個可以學習下西洋跳棋的程序。這個程序可以通過自我對弈來提升棋力，其水平最終甚至超過了薩繆爾本人。這是機器學習的第一個廣為人知的成功案例，它生動地展示了“讓計算機自己學習”是可行的。薩繆爾也是第一個提出并普及“Machine Learning”這個詞的人。
1957年，感知機（Perceptron）：弗蘭克·羅森布拉特基于MCP模型，提出了“感知機”。與MCP不同，感知機模型的權重參數是可以通過學習算法自動調整的。他甚至制造了硬件“Mark I Perceptron”，用于圖像識別。這引發了第一次AI熱潮，人們對“會思考的機器”充滿了樂觀的幻想。

第一次AI寒冬（20世紀70-80年代）：理性的沉淀

1969年，《感知機》一書的沖擊：AI領域的兩位領軍人物馬文·明斯基和西摩爾·派普特，出版了《感知機》一書。書中通過嚴謹的數學證明，指出了單層感知機無法解決“異或（XOR）”這類線性不可分問題。這一結論雖然是針對單層結構的，但在當時被許多人誤讀為整個神經網絡方法的根本性缺陷。這本著作如一盆冷水，澆滅了當時過于狂熱的期望，直接導致了神經網絡研究的資金被大量削減，AI進入了第一個“冬天”。
寒冬中的火種：盡管神經網絡研究進入低谷，但其他機器學習流派仍在悄然發展。決策樹算法（如ID3）、專家系統等符號主義AI方法在這一時期取得了重要進展。寒冬并未熄滅所有火種，反而促使研究者們進行更深刻的理性和基礎性思考。

復興與連接主義的回歸（20世紀80年代末-90年代）：柳暗花明

1986年，反向傳播算法（Backpropagation）的重新發現：雖然反向傳播的思想早已存在，但由戴維·魯姆哈特、杰弗里·辛頓和羅納德·威廉姆斯等人的工作，使其得到了廣泛傳播和應用。該算法有效地解決了多層神經網絡的權重訓練問題，攻克了《感知機》一書中提出的核心難題，讓神經網絡研究重獲新生。
20世紀90年代，統計學習的崛起：在神經網絡復興的同時，另一股強大的力量正在形成。以弗拉基米爾·瓦普尼克等人提出的支撐向量機（SVM）為代表的，基于嚴格統計學習理論（VC維理論）的方法論開始大放異彩。SVM以其優美的數學理論、出色的泛化能力和高效的凸優化求解，在許多中小型數據集的分類和回歸任務上，其表現常常優于當時的神經網絡。同時期，決策樹的集成方法，如隨機森林（Random Forest）和梯度提升機（Gradient Boosting Machine）也開始嶄露頭角。這個時代，是“統計機器學習”的黃金時代，各種精巧的淺層模型百花齊放。

第二次AI寒冬（2000年前后）：瓶頸與醞釀

進入21世紀初，盡管機器學習在特定領域應用廣泛，但其發展似乎又遇到了瓶頸。當時的神經網絡雖然理論上可以很深，但實際訓練中面臨著梯度消失/爆炸等問題，導致深層網絡的訓練極為困難。而SVM等模型雖然理論優美，但在處理如圖像、語音這類擁有海量、高維原始特征的任務時，顯得力不從心。整個領域似乎在等待一次新的突破。

深度學習革命（2006年至今）：王者歸來

2006年，深度信念網絡與逐層預訓練：杰弗里·辛頓等人提出了“深度信念網絡（DBN）”，并開創性地使用了“無監督逐層預訓練+有監督微調”的方法。這種方法像搭積木一樣，先讓網絡的每一層自己進行無監督學習，理解數據的基本特征，然后再用有標簽的數據對整個網絡進行精調。這巧妙地緩解了深度網絡訓練的困難，為“深度學習”一詞的誕生拉開了序幕。
2012年，AlexNet在ImageNet競賽中取得歷史性突破：由辛頓的學生亞歷克斯·克里熱夫斯基設計的深度卷積神經網絡AlexNet，在當年的ImageNet大規模視覺識別挑戰賽（ILSVRC）中，以遠超第二名（基于傳統方法）的驚人準確率奪冠。這一事件的沖擊力，不亞于深藍計算機戰勝卡斯帕羅夫。它無可辯駁地證明了，在處理復雜模式識別任務時，深度學習（特別是卷積神經網絡CNN）的強大威力。這一勝利，點燃了延續至今的深度學習革命之火。
至今：黃金時代：自2012年以來，我們見證了技術的爆炸式發展。從用于序列數據的循環神經網絡（RNN）及其變體LSTM，到解決其長程依賴問題的Transformer架構；從生成以假亂真圖像的生成對抗網絡（GAN），到驅動AlphaGo和ChatGPT的深度強化學習與大規模預訓練語言模型。深度學習不僅統一了人工智能的諸多領域，更以前所未有的深度和廣度，滲透到我們生活的方方面面。

這段歷史告訴我們，科學的發展從不是一條直線。它充滿了螺旋式的上升和周期性的起伏。思想的火花可能需要數十年的沉寂才能燎原，而看似不可逾越的瓶頸，也終將被新的智慧所突破。

1.2.2 群星閃耀時：那些塑造了AI紀元的大師們

技術史的宏大敘事，最終是由一個個鮮活的人來書寫的。在AI的殿堂里，有幾位巨匠的名字，我們必須銘記。他們的思想與貢獻，如北極星般指引著整個領域的前行。

艾倫·圖靈（Alan Turing）：如前所述，他是計算機科學與人工智能的“思想教父”。他提出的圖靈機模型定義了“可計算”的邊界，而圖靈測試則開啟了“機器智能”的哲學與實踐探索。
杰弗里·辛頓（Geoffrey Hinton）：被譽為“深度學習之父”之一。從80年代共同推廣反向傳播算法，到21世紀初用深度信念網絡開啟深度學習革命，再到培養出AlexNet的作者等一眾英才，辛頓以其數十年的堅持和洞察力，將神經網絡從寒冬帶入了盛夏。他因在深度學習領域的開創性貢獻，與另外兩位學者共同獲得了2018年的圖靈獎。
楊立昆（Yann LeCun）：另一位2018年圖靈獎得主，卷積神經網絡（CNN）的締造者。早在上世紀90年代，他就開發了LeNet-5，成功應用于銀行的支票手寫數字識別。CNN架構模擬了生物的視覺皮層機制，其“局部連接”和“權值共享”的設計，對于處理圖像等網格狀數據具有天然的優勢，是當今計算機視覺領域的基石。
約書亞·本吉奧（Yoshua Bengio）：2018年圖靈獎的第三位得主。他在深度學習的多個領域都做出了奠基性貢獻，尤其是在語言模型、注意力機制等方面。他與團隊的工作，為后來Transformer架構的誕生和自然語言處理的革命性突破鋪平了道路。同時，他也是一位極具人文關懷的科學家，持續關注AI的社會影響與倫理問題。

這三位學者常被并稱為“深度學習三巨頭”，他們的合作與良性競爭，共同塑造了我們今天所知的深度學習版圖。

弗拉基米爾·瓦普尼克（Vladimir Vapnik）：統計學習理論的巨擘，支撐向量機（SVM）的發明人。他的工作為機器學習提供了堅實的理論基礎（VC維理論），強調了控制模型復雜度、追求泛化能力的重要性。在深度學習浪潮之前，SVM是學術界和工業界最受推崇的監督學習算法之一。他的思想提醒我們，即使在經驗主義大行其道的今天，深刻的數學理論依然是指引我們前行的燈塔。

當然，群星閃耀，遠不止于此。從“人工智能”一詞的提出者約翰·麥卡錫，到決策樹算法的先驅羅斯·昆蘭，再到強化學習領域的泰斗理查德·薩頓……正是這一代代研究者的智慧接力，才匯聚成了今日人工智能的滔滔江河。向他們致敬的最好方式，就是站在他們的肩膀上，繼續探索這片智慧的星辰大海。

1.3 為何是Python？——數據科學的“通用語”

在開啟具體的編程學習之前，一個自然的問題是：為什么是Python？在眾多編程語言中，為何Python能夠脫穎而出，成為機器學習和數據科學領域事實上的“標準語言”？這并非偶然，而是其內在哲學與外在生態共同作用的結果。

1.3.1 Python的哲學：“禪”與“道”

任何一門成功的語言，背后都有一種獨特的設計哲學。Python的哲學，被精煉地總結在“Python之禪（The Zen of Python）”中。你可以在任何安裝了Python的環境中，通過在解釋器里輸入import this來一睹其真容。其中幾條，與數據科學的精神內核不謀而合：

優美勝于丑陋（Beautiful is better than ugly.）
明了勝于晦澀（Explicit is better than implicit.）
簡單勝于復雜（Simple is better than complex.）
可讀性很重要（Readability counts.）

這不僅僅是編程美學，更是科學研究的方法論。機器學習項目往往不是一次性的“代碼沖鋒”，而是一個需要反復實驗、迭代、驗證和與他人協作的探索過程。

可讀性與簡潔性：Python的語法非常接近自然語言，這使得代碼的閱讀和編寫都變得異常輕松。對于科學家、分析師這些可能并非計算機科班出身的使用者來說，學習曲線極為平緩。他們可以將更多的精力聚焦于問題本身和算法思想，而不是糾結于繁瑣的語法細節（如C++的指針或Java的樣板代碼）。一段Python代碼，往往更像是在描述解決問題的“偽代碼”，這使得團隊協作和知識分享變得極為高效。
“膠水語言”的特質：Python被譽為“膠水語言”，因為它能輕易地將其他語言（特別是C/C++）編寫的高性能模塊“粘合”在一起。機器學習的核心計算，如圖形處理、大規模矩陣運算，對性能要求極高。這些計算通常由底層的、用C++或CUDA編寫的高性能庫來完成。Python則扮演了一個優雅的“指揮官”角色：我們用Python來定義模型結構、組織數據流、進行實驗管理，而將真正的計算密集型任務交給后臺的C++引擎。這就實現了“開發效率”與“運行效率”的完美結合。我們享受著Python的簡潔，卻沒有犧牲關鍵任務的性能。

這種設計哲學，使得Python成為一座理想的橋梁，它連接了思想與實現，連接了研究與工程，連接了專家與初學者。

1.3.2 生態系統概覽：為何它能成為最優選擇

如果說哲學是Python的“靈魂”，那么其無與倫比的開源生態系統，就是它強健的“體魄”。圍繞著數據科學和機器學習，Python社區自發地構建起了一套完整、強大且高度協同的“工具鏈”。這套工具鏈覆蓋了從數據獲取、清洗、分析、建模到可視化的整個工作流。

讓我們來巡禮一下這個生態中的幾顆璀璨明珠，這些也是我們后續章節將會深入學習的核心工具：

NumPy (Numerical Python)：數據科學的基石。它提供了一個強大的N維數組對象（ndarray），以及對這些數組進行操作的大量高效函數。幾乎所有Python中的高級數據分析和機器學習庫，其底層都構建在NumPy之上。它將Python從一門通用腳本語言，變成了能夠與MATLAB等專業科學計算軟件相媲美的強大工具。
Pandas：數據分析與處理的瑞士軍刀。Pandas提供了兩種核心數據結構：Series（一維）和DataFrame（二維）。DataFrame可以被想象成一個內存中的、功能極其強大的Excel表格。它使得數據的讀取、清洗、轉換、篩選、聚合、分組等操作變得異常簡單直觀。可以說，在機器學習項目中，80%的時間花在數據預處理上，而Pandas正是讓這80%的時間變得高效而愉快的關鍵。
Matplotlib & Seaborn：數據可視化的雙璧。Matplotlib是Python中最基礎、最靈活的可視化庫，它提供了強大的底層繪圖接口，讓你可以定制幾乎任何類型的靜態、動態、交互式圖表。而Seaborn則是基于Matplotlib構建的更高級的統計圖形庫，它提供了更多美觀且面向統計分析的圖表模板，用更少的代碼就能生成信息含量豐富的可視化結果。“一圖勝千言”，這兩個庫是我們洞察數據、展示模型結果的“眼睛”。
Scikit-learn：傳統機器學習的集大成者。Scikit-learn是進入機器學習領域最重要、最友好的庫。它用一套高度一致、簡潔優雅的API，實現了絕大多數經典的機器學習算法（分類、回歸、聚類、降維等）。無論是初學者學習算法，還是從業者快速搭建基線模型，Scikit-learn都是不二之選。它的文檔極為完善，堪稱技術文檔的典范。本書的第二部分將重點圍繞Scikit-learn展開。
深度學習框架：TensorFlow & PyTorch：當問題復雜度超越了傳統機器學習的范疇，我們就需要進入深度學習的世界。在這個世界里，TensorFlow（由Google開發）和PyTorch（由Facebook開發）是兩大主流框架。它們提供了構建、訓練和部署大規模神經網絡所需的全部工具，包括自動微分、GPU加速、豐富的預置模型層等。雖然它們在設計哲學上有所不同（TensorFlow 2.x后也采納了PyTorch的動態圖思想），但都已成為驅動當今AI革命的核心引擎。
Jupyter Notebook / Lab：交互式科學計算的理想環境。Jupyter提供了一個基于Web的交互式計算環境，允許你將代碼、文本（Markdown）、數學公式（LaTeX）、可視化結果等組合在一個文檔中。這種“文學編程”的范式，極大地促進了探索性數據分析和研究過程的記錄與分享。它是數據科學家和機器學習研究者的“數字實驗室”和“工作臺”。

這套生態系統的力量在于其“網絡效應”：每一個庫都構建在其他庫之上，彼此無縫集成。你用Pandas清洗數據，得到的DataFrame可以直接喂給Scikit-learn進行建模，然后用Matplotlib將結果畫出來。這種流暢的體驗，是其他任何語言生態都難以比擬的。正是這個原因，最終使得Python戰勝了R、MATLAB、Java等競爭者，成為了數據科學的“通用語”。

1.4 破除迷思：AI是“神”還是“器”？

隨著AlphaGo的勝利和ChatGPT的驚艷表現，人工智能（AI）以前所未有的姿態進入了公眾視野。媒體的渲染、科幻作品的想象，使得AI的形象在人們心中變得模糊、甚至兩極分化：一些人視之為無所不能、即將取代人類的“神”；另一些人則憂心忡忡，將其視為可能失控的“潘多拉魔盒”。

作為即將踏入這個領域的實踐者，我們必須建立一個清醒、理性的認知：在可預見的未來，我們今天所談論和實踐的AI，本質上是一種“器”，而非“神”。 它是一種由人類設計，基于數學和數據，用于放大人類智慧、解決特定問題的強大工具。

1.4.1 機器學習的能力邊界與倫理挑戰

承認AI是“器”，意味著我們要清醒地認識到它的能力邊界。

數據依賴性：機器學習模型的能力，完全取決于其“喂養”的數據。模型的“智慧”是數據中蘊含模式的反映，其“偏見”也是數據中固有偏見的折射。如果訓練數據存在偏差（例如，在招聘模型中，歷史數據里男性工程師遠多于女性），那么模型就會學習并放大這種偏差，做出歧視性的判斷。模型無法創造數據中不存在的知識。
泛化能力的局限：模型在訓練數據上表現好，不代表在全新的、分布差異巨大的現實世界數據上依然表現好。這種從已知到未知的推廣能力，被稱為泛化（Generalization）。提升泛化能力是機器學習的核心挑戰之一。一個在加州房價數據上訓練得很好的模型，直接拿到中國市場來用，結果幾乎必然是災難性的。
缺乏常識與因果推理：目前的機器學習，尤其是深度學習，本質上是一種基于相關性的“模式匹配”。它擅長發現“A和B經常一起出現”，但通常無法理解“是不是因為A導致了B”。它缺乏人類與生俱來的大量背景知識和常識。一個能識別圖片中“馬”的模型，并不知道馬是一種動物，不能穿過墻壁。這種能力的缺失，使其在需要深度理解和推理的復雜決策場景中，依然非常脆弱。
可解釋性（Interpretability）的挑戰：特別是對于深度神經網絡這類復雜的“黑箱”模型，我們往往很難理解它為什么會做出某個具體的決策。一個模型拒絕了你的貸款申請，但它無法像人類信貸員那樣，給你一個清晰、合乎邏輯的理由。這種“知其然，而不知其所以然”的特性，在金融、醫療、司法等高風險領域，是不可接受的。

認識到這些邊界，自然會引出我們必須面對的倫理挑戰：

偏見與公平性（Bias and Fairness）：如何確保算法不會對特定人群產生系統性的歧視？這不僅僅是技術問題，更是社會正義問題。我們需要開發能夠檢測、量化并緩解偏見的算法，并在模型設計之初就將公平性作為核心目標之一。
隱私（Privacy）：在利用海量個人數據訓練模型的同時，如何保護用戶的隱私權？像聯邦學習（Federated Learning）和差分隱私（Differential Privacy）這樣的技術正在為此努力，它們旨在讓模型在不接觸原始敏感數據的情況下完成學習，或者在數據發布時加入數學上可保證的“噪聲”來保護個體信息。
責任（Accountability）：當一個自動駕駛汽車發生事故，或一個AI醫療診斷系統出現誤診時，責任該由誰來承擔？是用戶、開發者、公司，還是AI本身？這需要建立清晰的法律法規和問責框架，確保技術的每一個環節都有明確的責任主體。
安全與魯棒性（Safety and Robustness）：如何防止AI系統被惡意攻擊（例如，通過在停車標志上貼一個不起眼的貼紙，就讓自動駕駛的識別系統將其誤判為限速標志）？研究模型的“脆弱性”，發展“對抗性訓練”等防御技術，是確保AI系統在現實世界中安全可靠的關鍵。
失業與社會結構：AI自動化將在多大程度上取代人類工作，我們應如何應對由此帶來的社會結構性變遷？這需要政策制定者、教育家和全社會共同思考，如何進行教育改革、建立社會保障體系，以及創造新的工作崗位，以適應人機協作的新時代。

這些挑戰提醒我們，機器學習的實踐者，絕不能僅僅是一個埋頭于代碼和模型的“技術工匠”。我們必須成為一個負責任的“思考者”，時刻審視我們創造的技術可能帶來的深遠影響。

1.4.2 心法：以“出世”之心，做“入世”之事

面對機器學習的強大能力與深刻挑戰，我們應秉持怎樣的心態和原則來從事這項事業？在此，奶奶想與你分享一種“心法”，一種融合了東方智慧與科學精神的從業態度——以“出世”之心，做“入世”之事。

何為“出世”之心？

“出世”，并非消極避世，而是指一種超越具體事務、追求事物本源和規律的超然心態。它要求我們在精神層面保持高度的清醒、客觀與謙卑。

保持對知識的敬畏：要認識到我們所學的不過是滄海一粟。機器學習領域日新月異，沒有任何人能宣稱自己掌握了全部。保持空杯心態，持續學習，對未知保持好奇與敬畏，這是避免技術傲慢的根本。
追求真理，而非迎合指標：在項目中，我們常常會為了提升某個評估指標（如準確率）而無所不用其極。但“出世”之心提醒我們，要時刻反思這個指標是否真正反映了我們想要解決的現實問題。有時，0.1%的準確率提升可能伴隨著對某一群體公平性的巨大損害。我們的目標是解決問題，而不僅僅是優化數字。
旁觀者清，審視全局：在埋頭于特征工程和模型調優的“入世”狀態中，要時常抽離出來，像一個“出世”的旁觀者一樣審視自己的工作。問自己：我做的事情是否有潛在的負面影響？我的模型是否可能被濫用？我是否考慮了所有相關的利益方？這種自我審視，是技術倫理的第一道防線。
不執于“我”：不執著于“我”的模型、“我”的方法。科學的進步在于開放與協作。要樂于分享，敢于承認自己方法的局限，并積極吸收他人的智慧。一個算法、一個模型的價值，在于它能解決問題，而不在于它屬于誰。

何為“入世”之事？

“入世”，就是積極地投身于現實世界，用我們所學的知識去解決具體、實際的問題，創造真實的價值。它要求我們腳踏實地，精益求精。

問題驅動，而非技術驅動：要從真實的需求出發，而不是拿著“錘子”（某個炫酷的新模型）到處找“釘子”。深刻理解業務場景，與領域專家緊密合作，讓技術真正服務于目的。
動手實踐，精益求精：機器學習終究是一門實踐科學。“紙上得來終覺淺，絕知此事要躬行。” 必須親手處理數據，編寫代碼，訓練模型，分析結果。在每一個細節上追求卓越，代碼要清晰，實驗要嚴謹，結果要可復現。這是工匠精神的體現。
創造價值，勇于擔當：我們的最終目標，是利用機器學習技術，在醫療、教育、環保、科研等領域做出積極的貢獻。同時，也要勇于為自己創造的技術成果負責。如果發現它帶來了意想不到的負面后果，要有勇氣站出來承認并努力修正。

“出世”與“入世”的辯證統一

“出世”之心是“體”，是我們的世界觀和價值觀，它為我們指明方向，設定底線，讓我們不迷失在技術的洪流中。“入世”之事是“用”，是我們的方法論和行動力，它讓我們將理想轉化為現實，將智慧落地為價值。

只“出世”而無“入世”，則易流于空談，成為“坐而論道”的清談客。只“入世”而無“出世”，則易陷于“術”而忘了“道”，成為一個高效但可能盲目的“工具人”，甚至可能在不經意間“作惡”。

因此，真正的大家，必然是“出世”與“入世”的完美結合。他們既有仰望星空的深邃思考，又有腳踏實地的精湛技藝。

結語

親愛的讀者，本章即將結束。我們一同探討了學習的本質，回顧了AI的壯闊歷史，明確了Python的生態優勢，并最終落腳于從業者的內心修為。

希望這番“務虛”的討論，能為您接下來的“務實”學習，打下堅實的地基。因為最高明的技術，永遠由最清醒的頭腦和最正直的心靈所駕馭。

從下一章開始，我們將正式卷起袖子，進入Python與機器學習工具的實踐世界。請帶著這份對全局的認知和內心的準則，開始我們真正的筑基之旅。

第二章：工欲善其事——Python環境與核心工具鏈

2.1 “乾坤在握”：Anaconda與Jupyter Notebook的安裝與配置
2.2 “數據之舟”：NumPy數值計算基礎
2.3 “數據之魂”：Pandas數據分析利器
2.4 “眼見為實”：Matplotlib與Seaborn數據可視化

在上一章，我們探討了機器學習的宏大世界觀。現在，我們要將這些思想付諸實踐。實踐的第一步，便是構建一個穩定、可靠且功能強大的工作環境。本章將引導您完成從環境安裝到核心工具掌握的全過程，為您后續的學習掃清障礙。

我們將首先介紹并安裝Anaconda，這個被譽為數據科學“全家桶”的發行版，它能一站式解決Python環境管理和包安裝的難題。接著，我們將學習使用Jupyter Notebook，一個交互式的“數字實驗室”，它將成為我們探索、實驗和展示工作的主要平臺。

隨后，我們將深入學習三個數據科學的“奠基石”庫：

NumPy：我們的“數據之舟”，它為Python提供了強大的多維數組和高效的數值計算能力。
Pandas：我們的“數據之魂”，它提供了靈活的數據結構，讓處理和分析結構化數據變得輕而易舉。
Matplotlib & Seaborn：我們的“眼睛”，它們能將枯燥的數據轉化為富有洞察力的可視化圖表。

請務必對本章內容投入足夠的時間和耐心。熟練掌握這些工具，您會發現后續的學習將事半功倍。

2.1 “乾坤在握”：Anaconda與Jupyter Notebook的安裝與配置

在編程世界里，環境配置往往是勸退新手的“第一道坎”。不同項目可能需要不同版本的Python或依賴庫，如果將所有東西都裝在系統的主Python環境中，很快就會導致版本沖突和混亂，猶如一個堆滿了各種工具、零件卻雜亂無章的車庫。

為了解決這個問題，我們需要一個專業的“車庫管理員”——Anaconda。

什么是Anaconda？

Anaconda并不僅僅是Python，它是一個專注于數據科學的Python發行版。你可以把它理解為一個“大禮包”，里面包含了：

特定版本的Python解釋器。
Conda：一個強大的包管理器和環境管理器。
預裝好的數百個常用科學計算包：如NumPy, Pandas, Matplotlib, Scikit-learn等。你無需再一個個手動安裝，省去了大量的配置麻煩。

為何選擇Anaconda？——環境管理的智慧

Anaconda最核心的價值在于其附帶的conda工具，它能讓我們輕松創建相互隔離的虛擬環境（Virtual Environments）。

想象一下，你要同時進行兩個項目：

項目A，是一個老項目，需要使用Python 3.7和一個舊版的庫X (版本1.0)。
項目B，是一個新項目，你想使用最新的Python 3.11和庫X的新版本 (版本2.0)。

如果沒有環境隔離，這兩個項目根本無法在同一臺電腦上共存。而有了conda，你可以：

創建一個名為project_a_env的環境，在里面安裝Python 3.7和庫X 1.0。
再創建一個名為project_b_env的環境，在里面安裝Python 3.11和庫X 2.0。

這兩個環境如同兩個獨立的平行宇宙，互不干擾。你可以隨時通過一條簡單的命令在它們之間切換。這種“分而治之”的智慧，是專業開發實踐的基石。

安裝Anaconda

安裝過程非常直觀，與安裝普通軟件無異。

訪問官網：在瀏覽器中打開Anaconda的官方下載頁面 (anaconda.com/download)。網站通常會自動檢測你的操作系統（Windows, macOS, Linux）并推薦合適的版本。
選擇版本：選擇與你操作系統對應的最新Python 3.x版本的圖形化安裝包（Graphical Installer）進行下載。
執行安裝：
- 雙擊下載好的安裝包。
- 按照提示點擊“Next”或“Continue”。
- 在許可協議頁面，同意協議。
- 安裝類型選擇“Just Me”即可（除非你有特殊需求為電腦所有用戶安裝）。
- 關鍵步驟（Windows）：在“Advanced Options”界面，建議不要勾選“Add Anaconda to my PATH environment variable”（將Anaconda添加到系統環境變量）。雖然勾選看似方便，但長期來看容易引起與其他Python安裝的沖突。官方推薦使用“Anaconda Prompt”來啟動和管理conda。另一個選項“Register Anaconda as my default Python”可以勾選。
- 選擇安裝路徑（通常保持默認即可），然后開始安裝。過程可能需要幾分鐘。
驗證安裝：
- Windows: 在開始菜單中找到并打開“Anaconda Prompt (anaconda3)”。
- macOS/Linux: 打開你的終端（Terminal）。
- 在打開的命令行窗口中，輸入?conda --version?并回車。如果成功顯示出conda的版本號（如?conda 23.7.4），則證明Anaconda已安裝成功。

使用Conda創建和管理環境

現在，讓我們來實踐一下環境管理的威力。打開你的Anaconda Prompt或終端。

創建一個新的環境：我們為本書創建一個專屬的學習環境，命名為ml_book，并指定使用Python 3.9（一個穩定且兼容性好的版本）。
```
conda create --name ml_book python=3.9
```
Conda會詢問你是否要安裝一些基礎包，輸入y并回車。
激活環境：創建好后，需要“進入”這個環境才能使用它。
```
conda activate ml_book
```
激活后，你會發現命令行提示符前面多了(ml_book)的字樣，這表示你當前正處于這個獨立的環境中。
在環境中安裝庫：現在，我們在這個環境中安裝本書需要的核心庫。由于Anaconda的base環境已經自帶，我們這里僅作演示。例如，安裝seaborn。
```
conda install seaborn
```
Conda會自動處理依賴關系，一并安裝好所有需要的其他庫。
查看已安裝的庫：
```
conda list
```
退出環境：當你完成工作，可以退回到基礎環境。
```
conda deactivate
```
提示符前面的(ml_book)會消失。

Jupyter Notebook：你的交互式實驗室

環境搭好了，我們還需要一個好用的“工作臺”。Jupyter Notebook就是這樣一個理想的工具。它是一個基于Web的應用程序，允許你創建和共享包含實時代碼、公式、可視化和敘述性文本的文檔。

啟動Jupyter Notebook

確保你已經激活了你的工作環境（conda activate ml_book）。
在命令行中輸入：
```
jupyter notebook
```
執行后，你的默認瀏覽器會自動打開一個新標簽頁，地址通常是http://localhost:8888/tree?。這就是Jupyter的文件瀏覽器界面。命令行窗口不要關閉，因為它是Jupyter服務的后臺。

Jupyter Notebook核心概念

Notebook文件 (.ipynb)：你創建的每一個Jupyter文檔都是一個.ipynb文件，它用一種特殊格式（JSON）保存了你所有的代碼、文本和輸出。
單元格（Cell）：Notebook由一個個單元格組成。單元格主要有兩種類型：
- Code Cell（代碼單元格）：用來編寫和執行代碼（如Python代碼）。
- Markdown Cell（文本單元格）：用來編寫格式化的文本，就像你現在正在閱讀的這些文字一樣，可以包含標題、列表、鏈接、圖片等。
內核（Kernel）：每個Notebook都有一個獨立的“內核”在后臺運行。這個內核是你激活的conda環境的體現，它負責接收你在Code Cell中寫的代碼，執行它，然后將結果返回并顯示在單元格下方。

基本操作

新建Notebook：在Jupyter的文件瀏覽器頁面，點擊右上角的“New”，然后選擇“Python 3 (ipykernel)”或類似選項，即可創建一個新的Notebook。
切換單元格類型：在選中一個單元格后，可以在頂部的工具欄下拉菜單中選擇Code或Markdown。
執行單元格：選中一個單元格，按下?Shift + Enter，Jupyter會執行該單元格，并自動跳轉到下一個單元格。這是最常用的快捷鍵。
保存：點擊左上角的保存圖標，或使用快捷鍵Ctrl + S?(Windows/Linux) /?Cmd + S?(macOS)。

現在，請你親手嘗試：

創建一個新的Notebook。
在第一個單元格中，輸入?print("Hello, Machine Learning World!")，然后按Shift + Enter執行。
將第二個單元格的類型改為Markdown，輸入# 這是我的第一個Notebook標題，然后按Shift + Enter渲染文本。

恭喜！你已經成功搭建了專業的開發環境，并掌握了與它交互的基本方式。這個環境如同一片沃土，我們接下來要學習的NumPy、Pandas等工具，就是將要在這片土地上茁壯成長的參天大樹。

2.2 “數據之舟”：NumPy數值計算基礎

如果說數據是海洋，那NumPy (Numerical Python) 就是我們在這片海洋上航行的第一艘堅固快船。它是Python科學計算生態的絕對核心，幾乎所有上層庫（包括Pandas和Scikit-learn）都構建于它之上。

Python原生的列表（list）雖然靈活，但對于大規模數值運算，其性能不堪一擊。NumPy的核心是其ndarray（N-dimensional array）對象，這是一個由相同類型元素組成的多維數組。它的優勢在于：

性能：ndarray在內存中是連續存儲的，并且其核心運算由C語言編寫的底層代碼執行，速度遠超Python原生列表。
便捷：提供了大量用于數組操作的數學函數和線性代數運算，語法簡潔。

安裝NumPy

如果你遵循了上一節使用Anaconda，那么NumPy已經被預裝好了。如果沒有，只需在激活的環境中運行：

conda install numpy

導入NumPy

在代碼中，我們遵循一個廣泛接受的慣例，將NumPy導入并簡寫為np。

import numpy as np

2.2.1 從標量到張量：維度的哲學

在NumPy中，我們用不同的術語來描述不同維度的數據，這與物理學和深度學習中的“張量（Tensor）”概念一脈相承。理解維度，是理解數據結構的第一步。

標量（Scalar）：一個單獨的數字，如7。在NumPy中，它是一個0維數組。

s = np.array(7)
print(s)
print("維度:", s.ndim) # ndim屬性查看維度數量
# 輸出:
# 7
# 維度: 0

向量（Vector）：一列有序的數字，如[1, 2, 3]。它是一個1維數組。

v = np.array([1, 2, 3])
print(v)
print("維度:", v.ndim)
print("形狀:", v.shape) # shape屬性查看每個維度的大小
# 輸出:
# [1 2 3]
# 維度: 1
# 形狀: (3,)

矩陣（Matrix）：一個二維的數字表格，如[[1, 2], [3, 4]]。它是一個2維數組。

m = np.array([[1, 2, 3], [4, 5, 6]])
print(m)
print("維度:", m.ndim)
print("形狀:", m.shape)
# 輸出:
# [[1 2 3]
#  [4 5 6]]
# 維度: 2
# 形狀: (2, 3)  (代表2行3列)

張量（Tensor）：一個超過二維的數組。例如，一張彩色圖片可以表示為一個3維張量（高度，寬度，顏色通道RGB）。

t = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
print(t)
print("維度:", t.ndim)
print("形狀:", t.shape)
# 輸出:
# [[[1 2]
#   [3 4]]
#
#  [[5 6]
#   [7 8]]]
# 維度: 3
# 形狀: (2, 2, 2)

ndim（維度數）、shape（形狀）和dtype（數據類型）是ndarray最重要的三個屬性。在處理數據時，時刻關注這三個屬性，能幫你避免很多錯誤。

創建數組的常用方法

除了直接從列表創建，NumPy還提供了多種便捷的創建方式：

# 創建一個3行4列，所有元素為0的數組
zeros_arr = np.zeros((3, 4))# 創建一個2x3x2，所有元素為1的數組
ones_arr = np.ones((2, 3, 2))# 創建一個從0到9的數組（不包含10）
range_arr = np.arange(10)# 創建一個從0到1，包含5個等間距元素的數組
linspace_arr = np.linspace(0, 1, 5)# 創建一個3x3的單位矩陣
eye_arr = np.eye(3)# 創建一個2x3，元素為隨機數的數組（0到1之間）
rand_arr = np.random.rand(2, 3)# 創建一個2x3，元素為符合標準正態分布的隨機數
randn_arr = np.random.randn(2, 3)

2.2.2 核心操作：索引、切片、廣播機制

1. 索引與切片（Indexing and Slicing）

這與Python列表類似，但擴展到了多維。

# 以一個1維數組為例
a = np.arange(10) # [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]# 獲取單個元素
print(a[5]) # 輸出: 5# 切片：獲取從索引2到索引7（不含）的元素
print(a[2:7]) # 輸出: [2 3 4 5 6]# 以一個2維數組為例
m = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])# 獲取單個元素：第1行（索引從0開始），第2列
print(m[1, 2]) # 輸出: 6# 獲取整行
print(m[0, :]) # 輸出: [1 2 3]  (:代表該維度的所有元素)
# 或者簡寫為
print(m[0])# 獲取整列
print(m[:, 1]) # 輸出: [2 5 8]# 獲取子矩陣：第0、1行，和第1、2列
print(m[0:2, 1:3])
# 輸出:
# [[2 3]
#  [5 6]]

布爾索引（Boolean Indexing） 這是一個極其強大的功能，允許我們根據條件來選擇元素。

data = np.array([[1, 2], [3, 4], [5, 6]])# 找到data中所有大于3的元素
bool_idx = data > 3
print(bool_idx)
# 輸出:
# [[False False]
#  [False  True]
#  [ True  True]]# 使用這個布爾數組來索引，會返回所有對應位置為True的元素
print(data[bool_idx]) # 輸出: [4 5 6]# 也可以直接寫成一行
print(data[data > 3])

2. 數組運算

NumPy的數組運算是按元素進行的，這使得代碼非常簡潔。

x = np.array([[1, 2], [3, 4]])
y = np.array([[5, 6], [7, 8]])# 按元素加法
print(x + y)
# [[ 6  8]
#  [10 12]]# 按元素乘法
print(x * y)
# [[ 5 12]
#  [21 32]]# 矩陣乘法（點積）
print(np.dot(x, y))
# 或者使用@符號 (Python 3.5+)
print(x @ y)
# [[19 22]
#  [43 50]]

NumPy還提供了全套的通用函數（ufunc），如np.sqrt(), np.sin(), np.exp()等，它們也都按元素作用于整個數組。

3. 廣播機制（Broadcasting）

廣播是NumPy最神奇也最重要的特性之一。它描述了NumPy在處理不同形狀的數組進行算術運算時的規則。簡單來說，如果兩個數組的形狀不完全匹配，NumPy會嘗試“廣播”那個較小的數組，將其“拉伸”以匹配較大數組的形狀，從而使運算成為可能。

規則：從兩個數組的尾部維度開始逐一比較它們的size：

如果兩個維度size相同，或其中一個為1，則該維度兼容。
如果所有維度都兼容，則運算可以進行。
如果任一維度不兼容（size不同且沒有一個是1），則會報錯。

示例：

# 一個2x3的矩陣
a = np.array([[1, 2, 3], [4, 5, 6]])# 一個1x3的向量（或說行向量）
b = np.array([10, 20, 30])# a的形狀是(2, 3)，b的形狀是(3,)。
# NumPy會將b廣播，想象成把它復制了一遍，變成了[[10, 20, 30], [10, 20, 30]]
# 然后再與a進行按元素加法
print(a + b)
# 輸出:
# [[11 22 33]
#  [14 25 36]]# 另一個例子：給矩陣的每一列加上一個不同的值
# a的形狀是(2, 3)
# c的形狀是(2, 1)
c = np.array([[100], [200]])# NumPy會將c的第1維（列）進行廣播，變成[[100, 100, 100], [200, 200, 200]]
print(a + c)
# 輸出:
# [[101 102 103]
#  [204 205 206]]

廣播機制極大地提升了代碼的簡潔性和效率，避免了我們手動寫循環去擴展數組。理解并善用廣播，是衡量一個NumPy使用者是否熟練的重要標志。

2.3 “數據之魂”：Pandas數據分析利器

Pandas的名字來源于“Panel Data”（面板數據），這是一個計量經濟學術語，指多維度的結構化數據集。這個庫由Wes McKinney在2008年開發，初衷是為了解決金融數據分析中的實際問題。如今，它已成為Python數據分析的代名詞。

Pandas的核心價值在于，它提供了一套直觀、靈活且功能強大的數據結構，專門用于處理表格型（tabular）和異構（heterogeneous）數據。在真實世界中，我們遇到的大部分數據，如Excel表格、數據庫查詢結果、CSV文件，都是這種形式。

安裝Pandas

同樣，如果你使用Anaconda，Pandas已為你準備就緒。否則，請運行：

##########################
### 導入Pandas
### 社區慣例是將其導入為`pd`
##########################
conda install pandasimport pandas as pd

2.3.1 Series與DataFrame：結構化數據的“陰陽”

Pandas有兩個核心的數據結構，理解它們是掌握Pandas的關鍵。

1. Series：帶標簽的一維數組

你可以將Series想象成一個加強版的NumPy一維數組。它與ndarray的主要區別在于，Series有一個與之關聯的標簽數組，稱為索引（Index）。

# 從列表創建一個基本的Series
s = pd.Series([10, 20, 30, 40])
print(s)
# 輸出:
# 0    10
# 1    20
# 2    30
# 3    40
# dtype: int64

左邊的一列（0, 1, 2, 3）是默認生成的整數索引。右邊是我們的數據值。

Series的強大之處在于我們可以自定義索引：

# 創建一個帶有自定義索引的Series
sales = pd.Series([250, 300, 450], index=['北京', '上海', '深圳'])
print(sales)
# 輸出:
# 北京    250
# 上海    300
# 深圳    450
# dtype: int64# 可以像字典一樣通過標簽進行索引
print(sales['上海']) # 輸出: 300# 也可以像NumPy數組一樣進行切片和布爾索引
print(sales[sales > 280])
# 輸出:
# 上海    300
# 深圳    450
# dtype: int64

Series的index和values屬性可以分別訪問其索引和值（值為一個NumPy數組）。

2. DataFrame：二維的“超級表格”

DataFrame是Pandas最核心、最常用的數據結構。你可以把它看作：

一個共享相同索引的Series的集合。
一個帶有行索引（index）和列索引（columns）的二維表格。
一個功能極其強大的Excel電子表格或SQL數據表。

####################
# 從字典創建DataFrame，字典的key會成為列名
####################data = {'城市': ['北京', '上海', '廣州', '深圳'],'年份': [2020, 2020, 2021, 2021],'人口(萬)': [2154, 2428, 1867, 1756]
}
df = pd.DataFrame(data)
print(df)
# 輸出:
#     城市    年份  人口(萬)
# 0   北京  2020   2154
# 1   上海  2020   2428
# 2   廣州  2021   1867
# 3   深圳  2021   1756####################
# DataFrame
# 既有行索引（左邊的0, 1, 2, 3），也有列索引（'城市', '年份', '人口(萬)'）
########################################
# 查看DataFrame基本信息
# 在進行任何分析前，先“體檢”一下數據是個好習慣：
##################### 查看前5行
print(df.head())# 查看后5行
print(df.tail())# 查看索引、列名和數據類型
print(df.info())
# <class 'pandas.core.frame.DataFrame'>
# RangeIndex: 4 entries, 0 to 3
# Data columns (total 3 columns):
#  #   Column   Non-Null Count  Dtype
# ---  ------   --------------  -----
#  0   城市       4 non-null      object
#  1   年份       4 non-null      int64
#  2   人口(萬)    4 non-null      int64
# dtypes: int64(2), object(1)
# memory usage: 224.0+ bytes# 獲取描述性統計信息（對數值列）
print(df.describe())
#                年份        人口(萬)
# count    4.000000     4.000000
# mean  2020.500000  2051.250000
# std      0.577350   302.491322
# min   2020.000000  1756.000000
# 25%   2020.000000  1839.250000
# 50%   2020.500000  2010.500000
# 75%   2021.000000  2222.500000
# max   2021.000000  2428.000000

2.3.2 數據的“增刪改查”與“聚合分離”

Pandas的威力體現在它對數據進行復雜操作的簡潔性上。

1. 查（選擇數據）

這是最頻繁的操作。Pandas提供了兩種主要的索引方式：

.loc：**基于標簽（label）**的索引。
.iloc：**基于位置（integer position）**的索引。

# 假設我們給df設置一個更有意義的索引
df.index = ['BJ', 'SH', 'GZ', 'SZ']# --- 使用 .loc ---
# 選擇單行 (返回一個Series)
print(df.loc['SH'])# 選擇多行 (返回一個DataFrame)
print(df.loc[['BJ', 'SZ']])# 選擇行和列
print(df.loc['GZ', '人口(萬)']) # 輸出: 1867# 選擇多行多列
print(df.loc[['SH', 'GZ'], ['城市', '人口(萬)']])# --- 使用 .iloc ---
# 選擇第2行（索引為1）
print(df.iloc[1])# 選擇第0行和第3行
print(df.iloc[[0, 3]])# 選擇第2行、第1列的元素
print(df.iloc[2, 1]) # 輸出: 2021# --- 條件選擇 ---
# 選擇年份為2020的所有行
print(df[df['年份'] == 2020])# 選擇人口超過2000萬的城市名
print(df[df['人口(萬)'] > 2000]['城市'])

記住.loc用名字，.iloc用數字，是避免混淆的關鍵。

2. 增（添加數據）

# 添加新列
df['GDP(萬億)'] = [3.6, 3.9, 2.5, 3.0]
print(df)# 添加新行 (使用.loc)
df.loc['HZ'] = ['杭州', 2022, 1200, 1.8]
print(df)

3. 刪（刪除數據）

使用.drop()方法。它默認返回一個新對象，不修改原始DataFrame。

# 刪除列 (axis=1代表列)
df_no_gdp = df.drop('GDP(萬億)', axis=1)# 刪除行 (axis=0代表行)
df_no_hz = df.drop('HZ', axis=0)

4. 改（修改數據）

可以直接通過索引賦值來修改。

# 修改單個值
df.loc['BJ', '人口(萬)'] = 2189# 修改整列
df['年份'] = 2022# 根據條件修改
df.loc[df['城市'] == '上海', '人口(萬)'] = 2487

5. 聚合與分組（Groupby）

這是Pandas的“大殺器”，對應于SQL中的GROUP BY操作。它實現了“分離-應用-合并”（Split-Apply-Combine）的強大模式。

過程：

分離（Split）：根據某個或某些鍵將數據拆分成組。
應用（Apply）：對每個組獨立地應用一個函數（如求和、求平均）。
合并（Combine）：將結果合并成一個新的數據結構。

# 按“年份”分組，并計算每年的平均人口
avg_pop_by_year = df.groupby('年份')['人口(萬)'].mean()
print(avg_pop_by_year)# 按“年份”分組，并應用多個聚合函數
stats_by_year = df.groupby('年份')['人口(萬)'].agg(['mean', 'sum', 'count'])
print(stats_by_year)

groupby操作是探索性數據分析的核心，能幫助我們快速發現不同類別數據之間的關系。

Pandas的功能遠不止于此，還包括處理缺失數據、合并/連接多個DataFrame、時間序列分析等高級功能，我們將在后續章節的實戰中不斷遇到和學習。

2.4 “眼見為實”：Matplotlib與Seaborn數據可視化

數據分析的最終目的之一是獲得洞察（Insight）。而人類的大腦天生就對圖形信息比對數字表格更敏感。“一圖勝千言”，數據可視化正是連接數據與洞察的橋梁。

在Python生態中，Matplotlib是“教父”級別的可視化庫，它功能強大、可定制性極高。而Seaborn則是基于Matplotlib構建的、更側重于統計圖形的“美顏相機”，它能用更簡潔的代碼生成更美觀、信息更豐富的圖表。

導入

import matplotlib.pyplot as plt
import seaborn as sns# 在Jupyter Notebook中，通常會加上這行魔法命令，讓圖像直接內嵌在Notebook中顯示
%matplotlib inline

2.4.1 從點線圖到熱力圖：選擇合適的“畫筆”

不同的數據關系，需要用不同的圖表類型來呈現。

1. 折線圖（Line Plot）：最適合展示數據隨連續變量（尤其是時間）變化的趨勢。

# 假設我們有一周的銷售數據
days = np.arange(1, 8)
sales = np.array([50, 55, 47, 62, 60, 70, 68])plt.figure(figsize=(8, 4)) # 創建一個8x4英寸的畫布
plt.plot(days, sales, marker='o', linestyle='--') # marker是數據點的樣式，linestyle是線的樣式
plt.title("周銷售額趨勢") # 添加標題
plt.xlabel("天數") # 添加x軸標簽
plt.ylabel("銷售額") # 添加y軸標簽
plt.grid(True) # 顯示網格
plt.show() # 顯示圖像

2. 散點圖（Scatter Plot）：用于探索兩個數值變量之間的關系。

# 假設我們有房屋面積和價格的數據
area = np.random.randint(50, 150, size=100)
price = area * 1.2 + np.random.randn(100) * 20# 使用Seaborn繪制散點圖，更美觀
sns.scatterplot(x=area, y=price)
plt.title("房屋面積與價格關系")
plt.xlabel("面積 (平方米)")
plt.ylabel("價格 (萬元)")
plt.show()

3. 柱狀圖（Bar Plot）：用于比較不同類別的數據。

# 使用我們之前的城市人口DataFrame
sns.barplot(x='城市', y='人口(萬)', data=df)
plt.title("主要城市人口對比")
plt.show()

4. 直方圖（Histogram）：用于觀察單個數值變量的分布情況。

# 觀察價格數據的分布
sns.histplot(price, kde=True) # kde=True會同時繪制一條核密度估計曲線
plt.title("房價分布直方圖")
plt.show()

5. 熱力圖（Heatmap）：用顏色深淺來展示一個矩陣的值，非常適合展示變量之間的相關性。

# 計算df中數值列的相關系數矩陣
corr_matrix = df[['年份', '人口(萬)', 'GDP(萬億)']].corr()sns.heatmap(corr_matrix, annot=True, cmap='coolwarm') # annot=True在格子上顯示數值, cmap是顏色主題
plt.title("特征相關性熱力圖")
plt.show()

2.4.2 可視化之道：美學、信息與洞察

一幅好的數據可視化作品，應遵循幾個原則：

數據-墨水比（Data-Ink Ratio）：由可視化大師愛德華·塔夫特提出。核心思想是，一幅圖中絕大部分的“墨水”都應該用來展示數據本身，而應刪去所有無益于理解數據的裝飾性元素（如花哨的背景、3D效果等）。追求簡約和清晰。
選擇正確的圖表：明確你要表達的關系——是比較、分布、構成還是聯系？然后選擇最適合的圖表類型。用折線圖去比較類別數據，或者用餅圖去展示超過5個類別的構成，都是常見的錯誤。
清晰的標注：一幅圖必須是自包含的。它應該有明確的標題、坐標軸標簽（包含單位）、圖例等，讓讀者無需閱讀正文就能理解圖表的基本含義。
利用視覺編碼：除了位置（x, y坐標），我們還可以利用顏色、形狀、大小、透明度等視覺元素來編碼更多的信息維度。但要避免過度使用，以免造成視覺混亂。
講一個故事（Tell a Story）：最好的可視化不僅僅是呈現數據，它還在講述一個故事，引導讀者發現模式、得出結論。你的標題、注解和高亮顯示，都應該服務于這個故事。

結語

本章，我們從零開始，搭建了堅實的Python數據科學環境，并掌握了NumPy、Pandas、Matplotlib和Seaborn這四大金剛。這套工具鏈，是您未來探索廣闊數據世界的“標準裝備”。

請務必花時間親手實踐本章的所有代碼。嘗試讀取你自己的CSV文件，用Pandas進行清洗和分析，再用Matplotlib/Seaborn將其可視化。當你能自如地運用這些工具時，你就已經完成了從門外漢到數據科學“準入者”的蛻變。

從下一章開始，我們將正式進入機器學習的核心地帶，開始學習如何利用這些工具，去構建、訓練和評估真正的機器學習模型。我們的地基已經打好，是時候開始建造大廈了。

第三章：數據的心法——預處理與特征工程

3.1 “相數據”：理解你的數據
3.2 “凈數據”：數據清洗的修行
3.3 “點石成金”：特征工程的科學與藝術

在機器學習的宏偉藍圖中，數據預處理與特征工程扮演著承前啟后的關鍵角色。它們是連接原始數據與機器學習模型的橋梁，其質量直接決定了模型最終所能達到的高度。一個經過精心處理和設計的特征，其價值往往勝過一個復雜模型的微小調優。

本章，我們將秉持一種“格物致知”的精神，深入數據的內在肌理。我們將學習：

“相數據”：如何通過探索性數據分析（EDA）與數據進行初次“對話”，理解其脾性。
“凈數據”：如何像一位耐心的工匠，清理數據中的“雜質”——缺失值與異常值。
“點石成金”：如何施展特征工程的“魔法”，從現有數據中創造出更具信息量的特征，并將其轉化為模型能夠“消化”的格式。

這個過程，既有章法可循的科學，也有依賴經驗直覺的藝術。它是一場修行，考驗的是我們的耐心、細致與創造力。

3.1 “相數據”：理解你的數據

在拿到一個數據集后，最忌諱的就是不假思索地直接將其扔進模型。這好比醫生不經問診，就給病人開藥，是極其危險和不負責任的。我們的第一步，永遠是理解數據。這個過程，我們稱之為探索性數據分析（Exploratory Data Analysis, EDA）。

3.1.1 探索性數據分析（EDA）：與數據對話的藝術

EDA是由統計學大師約翰·圖基（John Tukey）提倡的一種數據分析方法論。它的核心思想是，在進行任何正式的假設檢驗之前，通過多種手段（主要是可視化和匯總統計）對數據進行開放式的探索，以發現其結構、異常、模式和關系。

這是一種偵探般的工作，我們的目標是回答關于數據的基本問題：

這個數據集中有多少行（樣本）和多少列（特征）？
每個特征是什么數據類型（數值型、類別型、文本、日期）？
數據中是否存在缺失值？比例如何？
數據的分布是怎樣的？（是正態分布，還是偏態分布？）
不同特征之間是否存在關聯？（例如，身高和體重是否正相關？）

讓我們以一個經典的“泰坦尼克號幸存者”數據集為例，來演示EDA的基本流程。首先，加載數據并進行初步檢視。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns# 加載數據 (Seaborn自帶了這個數據集)
df = sns.load_dataset('titanic')# 1. 查看數據維度
print("數據形狀:", df.shape)# 2. 查看前幾行，對數據有個直觀印象
print(df.head())# 3. 查看各列的數據類型和非空值數量
print(df.info())

從df.info()的輸出中，我們能立刻獲得大量信息：

共有891個樣本（行），15個特征（列）。
age（年齡）、deck（甲板號）、embarked（登船港口）等列存在缺失值（因為它們的非空計數少于891）。
survived,?pclass,?sex,?embarked?等是類別型特征，而?age,?fare?是數值型特征。

這就是與數據的第一輪“對話”，我們已經對它的“家底”有了大致了解。

3.1.2 描述性統計與分布可視化

接下來，我們要更深入地探查數據的內在特征。

1. 描述性統計

對于數值型特征，describe()方法是我們的得力助手。

print(df.describe())

這會輸出數值列的計數、平均值、標準差、最小值、四分位數和最大值。從中我們可以快速發現：

年齡（age）：乘客平均年齡約29.7歲，但年齡跨度很大（從0.42歲到80歲），且存在缺失值（count為714）。
票價（fare）：票價分布極不均勻，75%的乘客票價低于31美元，但最高票價竟達512美元，這暗示可能存在極端值（異常值）。

對于類別型特征，我們可以使用value_counts()來查看其取值分布。

# 查看性別分布
print(df['sex'].value_counts())# 查看生還情況分布
print(df['survived'].value_counts(normalize=True)) # normalize=True顯示比例

我們發現，乘客中男性遠多于女性，且總體生還率只有約38.4%。

2. 分布可視化

數字是抽象的，圖形是直觀的。我們將使用Matplotlib和Seaborn將統計結果可視化。

觀察單個數值變量的分布（直方圖/核密度圖）
```
sns.histplot(df['age'].dropna(), kde=True) # dropna()去掉缺失值
plt.title('乘客年齡分布')
plt.show()
```
從圖中可以看到，乘客以年輕人為主，呈右偏態分布。
觀察單個類別變量的分布（計數圖/柱狀圖）
```
sns.countplot(x='pclass', data=df)
plt.title('各船艙等級人數')
plt.show()
```
三等艙乘客數量最多。
探索特征與目標變量的關系 這是EDA的核心目的之一。例如，我們想知道“船艙等級”和“生還率”有何關系。
```
sns.barplot(x='pclass', y='survived', data=df)
plt.title('各船艙等級的生還率')
plt.ylabel('生還率')
plt.show()
```
一目了然，船艙等級越高（1等艙），生還率越高。這是一個極具信息量的發現。

探索兩個數值變量的關系（散點圖）

sns.scatterplot(x='age', y='fare', data=df)
plt.title('年齡與票價的關系')
plt.show()

探索多個變量間的關系（熱力圖/配對圖）

# 計算數值特征的相關性矩陣
corr = df[['survived', 'pclass', 'age', 'sibsp', 'parch', 'fare']].corr()
sns.heatmap(corr, annot=True, cmap='coolwarm')
plt.title('特征相關性熱力圖')
plt.show()
```    熱力圖顯示，`pclass`和`survived`有顯著的負相關（-0.34），`fare`和`survived`有正相關（0.26），這與我們之前的發現一致。

通過這一系列“望、聞、問、切”，我們對數據的特性、潛在的問題（缺失值、異常值）以及特征間的關系有了深刻的理解。這份理解，將指導我們下一步的“凈數據”和“點石成金”工作。

3.2 “凈數據”：數據清洗的修行

現實世界的數據是“骯臟”的。數據錄入錯誤、傳感器故障、用戶不愿填寫……種種原因導致了數據中充滿了缺失值（Missing Values）和異常值（Outliers）。數據清洗，就是將這些“雜質”處理掉的過程，它是一項細致且關鍵的修行。

3.2.1 缺失值的“舍”與“得”：刪除、插補與預測

處理缺失值，我們需要權衡利弊，做出“舍”與“得”的決策。

1. 識別缺失值

# 查看每列的缺失值數量
print(df.isnull().sum())# 查看缺失值比例
print(df.isnull().sum() / len(df) * 100)

在泰坦尼克數據中，age缺失約19.8%，deck缺失高達77.4%，embarked只缺失2個。

2. 處理策略

刪除（Dropping）：“舍”的決斷
- 刪除整列：如果一個特征的缺失比例過高（如deck的77%），它所能提供的信息已經非常有限，強行填充反而可能引入噪聲。此時，可以考慮直接刪除該列。
```
df_dropped_col = df.drop('deck', axis=1)
```
- 刪除整行：如果某個樣本（行）缺失了多個關鍵特征，或者數據集非常大而缺失的行數很少（如embarked只缺失2行），那么直接刪除這些行是簡單有效的做法。
```
df_dropped_row = df.dropna(subset=['embarked'])
```
優點：簡單直接，不會引入偏誤。缺點：會損失數據，如果缺失數據不是隨機的，可能會導致分析結果產生偏見。
插補（Imputation）：“得”的智慧 插補是用一個估算值來代替缺失值。這是更常用的方法。
- 用均值/中位數/眾數填充：這是最簡單的插補方法。
  - 對于數值型特征，如果數據分布比較對稱，可以用**均值（mean）填充；如果數據存在偏態或有異常值，用中位數（median）**更為穩健。
  - 對于類別型特征，可以用眾數（mode）（出現次數最多的值）來填充。
```
# 用年齡的中位數填充age列的缺失值
age_median = df['age'].median()
df['age'].fillna(age_median, inplace=True) # inplace=True直接在原DataFrame上修改# 用登船港口的眾數填充embarked列
embarked_mode = df['embarked'].mode()[0] # mode()返回一個Series，取第一個
df['embarked'].fillna(embarked_mode, inplace=True)
```
- 分組插補：簡單的全局均值/中位數忽略了數據內部的結構。我們可以做得更精細。例如，我們知道不同船艙等級的乘客年齡可能有差異，可以按pclass分組，用各組的中位數來填充。
```
# 偽代碼演示思想
# df['age'] = df.groupby('pclass')['age'].transform(lambda x: x.fillna(x.median()))
```
優點：保留了樣本，充分利用了數據。缺點：可能會低估數據的方差，引入一定偏誤。
預測模型插補 這是一種更高級的方法。我們可以將含有缺失值的列作為目標變量（y），其他列作為特征（X），訓練一個機器學習模型（如線性回歸、K近鄰）來預測缺失值。優點：通常是最準確的插補方法。缺點：實現復雜，計算成本高。

選擇哪種方法？ 這取決于缺失的比例、特征的重要性、數據的內在關系以及你愿意投入的成本。沒有絕對的“最優解”，只有“最合適”的解。

3.2.2 異常值的“辨”與“融”：識別與處理

異常值（Outliers）是指那些與數據集中其余數據點顯著不同的數據點。它們可能是錄入錯誤，也可能是真實但極端的情況。

1. 識別異常值（“辨”）

可視化識別：**箱形圖（Box Plot）**是識別異常值的利器。箱體外的點通常被認為是潛在的異常值。
```
sns.boxplot(x=df['fare'])
plt.show()
```
泰坦尼克票價的箱形圖清楚地顯示了大量的高價異常點。
統計方法識別：
- 3σ法則（3-Sigma Rule）：對于近似正態分布的數據，約99.7%的數據點會落在距離均值3個標準差的范圍內。超出這個范圍的點可被視為異常值。
- IQR法則（Interquartile Range）：這是箱形圖背后的數學原理。IQR = Q3（上四分位數） - Q1（下四分位數）。通常將小于?Q1 - 1.5 * IQR?或大于?Q3 + 1.5 * IQR?的點定義為異常值。

2. 處理異常值（“融”）

刪除：如果確定異常值是由于錯誤（如年齡輸入為200歲），可以直接刪除。但如果異常值是真實的（如CEO的超高薪水），刪除它們可能會丟失重要信息。
轉換（Transformation）：對數據進行數學轉換，如對數轉換（log transform），可以“壓縮”數據的尺度，減小異常值的影響。這對于處理右偏分布（如收入、票價）的數據特別有效。
```
df['fare_log'] = np.log1p(df['fare']) # log1p(x) = log(1+x)，避免log(0)
sns.histplot(df['fare_log'], kde=True)
plt.show()
```
可以看到，對數轉換后的票價分布更接近正態分布。
蓋帽（Capping/Winsorization）：將超出特定閾值（如99百分位數）的異常值，替換為該閾值。這既限制了異常值的極端影響，又保留了它們作為“高值”的信息。
```
p99 = df['fare'].quantile(0.99)
df_capped = df.copy()
df_capped.loc[df_capped['fare'] > p99, 'fare'] = p99
```

處理異常值同樣需要審慎。要結合業務理解，判斷一個“異常”點究竟是噪聲還是有價值的信號。

3.3 “點石成金”：特征工程的科學與藝術

如果說數據清洗是“打掃屋子”，那么特征工程就是“精心裝修”。特征工程是指利用領域知識和技術手段，從原始數據中提取、創造出對預測模型更有用的新特征的過程。 它是決定機器學習項目成敗的最關鍵因素。

3.3.1 特征提取與創造：從原始數據中提煉真金

從現有特征組合：在泰坦尼克數據中，有sibsp（兄弟姐妹/配偶數）和parch（父母/子女數）兩個特征。它們都代表了親人。我們可以將它們組合成一個更有意義的新特征——family_size（家庭成員總數）。
```
df['family_size'] = df['sibsp'] + df['parch'] + 1 # +1是加上自己
```
我們還可以根據家庭規模，創造一個類別特征，如is_alone（是否獨自一人）。
```
df['is_alone'] = (df['family_size'] == 1).astype(int) # astype(int)將布爾值轉為0/1
```
從復雜數據中提取：
- 日期時間：從一個日期2025-07-18，可以提取出年份、月份、星期幾、是否為周末等多個特征。
- 文本數據：從一段文本中，可以提取詞頻（TF-IDF）、情感傾向、關鍵詞等。
- 乘客姓名（Name）：看似無用，但仔細觀察，姓名中包含了Mr.,?Mrs.,?Miss.,?Master.等稱謂（Title）。這些稱謂反映了乘客的性別、年齡、婚姻狀況和社會地位，可能是非常有用的特征。
```
df['title'] = df['name'].str.extract(' ([A-Za-z]+)\.', expand=False)
print(df['title'].value_counts())
```

3.3.2 特征縮放與編碼：為模型準備“素食”

大多數機器學習模型都像“挑食的孩子”，它們無法直接“吃”下原始的、五花八門的數據。我們需要將所有特征都處理成它們喜歡的格式——數值型。

1. 類別特征編碼

獨熱編碼（One-Hot Encoding）：這是處理名義類別特征（Nominal Feature）（類別間沒有順序關系，如“顏色”：紅、綠、藍）最常用的方法。它會為每個類別創建一個新的二進制（0/1）特征。
```
# 對'embarked'列進行獨熱編碼
embarked_dummies = pd.get_dummies(df['embarked'], prefix='embarked')
df = pd.concat([df, embarked_dummies], axis=1)
```
pd.get_dummies是Pandas中實現獨熱編碼的便捷函數。
標簽編碼（Label Encoding）/ 序數編碼（Ordinal Encoding）：用于處理有序類別特征（Ordinal Feature）（類別間有明確的順序，如“學歷”：學士、碩士、博士）。它將每個類別映射到一個整數。
```
# 假設有學歷特征
# mapping = {'學士': 1, '碩士': 2, '博士': 3}
# df['education_encoded'] = df['education'].map(mapping)
```
注意：絕對不能對名義類別特征使用標簽編碼，因為這會錯誤地給模型引入一個不存在的順序關系（例如，模型會認為“藍色”比“紅色”大）。

2. 數值特征縮放（Scaling）

許多模型（如線性回歸、SVM、神經網絡）對特征的尺度非常敏感。如果一個特征的范圍是0-10000（如薪水），另一個是0-100（如年齡），模型會不成比例地被薪水這個特征所主導。特征縮放就是將所有特征調整到相似的尺度。

標準化（Standardization / Z-score Normalization）：將特征縮放到均值為0，標準差為1的分布。計算公式為 (x - mean) / std。這是最常用、最通用的縮放方法。
```
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
df['age_scaled'] = scaler.fit_transform(df[['age']])
```
歸一化（Normalization / Min-Max Scaling）：將特征縮放到一個固定的范圍，通常是****。計算公式為 (x - min) / (max - min)。當數據分布不符合高斯分布，或者你想保留0值時比較有用。
```
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
df['fare_scaled'] = scaler.fit_transform(df[['fare']])
```

3.3.3 特征選擇與降維：去蕪存菁，大道至簡

當我們創造了大量特征后，可能會引入冗余或不相關的特征，這會增加模型復雜度，降低泛化能力，甚至導致“維度災難”。因此，我們需要“去蕪存菁”。

1. 特征選擇（Feature Selection）

目標是從所有特征中，選出一個最優的子集。

過濾法（Filter Methods）：獨立于模型，根據特征本身的統計特性（如相關系數、卡方檢驗、信息增益）來打分和排序，然后選擇得分最高的特征。速度快，但沒有考慮特征間的組合效應。
包裝法（Wrapper Methods）：將特征選擇過程“包裝”在模型訓練中。它把特征子集的選擇看作一個搜索問題，用模型的性能作為評估標準來尋找最優子集。例如，遞歸特征消除（Recursive Feature Elimination, RFE）。效果好，但計算成本高。
嵌入法（Embedded Methods）：將特征選擇嵌入到模型構建的過程中。例如，**L1正則化（如Lasso回歸）**在訓練時會自動將不重要特征的系數懲罰為0，從而實現了自動的特征選擇。這是目前非常推崇的方法。

2. 降維（Dimensionality Reduction）

降維不是簡單地“選擇”特征，而是通過線性或非線性變換，將高維數據投影到低維空間，同時盡可能多地保留原始數據的信息，創造出全新的、更少的特征。

主成分分析（Principal Component Analysis, PCA）：這是最經典的線性降維方法。它的思想是，尋找一個新的坐標系，使得數據在第一個新坐標軸（第一主成分）上的方差最大，在第二個新坐標軸（第二主成分）上的方差次之，且與第一個正交，以此類推。然后我們只保留前k個方差最大的主成分，就實現了降維。 PCA在數據可視化（將高維數據降到2D或3D進行觀察）和消除多重共線性方面非常有用。我們將在后續章節中更詳細地學習和實踐它。

結語

本章，我們完成了一次從“原始數據”到“精煉特征”的完整修行。我們學會了如何與數據對話（EDA），如何為數據“沐浴更衣”（清洗），以及如何為其“梳妝打扮”（特征工程）。

請牢記，特征工程是機器學習中創造力和領域知識價值最大的體現。好的特征，能讓簡單的模型大放異彩；而差的特征，即使是再強大的模型也無力回天。

現在，我們的數據已經準備就緒，可以隨時“喂”給模型了。下一章，我們將正式開啟各類主流機器學習模型的學習之旅，將這些精心準備的“食材”，烹飪成一道道美味的“算法大餐”。

第四章：模型的羅盤——評估與選擇

4.1 “度量衡”：分類、回歸與聚類模型的評估指標
4.2 “執其兩端而用中”：偏差與方差的權衡
4.3 “他山之石”：交叉驗證的智慧
4.4 “尋路”：網格搜索與超參數調優

經過前三章的修煉，我們已經學會了搭建環境、駕馭工具，并掌握了數據的“心法”。我們手中已經有了經過精心提煉的“燃料”——干凈、規整的特征。現在，是時候將這些燃料注入各種強大的“引擎”——機器學習模型了。

但在我們一頭扎進形形色色的算法海洋之前，一個至關重要的問題擺在面前：我們如何判斷一個模型是好是壞？

在兩個模型之間，我們如何客觀地選擇那個更好的？一個模型在訓練數據上表現完美，我們就能相信它在未來的新數據上同樣出色嗎？如何為模型選擇最佳的“配置參數”，讓其發揮最大潛能？

本章，便是解答這些問題的“羅盤”。我們將系統地學習模型評估與選擇的完整框架。首先，我們會為不同類型的任務（分類、回歸、聚類）建立一套精確的“度量衡”，即評估指標。接著，我們將深入探討所有模型都無法回避的兩個核心矛盾——偏差與方差，并學習如何通過學習曲線來診斷它們。隨后，我們將掌握交叉驗證這一強大的技術，以獲得對模型性能更穩定、更可靠的評估。最后，我們將學習如何像一位經驗豐富的工程師一樣，系統地為模型尋找最優的超參數。

掌握本章內容，您將擁有一雙“慧眼”，能夠洞悉模型的內在狀態，科學地評估其優劣，并自信地做出選擇。這是從“會用模型”到“用好模型”的關鍵一步。

4.1 “度量衡”：分類、回歸與聚類模型的評估指標

沒有度量，就無法優化。評估指標，就是我們衡量模型性能的尺子。不同的任務，需要用不同的尺子來量。我們不能用量身高的尺子去量體重，同樣，我們也不能用回歸的指標去評估分類模型。

4.1.1 分類任務的“是非題”：混淆矩陣的深層解讀

分類任務是最常見的機器學習問題之一。其輸出是離散的類別，如“是/否”、“貓/狗/鳥”、“A/B/C類”。對于最基礎的二元分類問題（例如，判斷一封郵件是否為垃圾郵件），模型的所有預測結果可以歸入四種情況。這四種情況共同構成了一個名為**混淆矩陣（Confusion Matrix）**的表格，它是幾乎所有分類評估指標的基石。

基本概念：真正例(TP)、假正例(FP)、真負例(FN)、假負例(TN)

我們以一個“AI醫生”判斷病人是否患有某種疾病（“陽性”為患病，“陰性”為健康）的場景為例來理解這四個概念：

真正例 (True Positive, TP)：病人確實患病（真實為正），AI醫生也正確地預測其為陽性（預測為正）。——?判斷正確
假正例 (False Positive, FP)：病人其實很健康（真實為負），但AI醫生卻錯誤地預測其為陽性（預測為正）。這是“誤報”，也稱為第一類錯誤 (Type I Error)。——?判斷錯誤
真負例 (True Negative, TN)：病人確實很健康（真實為負），AI醫生也正確地預測其為陰性（預測為負）。——?判斷正確
假負例 (False Negative, FN)：病人其實患有該病（真實為正），但AI醫生卻錯誤地預測其為陰性（預測為負）。這是“漏報”，也稱為第二類錯誤 (Type II Error)。——?判斷錯誤

這四者可以用一個2x2的矩陣清晰地展示出來：

	預測為正 (Predicted: 1)	預測為負 (Predicted: 0)
真實為正 (Actual: 1)	TP (真正例)	FN (假負例)
真實為負 (Actual: 0)	FP (假正例)	TN (真負例)

在Scikit-learn中，我們可以輕松計算混淆矩陣：

from sklearn.metrics import confusion_matrix
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt# 使用上一章處理過的泰坦尼克數據（假設已完成缺失值填充和編碼）
# 為了演示，我們簡化一下特征
df = sns.load_dataset('titanic')
# ... (此處省略上一章的數據清洗和特征工程代碼) ...
# 假設我們得到了一個可用的df_processed，包含特征X和目標y
# X = df_processed[['pclass', 'age_scaled', 'fare_scaled', 'is_alone', ...]]
# y = df_processed['survived']# 偽代碼演示流程
# X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# model = LogisticRegression()
# model.fit(X_train, y_train)
# y_pred = model.predict(X_test)# 假設我們有真實值y_test和預測值y_pred
y_test = pd.Series([1, 0, 0, 1, 0, 1, 0, 1, 1, 0]) # 真實標簽
y_pred = pd.Series([1, 0, 1, 1, 0, 0, 0, 1, 1, 0]) # 模型預測cm = confusion_matrix(y_test, y_pred)
print("混淆矩陣:\n", cm)# 可視化混淆矩陣
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')
plt.xlabel('Predicted Label')
plt.ylabel('True Label')
plt.show()

混淆矩陣本身信息量巨大，但不夠直觀，我們需要從中提煉出更易于比較的單一數值指標。

從混淆矩陣到核心指標：準確率、精確率、召回率、F1分數

準確率 (Accuracy)
- 定義：預測正確的樣本數占總樣本數的比例。
- 公式：(TP + TN) / (TP + TN + FP + FN)
- 解讀：這是最直觀的指標，衡量了模型“整體上做對了多少”。
- 陷阱：在數據不平衡的場景下，準確率具有極大的誤導性。例如，在一個99%的郵件都是正常郵件的數據集中，一個無腦地將所有郵件都預測為“正常”的模型，其準確率高達99%，但它毫無用處，因為它一個垃圾郵件都找不出來。
精確率 (Precision)
- 定義：在所有被預測為正例的樣本中，有多少是真正的正例。
- 公式：TP / (TP + FP)
- 解讀：它衡量的是模型的“查準率”。高精確率意味著“我預測你是正例，你大概率真的是正例”。它關心的是預測結果的質量。
- 應用場景：對“誤報”懲罰很高的場景。例如，垃圾郵件過濾，我們不希望把重要的正常郵件（如面試通知）錯誤地判為垃圾郵件（FP），此時精確率比召回率更重要。
召回率 (Recall / Sensitivity / True Positive Rate)
- 定義：在所有真實為正例的樣本中，有多少被模型成功地預測了出來。
- 公式：TP / (TP + FN)
- 解讀：它衡量的是模型的“查全率”。高召回率意味著“所有真實的正例，我基本都找出來了”。它關心的是對真實正例的覆蓋能力。
- 應用場景：對“漏報”懲罰很高的場景。例如，在疾病診斷或金融欺詐檢測中，我們寧可“誤報”一些健康人或正常交易（FP較高，精確率下降），也絕不希望“漏掉”一個真正的病人或欺詐行為（FN很低，召回率高）。
F1分數 (F1-Score)
- 定義：精確率和召回率的調和平均數。
- 公式：2 * (Precision * Recall) / (Precision + Recall)
- 解讀：它是一個綜合性指標，試圖在精確率和召回率之間找到一個平衡。只有當兩者都比較高時，F1分數才會高。
- 應用場景：當你希望同時關注精確率和召回率，或者當兩者存在矛盾時，F1分數是一個很好的參考。

在Scikit-learn中，這些指標都可以輕松計算：

from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, classification_reportprint("Accuracy:", accuracy_score(y_test, y_pred))
print("Precision:", precision_score(y_test, y_pred))
print("Recall:", recall_score(y_test, y_pred))
print("F1 Score:", f1_score(y_test, y_pred))# 或者使用classification_report一次性輸出所有指標
print("\nClassification Report:\n", classification_report(y_test, y_pred))

精確率與召回率的權衡：在“寧可錯殺”與“絕不放過”之間

精確率和召回率通常是一對“矛盾”的指標。

想象一下，模型在內部并不是直接輸出“0”或“1”，而是輸出一個“是正例的概率”（0到1之間）。我們通過設定一個**閾值（Threshold）**來做出最終判斷，例如，默認閾值是0.5，概率>0.5就判為1，否則為0。

如果我們提高閾值（例如，提高到0.9），模型會變得非常“謹慎”。只有非常有把握的才判為正例。這樣，FP會減少，精確率會提高；但同時，很多“有點像但把握不大”的正例會被漏掉（FN增加），導致召回率下降。這對應了“寧可錯殺一千，絕不放過一個（敵人）”的反面，即“寧可放過（漏掉）一些可疑分子，也要保證抓到的都是鐵證如山的真兇”。
如果我們降低閾值（例如，降低到0.1），模型會變得非常“激進”。只要有一點點像正例，就判為正例。這樣，FN會減少，召回率會提高；但同時，很多負例會被誤判為正例（FP增加），導致精確率下降。這對應了“寧可錯殺一千，絕不放過一個”的策略。

理解這種權衡關系至關重要。在實際應用中，我們需要根據業務需求，選擇一個合適的閾值，來平衡精確率和召回率。而**精確率-召回率曲線（P-R Curve）**正是可視化這種權衡的工具。

精確率與召回率的權衡：在“寧可錯殺”與“絕不放過”之間

精確率和召回率通常是一對“矛盾”的指標，它們之間存在一種此消彼長的權衡關系。理解這種權衡，是做出有效業務決策的關鍵。

想象一下，大多數分類模型（如邏輯回歸、神經網絡）在內部并不是直接輸出“0”或“1”的硬性類別，而是輸出一個“樣本屬于正例的概率”，這是一個介于0和1之間的連續值。我們最終看到的“0”或“1”的預測結果，是這個概率值與一個我們設定的**決策閾值（Decision Threshold）**比較得來的。默認情況下，這個閾值通常是0.5。

如果?模型輸出概率 > 閾值，則預測為正例（1）。
如果?模型輸出概率 <= 閾值，則預測為負例（0）。

現在，讓我們看看調整這個閾值會發生什么：

提高決策閾值（例如，從0.5提高到0.9）：
- 影響：模型會變得非常“保守”或“挑剔”。只有當它“極度確信”一個樣本是正例時（概率高達90%以上），才會將其預測為正例。
- 結果：
  - 大量的“疑似”正例會被劃為負例，導致假負例（FN）增加，從而召回率（Recall）急劇下降。
  - 由于標準嚴苛，被預測為正例的樣本，其“含金量”會很高，假正例（FP）會減少，從而精確率（Precision）會提高。
- 類比：“寧可放過一千，不可錯殺一人”。適用于對誤報（FP）容忍度極低的場景，如向用戶推送高價值但打擾性強的廣告。
降低決策閾值（例如，從0.5降低到0.1）：
- 影響：模型會變得非常“激進”或“敏感”。只要有一點點可能是正例的跡象（概率超過10%），它就會將其預測為正例。
- 結果：
  - 大量的“疑似”正例會被成功捕獲，假負例（FN）會減少，從而召回率（Recall）會提高。
  - 由于標準寬松，很多負例會被錯誤地劃入正例，假正例（FP）會增加，從而精確率（Precision）會下降。
- 類比：“寧可錯殺一千，不可放過一個”。適用于對漏報（FN）容忍度極低的場景，如癌癥篩查。

精確率-召回率曲線（Precision-Recall Curve, P-R Curve） 為了系統地觀察這種權衡關系，我們可以繪制P-R曲線。該曲線的橫坐標是召回率，縱坐標是精確率。它是通過從高到低移動決策閾值，在每個閾值下計算一組(Recall, Precision)值，然后將這些點連接而成。

from sklearn.metrics import precision_recall_curve# 假設model已經訓練好，并且可以輸出概率
# y_scores = model.predict_proba(X_test)[:, 1] # 獲取正例的概率# 偽代碼演示
y_test = pd.Series([1, 0, 0, 1, 0, 1, 0, 1, 1, 0])
y_scores = pd.Series([0.9, 0.4, 0.6, 0.8, 0.3, 0.45, 0.2, 0.85, 0.7, 0.1]) # 模型輸出的概率precisions, recalls, thresholds = precision_recall_curve(y_test, y_scores)plt.figure(figsize=(8, 6))
plt.plot(recalls, precisions, marker='.')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall Curve')
plt.grid(True)
plt.show()

一根理想的P-R曲線會盡可能地靠近右上角（即在相同的召回率下，精確率盡可能高）。曲線下方的面積（AUC-PR）也可以作為一個綜合評估指標，面積越大，模型性能越好。

4.1.2 超越單一閾值：ROC曲線與AUC值的“全局觀”

P-R曲線非常適合評估在不平衡數據集上的模型性能。但還有一個更常用、更通用的評估工具——ROC曲線（Receiver Operating Characteristic Curve）。

ROC曲線的繪制：真正例率(TPR) vs. 假正例率(FPR)

ROC曲線描繪了兩個關鍵指標之間的關系：

真正例率 (True Positive Rate, TPR)：這其實就是我們已經學過的召回率（Recall）。它衡量模型“抓住了多少真病人”。
- TPR = TP / (TP + FN)
假正例率 (False Positive Rate, FPR)：它衡量的是，在所有真實的負例中，有多少被模型錯誤地預測為了正例。
- FPR = FP / (FP + TN)

ROC曲線的繪制過程與P-R曲線類似，也是通過不斷移動決策閾值，在每個閾值下計算一組(FPR, TPR)值，然后將這些點連接而成。

AUC的含義：模型整體排序能力的量化

ROC曲線解讀：
- 曲線上的每個點代表一個特定的決策閾值。
- 左下角(0,0)點：閾值設為1，模型將所有樣本都預測為負，TPR和FPR都為0。
- 右上角(1,1)點：閾值設為0，模型將所有樣本都預測為正，TPR和FPR都為1。
- 左上角(0,1)點：理想的完美模型，FPR為0（沒有誤報），TPR為1（沒有漏報）。
- 對角線（y=x）：代表一個“隨機猜測”模型。一個有價值的模型，其ROC曲線必須在對角線上方。
- 曲線越靠近左上角，說明模型在相同的“誤報成本”（FPR）下，能獲得更高的“查全率”（TPR），性能越好。
AUC (Area Under the Curve)： AUC值就是ROC曲線下方的面積。它是一個介于0和1之間的數值。
- AUC = 1：完美分類器。
- AUC = 0.5：隨機猜測模型。
- AUC < 0.5：模型性能差于隨機猜測（可能把標簽搞反了）。
- 0.5 < AUC < 1：模型具有一定的預測價值，值越大越好。

AUC有一個非常直觀的統計學解釋：它等于從所有正例中隨機抽取一個樣本，再從所有負例中隨機抽取一個樣本，該模型將正例的預測概率排在負例之前的概率。 因此，AUC衡量的是模型整體的排序能力，而不依賴于某個特定的決策閾值。

from sklearn.metrics import roc_curve, auc# y_scores 同樣是模型輸出的正例概率
fpr, tpr, thresholds = roc_curve(y_test, y_scores)
roc_auc = auc(fpr, tpr)plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (area = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--') # 繪制對角線
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.grid(True)
plt.show()

何時關注ROC/AUC，何時關注P-R曲線

當正負樣本分布相對均衡時，ROC/AUC是一個非常穩定且全面的評估指標。
當處理嚴重的數據不平衡問題時，P-R曲線通常能提供更多的信息。因為在極不平衡的數據中，FPR的分母（FP+TN）由于TN數量巨大，即使FP顯著增加，FPR的變化也可能不明顯，導致ROC曲線呈現出過于“樂觀”的結果。而P-R曲線的兩個指標（Precision和Recall）都聚焦于正例，對正例的預測變化更為敏感。

4.1.3 回歸任務的“度量尺”：衡量預測的“遠近”

回歸任務的目標是預測一個連續值，如房價、氣溫。評估回歸模型，就是衡量預測值與真實值之間的“距離”或“誤差”。

誤差的基本度量：MAE, MSE, RMSE

假設真實值為 y，預測值為 ?。

平均絕對誤差 (Mean Absolute Error, MAE)
- 公式：1/n * Σ|y - ?|
- 解讀：計算每個樣本的預測誤差的絕對值，然后取平均。它直接反映了預測誤差的平均大小，單位與目標變量相同，易于理解。
均方誤差 (Mean Squared Error, MSE)
- 公式：1/n * Σ(y - ?)2
- 解讀：計算每個樣本的預測誤差的平方，然后取平均。由于平方的存在，MSE對較大的誤差（離群點）給予了更高的權重。如果你的業務場景中，大的誤差是不可接受的，那么MSE是一個很好的懲罰指標。但其單位是目標變量單位的平方，不易解釋。
均方根誤差 (Root Mean Squared Error, RMSE)
- 公式：sqrt(MSE)
- 解讀：它就是MSE開根號。這樣做的好處是，其單位與目標變量恢復一致，同時保留了MSE對大誤差敏感的特性。RMSE可能是回歸任務中最常用的評估指標。

from sklearn.metrics import mean_absolute_error, mean_squared_errory_true_reg = [3, -0.5, 2, 7]
y_pred_reg = [2.5, 0.0, 2, 8]mae = mean_absolute_error(y_true_reg, y_pred_reg)
mse = mean_squared_error(y_true_reg, y_pred_reg)
rmse = np.sqrt(mse)print(f"MAE: {mae}")
print(f"MSE: {mse}")
print(f"RMSE: {rmse}")

相對度量：R2 (決定系數)的解釋與誤區

R2 (R-squared / Coefficient of Determination)
- 公式：1 - (Σ(y - ?)2) / (Σ(y - ?)2)?，其中???是真實值的平均值。
- 解讀：R2衡量的是模型所解釋的因變量方差的比例。通俗地說，它表示你的模型在多大程度上“解釋”了數據的變動。
  - R2 = 1：模型完美預測了所有數據。
  - R2 = 0：模型的表現等同于一個“基準模型”，這個基準模型總是預測所有樣本的值為真實值的平均數。
  - R2 < 0：模型表現比基準模型還差。
- 優點：提供了一個相對的性能度量（0%到100%），不受目標變量尺度的影響。
- 誤區：R2有一個致命缺陷——當你向模型中添加任何新的特征時，即使這個特征毫無用處，R2的值也幾乎總是會增加或保持不變，絕不會下降。這使得它在比較包含不同數量特征的模型時具有誤導性。為此，**調整R2 (Adjusted R-squared)**被提出，它對特征的數量進行了懲罰，是一個更公允的指標。

4.1.4 無監督任務的“內省”：聚類效果的評估

評估聚類（Clustering）這類無監督任務比監督學習更具挑戰性，因為我們通常沒有“正確答案”（真實標簽）。評估方法分為兩類：

有真實標簽時（外部評估）

在某些特殊情況（如學術研究或驗證算法），我們手頭有數據的真實類別。此時，我們可以比較聚類結果和真實標簽的吻合程度。

蘭德指數 (Rand Index, RI)：衡量兩組聚類（預測的和真實的）中，所有“點對”分類一致性的比例。
互信息 (Mutual Information, MI)：從信息論角度衡量兩組聚類共享的信息量。

無真實標簽時（內部評估）

這是更常見的情況。內部評估僅利用數據本身和聚類結果來進行。

輪廓系數 (Silhouette Coefficient)：這是最常用、最直觀的內部評估指標。它為每一個樣本計算一個輪廓分數，該分數衡量：
- a: 該樣本與其所在簇內其他所有點的平均距離（簇內凝聚度）。
- b: 該樣本與距離它最近的下一個簇內所有點的平均距離（簇間分離度）。
- 輪廓分數 =?(b - a) / max(a, b)
- 解讀：
  - 分數接近?+1：說明樣本遠離相鄰簇，很好地被分配到了當前簇（凝聚度和分離度都好）。
  - 分數接近?0：說明樣本位于兩個簇的邊界上。
  - 分數接近?-1：說明樣本可能被分配到了錯誤的簇。
- 整個數據集的輪廓系數是所有樣本輪廓分數的平均值。
Calinski-Harabasz指數 (CH Index)：通過計算簇間散度與簇內散度的比值來評估。比值越大，意味著簇間分離得越遠，簇內凝聚得越緊，聚類效果越好。

from sklearn.metrics import silhouette_score
from sklearn.cluster import KMeans# 假設X_cluster是待聚類的數據
# kmeans = KMeans(n_clusters=3, random_state=42, n_init=10)
# labels = kmeans.fit_predict(X_cluster)
# score = silhouette_score(X_cluster, labels)
# print(f"Silhouette Score: {score}")

4.2 “執其兩端而用中”：偏差與方差的權衡

掌握了評估指標，我們就有了一把尺子。但有時我們會發現，模型在一個數據集上表現優異，換個數據集就一塌糊涂。這背后，是所有監督學習模型都必須面對的一對核心矛盾——偏差（Bias）與方差（Variance）。

4.2.1 模型的兩種“原罪”：偏差(Bias)與方差(Variance)

想象我們用不同的訓練數據集（來自同一數據源）多次訓練同一個模型，然后去預測同一個測試點。

偏差：描述的是模型所有預測值的平均值與真實值之間的差距。高偏差意味著模型系統性地偏離了真相。
方差：描述的是模型不同次預測值之間的離散程度或散布范圍。高方差意味著模型對訓練數據的微小變化極其敏感。

一個好的模型，應該既沒有系統性的偏離（低偏差），又對數據的擾動不那么敏感（低方差）。

偏差：模型對真相的“固有偏見”

高偏差的根本原因是模型過于簡單，無法捕捉數據中復雜的真實規律。它就像一個固執的“老學究”，腦子里只有幾條簡單的規則（如一條直線），試圖用它去解釋一個復雜的世界（如一條曲線）。無論給他多少數據，他都堅持自己的“偏見”。

方差：模型對數據的“過度敏感”

高方差的根本原因是模型過于復雜，它不僅學習了數據中普適的規律，還把訓練數據中的噪聲和隨機性也當作了“真理”來學習。它就像一個“書呆子”，把訓練集這本“教科書”背得滾瓜爛熟，每一個細節都記得清清楚楚，但缺乏舉一反三的能力。換一本“模擬試卷”（測試集），他就傻眼了。

4.2.2 欠擬合與過擬合：模型學習的“執念”與“妄念”

偏差和方差的概念，最終體現在模型的兩種常見狀態上：

欠擬合(Underfitting)：學得太少，想得太簡單（高偏差）

表現：模型在訓練集上的表現就很差，在測試集上的表現同樣很差。
原因：通常是模型復雜度太低（如用線性模型去擬合非線性數據），或者特征太少。

過擬合(Overfitting)：學得太細，想得太復雜（高方差）

表現：模型在訓練集上表現極好，甚至接近完美，但在測試集上的表現卻大幅下降。訓練集和測試集性能之間存在巨大鴻溝。
原因：通常是模型復雜度過高（如一個深度很深的決策樹），或者數據量相對于模型復雜度來說太少。

偏差-方差權衡（Bias-Variance Trade-off）：模型復雜度與這兩者之間存在一個U型關系。

非常簡單的模型：高偏差，低方差。
非常復雜的模型：低偏差，高方差。我們的目標，是在這個U型曲線的谷底找到一個平衡點，使得總誤差（約等于偏差2 + 方差）最小。

4.2.3 診斷之道：學習曲線的可視化解讀

如何判斷我們的模型正處于欠擬合、過擬合還是理想狀態？**學習曲線（Learning Curves）**是一個強大的診斷工具。

學習曲線展示的是，隨著訓練樣本數量的增加，模型的訓練集得分和驗證集得分如何變化。

繪制學習曲線：訓練集與驗證集得分隨樣本量變化的軌跡

from sklearn.model_selection import learning_curve# model = LogisticRegression() # 或其他任何模型
# train_sizes, train_scores, validation_scores = learning_curve(
#     estimator=model,
#     X=X, y=y,
#     train_sizes=np.linspace(0.1, 1.0, 10), # 訓練樣本的比例
#     cv=5, # 交叉驗證折數
#     scoring='accuracy' # 評估指標
# )# # 計算均值和標準差
# train_scores_mean = np.mean(train_scores, axis=1)
# validation_scores_mean = np.mean(validation_scores, axis=1)# # 繪制曲線
# plt.plot(train_sizes, train_scores_mean, 'o-', color="r", label="Training score")
# plt.plot(train_sizes, validation_scores_mean, 'o-', color="g", label="Cross-validation score")
# plt.title("Learning Curve")
# plt.xlabel("Training examples")
# plt.ylabel("Score")
# plt.legend(loc="best")
# plt.grid()
# plt.show()

從曲線形態診斷模型是“欠”還是“過”

理想狀態：
- 隨著樣本增加，訓練得分和驗證得分都逐漸升高并最終收斂。
- 收斂時，兩條曲線靠得很近，且得分都很高。
高偏差（欠擬合）：
- 兩條曲線很早就收斂了，且收斂到一個比較低的得分水平。
- 兩條曲線靠得很近。
- 解讀：模型太簡單了，即使給它再多的數據，它也學不到更多東西了。性能的瓶頸在于模型本身。
高方差（過擬合）：
- 訓練得分一直很高，而驗證得分一直比較低。
- 兩條曲線之間存在明顯的、持續的差距（Gap）。
- 解讀：模型在訓練集上“死記硬背”，但泛化能力差。好消息是，隨著樣本量的增加，這個差距有縮小的趨勢，說明增加數據量可能有助于緩解過擬合。

4.2.4 應對之策：降低偏差與方差的常用策略

解決高偏差（欠擬合）：
1. 增加模型復雜度：換用更強大的模型（如從線性模型換到梯度提升樹或神經網絡）。
2. 獲取或創造更多特征：讓模型有更多的信息來源來學習。
3. 減少正則化：正則化是用來對抗過擬合的，如果模型已經欠擬合，應減小正則化強度。
解決高方差（過擬合）：
1. 增加數據量：這是最有效但往往也最昂貴的方法。
2. 降低模型復雜度：使用更簡單的模型，或者減少現有模型的參數（如降低決策樹的深度）。
3. 正則化（Regularization）：在損失函數中加入一個懲罰項，對模型的復雜性（如大的權重）進行懲罰。L1和L2正則化是經典方法。
4. 特征選擇/降維：移除不相關或冗余的特征。
5. 集成學習（Ensemble Methods）：如Bagging（隨機森林），通過平均多個不同模型的結果來降低方差。
6. Dropout（主要用于神經網絡）：在訓練過程中隨機“丟棄”一部分神經元，強迫網絡學習更魯棒的特征。

4.3 “他山之石”：交叉驗證的智慧

在診斷模型的過程中，我們反復提到了“驗證集”。一個常見的做法是將數據一次性劃分為訓練集、驗證集和測試集。但這種方法存在一個嚴重問題。

4.3.1 為何需要交叉驗證？簡單“訓練/測試集”劃分的陷阱

數據劃分的偶然性：你碰巧分到驗證集里的數據可能特別“簡單”或特別“困難”，導致你對模型性能的評估過于樂觀或悲觀。換一種隨機劃分方式，結果可能截然不同。
評估結果的不穩定：基于一次劃分的評估結果，其隨機性太大，不夠可靠。
數據浪費：在數據量本就不多的情況下，留出一部分數據只用于驗證，是一種浪費。

交叉驗證（Cross-Validation, CV）正是為了解決這些問題而生的智慧。

4.3.2 K-折交叉驗證（K-Fold Cross-Validation）：讓每一份數據都發光

K-折交叉驗證是應用最廣泛的交叉驗證技術。

K-折的執行流程：分割、訓練、驗證、取平均

分割：將整個訓練數據集隨機地、不重復地劃分為K個大小相似的子集（稱為“折”，Fold）。
循環：進行K次循環，在每一次循環中：
- 取其中1個折作為驗證集。
- 取其余的K-1個折合并作為訓練集。
- 在該訓練集上訓練模型，并在該驗證集上進行評估，得到一個性能得分。
取平均：將K次循環得到的K個性能得分進行平均，得到最終的、更穩健的交叉驗證得分。

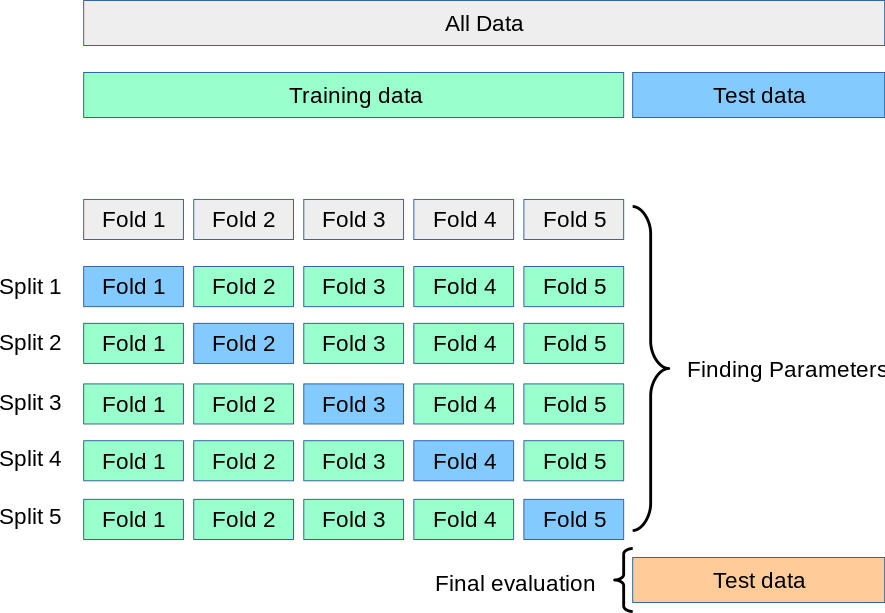
K-Fold Cross-Validation

優點：

所有數據都參與了訓練和驗證，數據利用率高。
得到的評估結果是K次評估的平均值，大大降低了偶然性，更為穩定和可靠。

如何選擇合適的K值？

K的常用取值是5或10。

K值較小（如3）：每次訓練的數據量較少（2/3），驗證集較大（1/3）。偏差較高，方差較低，計算成本也低。
K值較大（如10）：每次訓練的數據量較多（9/10），更接近于在全部數據上訓練。偏差較低，但由于不同折的訓練集重合度高，K個模型會比較相似，導致最終評估結果的方差可能較高。計算成本也更高。

4.3.3 特殊場景下的變體：分層K-折與留一法

分層K-折（Stratified K-Fold）：處理不平衡分類問題的利器

在分類問題中，如果直接用標準K-Fold，可能會出現某個折中正例或負例的比例與整體數據集差異很大的情況，甚至某個折中完全沒有某個類別的樣本。

分層K-折在進行數據劃分時，會確保每一個折中各個類別的樣本比例都與原始數據集中相應類別的比例大致相同。在處理不平衡分類問題時，這幾乎是必須使用的交叉驗證方法。

留一法（Leave-One-Out, LOO）：K-折的極端形式及其優缺點

留一法是K-折交叉驗證的一個特例，即K=N（N為樣本總數）。每次只留下一個樣本作為驗證集，其余N-1個樣本都作為訓練集。

優點：數據利用率最高，評估結果的偏差最低。
缺點：計算成本極高（需要訓練N個模型），且評估結果的方差通常也較高。一般只在數據集非常小的情況下使用。

4.4 “尋路”：網格搜索與超參數調優

我們已經知道如何可靠地評估一個模型了。但一個模型的性能，還受到另一類參數的深刻影響——超參數。

4.4.1 參數 vs. 超參數：模型自身的“修行”與我們施加的“點化”

參數 (Parameters)：模型從數據中學習得到的值。例如，線性回歸的權重w和偏置b。我們無法手動設置它們，它們是訓練過程的結果。
超參數 (Hyperparameters)：我們在模型訓練之前手動設置的參數。它們是模型的“配置選項”，控制著學習過程的行為。例如：
- K近鄰算法中的K值。
- 決策樹的max_depth（最大深度）。
- SVM中的懲罰系數C和核函數kernel。
- 神經網絡的學習率learning_rate。

超參數調優（Hyperparameter Tuning）的目的，就是為我們的模型找到一組能使其性能最佳的超參數組合。

4.4.2 傳統的尋路者：網格搜索（Grid Search）

網格搜索是一種簡單粗暴但有效的超參數搜索方法。

定義參數網格與暴力搜索

定義網格：為每一個你想要調優的超參數，定義一個候選值列表。這些列表組合在一起，就形成了一個多維的“網格”。
暴力搜索：遍歷網格中每一個可能的超參數組合。對每一個組合，使用交叉驗證來評估其性能。
選擇最優：選擇那個在交叉驗證中平均得分最高的超參數組合。

網格搜索與交叉驗證的結合（GridSearchCV）

Scikit-learn提供了GridSearchCV這個強大的工具，將網格搜索和交叉驗證完美地結合在了一起。

from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC# 1. 定義模型
model = SVC()# 2. 定義超參數網格
param_grid = {'C': [0.1, 1, 10, 100],'gamma': [1, 0.1, 0.01, 0.001],'kernel': ['rbf', 'linear']
}# 3. 創建GridSearchCV對象
# cv=5表示使用5折交叉驗證
grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=5, scoring='accuracy', verbose=2)# 4. 執行搜索 (在訓練數據上)
# grid_search.fit(X_train, y_train)# 5. 查看最佳參數和最佳得分
# print("Best Parameters:", grid_search.best_params_)
# print("Best Score:", grid_search.best_score_)# 6. 獲取最佳模型
# best_model = grid_search.best_estimator_

網格搜索的“維度詛咒”

網格搜索的主要缺點是計算成本高。如果超參數數量增多，或者每個超參數的候選值增多，需要嘗試的組合數量會呈指數級增長，這就是所謂的“維度詛咒”。

4.4.3 更聰明的探索者：隨機搜索（Random Search）

隨機搜索是對網格搜索的一個簡單而又常常更高效的替代方案。

從“地毯式”到“撒胡椒面式”的轉變

隨機搜索不再嘗試所有可能的組合，而是在指定的參數分布（如一個列表或一個連續分布）中，隨機地采樣固定數量（由n_iter參數指定）的超參數組合。

為何隨機搜索常常更高效？

研究表明，對于很多模型來說，其性能主要由少數幾個“關鍵”超參數決定。

網格搜索可能會在那些不重要的超參數上浪費大量時間進行精細的、不必要的嘗試。
隨機搜索則更有可能在相同的計算預算內，在那些“關鍵”超參數上探索到更多樣化的值，從而有更大幾率找到一個優秀的組合。

在Scikit-learn中，使用RandomizedSearchCV，其用法與GridSearchCV非常相似。

4.4.4 前沿的向導：貝葉斯優化等高級方法簡介

當超參數搜索的成本極高時（例如，訓練一個深度學習模型可能需要數天），網格搜索和隨機搜索這種“盲目”的探索就顯得效率低下了。

貝葉斯優化的思想：利用先驗信息指導下一次嘗試

貝葉斯優化是一種更智能的搜索策略。它將超參數與模型性能的關系看作一個需要學習的函數。

它首先嘗試幾個隨機點。
然后，它根據已有的（超參數組合，性能得分）結果，建立一個概率模型（代理模型），來“猜測”這個未知函數的樣子。
接著，它利用這個代理模型，去選擇下一個最有可能帶來性能提升的超參數組合進行嘗試（而不是隨機選）。
不斷重復2和3，直到達到預設的迭代次數。

它就像一個聰明的探礦者，會根據已經挖到的礦石信息，來判斷下一鏟子應該挖在哪里，而不是到處亂挖。

何時考慮使用更高級的調優方法

當單次模型評估的成本非常高昂，且超參數空間復雜時，就應該考慮使用貝葉斯優化（如hyperopt, scikit-optimize等庫）或其更先進的變體。

結語

本章，我們打造了一套完整的模型評估與選擇的“羅盤”。我們學會了如何用精確的“度量衡”來衡量模型，如何洞察“偏差與方差”這對核心矛盾，如何用“交叉驗證”的智慧獲得可靠的評估，以及如何用“網格/隨機搜索”的策略為模型找到最佳的“配置”。

這套框架是獨立于任何具體模型的通用方法論。掌握了它，您就擁有了在算法海洋中自信航行的能力。從下一章開始，我們將正式揚帆起航，逐一探索那些主流的機器學習模型。屆時，本章所學的一切，都將成為我們評估、診斷和優化這些模型的強大武器。

第二部分：術法萬千——主流機器學習模型詳解

核心目標： 深入剖析各類主流算法的原理、數學基礎和代碼實現。強調每個模型的適用場景、優缺點，并結合實例進行“庖丁解牛”式的講解。

第五章：監督學習之“判別”——分類算法

5.1 邏輯回歸：看似回歸，實為分類的智慧
5.2 K-近鄰（KNN）：“物以類聚，人以群分”的樸素哲學
5.3 支撐向量機（SVM）：“一劃開天”的數學之美
5.4 決策樹與隨機森林：“集思廣益”的集成智慧
5.5 樸素貝葉斯：“執果索因”的概率思維

歡迎來到機器學習的核心腹地。從本章開始，我們將學習具體的算法，將前幾章的理論、工具與方法論付諸實踐。我們將從監督學習中的**分類（Classification）**任務開始。分類，顧名思義，就是讓機器學會“分辨類別”，它旨在預測一個離散的目標變量。

生活中的分類問題無處不在：判斷一封郵件是否為垃圾郵件，識別一張圖片中的動物是貓還是狗，評估一筆交易是否存在欺詐風險，或者預測一位客戶是否會流失。這些都是分類算法大顯身手的舞臺。

本章將介紹五種最經典、最基礎、也是應用最廣泛的分類算法。它們各自代表了一種獨特的解決問題的哲學：邏輯回歸的概率建模、K-近鄰的類比推理、支撐向量機的幾何間隔、決策樹的邏輯規則以及樸素貝葉斯的概率推斷。

學習這些算法時，請重點關注：

它的核心思想是什么？
它是如何學習和預測的？
它的關鍵超參數有哪些，分別控制什么？
它的優缺點是什么，適用于哪些場景？

掌握了這些，您便能像一位經驗豐富的工匠，為不同的任務選擇最合適的工具。

5.1 邏輯回歸：看似回歸，實為分類的智慧

邏輯回歸（Logistic Regression）是您在分類領域遇到的第一個，也可能是最重要的算法之一。它的名字里雖然帶有“回歸”，但請不要被誤導，它是一個地地道道的分類算法。它因其簡單、高效、可解釋性強且輸出結果為概率而備受青睞，常常被用作解決實際問題的首選基線模型。

5.1.1 從線性回歸到邏輯回歸：跨越“預測值”到“預測概率”的鴻溝

要理解邏輯回歸，最好的方式是從我們熟悉的線性回歸出發。線性回歸的目標是擬合一條直線（或超平面）來預測一個連續值，其公式為： ? = w? + w?x? + w?x? + ... + w?x?

線性回歸的局限性 那我們能否直接用它來做分類呢？比如，我們規定 ? > 0.5 就判為類別1，否則為類別0。這樣做有兩個致命問題：

輸出范圍不匹配：線性回歸的輸出???是一個實數，范圍是?(-∞, +∞)。而我們想要的分類結果，最好是一個表示“概率”的、在?(0, 1)?區間內的值。直接比較???和0.5，物理意義不明確。
對離群點敏感：如果在數據中加入一個x值很大的離群點，線性回歸的擬合直線會被嚴重“拉偏”，可能導致原本正確的決策邊界發生巨大偏移，造成錯誤的分類。

我們需要一個“轉換器”，能將線性回歸 (-∞, +∞) 的輸出，優雅地“壓縮”到 (0, 1) 的概率區間內。

Sigmoid函數的引入 這個神奇的“轉換器”就是Sigmoid函數（也稱Logistic函數），它的數學形式如下： σ(z) = 1 / (1 + e??)

這里的 z 就是我們線性回歸的輸出 w? + w?x? + ...。Sigmoid函數具有非常優美的S型曲線形態：

無論輸入?z?多大或多小，其輸出?σ(z)?始終在?(0, 1)?區間內。
當?z = 0?時，σ(z) = 0.5。
當?z -> +∞?時，σ(z) -> 1。
當?z -> -∞?時，σ(z) -> 0。

通過將線性回歸的輸出 z 作為Sigmoid函數的輸入，我們就構建了邏輯回歸的核心模型： P(y=1 | X) = σ(z) = 1 / (1 + e?(w?X + b)) 這個公式的含義是：在給定特征 X 的條件下，樣本類別 y 為1的概率。

5.1.2 模型解讀：概率、決策邊界與損失函數

概率的解釋 邏輯回歸的輸出 P(y=1|X) 是一個真正的概率值，這極具價值。例如，一個癌癥預測模型輸出0.9，意味著它有90%的把握認為該病人患有癌癥。這個概率值本身就可以用于風險排序、設定不同的告警級別等。有了概率，分類就變得順理成章：

如果?P(y=1|X) > 0.5，則預測為類別1。
如果?P(y=1|X) <= 0.5，則預測為類別0。

決策邊界（Decision Boundary） 決策邊界是模型在特征空間中將不同類別分開的那條“線”或“面”。對于邏輯回歸，當 P(y=1|X) = 0.5 時，分類結果處于臨界狀態。這對應于 σ(z) = 0.5，也就是 z = w?X + b = 0。所以，邏輯回歸的決策邊界就是由 w?X + b = 0 這條方程所定義的線性邊界。

在二維空間中，它是一條直線。
在三維空間中，它是一個平面。
在高維空間中，它是一個超平面。

重要：邏輯回歸本身是一個線性分類器，它的決策邊界是線性的。如果數據的真實邊界是非線性的，基礎的邏輯回歸模型將表現不佳。（當然，通過特征工程，如添加多項式特征，可以使其學習非線性邊界）。

損失函數 模型如何學習到最優的權重 w 和偏置 b 呢？它需要一個**損失函數（Loss Function）**來衡量當前模型的預測與真實標簽之間的“差距”，然后通過優化算法（如梯度下降）來最小化這個損失。

對于邏輯回歸，我們不能使用線性回歸的均方誤差（MSE），因為它會導致一個非凸的損失函數，優化起來非常困難。我們使用的是對數損失（Log Loss），也稱為二元交叉熵損失（Binary Cross-Entropy Loss）。

對于單個樣本，其損失定義為：

如果真實標簽?y = 1：Loss = -log(p)，其中?p?是模型預測為1的概率。
如果真實標簽?y = 0：Loss = -log(1-p)。

直觀理解：

當真實標簽是1時，我們希望預測概率?p?越接近1越好。如果?p?趨近于1，-log(p)?就趨近于0，損失很小。如果模型錯誤地預測?p?趨近于0，-log(p)?會趨近于無窮大，給予巨大的懲罰。
當真實標簽是0時，情況正好相反。

這個分段函數可以優雅地寫成一個統一的式子： Loss = -[y * log(p) + (1 - y) * log(1 - p)] 整個訓練集的總損失就是所有樣本損失的平均值。模型訓練的目標，就是找到一組 w 和 b，使得這個總損失最小。

5.1.3 Scikit-learn實戰與正則化

代碼實現 在Scikit-learn中，使用邏輯回歸非常簡單。我們將以一個標準流程來展示其應用，這個流程也適用于后續將要學習的大多數模型。

# 導入必要的庫
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.preprocessing import StandardScaler
import pandas as pd
import seaborn as sns
import numpy as np# --- 準備數據 (假設使用泰坦尼克數據集) ---
# 為了代碼能獨立運行，我們快速進行一次極簡的數據預處理
df = sns.load_dataset('titanic')
df.drop(['deck', 'embark_town', 'alive', 'who', 'adult_male', 'class'], axis=1, inplace=True)
df['age'].fillna(df['age'].median(), inplace=True)
df['embarked'].fillna(df['embarked'].mode()[0], inplace=True)
df = pd.get_dummies(df, columns=['sex', 'embarked'], drop_first=True)
df.drop('name', axis=1, inplace=True) # 名字暫時不用
df.drop('ticket', axis=1, inplace=True) # 票號暫時不用X = df.drop('survived', axis=1)
y = df['survived']# 1. 劃分數據
# stratify=y 確保訓練集和測試集中，目標變量y的類別比例與原始數據一致，這在分類問題中很重要
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)# 2. 特征縮放 (對于邏輯回歸，特別是帶正則化的，這是個好習慣)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)# 3. 初始化并訓練模型
# penalty='l2'表示使用L2正則化，C是正則化強度的倒數
# solver='liblinear' 是一個適用于小數據集的優秀求解器
model = LogisticRegression(penalty='l2', C=1.0, solver='liblinear', random_state=42)
model.fit(X_train_scaled, y_train)# 4. 預測與評估
y_pred = model.predict(X_test_scaled)
print("--- 邏輯回歸基礎模型評估 ---")
print("混淆矩陣:\n", confusion_matrix(y_test, y_pred))
print("\n分類報告:\n", classification_report(y_test, y_pred))# 查看模型學習到的系數
# feature_names = X.columns
# coefs = pd.Series(model.coef_[0], index=feature_names).sort_values()
# print("\n模型系數:\n", coefs)

正則化參數（C） 邏輯回歸很容易過擬合，特別是當特征數量很多時。為了對抗過擬合，我們引入正則化。LogisticRegression類中最關鍵的超參數就是C和penalty。

penalty：指定使用哪種正則化，通常是'l1'或'l2'。
- L2正則化（默認）：懲罰那些值很大的權重，使得所有權重都趨向于變小，但不會變為0。它讓模型的決策邊界更平滑。
- L1正則化：同樣懲罰大權重，但它有一個特性，就是能將一些不重要的特征的權重直接懲罰為0，從而實現特征選擇。
C：正則化強度的倒數。它是一個正浮點數。
- C值越小，代表正則化懲罰越強，模型會更簡單，有助于防止過擬合（增加偏差，降低方差）。
- C值越大，代表正則化懲罰越弱，模型會更努力地去擬合訓練數據，可能導致過擬合（降低偏差，增加方差）。

C是我們需要通過交叉驗證來調優的最重要的超參數。下面我們使用GridSearchCV來尋找最優的C值。

# --- 使用GridSearchCV進行超參數調優 ---
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10, 100]}
grid_search = GridSearchCV(LogisticRegression(penalty='l2', solver='liblinear', random_state=42), param_grid, cv=5, scoring='accuracy')
grid_search.fit(X_train_scaled, y_train)print("\n--- 邏輯回歸超參數調優 ---")
print("最佳超參數:", grid_search.best_params_)
print("交叉驗證最佳得分:", grid_search.best_score_)# 使用最佳模型進行最終評估
best_model = grid_search.best_estimator_
y_pred_best = best_model.predict(X_test_scaled)
print("\n最佳模型在測試集上的分類報告:\n", classification_report(y_test, y_pred_best))

優缺點與適用場景

優點：
1. 簡單快速：訓練速度快，計算成本低，易于實現。
2. 可解釋性強：可以查看每個特征的權重coef_，理解特征對結果的影響方向和大小，便于向業務方解釋。
3. 輸出概率：結果為概率，而不僅僅是類別，這在很多場景下（如風險評估）非常有用。
4. 應用廣泛：是許多工業界應用（如廣告點擊率預測、金融風控）的基石和首選基線模型。
缺點：
1. 線性模型：模型假設是線性的，容易欠擬合，無法直接捕捉數據中的非線性關系。
2. 對特征工程依賴高：需要手動創造特征（如多項式特征）來幫助模型學習非線性。
3. 對多重共線性敏感：如果特征之間高度相關，模型權重的解釋性會下降。

適用場景：

作為任何分類問題的首選基線模型（Baseline Model）。在嘗試復雜模型前，先用邏輯回歸跑一個結果，可以幫你判斷問題的難度，并為后續優化提供一個比較的基準。
當需要一個可解釋的模型時。
當需要預測概率時。
對于大規模稀疏數據（如文本分類后的詞袋模型），邏輯回歸配合L1正則化常常表現出色。

5.2 K-近鄰（KNN）：“物以類聚，人以群分”的樸素哲學

K-近鄰（K-Nearest Neighbors, KNN）算法是機器學習中最簡單、最直觀的算法之一。它的核心思想完美地詮釋了中國的一句古話：“物以類聚，人以群分”。要判斷一個未知樣本的類別，只需看看它在特征空間中的“鄰居”們都屬于哪個類別即可。

5.2.1 算法核心思想：近朱者赤，近墨者黑

“懶惰學習”的代表 KNN是一種**懶惰學習（Lazy Learning）或稱基于實例的學習（Instance-based Learning）**算法。它與其他我們即將學習的算法（如邏輯回歸、SVM）有一個根本區別：

它沒有傳統意義上的“訓練”過程。所謂的“訓練”，僅僅是把所有訓練數據加載到內存中而已。它不會從數據中學習一個判別函數或模型參數。
真正的計算發生在“預測”階段。當一個新樣本需要被預測時，KNN才會開始工作。

三個核心要素 KNN的預測過程由三個核心要素決定：

K值的選擇：我們要看新樣本周圍的多少個“鄰居”。K是一個正整數。
距離度量：我們如何定義和計算樣本之間的“遠近”。
決策規則：根據K個鄰居的類別，如何做出最終的判決。最常見的是多數表決（Majority Voting）。

預測步驟：

計算未知樣本與訓練集中每一個樣本之間的距離。
找出距離最近的K個訓練樣本（即K個“鄰居”）。
統計這K個鄰居的類別。
將出現次數最多的那個類別，作為未知樣本的預測結果。

5.2.2 距離的度量與K值的選擇

常見的距離公式 距離度量是KNN的基石。最常用的距離是歐氏距離（Euclidean Distance），也就是我們初中就學過的兩點間直線距離公式。對于兩個n維向量 x 和 y： d(x, y) = sqrt(Σ(x? - y?)2)

此外，還有其他距離度量方式，如：

曼哈頓距離（Manhattan Distance）：d(x, y) = Σ|x? - y?|，想象在城市街區中只能沿格線行走時的距離。
閔可夫斯基距離（Minkowski Distance）：是歐氏距離和曼哈頓距離的推廣。

K值選擇的藝術 K值的選擇對KNN的性能至關重要，它直接影響著模型的偏差和方差。

較小的K值（如 K=1）：
- 模型非常“敏感”，容易受到噪聲點的影響。
- 決策邊界會變得非常復雜、不規則。
- 這會導致低偏差，但高方差，容易過擬合。
較大的K值（如 K=N，N為訓練樣本總數）：
- 模型非常“遲鈍”，無論新樣本在哪里，都會被預測為訓練集中數量最多的那個類別。
- 決策邊界會變得非常平滑。
- 這會導致高偏差，但低方差，容易欠擬合。

因此，選擇一個合適的K值是在偏差和方差之間做權衡。通常，我們會通過交叉驗證來尋找一個最優的K值。一個經驗法則是，K值通常選擇一個較小的奇數（以避免投票時出現平局）。

5.2.3 Scikit-learn實戰與數據標準化的重要性

代碼實現

from sklearn.neighbors import KNeighborsClassifier# 假設X_train_scaled, X_test_scaled, y_train, y_test已準備好# 初始化并訓練模型 (fit只是存儲數據)
knn = KNeighborsClassifier(n_neighbors=5) # 先選擇一個經驗值K=5
knn.fit(X_train_scaled, y_train)# 預測與評估
y_pred_knn = knn.predict(X_test_scaled)
print("--- KNN基礎模型評估 (K=5) ---")
print(classification_report(y_test, y_pred_knn))# 使用GridSearchCV尋找最優K值
param_grid_knn = {'n_neighbors': np.arange(1, 31, 2)} # 嘗試1到30之間的所有奇數
grid_search_knn = GridSearchCV(KNeighborsClassifier(), param_grid_knn, cv=5, scoring='accuracy')
grid_search_knn.fit(X_train_scaled, y_train)print("\n--- KNN超參數調優 ---")
print("最佳K值:", grid_search_knn.best_params_)
print("交叉驗證最佳得分:", grid_search_knn.best_score_)

數據標準化的必要性 對于KNN這類基于距離度量的模型，進行特征縮放（如標準化）是至關重要的，甚至是強制性的。

想象一個場景，我們有兩個特征：年齡（范圍20-80）和薪水（范圍5000-50000）。在計算歐氏距離時，薪水這個特征的數值差異會遠遠大于年齡的差異，從而在距離計算中占據絕對主導地位。這會使得年齡這個特征幾乎不起作用，這顯然是不合理的。

通過標準化（StandardScaler），我們將所有特征都轉換到同一個尺度下（均值為0，標準差為1），使得每個特征在距離計算中都有平等“話語權”。

優缺點與適用場景

優點：
1. 思想簡單，易于理解和實現。
2. 模型靈活：可以學習任意復雜的決策邊界。
3. 無需訓練：對于需要快速上線、數據不斷更新的場景有優勢。
缺點：
1. 計算成本高昂：預測一個新樣本需要與所有訓練樣本計算距離，當訓練集很大時，非常耗時。
2. 對內存需求大：需要存儲整個訓練集。
3. 對不平衡數據敏感：數量多的類別在投票中占優勢。
4. 對維度詛咒敏感：在高維空間中，所有點之間的距離都趨向于變得遙遠且相近，“鄰居”的概念變得模糊。

適用場景：

小到中等規模的數據集。
當問題的決策邊界高度非線性時。
作為一種快速的基線模型。

5.3 支撐向量機（SVM）：“一劃開天”的數學之美

支撐向量機（Support Vector Machine, SVM）是機器學習領域最強大、最優雅的算法之一。它誕生于上世紀90年代，在深度學習浪潮來臨之前，曾一度被認為是監督學習中效果最好的“大殺器”。SVM的核心思想是基于幾何間隔，尋找一個“最優”的決策邊界。

5.3.1 核心思想：尋找最大間隔的“最優”決策邊界

對于一個線性可分的二分類問題，能將兩類樣本分開的直線（或超平面）有無數條。邏輯回歸會找到其中一條，但SVM追求的是最好的那一條。

什么是“最好”？ SVM認為，最好的決策邊界應該是那條離兩邊最近的樣本點最遠的邊界。這條邊界就像在兩軍對壘的戰場中央劃下的一道“停火線”，它使得雙方（不同類別的樣本）都離這條線有盡可能大的“緩沖地帶”。

間隔（Margin）與支持向量（Support Vectors）

決策邊界：就是中間那條實線的超平面?w?x + b = 0。
間隔（Margin）：是決策邊界與兩側距離它最近的樣本點之間的垂直距離。SVM的目標就是最大化這個間隔。
支持向量（Support Vectors）：那些恰好落在間隔邊界上的樣本點。它們就像支撐起整個間隔的“樁子”。一個驚人的事實是：最終的決策邊界完全由這些支持向量決定，與其他樣本點無關。即使移動或刪除非支持向量的樣本點，決策邊界也不會改變。這使得SVM非常高效且魯棒。

從線性可分到線性不可分：軟間隔（Soft Margin） 現實世界的數據往往不是完美線性可分的，總會有一些噪聲點或“越界”的樣本。為了處理這種情況，SVM引入了**軟間隔（Soft Margin）**的概念。

軟間隔允許一些樣本點“犯規”，即可以處在間隔之內，甚至可以被錯誤分類。但這種“犯規”是要付出代價的。SVM引入了一個懲罰系數超參數 C：

C?控制了我們對“犯規”的容忍程度。
較大的C值：代表對犯規的懲罰很重，SVM會努力將所有樣本都正確分類，這可能導致間隔變窄，模型變得復雜，容易過擬合。
較小的C值：代表對犯規比較寬容，允許一些錯誤分類，以換取一個更寬的間隔。這會使模型更簡單，泛化能力可能更強，但可能欠擬合。

C是在偏差和方差之間進行權衡的關鍵。

5.3.2 核技巧（Kernel Trick）：低維到高維的“乾坤大挪移”

SVM最強大的武器是核技巧（Kernel Trick）。對于那些在原始特征空間中線性不可分的數據（例如，一個環形分布），SVM可以通過核技巧，巧妙地將其映射到一個更高維度的空間，使得數據在這個高維空間中變得線性可分。

核函數的魔力 想象一下，我們把二維平面上的一張紙（數據），通過某種方式向上“彎曲”，變成一個三維的碗狀。原本在紙上無法用一條直線分開的同心圓，在三維空間中就可以用一個水平面輕易地分開了。

核函數的神奇之處在于：它讓我們無需真正地去計算數據在高維空間中的坐標，就能得到數據點在高維空間中的內積結果。這極大地節省了計算量，使得在高維空間中尋找決策邊界成為可能。

常見的核函數

線性核（Linear Kernel）：kernel='linear'。實際上就是不做任何映射，在原始空間中尋找線性邊界。
多項式核（Polynomial Kernel）：kernel='poly'。可以將數據映射到多項式空間。
高斯徑向基核（Gaussian Radial Basis Function, RBF）：kernel='rbf'。這是最常用、最強大的核函數。它可以將數據映射到無限維空間，能夠學習任意復雜的非線性決策邊界。

5.3.3 Scikit-learn實戰與關鍵超參數

代碼實現

from sklearn.svm import SVC# 假設X_train_scaled, X_test_scaled, y_train, y_test已準備好# 初始化并訓練模型 (使用RBF核)
svm_model = SVC(kernel='rbf', C=1.0, gamma='scale', random_state=42)
svm_model.fit(X_train_scaled, y_train)# 預測與評估
y_pred_svm = svm_model.predict(X_test_scaled)
print("--- SVM基礎模型評估 ---")
print(classification_report(y_test, y_pred_svm))# 使用GridSearchCV進行超參數調優
param_grid_svm = {'C': [0.1, 1, 10],'gamma': ['scale', 0.1, 0.01],'kernel': ['rbf', 'linear']
}
grid_search_svm = GridSearchCV(SVC(random_state=42), param_grid_svm, cv=3, scoring='accuracy') # cv=3以加快速度
grid_search_svm.fit(X_train_scaled, y_train)print("\n--- SVM超參數調優 ---")
print("最佳超參數:", grid_search_svm.best_params_)
print("交叉驗證最佳得分:", grid_search_svm.best_score_)

關鍵超參數 對于使用RBF核的SVM，有兩個至關重要的超參數需要調優：

C?(懲罰系數)：如前所述，控制著對錯誤分類的懲罰力度，權衡著間隔寬度和分類準確性。
gamma?(核系數)：它定義了單個訓練樣本的影響范圍。
- 較小的gamma值：意味著影響范圍大，決策邊界會非常平滑，模型趨向于欠擬合（高偏差）。
- 較大的gamma值：意味著影響范圍小，只有靠近的樣本點才會對決策邊界產生影響，這會導致決策邊界非常曲折、復雜，模型趨向于過擬合（高方差）。

C和gamma通常需要一起進行網格搜索來尋找最優組合。

優缺點與適用場景

優點：
1. 在高維空間中非常有效，甚至當維度數大于樣本數時。
2. 內存效率高，因為它只使用一部分訓練點（支持向量）來做決策。
3. 非常通用，通過選擇不同的核函數，可以適應各種數據和決策邊界。
缺點：
1. 當樣本數量遠大于特征數量時，性能和速度通常不如一些集成模型（如隨機森林）。
2. 對缺失數據敏感。
3. 結果不易解釋，特別是使用非線性核時，它不像邏輯回歸或決策樹那樣直觀。
4. 沒有直接的概率輸出（雖然可以通過一些方法間接計算）。

適用場景：

復雜但中小型的數據集。
高維數據，如圖像識別、文本分類。
當需要一個非線性分類器時，SVM（特別是RBF核）是一個強大的選擇。

5.4 決策樹與隨機森林：“集思廣益”的集成智慧

決策樹（Decision Tree）是一種非常符合人類直覺的分類模型。它通過學習一系列“if-then”規則，來構建一個樹形的決策結構。而隨機森林（Random Forest）則是通過“集體智慧”，將許多棵決策樹組合起來，形成一個更強大、更穩健的模型。

5.4.1 決策樹：像人一樣思考的樹形結構

構建過程 決策樹的構建是一個遞歸的過程，目標是生成一棵泛化能力強、不純度低的樹。

選擇根節點：從所有特征中，選擇一個“最好”的特征作為樹的根節點。
分裂：根據這個最優特征的取值，將數據集分裂成若干個子集。
遞歸：對每個子集，重復步驟1和2，即選擇該子集下的最優特征進行分裂，生成新的子節點。
停止：當滿足停止條件時（如節點下的所有樣本都屬于同一類別，或達到預設的樹深），該節點成為葉子節點，不再分裂。

如何選擇最優特征進行分裂 “最好”的特征，是指那個能讓分裂后的數據集**“不純度”下降最大**的特征。我們希望每次分裂后，各個子集內部的類別盡可能地“純粹”（即大部分樣本屬于同一個類別）。衡量不純度的常用指標有：

基尼不純度（Gini Impurity）：Scikit-learn中的默認選擇。它衡量的是從數據集中隨機抽取兩個樣本，其類別標簽不一致的概率。基尼不純度越小，數據集越純。
信息增益（Information Gain）：基于信息熵（Entropy）的概念。信息熵衡量的是數據的不確定性。信息增益就是父節點的信息熵減去所有子節點信息熵的加權平均。信息增益越大，說明這次分裂帶來的“確定性”提升越大。

可視化與可解釋性 決策樹最大的優點之一就是高度的可解釋性。我們可以將訓練好的決策樹可視化出來，清晰地看到它的每一個決策規則。這使得它成為一個“白盒”模型，非常便于向非技術人員解釋。

剪枝（Pruning） 如果不加限制，決策樹會一直生長，直到每個葉子節點都只包含一個樣本，這會導致嚴重的過擬合。為了防止這種情況，我們需要對樹進行“剪枝”。

預剪枝（Pre-pruning）：在樹的生長過程中，通過設定一些條件提前停止分裂。常用的超參數包括：
- max_depth：樹的最大深度。
- min_samples_split：一個節點要分裂，至少需要包含的樣本數。
- min_samples_leaf：一個葉子節點至少需要包含的樣本數。
后剪枝（Post-pruning）：先生成一棵完整的決策樹，然后自底向上地考察非葉子節點，如果將該節點替換為葉子節點能提升模型的泛化性能，則進行剪枝。

5.4.2 集成學習入門：從“一個好漢”到“三個臭皮匠”

集成學習（Ensemble Learning）是一種強大的機器學習范式，它不依賴于單個模型，而是將多個弱學習器（weak learners）組合起來，形成一個強大的強學習器。俗話說“三個臭皮匠，頂個諸葛亮”，這就是集成學習的核心思想。

Bagging思想 Bagging（Bootstrap Aggregating的縮寫）是集成學習中最基礎的思想之一。它的目標是降低模型的方差。

自助采樣（Bootstrap）：從原始訓練集中，進行有放回地隨機抽樣，生成多個大小與原始數據集相同的自助樣本集。由于是有放回抽樣，每個自助樣本集中會包含一些重復樣本，也有些原始樣本未被抽到。
獨立訓練：在每個自助樣本集上，獨立地訓練一個基學習器（如一棵決策樹）。
聚合（Aggregating）：對于分類任務，使用多數表決的方式，將所有基學習器的預測結果進行投票，得出最終的集成預測。對于回歸任務，則取所有基學習器預測結果的平均值。

5.4.3 隨機森林（Random Forest）：決策樹的“集體智慧”

隨機森林就是以決策樹為基學習器的Bagging集成模型，并且在Bagging的基礎上，引入了進一步的“隨機性”。

“雙重隨機”的核心

樣本隨機（行抽樣）：繼承自Bagging，每個基決策樹都在一個自助樣本集上訓練。
特征隨機（列抽樣）：這是隨機森林的獨創。在每個節點進行分裂時，不是從所有特征中選擇最優特征，而是先從所有特征中隨機抽取一個子集（通常是sqrt(n_features)個），然后再從這個子集中選擇最優特征進行分裂。

為何隨機森林通常優于單棵決策樹

降低方差：Bagging的聚合過程本身就能有效降低方差。
增加模型多樣性：“特征隨機”這一步，使得森林中的每棵樹都長得“各不相同”，因為它們在每個節點上看到的“世界”（特征子集）都不同。這降低了樹與樹之間的相關性，使得投票結果更加穩健，進一步降低了整體模型的方差，有效防止了過擬合。

5.4.4 Scikit-learn實戰與特征重要性

代碼實現

from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier# --- 決策樹 ---
dt_model = DecisionTreeClassifier(max_depth=5, random_state=42)
dt_model.fit(X_train, y_train) # 決策樹對縮放不敏感，可以直接用原始數據
y_pred_dt = dt_model.predict(X_test)
print("--- 決策樹模型評估 ---")
print(classification_report(y_test, y_pred_dt))# --- 隨機森林 ---
rf_model = RandomForestClassifier(n_estimators=100, max_depth=5, random_state=42, n_jobs=-1)
rf_model.fit(X_train, y_train)
y_pred_rf = rf_model.predict(X_test)
print("\n--- 隨機森林模型評估 ---")
print(classification_report(y_test, y_pred_rf))

n_estimators是森林中樹的數量，n_jobs=-1表示使用所有CPU核心并行計算。

特征重要性（Feature Importance） 隨機森林還有一個非常有用的副產品——特征重要性。模型可以評估每個特征在所有樹的決策中所做的貢獻大小（通常是基于該特征帶來的不純度下降總量）。這為我們理解數據和篩選特征提供了極佳的洞察。

importances = rf_model.feature_importances_
feature_importances = pd.Series(importances, index=X.columns).sort_values(ascending=False)plt.figure(figsize=(10, 6))
sns.barplot(x=feature_importances, y=feature_importances.index)
plt.title('Feature Importances in Random Forest')
plt.show()

優缺點與適用場景

優點：
1. 性能強大：通常能獲得非常高的準確率，是許多競賽和工業應用中的主力模型。
2. 抗過擬合能力強：雙重隨機性使其非常穩健。
3. 對缺失值和異常值不敏感。
4. 無需特征縮放。
5. 能處理高維數據，并能輸出特征重要性。
缺點：
1. 可解釋性差：相比單棵決策樹，隨機森林是一個“黑盒”模型，難以解釋其內部決策邏輯。
2. 計算和內存開銷大：需要訓練和存儲數百棵樹。
3. 在某些噪聲很大的數據集上，可能會過擬合。

適用場景：

幾乎適用于任何分類（或回歸）問題，是工具箱中必備的“瑞士軍刀”。
當需要一個高性能、開箱即用的模型時。
用于特征選擇和數據探索。

5.5 樸素貝葉斯：“執果索因”的概率思維

樸素貝葉斯（Naive Bayes）是一類基于貝葉斯定理和特征條件獨立性假設的簡單概率分類器。盡管它的假設非常“樸素”，但在許多現實場景，尤其是文本分類中，其表現卻出人意料地好。

5.5.1 貝葉斯定理：概率論的基石

貝葉斯定理描述了兩個條件概率之間的關系。它的核心思想是根據“結果”來反推“原因”的概率。 P(A|B) = [P(B|A) * P(A)] / P(B)

在分類任務中，我們可以將其改寫為： P(類別 | 特征) = [P(特征 | 類別) * P(類別)] / P(特征)

P(類別 | 特征)：后驗概率（Posterior）。這是我們想求的，即在看到這些特征后，樣本屬于某個類別的概率。
P(特征 | 類別)：似然（Likelihood）。在某個類別下，出現這些特征的概率。這是模型需要從訓練數據中學習的。
P(類別)：先驗概率（Prior）。在不看任何特征的情況下，某個類別本身出現的概率。可以從訓練數據中直接統計。
P(特征)：證據（Evidence）。這些特征出現的概率。在預測時，對于所有類別，它是一個常數，因此可以忽略。

所以，樸素貝葉斯的預測過程就是：對于一個新樣本，計算它屬于每個類別的后驗概率，然后選擇后驗概率最大的那個類別作為預測結果。

5.5.2 “樸素”在何處？特征條件獨立性假設

計算P(特征 | 類別)，即P(特征?, 特征?, ... | 類別)，是非常困難的。為了簡化計算，樸素貝葉斯做出了一個非常強的假設：

特征條件獨立性假設：它假設在給定類別的情況下，所有特征之間是相互獨立的。 P(特征?, 特征?, ... | 類別) = P(特征? | 類別) * P(特征? | 類別) * ...

這個假設就是“樸素”一詞的來源。在現實中，特征之間往往是有關聯的（例如，在文本中，“機器學習”和“算法”這兩個詞就經常一起出現）。但這個看似不合理的假設，卻極大地簡化了計算，并使得樸素貝葉斯在實踐中依然表現良好。

不同類型的樸素貝葉斯 根據特征數據的不同分布，樸素貝葉斯有幾種常見的變體：

高斯樸素貝葉斯（GaussianNB）：假設連續型特征服從高斯分布（正態分布）。
多項式樸素貝葉斯（MultinomialNB）：適用于離散型特征，特別是文本分類中的詞頻計數。
伯努利樸素貝葉斯（BernoulliNB）：適用于二元特征（特征出現或不出現），也是文本分類的常用模型。

5.5.3 Scikit-learn實戰與文本分類應用

樸素貝葉斯最經典、最成功的應用領域莫過于文本分類。我們將以一個經典的垃圾郵件過濾為例，展示其工作流程。在文本處理中，我們通常使用MultinomialNB或BernoulliNB。

代碼實現 為了處理文本，我們首先需要將文字轉換成機器可以理解的數值形式。最常用的方法是詞袋模型（Bag-of-Words），它將每篇文檔表示為一個向量，向量的每個維度代表一個詞，值可以是該詞在文檔中出現的次數（詞頻）。Scikit-learn的CountVectorizer可以幫我們完成這個轉換。

make_pipeline是一個非常有用的工具，它可以將“特征提取”（如CountVectorizer）和“模型訓練”（如MultinomialNB）這兩個步驟串聯成一個無縫的處理流程。

from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
import pandas as pd# 假設我們有一個包含郵件文本和標簽的數據集
# 為了演示，我們創建一個簡單的數據集
data = {'text': ["SPECIAL OFFER! Buy now and get a 50% discount!","Hi Bob, can we schedule a meeting for tomorrow?","Congratulations! You've won a free cruise trip!","Please find the attached document for your review.","Limited time offer: exclusive access to cheap viagra.","Project update and next steps for our meeting.","URGENT: Your account has been compromised! Click here to secure it.","Thanks for your email, I will look into the document."],'label': ['spam', 'ham', 'spam', 'ham', 'spam', 'ham', 'spam', 'ham']
}
df_mail = pd.DataFrame(data)X_mail = df_mail['text']
y_mail = df_mail['label']# 劃分訓練集和測試集
X_train_mail, X_test_mail, y_train_mail, y_test_mail = train_test_split(X_mail, y_mail, test_size=0.25, random_state=42)# 1. 創建一個處理流程管道
# CountVectorizer: 將文本轉換為詞頻計數向量。
# MultinomialNB: 使用多項式樸素貝葉斯分類器。
pipeline = make_pipeline(CountVectorizer(), MultinomialNB())# 2. 訓練模型 (管道會自動先對X_train_mail做transform，然后用轉換后的數據訓練模型)
pipeline.fit(X_train_mail, y_train_mail)# 3. 預測與評估
y_pred_mail = pipeline.predict(X_test_mail)
print("--- 樸素貝葉斯在測試集上的評估 ---")
print(classification_report(y_test_mail, y_pred_mail))# 4. 預測新郵件
print("\n--- 預測新郵件 ---")
new_emails = ["Dear customer, your invoice is attached.","Claim your free prize now!"
]
predictions = pipeline.predict(new_emails)
proba_predictions = pipeline.predict_proba(new_emails)for email, pred, proba in zip(new_emails, predictions, proba_predictions):# pipeline.classes_ 可以查看類別的順序class_order = pipeline.classes_print(f"郵件: '{email}'")print(f"預測結果: {pred}")print(f"屬于各類的概率: {dict(zip(class_order, proba))}\n")

優缺點與適用場景

優點：
1. 算法簡單，訓練速度極快：計算開銷小，因為它只需要做一些計數和概率計算，沒有復雜的迭代優化過程。
2. 對小規模數據表現很好：在數據量不大的情況下，依然能獲得不錯的性能。
3. 能處理多分類問題，且表現穩定。
4. 在特征條件獨立性假設成立或近似成立時（如文本分類中，詞與詞的關聯性被簡化），效果甚至可以媲美復雜模型。
缺點：
1. “樸素”的假設在現實中幾乎不成立，這限制了其預測精度的上限。如果特征之間存在很強的關聯性，模型的表現會大打折扣。
2. 對輸入數據的表達形式很敏感。
3. 零概率問題：由于概率是連乘的，如果某個特征在訓練集的某個類別中從未出現過，會導致其條件概率為0，從而使得整個后驗概率計算結果為0，無論其他特征如何。這個問題需要通過**拉普拉斯平滑（Laplace Smoothing）**來解決（Scikit-learn中的實現已默認處理）。

適用場景：

文本分類：這是樸素貝葉斯最經典、最成功的應用場景，如垃圾郵件過濾、新聞主題分類、情感分析等。
作為一種快速、簡單的基線模型：與邏輯回歸類似，它可以為更復雜的模型提供一個性能參考基準。
適用于特征之間關聯性較弱的問題。

結語

本章，我們系統地學習了五種主流的監督學習分類算法。我們從邏輯回歸的概率視角出發，感受了其作為基線模型的穩健與可解釋性；接著，我們體會了K-近鄰“近朱者赤”的樸素哲學，并認識到數據標準化的重要性；然后，我們領略了支撐向量機在線性與非線性世界中尋找“最大間隔”的數學之美；隨后，我們深入探索了決策樹與隨機森林如何從“個體智慧”走向“集體智慧”，并見識了集成學習的強大威力；最后，我們回歸概率的本源，理解了樸素貝葉斯“執果索因”的推斷邏輯及其在文本世界的卓越表現。

這五種算法，如同五位性格迥異的武林高手，各有其獨門絕技和適用之地。沒有哪一個算法是永遠的“天下第一”，真正的“高手”在于能夠洞悉問題的本質，為之匹配最合適的“招式”。

至此，我們完成了對“判別”類任務的探索。在下一章，我們將轉向監督學習的另一個重要分支——“預測”類任務，深入學習各類回歸算法，探索如何精準地預測連續的數值。請帶著本章的收獲，準備好進入新的智慧之境。

第六章：監督學習之“預測”——回歸算法

6.1 線性回歸：從簡單到多元，探尋變量間的線性關系
6.2 嶺回歸與Lasso回歸：正則化下的“中庸之道”
6.3 多項式回歸：用曲線擬合復雜世界
6.4 回歸樹與集成回歸模型（例如 GBDT, XGBoost）

在前一章，我們探索了如何讓機器學會“判別”事物的類別。本章，我們將開啟監督學習的另一扇大門——回歸（Regression）。回歸任務的目標是預測一個連續的數值型輸出。它構成了現代數據科學和機器學習的基石，應用場景無處不在：

經濟金融：預測股票價格、GDP增長率、公司營收。
房地產：根據房屋特征（面積、位置、房齡）預測其售價。
氣象學：預測明天的最高溫度、降雨量。
商業運營：預測網站的訪問量、產品的銷量、廣告的點擊率。

本章，我們將從最經典、最基礎的線性回歸出發，理解變量間線性關系的建模方式。接著，我們將學習如何通過正則化技術（嶺回歸與Lasso回歸）來約束和優化線性模型，使其更加穩健。然后，我們會看到如何利用多項式特征，讓線性模型也能擬合復雜的非線性關系。最后，我們將邁向當今最強大的一類回歸工具——以回歸樹為基礎的集成模型，如隨機森林、GBDT和XGBoost，它們是無數數據科學競賽和工業應用中的性能王者。

準備好，讓我們一起探尋預測連續變量的奧秘，學習如何為復雜世界建立精準的量化模型。

6.1 線性回歸：從簡單到多元，探尋變量間的線性關系

線性回歸是回歸算法家族的“開山鼻祖”。它的思想簡單而強大：假設目標變量與一個或多個特征變量之間存在線性關系。盡管簡單，但它至今仍是應用最廣泛的模型之一，并且是理解更復雜回歸算法的重要基礎。

6.1.1 簡單線性回歸：一元一次方程的“機器學習”視角

簡單線性回歸只涉及一個特征變量（自變量 x）和一個目標變量（因變量 y）。

模型形式 我們試圖找到一條直線，來最好地擬合數據點。這條直線的方程，就是我們初中數學學過的一元一次方程： ? = wx + b 在機器學習語境下：

??(y-hat) 是模型的預測值。
x?是輸入的特征值。
w?(weight) 是權重或系數，代表特征?x?的重要性，幾何上是直線的斜率。
b?(bias) 是偏置或截距，代表當所有特征為0時模型的基準輸出，幾何上是直線在y軸上的截距。

機器學習的“訓練”過程，就是要根據已有的 (x, y) 數據點，自動地找到最優的 w 和 b。

損失函數：最小二乘法（Least Squares） 如何評判一組 w 和 b 是不是“最優”的？我們需要一個標準來衡量模型的“好壞”。對于回歸問題，最直觀的想法是看真實值 y 和預測值 ? 之間的差距。

最小二乘法就是這個標準。它定義了模型的損失函數（Loss Function）或成本函數（Cost Function）為所有樣本的預測誤差的平方和。這個值通常被稱為殘差平方和（Residual Sum of Squares, RSS）。 Loss(w, b) = Σ(y? - ??)2 = Σ(y? - (wx? + b))2

幾何意義：這個損失函數代表了所有數據點到擬合直線的垂直距離的平方和。 代數意義：我們的目標是找到一組 w 和 b，使得這個 Loss 值最小。

求解方法簡介 如何找到最小化損失函數的 w 和 b？主要有兩種方法：

正規方程（Normal Equation）：一種純數學的解法。通過對損失函數求偏導并令其為零，可以直接解出一個封閉形式的數學公式，一次性計算出最優的?w?和?b。它的優點是精確，無需迭代；缺點是當特征數量非常大時，矩陣求逆的計算成本極高。
梯度下降（Gradient Descent）：一種迭代式的優化算法。它就像一個蒙著眼睛下山的人，從一個隨機的?(w, b)?點出發，每次都沿著當前位置**最陡峭的下坡方向（梯度的反方向）**走一小步，不斷迭代，直到走到山谷的最低點（損失函數的最小值點）。它是絕大多數機器學習模型（包括深度學習）的核心優化算法。

6.1.2 多元線性回歸：從“線”到“面”的擴展

現實世界中，一個結果往往由多個因素共同決定。例如，房價不僅與面積有關，還與地段、房齡、樓層等多個特征有關。這時，我們就需要使用多元線性回歸（Multiple Linear Regression）。

模型形式 它只是簡單線性回歸的直接擴展，從一個特征擴展到 n 個特征： ? = w?x? + w?x? + ... + w?x? + b 或者用更簡潔的向量形式表示： ? = w?X + b 這里的 w 是一個權重向量，X 是一個特征向量。在三維空間中，它擬合的是一個平面；在更高維的空間中，它擬合的是一個超平面。

核心假設 為了讓多元線性回歸的結果可靠且具有良好的解釋性，它依賴于幾個核心假設，常被總結為**“LINE”**原則：

線性（Linearity）：特征和目標變量之間存在線性關系。
獨立性（Independence）：樣本的誤差（殘差）之間相互獨立。
正態性（Normality）：誤差服從正態分布。
同方差性（Equal variance / Homoscedasticity）：誤差的方差在所有預測值水平上是恒定的。

在實際應用中，這些假設不一定能完美滿足，但了解它們有助于我們診斷模型的問題。

6.1.3 Scikit-learn實戰與模型解讀

代碼實現 Scikit-learn讓使用線性回歸變得異常簡單。我們將使用經典的波士頓房價數據集進行演示。這個數據集包含了影響房價的多種因素（如犯罪率、房間數、學生教師比等），我們的目標是建立一個模型來預測房價。

# 導入必要的庫
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns# --- 數據準備 ---
# 加載數據 (Scikit-learn 1.2后，波士頓房價數據集因倫理問題被移除，我們從其他源加載)
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None )
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]
feature_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']
X = pd.DataFrame(data, columns=feature_names)
y = pd.Series(target, name='PRICE')# 1. 劃分數據
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 2. 初始化并訓練模型
# Scikit-learn的LinearRegression默認使用正規方程求解
lr_model = LinearRegression()
lr_model.fit(X_train, y_train)# 3. 預測
y_pred = lr_model.predict(X_test)# 4. 評估
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
r2 = r2_score(y_test, y_pred)print("--- 線性回歸模型評估 ---")
print(f"均方誤差 (MSE): {mse:.2f}")
print(f"均方根誤差 (RMSE): {rmse:.2f}")
print(f"R^2 分數: {r2:.2f}")

系數解讀（Coefficients） 線性回歸的一大優點是其可解釋性。我們可以直接查看模型學習到的權重（系數），來理解每個特征對預測結果的影響。

# 查看截距和系數
print(f"\n截距 (b): {lr_model.intercept_:.2f}")
coefficients = pd.Series(lr_model.coef_, index=X.columns).sort_values()
print("系數 (w):\n", coefficients)# 可視化系數
plt.figure(figsize=(10, 6))
coefficients.plot(kind='bar')
plt.title('Coefficients of the Linear Regression Model')
plt.show()

如何解讀系數？ 以RM（平均每戶住宅的房間數）為例，其系數為正數（約2.94），則意味著在其他所有特征保持不變的情況下，房間數每增加1個單位，預測的房價平均會增加約2.94萬美元。反之，LSTAT（低地位人口比例）的系數為負數（約-0.55），則說明該比例越高，預測的房價越低。

重要提示：只有當所有特征處于相同或相似的尺度時，我們才能直接比較系數的絕對值大小來判斷特征的相對重要性。否則，一個單位變化很大的特征（如總資產）即使系數很小，其影響力也可能超過一個單位變化很小的特征（如年齡）。因此，在解讀系數重要性之前，通常需要對數據進行標準化。

評估指標 除了在第四章學過的MAE, MSE, RMSE，回歸任務中最常用的相對評估指標是R2 (R-squared)。

R2，即決定系數，衡量的是模型能夠解釋的目標變量方差的百分比。R2越接近1，說明模型的擬合效果越好。一個R2為0.67的模型，意味著它能解釋67%的房價變動。剩下的33%則是由模型未包含的其他因素引起的。

6.2 嶺回歸與Lasso回歸：正則化下的“中庸之道”

普通線性回歸（也稱OLS，Ordinary Least Squares）雖然簡單，但它有兩個主要的“煩惱”：過擬合和多重共線性。正則化回歸就是為了解決這些問題而生的。

6.2.1 線性回歸的“煩惱”：過擬合與多重共線性

過擬合現象：當特征數量很多，特別是相對于樣本數量而言時，線性回歸模型會變得過于復雜。它會試圖去完美擬合訓練數據中的每一個點，包括噪聲。這會導致模型的系數（權重?w）變得異常大，模型在訓練集上表現很好，但在測試集上表現很差。
多重共線性（Multicollinearity）：當兩個或多個特征高度相關時（例如，“房屋面積”和“房間數”），線性回歸的系數會變得非常不穩定。稍微改變一下訓練數據，系數的值就可能發生劇烈變化，甚至正負顛倒。這使得我們無法再信任系數的解釋性。

正則化通過在損失函數中加入一個懲罰項，來對模型的復雜度（即系數的大小）進行約束，從而緩解這些問題。

6.2.2 嶺回歸（Ridge Regression）：在“山嶺”上保持平衡

嶺回歸在線性回歸的原始損失函數（RSS）的基礎上，增加了一個L2正則化項。

L2正則化 Loss_Ridge = Σ(y? - ??)2 + α * Σ(w?)2

Σ(w?)2?是所有特征系數的平方和。
α?(alpha) 是一個超參數，用于控制正則化的強度。

超參數Alpha（α）

當?α = 0?時，嶺回歸就退化為普通的線性回歸。
當?α?增大時，對大系數的懲罰就越強，模型會迫使所有系數都向0收縮，但不會完全等于0。
當?α -> ∞?時，所有系數都將無限趨近于0，模型變為一條水平線（只剩下截距）。

效果通過懲罰大系數，嶺回歸可以有效地防止模型過擬合。同時，在處理多重共線性問題時，它傾向于將相關特征的系數“均分”權重，而不是像普通線性回歸那樣隨意地給一個很大的正系數和另一個很大的負系數，從而使模型更加穩定。

6.2.3 Lasso回歸（Least Absolute Shrinkage and Selection Operator）：稀疏性的力量

Lasso回歸與嶺回歸非常相似，但它使用的是L1正則化項。

L1正則化 Loss_Lasso = Σ(y? - ??)2 + α * Σ|w?|

Σ|w?|?是所有特征系數的絕對值之和。

稀疏解與特征選擇 L1正則化與L2正則化有一個關鍵的區別：L1正則化能夠將一些不重要的特征的系數完全壓縮到0。

幾何上，L2的懲罰項是圓形，而L1是菱形。損失函數的等高線在與菱形的頂點相交時，更容易使得某些坐標軸上的系數為0。
這個特性使得Lasso回歸具有自動進行特征選擇的能力。訓練完一個Lasso模型后，那些系數不為0的特征，就是模型認為比較重要的特征。這種產生“稀疏解”（大部分系數為0）的能力在特征數量龐大的場景中非常有用。

6.2.4 Scikit-learn實戰與彈性網絡（Elastic Net）

代碼實現 使用正則化回歸時，對數據進行標準化是至關重要的，因為懲罰項是基于系數的大小的，如果特征尺度不同，懲罰就會不公平。

from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Ridge, Lasso, ElasticNet
from sklearn.model_selection import GridSearchCV# 標準化數據
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)# --- 嶺回歸 ---
ridge = Ridge(alpha=1.0)
ridge.fit(X_train_scaled, y_train)
print(f"嶺回歸在測試集上的R^2: {ridge.score(X_test_scaled, y_test):.2f}")# --- Lasso回歸 ---
lasso = Lasso(alpha=0.1)
lasso.fit(X_train_scaled, y_train)
print(f"Lasso回歸在測試集上的R^2: {lasso.score(X_test_scaled, y_test):.2f}")
print(f"Lasso選出的特征數量: {np.sum(lasso.coef_ != 0)}")# --- 使用GridSearchCV尋找最優alpha ---
param_grid = {'alpha': [0.001, 0.01, 0.1, 1, 10, 100]}
ridge_cv = GridSearchCV(Ridge(), param_grid, cv=5)
ridge_cv.fit(X_train_scaled, y_train)
print(f"\n嶺回歸最優alpha: {ridge_cv.best_params_['alpha']}")

彈性網絡（Elastic Net） 彈性網絡是嶺回歸和Lasso回歸的結合體，它同時使用了L1和L2兩種正則化。 Loss_ElasticNet = RSS + α * [ l1_ratio * Σ|w?| + (1 - l1_ratio) * 0.5 * Σ(w?)2 ]

它有兩個超參數：alpha?控制整體正則化強度，l1_ratio?控制L1和L2懲罰的比例。
當?l1_ratio = 1?時，它就是Lasso；當?l1_ratio = 0?時，它就是Ridge。

何時選擇

嶺回歸：是默認的首選。當你知道大部分特征都有用時，它通常表現更好。
Lasso回歸：當你懷疑很多特征是無用或冗余的，并希望模型能幫你自動篩選特征時，Lasso是絕佳選擇。
彈性網絡：當存在高度相關的特征群組時，Lasso傾向于只隨機選擇其中一個特征，而彈性網絡則能像嶺回歸一樣，將這個群組的特征都選入模型。因此，在有共線性且需要特征選擇時，彈性網絡是最好的選擇。

6.3 多項式回歸：用曲線擬合復雜世界

6.3.1 超越線性：當關系不再是直線

線性回歸有一個很強的假設：特征和目標變量之間是線性關系。但現實世界中，很多關系是曲線形的。例如，施肥量與作物產量之間的關系，可能一開始是正相關的，但施肥過多后，產量反而會下降，形成一個拋物線關系。

6.3.2 “偽裝”的線性回歸：特征工程的力量

多項式回歸并不是一種新的回歸算法，它本質上仍然是線性回歸。它的巧妙之處在于，通過特征工程的手段，對原始數據進行“升維”，從而讓線性模型能夠擬合非線性數據。

多項式特征生成 假設我們有一個特征 x。我們可以手動創造出它的高次項，如 x2, x3 等，并將這些新特征加入到模型中。 y = w?x + w?x2 + w?x3 + b 這個模型對于 y 和 x 來說是非線性的，但如果我們把 x?_new = x, x?_new = x2, x?_new = x3 看作是三個新的、獨立的特征，那么模型就變成了： y = w?x?_new + w?x?_new + w?x?_new + b 這又回到了我們熟悉的多元線性回歸的形式！

Scikit-learn的PolynomialFeatures可以自動幫我們完成這個特征生成的過程。

6.3.3 Scikit-learn實戰與過擬合的風險

代碼實現

from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline# 為了可視化，我們創建一個簡單的非線性數據集
np.random.seed(42)
X_poly = np.sort(5 * np.random.rand(80, 1), axis=0)
y_poly = np.sin(X_poly).ravel() + np.random.randn(80) * 0.1plt.scatter(X_poly, y_poly)
plt.title("Simple Non-linear Data")
plt.show()# 使用不同階數的多項式回歸進行擬合
plt.figure(figsize=(12, 8))
for degree in [1, 3, 10]:# 創建一個包含多項式特征生成和線性回歸的管道poly_reg = make_pipeline(PolynomialFeatures(degree=degree), LinearRegression())poly_reg.fit(X_poly, y_poly)X_fit = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]y_fit = poly_reg.predict(X_fit)plt.plot(X_fit, y_fit, label=f'degree={degree}')plt.scatter(X_poly, y_poly, edgecolor='b', s=20, label='data points')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()

階數（Degree）的選擇

degree=1：就是普通的線性回歸，無法擬合曲線，出現欠擬合。
degree=3：較好地擬合了數據的真實趨勢。
degree=10：模型變得異常扭曲，試圖穿過每一個數據點，包括噪聲點。這在訓練集上誤差會很小，但在新數據上表現會很差，是典型的過擬合。

階數是多項式回歸中最重要的超參數，需要通過交叉驗證來選擇。通常，我們很少使用超過4或5階的多項式，因為高階多項式非常容易過擬合，且模型會變得不穩定。

6.4 回歸樹與集成回歸模型：從規則到智慧的升華

線性模型家族雖然強大，但它們都基于一個固定的函數形式。而基于樹的模型，則提供了一種完全不同的、非參數化的解決思路。

6.4.1 回歸樹（Regression Tree）：用樹形結構做預測

回歸樹的結構與我們在分類任務中學到的決策樹完全相同，但在兩個關鍵點上有所區別：

分裂準則：分類樹使用基尼不純度或信息增益來選擇分裂點，目標是讓分裂后的節點類別更“純粹”。而回歸樹的目標是讓分裂后的每個節點內的預測誤差最小化。最常用的分裂準則就是均方誤差（MSE）。在每個節點，樹會遍歷所有特征的所有可能分裂點，選擇那個能使分裂后的兩個子節點的MSE之和最小的分裂方式。
葉節點輸出：分類樹的葉節點輸出是該節點樣本的眾數類別。而回歸樹的葉節點輸出是落在該葉節點所有訓練樣本的目標值的平均值。

模型特點 回歸樹的預測函數是一個分段常數函數。它將特征空間劃分為若干個矩形區域，在每個區域內，預測值都是一個固定的常數。

6.4.2 隨機森林回歸（Random Forest Regressor）

單棵回歸樹同樣存在容易過擬合的問題。隨機森林通過Bagging的思想，將多棵回歸樹集成起來，極大地提升了模型的性能和穩定性。

工作原理：與分類隨機森林完全一致，通過“樣本隨機”和“特征隨機”構建一個由多棵“各不相同”的回歸樹組成的森林。
預測方式：對于一個新的樣本，森林中的每棵樹都會給出一個預測值。隨機森林的最終預測結果是所有樹預測值的平均值。

Scikit-learn實戰

from sklearn.ensemble import RandomForestRegressor# 使用波士頓房價數據
rf_reg = RandomForestRegressor(n_estimators=100, random_state=42, n_jobs=-1)
rf_reg.fit(X_train, y_train) # 樹模型對數據縮放不敏感
print(f"\n隨機森林回歸在測試集上的R^2: {rf_reg.score(X_test, y_test):.2f}")

6.4.3 梯度提升決策樹（GBDT）：在“錯誤”中不斷進步

梯度提升決策樹（Gradient Boosting Decision Tree, GBDT）是另一種強大的集成方法，它采用的是Boosting思想。

Boosting思想 與Bagging并行訓練不同，Boosting是一種串行的、循序漸進的集成方式。

首先，訓練一個簡單的基學習器（如一棵很淺的決策樹）。
計算當前模型在所有樣本上的殘差（Residuals），即?真實值 - 預測值。這些殘差就是模型尚未學好的“錯誤”。
接下來，訓練第二棵樹，但這棵樹的學習目標不再是原始的?y，而是上一輪的殘差。它專門學習如何彌補第一棵樹的不足。
將第二棵樹的預測結果（按一定比例，即學習率）加到第一棵樹的預測結果上，形成一個新的集成模型。
不斷重復步驟2-4，每一棵新樹都在學習前面所有樹集成起來的模型的殘差。

最終，GBDT的預測結果是所有樹的預測結果的加權和。它通過這種“在錯誤中不斷進步”的方式，逐步構建出一個非常精準的模型。

Scikit-learn實戰

from sklearn.ensemble import GradientBoostingRegressorgbrt = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=42)
gbrt.fit(X_train, y_train)
print(f"GBDT回歸在測試集上的R^2: {gbrt.score(X_test, y_test):.2f}")

6.4.4 XGBoost：極致的工程實現與性能王者

XGBoost（eXtreme Gradient Boosting）是GBDT的一種高效、靈活且可移植的工程實現。它在算法和工程層面都做了大量的優化，使其成為數據科學競賽和工業界最受歡迎的模型之一。

核心優勢

正則化：XGBoost在損失函數中直接加入了對樹的復雜度的正則化項（如葉子節點的數量和葉子節點輸出值的L2范數），這比GBDT單純依靠學習率和剪枝來控制過擬合要更勝一籌。
高效的并行處理：雖然樹的生成是串行的，但在每個節點尋找最佳分裂點時，XGBoost可以高效地進行并行計算。
內置交叉驗證：可以在訓練過程中直接進行交叉驗證。
處理稀疏數據和缺失值：有專門的優化算法來處理稀疏數據和自動處理缺失值。
緩存感知和核外計算：在工程上做了很多優化，使得它能處理超出內存的大規模數據集。

代碼實現 XGBoost是一個獨立的庫，需要單獨安裝 (pip install xgboost)。

import xgboost as xgbxgb_reg = xgb.XGBRegressor(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=42,objective='reg:squarederror')
xgb_reg.fit(X_train, y_train)
print(f"XGBoost回歸在測試集上的R^2: {xgb_reg.score(X_test, y_test):.2f}")

結語

本章，我們從最基礎的線性回歸出發，一路探索了回歸算法的廣闊天地。我們學習了如何用正則化來約束線性模型，如何用多項式特征來捕捉非線性，最終登上了以隨機森林、GBDT和XGBoost為代表的集成模型的性能高峰。

您現在已經掌握了解決兩類最核心的監督學習問題——分類與回歸——的強大工具集。線性模型家族為我們提供了良好的可解釋性和基準，而樹的集成模型則為我們追求極致性能提供了保障。

到目前為止，我們所學的都是“監督學習”，即數據都帶有明確的“答案”（標簽）。在下一章，我們將進入一個全新的、更具探索性的領域——無監督學習。在那里，數據沒有標簽，我們的任務是從數據本身發現隱藏的結構、模式和群體。這將是一場全新的智慧探險。

第七章：無監督學習之“歸納”——聚類與降維

7.1 K-均值聚類（K-Means）：尋找數據中的“引力中心”
7.2 層次聚類：構建數據的“家族譜系”
7.3 DBSCAN：基于密度的“社區發現”
7.4 主成分分析（PCA）：在紛繁中見本質的降維之道

至此，我們旅程的前半段始終有一位“向導”——數據標簽。它告訴我們什么是對的，什么是錯的，我們的模型則努力學習這位向導的智慧。然而，在浩瀚的數據宇宙中，絕大多數的“星辰”（數據）都是未經標注的。如何從這些看似混沌的數據中發現秩序、歸納結構、提煉精華？這便是無監督學習的使命。

無監督學習，是一場沒有標準答案的探索。它要求我們放棄對“預測”的執念，轉而擁抱對“發現”的熱情。本章，我們將聚焦于無日志學習的兩大核心任務：

聚類（Clustering）：旨在將數據集中的樣本劃分為若干個內部相似、外部相異的“簇”（Cluster）。它幫助我們回答“數據可以被自然地分成哪些群體？”這個問題。
降維（Dimensionality Reduction）：旨在用一組數量更少的變量來概括原始數據中的主要信息。它幫助我們回答“數據的核心本質是什么？”這個問題。

掌握無監督學習，意味著您將擁有一雙能夠穿透數據表象、洞察其內在結構的“慧眼”。這不僅是數據預處理的關鍵步驟，其本身就能帶來深刻的商業洞察，如客戶分群、異常檢測、文本主題挖掘等。

7.1 K-均值聚類（K-Means）：尋找數據中的“引力中心”

K-均值（K-Means）是聚類算法中最著名、最簡單、也是應用最廣泛的算法之一。它是一種基于原型（Prototype-based）的聚類方法，試圖找到每個簇的“原型”——即質心（Centroid），然后將每個樣本劃分給離它最近的質心所代表的簇。

7.1.1 核心思想：物以類聚，迭代為王

算法目標 K-Means的最終目標，是將 n 個樣本劃分為 K 個簇，并使得所有簇的**簇內平方和（Within-Cluster Sum of Squares, WCSS）**最小。WCSS衡量的是每個簇內所有樣本點到其質心的距離平方之和。這個值越小，說明簇內的樣本越緊密，聚類效果越好。

迭代步驟 K-Means通過一個簡單而優美的迭代過程來逼近這個目標：

初始化：隨機選擇?K?個數據點作為初始的質心。
分配（Assignment）：遍歷每一個數據點，計算它到所有?K?個質心的距離，并將其分配給距離最近的那個質心所代表的簇。
更新（Update）：對于每一個簇，重新計算其質心。新的質心是該簇內所有數據點的平均值。
重復：不斷重復步驟2和步驟3，直到質心的位置不再發生顯著變化（或達到預設的迭代次數），算法收斂。

這個過程就像在數據平原上尋找 K 個“引力中心”，數據點不斷被最近的中心吸引，而中心的位置又根據被吸引來的點的分布而調整，最終達到一個穩定的平衡狀態。

7.1.2 算法的“阿喀琉斯之踵”：K值選擇與初始點敏感性

K-Means雖然強大，但它有兩個著名的“軟肋”。

K值的確定 算法開始前，我們必須手動指定簇的數量 K。這個 K 值應該如何確定？

肘部法則（Elbow Method）：我們可以嘗試多個不同的?K?值（例如從2到10），并計算每個?K?值下最終的WCSS。然后，將?K?值作為橫坐標，WCSS作為縱坐標，繪制一條曲線。通常，這條曲線會像一個手臂，隨著?K?的增加，WCSS會迅速下降，但到某個點后，下降速度會變得非常平緩。這個“拐點”，即“肘部”，通常被認為是比較合適的?K?值。
輪廓系數（Silhouette Score）：這是一個更嚴謹的指標（我們在第四章已經介紹過）。它同時衡量了簇的內聚度和分離度。我們可以為每個?K?值計算其輪廓系數的平均值，然后選擇那個使得輪廓系數最大的?K?值。

初始點敏感性 K-Means的最終結果在一定程度上依賴于初始質心的選擇。不同的隨機初始化可能會導致完全不同的聚類結果，甚至陷入一個局部最優解。

K-Means++ 為了解決這個問題，**K-Means++**被提了出來。它是一種更智能的初始化策略，其核心思想是：初始的 K 個質心應該盡可能地相互遠離。Scikit-learn中的KMeans默認使用的就是K-Means++初始化（init='k-means++'），這在很大程度上緩解了初始點敏感性的問題。

7.1.3 Scikit-learn實戰與模型假設

代碼實現 在Scikit-learn中，實現K-Means聚類非常直觀。我們將通過一個完整的流程，包括尋找最優K值、訓練模型和可視化結果，來展示其應用。

# 導入必要的庫
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
from sklearn.metrics import silhouette_score
import numpy as np# 1. 生成模擬數據
# 我們創建一些符合K-Means假設的數據，即球狀、大小相似的簇
X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.8, random_state=42)
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], s=50)
plt.title("Simulated Data for Clustering")
plt.show()# 2. 使用肘部法則和輪廓系數尋找最優K
wcss = []
silhouette_scores = []
k_range = range(2, 11) # K值至少為2才有意義for k in k_range:# n_init=10 表示算法會用10個不同的初始質心運行10次，并選擇WCSS最小的結果kmeans = KMeans(n_clusters=k, init='k-means++', random_state=42, n_init=10)kmeans.fit(X)wcss.append(kmeans.inertia_) # inertia_ 屬性就是WCSS# 計算輪廓系數score = silhouette_score(X, kmeans.labels_)silhouette_scores.append(score)# 繪制肘部法則圖
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(k_range, wcss, marker='o')
plt.title('Elbow Method')
plt.xlabel('Number of clusters (K)')
plt.ylabel('WCSS')# 繪制輪廓系數圖
plt.subplot(1, 2, 2)
plt.plot(k_range, silhouette_scores, marker='o')
plt.title('Silhouette Score for each K')
plt.xlabel('Number of clusters (K)')
plt.ylabel('Silhouette Score')
plt.tight_layout()
plt.show()# 從圖中我們可以清晰地看到，K=4是最佳選擇（肘部點，輪廓系數最高）# 3. 訓練最終的K-Means模型
best_k = 4
kmeans_final = KMeans(n_clusters=best_k, init='k-means++', random_state=42, n_init=10)
y_kmeans = kmeans_final.fit_predict(X)# 4. 結果可視化
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
centers = kmeans_final.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75, marker='X', label='Centroids')
plt.title(f'K-Means Clustering Result (K={best_k})')
plt.legend()
plt.show()# 5. 打印最終的輪廓系數
final_score = silhouette_score(X, y_kmeans)
print(f"Final Silhouette Score for K={best_k}: {final_score:.3f}")

模型假設 理解K-Means的隱含假設至關重要，因為它決定了算法的適用范圍：

簇是凸形的、球狀的（Isotropic）：由于K-Means使用基于歐氏距離的質心來定義簇，它天然地傾向于發現球狀的簇。
所有簇的大小（樣本量）和密度大致相同。
每個樣本都屬于某個簇：K-Means會將所有點都分配給一個簇，它無法識別離群點或噪聲。

如果數據的真實簇結構是細長的、環形的，或者大小、密度差異巨大，K-Means的表現就會很差。這時，我們就需要求助于下面將要介紹的其他聚類算法。

7.2 層次聚類：構建數據的“家族譜系”

層次聚類（Hierarchical Clustering）提供了一種與K-Means完全不同的視角。它不要求我們預先指定簇的數量，而是通過構建一個嵌套的簇的層次結構，來展現數據點之間的親疏關系，就像一個家族的族譜一樣。

7.2.1 兩種策略：自底向上（凝聚）與自頂向下（分裂）

凝聚型層次聚類（Agglomerative Clustering）：這是最常用的方法。
1. 開始：將每一個數據點都視為一個獨立的簇。
2. 合并：找到最接近的兩個簇，將它們合并成一個新的簇。
3. 重復：不斷重復合并步驟，直到所有數據點都合并成一個唯一的、巨大的簇。
分裂型層次聚類（Divisive Clustering）：過程正好相反。
1. 開始：所有數據點都在一個大簇里。
2. 分裂：以某種方式將當前最“不協調”的簇分裂成兩個子簇。
3. 重復：不斷重復分裂步驟，直到每個數據點都自成一簇。

我們將重點關注更主流的凝聚型方法。

7.2.2 核心要素：鏈接標準（Linkage Criteria）

在凝聚型聚類的合并步驟中，我們如何定義兩個簇之間的“距離”？這就是鏈接標準要解決的問題。

Ward鏈接（Ward's Linkage）：Scikit-learn中的默認選項。它會合并那兩個能使總的簇內方差增加最小的簇。它傾向于產生大小相似的球狀簇，通常表現非常穩健。
完全鏈接（Complete Linkage）：簇間距離定義為兩個簇中最遠的兩個點之間的距離。它傾向于產生緊湊的球狀簇。
平均鏈接（Average Linkage）：簇間距離定義為兩個簇中所有點對之間距離的平均值。
單一鏈接（Single Linkage）：簇間距離定義為兩個簇中最近的兩個點之間的距離。它可以處理非球狀的簇，但對噪聲非常敏感。

7.2.3 Scikit-learn實戰與樹狀圖（Dendrogram）解讀

代碼實現 層次聚類的美妙之處在于，我們可以通過樹狀圖（Dendrogram）來可視化整個合并過程。

from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram, linkage# 使用之前的數據X# 1. 生成鏈接矩陣
# 'ward'鏈接方法計算的是簇間方差，而不是距離，所以它通常與歐氏距離配合使用
linked = linkage(X, method='ward')# 2. 繪制樹狀圖
plt.figure(figsize=(12, 7))
dendrogram(linked,orientation='top',labels=None, # 如果樣本少，可以傳入標簽distance_sort='descending',show_leaf_counts=True)
plt.title('Hierarchical Clustering Dendrogram (Ward Linkage)')
plt.xlabel('Sample index')
plt.ylabel('Distance (Ward)')
plt.show()

樹狀圖解讀

橫軸代表數據樣本。
縱軸代表簇之間的距離或不相似度。
每一條豎線代表一個簇。
連接兩條豎線的橫線表示一次合并，橫線的高度就是這次合并時兩個簇的距離。

如何根據樹狀圖決定簇的數量？ 我們可以畫一條水平線橫切整個樹狀圖。這條水平線與多少條豎線相交，就意味著我們將數據分成了多少個簇。一個常用的方法是，尋找那段最長的、沒有被橫線穿過的豎線，然后在這段中間畫一條水平線。

# 3. 訓練AgglomerativeClustering模型
# 假設我們從樹狀圖中決定n_clusters=4
agg_cluster = AgglomerativeClustering(n_clusters=4, linkage='ward')
y_agg = agg_cluster.fit_predict(X)# 4. 結果可視化
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=y_agg, s=50, cmap='viridis')
plt.title('Agglomerative Clustering Result (K=4)')
plt.show()

7.3 DBSCAN：基于密度的“社區發現”

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一種完全不同的聚類范式。它不基于距離中心或層次關系，而是基于密度。

7.3.1 超越幾何中心：從“密度”出發看世界

核心思想 DBSCAN認為，一個簇是由密度可達（density-reachable）的點的集合。通俗地說，一個點屬于某個簇，是因為它周圍“足夠稠密”。

兩個關鍵參數

鄰域半徑 (eps)：定義了一個點的“鄰域”范圍。它是一個距離值。
最小點數 (min_samples)：要成為一個“稠密”區域，一個點的鄰域內至少需要包含多少個其他點（包括它自己）。

點的分類 根據這兩個參數，DBSCAN將所有點分為三類：

核心點（Core Point）：在其eps鄰域內，至少有min_samples個點的點。它們是簇的“心臟”。
邊界點（Border Point）：它不是核心點，但它落在了某個核心點的eps鄰域內。它們是簇的“邊緣”。
噪聲點（Noise Point / Outlier）：既不是核心點，也不是邊界點。它們是離群的、孤獨的點。

算法流程：從一個任意點開始，如果它是核心點，就以它為中心，通過密度可達關系不斷擴張，形成一個簇。然后繼續處理下一個未被訪問的點。

7.3.2 DBSCAN的獨特優勢：發現任意形狀的簇與識別噪聲

處理非球形簇：由于DBSCAN不關心點到中心的距離，只關心密度，因此它可以輕松地發現任意形狀的簇，如環形、月牙形、蛇形等，這是K-Means和層次聚類難以做到的。
自動識別離群點：DBSCAN不需要預先指定簇的數量。它會根據密度自動確定簇的數量，并將任何不屬于任何簇的點標記為噪聲（通常標簽為-1）。

7.3.3 Scikit-learn實戰與參數選擇的挑戰

代碼實現

from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons# 生成月牙形數據
X_moon, y_moon = make_moons(n_samples=200, noise=0.05, random_state=42)# 訓練DBSCAN模型
# eps和min_samples的選擇非常關鍵，需要調試
dbscan = DBSCAN(eps=0.3, min_samples=5)
y_db = dbscan.fit_predict(X_moon)# 結果可視化
plt.figure(figsize=(8, 6))
plt.scatter(X_moon[:, 0], X_moon[:, 1], c=y_db, s=50, cmap='viridis')
plt.title('DBSCAN Clustering on Moons Dataset')
plt.show()

參數選擇的挑戰 DBSCAN的性能高度依賴于eps和min_samples的選擇。

min_samples通常根據領域知識設定，一個經驗法則是將其設為2 * D，其中D是數據的維度。
eps的選擇更具挑戰性。一個常用的輔助方法是K-距離圖（K-distance plot）：
1. 計算每個點到其第k個最近鄰的距離（這里的k就是min_samples-1）。
2. 將這些距離從大到小排序，并繪制出來。
3. 圖形中同樣會出現一個“肘部”，這個肘部對應的距離值，就是一個很好的eps候選值。

7.4 主成分分析（PCA）：在紛繁中見本質的降維之道

主成分分析（Principal Component Analysis, PCA）是無監督學習中應用最廣泛的降維技術。它旨在將高維數據投影到一個低維空間中，同時盡可能多地保留原始數據的方差（信息）。

7.4.1 降維的意義：為何我們需要“化繁為簡”

克服維度詛咒：當特征維度非常高時，數據會變得異常稀疏，模型性能下降，計算成本劇增。降維可以有效緩解這個問題。
數據可視化：我們的肉眼只能感知二維或三維空間。PCA可以將上百維的數據降到2D或3D，讓我們能夠直觀地觀察數據的分布、結構和聚類趨勢。
降低計算成本與噪聲：去除冗余和次要的特征，可以加快模型訓練速度，并可能通過濾除噪聲來提升模型性能。

7.4.2 PCA的核心思想：尋找最大方差的方向

PCA的本質是進行一次坐標系的旋轉。它要找到一個新的坐標系，使得數據在這個新坐標系下的表示具有兩個特點：

方差最大化：第一個新坐標軸（即第一主成分）的方向，必須是原始數據方差最大的方向。因為方差越大，代表數據在該方向上攜帶的信息越多。第二個新坐標軸（第二主成分）則是在與第一個軸正交（垂直）的前提下，方差次大的方向，以此類推。
不相關性：所有新的坐標軸（主成分）之間都是線性無關（正交）的。

主成分（Principal Components）就是這些新的坐標軸。它們是原始特征的線性組合。

可解釋方差比（Explained Variance Ratio） PCA完成后，我們可以計算每個主成分“解釋”了多少原始數據的方差。例如，如果前兩個主成分的累計可解釋方差比為0.95，就意味著我們用這兩個新的特征，保留了原始數據95%的信息。

7.4.3 Scikit-learn實戰與應用

代碼實現 PCA對特征的尺度非常敏感。如果一個特征的方差遠大于其他特征，那么PCA會主要被這個特征所主導。因此，在使用PCA之前，對數據進行標準化（StandardScaler）是一個至關重要的預處理步驟。Scikit-learn的PCA實現會自動對數據進行中心化（減去均值），但標準化的步驟需要我們自己完成。

我們將使用一個經典的手寫數字數據集（Digits）來演示PCA的應用。這個數據集的每個樣本有64個特征（一個8x8像素的圖像），我們的目標是將其降維以便于可視化。

# 導入必要的庫
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_digits
import matplotlib.pyplot as plt
import numpy as np# 1. 加載數據
# Digits數據集，每個樣本是64維的向量
digits = load_digits()
X_digits = digits.data
y_digits = digits.targetprint(f"Original data shape: {X_digits.shape}")# 2. 數據標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X_digits)# 3. 應用PCA進行降維 (目標是降到2維以便可視化)
# n_components可以是一個整數，也可以是一個(0,1)之間的浮點數
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)print(f"Data shape after PCA: {X_pca.shape}")# 4. 查看可解釋方差比
# explained_variance_ratio_ 屬性是一個數組，包含了每個主成分解釋的方差比例
print(f"\nExplained variance ratio of the first component: {pca.explained_variance_ratio_[0]:.3f}")
print(f"Explained variance ratio of the second component: {pca.explained_variance_ratio_[1]:.3f}")
print(f"Total explained variance by 2 components: {np.sum(pca.explained_variance_ratio_):.3f}")
# 這個結果告訴我們，僅用2個主成分，就保留了原始64維數據約28.7%的方差（信息）。# 5. 可視化降維后的數據
plt.figure(figsize=(10, 8))
scatter = plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y_digits, cmap='jet', alpha=0.7, s=40)
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.title('PCA of Digits Dataset (64D -> 2D)')
plt.legend(handles=scatter.legend_elements()[0], labels=digits.target_names)
plt.colorbar(label='Digit Label')
plt.grid(True)
plt.show()

從可視化結果中，我們可以清晰地看到，即使只用了兩個主成分，不同數字的類別也已經在二維平面上呈現出了明顯的分離趨勢。這就是PCA在數據探索和可視化方面的強大威力。

選擇主成分數量 在實際應用中，我們不一定總想降到2維。如何選擇一個既能顯著降維、又能保留足夠信息的維度 k？

根據累計可解釋方差比：這是最常用的方法。我們可以設定一個閾值（例如，希望保留95%的方差），然后運行PCA，讓它自動選擇能達到這個閾值的最小組件數。
碎石圖（Scree Plot）：將所有主成分按其解釋的方差大小排序并繪制出來。圖形中通常也會出現一個“肘部”，肘部之前的主成分通常被認為是重要的，可以保留。

# 方法一：設定可解釋方差比閾值
# n_components=0.95 表示選擇能保留95%方差的最少數量的主成分
pca_95 = PCA(n_components=0.95)
X_pca_95 = pca_95.fit_transform(X_scaled)
print(f"\nNumber of components to explain 95% variance: {pca_95.n_components_}")# 方法二：繪制碎石圖來輔助決策
pca_full = PCA().fit(X_scaled) # 不指定n_components，計算所有主成分
plt.figure(figsize=(8, 6))
plt.plot(np.cumsum(pca_full.explained_variance_ratio_), marker='o', linestyle='--')
plt.xlabel('Number of Components')
plt.ylabel('Cumulative Explained Variance Ratio')
plt.title('Scree Plot for PCA')
plt.axhline(y=0.95, color='r', linestyle='-', label='95% threshold')
plt.legend()
plt.grid(True)
plt.show()

從碎石圖中，我們可以看到，大約需要28個主成分才能保留95%的方差，這依然實現了超過一半的維度約減。

應用案例

數據可視化：如上例所示，將高維數據投影到2D或3D空間，以洞察其內在結構。
作為機器學習模型的預處理步驟：先用PCA對數據降維，再將降維后的數據輸入到分類或回歸模型中。
- 優點：可以顯著加快模型訓練速度，并可能通過濾除噪聲和共線性來提升模型性能。
- 缺點：降維后的新特征是原始特征的線性組合，失去了原有的物理意義，導致模型的可解釋性下降。

結語

本章，我們踏入了無監督學習的奇妙世界。這是一片充滿未知與驚喜的土地，在這里，我們不再是跟隨“標簽”的學徒，而是成為了主動發現數據奧秘的“探險家”。

我們學會了三種主流的聚類方法：

K-Means，以其簡潔高效，為我們尋找數據的“引力中心”。
層次聚類，通過構建數據的“家族譜系”，為我們展現了樣本間由近及遠的完整親緣關系。
DBSCAN，則獨辟蹊徑，從“密度”的視角出發，發現了隱藏在數據中的任意形狀的“社區”，并智慧地識別出了離群的“獨行者”。

同時，我們還掌握了PCA這一強大的降維“神器”。它教會我們如何在紛繁復雜的數據中，通過尋找最大方差的方向，抓住其主要矛盾，提煉其核心本質，實現“化繁為簡”的智慧。

至此，您已經構建了機器學習知識體系的“四梁八柱”：監督學習的分類與回歸，無監督學習的聚類與降維。這為您解決絕大多數現實世界中的機器學習問題打下了堅實的基礎。您已經從一個求知者，成長為了一位擁有完整工具箱的實踐者。

在本書的最后一章，我們將把目光投向更遠的地平線，簡要介紹一些更前沿、更令人興奮的領域，如深度學習的神經網絡、模型部署的工程實踐等，為您的持續學習與成長之旅點亮前行的燈塔。

第八章：集成學習——從“三個臭皮匠”到“諸葛亮”

8.1 Bagging思想：隨機森林的再思考
8.2 Boosting思想：從AdaBoost到梯度提升樹（GBDT）
8.3 Stacking/Blending：模型的“圓桌會議”
8.4 XGBoost與LightGBM：工業界的“大殺器”詳解

在我們的機器學習探索之旅中，我們已經結識了眾多各具特色的算法模型。它們如同身懷絕技的俠客，在各自擅長的領域里表現出色。然而，一個自然而然的問題是：我們能否將這些“個體英雄”的力量集結起來，形成一個戰無不勝的“夢之隊”？

集成學習（Ensemble Learning）正是對這個問題最響亮的回答。它并非一種具體的算法，而是一種強大的元算法框架（Meta-algorithm Framework）。其核心思想是，通過構建并結合多個學習器來完成學習任務，以期獲得比任何單個學習器都顯著優越的泛化性能。

本章，我們將深入探討集成學習的三大主流思想：

Bagging：通過并行訓練多個獨立模型并取其平均，來降低方差，追求“穩定壓倒一切”。隨機森林是其最杰出的代表。
Boosting：通過串行訓練，讓模型在前輩的“錯誤”中不斷學習和進化，來降低偏差，追求“精益求精”。GBDT是其核心思想的體現。
Stacking：通過分層結構，讓不同模型各司其職，再由一個“元模型”來學習如何最好地融合它們的智慧，追求“博采眾長”。

最后，我們將詳細拆解在當今工業界和數據科學競賽中叱咤風云的兩大“神器”——XGBoost和LightGBM，看看它們是如何將Boosting思想推向工程和算法的極致。準備好，讓我們一起見證“三個臭皮-匠”如何通過智慧的組織，升華為運籌帷幄的“諸葛亮”。

8.1 Bagging思想：隨機森林的再思考

Bagging是集成學習中最基礎、最直觀的思想之一。它的策略簡單而有效：通過引入隨機性來構建多個略有不同的模型，然后通過“民主投票”的方式匯集它們的預測，以獲得一個更穩定、更可靠的最終結果。

8.1.1 核心思想：通過“隨機”降低“方差”

Bagging是集成學習中最基礎、最直觀的思想之一。它的策略簡單而有效：通過引入隨機性來構建多個略有不同的模型，然后通過“民主決策”的方式匯集它們的預測，以獲得一個更穩定、更可靠的最終結果。

自助采樣法（Bootstrap Aggregating） Bagging這個詞本身就是Bootstrap Aggregating的縮寫，完美地概括了其兩個核心步驟：

自助采樣（Bootstrap）：這是Bagging引入隨機性的關鍵手段。假設我們有?N?個樣本的原始訓練集。我們進行有放回的隨機抽樣?N?次，得到一個同樣大小為?N?的“自助樣本集”。由于是有放回抽樣，這個新的數據集中會不可避免地包含一些重復樣本，同時，原始數據中約有36.8%（數學上趨近于?1/e）的樣本從未被抽到。這個過程模擬了從原始數據分布中多次采樣的過程，創造了數據的多樣性。
聚合（Aggregating）：我們重復上述自助采樣過程?M?次，得到?M?個不同的自助樣本集。然后，我們在這?M?個數據集上獨立地、并行地訓練?M?個基學習器（例如，M?棵決策樹）。

并行訓練與投票/平均

并行訓練：由于?M?個基學習器的訓練過程互不依賴，它們可以完全并行進行，這使得Bagging的訓練效率很高。
決策方式：
- 對于分類任務，最終結果由?M?個基學習器進行多數投票（Majority Voting）決定。
- 對于回歸任務，最終結果是?M?個基學習器預測值的平均值。

方差降低的直觀解釋 Bagging的主要作用是降低模型的方差。方差衡量的是模型在不同訓練數據集上的預測結果的波動性。高方差模型（如未剪枝的決策樹）容易過擬合，對訓練數據的微小變化非常敏感。

Bagging通過在略有不同的數據子集上訓練出多個這樣的高方差模型，每個模型都從一個略微不同的“視角”來看待數據。雖然單個模型可能仍然存在過擬合，但它們的“錯誤”是各不相同的、不相關的。通過投票或平均，這些五花八門的錯誤在很大程度上被相互抵消了，最終留下的是數據中穩定、普適的規律，從而使得集成模型的整體方差大大降低。這就像投資組合一樣，通過持有多個不完全相關的資產來分散風險。

8.1.2 隨機森林（Random Forest）的再審視

我們在第五章已經學習過隨機森林，現在我們可以從Bagging的視角來更深刻地理解它。隨機森林是以決策樹為基學習器的Bagging集成模型，并且在Bagging的基礎上，更進了一步，引入了更強的隨機性。

超越普通Bagging：特征隨機化 隨機森林引入了“雙重隨機性”：

行采樣（樣本隨機）：繼承自Bagging的自助采樣。
列采樣（特征隨機）：這是隨機森林的獨創。在構建每棵決策樹的每個節點時，并不是從全部特征中選擇最優分裂點，而是先從全部特征中隨機抽取一個子集（例如，對于分類問題，通常是?sqrt(n_features)?個），然后再從這個子集中選擇最優特征。

這個“特征隨機化”的步驟，進一步降低了森林中樹與樹之間的相關性。如果不用特征隨機化，那么在每個自助樣本集上，那些強特征很可能總是被優先選中，導致森林中的樹長得“千篇一律”，相關性很高。而引入特征隨機化后，即使是弱特征也有機會在某些樹的某些節點上成為最優選擇，這使得森林中的樹更加“多樣化”。更多樣化的模型，在聚合時能更有效地抵消誤差，從而帶來更強的泛化能力。

包外（Out-of-Bag, OOB）估計 由于自助采樣平均約有36.8%的數據未被用于訓練某一棵特定的樹，這些數據被稱為該樹的包外（Out-of-Bag）數據。我們可以利用這些“免費”的、未被模型見過的數據來評估模型的性能，而無需再單獨劃分一個驗證集或進行交叉驗證。

對于每個樣本，找到所有沒有用它來訓練的樹，讓這些樹對它進行預測，然后將這些預測結果聚合起來，得到該樣本的OOB預測。最后，用所有樣本的OOB預測和真實標簽來計算模型的OOB得分。在Scikit-learn中，只需在創建RandomForestClassifier或RandomForestRegressor時設置oob_score=True即可。

8.1.3 Scikit-learn實戰與Bagging的泛化

代碼實現 Scikit-learn提供了通用的BaggingClassifier和BaggingRegressor，它們允許我們將任何基學習器進行Bagging集成。

from sklearn.ensemble import BaggingClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 生成數據
X, y = make_classification(n_samples=500, n_features=20, n_informative=15, n_redundant=5, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)# 1. 單個決策樹模型
tree = DecisionTreeClassifier(random_state=42)
tree.fit(X_train, y_train)
y_pred_tree = tree.predict(X_test)
print(f"單個決策樹模型的準確率: {accuracy_score(y_test, y_pred_tree):.4f}")# 2. 使用Bagging集成決策樹模型 (這實際上就是隨機森林的簡化版，沒有特征隨機)
bagging_tree = BaggingClassifier(estimator=DecisionTreeClassifier(random_state=42),n_estimators=100,max_samples=1.0, # 使用全部樣本大小的自助采樣bootstrap=True,random_state=42,n_jobs=-1
)
bagging_tree.fit(X_train, y_train)
y_pred_bagging = bagging_tree.predict(X_test)
print(f"Bagging決策樹模型的準確率: {accuracy_score(y_test, y_pred_bagging):.4f}")

通常，我們會看到集成后的模型性能比單個模型更加穩定和優越。

基學習器的選擇 Bagging的核心是降低方差，因此它對于那些本身是低偏差、高方差的模型（即容易過擬合的復雜模型）效果最好。這就是為什么它與決策樹（特別是未剪枝的決策樹）是“天作之合”。將Bagging應用于本身就是高偏差的簡單模型（如邏輯回歸），通常不會帶來顯著的性能提升。

8.2 Boosting思想：從AdaBoost到梯度提升樹（GBDT）

如果說Bagging是“群策群力、民主決策”，那么Boosting就是“精英培養、迭代優化”。Boosting家族的算法通過一種串行的方式，讓模型在前輩的“錯誤”中不斷學習和進化，最終將一群“弱學習器”提升為一個強大的“強學習器”。

8.2.1 核心思想：在“錯誤”中迭代，化“弱”為“強”

串行訓練的哲學 Boosting的訓練過程是串行的，這意味著基學習器必須一個接一個地、按順序進行訓練。

首先，訓練一個初始的基學習器。
然后，根據這個基學習器的表現，調整數據的權重或學習目標，使得那些被錯分或預測誤差大的樣本在下一輪訓練中受到更多的“關注”。
接著，在調整后的數據上訓練第二個基學習器。
不斷重復這個過程，每一輪都致力于彌補前一輪模型的“短板”。
最終，將所有基學習器進行加權組合，得到最終的強學習器。

Boosting與Bagging的根本區別

訓練方式：Bagging是并行的，模型間獨立；Boosting是串行的，模型間相互依賴。
核心目標：Bagging主要降低方差（variance），通過平均來平滑模型的波動；Boosting主要降低偏差（bias），通過不斷修正錯誤來提升模型的準確度。
樣本權重：Bagging中樣本權重不變；Boosting中樣本權重會動態調整。

8.2.2 AdaBoost（Adaptive Boosting）：關注被錯分的樣本

AdaBoost（自適應提升）是Boosting家族的早期代表，其思想非常直觀。

初始化：為每個訓練樣本分配相等的權重。
迭代：在每一輪中：
- 在帶權的訓練數據上訓練一個弱學習器（通常是決策樹樁，即深度為1的決策樹）。
- 計算這個弱學習器的錯誤率。
- 根據錯誤率計算該學習器的權重（錯誤率越低，權重越大）。
- 更新樣本權重：提升那些被當前弱學習器錯分的樣本的權重，降低那些被正確分類的樣本的權重。
組合：最終的模型是所有弱學習器的加權投票結果，表現好的學習器擁有更大的“話語權”。

8.2.3 梯度提升樹（GBDT）：擬合殘差的智慧

梯度提升樹（Gradient Boosting Decision Tree）是Boosting思想更通用、更強大的體現。它不再像AdaBoost那樣通過調整樣本權重，而是通過一種更巧妙的方式來關注“錯誤”——直接擬合錯誤的本身。

殘差（Residuals）作為學習目標 對于回歸問題，GBDT的流程非常清晰：

用一個簡單的模型（如所有樣本的均值）作為初始預測。
計算當前模型的殘差，即?真實值 - 預測值。
訓練一棵新的決策樹，但這棵樹的學習目標不再是原始的?y，而是上一輪的殘差。
將這棵“殘差樹”的預測結果乘以一個學習率（learning_rate），然后加到上一輪的預測結果上，得到新的預測。
不斷重復步驟2-4，每一棵新樹都在努力修正前面所有樹留下來的“集體錯誤”。

梯度下降的視角 為何叫“梯度”提升？因為從更數學化的角度看，上述擬合殘差的過程，等價于在函數空間中，讓模型沿著損失函數的負梯度方向進行優化。對于回歸問題常用的MSE損失函數，其負梯度恰好就是殘差。這個視角將Boosting統一到了梯度下降的框架下，使其可以推廣到任何可微分的損失函數，從而也能處理分類問題。

學習率（Learning Rate） 學習率（也稱shrinkage）是一個非常關鍵的超參數（通常設為一個小值，如0.1）。它控制了每一棵樹對最終結果的貢獻度，即每次“進步”的步長。較小的學習率意味著需要更多的樹（n_estimators）才能達到好的效果，但通常能讓模型具有更好的泛化能力，防止過擬合。

8.3 Stacking/Blending：模型的“圓桌會議”

如果說Bagging是“一人一票”，Boosting是“老師帶學生”，那么Stacking（堆疊）就是一場“圓桌會議”。它邀請不同領域的“專家”（異構的基學習器），讓他們各自發表意見，最后由一位更高級的“主席”（元學習器）來綜合所有意見，做出最終的裁決。

8.3.1 核心思想：讓模型“各抒己見”，再由“主席”定奪

分層結構 Stacking通常包含兩層模型：

基學習器層（Level 0）：包含多個（通常是不同類型的）基學習器。例如，我們可以同時使用邏輯回歸、SVM、隨機森林和KNN作為基學習器。
元學習器（Meta-learner, Level 1）：只有一個模型，它的任務是學習如何最好地組合基學習器的預測結果。元學習器通常選擇一個相對簡單的模型，如邏輯回歸或嶺回歸。

Stacking的工作流程

將訓練集劃分為訓練子集和測試子集。
在訓練子集上訓練多個基學習器。
讓這些訓練好的基學習器對測試子集進行預測，這些預測結果將構成元學習器的新特征。
元學習器就以這些新特征作為輸入，以測試子集的真實標簽作為目標，進行訓練。
在預測新數據時，先將數據輸入到所有基學習器中得到預測，再將這些預測作為新特征輸入到元學習器中，得到最終的預測結果。

8.3.2 避免“信息泄露”：交叉驗證在Stacking中的妙用

上述簡單流程有一個嚴重的問題：基學習器在預測時看到了它們用來訓練的數據，這會導致“信息泄露”，使得元學習器過擬合。

K-折交叉預測 為了解決這個問題，標準的Stacking流程使用了K-折交叉驗證的思想：

將原始訓練集劃分為?K?折。
進行?K?次循環。在第?i?次循環中：
- 用除了第?i?折之外的?K-1?折數據來訓練所有的基學習器。
- 讓訓練好的基學習器對第?i?折數據進行預測。這?K?次循環下來，我們就得到了對整個原始訓練集的一個“干凈”的預測，這些預測將作為元學習器的訓練特征。
在生成元學習器的訓練數據后，還需要用完整的原始訓練集重新訓練一遍所有的基學習器，以便它們在未來預測新數據時能利用所有信息。

Blending Blending是Stacking的一種簡化形式。它不再使用復雜的K-折交叉，而是直接將原始訓練集劃分為一個更小的訓練集和一個留出集（hold-out set）。基學習器在訓練集上訓練，然后在留出集上進行預測，用這些預測來訓練元學習器。Blending更簡單，但數據利用率較低。

8.3.3 Scikit-learn實戰與模型多樣性的重要性

代碼實現 Scikit-learn 0.22版本后，提供了官方的StackingClassifier和StackingRegressor，使得實現Stacking變得非常方便。

from sklearn.ensemble import StackingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier# 定義基學習器
estimators = [('rf', RandomForestClassifier(n_estimators=10, random_state=42)),('svr', SVC(random_state=42, probability=True)) # probability=True很重要
]# 定義元學習器
final_estimator = LogisticRegression()# 構建Stacking模型
# cv=5表示使用5折交叉驗證來生成元學習器的訓練數據
stacking_clf = StackingClassifier(estimators=estimators, final_estimator=final_estimator,cv=5
)# 訓練和預測
stacking_clf.fit(X_train, y_train)
y_pred_stacking = stacking_clf.predict(X_test)
print(f"\nStacking模型的準確率: {accuracy_score(y_test, y_pred_stacking):.4f}")

“和而不同” Stacking成功的關鍵在于基學習器的多樣性。如果所有的基學習器都是同質的，或者它們的預測結果高度相關，那么元學習器就學不到什么有用的組合信息。因此，在選擇基學習器時，我們應該盡量選擇那些“思考方式”不同、錯誤模式也不同的模型。例如，將線性模型（邏輯回歸）、基于距離的模型（KNN）和基于樹的模型（隨機森林）組合在一起，通常會比組合三個不同參數的隨機森林效果更好。

8.4 XGBoost與LightGBM：工業界的“大殺器”詳解

XGBoost和LightGBM都是對GBDT思想的極致工程實現和算法優化，它們憑借卓越的性能和效率，成為了當今數據科學領域應用最廣泛的模型。

8.4.1 XGBoost（eXtreme Gradient Boosting）：GBDT的極致進化

XGBoost在GBDT的基礎上，從算法和工程兩個層面都進行了深度優化。

算法層面的優化：
- 正則化：XGBoost在損失函數中直接加入了對樹的復雜度的正則化項，包括對葉子節點數量（T）和葉子節點輸出值（w）的L2正則化。這使得XGBoost能更好地控制過擬合。
- 二階泰勒展開：傳統的GBDT只利用了損失函數的一階梯度信息，而XGBoost對損失函數進行了二階泰勒展開，同時利用了一階和二階梯度信息，使得模型能更精準地向最優解逼近。
工程層面的革新：
- 并行化：雖然樹的生成是串行的，但在每個節點尋找最佳分裂點時，XGBoost可以高效地對特征進行并行計算。
- 緩存感知與核外計算：在工程上做了很多優化，使得它能處理超出內存的大規模數據集。
- 內置稀疏數據處理：能自動處理缺失值和稀疏特征。

為何稱王：XGBoost通過這些優化，實現了速度與精度的完美結合，使其在很長一段時間內統治了各大機器學習競賽。

8.4.2 LightGBM（Light Gradient Boosting Machine）：更快、更輕、更強

LightGBM是微軟推出的一個GBDT框架，它的目標是“更快、更輕”。

基于直方圖的算法：傳統的GBDT在尋找分裂點時需要遍歷所有數據點。LightGBM則先將連續的浮點數特征離散化為K個整數箱（bins），并構建一個寬度為K的直方圖。后續尋找分裂點時，只需在這些箱的邊界上進行，極大地提升了效率和降低了內存消耗。
帶深度限制的Leaf-wise生長策略：傳統的GBDT和XGBoost大多采用Level-wise（按層）的生長策略，它對同一層的所有葉子節點進行無差別分裂，容易產生很多不必要的分裂。LightGBM則采用Leaf-wise（按葉子）的生長策略，每次都從當前所有葉子中，找到那個分裂增益最大的葉子進行分裂。這種策略在分裂次數相同時，能獲得更高的精度，但可能導致樹的深度過深而過擬合，因此需要通過max_depth來限制。

應用場景：由于其卓越的效率，LightGBM在處理大規模數據集時，通常比XGBoost更快，性能也極具競爭力。

8.4.3 實戰對比與選擇之道

代碼實現 XGBoost和LightGBM都是獨立的庫，需要單獨安裝 (pip install xgboost lightgbm)。它們的API與Scikit-learn高度兼容。

import xgboost as xgb
import lightgbm as lgb# XGBoost
xgb_clf = xgb.XGBClassifier(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=42, use_label_encoder=False, eval_metric='logloss')
xgb_clf.fit(X_train, y_train)
y_pred_xgb = xgb_clf.predict(X_test)
print(f"\nXGBoost模型的準確率: {accuracy_score(y_test, y_pred_xgb):.4f}")# LightGBM
lgb_clf = lgb.LGBMClassifier(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=42)
lgb_clf.fit(X_train, y_train)
y_pred_lgb = lgb_clf.predict(X_test)
print(f"LightGBM模型的準確率: {accuracy_score(y_test, y_pred_lgb):.4f}")

何時用哪個

數據規模：
- 對于中小規模的數據集（幾萬到幾十萬行），XGBoost和LightGBM性能相近，XGBoost的社區和文檔更成熟。
- 對于大規模的數據集（百萬行以上），LightGBM的速度優勢會非常明顯。
調參：兩者都有大量的超參數可以調優。XGBoost的參數更直觀一些，而LightGBM由于其獨特的生長策略，調參時需要特別注意控制過擬合。
一般建議：在新的項目中，可以優先嘗試LightGBM，因為它通常能以更快的速度獲得一個非常有競爭力的基線模型。如果對精度有極致要求，可以再精調XGBoost進行比較。

結語

本章，我們深入探索了集成學習的宏偉殿堂。我們理解了Bagging如何通過并行和隨機來追求穩定，領悟了Boosting如何通過串行和迭代來追求卓越，也見識了Stacking如何通過分層和融合來追求協同。最后，我們拆解了XGBoost和LightGBM這兩柄工業界的“神兵利器”。

掌握集成學習，意味著您不再將模型視為孤立的個體，而是學會了如何成為一名運籌帷幄的“將軍”，將不同的兵種（模型）排兵布陣，以集體的智慧去攻克最艱難的堡壘。

至此，我們已經完成了對主流機器學習算法的全面學習。在本書的最后一章，我們將把視野投向更廣闊的未來，探討如何將我們學到的知識付諸實踐，并為您的下一步學習指明方向。

第九章：神經網絡入門——通往深度學習的橋梁

9.1 從生物神經元到感知機模型
9.2 多層感知機（MLP）與反向傳播算法
9.3 激活函數：為神經網絡注入“靈魂”
9.4 使用Scikit-Learn與Keras/TensorFlow構建你的第一個神經網絡

在我們迄今為止的旅程中，我們已經探索了眾多強大的機器學習算法。這些算法在處理結構化數據、進行分類、回歸和聚類任務時表現出色。然而，當面對如圖像、聲音、自然語言等極其復雜、高維且非結構化的數據時，傳統機器學習算法往往會遇到瓶頸。為了應對這些挑戰，一個源于生物學靈感、擁有強大表征學習能力的領域應運而生——人工神經網絡（Artificial Neural Networks, ANN），它構成了現代深度學習（Deep Learning）的基石。

本章是您從經典機器學習邁向深度學習的關鍵橋梁。我們將追本溯源，從模擬生物神經元的最簡單模型“感知機”開始，逐步揭示神經網絡如何通過增加層次（“深度”）來獲得學習復雜模式的能力。我們將深入探討驅動其學習的“靈魂”算法——反向傳播，并巡禮那些為網絡注入非線性“活力”的激活函數。

最后，我們將從我們熟悉的Scikit-Learn平穩過渡到工業界標準的深度學習框架Keras/TensorFlow，親手搭建、訓練并評估您的第一個神經網絡。這不僅是學習一種新的模型，更是開啟一種全新的、以“端到端”學習為核心的解決問題的思維方式。

9.1 從生物神經元到感知機模型

人工神經網絡的最初構想，是對人腦基本處理單元——神經元——的一次大膽而簡化的模仿。理解這個靈感之源，能幫助我們更好地把握其核心設計哲學。

9.1.1 靈感之源：大腦神經元的工作機制

一個典型的生物神經元由以下幾個部分組成：

樹突（Dendrites）：像天線一樣，接收來自其他成千上萬個神經元的信號。
細胞體（Soma）：將所有接收到的信號進行整合處理。
軸突（Axon）：如果整合后的信號強度超過了一個特定的激活閾值（Activation Threshold），細胞體就會產生一次電脈沖（動作電位），并通過軸突將這個信號傳遞出去。
突觸（Synapse）：軸突的末梢，通過釋放化學物質（神經遞質）將信號傳遞給下一個神經元的樹突。突觸的連接強度是可以變化的，這被認為是學習和記憶的生物學基礎。

這個過程可以被高度簡化為：多個輸入信號被加權求和，當總和超過一個閾值時，神經元被“激活”并產生一個輸出信號。

9.1.2 感知機（Perceptron）：最早的神經網絡模型

1957年，心理學家弗蘭克·羅森布拉特（Frank Rosenblatt）受生物神經元的啟發，提出了感知機模型。這不只是一個抽象的概念，而是第一個用算法精確定義的、可學習的神經網絡模型，是人工神經網絡領域的“開山鼻祖”。

數學形式 一個接收 n 個輸入的感知機，其工作流程可以分解為以下幾步：

輸入與權重：模型接收一個輸入向量?x = (x?, x?, ..., x?)。每個輸入?x??都被賦予一個相應的權重?w?，這個權重代表了該輸入信號的重要性。此外，還有一個偏置項?b（bias），可以理解為一個可學習的激活閾值。
加權和（Net Input）：將所有輸入信號與其對應的權重相乘，然后求和，最后加上偏置項。這個過程計算出一個凈輸入值?z。?z = (w?x? + w?x? + ... + w?x?) + b = w · x + b
激活函數（Activation Function）：將凈輸入值?z?傳遞給一個激活函數。在經典的感知機中，這個函數是一個簡單的單位階躍函數（Heaviside Step Function）。?y = f(z) = 1?如果?z ≥ 0?y = f(z) = 0?如果?z < 0?最終的輸出?y?就是模型的預測結果（通常是類別1或類別0）。

學習規則 感知機的學習過程非常直觀：對于一個訓練樣本，如果預測錯誤，就調整權重。

如果真實標簽是1，但模型預測為0（即?z < 0），說明權重太小了，需要增大。更新規則為：w_new = w_old + η * x，b_new = b_old + η。（η是學習率）
如果真實標簽是0，但模型預測為1（即?z ≥ 0），說明權重太大了，需要減小。更新規則為：w_new = w_old - η * x，b_new = b_old - η。這個過程會一直迭代，直到模型能正確分類所有訓練樣本。

幾何意義 w · x + b = 0 這個方程在二維空間中定義了一條直線，在三維空間中定義了一個平面，在更高維空間中則定義了一個超平面（Hyperplane）。這個超平面恰好是決策的邊界。感知機的任務，就是通過學習調整權重 w 和偏置 b，來找到這樣一個超平面，將特征空間一分為二，使得一邊的點被預測為一類，另一邊的點被預測為另一類。因此，感知機本質上是一個線性二分類器。

感知機的局限性 感知機的輝煌是短暫的。1969年，人工智能領域的兩位巨擘馬文·明斯基（Marvin Minsky）和西摩爾·佩珀特（Seymour Papert）在他們的著作《感知機》中，系統地指出了其致命缺陷：感知機只能解決線性可分問題。

最著名的反例就是**“異或（XOR）”問題**。對于輸入(0,0)和(1,1)，XOR輸出0；對于(0,1)和(1,0)，XOR輸出1。你無法在二維平面上用一條直線將這兩組點（(0,0),(1,1) vs (0,1),(1,0)）分開。這個看似簡單的問題，卻成了單層感知機的“滑鐵盧”。這一發現極大地打擊了當時對神經網絡的熱情，使其研究進入了長達十余年的“寒冬”。然而，也正是這個局限性，迫使研究者們思考：單個神經元不行，那多個神經元組合起來呢？

9.2 多層感知機（MLP）與反向傳播算法

要突破線性枷鎖，就需要構建更復雜的模型。解決方案是將多個感知機（或更通用的神經元）堆疊起來，形成多層感知機（Multi-Layer Perceptron, MLP）。

9.2.1 突破線性枷鎖：從單層到多層

網絡結構 一個MLP至少包含三層：

輸入層（Input Layer）：接收原始的特征數據。它不算作真正的計算層，只是數據的入口。
隱藏層（Hidden Layers）：位于輸入層和輸出層之間，可以有一層或多層。這些層對輸入數據進行一系列非線性的變換，是神經網絡“魔力”的核心所在。
輸出層（Output Layer）：產生最終的預測結果。

“深度”的由來 當一個神經網絡包含一個或多個隱藏層時，我們就開始稱其為深度神經網絡（Deep Neural Network, DNN），這也是“深度學習”一詞的來源。每一層隱藏層都可以看作是對前一層輸出的特征進行更高層次、更抽象的組合與表達。例如，在圖像識別中，第一層可能學習到邊緣和角點，第二層可能將邊緣組合成眼睛、鼻子等部件，第三層則可能將這些部件組合成一張人臉。正是這種層次化的特征學習能力，使得深度網絡能夠解決像XOR這樣復雜的非線性問題。

通用近似定理（Universal Approximation Theorem） 這個重要的理論指出：一個包含單個隱藏層、且該隱藏層有足夠多神經元并使用非線性激活函數的MLP，可以以任意精度近似任何連續函數。這從理論上保證了神經網絡的強大表達能力。它告訴我們，只要網絡“足夠寬”，它就能擬合出任意復雜的形狀。而“深度”學習則進一步表明，增加網絡的深度（層數）通常比增加寬度（神經元數量）更有效率。

9.2.2 反向傳播（Backpropagation）：神經網絡的“靈魂”算法

有了多層結構，我們如何有效地訓練這個包含成千上萬個權重的復雜網絡呢？答案就是反向傳播算法，它與梯度下降法相結合，構成了現代神經網絡訓練的基石。

核心思想 反向傳播的核心是微積分中的鏈式法則（Chain Rule）。它是一種高效計算復雜函數梯度的方法。

前向傳播（Forward Pass）：將一個訓練樣本輸入網絡，信號從輸入層逐層向前傳播，經過每一層的計算，最終在輸出層得到一個預測值。
計算損失（Loss Calculation）：將預測值與真實標簽進行比較，通過一個損失函數（如分類任務的交叉熵損失，回歸任務的均方誤差損失）來量化模型的“錯誤”程度。
反向傳播（Backward Pass）：
- 首先，計算損失函數對輸出層權重的梯度。
- 然后，利用鏈式法則，將這個“誤差信號”逐層向后（反向）傳播。在每一層，我們都計算出損失對該層權重的梯度。
- 這個過程就像是在“追究責任”：輸出層的誤差有多大“責任”應該由倒數第二層承擔？倒數第二層的誤差又該如何分配給更前一層的權重？反向傳播完美地解決了這個“責任分配”問題。

梯度下降的再次登場 一旦通過反向傳播計算出了網絡中所有權重相對于總損失的梯度，接下來的步驟就和我們熟悉的梯度下降完全一樣了：用這些梯度來更新每一個權重，使得總損失向著減小的方向移動一小步。 w_new = w_old - η * (?Loss / ?w) 這個“前向傳播 -> 計算損失 -> 反向傳播 -> 更新權重”的循環，會通過成千上萬個訓練樣本不斷迭代，最終將網絡訓練到一個能夠很好地完成任務的狀態。

9.3 激活函數：為神經網絡注入“靈魂”

在MLP的討論中，我們提到了“非線性激活函數”。它是將簡單的線性模型轉變為強大的非線性學習機器的關鍵。

9.3.1 為何需要非線性激活函數？

想象一下，如果我們使用的激活函數是線性的（例如 f(z) = z）。那么，一個隱藏層的輸出就是其輸入的線性組合。當這個輸出再作為下一層的輸入時，最終整個網絡的輸出仍然只是原始輸入的某種線性組合。這意味著，無論你堆疊多少層，整個網絡本質上等價于一個單層的線性模型。它將失去學習復雜非線性關系的能力，退化成一個普通的線性分類器或回歸器。

因此，非線性激活函數是賦予神經網絡深度和表達能力的“靈魂”。

9.3.2 常用激活函數巡禮

Sigmoid：f(z) = 1 / (1 + e??)
- 特點：將任意實數壓縮到?(0, 1)?區間，常用于二分類問題的輸出層（表示概率）。
- 缺點：當輸入值非常大或非常小時，其導數（梯度）趨近于0，這會導致**梯度消失（Vanishing Gradients）**問題，使得深層網絡的訓練非常困難。
Tanh（雙曲正切）：f(z) = (e? - e??) / (e? + e??)
- 特點：將任意實數壓縮到?(-1, 1)?區間，是“以0為中心”的，通常比Sigmoid收斂更快。
- 缺點：同樣存在梯度消失問題。
ReLU（Rectified Linear Unit）：f(z) = max(0, z)
- 特點：現代神經網絡最常用的激活函數。它計算非常簡單（一個閾值判斷），并且在正數區間的梯度恒為1，極大地緩解了梯度消失問題，使得訓練深層網絡成為可能。
- 缺點：當輸入為負數時，其梯度為0，可能導致某些神經元永遠無法被激活，即**“死亡ReLU問題”（Dying ReLU Problem）**。
Leaky ReLU, PReLU, ELU：這些都是對ReLU的改進，試圖解決“死亡ReLU問題”。例如，Leaky ReLU在輸入為負數時，會給一個非常小的正斜率（如0.01），而不是0。
Softmax：f(z?) = e?? / Σ?(e??)
- 特點：它不是作用于單個神經元，而是作用于整個輸出層。它能將輸出層的一組任意實數值，轉換為一個和為1的概率分布。因此，它是多分類問題輸出層的標準選擇。

9.4 使用Scikit-Learn與Keras/TensorFlow構建你的第一個神經網絡

理論學習之后，最好的消化方式就是動手實踐。我們將從我們熟悉的Scikit-Learn開始，然后邁向更專業的深度學習框架。

9.4.1 Scikit-Learn中的`MLPClassifier`與`MLPRegressor`

Scikit-Learn為我們提供了一個易于使用的MLP實現，非常適合進行快速的原型驗證。

代碼實現

from sklearn.neural_network import MLPClassifier
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler# 使用月牙形數據，這是一個典型的非線性可分問題
X, y = make_moons(n_samples=200, noise=0.2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)# 神經網絡對特征尺度敏感，標準化是重要步驟
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)# 構建和訓練MLP
# hidden_layer_sizes=(10, 5) 表示兩個隱藏層，第一個10個神經元，第二個5個
mlp = MLPClassifier(hidden_layer_sizes=(10, 5), max_iter=1000, random_state=42)
mlp.fit(X_train_scaled, y_train)print(f"Scikit-Learn MLP Accuracy: {mlp.score(X_test_scaled, y_test):.4f}")

核心超參數

hidden_layer_sizes: 一個元組，定義了每個隱藏層的神經元數量。
activation: 激活函數，默認為'relu'。
solver: 權重優化的求解器，默認為'adam'，一個高效的梯度下降變體。
alpha: L2正則化的強度。

局限性：Scikit-Learn的MLP實現功能相對基礎，不支持GPU加速，也無法方便地構建如卷積神經網絡（CNN）、循環神經網絡（RNN）等復雜的網絡結構。當我們需要更大的靈活性和性能時，就需要轉向專業的深度學習框架。

9.4.2 邁向專業框架：TensorFlow與Keras簡介

TensorFlow：由Google開發的開源深度學習平臺。它是一個強大的底層引擎，提供了構建和部署大規模機器學習模型所需的全套工具。
Keras：一個高級神經網絡API，以其用戶友好、模塊化和可擴展性而聞名。它現在已經正式成為TensorFlow項目的官方高級API。

它們的關系可以理解為：Keras是“前端”，負責以簡單直觀的方式定義網絡結構；TensorFlow是“后端”，負責在底層高效地執行計算。

9.4.3 Keras實戰：序貫模型（Sequential API）入門

Keras最簡單的模型是序貫模型（Sequential Model），它允許我們像堆疊積木一樣，一層一層地構建網絡。

代碼實現

# 需要先安裝tensorflow: pip install tensorflow
import tensorflow as tf
from tensorflow import keras# 1. 構建模型
# Sequential模型是一個線性的層堆棧
model = keras.Sequential([# Dense層就是全連接層。input_shape只需在第一層指定。keras.layers.Dense(10, activation='relu', input_shape=(X_train_scaled.shape[1],)),keras.layers.Dense(5, activation='relu'),# 輸出層，因為是二分類，用一個sigmoid神經元keras.layers.Dense(1, activation='sigmoid')
])# 2. 編譯模型
# 在這里我們定義損失函數、優化器和評估指標
model.compile(optimizer='adam',loss='binary_crossentropy', # 二分類交叉熵metrics=['accuracy'])# 打印模型概覽
model.summary()# 3. 訓練模型
# epochs: 訓練輪數; batch_size: 每批次樣本數
history = model.fit(X_train_scaled, y_train, epochs=100, batch_size=16, verbose=0) # verbose=0不打印過程# 4. 評估模型
loss, accuracy = model.evaluate(X_test_scaled, y_test)
print(f"\nKeras MLP Accuracy: {accuracy:.4f}")

代碼對比：通過與Scikit-Learn的對比，我們可以看到Keras的實現更加清晰和模塊化。每一層都是一個獨立的對象，我們可以自由地組合它們。compile和fit的步驟也讓我們對訓練過程有了更精細的控制。這種設計哲學，為我們未來構建更復雜的深度學習模型鋪平了道路。

結語

本章，我們成功地搭建了從經典機器學習通往深度學習的橋梁。我們從生物學的靈感出發，理解了感知機的誕生與局限，見證了多層感知機如何通過“深度”和“非線性”打破枷鎖。我們揭開了反向傳播算法的神秘面紗，并熟悉了激活函數這個神經網絡的“靈魂”家族。

最重要的是，我們跨出了從使用便捷工具到掌握專業框架的關鍵一步。您現在已經具備了使用Keras/TensorFlow構建和訓練神經網絡的基本能力。

這并非我們旅程的終點，而是一個更宏大、更激動人心的起點。深度學習的世界廣闊無垠，卷積神經網絡在計算機視覺中叱咤風云，循環神經網絡在自然語言處理中大放異彩。愿本章所學，能成為您探索這個新世界的堅實基石和不竭動力。

第三部分：登堂入室——高級專題與實戰演練

核心目標： 將理論知識應用于真實世界的復雜問題。提供從數據獲取到模型部署的全流程項目指導，并介紹更前沿的領域，開拓學習者視野。

?第十章：實戰項目一：金融風控——信用卡欺詐檢測

10.1 問題定義與數據探索：理解不平衡數據
10.2 特征工程與采樣技術（SMOTE）
10.3 模型選擇、訓練與評估
10.4 解釋性分析：模型為何做出這樣的決策？ (SHAP/LIME)

歡迎來到我們的第一個綜合實戰項目。在本章中，我們將化身為一名金融科技公司的數據科學家，直面一個極具挑戰性且價值巨大的任務：構建一個信用卡欺詐檢測模型。這個項目將不再是孤立地學習某個算法，而是要求我們綜合運用數據探索、特征工程、模型訓練、評估和解釋等一系列技能，來解決一個真實的商業問題。

我們將要處理的數據有一個非常顯著的特點——嚴重的類別不平衡。在現實世界中，絕大多數的信用卡交易都是合法的，欺詐交易只占極小的一部分。這種不平衡性給模型訓練帶來了巨大的挑戰，也使得我們必須重新審視和選擇合適的評估指標。

本章的目標不僅是構建一個高精度的模型，更是要經歷一個完整的、端到端的數據科學項目流程。我們將學習如何處理不平衡數據，如何在多個模型和策略中進行權衡，以及如何利用先進的工具來“打開”模型的黑箱，理解其決策背后的邏輯。這對于在金融、醫療等高風險領域建立可信賴的AI系統至關重要。

10.1 問題定義與數據探索：理解不平衡數據

在動手寫代碼之前，首要任務是清晰地理解問題和我們手中的數據。

10.1.1 業務背景與問題定義

業務目標：銀行或金融機構的核心訴求是，在不影響絕大多數正常用戶交易體驗的前提下，盡可能準確、快速地識別出欺詐交易，以減少資金損失。這里存在一個天然的權衡：
- 漏報（False Negative）：將欺詐交易誤判為正常交易。這是最嚴重的錯誤，直接導致資金損失。
- 誤報（False Positive）：將正常交易誤判為欺詐交易。這會給用戶帶來不便（如交易被拒，需電話核實），影響用戶體驗。
- 我們的模型需要在降低漏報率（即提高召回率）和控制誤報率（即提高精確率）之間找到一個最佳平衡點。
機器學習問題定性：這是一個典型的二分類問題。輸入是交易的各項特征，輸出是兩個類別之一：0（正常）或 1（欺詐）。其核心難點在于“欺詐”這個類別是極少數類。

10.1.2 數據集介紹與探索性數據分析（EDA）

我們將使用Kaggle上一個非常經典的“信用卡欺詐檢測”數據集。

數據加載與初步觀察

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns# 加載數據
df = pd.read_csv('creditcard.csv')# 查看數據基本信息
print(df.head())
print(df.info())
print(df.describe())# 檢查缺失值
print("\n缺失值檢查:")
print(df.isnull().sum().max())

特征分析：數據包含31列。Time是自第一筆交易以來的秒數。Amount是交易金額。Class是我們的目標變量（1表示欺詐，0表示正常）。V1到V28是經過**主成分分析（PCA）**處理后的特征，這是為了保護用戶隱私和數據安全。PCA處理過后的特征已經去除了原始意義，并且尺度相對統一，但Time和Amount還保留著原始尺度。

不平衡性可視化 這是理解本問題的關鍵第一步。

# 查看類別分布
class_counts = df['Class'].value_counts()
print("\n類別分布:")
print(class_counts)# 繪制計數圖
plt.figure(figsize=(8, 6))
sns.countplot(x='Class', data=df)
plt.title(f'Class Distribution \n (0: Normal || 1: Fraud)')
plt.show()# 計算比例
fraud_percentage = (class_counts[1] / class_counts.sum()) * 100
print(f"欺詐交易占比: {fraud_percentage:.4f}%")

我們會發現，欺詐交易的數量（492筆）相對于正常交易（284,315筆）來說微乎其微，占比僅為約0.1727%。這種懸殊的比例是我們在后續所有工作中都必須牢記的核心背景。

Amount和Time特征的分布

我們來觀察一下這兩個未經PCA處理的特征與欺詐行為的關系。

fig, axes = plt.subplots(1, 2, figsize=(18, 4))# 交易金額分布
sns.histplot(df['Amount'], ax=axes[0], bins=50, kde=True)
axes[0].set_title('Distribution of Transaction Amount')# 交易時間分布
sns.histplot(df['Time'], ax=axes[1], bins=50, kde=True)
axes[1].set_title('Distribution of Transaction Time')plt.show()# 查看欺詐交易和正常交易在Amount上的差異
print("\n交易金額描述 (正常 vs 欺詐):")
print(df.groupby('Class')['Amount'].describe())

通過對Amount的描述性統計，我們可能會發現欺詐交易的平均金額與正常交易有所不同。同時，我們也可以繪制欺詐交易和正常交易在Time和Amount上的分布圖，來更直觀地尋找差異。

# 欺詐和正常交易的金額與時間分布對比
fig, axes = plt.subplots(2, 1, figsize=(12, 10), sharex=True)sns.histplot(df.loc[df['Class'] == 1, 'Amount'], bins=30, ax=axes[0], color='r', label='Fraud')
axes[0].set_title('Amount Distribution for Fraudulent Transactions')
axes[0].legend()sns.histplot(df.loc[df['Class'] == 0, 'Amount'], bins=30, ax=axes[1], color='b', label='Normal')
axes[1].set_title('Amount Distribution for Normal Transactions')
axes[1].legend()plt.xlim((0, 5000)) # 限制x軸范圍以便觀察
plt.show()

我們已經看到了Amount和Time的整體分布，現在讓我們更細致地比較一下正常交易與欺詐交易在這兩個維度上的差異。

# 欺詐和正常交易的金額與時間分布對比
fig, axes = plt.subplots(2, 2, figsize=(18, 10))# --- Amount 對比 ---
sns.kdeplot(df.loc[df['Class'] == 0, 'Amount'], ax=axes[0, 0], label='Normal', fill=True)
sns.kdeplot(df.loc[df['Class'] == 1, 'Amount'], ax=axes[0, 1], label='Fraud', fill=True, color='r')
axes[0, 0].set_title('Amount Distribution (Normal)')
axes[0, 1].set_title('Amount Distribution (Fraud)')
axes[0, 0].set_xlim(-50, 500) # 限制范圍以便觀察
axes[0, 1].set_xlim(-50, 500)# --- Time 對比 ---
# 時間特征以秒為單位，跨度為兩天，可能存在晝夜模式
sns.kdeplot(df.loc[df['Class'] == 0, 'Time'], ax=axes[1, 0], label='Normal', fill=True)
sns.kdeplot(df.loc[df['Class'] == 1, 'Time'], ax=axes[1, 1], label='Fraud', fill=True, color='r')
axes[1, 0].set_title('Time Distribution (Normal)')
axes[1, 1].set_title('Time Distribution (Fraud)')plt.tight_layout()
plt.show()

觀察與發現：

金額（Amount）：正常交易的金額分布非常廣泛，而欺詐交易的金額似乎更集中在較小的數值區域。這可能是一個有用的信號。
時間（Time）：正常交易的時間分布呈現出明顯的周期性，有兩個低谷，這很可能對應著深夜交易量減少的模式。而欺詐交易的時間分布則顯得更加均勻，似乎全天候都在發生。

這些初步的EDA（探索性數據分析）給了我們信心，說明這些特征中確實包含了可以用于區分兩類交易的信息。

10.2 特征工程與采樣技術

在將數據喂給模型之前，我們需要進行一些必要的準備工作。

10.2.1 特征標準化

Amount和Time特征的數值范圍（Amount可以上萬，Time可以達到十幾萬）與其他經過PCA處理的V1-V28特征（大多集中在0附近）差異巨大。如果直接使用，可能會導致那些數值范圍大的特征在模型訓練中占據主導地位，特別是對于那些對尺度敏感的算法（如邏輯回歸、SVM、神經網絡）。因此，標準化是必不可少的步驟。

RobustScaler是一個不錯的選擇，因為它使用四分位數進行縮放，對于異常值不那么敏感，而金融數據中往往存在一些極端的大額交易。

from sklearn.preprocessing import RobustScaler# 創建RobustScaler實例
rob_scaler = RobustScaler()# 對Amount和Time進行縮放
df['scaled_amount'] = rob_scaler.fit_transform(df['Amount'].values.reshape(-1,1))
df['scaled_time'] = rob_scaler.fit_transform(df['Time'].values.reshape(-1,1))# 刪除原始的Time和Amount列
df.drop(['Time','Amount'], axis=1, inplace=True)# 將scaled_amount和scaled_time移動到前面，方便查看
scaled_amount = df['scaled_amount']
scaled_time = df['scaled_time']
df.drop(['scaled_amount', 'scaled_time'], axis=1, inplace=True)
df.insert(0, 'scaled_amount', scaled_amount)
df.insert(1, 'scaled_time', scaled_time)print("標準化后的數據頭部:")
print(df.head())

10.2.2 應對類別不平衡：采樣技術

這是本項目最核心的挑戰。如果直接在原始的不平衡數據上訓練，大多數模型會學到一個“偷懶”的策略：將所有交易都預測為正常。這樣做雖然能達到99.8%以上的準確率，但它完全沒有識別出任何欺詐交易，對于我們的業務目標來說毫無價值。

下采樣（Undersampling） 最簡單的方法是隨機刪除多數類（正常交易）的樣本，使其數量與少數類（欺詐交易）相匹配。

優點：速度快，數據集變小，訓練成本降低。
缺點：會丟失大量信息。被刪除的正常交易樣本中可能包含了區分正常與欺詐的重要模式。

過采樣（Oversampling） 與下采樣相反，我們可以增加少數類樣本的數量，通常通過隨機復制來實現。

優點：沒有信息丟失。
缺點：由于是簡單復制，容易導致模型對特定的少數類樣本過擬合。

10.2.3 SMOTE：更智能的過采樣

為了解決簡單過采樣的過擬合問題，SMOTE（Synthetic Minority Over-sampling Technique）被提了出來。

核心思想：SMOTE不是簡單地復制少數類樣本，而是合成新的、看起來很真實的少數類樣本。其過程是：
1. 隨機選擇一個少數類樣本?A。
2. 找到它在少數類樣本中的?k?個最近鄰（k通常為5）。
3. 從這?k?個近鄰中隨機選擇一個樣本?B。
4. 在?A?和?B?之間的連線上隨機取一點，作為新的合成樣本。這個新樣本的計算公式是?A + λ * (B - A)，其中?λ?是一個0到1之間的隨機數。
效果：通過這種方式，SMOTE為少數類生成了新的、多樣化的樣本，擴大了少數類的決策區域，有助于模型學習到更魯棒的分類邊界。

代碼實現

我們將使用一個非常流行的庫 imbalanced-learn 來實現SMOTE。如果尚未安裝，請先運行：

pip install -U imbalanced-learn

現在，讓我們在代碼中實際應用SMOTE。關鍵在于，SMOTE只能應用于訓練集，絕不能應用于測試集。因為測試集必須保持其原始的、真實的數據分布，以公正地評估模型的泛化能力。

from sklearn.model_selection import train_test_split
from imblearn.over_sampling import SMOTE
import pandas as pd# 假設 df 是我們已經完成特征標準化的DataFrame
# X 是特征, y 是標簽
X = df.drop('Class', axis=1)
y = df['Class']# 1. 首先，劃分訓練集和測試集
# 使用 stratify=y 來確保訓練集和測試集中的類別比例與原始數據集一致
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42, stratify=y)print("--- 數據劃分后 ---")
print("原始訓練集中的類別分布:")
print(y_train.value_counts())
print("\n原始測試集中的類別分布:")
print(y_test.value_counts())# 2. 創建SMOTE實例并應用于訓練集
print("\n--- 應用SMOTE ---")
smote = SMOTE(random_state=42)
X_train_smote, y_train_smote = smote.fit_resample(X_train, y_train)# 3. 檢查SMOTE處理后訓練集的類別分布
print("\nSMOTE處理后訓練集的類別分布:")
print(y_train_smote.value_counts())

代碼解讀：

我們首先將整個數據集劃分為訓練集和測試集。這是至關重要的一步。
然后，我們創建了一個SMOTE對象。
最關鍵的一行是?smote.fit_resample(X_train, y_train)。fit_resample方法會學習訓練數據中少數類的分布，并生成新的合成樣本，最終返回一個類別完全平衡的新訓練集?X_train_smote?和?y_train_smote。
從輸出可以看到，經過SMOTE處理后，訓練集中的少數類（欺詐）樣本數量被提升到與多數類（正常）相同，而測試集則保持原樣，這完全符合我們的要求。

現在，我們擁有了一個經過SMOTE處理、類別平衡的訓練集 (X_train_smote, y_train_smote)，以及一個原始的、不平衡的測試集 (X_test, y_test)。接下來，我們就可以放心地使用這個新的訓練集來訓練我們的模型了。

10.3 模型選擇、訓練與評估

現在，我們準備好進入模型構建階段了。

10.3.1 選擇合適的評估指標

正如之前所說，**準確率（Accuracy）**在這里是完全不可信的。我們需要關注那些能真實反映模型在不平衡數據上表現的指標：

精確率（Precision）：TP / (TP + FP)。在所有被模型預測為“欺詐”的交易中，真正是欺詐的比例。它衡量了模型的查準率，高精確率意味著低的誤報率。
召回率（Recall）：TP / (TP + FN)。在所有真正的欺詐交易中，被模型成功識別出來的比例。它衡量了模型的查全率，高召回率意味著低的漏報率。
F1-Score：精確率和召回率的調和平均數，是兩者的綜合考量。
PR曲線（Precision-Recall Curve）：以召回率為橫軸，精確率為縱軸繪制的曲線。曲線下的面積（AUC-PR）是衡量模型整體性能的優秀指標，尤其是在不平衡場景下。一個理想模型的PR曲線會盡可能地靠近右上角。

10.3.2 模型訓練與比較

我們將進行一個對比實驗，看看不同數據處理策略對模型性能的影響。

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, precision_recall_curve, auc
from imblearn.over_sampling import SMOTE# 準備數據
X = df.drop('Class', axis=1)
y = df['Class']# 劃分原始數據集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42, stratify=y)# --- 1. 在原始不平衡數據上訓練 ---
print("--- 1. 訓練于原始不平衡數據 ---")
lr_original = LogisticRegression(solver='liblinear')
lr_original.fit(X_train, y_train)
y_pred_original = lr_original.predict(X_test)
print(classification_report(y_test, y_pred_original, target_names=['Normal', 'Fraud']))# --- 2. 使用SMOTE處理數據并訓練 ---
print("\n--- 2. 訓練于SMOTE處理后的數據 ---")
smote = SMOTE(random_state=42)
X_train_smote, y_train_smote = smote.fit_resample(X_train, y_train)print("SMOTE處理后訓練集類別分布:")
print(y_train_smote.value_counts())lr_smote = LogisticRegression(solver='liblinear')
lr_smote.fit(X_train_smote, y_train_smote)
y_pred_smote = lr_smote.predict(X_test)
print(classification_report(y_test, y_pred_smote, target_names=['Normal', 'Fraud']))

結果分析：

在原始數據上訓練的模型，其對欺詐類（Fraud）的**召回率（recall）**會非常低，這意味著它漏掉了大量的欺詐交易。
在SMOTE處理過的數據上訓練的模型，其對欺詐類的召回率會顯著提升，但**精確率（precision）**可能會有所下降。這是一種典型的權衡。

10.3.3 精調與決策

僅僅得到預測類別是不夠的，我們還需要利用預測概率來做更精細的決策。

閾值移動（Threshold Moving） 大多數分類器默認使用0.5作為分類閾值。我們可以通過調整這個閾值，來主動地在精確率和召回率之間進行權衡。

# 獲取SMOTE模型在測試集上的預測概率
y_proba_smote = lr_smote.predict_proba(X_test)[:, 1]# 計算PR曲線
precision, recall, thresholds = precision_recall_curve(y_test, y_proba_smote)
auc_pr = auc(recall, precision)# 繪制PR曲線
plt.figure(figsize=(8, 6))
plt.plot(recall, precision, label=f'Logistic Regression (AUC-PR = {auc_pr:.2f})')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall Curve')
plt.legend(loc='best')
plt.grid(True)
plt.show()

通過觀察PR曲線，業務決策者可以選擇一個最符合他們風險偏好的點。例如，如果銀行對漏報的容忍度極低，他們可能會選擇一個高召回率、中等精確率的閾值點。

10.4 解釋性分析：模型為何做出這樣的決策？

一個模型即使表現再好，如果它是一個完全的“黑箱”，在金融風控這樣的高風險領域也很難被完全信任和采納。我們需要知道模型做出決策的依據。

10.4.1 模型可解釋性的重要性

建立信任：讓業務人員和監管機構相信模型是可靠的。
模型調試：理解模型的錯誤，發現其決策邏輯的漏洞。
發現新知：從模型的決策模式中，可能會發現一些人類專家未曾注意到的欺詐模式。
滿足合規：很多地區的法規（如GDPR）要求對算法決策給出解釋。

10.4.2 SHAP（SHapley Additive exPlanations）簡介

SHAP是一個基于博弈論中沙普利值（Shapley Value）的、強大的模型解釋框架。

核心思想：它將模型的單次預測結果看作是所有特征共同協作完成的“收益”，而SHAP值則公平地將這份“收益”（即預測值與基準值的差異）分配給每一個特征，量化了每個特征的貢獻。
SHAP值的含義：對于某個預測，一個特征的SHAP值為正，表示該特征將預測推向了正類（欺詐）；為負，則表示推向了負類（正常）。

10.4.3 使用SHAP進行模型解釋

我們將使用shap庫來解釋我們訓練的LightGBM或XGBoost模型（因為它們通常性能更好，也更值得解釋）。

pip install shap

import lightgbm as lgb
import shap# 在SMOTE數據上訓練一個LightGBM模型
lgbm = lgb.LGBMClassifier(random_state=42)
lgbm.fit(X_train_smote, y_train_smote)# 1. 創建SHAP解釋器
explainer = shap.TreeExplainer(lgbm)# 2. 計算測試集的SHAP值
shap_values = explainer.shap_values(X_test)# 3. 全局解釋：特征重要性圖 (Summary Plot)
# shap_values[1] 對應正類（欺詐）的SHAP值
shap.summary_plot(shap_values[1], X_test, plot_type="dot")

Summary Plot解讀：

每一行代表一個特征，按其全局重要性排序。
每個點代表一個樣本。
點的顏色表示該樣本上該特征的原始值（紅色高，藍色低）。
點在橫軸上的位置表示該樣本上該特征的SHAP值。
從圖中我們可以看到，例如，V14特征值較低（藍色）時，其SHAP值為正，強烈地將預測推向“欺詐”；而V12特征值較高（紅色）時，其SHAP值為負，將預測推向“正常”。

個體解釋：力圖（Force Plot） 我們還可以對單個預測進行解釋。

# 解釋第一個測試樣本
shap.initjs() # 初始化JS環境以便在notebook中繪圖
shap.force_plot(explainer.expected_value[1], shap_values[1][0,:], X_test.iloc[0,:])

Force Plot解讀：

基準值（base value）：是模型在整個數據集上的平均預測概率。
紅色部分：是將預測概率推高的特征。
藍色部分：是將預測概率拉低的特征。
這個圖清晰地展示了對于這一個特定的交易，是哪些特征以及它們的取值，共同作用導致了最終的預測結果。

結語

通過這個實戰項目，我們走完了一個完整的數據科學流程。我們從理解一個充滿挑戰的業務問題開始，通過細致的數據探索發現了核心難點——類別不平衡。我們學習并應用了SMOTE技術來處理這個問題，并選擇了合適的評估指標來公正地評價我們的模型。最后，我們還利用SHAP這一強大工具，打開了模型的“黑箱”，窺探了其決策的內在邏輯。

這不僅僅是一次技術的演練，更是一次思維的升華。您現在所掌握的，已經不再是零散的知識點，而是一套可以遷移到其他領域的、解決實際問題的完整方法論。

第十一章：實戰項目二：自然語言處理——文本情感分析

11.1 文本數據的預處理：分詞、停用詞與向量化（TF-IDF, Word2Vec）
11.2 從傳統模型到簡單神經網絡的情感分類
11.3 主題模型（LDA）：挖掘文本背后的隱藏主題

在完成了對結構化數字世界的探索之后，我們的實戰旅程將轉向一個更貼近人類智慧核心的領域——自然語言處理（Natural Language Processing, NLP）。本項目中，我們將挑戰一個NLP中最經典、也最具商業價值的任務之一：文本情感分析（Sentiment Analysis）。

我們的目標是教會機器去“閱讀”一段文本（例如一條電影評論、一條產品反饋），并判斷其中蘊含的情感是積極的、消極的還是中性的。這項技術是構建智能客服、進行輿情監控、分析用戶反饋等眾多應用的核心。

與上一個項目不同，我們這次面對的不再是整齊的、數值化的數據，而是由詞語、句子和段落組成的非結構化文本。因此，本章的重點將首先聚焦于如何將這些人類語言“翻譯”成機器能夠理解的數學語言——即文本向量化。我們將探索從經典的TF-IDF到更現代的Word2Vec詞嵌入技術。

隨后，我們將分別使用傳統機器學習模型和簡單的神經網絡來構建情感分類器，并比較它們的性能。最后，我們還將學習一種強大的無監督技術——主題模型（LDA），它能幫助我們自動地從海量文本中挖掘出人們正在討論的核心話題，為我們提供超越情感分類的更深層次洞察。

11.1 文本數據的預處理：分詞、停用詞與向量化

在NLP中，原始文本數據往往是“嘈雜”的，需要經過一系列精心的預處理和轉換，才能被機器學習模型所用。這個過程的好壞，直接決定了整個項目的成敗。

11.1.1 NLP的第一步：文本清洗與規范化

我們將以一個IMDb電影評論數據集為例，這個數據集中包含了5萬條帶有正面或負面標簽的電影評論。

數據加載與清洗流程

import pandas as pd
import re# 假設數據已加載到DataFrame df 中，包含 'review' 和 'sentiment' 兩列
# df = pd.read_csv('IMDB_Dataset.csv')# 示例數據
data = {'review': ["This movie was awesome! The acting was great.", "A truly TERRIBLE film. 1/10. Don't waste your time.","<br /><br />What a masterpiece!"],'sentiment': ['positive', 'negative', 'positive']}
df = pd.DataFrame(data)def clean_text(text):# 1. 轉換為小寫text = text.lower()# 2. 移除HTML標簽text = re.sub(r'<.*?>', '', text)# 3. 移除標點符號和數字text = re.sub(r'[^a-z\s]', '', text)# 4. 移除多余的空格text = re.sub(r'\s+', ' ', text).strip()return textdf['cleaned_review'] = df['review'].apply(clean_text)
print(df[['review', 'cleaned_review']])

11.1.2 分詞（Tokenization）與停用詞（Stop Words）

清洗完成后，我們需要將連續的文本切分成獨立的單元，即“詞元”（Token）。

分詞：對于英文，分詞相對簡單，通常按空格和標點來切分。對于中文等沒有明確單詞邊界的語言，則需要使用專門的分詞算法庫（如jieba）。
停用詞：文本中有很多詞，如“a”, “the”, “is”, “in”等，它們頻繁出現但幾乎不攜帶任何情感信息。這些詞被稱為“停用詞”，通常需要被移除，以減少噪聲和計算量。

import nltk
# nltk.download('stopwords') # 首次使用需要下載
# nltk.download('punkt')
from nltk.corpus import stopwords
from nltk.tokenize import word_tokenizestop_words = set(stopwords.words('english'))def tokenize_and_remove_stopwords(text):tokens = word_tokenize(text)filtered_tokens = [word for word in tokens if word not in stop_words]return filtered_tokensdf['tokens'] = df['cleaned_review'].apply(tokenize_and_remove_stopwords)
print("\n分詞與移除停用詞后:")
print(df[['cleaned_review', 'tokens']])

11.1.3 將文本轉化為向量：從詞袋到詞嵌入

這是最關鍵的一步：將詞元列表轉換為數值向量。

TF-IDF（Term Frequency-Inverse Document Frequency） TF-IDF是詞袋模型（BoW）的一種經典升級。它認為一個詞的重要性與它在**當前文檔中出現的頻率（TF）成正比，與它在所有文檔中出現的頻率（IDF）**成反比。一個詞在當前文檔里出現次數多，但在其他文檔里很少出現，那么它很可能就是當前文檔的關鍵詞，應該被賦予高權重。

from sklearn.feature_extraction.text import TfidfVectorizer# 為了使用TfidfVectorizer，我們需要將詞元列表重新組合成字符串
df['processed_text'] = df['tokens'].apply(lambda x: ' '.join(x))tfidf_vectorizer = TfidfVectorizer(max_features=5000) # 限制最大特征數為5000
X_tfidf = tfidf_vectorizer.fit_transform(df['processed_text'])print("\nTF-IDF向量的維度:")
print(X_tfidf.shape) # (文檔數, 特征數)
# 這是一個稀疏矩陣

詞嵌入（Word Embeddings） TF-IDF雖然經典，但它有一個重大缺陷：它無法理解詞與詞之間的語義關系。在TF-IDF看來，“good”, “excellent”, “superb”是三個完全不同的、毫無關聯的詞。

詞嵌入技術解決了這個問題。

核心思想：它將每個詞映射到一個低維（如100維或300維）、稠密的浮點數向量。這個映射是通過在大量文本上訓練一個神經網絡來學習的，其學習目標是讓上下文相似的詞，其對應的向量在向量空間中也相互靠近。例如，“king”的向量會和“queen”的向量很接近。
Word2Vec：是Google在2013年推出的一個里程碑式的詞嵌入模型。它有兩種主要的訓練算法：
- CBOW (Continuous Bag-of-Words)：根據上下文詞來預測中心詞。
- Skip-gram：根據中心詞來預測上下文詞。
使用預訓練模型：訓練一個高質量的Word2Vec模型需要海量的文本和巨大的計算資源。幸運的是，我們可以直接使用Google、Facebook等機構在大規模語料庫（如維基百科、新聞文章）上訓練好的預訓練詞嵌入模型。

11.2 從傳統模型到簡單神經網絡的情感分類

現在我們有了兩種將文本表示為向量的方法，可以開始構建分類模型了。

11.2.1 使用TF-IDF與傳統機器學習模型

TF-IDF產生的高維稀疏向量，與邏輯回歸、樸素貝葉斯等線性模型是“天作之合”。

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
from sklearn.preprocessing import LabelEncoder# 準備標簽
le = LabelEncoder()
y = le.fit_transform(df['sentiment'])# 劃分數據
X_train, X_test, y_train, y_test = train_test_split(X_tfidf, y, test_size=0.2, random_state=42)# 訓練邏輯回歸模型
lr_model = LogisticRegression(solver='liblinear', random_state=42)
lr_model.fit(X_train, y_train)# 評估
y_pred = lr_model.predict(X_test)
print("--- TF-IDF + 邏輯回歸 模型評估 ---")
# 由于我們的示例數據太少，這里只展示流程，真實數據集上才能看到有意義的結果
# print(classification_report(y_test, y_pred, target_names=le.classes_))
print("模型訓練完成。在真實數據集上，此方法通常能獲得非常好的基線性能。")

11.2.2 使用Word2Vec與神經網絡

使用詞嵌入時，我們需要先將一條評論中的所有詞向量聚合成一個能代表整條評論的句子向量。最簡單的方法是取平均值。

# 假設我們已經加載了一個預訓練的Word2Vec模型 (例如 gensim.models.KeyedVectors.load_word2vec_format)
# word2vec_model = ...
# embedding_dim = word2vec_model.vector_size# 此處為演示，我們創建一個假的Word2Vec模型
embedding_dim = 100
vocab = set(word for tokens_list in df['tokens'] for word in tokens_list)
word2vec_model = {word: np.random.rand(embedding_dim) for word in vocab}def sentence_to_vector(tokens, model, embedding_dim):# 將句子中所有詞的向量相加，然后除以詞數vectors = [model[word] for word in tokens if word in model]if not vectors:return np.zeros(embedding_dim)return np.mean(vectors, axis=0)# 為每條評論創建句子向量
X_w2v = np.array([sentence_to_vector(tokens, word2vec_model, embedding_dim) for tokens in df['tokens']])print("\nWord2Vec句子向量的維度:")
print(X_w2v.shape)# 劃分數據
X_train_w2v, X_test_w2v, y_train_w2v, y_test_w2v = train_test_split(X_w2v, y, test_size=0.2, random_state=42)# 使用Keras構建一個簡單的MLP
import tensorflow as tf
from tensorflow import kerasmodel = keras.Sequential([keras.layers.Dense(64, activation='relu', input_shape=(embedding_dim,)),keras.layers.Dropout(0.5), # Dropout層用于防止過擬合keras.layers.Dense(1, activation='sigmoid') # 二分類輸出
])model.compile(optimizer='adam',loss='binary_crossentropy',metrics=['accuracy'])# 訓練
# model.fit(X_train_w2v, y_train_w2v, epochs=10, batch_size=32, validation_split=0.1)
print("\n--- Word2Vec + 神經網絡 模型 ---")
print("模型構建完成。這種方法能捕捉詞匯的語義信息，在更復雜的NLP任務中潛力巨大。")

性能對比：在簡單的情感分析任務中，精心調優的TF-IDF+邏輯回歸模型有時甚至不輸于簡單的神經網絡。但詞嵌入+神經網絡的架構具有更強的擴展性，是通往更高級NLP模型（如RNN、LSTM、Transformer）的必經之路。

11.3 主題模型（LDA）：挖掘文本背后的隱藏主題

情感分析告訴我們人們的評價是“好”是“壞”，但我們還想知道，他們到底在討論什么？

11.3.1 無監督的探索：什么是主題模型？

主題模型是一種無監督學習技術，它能在不知道任何標簽的情況下，自動地從大量文檔中發現隱藏的“主題”結構。

LDA（Latent Dirichlet Allocation）?是最著名的主題模型。它的核心思想非常符合直覺：
1. 一篇文章被看作是多個主題的概率混合。例如，一篇影評可能是70%的“劇情”主題 + 20%的“演員”主題 + 10%的“配樂”主題。
2. 一個主題被看作是多個詞語的概率分布。例如，“劇情”主題下，“plot”, “story”, “character”這些詞出現的概率會很高。

11.3.2 LDA的實現與結果解讀

LDA的輸入不能是TF-IDF，而必須是基于詞頻計數的詞袋模型矩陣。

from sklearn.feature_extraction.text import CountVectorizer
from sklearn.decomposition import LatentDirichletAllocation# 1. 創建詞頻計數向量器
count_vectorizer = CountVectorizer(max_df=0.95, min_df=2, max_features=1000, stop_words='english')
X_counts = count_vectorizer.fit_transform(df['cleaned_review']) # 使用清洗后的文本# 2. 訓練LDA模型
# n_components 就是我們想要發現的主題數量
num_topics = 5
lda = LatentDirichletAllocation(n_components=num_topics, random_state=42)
lda.fit(X_counts)# 3. 結果解讀：打印每個主題下最重要的詞
def print_top_words(model, feature_names, n_top_words):for topic_idx, topic in enumerate(model.components_):message = f"Topic #{topic_idx}: "message += " ".join([feature_names[i]for i in topic.argsort()[:-n_top_words - 1:-1]])print(message)print("\n--- LDA 主題發現結果 ---")
feature_names = count_vectorizer.get_feature_names_out()
print_top_words(lda, feature_names, 10)

結果解讀：通過觀察每個主題下的高頻詞，我們可以人為地去“命名”和理解這個主題。例如，如果一個主題下都是“action”, “fight”, “explosion”，我們就可以將其標記為“動作場面”主題。

11.3.3 應用場景與洞察

商業洞察：對于一個手機廠商，通過對海量用戶評論運行LDA，可以自動發現用戶最關心的幾個方面是“電池續航”、“拍照效果”、“屏幕質量”還是“系統流暢度”，從而指導產品改進。
內容聚合與推薦：將新聞文章按主題進行分類，為用戶推薦他們感興趣主題下的其他文章。
輿情監控：分析社交媒體上關于某個事件的討論，看公眾的討論焦點在哪些方面。

結語

在本章中，我們成功地進入了自然語言處理的世界。我們掌握了處理文本數據的一整套流程：從清洗、分詞，到使用TF-IDF和Word2Vec進行向量化。我們構建了能夠判斷文本情感的分類模型，并體驗了從傳統方法到神經網絡的演進。最后，我們還學習了如何使用LDA這一無監督利器，從文本中挖掘出更深層次的、人類難以直接發現的主題結構。

您現在已經具備了分析文本數據的基本能力，為您打開了通往智能問答、機器翻譯、文本生成等更高級NLP領域的大門。

第十二章：模型部署與工程化——讓模型“活”起來

12.1 模型持久化：序列化與保存
12.2 使用Flask/FastAPI構建API服務
12.3 Docker容器化：為模型打造一個“家”
12.4 MLOps初探：自動化、監控與再訓練

經過前面章節的艱苦跋涉，我們已經成功訓練出了能夠解決特定問題的機器學習模型。它們在我們的開發環境中表現優異，但這只是萬里長征的第一步。一個真正有價值的模型，必須能夠走出實驗室，被集成到實際的應用程序中，為用戶提供持續、可靠的服務。這個過程，就是模型部署與工程化。

本章，我們將聚焦于如何將我們精心訓練的模型，從一個靜態的文件，轉變為一個動態的、可交互的、健壯的在線服務。我們將學習如何保存和加載模型，如何用Web框架為其創建一個API接口，如何用Docker將其打包成一個標準化的、可移植的“集裝箱”，最后，我們還將初步探討MLOps的理念，了解如何對“活”起來的模型進行持續的生命周期管理。

掌握本章內容，意味著您將打通從數據到價值的“最后一公里”，讓您的算法真正落地生根，開花結果。

12.1 模型持久化：序列化與保存

12.1.1 為何需要持久化？

模型持久化，就是將內存中訓練好的模型對象，以文件的形式保存到硬盤上。這是模型部署的絕對前提。

保存勞動成果：許多復雜的模型（尤其是深度學習模型）訓練過程可能需要數小時甚至數天。將訓練好的模型保存下來，我們就可以在任何時候重新加載它，而無需再次進行耗時耗力的訓練。
實現部署遷移：我們通常在一個環境（如配備GPU的開發服務器）中訓練模型，而在另一個或多個環境（如生產服務器集群）中使用模型。持久化使得我們可以輕松地將模型文件從一個地方復制到另一個地方。

12.1.2 Python中的序列化工具：`pickle`與`joblib`

序列化是將Python對象結構轉換為字節流的過程，以便將其存儲在文件中或通過網絡傳輸。

pickle：是Python標準庫中內建的序列化模塊。它功能強大，可以序列化幾乎任何Python對象。
joblib：是一個由Scikit-learn社區維護的庫，其序列化功能（joblib.dump和joblib.load）在處理包含大型NumPy數組的對象時，比pickle更高效。因此，對于Scikit-learn訓練出的模型，官方推薦使用joblib。

12.1.3 實戰演練：保存與加載Scikit-learn模型

讓我們以之前訓練的信用卡欺詐檢測模型（例如，在SMOTE數據上訓練的LightGBM模型）為例。

保存模型 在一個訓練腳本（例如train.py）的末尾，我們可以添加如下代碼：

# train.py
import joblib
import lightgbm as lgb
from sklearn.model_selection import train_test_split
from imblearn.over_sampling import SMOTE
import pandas as pd# ... (此處省略數據加載、預處理、SMOTE和模型訓練的代碼) ...
# 假設 lgbm_model 是我們已經訓練好的模型對象
# df = pd.read_csv('creditcard.csv')
# ... (預處理) ...
# X_train_smote, y_train_smote = ... (SMOTE) ...
# lgbm_model = lgb.LGBMClassifier(random_state=42)
# lgbm_model.fit(X_train_smote, y_train_smote)# 定義保存路徑和文件名
model_filename = 'fraud_detection_lgbm.joblib'# 使用joblib.dump保存模型
# compress=3 是一個可選參數，表示壓縮級別，可以減小文件大小
joblib.dump(lgbm_model, model_filename, compress=3)print(f"模型已保存到: {model_filename}")

加載并使用模型 現在，我們可以在一個全新的Python腳本（例如predict.py）中，加載這個模型并用它來進行預測，完全脫離原始的訓練數據和訓練過程。

# predict.py
import joblib
import numpy as np# 加載模型
try:loaded_model = joblib.load('fraud_detection_lgbm.joblib')print("模型加載成功！")
except FileNotFoundError:print("錯誤：找不到模型文件。請先運行訓練腳本。")exit()# 準備一條新的、待預測的數據樣本
# 特征維度和順序需要與訓練時嚴格一致
# 這里的new_data是一個示例，實際應用中它會來自API請求
# 假設有 scaled_time, scaled_amount, V1-V28，共30個特征
new_data = np.random.rand(1, 30) # 使用加載的模型進行預測
prediction = loaded_model.predict(new_data)
prediction_proba = loaded_model.predict_proba(new_data)print(f"\n對新數據的預測類別: {'欺詐' if prediction[0] == 1 else '正常'}")
print(f"預測為'正常'的概率: {prediction_proba[0][0]:.4f}")
print(f"預測為'欺詐'的概率: {prediction_proba[0][1]:.4f}")

重要注意事項：版本依賴 序列化和反序列化（加載）過程對庫的版本非常敏感。如果在Python 3.8和LightGBM 3.2版本下保存的模型，嘗試在Python 3.9和LightGBM 4.0的環境下加載，很可能會失敗。因此，在部署時，確保生產環境的庫版本與訓練環境的庫版本嚴格一致是至關重要的。我們稍后將看到的Docker，正是解決這個問題的利器。

12.2 使用Flask/FastAPI構建API服務

模型文件本身還不能對外提供服務。我們需要一個程序，它能監聽網絡請求，接收傳入的數據，調用模型進行預測，然后將結果返回給請求方。這個程序就是API服務。

12.2.1 API：模型與外界溝通的“窗口”

API（Application Programming Interface）：應用程序編程接口。它定義了不同軟件組件之間如何相互通信。對于我們的模型，就是定義一個接收輸入數據、返回預測結果的標準化網絡接口。
RESTful API：一種流行的API設計風格，它使用標準的HTTP方法（如GET, POST, PUT, DELETE）來操作資源。我們的預測服務通常會使用POST方法，因為客戶端需要向服務器發送包含特征數據的請求體。數據交換格式通常是JSON。

12.2.2 輕量級Web框架簡介

Flask：經典、靈活、易于上手的Python Web框架，是許多人入門Web開發和API構建的首選。
FastAPI：一個現代、高性能的Web框架。它基于Python 3.6+的類型提示，并因此獲得了兩大“殺手級”特性：
1. 極高的性能：可與NodeJS和Go相媲美。
2. 自動生成交互式API文檔：基于OpenAPI（以前稱為Swagger）和JSON Schema標準，極大地方便了API的測試和協作。基于這些優點，我們選擇FastAPI來構建我們的服務。

12.2.3 實戰演練：使用FastAPI包裝我們的模型

首先，安裝FastAPI和其運行所需的ASGI服務器Uvicorn： pip install fastapi "uvicorn[standard]"

然后，我們創建一個名為main.py的文件。

# main.py
from fastapi import FastAPI, HTTPException
from pydantic import BaseModel, Field
import joblib
import numpy as np
from typing import List# 1. 創建FastAPI應用實例
app = FastAPI(title="信用卡欺詐檢測API", description="一個使用LightGBM模型進行欺詐檢測的API")# 2. 定義輸入數據的模型 (數據契約)
# 使用pydantic的BaseModel來定義請求體的數據結構和類型
class Transaction(BaseModel):features: List[float] = Field(..., example=[0.1, -0.2, ..., 1.5], description="包含30個特征的列表")class Config:schema_extra = {"example": {"features": list(np.random.rand(30))}}# 3. 加載我們訓練好的模型
try:model = joblib.load('fraud_detection_lgbm.joblib')
except FileNotFoundError:# 在實際應用中，如果模型加載失敗，服務應該無法啟動# 這里為了簡單起見，我們只打印錯誤model = Noneprint("錯誤：模型文件未找到！API將無法工作。")# 4. 創建API端點 (endpoint)
@app.post("/predict", summary="進行欺詐檢測預測")
def predict_fraud(transaction: Transaction):"""接收一筆交易的特征數據，返回其是否為欺詐的預測結果和概率。- **transaction**: 包含特征列表的JSON對象。- **返回**: 包含預測類別和概率的JSON對象。"""if model is None:raise HTTPException(status_code=503, detail="模型當前不可用，請聯系管理員。")# 將輸入的列表轉換為NumPy數組，并reshape成(1, n_features)的形狀features_array = np.array(transaction.features).reshape(1, -1)if features_array.shape[1] != 30: # 假設我們的模型需要30個特征raise HTTPException(status_code=400, detail=f"輸入特征數量錯誤，需要30個，但收到了{features_array.shape[1]}個。")# 使用模型進行預測prediction = model.predict(features_array)probability = model.predict_proba(features_array)# 準備返回結果return {"is_fraud": int(prediction[0]), # 預測類別 (0: 正常, 1: 欺詐)"probability_normal": float(probability[0][0]),"probability_fraud": float(probability[0][1])}# 創建一個根端點，用于健康檢查
@app.get("/", summary="API健康檢查")
def read_root():return {"status": "ok", "message": "歡迎來到欺詐檢測API！"}

運行API服務 在終端中，切換到main.py所在的目錄，然后運行： uvicorn main:app --reload

main: 指的是main.py文件。
app: 指的是我們在main.py中創建的FastAPI對象app。
--reload: 這個參數會讓服務器在代碼文件被修改后自動重啟，非常適合開發階段。

測試API 服務運行后，打開瀏覽器訪問 http://127.0.0.1:8000/docs 。你會看到FastAPI自動生成的交互式API文檔（Swagger UI）。你可以在這個頁面上直接測試你的/predict端點，輸入示例數據，然后點擊“Execute”，就能看到服務器返回的預測結果。這極大地提高了開發和調試的效率。

12.3 Docker容器化：為模型打造一個“家”

我們的API服務現在可以在本地運行了，但如果想把它部署到另一臺服務器或云上，就會遇到“在我電腦上能跑”的經典困境。Docker正是為了解決這個問題而生的。

12.3.1 “在我電腦上能跑”的困境

問題的根源在于環境依賴的差異：

Python版本不同。
scikit-learn,?lightgbm,?fastapi等庫的版本不同。
甚至操作系統底層的一些依賴庫也可能不同。

12.3.2 Docker的核心思想：集裝箱式的標準化

Docker通過“容器化”技術，將我們的應用程序及其所有依賴（代碼、運行時、庫、環境變量）打包到一個標準化的、可移植的單元中，這個單元就是容器。

鏡像（Image）：一個只讀的模板，是容器的“藍圖”。
容器（Container）：鏡像的一個可運行實例。它與宿主系統和其他容器相互隔離，擁有自己獨立的文件系統和網絡空間。
Dockerfile：一個文本文件，像一份“菜譜”，定義了構建一個Docker鏡像所需的所有步驟。

12.3.3 實戰演練：將我們的FastAPI服務打包成Docker鏡像

創建requirements.txt文件 這個文件列出了我們項目的所有Python依賴。
```
fastapi
uvicorn[standard]
scikit-learn
lightgbm
joblib
numpy
```

編寫Dockerfile 在項目根目錄下創建一個名為Dockerfile（沒有擴展名）的文件。

# 1. 選擇一個官方的Python運行時作為基礎鏡像
FROM python:3.9-slim# 2. 設置工作目錄
WORKDIR /app# 3. 復制依賴文件到工作目錄
COPY requirements.txt .# 4. 安裝依賴
RUN pip install --no-cache-dir -r requirements.txt# 5. 復制項目的所有文件到工作目錄
COPY . .# 6. 暴露端口，讓容器外的世界可以訪問
EXPOSE 8000# 7. 定義容器啟動時要執行的命令
CMD ["uvicorn", "main:app", "--host", "0.0.0.0", "--port", "8000"]

構建與運行 確保你的機器上已經安裝了Docker。在終端中，確保你在Dockerfile所在的目錄下，然后執行：
- 構建鏡像： docker build -t fraud-detection-api . （-t參數為鏡像命名，.表示使用當前目錄的Dockerfile）
- 運行容器： docker run -p 8000:8000 fraud-detection-api （-p 8000:8000將宿主機的8000端口映射到容器的8000端口）

現在，你的API服務就在一個隔離的、標準化的容器中運行了。你可以再次訪問http://127.0.0.1:8000/docs來驗證它。這個容器可以被輕松地部署到任何安裝了Docker的服務器或云平臺上，完美地解決了環境依賴問題。

12.4 MLOps初探：自動化、監控與再訓練

我們已經成功部署了模型，但這只是一個靜態的部署。在真實世界中，數據是不斷變化的，模型的生命周期管理是一個持續的過程。

12.4.1 超越一次性部署：模型的生命周期管理

模型退化（Model Decay）：隨著時間的推移，現實世界的數據分布可能會發生變化（例如，欺詐手段更新了），導致模型的預測性能逐漸下降。這就是“模型退化”。
MLOps（Machine Learning Operations）：它借鑒了軟件工程中DevOps的理念，是一套旨在實現機器學習模型開發（Dev）、部署和運維（Ops）自動化與標準化的實踐和原則。其目標是縮短模型迭代周期，提高部署質量和可靠性。

12.4.2 MLOps的核心理念

CI/CD for ML：將持續集成/持續部署的思想應用于機器學習。
- CI（持續集成）：代碼（包括數據處理、模型訓練代碼）的任何變更都會自動觸發測試和驗證。
- CD（持續交付/部署）：一旦模型通過所有測試，就會被自動部署到生產環境。
自動化流水線（Pipeline）：將數據獲取、預處理、特征工程、模型訓練、評估、版本控制、部署等環節串聯成一個自動化的工作流。
監控（Monitoring）：持續監控線上模型的性能。
- 技術指標：API的延遲、QPS、錯誤率。
- 模型指標：預測結果的分布是否穩定？輸入特征的分布是否發生了數據漂移（Data Drift）？如果能獲取到真實標簽，模型的準確率、召回率是否下降？
再訓練（Retraining）：建立觸發機制（如性能下降到某個閾值，或定期如每周/每月），自動使用最新的數據對模型進行再訓練，并生成新版本的模型，然后通過流水線進行評估和部署。

12.4.3 工具與展望

MLOps是一個龐大而復雜的領域，通常需要專門的工具和平臺來支撐。

開源工具：
- 實驗追蹤與模型注冊：MLflow,?DVC
- 工作流編排：Kubeflow,?Airflow
- 模型服務：Seldon Core,?KServe
云平臺服務：各大云廠商都提供了端到端的MLOps解決方案，如Amazon SageMaker,?Google AI Platform (Vertex AI),?Azure Machine Learning。它們將上述許多功能集成在了一起，降低了實施MLOps的門檻。

結語

本章，我們完成了從算法到服務的關鍵一躍。我們學會了如何保存和加載模型，如何用FastAPI為其穿上API的“外衣”，如何用Docker為其打造一個標準化的“家”，并最終將視野投向了MLOps這片更廣闊的星辰大海。

至此，我們已經走完了一名數據科學家從入門到實踐的全過程。您不僅掌握了機器學習的核心理論與算法，更具備了將模型付諸實踐、創造真實價值的工程能力。這并非終點，而是一個全新的、激動人心的起點。愿您帶著這份完整的知識體系，在數據科學的道路上，不斷探索，不斷創造，行穩致遠。

第十三章：超越經典——未來展望與進階路徑

13.1 深度學習概覽：CNN、RNN的世界
13.2 強化學習：與環境交互的智能體
13.3 圖神經網絡、聯邦學習等前沿簡介
13.4 “知行合一”：如何持續學習與成長

親愛的讀者，當您抵達本書的終章，您已不再是旁觀者，而是身懷絕技的入局者。您所掌握的經典機器學習理論與實踐，是理解這個數據驅動時代的堅固基石。然而，技術的地平線總在不斷向遠方延伸，引領浪潮之巔的，正是深度學習那璀璨的群星。

本章，我們將以一種前所未有的深度，去探索深度學習的核心分支。我們不再滿足于概念的羅列，而是要深入其設計的哲學，剖析其數學的肌理，追溯其演化的邏輯。我們將探討每一個模型誕生的“動機”——它解決了前輩的何種“困境”？我們還將提供一份詳盡的“進階路線圖”，包含必讀的“圣經級”論文及可上手的“里程碑式”項目和值得關注的“前沿方向”。

這不僅是知識的傳遞，更是一次思維的淬煉。愿您在本章的引領下，完成從“模型使用者”到“算法思想家”的蛻變。

13.1 深度學習進階：從“萬金油”到“特種兵”的架構演化

我們在第九章學習的多層感知機（MLP），本質上是一種強大的“通用函數擬合器”。它將輸入數據“一視同仁”地展平為一維向量，并通過全連接層進行變換。這種“萬金油”式的設計，在處理缺乏內在結構的數據時表現尚可。但當面對具有精巧結構的數據——如圖像中像素的空間排列、語言中詞語的時間序列——MLP的“一視同仁”就變成了它的“阿喀琉斯之踵”。它不僅會因參數量爆炸而陷入“維度災難”，更會粗暴地破壞掉數據中最寶貴的結構信息。

深度學習的革命性突破，正在于它發展出了一系列“特種兵”式的網絡架構。這些架構內置了針對特定數據結構的歸納偏置（Inductive Bias），即一種基于先驗知識的“世界觀”假設。正是這些“偏見”，讓模型能更高效、更深刻地學習。

13.1.1 卷積神經網絡（CNN）：為“空間”而生的視覺大師

1. 動機與哲學：為何卷積？

困境：用MLP處理一張僅為224x224x3的彩色圖像（ImageNet競賽的經典尺寸），輸入層神經元數量高達150,528個。若第一個隱藏層有4096個神經元（AlexNet的配置），僅這一層的權重參數就將達到驚人的 6億（150528 * 4096）！這在計算上難以承受，在數據上極易過擬合。更致命的是，它完全忽略了圖像的兩個基本先驗：
1. 局部相關性（Locality）：一個像素的含義，與其緊鄰的像素關系最密切。遠隔千里的兩個像素幾乎沒有直接關聯。
2. 平移不變性（Translation Invariance）：一只貓，無論出現在圖像的左上角還是右下角，它仍然是一只貓。我們尋找的特征（如貓的耳朵）應該與位置無關。
哲學突破：引入“空間”的歸納偏置 CNN的設計哲學，就是將這兩個“先驗”硬編碼到網絡結構中。它不再將圖像看作扁平的向量，而是看作一個有長、寬、深（通道）的三維張量。

2. 核心武器庫：CNN的兩大基石

基石一：局部感受野（Local Receptive Fields）與卷積（Convolution）
- 機制：CNN不再進行全連接，而是定義了一個個小的、共享的卷積核（Kernel/Filter）。每個神經元只“看”輸入圖像的一小塊區域（即局部感受野），這個區域的大小就是卷積核的大小（如3x3, 5x5）。卷積核內包含一組可學習的權重，它在整個輸入圖像上按步長（Stride）滑動，每滑動到一個位置，就與該位置的局部圖像塊進行點積運算，從而得到一個輸出值。所有輸出值共同構成一張特征圖（Feature Map）。
- 意義：這完美地體現了“局部相關性”。每個輸出值都只由一小片局部信息計算而來。一個卷積核，就像一個可學習的“模式探測器”，專門負責尋找一種特定的微觀模式，如水平邊緣、綠色斑塊或某個特定的紋理。
基石二：參數共享（Parameter Sharing）與池化（Pooling）
- 機制：
  - 參數共享：用于生成同一張特征圖的那個卷積核，其內部的權重在滑動到圖像的任何位置時都是完全相同的。這意味著，網絡用同一套參數去尋找圖像中所有位置的同一種特征。
  - 池化：在卷積層之后，通常會接一個池化層（如最大池化Max Pooling）。它將特征圖劃分為若干個不重疊的區域（如2x2），并從每個區域中取最大值作為輸出。
- 意義：
  - 參數共享是CNN最天才的設計。它直接將“平移不變性”的假設注入了模型，并使得模型的參數量從“億”級別驟降到“萬”甚至“千”級別，極大地提高了模型的泛化能力和訓練效率。
  - 池化操作則提供了另一種形式的平移不變性，并實現了對特征圖的降采樣，既減少了后續計算量，又增大了上層神經元的“感受野”（即它能看到的原始圖像區域范圍）。

3. 架構演化與進階路徑

階段一：奠基與驗證 (LeNet-5, AlexNet)
- 必讀論文：無需讀LeCun 1998年的論文，可以直接看Krizhevsky等人2012年的《ImageNet Classification with Deep Convolutional Neural Networks》(AlexNet)。這篇論文是引爆深度學習革命的“宇宙大爆炸”奇點。
- 學習要點：理解經典的“卷積-激活-池化”堆疊模式。注意AlexNet如何使用ReLU激活函數代替Sigmoid/Tanh來解決梯度消失問題，以及如何使用Dropout來對抗過擬合。
- 實踐項目：在PyTorch或TensorFlow中，從零開始搭建一個類似LeNet-5或簡化版AlexNet的結構，在MNIST或CIFAR-10數據集上進行訓練。目標是親手實現卷積層、池化層、全連接層的連接，并觀察模型從隨機權重開始學習到有效特征的過程。
階段二：走向深度 (VGG, GoogLeNet)
- 必讀論文：《Very Deep Convolutional Networks for Large-Scale Image Recognition》(VGG) 和《Going Deeper with Convolutions》(GoogLeNet)。
- 學習要點：
  - VGG：探索了“深度”的力量。它證明了通過堆疊非常小的（3x3）卷積核，可以構建出比使用大卷積核更深、更有效的網絡。其結構非常規整，易于理解。
  - GoogLeNet：引入了創新的Inception模塊，在一個網絡層中并行地使用不同尺寸的卷積核和池化操作，然后將結果拼接起來。這讓網絡可以自適應地選擇最合適的感受野來捕捉特征，實現了“寬度”和“深度”的結合。
- 實踐項目：學習使用Keras或PyTorch的API，加載一個預訓練（Pre-trained）的VGG16或InceptionV3模型。然后，替換掉其頂部的全連接層，換上你自己定義的分類頭，在一個新的、較小的數據集上（如貓狗分類）進行遷移學習（Transfer Learning）。這是工業界應用CNN最核心、最高效的范式。
階段三：跨越瓶頸 (ResNet)
- 必讀論文：何愷明等人的《Deep Residual Learning for Image Recognition》(ResNet)，這是計算機視覺領域引用量最高的論文之一，思想深刻而優美。
- 學習要點：當網絡堆得非常深時，會出現“退化”現象（Deeper is not better）。ResNet天才地引入了殘差連接（Residual Connection）/快捷連接（Shortcut Connection）。它允許輸入信號可以“跳過”一個或多個層，直接加到后續層的輸出上。這使得網絡需要學習的不再是完整的映射H(x)，而是一個更容易學習的殘差F(x) = H(x) - x。如果某個層是多余的，網絡只需將F(x)學習為0即可，這比讓它學習一個恒等映射H(x)=x要容易得多。這一結構極大地緩解了深度網絡的梯度消失和退化問題，使得訓練成百上千層的網絡成為可能。
- 實踐項目：在代碼中親手實現一個“殘差塊（Residual Block）”。然后，嘗試將你之前搭建的“平原網絡（Plain Network）”改造為“殘差網絡”，并比較兩者在更深層數下的訓練收斂性和最終性能。
前沿方向：
- 輕量化網絡：MobileNet, ShuffleNet等，為在移動端和嵌入式設備上高效運行而設計。
- 注意力機制：Squeeze-and-Excitation Networks (SENet)等，讓網絡學習不同通道特征的重要性。
- 新架構探索：Vision Transformer (ViT) 將Transformer架構成功應用于視覺，挑戰了CNN的統治地位。

13.1.2 循環神經網絡（RNN）及其變體：為“時間”而生的序列詩人

1. 動機與哲學：為何循環？

困境：無論是MLP還是CNN，它們都內含一個根本性的假設——輸入數據（或特征）之間是相互獨立的（i.i.d. assumption）。這個假設在處理如語言、語音、金融時間序列等數據時，是完全錯誤的。對于序列數據，**順序（Order）和上下文（Context）**是其靈魂。一個詞的意義，嚴重依賴于它前面的詞；今天的股價，與昨天的股價息息相關。CNN雖然能捕捉局部空間模式，但其固定大小的卷積核無法靈活處理長短不一、依賴關系復雜的序列。
哲學突破：引入“時間”的歸納偏置 RNN的設計哲學，是將“時間”和“記憶”的概念，直接編碼到其網絡結構中。它不再將序列視為一個靜態的整體，而是將其視為一個隨時間演化的動態過程。

2. 核心武器庫：循環、狀態與門控

基石一：循環連接（Recurrent Connection）與隱藏狀態（Hidden State）
- 機制：RNN的核心在于其神經元（或一層神經元）擁有一個自連接的循環邊。在處理序列的第?t?個元素?x_t?時，RNN的計算單元不僅接收?x_t?作為輸入，還接收來自上一個時間步?t-1?的輸出，即隱藏狀態?h_{t-1}。它將兩者結合起來，計算出當前時間步的隱藏狀態?h_t。這個過程可以用公式表達為：h_t = f(W * x_t + U * h_{t-1} + b)，其中?W?和?U?是可學習的權重矩陣，f?是激活函數（通常是tanh）。
- 意義：隱藏狀態?h_t?成為了網絡的**“記憶”。它理論上編碼了從序列開始到當前時刻?t?的所有歷史信息。在整個序列處理過程中，權重矩陣?W?和?U?是共享**的，這與CNN中卷積核的參數共享異曲同工，極大地減少了參數量，并使得模型能處理任意長度的序列。
基石二：門控機制（Gating Mechanism）——對抗遺忘的智慧
- 困境：長期依賴問題（Long-Term Dependencies Problem）?經典的RNN在實踐中難以學習到相隔較遠的詞之間的依賴關系。這是因為在反向傳播（BPTT）過程中，梯度需要穿越很長的時間步進行連乘。如果激活函數的導數長期小于1，梯度會指數級衰減，導致梯度消失（Vanishing Gradients）；反之則會導致梯度爆炸（Exploding Gradients）。這使得網絡幾乎無法根據遙遠未來的誤差來調整遙遠過去的權重。
- 解決方案：長短期記憶網絡（LSTM）?LSTM并非簡單地用一個更復雜的激活函數，而是設計了一套精巧的內部記憶管理系統。其核心是一個獨立的細胞狀態（Cell State, C_t），可以看作是一條信息高速公路，信息在上面可以很順暢地流動而不發生劇烈變化。同時，LSTM引入了三個“門”結構（本質上是帶有Sigmoid激活函數的全連接層，輸出0到1之間的值，代表信息的通過率）來精密地控制這條高速公路：
  1. 遺忘門（Forget Gate）：決定應該從上一個細胞狀態?C_{t-1}?中遺忘掉哪些舊信息。
  2. 輸入門（Input Gate）：決定當前時刻有哪些新信息?x_t?應該被存入到細胞狀態中。
  3. 輸出門（Output Gate）：決定當前細胞狀態?C_t?的哪些部分應該被輸出為當前時刻的隱藏狀態?h_t。這種設計使得LSTM能夠有選擇地、動態地遺忘、記憶和輸出信息，從而有效地捕捉長期依賴。
- 簡化方案：門控循環單元（GRU）?GRU是LSTM的一個流行變體。它將遺忘門和輸入門合并為單一的更新門（Update Gate），并融合了細胞狀態和隱藏狀態。GRU的參數更少，計算效率更高，在許多任務上能取得與LSTM相當的性能，是實踐中一個值得嘗試的優秀替代方案。

3. 架構演化與進階路徑

階段一：理解循環與記憶
- 必讀文獻：Chris Olah的博客文章《Understanding LSTM Networks》是全世界公認的、圖文并茂的最佳入門材料，比直接閱讀原始論文更直觀。
- 學習要點：不要滿足于API調用，必須親手在紙上或白板上畫出LSTM單元的內部數據流圖。清晰地理解輸入?x_t?和?h_{t-1}?是如何通過三個門和細胞狀態，最終計算出?h_t?和?C_t?的。這是后續所有學習的基礎。
- 實踐項目：使用Keras或PyTorch，搭建一個字符級的RNN/LSTM語言模型。在一段文本（如莎士比亞的著作）上進行訓練，然后讓它從一個種子字符開始，自動生成新的文本。觀察它是否能學習到單詞拼寫、空格、換行等語法規則，這是檢驗你是否真正理解序列建模的“試金石”。
階段二：序列到序列（Seq2Seq）與注意力機制
- 必讀論文：《Sequence to Sequence Learning with Neural Networks》和《Neural Machine Translation by Jointly Learning to Align and Translate》。
- 學習要點：
  - Seq2Seq架構：理解其經典的**編碼器-解碼器（Encoder-Decoder）**結構。編碼器（一個RNN/LSTM）將整個輸入序列壓縮成一個固定長度的上下文向量（Context Vector），解碼器（另一個RNN/LSTM）則以這個向量為初始狀態，逐個生成輸出序列的元素。
  - 瓶頸：這個固定長度的上下文向量成為了信息瓶頸，難以承載長輸入序列的全部信息。
  - 注意力機制（Attention）：這是解決瓶頸的天才之舉。它允許解碼器在生成每一個輸出詞時，不再只依賴那個固定的上下文向量，而是可以“回顧”編碼器的所有隱藏狀態，并為它們計算一個“注意力權重”，然后對這些隱藏狀態進行加權求和。這樣，解碼器在每一步都能動態地、有選擇地聚焦于輸入序列中最相關的部分。
- 實踐項目：實現一個帶注意力機制的Seq2Seq模型，用于完成一個簡單的任務，如日期格式轉換（“2024-07-21” -> “July 21, 2024”）或簡單的機器翻譯。
階段三：Transformer的崛起（詳見下一節） RNN及其變體雖然強大，但其固有的順序計算特性使其難以在現代GPU上高效并行化，限制了其處理超長序列和構建超大規模模型的能力。這直接催生了下一代革命性架構的誕生。

13.1.3 注意力機制與Transformer：并行時代的NLP王者

1. 動機與哲學：為何拋棄循環？

困境：RNN的“循環”既是其優點（記憶），也是其致命弱點。t時刻的計算必須等待t-1時刻完成，這種順序依賴使其無法利用GPU強大的并行計算能力。在處理長文檔時，這種串行計算的效率低下問題尤為突出。此外，即使有LSTM/GRU，信息在序列中傳遞的路徑依然很長，捕捉超長距離依賴仍然是一個挑戰。
哲學突破：將“重要性”的計算并行化 注意力機制的成功啟發了研究者們：如果模型可以直接計算出序列中任意兩個位置之間的依賴關系，而無需通過循環結構逐步傳遞信息，那么是否可以完全拋棄循環？Transformer的回答是：可以！ 它的核心哲學是，序列中一個元素的表示，應該由整個序列中所有元素根據其重要性進行加權求和來定義。

2. 核心武器庫：自注意力機制

機制：縮放點積注意力（Scaled Dot-Product Attention）?這是Transformer的靈魂。對于輸入序列中的每一個元素（Token），我們都通過線性變換為其生成三個可學習的向量：
1. 查詢（Query, Q）：代表了當前元素為了理解自己，需要去“查詢”其他元素的信息。
2. 鍵（Key, K）：代表了序列中每個元素所攜帶的、可供“查詢”的“標簽”信息。
3. 值（Value, V）：代表了序列中每個元素實際包含的“內容”信息。計算過程分為三步：
4. 計算注意力分數：將當前元素的Q向量，與所有元素的K向量進行點積。這個分數直觀地衡量了“查詢”與“鍵”的匹配程度。
5. 縮放與歸一化：將得到的分數除以一個縮放因子（通常是K向量維度的平方根），以防止梯度過小，然后通過Softmax函數將其歸一化為和為1的概率分布。這就是“注意力權重”。
6. 加權求和：用得到的注意力權重，去加權求和所有元素的V向量。最終的結果，就是當前元素融合了全局上下文信息后的新表示。
關鍵增強：
- 多頭注意力（Multi-Head Attention）：并行地運行多次獨立的自注意力計算。每一“頭”都學習將Q, K, V投影到不同的表示子空間中，從而讓模型能夠同時關注來自不同方面、不同位置的信息。這就像我們讀書時，可以同時關注一句話的語法結構、語義內涵和情感色彩。
- 位置編碼（Positional Encoding）：由于自注意力機制本身不包含任何關于順序的信息（它是一個“集合”操作），我們需要顯式地為輸入序列添加“位置編碼”向量，將詞的位置信息注入模型。

3. 架構演化與進階路徑

階段一：奠基與理解
- 必讀論文：《Attention Is All You Need》。這篇論文簡潔、有力，是現代NLP的“新約圣經”。每一個有志于深度學習的人都應該反復精讀。
- 學習要點：徹底理解自注意力機制的矩陣運算形式。明白Q, K, V矩陣的維度變化。理解為何需要位置編碼，以及殘差連接和層歸一化（Layer Normalization）在Transformer塊中的關鍵作用。
- 實踐項目：使用PyTorch或TensorFlow，從零開始實現一個完整的、包含多頭自注意力和前饋網絡（Feed-Forward Network）的Transformer編碼器塊。這是檢驗你是否真正理解其內部工作原理的終極測試。
階段二：預訓練語言模型（Pre-trained Language Models, PLMs）
- 必讀論文：《BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding》和OpenAI關于GPT系列模型的博客文章或論文。
- 學習要點：理解遷移學習在NLP領域的應用，即“預訓練-微調（Pre-train, Fine-tune）”范式。
  - BERT：學習其核心的**掩碼語言模型（Masked Language Model, MLM）**預訓練任務，以及它如何通過雙向Transformer編碼器實現對上下文的深度雙向理解。
  - GPT：學習其經典的**自回歸語言模型（Autoregressive LM）**預訓練任務，以及它如何通過單向Transformer解碼器結構，在文本生成任務上表現出色。
- 實踐項目：熟練掌握Hugging Face的transformers庫。加載一個預訓練的BERT模型，并將其在一個下游文本分類任務（如GLUE基準測試中的一個）上進行微調。然后，加載一個預訓練的GPT-2模型，體驗其強大的文本生成和零樣本/少樣本學習能力。
階段三：效率與未來
- 學習要點：標準Transformer的計算和內存復雜度與序列長度的平方成正比，這限制了其處理長文檔或高分辨率圖像。因此，大量的研究工作致力于高效Transformer，如Longformer, Reformer, Linformer等，它們通過各種稀疏注意力或低秩近似的方法來降低復雜度。
- 前沿方向：
  - 多模態融合：CLIP, DALL-E等模型展示了如何使用Transformer架構來聯合理解圖像和文本，實現了驚人的跨模態生成和理解能力。
  - 模型即服務：隨著模型規模（如GPT-3/4）變得越來越龐大，普通研究者和開發者難以自行訓練或部署。學習如何通過API來調用這些超大規模模型，并將其作為一種強大的“AI即服務”來構建應用，正變得越來越重要。
  - 架構統一：Transformer架構正從NLP領域“溢出”，在計算機視覺（Vision Transformer, ViT）、語音處理、甚至強化學習中都取得了巨大成功，展現出成為一種“通用智能計算架構”的潛力。

13.2 強化學習：在“試錯”中學習最優決策的智能體

13.2.1. 動機與哲學：超越“標簽”的智慧

困境：監督學習需要大量的、高質量的標注數據，這在許多現實場景中是昂貴甚至不可能獲得的（如下棋、機器人控制）。無監督學習擅長發現數據中的模式，但通常不直接導向一個最優的“決策”或“行為”。當我們的問題核心是序貫決策（Sequential Decision Making），即需要在一系列時間步驟中做出最優選擇以達成一個長期目標時，這兩種范式都顯得力不從心。
哲學突破：從“交互”中涌現智能 強化學習（RL）的哲學根植于生物心理學的行為主義。它不依賴于一個“教師”給出的正確答案，而是讓一個智能體（Agent）直接與一個環境（Environment）進行交互。智能體通過“試錯（Trial-and-Error）”來探索環境，環境則通過一個獎勵信號（Reward Signal）來反饋智能體行為的好壞。智能體的唯一目標，就是學習一個策略（Policy），以最大化其在生命周期內獲得的累積獎勵。這種從稀疏、延遲的獎勵信號中學習復雜行為的能力，是RL最迷人、也最具挑戰性的地方。

13.2.2. 核心武器庫：價值、策略與模型

RL算法的汪洋大海，可以從三個核心視角來劃分：對**價值（Value）的估計、對策略（Policy）的直接學習，以及對環境模型（Model）**的構建。

基石一：價值函數（Value Function）——衡量“好壞”的標尺
- 機制：價值函數是RL的基石。它不去直接回答“該做什么”，而是回答“當前狀態或行為有多好”。
  - 狀態價值函數?V(s)：表示從狀態?s?出發，遵循當前策略?π，未來能獲得的期望累積獎勵。
  - 動作價值函數?Q(s, a)（Q-function）：表示在狀態?s?下，執行動作?a，然后遵循當前策略?π，未來能獲得的期望累d積獎勵。Q函數比V函數更直接地指導決策，因為我們只需在當前狀態下選擇能帶來最大Q值的動作即可。
- 核心算法：Q-Learning 與 DQN?Q-Learning是一種經典的離策略（Off-policy）時間差分（TD）學習算法。它通過不斷迭代貝爾曼最優方程?Q(s, a) = R + γ * max_{a'} Q(s', a')?來直接逼近最優的動作價值函數Q*，而無需知道環境的具體模型。 **深度Q網絡（Deep Q-Network, DQN）是其里程碑式的延伸。它使用一個深度神經網絡來近似Q函數，從而能處理高維的狀態輸入（如游戲畫面像素）。DQN通過引入經驗回放（Experience Replay）和目標網絡（Target Network）**兩大技巧，成功地解決了使用非線性函數近似器帶來的訓練不穩定性問題，開啟了深度強化學習的時代。
基石二：策略函數（Policy Function）——直接指導“行動”的指南
- 機制：基于價值的方法在處理連續動作空間或隨機策略時會遇到困難。基于策略的方法則選擇直接參數化策略本身，即學習一個函數?π(a|s; θ)，輸入狀態?s，直接輸出執行每個動作?a?的概率分布。
- 核心算法：策略梯度（Policy Gradient）?其核心思想非常直觀：如果一個動作最終導向了好的結果（高獎勵），那么就調整參數?θ，增大這個動作被選中的概率；反之則減小。REINFORCE算法是其最基礎的形式。然而，策略梯度方法通常具有高方差，收斂較慢。 **行動者-評論家（Actor-Critic, A-C）**架構是解決此問題的主流方案。它結合了價值和策略學習：
  - 行動者（Actor）：即策略網絡，負責輸出動作。
  - 評論家（Critic）：即價值網絡，負責評估行動者所選動作的好壞，并提供一個更低方差的梯度信號來指導行動者的更新。A2C (Advantage Actor-Critic)?和其異步版本?A3C?是其中的杰出代表。
基石三：環境模型（Environment Model）——在“想象”中規劃未來
- 機制：上述兩類方法都屬于無模型（Model-Free）RL，它們直接從與真實環境的交互中學習。而有模型（Model-Based）RL則試圖先學習一個環境的模型，即學習狀態轉移函數?P(s'|s, a)?和獎勵函數?R(s, a)。一旦有了模型，智能體就可以在“腦內”進行模擬和規劃，而無需與真實環境進行昂貴甚至危險的交互。
- 優勢與挑戰：有模型方法通常具有更高的樣本效率（Sample Efficiency）。然而，學習一個足夠精確的環境模型本身就是一個巨大的挑戰，模型誤差可能會被規劃過程放大。AlphaGo及其后繼者AlphaZero是結合了無模型學習（蒙特卡洛樹搜索）和有模型學習（價值/策略網絡）的巔峰之作。

13.3.3. 進階路徑

階段一：奠基與核心概念
- 必讀文獻：Richard Sutton 和 Andrew Barto 的《Reinforcement Learning: An Introduction (2nd Edition)》。這本書是RL領域的“圣經”，其地位無可撼動。前兩部分關于MDP、動態規劃、蒙特卡洛和TD學習的內容是理解一切后續算法的基礎。
- 學習要點：深刻理解探索與利用的權衡（Exploration vs. Exploitation Trade-off）。區分**同策略（On-policy）與離策略（Off-policy）**學習的本質區別。掌握貝爾曼方程的推導和意義。
- 實踐項目：使用Python和NumPy，在一個簡單的網格世界（Gridworld）環境中，親手實現Q-Learning和SARSA算法。然后，進入OpenAI Gym的“經典控制”環境，使用PyTorch或TensorFlow實現一個DQN來解決“車桿（CartPole-v1）”問題。
階段二：現代深度RL算法
- 必讀文獻：DQN、A3C、TRPO/PPO、DDPG/TD3、SAC的原始論文。這些是現代深度RL算法的基石。
- 學習要點：
  - 策略梯度：深入理解REINFORCE算法的推導，明白為何需要引入基線（Baseline）來減小方差。
  - Actor-Critic：理解A2C/A3C如何通過優勢函數（Advantage Function）來穩定訓練。
  - 信任區域/近端策略優化（TRPO/PPO）：理解其如何通過限制策略更新的步長來保證學習過程的穩定性，PPO是目前應用最廣泛、最魯棒的算法之一。
  - 連續控制：學習DDPG/TD3/SAC等算法是如何將DQN和Actor-Critic思想擴展到連續動作空間的。
- 實踐項目：在OpenAI Gym的MuJoCo或PyBullet物理仿真環境中，使用一個成熟的RL庫（如Stable Baselines3）來訓練PPO或SAC算法，讓一個模擬機器人學會行走或完成特定任務。
階段三：前沿與挑戰
- 學習要點：
  - 離線強化學習（Offline RL）：如何從一個固定的、歷史交互數據集中學習策略，而無需與環境進行新的交互？這在醫療、金融等無法自由探索的領域至關重要。
  - 多智能體強化學習（Multi-Agent RL, MARL）：當環境中存在多個相互影響的智能體時，如何學習合作或競爭的策略？
  - 基于模型的RL：學習Dreamer等算法，看它們如何通過在“想象”中學習，實現驚人的樣本效率。
  - 探索問題：如何設計更有效的內在激勵（Intrinsic Motivation）機制，來鼓勵智能體在稀疏獎勵環境中進行有意義的探索？

13.3 新興前沿：重塑AI邊界的新范式

13.3.1 圖神經網絡（GNN）：解鎖關系數據的力量

深度剖析：GNN的核心思想是消息傳遞（Message Passing），它是一個迭代的過程。在每一輪迭代中，每個節點都會：1)?收集其所有鄰居節點的特征表示；2) 通過一個可學習的函數（如一個小型MLP）將這些信息進行聚合；3) 將聚合后的信息與自己上一輪的表示相結合，更新為自己本輪的新表示。經過?k?輪迭代，每個節點的最終表示就編碼了其k跳鄰居內的全部結構信息。GCN、GraphSAGE、GAT等模型的主要區別在于它們使用了不同的聚合和更新函數。
進階路徑：學習PyTorch Geometric (PyG) 或 Deep Graph Library (DGL) 這兩個主流的GNN庫。從在一個社交網絡數據集（如Cora）上實現一個簡單的GCN進行節點分類開始。

13.3.2 聯邦學習（Federated Learning）：數據隱私時代的協同智能

深度剖析：其標準流程（FedAvg算法）為：1)?分發：中央服務器將全局模型分發給所有參與的客戶端。2)?本地訓練：每個客戶端使用自己的本地數據，對模型進行多輪梯度下降訓練。3)?上傳：客戶端將訓練后的模型權重更新（而非原始數據）加密后上傳給服務器。4)?聚合：服務器將收集到的所有更新進行加權平均，用來更新全局模型。這個過程循環往復。其核心挑戰在于如何處理客戶端之間的數據異構性（Non-IID data）、通信開銷以及安全性問題。
進階路徑：了解FedAvg算法的理論基礎。可以嘗試使用Flower或PySyft等聯邦學習框架，模擬一個簡單的聯邦學習環境。

13.3.3 自監督學習（Self-supervised Learning, SSL）：無標簽數據中的“煉金術”

深度剖析：SSL是近年來深度學習領域最激動人心的突破之一，它極大地降低了對人工標注數據的依賴。其成功的關鍵在于設計精巧的代理任務（Pretext Task）。SSL可以分為兩大流派：
1. 生成式（Generative）：如BERT的掩碼語言模型和圖像修復（Image Inpainting），它們學習恢復被破壞的部分輸入。
2. 對比式（Contrastive）：如SimCLR, MoCo，它們的核心思想是“將相似的樣本在表示空間中拉近，將不相似的樣本推遠”。通過對同一個樣本進行不同的數據增強（如旋轉、裁剪）來構造“正樣本對”，而將其他樣本視為“負樣本對”，然后通過一個對比損失函數（如InfoNCE Loss）來學習表示。
進階路徑：精讀SimCLR和BERT的論文，理解對比學習和掩碼建模的精髓。在實踐中，學習如何使用在ImageNet上通過自監督學習預訓練好的視覺模型（如MoCo, DINO），并將其用于下游任務的遷移學習。

13.4 “知行合一”：從優秀到卓越的終身成長之道

技術的學習永無止境，但成長之道有法可循。

構建“反脆弱”的知識體系：不要只滿足于學習當前最“火”的模型。更要去理解那些跨越時間、更加本質的思想，如貝葉斯推斷、信息論、優化理論、因果推斷。這些是理解和創造新模型的基礎。在構建T型知識結構時，讓這些基礎理論成為你“T”字那堅實的橫梁。
從“復現”到“批判”的思維升級：
- 復現是學習的基石，但批判是創新的開始。在閱讀論文時，不要全盤接受。要主動思考：作者的核心假設是什么？這個假設在哪些場景下可能不成立？實驗部分是否公平？有沒有更簡單的方法能達到類似的效果？這個思想能否被遷移到我自己的問題中？
- “Ablation Study”（消融研究）是論文中最值得關注的部分。它通過移除或替換模型的某個組件來觀察性能變化，這揭示了模型成功的真正原因。在自己的項目中，也要養成進行嚴謹消融研究的習慣。
打造你的“代表作”：
- 與其做十個淺嘗輒止的課程項目，不如集中精力，用半年甚至一年的時間，打造一個完整、深入、有影響力的個人項目。這個項目應該能體現你的技術深度、工程能力和對某個領域的獨特思考。它可以是一個性能優異的Kaggle競賽方案，一個被他人使用的開源工具，或是一篇發表在頂會Workshop上的論文。這個“代表作”將成為你最閃亮的名片。
建立你的“知識復利”系統：
- 費曼學習法：將復雜的概念用最簡單的語言解釋給不懂行的人聽。這個過程會強迫你直面自己理解的模糊之處。寫技術博客、做內部技術分享都是絕佳的實踐。
- 建立連接：知識的價值在連接中放大。積極參與線上（Twitter, Reddit）和線下（Meetup, 學術會議）的討論。向你尊敬的學者或工程師禮貌地提問，與志同道合的伙伴組成學習小組。在交流、分享、辯論中，你的認知會以指數方式成長。

結語

親愛的讀者，我們共同的旅程至此真正地畫上了一個句號，但它更像是一個省略號，預示著無限的可能。我們從Python的基礎語法出發，一路披荊斬棘，穿越了經典機器學習的崇山峻嶺，深入了深度學習的奇詭洞天，最終抵達了人工智能未來的海岸。

這本書傾注了我們對知識的敬畏，對實踐的尊重，以及對未來的熱望。如果它能在您的書架上占據一席之地，在您探索的道路上偶爾為您照亮一小片前路，那將是我們最大的榮幸。

記住，真正的“精通”，不是無所不知，而是永遠保有一顆學徒的心。

The journey is the reward.

附錄?

A. 數學基礎回顧（線性代數、微積分、概率論核心概念）
B. 常用工具與庫速查手冊
C. 術語表（中英對照）
D. 推薦閱讀與資源列表

A. 數學基礎回顧

本附錄并非一本詳盡的數學教科書，而是為機器學習實踐者量身打造的“急救包”與“概念地圖”。我們聚焦于那些在理解和實現算法時最核心、最常用的數學概念，旨在幫助您快速回顧、建立直覺，并將抽象的數學符號與具體的算法行為聯系起來。

A.1 線性代數：描述空間與變換的語言

核心地位：在機器學習中，數據被表示為向量，數據集是矩陣，算法是作用于這些向量和矩陣的變換。線性代數是這一切的底層語言。
核心概念回顧：
- 標量、向量、矩陣、張量：從0維到n維的數據容器。理解它們在NumPy中的對應（scalar,?1D-array,?2D-array,?nD-array）。
- 矩陣運算：
  - 加法與數乘：對應圖像的亮度調整等。
  - 矩陣乘法（Matrix Multiplication）：核心中的核心。理解其“行對列”的計算規則，以及它代表的線性變換。神經網絡的每一層本質上都是一次矩陣乘法加一個非線性激活。A * B。
  - 哈達瑪積（Hadamard Product）/ 逐元素乘積：兩個形狀相同的矩陣對應元素相乘。在NumPy中是?A * B，而矩陣乘法是?A @ B?或?np.dot(A, B)。
- 特殊矩陣：
  - 單位矩陣（Identity Matrix）：線性變換中的“不變”操作。
  - 轉置矩陣（Transpose Matrix）：A^T，行列互換。在計算梯度、變換向量空間時極其常用。
  - 逆矩陣（Inverse Matrix）：A?1，線性變換的“撤銷”操作。用于求解線性方程組。
- 線性方程組?Ax = b：理解其在最小二乘法（Normal Equation）中的應用。
- 范數（Norm）：衡量向量或矩陣的“大小”。
  - L1范數：向量元素絕對值之和。傾向于產生稀疏解（Lasso回歸）。
  - L2范數：向量元素平方和的平方根（歐幾里得距離）。正則化的常用工具（Ridge回歸）。
- 特征值與特征向量（Eigenvalues and Eigenvectors）：Av = λv。矩陣A作用于其特征向量v，效果等同于對v進行縮放，縮放比例即特征值λ。這是**主成分分析（PCA）**的靈魂，特征向量定義了數據變化的主方向，特征值衡量了該方向上的方差大小。
- 奇異值分解（SVD）：A = UΣV^T。一種更通用的矩陣分解方法，可用于任意矩陣。PCA、推薦系統、圖像壓縮等領域的核心技術。

A.2 微積分：描述變化與優化的語言

核心地位：機器學習的“學習”過程，本質上是一個優化過程，即尋找一組模型參數，使得損失函數最小。微積分，特別是微分學，是實現這一目標的唯一工具。
核心概念回顧：
- 導數（Derivative）：f'(x)，衡量一元函數在某一點的瞬時變化率。在優化中，它指明了函數值上升最快的方向。
- 偏導數（Partial Derivative）：?f/?x_i，多元函數中，固定其他變量，對其中一個變量求導。它衡量了函數在某個坐標軸方向上的變化率。
- 梯度（Gradient）：?f，由所有偏導數組成的向量。它指向函數在當前點上升最快的方向。因此，負梯度方向就是函數下降最快的方向。
- 梯度下降法（Gradient Descent）：θ = θ - η * ?J(θ)。這是機器學習中最核心的優化算法。我們沿著負梯度方向，以學習率η為步長，迭代地更新參數θ，以期找到損失函數J(θ)的最小值。
- 鏈式法則（Chain Rule）：dy/dx = dy/du * du/dx。這是**反向傳播算法（Backpropagation）**的數學基石。它使得我們能夠計算一個深度、復雜的神經網絡中，最終的損失對于網絡中任意一層參數的梯度。
- 雅可比矩陣（Jacobian Matrix）與海森矩陣（Hessian Matrix）：
  - 雅可比：一階偏導數組成的矩陣，是梯度的推廣。
  - 海森：二階偏導數組成的矩陣。它描述了函數的局部曲率，可用于判斷臨界點是極大、極小還是鞍點。牛頓法等二階優化方法會用到它。

A.3 概率論：描述不確定性的語言

核心地位：世界是充滿不確定性的，數據是有噪聲的，模型是概率性的。概率論為我們提供了一套嚴謹的框架來量化、建模和推理這種不確定性。
核心概念回顧：
- 隨機變量（Random Variable）：離散型與連續型。
- 概率分布（Probability Distribution）：
  - 概率質量函數（PMF）（離散）與概率密度函數（PDF）（連續）。
  - 常見分布：伯努利（單次硬幣）、二項（多次硬幣）、分類（單次骰子）、多項（多次骰子）、高斯（正態分布，自然界最常見）、泊松（單位時間事件發生次數）。
- 期望（Expectation）：E[X]，隨機變量的長期平均值。
- 方差（Variance）：Var(X)，衡量隨機變量取值偏離其期望的程度。
- 條件概率（Conditional Probability）：P(A|B)，在事件B發生的條件下，事件A發生的概率。這是所有概率模型的基礎。
- 貝葉斯定理（Bayes' Theorem）：P(H|D) = [P(D|H) * P(H)] / P(D)。
  - 后驗概率?P(H|D)?= (?似然?P(D|H)?*?先驗?P(H)?) /?證據?P(D)
  - 這是樸素貝葉斯分類器、貝葉斯推斷和許多現代生成模型的理論核心。它告訴我們如何根據觀測到的數據（證據），來更新我們對一個假設（模型參數）的信念。
- 最大似然估計（Maximum Likelihood Estimation, MLE）：一種參數估計方法。尋找一組參數，使得當前觀測到的這批數據出現的概率最大。這是頻率學派的核心思想。
- 最大后驗概率估計（Maximum A Posteriori, MAP）：貝葉斯學派的參數估計方法。它在最大似然的基礎上，額外考慮了參數本身的先驗分布，即argmax_θ P(D|θ)P(θ)。正則化項（如L1, L2）通常可以被解釋為對參數引入了某種先驗分布。

B. 常用工具與庫速查手冊

Jupyter Notebook / Lab
- Shift + Enter: 運行當前單元格并跳轉到下一個
- Ctrl + Enter: 運行當前單元格
- Esc?->?M: 切換到Markdown模式
- Esc?->?Y: 切換到代碼模式
- Esc?->?A?/?B: 在上方/下方插入單元格
- %matplotlib inline: 在Notebook中顯示Matplotlib圖像
- !pip install [package]: 在Notebook中執行Shell命令
NumPy
- np.array([list]): 創建數組
- np.arange(start, stop, step): 創建等差序列
- np.linspace(start, stop, num): 創建等分序列
- arr.shape,?arr.ndim,?arr.size: 查看形狀、維度、元素數
- arr.reshape(new_shape): 重塑數組
- arr[slice]: 索引與切片
- arr.T: 轉置
- np.dot(a, b)?or?a @ b: 矩陣乘法
- np.sum(),?np.mean(),?np.std(): 聚合函數（可指定axis）
- np.linalg.inv(A): 求逆矩陣
- np.linalg.eig(A): 求特征值和特征向量
Pandas
- pd.read_csv(filepath): 讀取CSV
- df.head(),?df.tail(),?df.info(),?df.describe(): 數據速覽
- df['column_name']?or?df.column_name: 選擇列（Series）
- df[['col1', 'col2']]: 選擇多列（DataFrame）
- df.loc[row_label, col_label]: 基于標簽的索引
- df.iloc[row_index, col_index]: 基于位置的索引
- df.isnull().sum(): 查看每列的缺失值數量
- df.fillna(value): 填充缺失值
- df.dropna(): 刪除有缺失值的行/列
- df.groupby('key_column').agg({'data_col': 'mean'}): 分組聚合
- pd.concat([df1, df2]): 拼接
- pd.merge(df1, df2, on='key'): 合并
Matplotlib / Seaborn
- import matplotlib.pyplot as plt
- import seaborn as sns
- plt.figure(figsize=(w, h)): 創建畫布
- plt.plot(x, y): 折線圖
- plt.scatter(x, y): 散點圖
- plt.hist(data, bins=n): 直方圖
- sns.heatmap(corr_matrix, annot=True): 熱力圖
- sns.pairplot(df, hue='category_col'): 變量關系對圖
- plt.title(),?plt.xlabel(),?plt.ylabel(),?plt.legend(): 添加圖表元素
- plt.show(): 顯示圖像
Scikit-learn (通用API模式)
1. from sklearn.module import Model
2. model = Model(hyperparameters)
3. model.fit(X_train, y_train)
4. predictions = model.predict(X_test)
5. score = model.score(X_test, y_test)
- 預處理:?StandardScaler,?MinMaxScaler,?OneHotEncoder,?LabelEncoder
- 模型選擇:?train_test_split,?GridSearchCV,?cross_val_score
- 評估:?confusion_matrix,?classification_report,?mean_squared_error,?r2_score

C. 術語表（中英對照）

人工智能 (Artificial Intelligence, AI)
機器學習 (Machine Learning, ML)
深度學習 (Deep Learning, DL)
監督學習 (Supervised Learning)
無監督學習 (Unsupervised Learning)
強化學習 (Reinforcement Learning)
特征 (Feature)
標簽 (Label)
訓練集 (Training Set)
驗證集 (Validation Set)
測試集 (Test Set)
過擬合 (Overfitting)
欠擬合 (Underfitting)
偏差-方差權衡 (Bias-Variance Trade-off)
損失函數 (Loss Function) / 成本函數 (Cost Function)
梯度下降 (Gradient Descent)
學習率 (Learning Rate)
反向傳播 (Backpropagation)
正則化 (Regularization) (L1, L2)
分類 (Classification)
回歸 (Regression)
聚類 (Clustering)
降維 (Dimensionality Reduction)
邏輯回歸 (Logistic Regression)
支撐向量機 (Support Vector Machine, SVM)
決策樹 (Decision Tree)
隨機森林 (Random Forest)
梯度提升 (Gradient Boosting) (GBDT, XGBoost, LightGBM)
K-均值 (K-Means)
主成分分析 (Principal Component Analysis, PCA)
神經網絡 (Neural Network, NN)
卷積神經網絡 (Convolutional Neural Network, CNN)
循環神經網絡 (Recurrent Neural Network, RNN)
長短期記憶網絡 (Long Short-Term Memory, LSTM)
注意力機制 (Attention Mechanism)
變換器 (Transformer)
準確率 (Accuracy)
精確率 (Precision)
召回率 (Recall)
F1分數 (F1-Score)
ROC曲線 (Receiver Operating Characteristic Curve)
曲線下面積 (Area Under the Curve, AUC)
超參數 (Hyperparameter)
批處理 (Batch)
周期 (Epoch)

D. 推薦閱讀與資源列表

經典書籍

《深度學習》(Deep Learning)?by Ian Goodfellow, Yoshua Bengio, and Aaron Courville.
- 俗稱“花書”。理論深度無出其右，是系統性理解深度學習數學原理的必讀之作。
《機器學習》(Machine Learning)?by 周志華.
- 俗稱“西瓜書”。內容全面，覆蓋廣泛，是國內最經典的機器學習教材之一。

在線課程

Coursera - Machine Learning by Andrew Ng (吳恩達)
- 機器學習的“啟蒙圣經”，無數人的AI入門第一課。直觀、易懂。
Coursera - Deep Learning Specialization by Andrew Ng
- 吳恩達老師的深度學習系列課程，系統性地介紹了深度學習的各項技術。

實用網站與工具

Kaggle: 全球最大的數據科學競賽平臺。是實踐、學習、交流和求職的絕佳場所。
Papers with Code: 將學術論文、代碼實現、數據集和SOTA（State-of-the-art）排行榜完美結合的網站，是追蹤領域前沿的利器。
Hugging Face: 提供了transformers庫，是NLP領域事實上的標準工具庫。其模型中心（Model Hub）和數據集（Datasets）庫也極為強大。

技術博客

Chris Olah's Blog: 對LSTM、注意力機制等復雜概念的圖文解釋已成經典。
Jay Alammar's Blog (The Illustrated Transformer/BERT): 用極其精美的圖示，將Transformer等復雜模型講解得一清二楚。
Lilian Weng's Blog: OpenAI研究員的博客，對RL、LLM等前沿領域有系統性、高質量的總結。

后記

親愛的讀者朋友們：

當您讀到這里時，我們共同的旅程已然畫上了一個句點。我仿佛能看到，燈光下，您輕輕合上書卷，長舒一口氣。您的目光或許會望向窗外，那片由數據、代碼和算法交織而成的、既熟悉又嶄新的世界，在您眼中，已然呈現出與初見時截然不同的風景。

我們一同走過了這段不平凡的道路。

我們始于“仰望星空”。在第一章，我們探討了何為學習，何為智能，我們追溯了機器學習那波瀾壯闊的思想史，也校準了我們作為探索者的“心法”——以“出世”之心，做“入世”之事。我們約定，技術是“器”，而駕馭它的，必須是一顆清明、審慎且充滿人文關懷的心。

隨后，我們開始了“腳踏實地”的筑基之旅。在第二章，我們磨利了手中的“神兵”——Python、NumPy、Pandas、Matplotlib。它們不再是冰冷的庫，而是我們感知數據、理解數據、與數據對話的延伸。我們學會了如何為數據“相面”，如何為它們“凈身”，如何在蕪雜中“點石成金”。第三章的預處理與特征工程，是我們從“工匠”走向“藝術家”的第一步，我們懂得了，好的模型始于好的數據，而好的數據，源于深刻的理解與精心的雕琢。

接著，我們進入了算法的“核心殿堂”。我們手持在第四章精心打磨的“度量衡”——那些評估模型好壞的標尺，開始系統地學習各類主流算法。從監督學習的“判別”與“預測”（第五、六章），到無監督學習的“歸納”與“發現”（第七章），我們像一位經驗豐富的將軍，檢閱了邏輯回歸的簡約、支撐向量機的精巧、決策樹的直觀、K-均值的樸素、PCA的深刻。我們不再滿足于model.fit()的表象，而是深入到每個算法的假設、邊界和數學原理之中。

當單一模型的智慧略顯單薄時，我們領悟了“集腋成裘”的集成思想。第八章的Bagging與Boosting，讓我們看到了“三個臭皮匠”如何通過協作與迭代，最終超越“諸葛亮”。我們見證了XGBoost與LightGBM這些工業界“大殺器”的威力，也理解了其背后深刻的統計學與優化思想。

然后，我們勇敢地叩響了“未來之門”。第九章的神經網絡，為我們搭建了通往深度學習的橋梁。我們從生物神經元的啟發開始，親手構建了多層感知機，理解了反向傳播的精髓。這扇門背后，是CNN對空間的洞察，是RNN對時間的記憶，是Transformer對語言的重塑。

理論的深度，最終要在實踐的土壤中開花結果。我們投身于兩個“真實戰場”。在第十章的金融風控中，我們直面了數據不平衡的挑戰，學會了用SMOTE創造智慧，用SHAP洞察模型的“內心”。在第十一章的文本情感分析中，我們學會了如何將非結構化的語言，轉化為機器可以理解的向量，并挖掘其背后的情感與主題。這不再是玩具項目，而是充滿約束、妥協與創造性解決問題的真實演練。

最后，我們完成了從“煉丹師”到“工程師”與“思想家”的最后一躍。第十二章讓我們學會了如何將模型封裝、部署，讓它走出實驗室，“活”在真實世界里，服務于人。而第十三章，我們再次抬頭，將目光投向了更遠的地平線——強化學習的交互智慧、圖神經網絡的關系洞察、自監督學習的無盡潛力。我們繪制了一張持續成長的地圖，因為我們深知，在這片領域，“畢業”即是“落后”的開始。

回顧這段旅程，我希望您收獲的，不僅僅是一套“屠龍之技”。如果是那樣，奶奶就失敗了。

我更希望您收獲的，是一種“思維范式”的轉變。您學會了如何將一個模糊的現實問題，解構、抽象為一個可以被數學定義的機器學習問題；您學會了在面對一堆看似雜亂無章的數據時，如何通過探索、清洗、轉換，發現其內在的結構與價值；您學會了在眾多模型中，如何根據問題的特性、數據的形態和業務的目標，做出權衡與選擇；您更學會了如何批判性地看待模型的輸出，理解其能力邊界，并警惕其潛在的偏見與風險。

我希望您收獲的，是一種“學習能力”的內化。我們不可能在一本書里窮盡所有知識。但通過對幾個核心算法進行“解剖麻雀”式的深度挖掘，您應該已經掌握了學習任何新模型的方法論：追溯其動機，理解其核心假設，剖析其數學原理，進行代碼實踐，并探索其應用邊界。這套方法，將是您未來面對層出不窮的新技術時，最可靠的武器。

我最希望您收獲的，是一種“知行合一”的信念。知識若不化為行動，便如錦衣夜行；行動若無知識指引，則易陷入迷途。請務必將書中所學，應用到您所熱愛的領域中去。去解決一個實際的問題，哪怕它很小；去參加一場Kaggle競賽，哪怕名次不佳；去寫一篇技術博客，哪怕讀者寥寥；去為開源社區貢獻一行代碼，哪怕只是修正一個拼寫錯誤。每一次微小的實踐，都是在為您內心的知識大廈，添上一塊堅實的磚瓦。

親愛的朋友，人工智能的時代洪流已至，它正以前所未有的力量，重塑著我們世界的每一個角落。這股力量，既可以創造巨大的福祉，也可能帶來前所未有的挑戰。而您，作為掌握了這股力量核心技術的人，您的每一次選擇，每一次創造，都將是這股洪流中一朵重要的浪花。

請永遠保持那份好奇心。對未知保持敬畏，對問題窮根究底。

請永遠懷有那份同理心。記住技術最終是為人服務的，去理解用戶的痛點，去關懷技術可能影響到的每一個人。

請永遠堅守那份責任心。確保你的模型是公平的、透明的、可靠的，用你的智慧去“作善”，而非“作惡”。

在古老的禪宗故事里，弟子問禪師：“師父，開悟之后，您做什么？”禪師答：“開悟前，砍柴，擔水；開悟后，砍柴，擔水。”

那么，在讀完這本書，掌握了機器學習的種種“法門”之后，我們該做什么呢？

答案或許也是一樣：回到你的生活，回到你的工作，回到你關心的問題中去。只是這一次，你的“斧頭”更鋒利了，你的“扁擔”更堅固了，你看待“柴”與“水”的眼光，也變得更加深邃、更加智慧了。

感謝您，選擇與我們一同走過這段旅程。前路漫漫，亦燦燦。現在，請合上書，走出書齋，去那片廣闊的智慧荒原上，點燃屬于您自己的、那獨一無二的火把。

愿智慧之光，永遠照亮您前行的道路，再會！