?
目錄
Collection簡介
Collection的遍歷方式
迭代器遍歷
增強for遍歷
Lambda表達式遍歷
?List集合
?List集合的遍歷方式
列表迭代器遍歷以及普通for循環
數據結構
棧
隊列
數組
鏈表
單向鏈表
雙向鏈表
二叉樹
遍歷方式
普通二叉樹
二叉查找樹
平衡二叉樹
旋轉機制
紅黑樹
ArrayList集合底層原理
?LinkedList集合的底層原理
泛型深入
JDK5之前
JDK5之后
泛型的定義
泛型類
泛型方法
?泛型接口
?泛型的繼承
泛型的通配符
Set集合
HashSet實現類
底層原理
LinkedHashSet底層原理
?TreeSet
?應用場景
?
本篇文章是我聽b站阿偉老師講課的一個總結。
Collection簡介
Collection接口:單列接口(單列集合的祖宗接口,它的功能是全部單列集合都可以繼承使用的。)
Map接口:雙列集合(下一期講)
紅色邊框是接口,藍色邊框表示implement接口的類?
Collection接口:List接口和Set接口繼承Collection接口
List接口:有三個實現類:ArrayList、LinkedList、Vector
Set接口:有兩個實現類:HashSet、TreeSet;同時在HashSet中,LinkedHashSet又繼承于它
List系列集合:添加的元素是有序、可重復、有索引
Set系列集合:添加的元素是無序、不重復、無索引
常見方法
public boolean add(E e):把給定的對象添加到當前集合中
public void clear ():清空集合中所有的元素
public boolean remove (E e):把給定的對象在當前集合中刪除
public boolean contains (Object obj):判斷當前集合中是否包含給定的對象
public boolean isEmpty():判斷當前集合是否為空
public int size():返回集合中元素的個數/集合
注意:
Set沒有索引不能通過普通for來進行遍歷。
普通for遍歷只有list接口的實現類能用(因為它有索引)。
Collection的遍歷方式
迭代器遍歷
迭代器不依賴索引。
迭代器在java中有一個類是Iterator,迭代器是集合專用的遍歷方式。
Collection集合獲取迭代器的方法:Iterator<E>? iterator() 返回迭代器對象,默認指向當前集合的0索引。
Iterator中的常用方法:
boolean hasNext()? 判斷當前位置是否有元素,有元素返回true,沒有元素返回false
E next()? 獲取當前位置的元素,并將迭代器對象移向下一個位置。
舉例:?
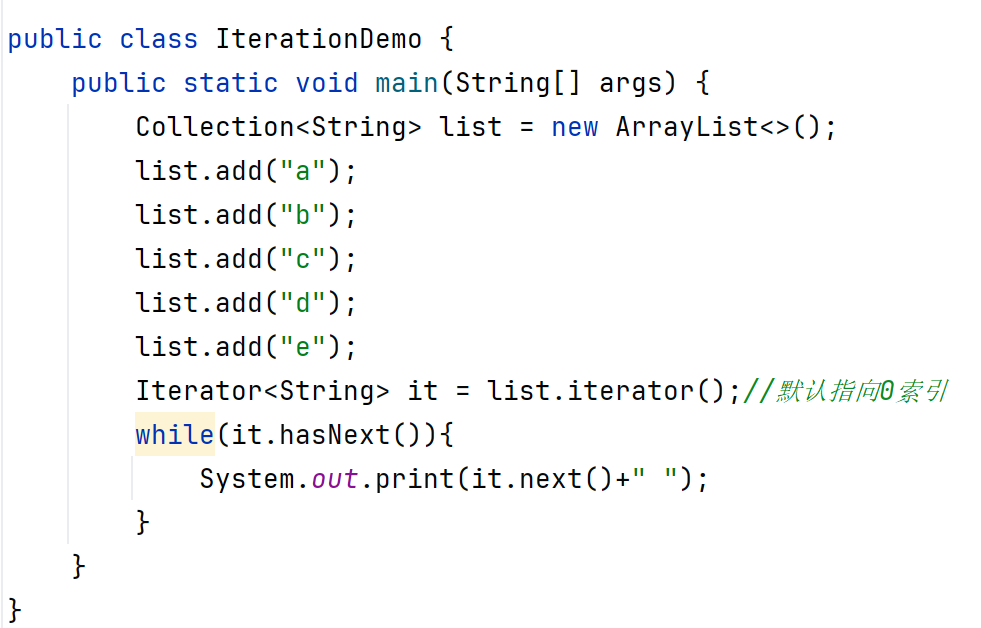
細節:
1、如果指針已經指向如上代碼元素e后面的數,e后面沒有數字,還要強行獲取當前元素,就會報錯NoSuchElementException.
2、迭代器遍歷完畢,指針不會復位。(如果還要遍歷集合第二遍,只能重新獲取一個迭代器)
3、循環中只能用一次next方法。(因為如果在一個循環中有兩次或者多次next方法時,如果在第一次或者前幾次用next方法已經遍歷結束了,在下一次next方法就會報錯,因為沒有元素了)
4、迭代器遍歷時,不能用集合的方式進行增加或者刪除。

增強for遍歷
增強for的底層就是迭代器,為了簡化迭代器的代碼書寫的。
它是JDK5之后出現的,內部原理就是一個Iterator迭代器。
所有的單列集合和數組才能用增強for進行遍歷
格式:
for(元素的數據類型? 變量名:數組或者集合){......}
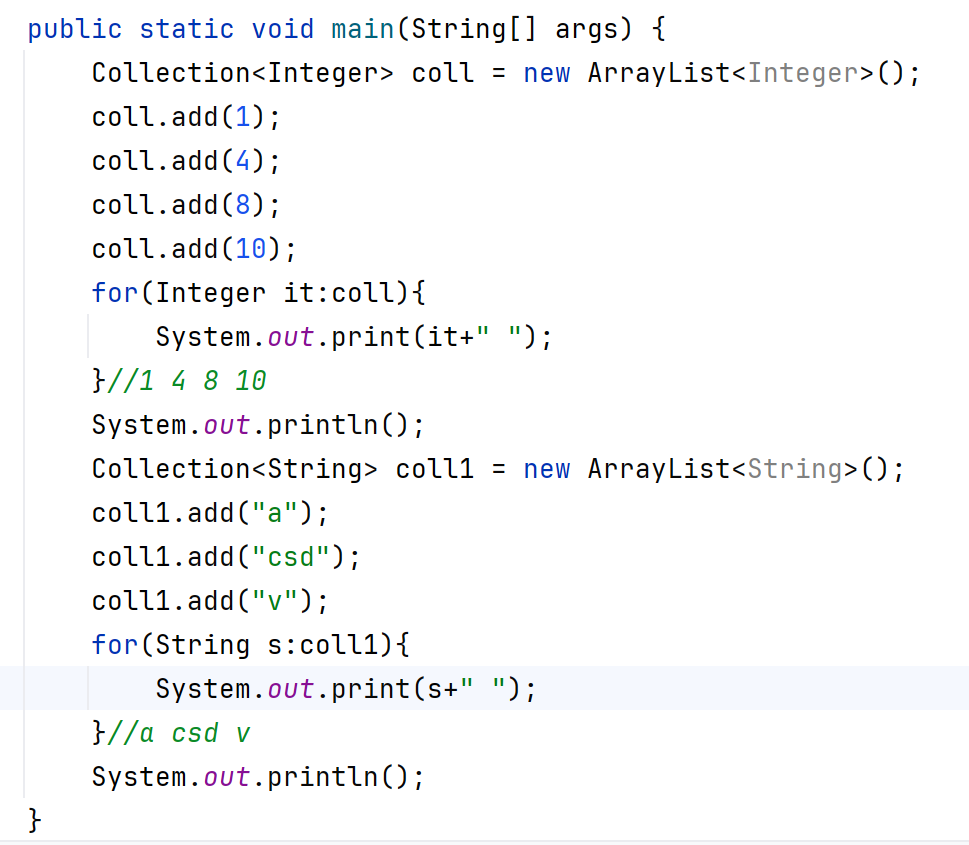
細節:
修改增強for中的變量(例如如上代碼的it、s),不會改變集合中原本的數據,他只是一個接收集合或數組中數據的變量而已。
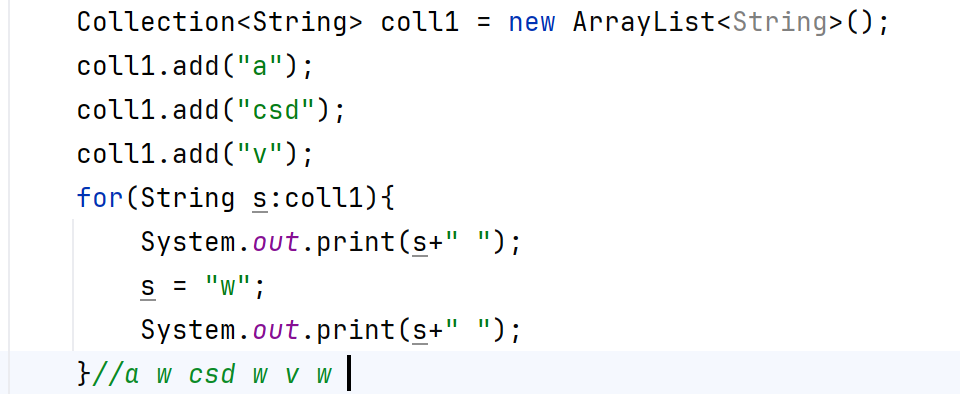
Lambda表達式遍歷
利用的方法:default void forEach(Consumer<? super T> action):?
Consumer是一個函數類接口
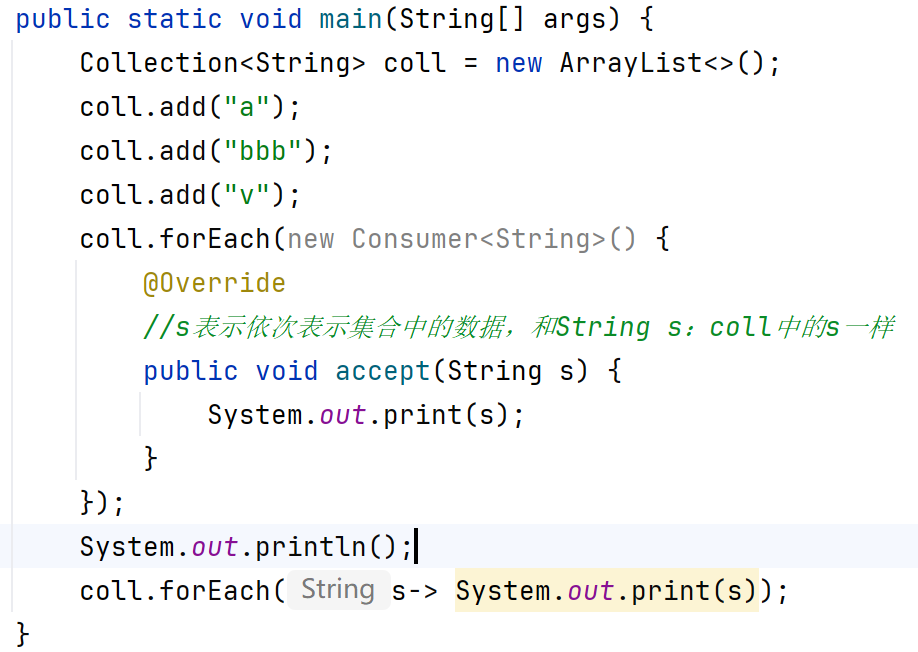
?List集合
特點:
有序:存和取的元素順序一致。
有索引:可以通過索引操作元素。
可重復:存儲的元素可以重復。
Collection的方法List都繼承了;List集合因為有索引,所以多了很多索引操作的方法。
void add(int index,E element)? 在此集合中的指定位置插入指定的元素
E remove(int index)? 刪除指定索引處的元素,返回被刪除的元素
E set (int index,E element)? 修改指定索引處的元素,返回被修改的元素
E get(int index)? 返回指定索引處的元素

?List集合的遍歷方式
List接口繼承于Collection,所以上邊講的Collection接口的遍歷方式在List中同樣適用,但是List也有它自己獨特的遍歷方式。
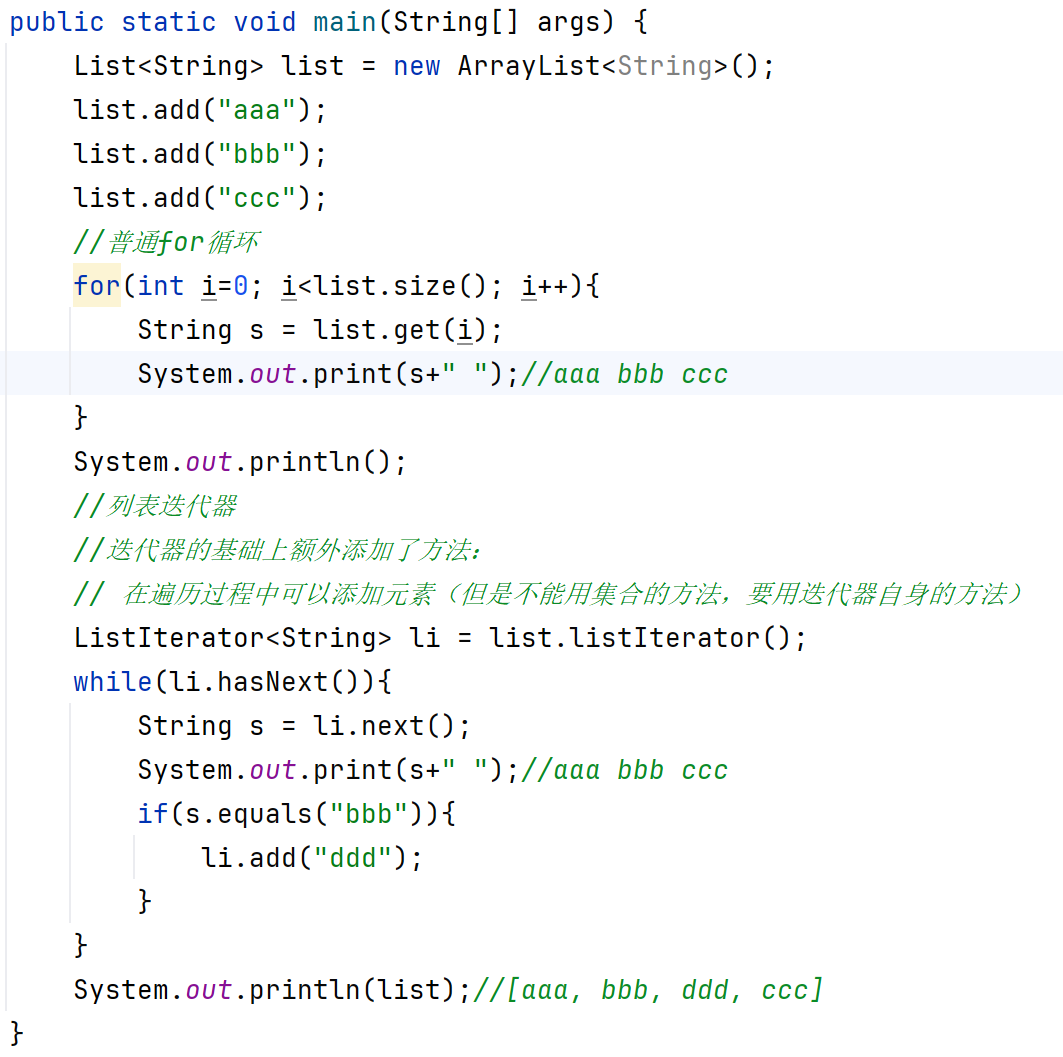
列表迭代器遍歷以及普通for循環
?列表迭代器遍歷(他自己獨特的遍歷方式)
普通for循環(因為List集合存在索引)
數據結構
數據結構是計算機底層存儲、組織數據的方式。是指數據之間是以什么方式排列在一起。
數據結構是為了更加方便的管理和使用數據,需要結合具體的業務場景來進行選擇。
一般情況下,精心選擇的數據結構可以帶來更高的運行或者存儲效率。
棧
先進后出
隊列
先進先出
數組
查詢速率快(有索引、地址值來查詢),刪除元素和添加元素效率低(查詢快,增刪慢)
鏈表
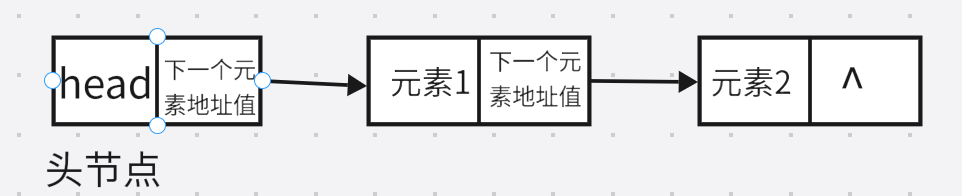
單向鏈表
查詢慢,無論查詢那個數據都要從頭開始找;增刪快。
每一個元素都被稱為結點,每一個節點都是一個獨立的對象,在內存中是不連續的,每個結點包含數據值和下一個結點的地址值。
鏈表有頭節點
雙向鏈表
頭結點的上一個元素地址值為空,尾結點的下一個元素地址值為空
可以提高查詢效率,不僅可以從前往后查詢,還可以從后往前查詢
當題目要求查第幾個元素時,如果離頭結點比較近那么就從前往后查,如果離尾結點比較近,就從后往前查

二叉樹
二叉樹中,任意節點的度<=2
遍歷方式
所有的二叉樹都可以用這個遍歷方式
前序遍歷:
從根節點開始,按照當前節點,左子節點,右子節點的順序開始遍歷
中序遍歷:
從最左邊的節點開始,按照左子節點,當前節點,右子節點的順序開始遍歷
后序遍歷:
從最左邊的節點開始,按照左子節點,右子節點,當前節點的順序開始遍歷
層序遍歷:
從根節點開始,一層一層的遍歷(從左到右)
普通二叉樹
查找很慢
二叉查找樹
又叫二叉排序樹或者二叉搜索樹
任意節點左子樹上的值都小于當前節點
任意節點右子樹上的值都大于當前節點
添加節點時,小的存左邊,大的存右邊,一樣的不存
查找也是一樣的原理。
弊端:如果添加的元素時按升序或者降序添加時,他就只有右子樹或者左子樹。這樣查詢效率就會很慢。因此,如果要使左右子樹差不多高,就涉及到了平衡二叉樹。
平衡二叉樹
任意節點左右字數高度差不超過1(由二叉查找樹演變而來,本質也是個二叉查找樹)
怎么保證樹的平衡?
旋轉機制
觸發時機:當添加一個節點之后,該樹不再是一顆平衡二叉樹
左旋(逆時針)
確定支點:從添加的結點開始,不斷的往父節點找不平衡的節點
找到后,把支點左旋,變成左子節點
如果支點存在左子樹,那么這個左子樹,肯定介于支點的父節點以及支點之間,他自然而然的變成支點父節點的右子樹;支點的父節點變為支點的左子樹。
右旋(順時針)
和左旋原理一樣,只不過反過來就可以了
需要旋轉的四種情況:
1、左左:當根節點左子樹的左子樹有節點插入,導致二叉樹不平衡(一次右旋)
2、左右:當根節點左子樹的右子樹有節點插入,導致二叉樹不平衡(先局部左旋,再整體右旋)
3、右右:當根節點右子樹的右子樹有節點插入,導致二叉樹不平衡(一次左旋)
4、右左:當根節點右子樹的左子樹有節點插入,導致二叉樹不平衡(先局部右旋,再整體左旋)
紅黑樹
增刪改查性能都很好
是一種自平衡的二叉查找樹。(之前被叫做二叉查找B數)
特殊的二叉查找樹;但是不是高度平衡的;條件:特有的紅黑規則
紅黑規則:
1、每一個節點要么是紅色,要么是黑色。
2、根節點必須是黑色
3、如果一個節點沒有子節點或者父節點,則該節點相應的指針屬性值為Nil,這些Nil視為葉節點,每個葉節點(Nil)是黑色的。
4、如果某一個節點是紅色,那么它的子節點必須是黑色(不能出現兩個紅色節點相連的情況)
5、對于每一個節點,從該節點到其所有后代葉節點的簡單路徑上,均包含相同數目的黑色節點。
添加節點時,默認添加節點的顏色是紅色的,這樣效率更高。
添加時:如果是根節點,直接變為黑色
非根節點:父節點是黑色:不需要進行任何操作
? ? ? ? ? ? ? ? ??父節點是紅色:1、叔叔紅色:1)將“父”設為黑色,將“叔叔”設為黑色
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 2)將“祖父”設為“紅色”
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 3)如果祖父為根,再將根變回黑色
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 4)如果祖父非根,將祖父設置為當前節點再進行其他判斷
? ? ? ? ? ? ? ? ? ? ? ? 2、叔叔黑色,當前節點為父的右孩子:把父設置為當前節點并左旋,再進行判斷
? ? ? ? ? ? ? ? ? ? ? ?2、叔叔黑色,當前節點為父的左孩子:1)將“父”設為“黑色”
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?2)將“祖父”變為“紅色”? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?3)以祖父為支點進行右旋
ArrayList集合底層原理
擴容機制:
1、利用空參構造的集合,在底層創建一個默認長度為0的數組。?
2、添加第一個元素時,底層會創建一個新的長度為10的數組。
這個數組的名字叫做:elementDate;size來記錄數組里面的元素個數,以及下一個要存入的數的索引。
3、當又存滿時,會再次創建一個新數組,把原來的元素都拷貝到新數組當中,新數組擴容1.5倍。
4、當又存滿了,第一種情況:會再次擴容1.5倍。
第二種情況:如果一次添加多個元素(比如addAll方法的list2.addAll(list1)在一個集合中添加另一個集合的所有元素),1.5倍還放不下,則新創建數組的長度為實際長度為基準。
這兩種情況,都會創建一個新的數組,開拷貝舊數組的元素,用copyOf()方法(Arrays類中的一個靜態方法)拷貝。新數組的名字和舊數組一樣。
?LinkedList集合的底層原理
?底層數據結構是雙鏈表,查詢慢,增刪快,但是如果操作的是首尾元素,數據也是極快的。
LinkedList本身提供了很多直接操作首尾元素的特有API
public void addFirst(E e)在該列表開頭插入指定的元素
public void addLast (E e):將指定的元素追加到此列表的末尾
public E getFirst():返回此列表中的第一個元素
public E getLast):返回此列表中的最后一個元素
public E removeFirst():從此列表中刪除并返回第一個元素
public E removeLast):從此列表中刪除并返回最后一個元素
可以自己去API看看Collection接口中的add方法源碼。
泛型深入
泛型是JDK5中引入的特性,可以在編譯階段約束操作的數據類型,并進行檢查。
泛型的格式:<數據類型>
注意:泛型只能支持引用數據類型
JDK5之前
沒有泛型

JDK5之后
泛型的好處:統一數據類型
擴展:Java中的泛型是偽泛型(比如集合的泛型String類型的,那么加入這個集合時,會檢驗是不是String,但是加入進去之后,就會變成Object類型的,但當外面要獲取數據時,底層就會把Object按照泛型強轉為String類型)(當在Java文件中編譯的時候這個泛型會顯示出來,但在它轉成字節碼class文件時,這個泛型就會消失)
泛型不能寫基本數據類型
指定泛型的具體類型后,傳遞數據時,可以傳入該類類型或者子類類型。
如果不寫泛型默認是Object
泛型的定義
類后面——泛型類、方法上面——泛型方法、接口后面——泛型接口
泛型類
當一個類中,某個變量的數據類型不確定時,就可以定義帶有泛型的類
格式:修飾符 class 類名<類型>{}
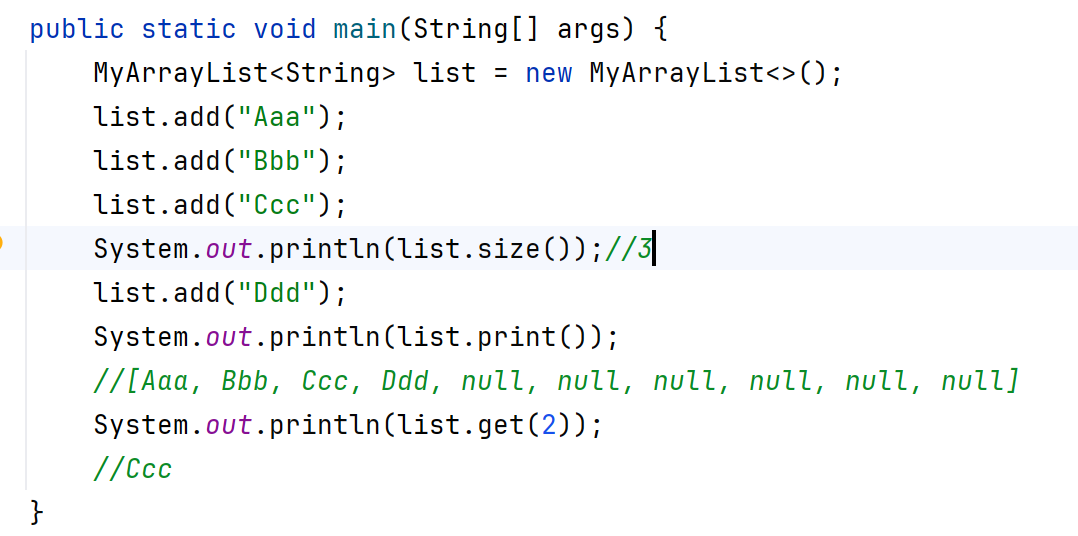
舉例:public class ArrayList<E>{}我們在使用的時候比如ArrayList<String> list = new ArrayList<>();這時這個E就確定為String類型
這個E可以理解為變量,不是用來記錄數據的,而是記錄數據的類型,可以寫成T、E、K、V等
 ?
?
泛型方法
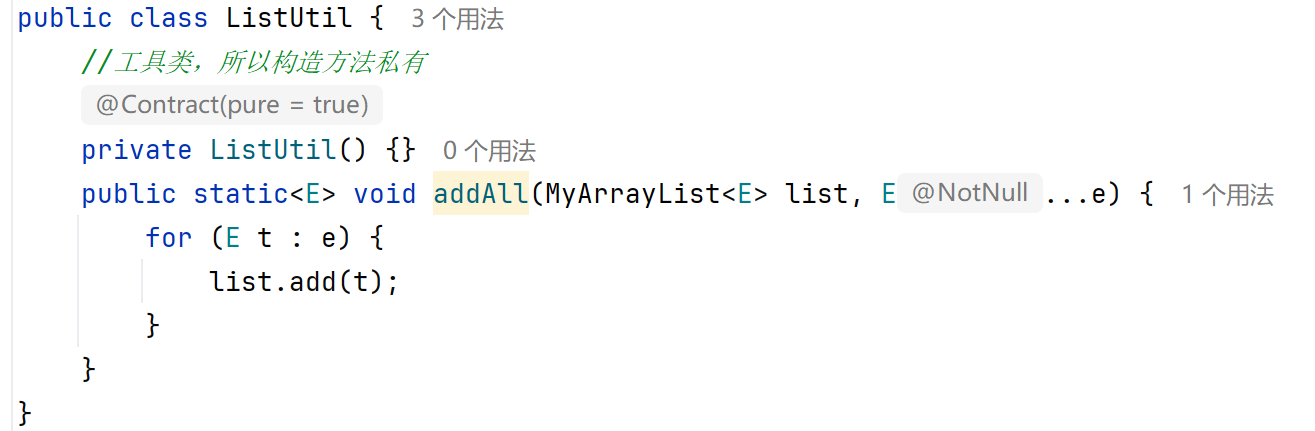
方法中形參類型不確定時,可以使用類名后面定義的泛型<E>
方法一:使用類名后面定義的泛型(所有方法都能使用)
如上代碼便是這種方法一。
方法二:在方法申明上定義自己的泛型(只能在本方法上使用)
格式:修飾符<類型> 返回值類型 方法名(類型 變量名){}
舉例:public<K> void swim(K k){}
K可以理解為變量,不是用來記錄數據的,而是記錄數據的類型,可以寫成T、E、K、V等
 ?
?
?泛型接口
格式:修飾符 interface 接口名<類型>{}
舉例:public interface List<E>{}
如何使用一個帶泛型的接口
方法一:實現類給出具體的類型

方法二:實現類延續泛型,創建對象再確定
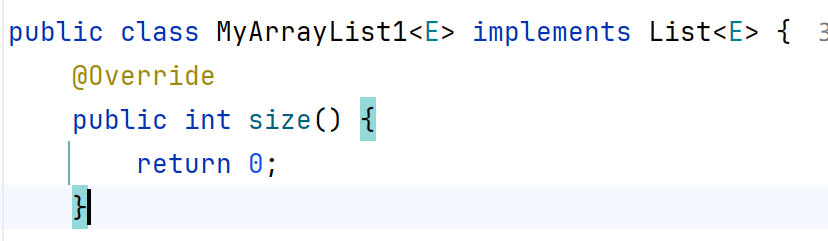
?泛型的繼承
泛型不具備繼承性,但是數據具備繼承性
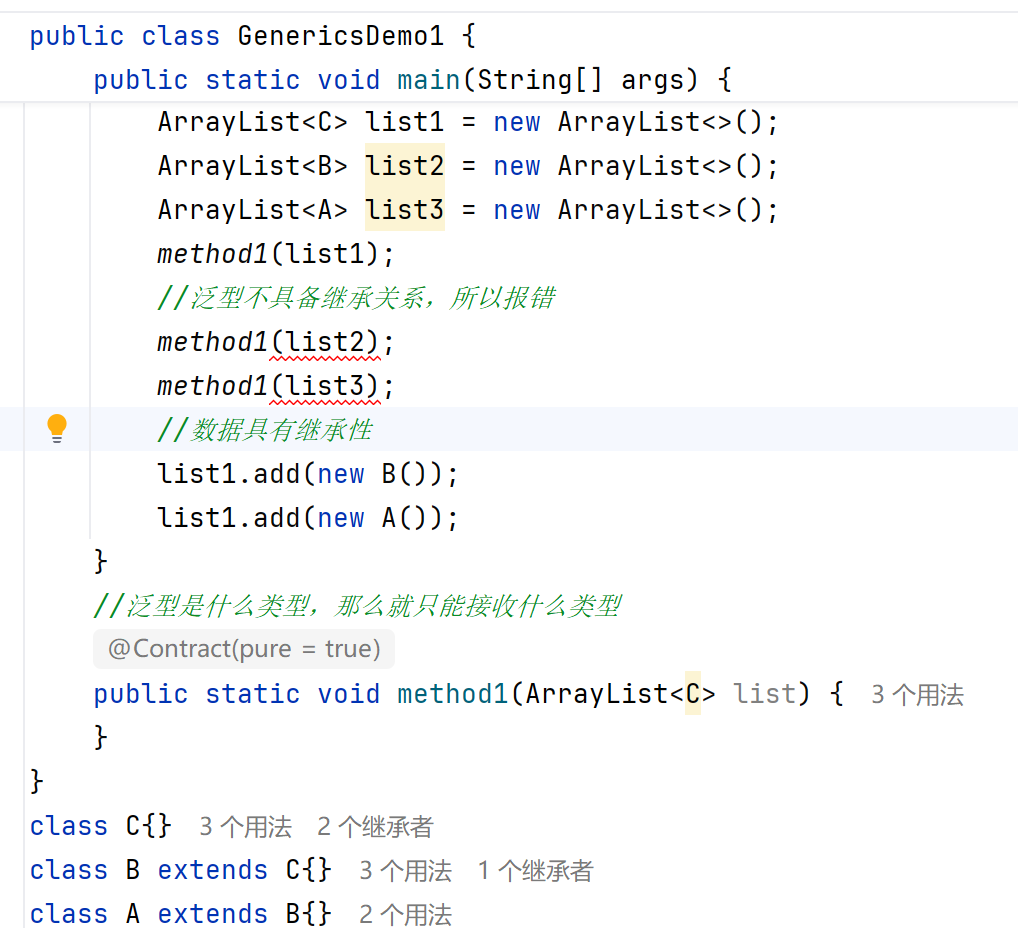
泛型的通配符
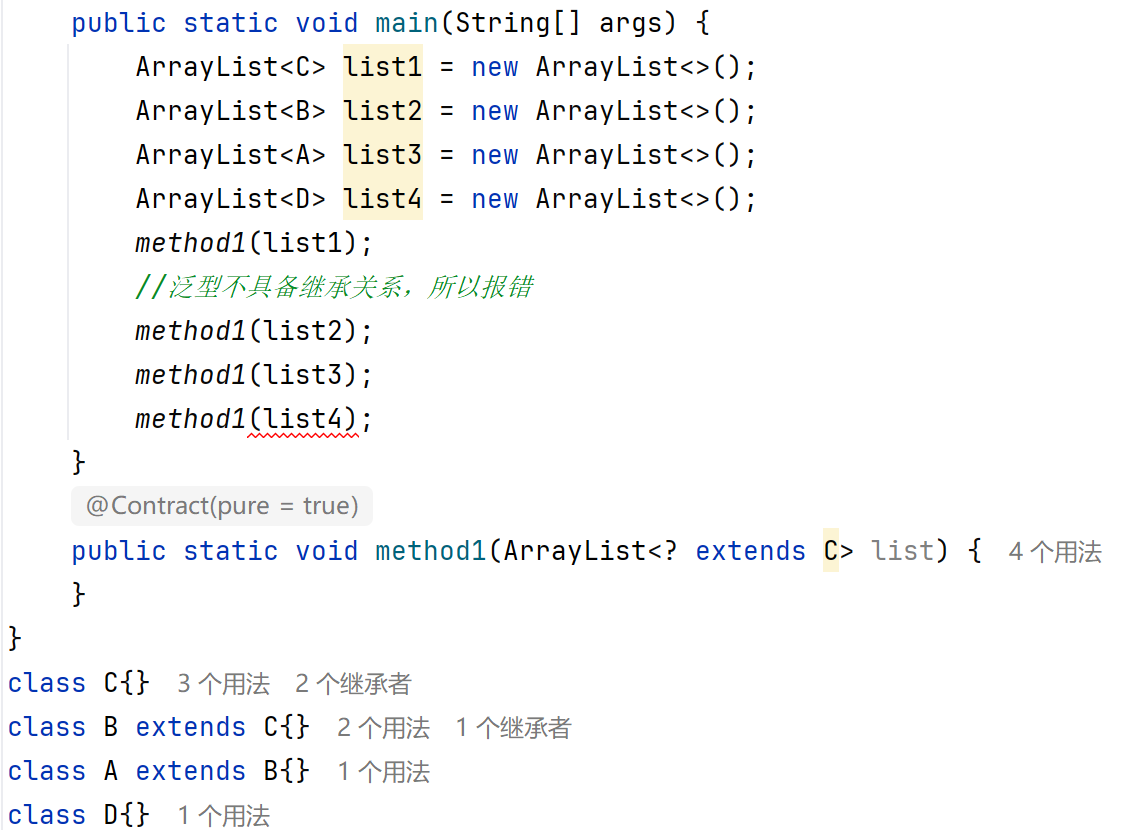
對于以上,如果我們非要讓他能夠傳遞A,B,C三種繼承類型時,該怎么辦?
有人會想到:
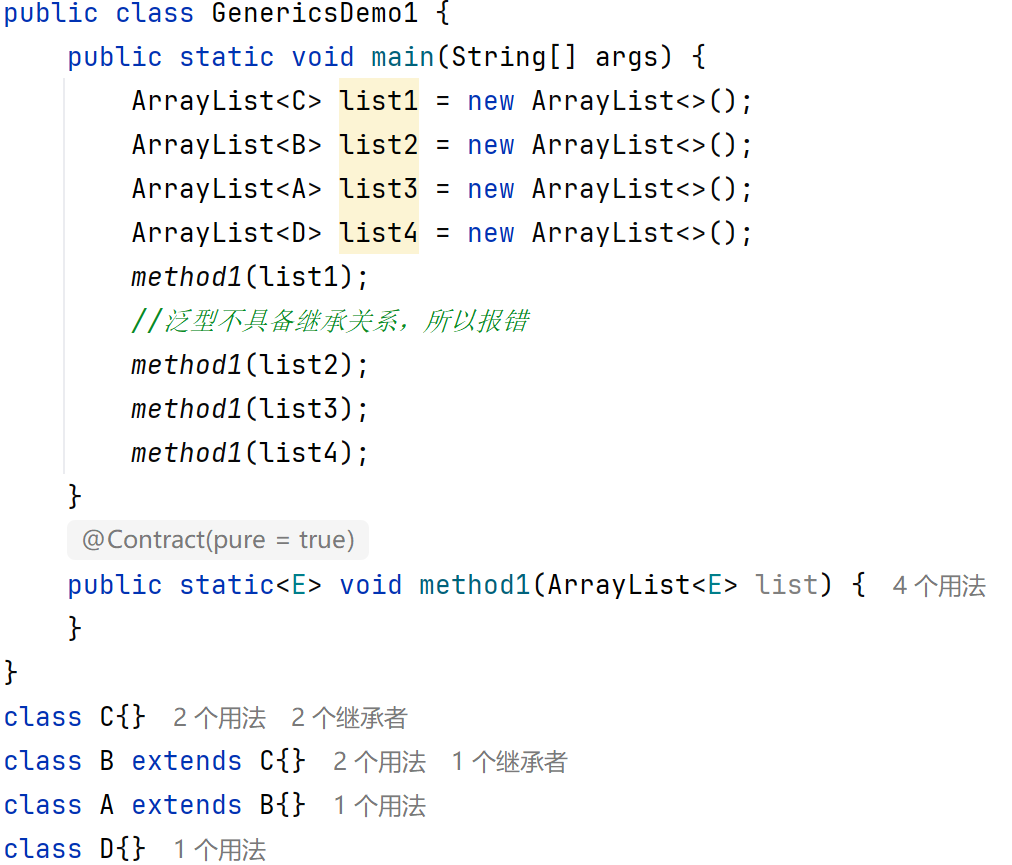
?這個雖然能傳遞,但是D類型他不在繼承之內,也可以傳遞,他可以傳遞任何類型。
?這時就能傳遞通配符
?也表示不確定的類型,它可以進行類型的限定
?extends E:表示可以傳遞E或者E所有的子類類型
?super E:表示可以傳遞E或者E所有的父類類型
只傳問號時,和上面代碼一個意思,也可以傳遞D:
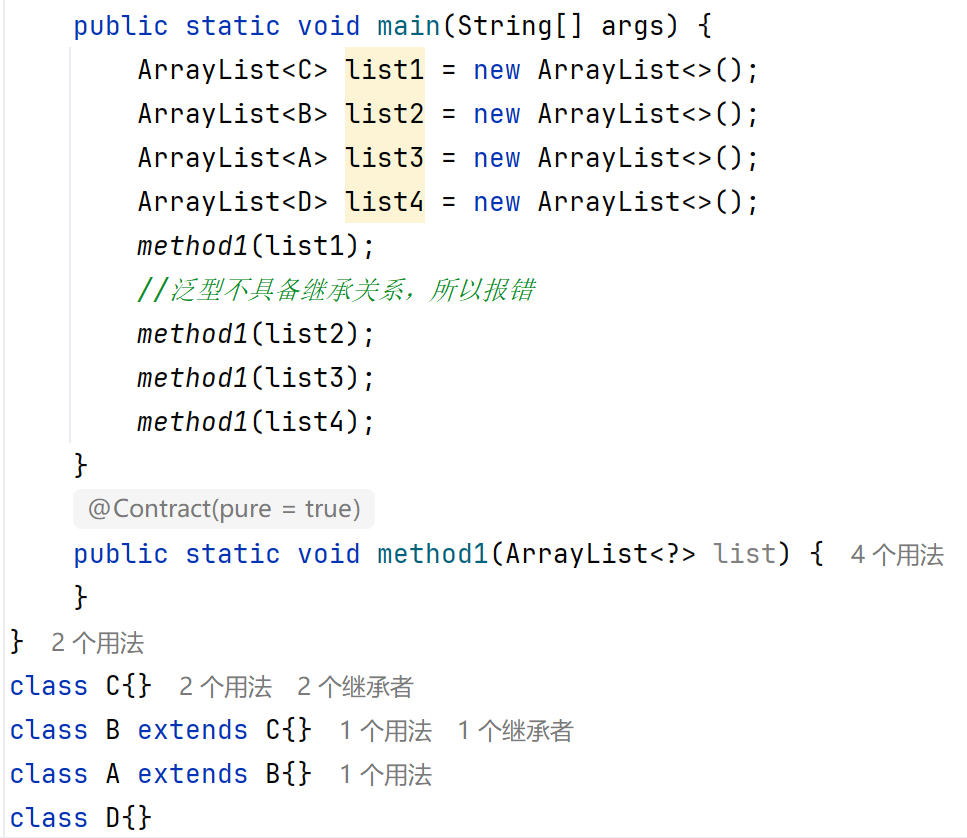
其他兩種情況
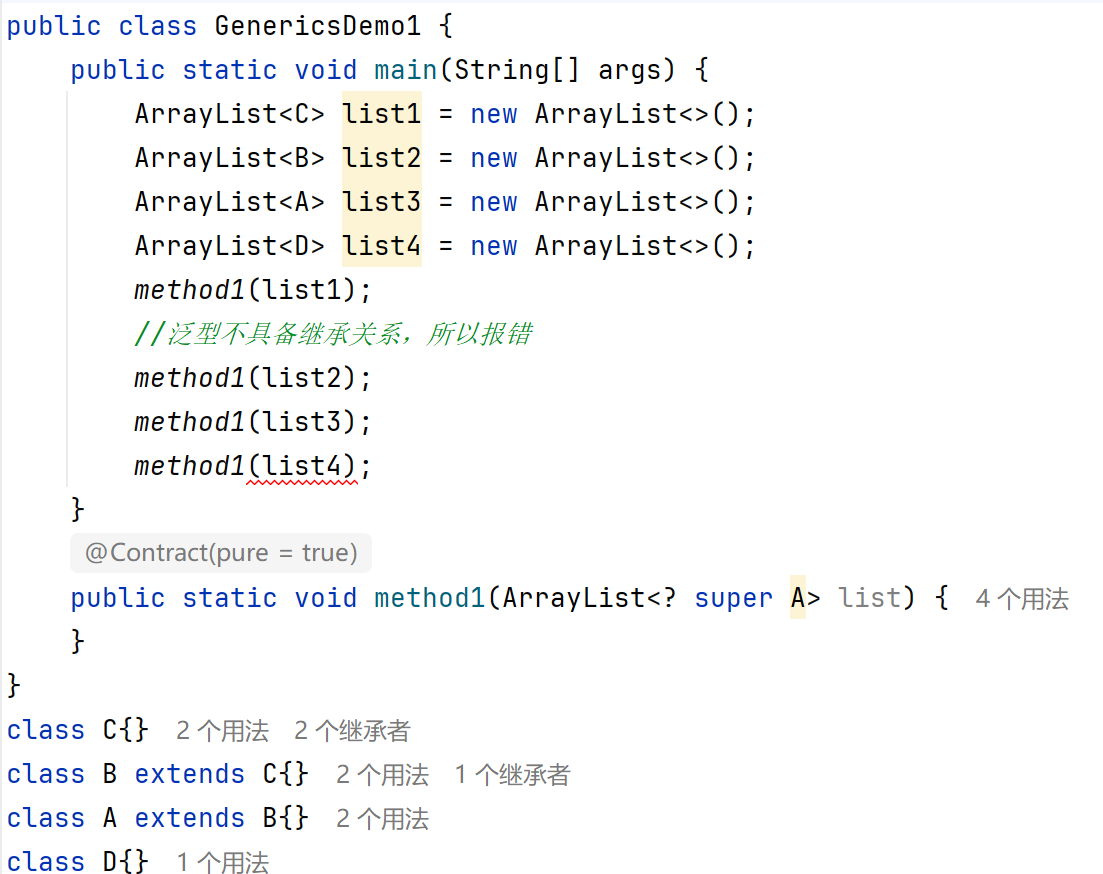
Vector已經被淘汰了,就不講了。
Set集合
Set接口的方法上基本上與Collection的API一致
特點:
無序:存取順序不一致,假如存是1234,那么取就可能是2431、1342等等。
不重復:可以去除重復。
無索引:沒有帶索引的方法,不能使用普通for循環遍歷,也不能通過索引來獲取元素。
只可以通過迭代器遍歷、增強for遍歷、Lambda表達式遍歷

實現類
HashSet:無序、不重復、無索引
LinkedHashSet:有序、不重復、無索引
TreeSet:可排序、不重復、無索引
示例Set接口繼承Collection接口中的方法

HashSet實現類
HashSet集合底層采取哈希表存儲數據;哈希表是一種對于增刪改查數據性能都較好的結構。
哈希表的組成:JDK8之前:數組+鏈表;JDK8之后:數組+鏈表+紅黑樹
哈希值
1、根據hashCode方法算出來的int類型的整數
2、該方法定義在Object類中,所有對象都可以調用,默認使用地址值進行計算
3、一般情況下,會重寫hashCode方法,利用對象內部的屬性值計算哈希值
對象的哈希值特點
1、如果沒有重寫hashCode方法,不同對象計算出的哈希值是不同的
2、如果已經重寫hashcode方法,不同的對象只要屬性值相同,計算出的哈希值就是一樣的
3、在小部分情況下,不同的屬性值或者不同的地址值計算出來的哈希值也有可能一樣。(哈希碰撞)
Alt+Insert鍵系統自動重寫hashCode(),equals()兩個方法。
底層原理
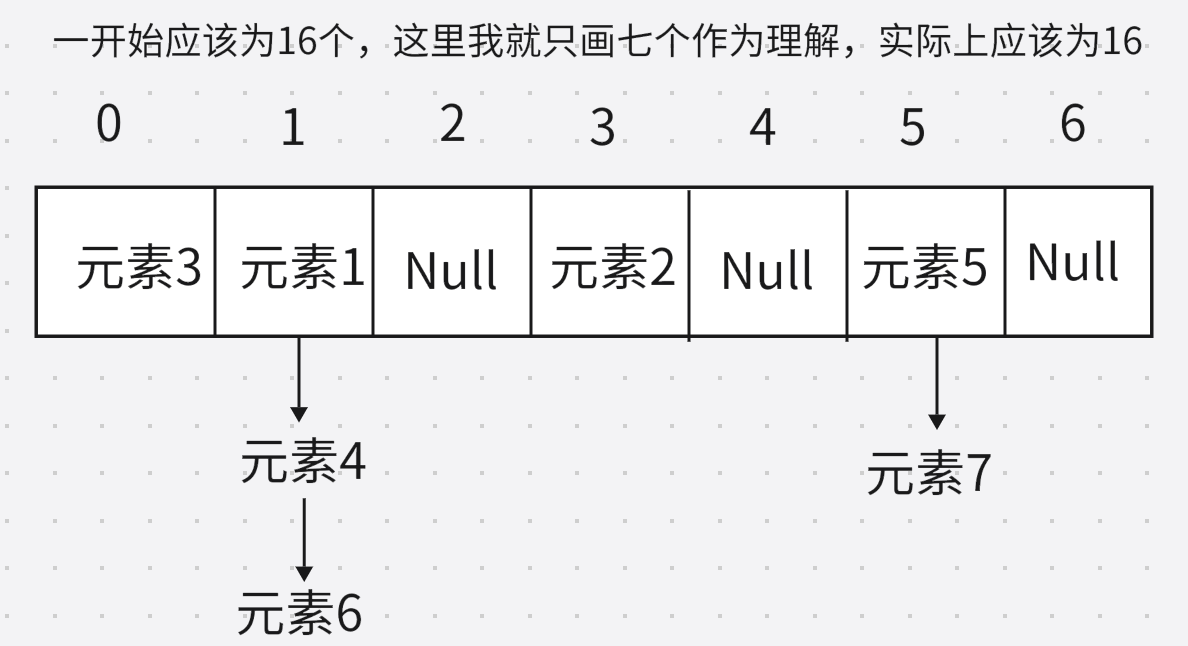
1、創建一個默認長度為16,默認加載因子0.75的數組,數組名table(HashSet<String> set = new HashSet<>();)
2、根據元素的哈希值跟數組的長度計算出應存入的位置(int index=(數組長度-1)&哈希值)
3、判斷當前位置是否為null,如果是null直接存入
4、如果位置不為null,表示有元素,則調用equals方法比較屬性值
5、一樣時不存? ?不一樣時存入數組,形成鏈表
JDK8以前:新元素存入數組,老元素掛在新元素下面
JDK8以后:新元素直接掛在老元素下面
解釋:當存入16*0.75=12個元素時,數組會自動擴容為兩倍16->32。當鏈表長度大于8并且數組長度大于等于64,那么當前長度大于8的鏈表會自動轉為紅黑樹。
如果集合中存儲的時自定義對象(比如Student、Teacher,因為這樣才能保證去重,重寫方法按照屬性值來判斷是否重復,如果按照地址值的話,無法保證去重;String、Integer在java底層已經重寫好了,我們直接用就可以),必須要重寫hasCode和equals方法。
?HashSet為什么存和取順序不一樣?
會從0索引開始,一個一個進行遍歷,如果有索引中有鏈表,會把鏈表遍歷結束,再開始下一個索引。
?HashSet為什么沒有索引?
因為是數組+鏈表+紅黑樹混合組成。
HashSet是利用什么機制保證數據去重的?
利用hashCode方法與equals方法保證的
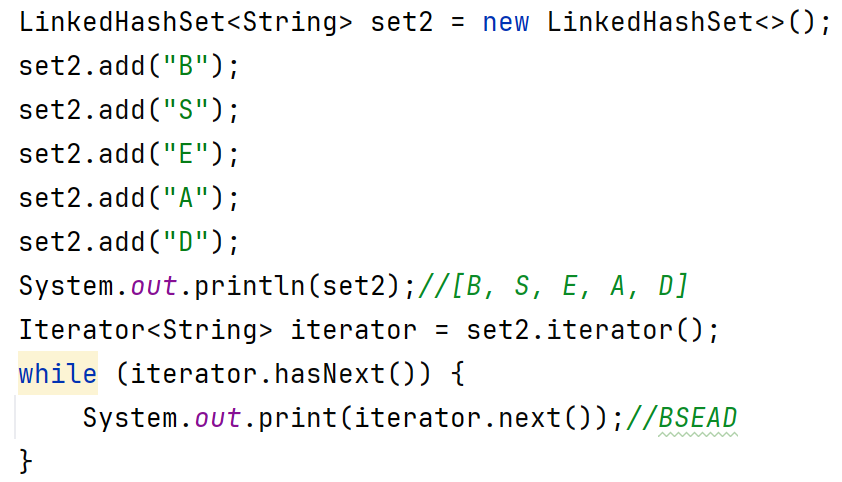
LinkedHashSet底層原理
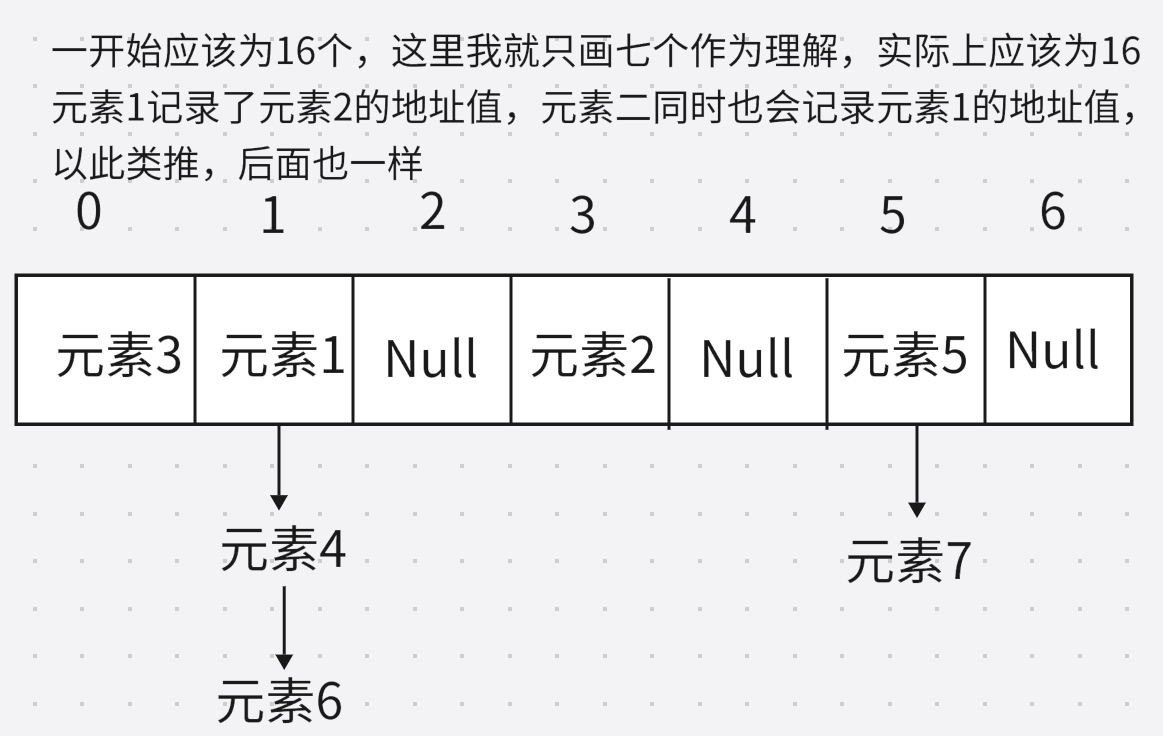
有序:保證存儲和取出的元素順序一致。
原理:底層依然是哈希表,只是每個元素又額外的多了一個雙鏈表的機制記錄存儲的順序。
?TreeSet
?可排序:默認從小到大排序。
TreeSet底層基于紅黑樹的數據結構實現排序的,增刪改查性能都較好。
對于數值類型:Integer、Double等,默認從小到大排列
對于字符、字符串類型:按照字符在ASCll碼表中的數字升序排列。
?字符串里面內容比較多,從首字母的ASCll值開始挨個比較(一樣時比較第二個),和字符長度無關。
對于自定義類型:
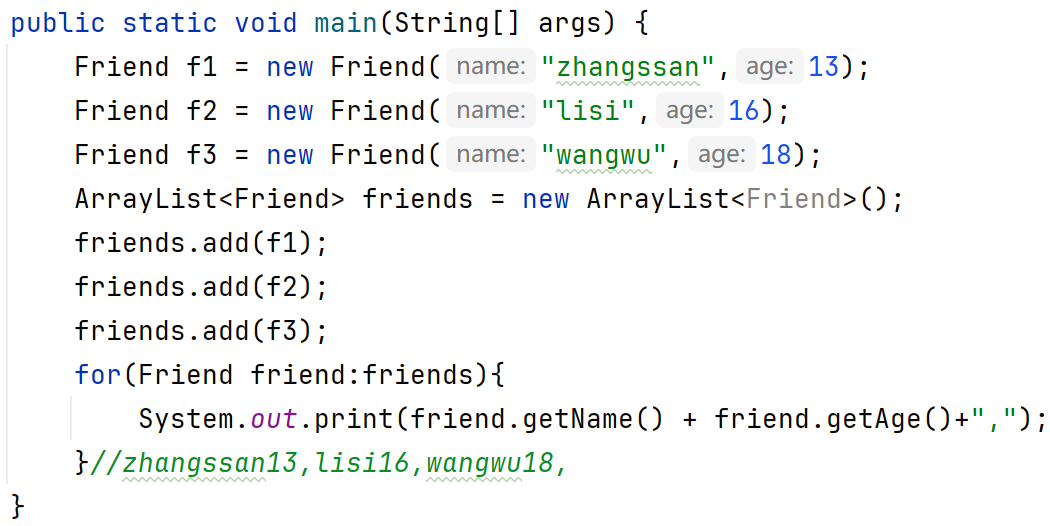
方式一:默認排序/自然排序:Javabean類實現Comparable接口指定比較規則
重寫compareTo方法的o表示當前紅黑樹的根節點對象,this表示要插入的對象。如果年齡小插左邊發現已經又對象了,那么底層會繼續調用compareTo方法,以此類推,如果添加進去發現不滿足紅黑樹,那么會按照紅黑樹規則來調整成紅黑樹。


 ?
?
方式二:比較器排序:創建TreeSet對象時,傳遞比較器Comparator指定規則。
使用規則:默認使用方式一,如果方式一不滿足需求,那么才會使用方式二。(比如像String與Integer這兩個類像重寫排序規則)(如果方式一與方式二同時存在,系統會用方式二)

?應用場景
1. 如果想要集合中的元素可重復:用ArrayList集合,基于數組的。(用的最多)
2. 如果想要集合中的元素可重復,而且當前的增刪操作明顯多于查詢:用LinkedList集合,基于鏈表的。
3. 如果想對集合中的元素去重:用HashSet集合,基于哈希表的。(用的最多)
4. 如果想對集合中的元素去重,而且保證存取順序:用LinkedHashSet集合,基于哈希表和雙鏈表,效率低于HashSet。
5. 如果想對集合中的元素進行排序:用TreeSet集臺,基于紅黑樹。


)







:單機模式部署與基礎操作詳解)

教程:從加載到球面映射)


)



