第三四章 基本圖形生成算法

圖形生成

概念：如何在指定的輸出設備上，根據坐標描述，構造基本二維幾何圖形

基本二維幾何圖形：點、直線、圓、多邊形域、字符串及相關屬性等。

圖形生成的概念

是在指定的輸出設備上，根據坐標描述構造二維幾何圖形。

圖形的掃描轉換：在光柵顯示器等數字設備上，確定一個醉駕逼近于圖形的像素集的過程。

光柵化

光柵就是德語中屏幕的意思，光柵化就是把圖形畫在屏幕上的過程，即將幾何圖形轉化為像素化圖像的過程。

基本過程：

1. 確定最佳逼近圖形的像素集合。
2. 用圖形的顏色或其它屬性，按照掃描順序，對像素進行某種寫操作，完成圖形在屏幕上的顯示。

直線段和圓的光柵化

直線段和圓是最基本的圖形元素，包括以下幾種算法：

直線光柵化算法：DDA算法、Bresenham算法

圓光柵化算法：Bresenham畫圓算法、中點算法、中點整數算法、中點整數優化算法。

直線的光柵化算法

要求：直、精確的起始點、亮度顏色均勻且沿直線不變，與直線長度、方向無關、快。

DDA算法

David F.Rogers的描述（適用于所有象限）

步驟如下：

1. 如果已知第$i$點的坐標，利用步長$StepX$和$StepY$，得到第$i+1$點的坐標，$i+1$點的坐標為：

$$x_{i+1}=x_i+StepX{y}_{i+1}=y_i+K?StepX$$

1. 如圖所示，$K<1,StepX=1，StepY=k$，將直線上每個點的坐標四舍五入，得到光柵點的位置：

   

James D.Foley的描述（只適用于第一象限，且K<1）

令：

$$k=\frac{y_2?y_1}{x_2?x_1}$$

有：

$$y_{i+1}=y_i+k?StepX$$

若$0<k<1$，則$△x>△y$。

因為光柵單位為1，每次$x$方向增加1，y方向增加k，得到下一個直線點。

現有算法描述分析

Rogers：

采用$x_{i+1}=x_i+StepX{y}_{i+1}=y_i+K?StepX$，逼近點并不是直線最好的逼近

D.Foley：可能引起累積誤差

未分析直線端點不在像素點的情況，且只給出$0°$-$45°$的第一卦限的情況。

每次步長為一個單位，減少累積誤差。

本教程描述——任意方向插補算法

if (fabs(dy)<fabs(dx)) {     //X方向長 ， 斜率 <=1Length=abs(Round(xe)-Round(xs));Flag=1; //最大的插補長度和方向標記ix= Round(xs); //初始 X點idx=isign(dx); //X方向單位增量y= ys+dy/dx*((float)(ix)-xs); //初始 Y點修正dy=dy/fabs(dx); //Y方向斜率增量
}else { // Y方向長 ， 斜率 >1Length=abs(Round(ye)-Round(ys));Flag=0;iy= Round(ys); //初始 Y點idy=isign(dy); //Y方向單位增量x= xs+dx/dy*((float)(iy)-ys); //初始 X點修正dx=dx/fabs(dy); //X方向斜率增量
}

Bresenham算法

Bresenham算法：

從另一個角度看直線光柵化顯示算法的原理：由直線的斜率確定選擇在$x$方向或$y$方向上每次遞增1個單位，另一變量遞增量為0或1，取決于實際直線與網格點的距離，四舍五入。

1. 基本原理

   假定直線斜率k在$0$-$1$之間，此時，$x$方向每次遞增一個單位，決定$y$方向每次遞增0或1。

   (斜率大于1，y每次遞增1，小于1，x每次遞增1）

   假設：當前點為$(x_i,y)$，當前光柵點為$(x_i,y_i)$

   則下一點為： ( x i + 1 , y + k ) , k ∈ { 0 , 1 } (x_i+1,y+k),k\in\{0,1\} (xi?+1,y+k),k∈{0,1}

   

   記直線與它垂直方向最近的下光柵點誤差為$d$。

   當$d<0.5$：下一像素點為$(x_i+1,y_i)$

   當$d>0.5$：下一像素點為$(x_i+1,y_i+1)$

1. 對bresenham的簡化

   令$e=d?0.5$，關于d的判別式和初值可簡化成：

   $e<0$：取$(x_i+1,y_i)$

   $e>0$：取$(x_i+1,y_i+1)$，$e=e?1$

2. 整數Bresenham算法

   上述Bresenham算法在計算直線斜率和誤差項時需要浮點運算和除法，采用整數算術運算和避免除法可以加快算法速度。

   只需作以下變換：

   初值：

   $$Error=△y/△x?0.5$$

   經過簡單變換：

   $$NError=2?Error?△x=2△y?△x$$

   便得到了整數算法。

3. 一般Bresenham算法

   為了使第一卦限的Bresenham算法適用于一般直線，進行如下改造：

   1. 當直線斜率$|k|>1$時，改為y的增量總為1，判斷$x$是否需要增加1
   2. $x$或$y$的增量可能是1或-1，視直線所在象限決定。

圓光柵化算法

簡單方程方法

圓的極坐標方程為：

$$\begin{gathered} x=R\cos \theta \\ y=R\sin \theta \end{gathered}$$

每次給 $\theta$ $\theta$${\theta }_{i+1}={\theta }_i+△\theta$

那么：

$$\begin{gathered} x_{i+1}=round(R\cos {\theta }_{i+1}) \\ {y}_{i+1}=round(R\sin {\theta }_{i+1}) \end{gathered}$$

利用圓的八方對稱畫圓

Bresenham畫圓算法

以圓心為坐標原點，建立局部坐標系

先考慮第一象限的八分之一圓弧：

設$P_{i?1}(x_{i?1},y_{i?1})$為已確定的逼近像素點

當$x_i=x_{i?1}+1$時，要決定$y_i$的取值

令$E(\frac{R}{\sqrt{2}},\frac{R}{\sqrt{2}})$

$$\begin{gathered} D(S_i)=[(x_{i?1}+1{)}^2+y_{i?1}^2]?R^2 \\ D(T_i)=[(x_{i?1}+1{)}^2+(y_{i?1}?1{)}^2]?R^2 \end{gathered}$$

若$|D(S_i)|\ge |D(T_I)|$,則$T_i$比$S_i$更接近實際的圓弧， 應選$T_i$
反之，選擇$S_i$。

令$d_i=|D(S_i)|?|D(T_i)|$

于是，$d_i\ge 0$時，選$T_i$，反之，選擇$S_i$。

分析情況ABCDE，可以將$d_i$改寫為：

$$\begin{array}{rl}{d}_i=& D(S_i)+D(T_i)\\ =& [(x_{i?1}+1{)}^2+y_{i?1}^2]?R^2+[(x_{i?1}+1{)}^2+(y_{i?1}?1{)}^2]?R^2\end{array}\text{\hspace{1em}?}$$

用$i+1$代替上式中的$i$，得：

$$\begin{array}{rl}{d}_{i+1}=& [(x_i+1{)}^2+y_i^2]?R^2+[(x_i+1{)}^2+(y_i?1{)}^2]?R^2\end{array}\text{\hspace{1em}?}$$

用$d_{i+1}?d_i$，得：

$$d_{i+1}?d_i=2[(x_i+1{)}^2?(x_{i?1}+1{)}^2]+(y_i^2?y_{i?1}^2)+(y_i?1{)}^2?(y_{i?1}?1{)}^2$$

改進：

若$d_i\ge 0,$選$T_i$，此時：

$$\begin{gathered} x_i=x_{i?1}+1 \\ {y}_i=y_{i?1}?1 \\ {d}_{i+1}=d_i+4(x_{i?1}?y_{i?1})+10 \end{gathered}$$

反之，選$S_i$，此時

$$\begin{gathered} x_i=x_{i?1}+1 \\ {y}_i=y_{i?1} \\ {d}_{i+1}=d_i+4x_{i?1}+6 \end{gathered}$$

$d_i$的初值$d_1$可以由$(1)$求出，將$i=1,x_0=0,y_0=R$帶入，得：

$$d_1=3?2R$$

顯然，改進方法的計算量更小，效率高。

中點圓算法

設$d$為點$p(x,y)$到圓心的距離，有：

$$d=F(x,y)=x^2+y^2?R^2$$

以圓的下 2個可選像素 中點的函數值 d的符號 決定選擇 2個可選像素 T和 B中哪一個更接近圓而作為圓的顯示點 ：

$$d_M=F(x_M,y_M)=F(x_p+1,y_p?0.5)=(x_p+1{)}^2+(y_p?0.5{)}^2?R^2$$

如果$d_M\le 0$，表示下一個中點M在圓內，用T逼近，得：

$$\begin{gathered} d_{MT}=F(x_{MT},y_{MT})=F(x_p+2,y_p?0.5)=(x_p+2{)}^2+(y_p?0.5{)}^2?R^2 \\ △d_{MT}=d_{MT}?d_M=2x_p+3 \end{gathered}$$

反之，表示下一中點M在園外，用B逼近，得：

$$\begin{gathered} d_{MB}=F(x_{MB},y_{MB})=F(x_p+2,y_p?1.5) \\ △d_{MB}=d_{MB}?d_M=2x_p?2y_p+5 \end{gathered}$$

綜上，中點圓算法為：

根據中點d的值，決定顯示的光柵點，更新$△d$$(△d_{MT}或{△}_{MB})$，更新d。

初值

由$x_0=0,y_0=R$
得$x_{M0}=0+1=1,y_{M0}=R?0.5$
$d_{M0}=F(x_{M0},y_{M0})=1.25?R$

中點圓整數算法

為了將其改造為整數計算，定義新變量：$D=d?0.25$
判別式$d<0$等價于$D<?0.25$
在D為整數的情況下，$D<?0.25$等價于$D<0$
仍將D寫為d（新的初值$d=1?radius$)，可得到中點圓整數算法

橢圓光柵化算法

設橢圓方程為：

$$F(x,y)=b^2{x}^2+a^2{y}^2?a^2{b}^2=0$$

該橢圓上一點$(x,y)$處的法向量為：

$$N(x,y)=\frac{?F}{?x}i+\frac{?F}{?y}j=2b^{2}xi+2a^{2}yj$$

在上半部分，法向量y的分量更大而在下部分, 法向量的x分量更大, 因而, 在上部分若當前最佳逼近理想橢圓弧的像素(xP,yP)滿足下列不等式：

$$b^2(x_p+1)<a^2(y_p?0.5)$$

在上半部分，假設橫坐標為$x_p$的像素中，與橢圓弧更接近的點是$(x_p,y_p)$,那么下一對候選像素的中點為$(x_p+1,y_p?0.5)$,判別式為：

$$d_1=F(x_p+1,y_p?0.5)=b^2(x_p+1{)}^2+a^2(y_p?0.5{)}^2?a^2{b}^2$$

若$d_1<0$，中點在橢圓內，則取正右方像素，判別式更新：

$$d_1^{,}=F(x_p+2,y_p?0.5)$$

若$d_1\ge 0$，中點在橢圓外，此時取右下方像素，更新判別式：

$$d_1^{\prime }=F(x_p+2,y_p?1.5)$$

由于弧的起點為$(0,b)$，第一中點為$(1,b?0.5)$,對應判別式為：

$$d_{10}=F(1,b?0.5)$$

**在下部分，**改為從正下方和右下方兩個像素選擇下一像素，計算與上半部分類似。

基本多邊形掃描轉換與區域填充

多邊形的掃描轉換，主要通過確定穿越區域的掃描線覆蓋區間來填充。

區域填充是從給定的位置開始涂描，直到指定的邊界條件為止。

多邊形的掃描轉換

頂點表示：用多邊形的頂點序列刻畫多邊形。

點陣表示：用位于多邊形內的像素集合來刻畫多邊形。

掃描轉換多邊形：從多邊形的頂點信息出發，求出位于其內部的各個像素，并將顏色值寫入幀緩存中相應單元的過程。

基本問題有：

1. 如何判斷一個點是否位于多邊形區域內？

   點在多邊形內的包含性檢驗方法：檢驗夾角之和、射線法檢驗交點數。

轉角法：若夾角和為0，則點$p$在多邊形外；若夾角和為360，則點$p$在多邊形內。

射線法：交點數為偶數，點在多邊形外；交點數為奇數，點在多邊形之內。

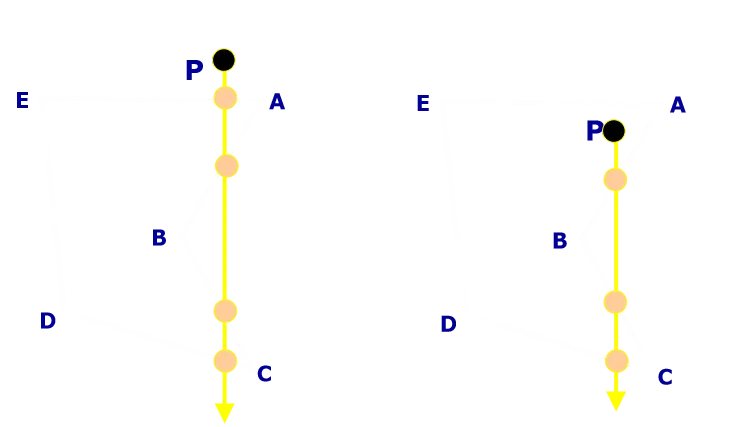
1. 逐點測試效率太低

采用包圍盒法：對凸多邊形效果好，但凹多邊形效率仍然低下。

掃描線填充算法：

掃描線填充算法：按掃描線順序，測試點的連貫性。

種子填充算法：從內部一個種子點出發，測試點的連貫性。

X-掃描線算法

基本思想：

按掃描線順序，計算掃描線與多邊形的相交區間；再用要求的顏色顯示區間的所有像素。

算法步驟：

1. 確定多邊形所占有的最大掃描線數，得到多邊形頂點的最小、最大$y$值$(y_{min}和y_{max})$。
2. 從$y=y_{min}$到$y=y_{max}$，每次用一條掃描線進行填充。
3. 對一條掃描線填充的過程分為四個步驟：求交、排序、交點配對、區間填色。

取整規則

交點的取整規則：使生成的像素全部位于多邊形之內。

為什么不采用四舍五入的規則？四舍五入可能導致部分像素位于多邊形之外，從而不可用。

假定非水平邊和掃描線y=e相交，交點橫坐標為$x$，規則如下：

1. $x$為小數，即交點落在掃描線上兩個相鄰像素間時：

   1. 交點位于左邊界上，向右取整。

   2. 交點位于右邊界上，向左取整。

      

2. 邊界上像素的取舍：為了避免填充擴大化，規定落在右邊邊界上的像素不予填充。

   • 具體實現時，對掃描線與多邊形相交區間左閉右開。

     

3. 當掃描線與多邊形頂點相交時：交點的取舍，保證交點正確配對。

   • 交點配對：當掃描線與多邊形的頂點相交時：

     • 若共享頂點的兩條邊落在掃描線兩邊，交點只算一個。
     • 若共享頂點的兩條邊落在掃描線同一邊，交點作為零或兩個。

   • 實際處理中，只要檢查頂點的兩條邊的另外兩個端點的Y值，兩個Y值中，大于交點Y值的個數為0\1\2，來決定取0\1\2個交點。

     

改進的有效邊表算法（Y連貫性算法）

改進原理：

• 處理一條掃描線時，僅對有效邊求交。
• 利用掃描線的連貫性。
• 利用多邊形邊的連貫性。

有效邊：與當前掃描線相交的多邊形的邊，也稱為活性邊。
有效邊表：把有效邊按與掃描線交點x坐標遞增的順序存放在一個鏈表中，此鏈表稱為有效邊表。

有效邊表中，每個結點的存儲方式：

$$x{|}_{y_{min}}{y}_{max}\frac{1}{k}next$$

構造邊表：

1. 首先構造一個縱向鏈表，鏈表的長度為多邊形所占有的最大掃描線數，鏈表的每個結點，稱為一個桶，對應多邊形覆蓋的每一條掃描線。

2. 將每條邊的信息鏈入與該邊最小y坐標（$y_{min}$ ）相對應的桶處。
   (也就是說，若某邊的較低端點為$y_{min}$，則該邊放在相應的掃描線桶中。）

3. 每條數據邊形成一個結點，內容包括：

   1. 掃描線與該邊的初始交點x（較低端點的x值）
   2. $\frac{1}{k}$
   3. 該邊的最大$y$值$y_{max}$

4. 同一桶中，若干條邊按$x$由小到大排序，若相等，按照$\frac{1}{k}$由小到大排序。

   

算法步驟：

1. 初始化：構造邊表，AET表置空。
2. 將第一個不空的ET表中的邊與AET表合并。
3. 由AET表中取出交點對進行填充。填充之后刪除$y=y_{max}$的邊。
4. $y_{i+1}=y_i+1$,根據$x_{i+1}=x_i+1/k$計算并修改AET表，同時合并ET表中$y=y_i+1$桶中的邊，按次序插入到AET表中，形成新的AET表。
5. AET表不為空則轉到3，否則end。

邊緣填充算法

基本思想：按任意順序，處理多邊形的每條邊。

處理時，先求出該邊與掃描線的交點，再對掃描線上交點右方的所有像素取反。

算法簡單，但對于復雜圖形，每一個像素可能被訪問多次。

柵欄填充算法

柵欄指的是一條過多邊形頂點且與掃描線垂直的直線。它把多邊形分為兩半。

基本思想：按任意順序處理多邊形的每一條邊，但處理每條邊與掃描線的交點時，將交點與柵欄之間的像素取反。
這種算法盡管減少了被重復訪問像素的數目，但仍有一些像素被重復訪問。

邊界標志算法

基本思想：先用特殊的顏色在幀緩存中將多邊形的邊界勾畫出來，然后將著色的像素點依 x 坐標遞增的順序配對，再把每一對像素構成的區間置為填充色。
分為兩個步驟：打標記-多邊形掃描轉化（利用直線的掃描轉換實現），填充。

當用軟件實現本算法時，速度與改進的有效邊表算法相當，但本算法用硬件實現后速度會有很大提高

區域填充

基本概念：從區域內的某一個像素點（種子點）開始，由內向外將填充色擴展到整個區域內的過程
區域：已經表示成點陣形式的填充圖形，它是相互連通的一組像素的集合。

邊界表示法：把位于給定區域的邊界上的像素一一列舉出來的方法。
邊界表示法中，由于邊界由特殊顏色指定，填充算法可以逐個像素地向外處理，直到遇到邊界顏色為止，這種方法稱為邊界填充算法。

內點表示法：枚舉出給定區域內所有像素的表示方法。

以內點表示法為基礎的區域填充算法稱為泛填充算法。

4連通區域、8連通區域：

連通性：4連通可看作8連通區域，但對邊界有要求。

邊界填充算法

算法的輸入：種子點坐標(x,y)，填充色以及邊界顏色。

利用堆棧實現簡單的種子填充算法。

• 算法從種子點開始檢測相鄰位置是否是邊界顏色。
• 若不是就用填充色著色。
• 檢測該像素點的相鄰位置。
• 直到檢測完區域邊界顏色范圍內的所有像素為止。

特點：

• 可以用于填充帶有內孔的平面區域。
• 把太多的像素壓入堆棧，降低了效率，同時需要較大的存儲空間。
• 遞歸執行，算法簡單，但效率不高，區域內每一像素都引起一次遞歸，進/出棧費時費內存。
• 通過沿掃描線填充水平像素段，來代替處理4-鄰接點和8-鄰接點。

掃描線種子算法

掃描線通過在任意不間斷掃描線區間中只取一個種子像素的方法使堆棧的尺寸極小化。
不間斷區間是指在一條掃描線上的一組相鄰像素。

基本過程：當給定種子點時，首先填充種子點所在的掃描線上的位于給定區域的一個區段，然后確定與這一區段相通的上下兩條掃描線上位于給定區域內的區段，并依次保存下來，重復以上過程。

算法步驟：在任意一個掃描線與多邊形的相交區間中, 只取一個種子像素, 并將種子像素入棧, 當棧非空時作如下四步操作:

1. 棧頂像素出棧
2. 沿掃描線對出棧像素的左右像素進行填充, 直至遇到邊界像素為止, 也就是對包含出棧像素的整個區間進行填充
3. 上述區間內最左最右的像素分別記為xl和xr
4. 在區間［xl, xr］中檢查與當前掃描線相鄰的上下兩條掃描線的有關像素是否全為邊界像素或已填充的像素, 若存在非邊界、 非填充的像素, 則把每一區間的最右像素入棧。

字符處理

ASCII碼：“美國信息交換用標準代碼集”(American Standard Code for Information Interchange)

國際碼：“中華人民共和國國家標準信息交換編碼，簡稱為國際碼，代號GB2312－80

字庫：字庫中儲存了每個字符的圖形信息

點陣字符

在點陣表示中，每個字符由一個點陣位圖來表示，顯示時，形成字符的像素圖案。

特點： 定義和顯示直接、簡單、存儲需要耗費大量空間。

改進：從一組點陣字符生成不同尺寸和不同字體的其他字符、采用壓縮技術。

矢量字符

矢量字符采用直線和曲線段來描述字符形狀，矢量字符庫中記錄的是筆劃信息；顯示時：解釋字符的每個筆劃信息。

輪廓字型法采用直線或二、三次曲線的集合來描述一個字符的輪廓線，輪廓線構成了一個或若干個封閉區域，顯示時只要填充這些區域就可產生相應的字符

• 顯示時可以“無極放縮”
• 占用空間少，美觀，變換方便

屬性處理

圖素或圖段的外觀由其屬性決定。

圖形軟件中實現屬性選擇的方法是提供一張系統當前屬性值表，通過調用標準函數提供屬性值表的設置和修改。進行掃描轉換時，系統使用屬性值表中的當前屬性值進行顯示和輸出。

線寬

線刷子：垂直刷子、水平刷子

線刷子特點：

• 實現簡單、效率高
• 斜線與水平(或垂直)線不一樣粗
• 當線寬為偶數個像素時，線的中心將偏移半個像素
• 利用線刷子生成線的始末端總是水平或垂直的，看起來不太自然

解決方法：添加線帽

方帽：調整端點位置，使粗線的顯示具有垂直于線段路徑的正方形端點。

凸方帽：簡單將線向兩頭延伸一半線寬并添加方帽。

圓帽：通過對每個方帽添加一個填充的半圓得到。

當比較接近水平的線與比較接近垂直的線匯合時，匯合處外角將有缺口。

解決方法：斜角連接、圓角連接、斜切連接。

方刷子：

方刷子繪制的線條（斜線）比用線刷子所繪制的線條要粗一些，斜線與水平（或垂直）線不一樣粗。線條自然地帶有一個“方線帽”。

利用像素模板進行線寬處理：

用等距線方法:
線寬均勻、端口處與邊垂直、生成的圖形質量高。

線型

用位屏蔽器實現

位屏蔽器中每一位對應的是一個像素，而不是單位長度，不能滿足要求
線型中的筆劃長度與直線長度有關
斜線筆劃長度比水平或垂直線筆劃長
對工程圖，這種變化是不允許的，不符合國標規定

用像素段方法實現：針對不同的線型，畫線程序沿路徑輸出一些連續像素段，在每兩個實心段之間有一段中間空白段，他們的長度（像素數目）可用像素模板(pixel mask)指定
如何保證任何方向的劃線長度近似相等呢？

• 可根據線的斜率來調整實心段和中間空白段的像素數目。

曲線的線性和線寬

采用像素模板的方法對圓的線型處理：

• 從一個八分象限轉入下一個八分象限時要交換像素的位置，以保持劃線長度近似相等。
• 在沿圓周移動時調整畫每根劃線的像素數目以保證劃線長度近似相等。
• 改進：采用沿等角弧畫像素代替用等長區間的像素模板來生成等長劃線。

曲線的線寬

線刷子：經過曲線斜率為1和-1處，必須切換刷子
（曲線接近水平與垂直的地方，線條更粗）

方刷子：接近水平垂直的地方，線條更細
（要顯示一致的曲線寬度可通過旋轉刷子方向以使其在沿曲線移動時與斜率方向一致）

圓弧刷子：采用填充方法

區域填充屬性

區域填充屬性選擇包括顏色、圖案和透明度。

確定區域與模板之間的位置關系（對齊方式）

反走樣

用離散量表示連續量引起的失真，就叫做走樣。

產生原因：數學意義上的圖形是由無限多個連續的、面積為零的點構成；
光柵顯示器上，用有限多個離散的，具有一定面積的像素來近似地表示他們

走樣現象：

1. 光柵圖形產生的階梯形
2. 圖形中包含相對微小的物體時

用于減少或消除這種效果的技術，稱為反走樣

簡單的方法：過取樣（后濾波）、區域取樣（前濾波）

分辨率提高一倍，階梯程度減小一倍

過取樣

在高于顯示分辨率的較高分辨率下用點取樣方法計算，然后對幾個像素的屬性進行平均得到較低分辨率下的像素屬性。

簡單過取樣：在x，y方向把分辨率都提高一倍，使每個像素對應4個子像素，然后掃描轉換求得各子像素的顏色亮度，再對4個像素的顏色亮度進行平均，得到較低分辨率下的像素顏色亮度。。

重疊過取樣

為了得到更好的效果，在對一個像素點進行著色處理時，不僅僅只對其本身的子像素進行采樣，同時對其周圍的多個像素的子像素進行采樣，來計算該點的顏色屬性

基于加權模板的過取樣

前面在確定像素的亮度時，僅僅是對所有子像素的亮度進行簡單的平均。更常見的做法是給接近像素中心的子像素賦予較大的權值，即對所有子像素的亮度進行加權平均。

簡單的區域取樣

在整個像素區域內進行采樣，這種技術稱為區域取樣。

由于像素的亮度是作為一個整體被確定的，不需要劃分子像素，故也被稱為前置濾波。

如何計算直線段與像素相交區域的面積？

1. 將屏幕像素分割成n個更小的子像素
2. 計算中心落在直線段內的子像素的個數m
3. m/n為線段與像素相交區域面積的近似值。

在過取樣中，我們對所有子像素的亮度進行簡單平均或加權平均來確定像素的亮度。

在區域取樣中，我們使用覆蓋像素的連續的加權函數（Weighting Function）或濾波函數(Filtering Function)來確定像素的亮度。

將加權函數在整個二維顯示圖形上積分，得到具有一定體積的濾波器（Filter），該濾波器的體積為1
將加權函數在顯示圖形上進行積分，得到濾波器的一個子體，該子體的體積介于0到1之間，用它來表示像素的亮度。

特點：

接近理想直線的像素將被分配更多的灰度值。
相鄰兩個像素的濾波器相交，有利于縮小直線條上相鄰像素的灰度差。