2025年五一數學建模競賽 A題

基于歷史數據與模式識別的道路車流量推測模型研究

摘要

交通擁堵是現代城市面臨的嚴峻挑戰，準確預測道路車流量對于交通管理、信號配時優化和出行規劃至關重要。本文聚焦于利用有限的歷史觀測數據和已知的交通流模式，推測特定路段（包括主路和多個支路）的詳細車流量變化。通過構建和應用多種數學模型，旨在解決不同交通流特征下的車流量推測問題，并探討數據誤差和采樣策略對推測精度的影響。

針對問題一：本文利用線性回歸和分段線性回歸模型，根據支路車流量的線性增長和先增后減趨勢，推測了特定時間段內兩條支路的車流量函數。

針對問題二：本文將模型應用擴展至四條具有不同變化規律（穩定、線性增長、線性減少、周期性）的支路，分別采用常數模型、線性模型和周期函數模型（如正弦函數或傅里葉級數）進行擬合與推測。

針對問題三：本文特別考慮了交通信號燈對車流量的周期性影響，通過模運算分析周期內流量模式，并應用傅里葉級數等周期模型對受信號燈控制的支路車流量進行建模。

針對問題四：本文探討了觀測數據中可能存在的誤差問題，通過分析擬合殘差來評估誤差特性，并提出了數據平滑、魯棒擬合等方法來推測更接近“實際”的車流量。

針對問題五：本文從模型復雜度和信息論角度分析了確定車流量函數所需的最少數據記錄時刻問題，強調了在關鍵特征點（如起止點、極值點、轉折點）進行采樣以及滿足奈奎斯特采樣定理的重要性

最后，本文分析了模型的優缺點，討論了模型的改進方向并對模型進行了簡單的推廣。

一、問題的背景和重述

1.1問題的背景

隨著城市化進程加速和機動車保有量持續增長，交通擁堵已成為制約城市運行效率和影響居民生活質量的普遍問題。精確掌握道路交通流量的時變規律，是實施有效交通管理和控制、優化信號燈配時、提供智能出行誘導服務以及規劃交通基礎設施的基礎。然而，在實際應用中，交通數據的獲取往往受限于監測設備的布設范圍和成本，可能僅能獲得部分路段（如主干道）或匯總性的數據。如何利用這些有限的信息，結合對交通流行為模式的理解，來推測和還原更詳細的路網交通狀態（例如各支路的具體流量），是一個具有重要理論價值和實際應用意義的研究課題。

1.2問題的重述

本文旨在研究如何基于給定的歷史數據和交通流模式描述，建立數學模型以推測道路（特別是支路）的車流量函數。具體研究問題如下：
問題1：已知主路歷史數據和兩條支路的車流量變化趨勢（支路1線性增長，支路2先線性增長后線性減少），推測這兩條支路在特定時間段（6:58至8:58）的車流量函數。
問題2：推測四條具有不同變化規律的支路的車流量函數：支路1穩定，支路2線性增長，支路3線性減少，支路4呈周期性波動。
問題3：在一個受交通信號燈（周期為18個時間單位）影響的特殊路段，推測支路1、2和受控的支路3的車流量函數。
問題4：考慮到監測數據可能存在誤差，如何在包含誤差的數據基礎上，推測“實際”的車流量，并可能描述誤差的特性。
問題5：為了能夠準確推測出上述問題中描述的各種車流量函數，確定最少需要記錄哪些時刻的數據點。

二、問題的分析

本系列問題旨在通過數學建模的方法，解決基于不完全信息和特定模式描述下的交通流量推測問題。核心在于為不同特征的交通流選擇合適的數學函數進行擬合與預測，并考慮實際應用中的復雜因素。
針對問題1：此問題是基礎的函數擬合應用。關鍵在于根據“線性增長”和“先增后減”的描述選擇正確的函數形式（一次多項式和分段一次多項式），并利用（可能需要從主路數據分離出的）支路數據通過最小二乘法估計模型參數。需要進行時間坐標的轉換，并確定分段模型的轉折點。
針對問題2：此問題將模型庫擴展到常數、負斜率線性函數以及周期函數。周期性流量的建模是難點，需要選擇合適的周期函數（如正弦函數或傅里葉級數），并估計其振幅、頻率、相位和均值等參數。可能需要非線性擬合技術或頻譜分析輔助。
針對問題3：此問題引入了外部周期性干擾（交通信號燈）。關鍵在于識別和建模這種由信號燈控制產生的特定周期（18個時間單位）的流量波動模式。可以通過分析時間模周期下的流量分布來選擇合適的周期函數（如傅里葉級數或自定義脈沖函數）進行擬合。
針對問題4：此問題關注數據質量和模型魯棒性。需要分析模型擬合后的殘差（觀測值-擬合值），以判斷誤差的性質（隨機噪聲還是系統偏差）和大小。可以采用數據平滑技術（如移動平均、濾波器）預處理數據，或使用魯棒回歸方法減少異常值的影響，從而得到更可靠的“真實”流量估計。
針對問題5：此問題涉及采樣理論和模型辨識度。最少所需數據點數與模型的自由參數數量相關。理論上k個參數需要至少k個獨立數據點。但為了捕捉函數形態和保證擬合穩健性，需要更多且分布在關鍵位置（如起止點、極值點、趨勢轉折點）的數據。對于周期信號，采樣頻率需滿足奈奎斯特準則以避免混疊。

三、模型假設

1、數據代表性假設： 提供的歷史數據能夠準確反映相應時間段內典型的交通流量變化模式。

2、模式一致性假設： 問題中描述的各支路交通流模式（如線性增長、周期性等）在整個分析時間段內是持續有效的。

3、時間連續性與離散測量假設： 假設交通流量隨時間連續變化（或在宏觀層面可視為連續），但我們獲得的是離散時間點的測量數據。

4、參數恒定性假設： 在所分析的時間段內，描述交通流模式的模型參數（如增長率、周期、振幅等）保持不變。

5、時間坐標轉換假設： 所有涉及的時間點都可以無歧義地轉換為統一的數值時間坐標（例如，從起始時刻計數的分鐘數）用于計算。

6、信號燈影響規律性假設（針對問題3）： 交通信號燈的周期（18個時間單位）是精確的，其對支路3車流量的影響模式在每個周期內是穩定重復的。

四、符號及變量說明

五、模型的建立與求解

問題一：基于線性回歸的支路車流量推測

解題思路：

• 根據支路1的線性增長和支路2的先增后減趨勢，分別建立線性函數和分段線性函數模型。
• 利用主路歷史數據，通過最小二乘法擬合支路車流量函數。
• 確定分段模型的轉折點，并調整參數以保證函數的連續性。

解題過程：

1. 數據可視化，找到支路2的峰值時間點。
2. 分別對支路1和支路2建立線性模型和分段線性模型。
3. 通過假設和啟發式方法確定支路1的增長率和截距。
4. 根據連續性條件，求解支路2的參數。
5. 輸出支路1和支路2的車流量函數表達式，并進行可視化。

問題二：組合流量模型的構建與參數估計

解題思路：

• 構建包含穩定流、線性增長流和周期性流的組合流量模型。
• 考慮支路1和支路2的2分鐘時延，通過非線性優化方法估計所有未知參數。
• 使用遍歷搜索法確定未知轉折點，并優化模型參數。

解題過程：

1. 定義各支路流量模型的形式，包括穩定流、線性增長流和周期性流。
2. 構建總流量模型，考慮支路的時延。
3. 使用非線性優化方法（如lsqnonlin）估計模型參數。
4. 遍歷搜索未知轉折點，找到使誤差最小的轉折點。
5. 輸出各支路流量函數表達式，并進行可視化。

問題三：考慮交通信號燈的復雜流量模型

解題思路：

• 引入交通信號燈的周期性影響，建立考慮信號燈周期性開關效應的流量模型。
• 使用整數參數遍歷搜索與非線性最小二乘相結合的混合優化策略，估計模型參數。
• 考慮支路1和支路2的2分鐘時延，以及支路3受交通燈控制的特性。

解題過程：

1. 定義交通信號燈的狀態函數，確定綠燈和紅燈的時間區間。
2. 構建各支路流量模型，考慮交通信號燈的周期性影響。
3. 使用混合優化策略，遍歷搜索整數參數（如轉折點），并結合非線性優化估計連續參數。
4. 輸出各支路流量函數表達式，并進行可視化。

問題四：考慮數據誤差的流量模型優化

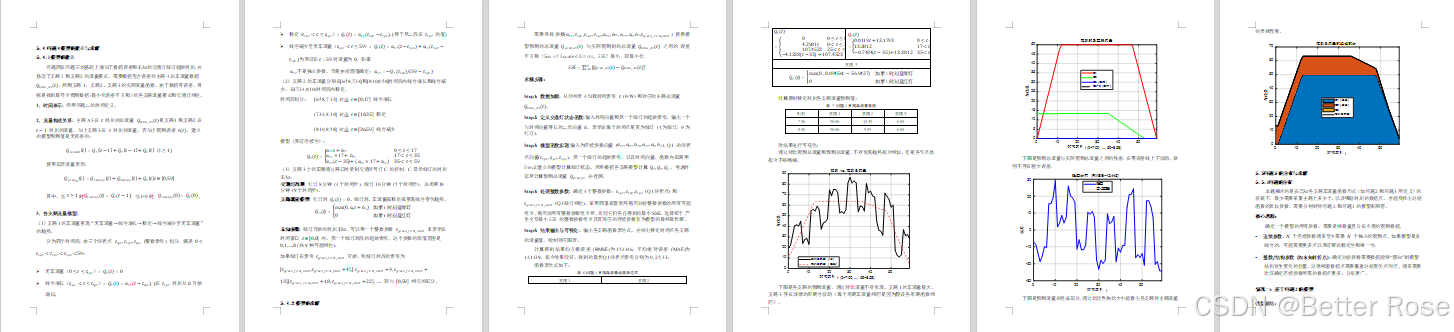
解題思路：

• 在問題三的基礎上，考慮數據誤差和未知的交通燈綠燈起始時刻。
• 引入參數邊界約束、目標函數懲罰項，利用先驗知識改進初始值猜測。
• 使用增強的混合優化算法對數據進行擬合。

解題過程：

1. 定義各支路流量模型，考慮數據誤差和未知的交通燈綠燈起始時刻。
2. 引入參數邊界約束和目標函數懲罰項，優化模型參數。
3. 使用混合優化策略，遍歷搜索整數參數（如轉折點和綠燈起始時刻），并結合非線性優化估計連續參數。
4. 輸出各支路流量函數表達式，并進行可視化。

問題五：最少數據采樣問題分析

解題思路：

• 分析模型參數辨識度，確定各支路流量函數所需的最少數據采樣點。
• 通過理論分析和模擬測試，驗證數據點的分布和數量對模型擬合的影響。

解題過程：

1. 理論分析模型參數與數據點的關系，確定最少數據點需求。
2. 使用代碼測試不同數據子集的擬合效果，逐步減少數據點并觀察誤差變化。
3. 根據誤差閾值，確定最少觀測數據點的數量和具體時刻。

關鍵代碼

完整論文，請看下方