Hello ！朋友們，這是我在學習過程中梳理的筆記，以作以后復習回顧，有時略有潦草，一些話是我用自己的話描述的，可能不夠準確，還是感謝大家的閱讀！

目錄

一、并查集Quickfind

二、兩種算法

1）QuickFind[快查找]

思想：

代碼框架：

2）QuickUnion[快合并]

思想：

基于size的算法優化：元素少的樹，嫁接到元素多的樹

基于rank的算法改進：矮的樹，嫁接到高的樹

路徑壓縮：所有元素都指向根結點

代碼實現步驟：

代碼框架：

---

一、并查集Quickfind

并查集是一種用于處理不相交集合的合并與查詢問題的數據結構。以下是其相關概念：

• 基本操作
  • 合并（Union）：將兩個不相交的集合合并為一個集合。
  • 查找（Find）：確定一個元素屬于哪個集合，通常返回該集合的代表元素。
• 實現原理
  • 并查集通常使用樹結構來實現，每個集合對應一棵樹。樹中的節點代表集合中的元素，根節點作為集合的代表元素。
  • 用一個數組來存儲每個元素的父節點信息，通過不斷查找父節點，最終找到根節點，從而確定元素所屬的集合。
• 路徑壓縮優化：在查找操作中，為了提高效率，可以采用路徑壓縮的優化方法。即在查找元素的根節點時，將路徑上的所有節點直接連接到根節點，這樣下次查找時就可以更快地找到根節點。
• 應用場景
  • 連通性問題：判斷圖中兩個節點是否連通，例如在網絡拓撲中，判斷兩個設備是否通過網絡連接。
  • 最小生成樹：在構建最小生成樹的過程中，用于判斷兩個頂點是否在同一個連通分量中，避免形成環。
  • 集合劃分：將一組元素劃分為不同的不相交集合，例如將一群人按照不同的興趣愛好劃分成不同的小組。

二、兩種算法

并查集有兩種算法，一種是快查找（QuickFind），另一種是快合并（QuickUnion)，兩種都要實現查找和和合并，只不過使用的不同的方法。

1）QuickFind[快查找]

查找效率：O(1)? ? 合并效率：O(N)

思想：

查找：查找兩個數是否在一組，借用索引，看兩個數的ID是否相等

合并：合并兩個組，將第二個組里所有的值的組號改為第一個組的組號

代碼框架：

2）QuickUnion[快合并]

查找效率：O(logN)? ? 合并效率：O(logN)

思想：

查找：查看兩個數是否在一組，看兩個數根ID是不是同一個，相等則是同一個，不等則不是同一組。

合并：不是合并a,b,而是a的根節點和b的根結點進行合并【合并a合并到b，b合并到a都不一定是最好的，所以需要優化算法】（掌握一個就可以）

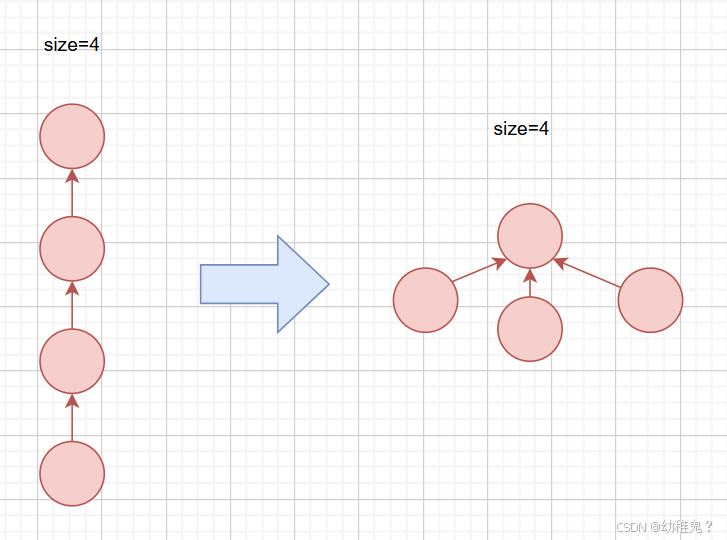
• 基于size的算法優化：元素少的樹，嫁接到元素多的樹

• （目前我是這樣理解的，不知道有沒有錯）

• 基于rank的算法改進：矮的樹，嫁接到高的樹

• 

• 路徑壓縮：所有元素都指向根結點

• 
• 使路徑上的所有結點都指向根結點，從而降低樹的高度

代碼實現步驟：

1、申請空間：根據需要給每個部分都申請出空間

2、初始化：給每個部分賦上初始的值

找索引

找根ID

3、查找：（判斷兩個元素是否在一個集合，返回0，1）判斷兩個元素的根結點是否相同，則需要找到該借點，然后沿著起父節點找到根結點，最后比較根ID的值。

4、合并：

5、釋放空間：

代碼框架：

?