一問看懂——支持向量機SVM（Support Vector Machine）

蕪湖~~~支持向量機（SVM）

1. 引言

2. 基本思想

3. 數學模型

3.1 超平面定義

3.2 分類間隔與目標函數

3.3 軟間隔與松弛變量

4. 核函數方法（Kernel Trick）

4.1 核函數定義

4.2 常用核函數

5. SVM 的幾種類型

6. SVM 的訓練與預測流程

6.1 模型訓練

6.2 模型預測

7. 優點與局限

7.1 優點

7.2 局限

8. SVM 與多分類問題

9.代碼示例

9. 應用場景

10. 小結

蕪湖~~~支持向量機（SVM）

1. 引言

????????支持向量機（Support Vector Machine，簡稱 SVM）是一種基于統計學習理論的監督學習模型，最早由 Vladimir Vapnik 等人提出，廣泛應用于分類（Classification）與回歸（Regression）任務中。由于其優越的泛化能力和堅實的理論基礎，SVM 成為現代機器學習領域的重要算法之一，特別適合于高維、小樣本以及非線性問題。

2. 基本思想

SVM 的核心思想是：

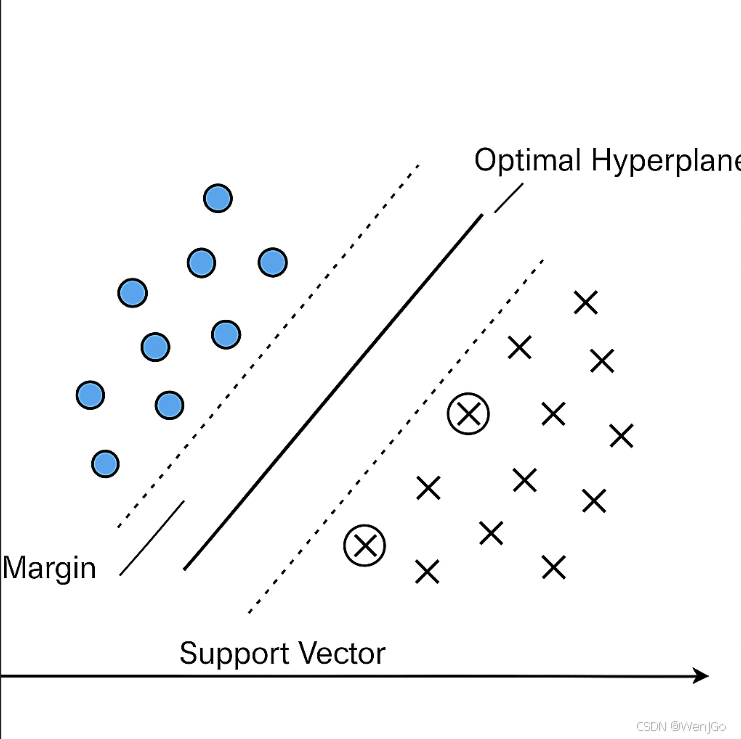
在特征空間中尋找一個最優分離超平面（Optimal Hyperplane），使得該超平面能夠最大限度地將不同類別的樣本分隔開，并具有? ?最大化間隔（Margin Maximization）的特性。

????????如下圖所示，對于線性可分問題，SVM 會選取離兩個類別最近樣本點（即支持向量）距離最大的分割平面作為最終分類器。

3. 數學模型

3.1 超平面定義

在 n 維空間中，一個超平面的定義如下：

$w^T x + b = 0$

其中：

w：法向量，決定超平面方向；
b ：偏置項，決定超平面距離原點的位置；
x ：輸入樣本。

3.2 分類間隔與目標函數

對于樣本 $(x_i, y_i)$ ，其分類間隔定義為：

$\gamma_i = \frac{y_i(w^T x_i + b)}{\|w\|}$

SVM 的目標是最大化所有樣本的最小分類間隔，即：

$\max_{w,b} \min_i \gamma_i$

為簡化計算，通常轉化為以下凸優化問題（硬間隔 SVM）：

$\min_{w,b} \frac{1}{2} \|w\|^2 \quad \text{s.t.} \quad y_i(w^T x_i + b) \geq 1$

3.3 軟間隔與松弛變量

當數據線性不可分時，引入松弛變量 $\xi_i$ 和懲罰系數 C，得到軟間隔 SVM：

$\min_{w,b,\xi} \frac{1}{2} \|w\|^2 + C \sum_i \xi_i \quad \text{s.t.} \quad y_i(w^T x_i + b) \geq 1 - \xi_i,\quad \xi_i \geq 0$

其中：

C ：控制對誤分類的懲罰程度；
$\xi_i$ ：表示樣本違反間隔的程度。

4. 核函數方法（Kernel Trick）

????????許多實際問題是非線性可分的。SVM 借助核函數技術將數據映射到高維特征空間，在高維空間中實現線性可分。

4.1 核函數定義

核函數 $K(x_i, x_j)$ 實際上是一個隱式內積：

$K(x_i, x_j) = \phi(x_i)^T \phi(x_j)$

其中 $\phi(\cdot)$ 是非線性映射函數，無需顯式計算。

4.2 常用核函數

核函數	表達式	說明
線性核（Linear）	$K(x_i, x_j) = x_i^T x_j$	適用于線性問題
多項式核（Polynomial）	$K(x_i, x_j) = (\gamma x_i^T x_j + r)^d$	控制多項式的復雜度
RBF核（高斯核）	$K(x_i, x_j) = \exp(-\gamma \\|x_i - x_j\\|^2)$	廣泛使用，處理非線性問題
Sigmoid核	$K(x_i, x_j) = \tanh(\gamma x_i^T x_j + r)$	類似神經網絡激活函數

5. SVM 的幾種類型

類型	描述
C-SVC	最常用的分類 SVM，帶懲罰系數 C
NU-SVC	用參數 $\nu$ 替代 C 控制支持向量數量
EPS-SVR	支持向量回歸（SVR）類型，用于回歸問題
NU-SVR	用 $\nu$ 形式的回歸模型

6. SVM 的訓練與預測流程

6.1 模型訓練

輸入：訓練樣本（特征向量 + 標簽）
設置 SVM 參數（核函數、C、γ等）
求解優化問題（使用 SMO、梯度下降等方法）
得到模型（支持向量、權重、偏置）

6.2 模型預測

預測函數定義為：

$f(x) = \text{sign} \left( \sum_i \alpha_i y_i K(x_i, x) + b \right)$

其中， $\alpha_i$ 是拉格朗日乘子，僅對支持向量不為零。

7. 優點與局限

7.1 優點

理論基礎堅實（VC維理論）
對高維、小樣本數據表現良好
可處理非線性問題（通過核方法）
具有稀疏解（依賴于少數支持向量）

7.2 局限

對大規模數據訓練速度慢，內存消耗大
核函數和參數選擇依賴經驗
不易處理多分類問題（需借助一對一/一對多策略）

8. SVM 與多分類問題

SVM 原生為二分類模型，但可通過以下策略擴展為多分類：

一對一（One-vs-One, OvO）：為每兩個類別訓練一個分類器，投票決定最終分類；
一對多（One-vs-Rest, OvR）：為每一個類別與其余類別訓練一個分類器，選擇概率最大者；
結構 SVM：直接擴展的多類模型（不常見于 OpenCV 實現中）。

9.代碼示例

基于 Python 的 scikit-learn 和 matplotlib 實現。這個代碼會：

創建兩類可分數據；
用 SVM 訓練分類器；
可視化：
- 支持向量（用圈標出）
- 決策邊界（黑線）
- 間隔邊界（虛線）

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs# 生成兩個類別的樣本數據
X, y = make_blobs(n_samples=40, centers=2, random_state=6)# 擬合一個線性支持向量分類器
clf = svm.SVC(kernel='linear', C=1.0)
clf.fit(X, y)# 獲取模型的參數
w = clf.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(min(X[:, 0]) - 1, max(X[:, 0]) + 1)
yy = a * xx - (clf.intercept_[0]) / w[1]# 計算邊界線（間隔）
margin = 1 / np.linalg.norm(w)
yy_down = yy - np.sqrt(1 + a ** 2) * margin
yy_up = yy + np.sqrt(1 + a ** 2) * margin# 繪圖
plt.figure(figsize=(8, 6))# 分類點
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm, s=30)# 決策邊界
plt.plot(xx, yy, 'k-')# 間隔邊界
plt.plot(xx, yy_down, 'k--')
plt.plot(xx, yy_up, 'k--')# 支持向量
plt.scatter(clf.support_vectors_[:, 0],clf.support_vectors_[:, 1],s=150, facecolors='none', edgecolors='k', linewidths=1.5, label='Support Vectors')plt.legend()
plt.title("SVM Decision Boundary with Margin and Support Vectors")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.grid(True)
plt.show()

9. 應用場景

SVM 被廣泛應用于以下任務：

圖像分類、人臉識別、字符識別（如 OCR）
基因數據分析與醫學診斷
文字情感分類與垃圾郵件檢測
股票趨勢預測與回歸任務

10. 小結

????????支持向量機是一種功能強大的分類與回歸工具，其“最大間隔 + 核技巧”的方法為機器學習提供了堅實的模型選擇方式。在合適的參數和核函數配置下，SVM 能夠提供強魯棒性與良好的泛化能力。對于中小規模問題，SVM 是值得優先嘗試的模型之一。

用一句最簡單的話講明白SVM支持向量機

????????SVM支持向量機是一種機器學習算法，它通過找到一個最優的超平面來分類數據點，使得不同類別的數據點盡可能分開。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/diannao/77430.shtml
繁體地址，請注明出處：http://hk.pswp.cn/diannao/77430.shtml
英文地址，請注明出處：http://en.pswp.cn/diannao/77430.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！