代碼隨想錄算法訓練Day57|LeetCode200-島嶼數量、LeetCode695-島嶼的最大面積

島嶼數量

題目描述

力扣200-島嶼數量

給你一個由 '1'（陸地）和 '0'（水）組成的的二維網格，請你計算網格中島嶼的數量。

島嶼總是被水包圍，并且每座島嶼只能由水平方向和/或豎直方向上相鄰的陸地連接形成。

此外，你可以假設該網格的四條邊均被水包圍。

示例 2：

輸入：grid = [["1","1","0","0","0"],["1","1","0","0","0"],["0","0","1","0","0"],["0","0","0","1","1"]
]
輸出：3

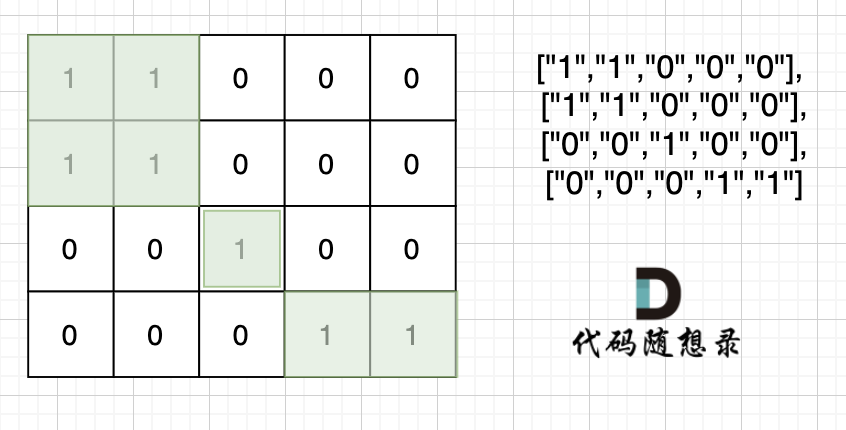
本題思路，是用遇到一個沒有遍歷過的節點陸地，計數器就加一，然后把該節點陸地所能遍歷到的陸地都標記上。在遇到標記過的陸地節點和海洋節點的時候直接跳過。這樣計數器就是最終島嶼的數量。

那么如果把節點陸地所能遍歷到的陸地都標記上呢，就可以使用 DFS，BFS或者并查集。

廣度優先搜索 BFS

不少同學用廣搜做這道題目的時候，超時了。這里有一個廣搜中很重要的細節：

根本原因是==只要加入隊列就代表走過，就需要標記，而不是從隊列拿出來的時候再去標記走過==。

很多同學可能感覺這有區別嗎？

如果從隊列拿出節點，再去標記這個節點走過，就會發生下圖所示的結果，會導致很多節點重復加入隊列。

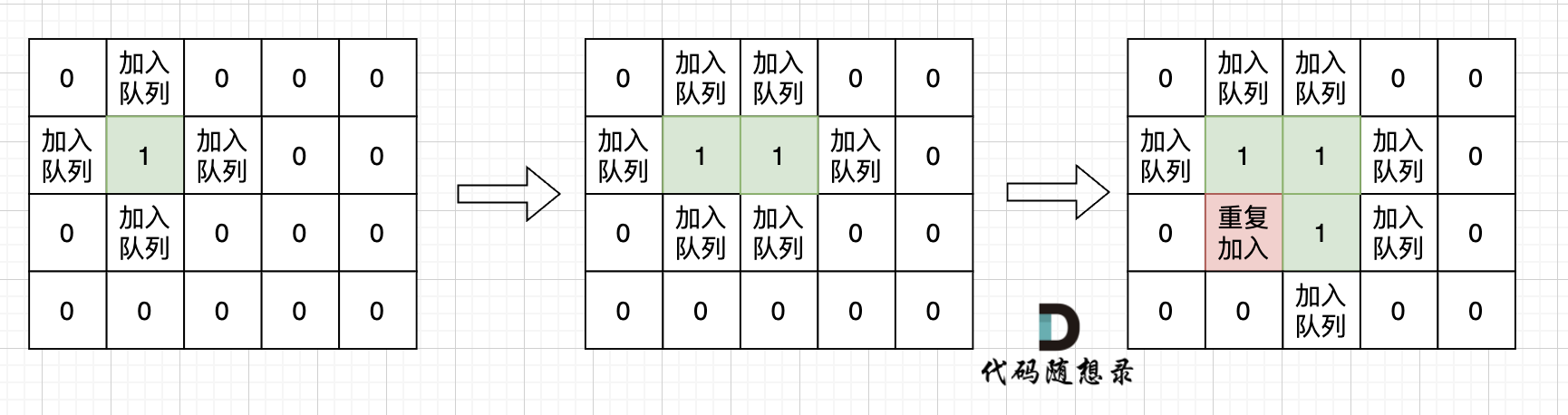
 `visited[x][y] = true;` 放在的地方，著去取決于我們對 代碼中隊列的定義，隊列中的節點就表示已經走過的節點。 **所以只要加入隊列，立即標記該節點走過**。

本題完整廣搜代碼：

class Solution {private static final int[][] dir = { { 0, 1 }, { 1, 0 }, { -1, 0 }, { 0, -1 } }; // 四個方向private void bfs(char[][] grid, boolean[][] visited, int x, int y) {//用于將當前陸地相連的陸地都進行標記Queue<int[]> queue = new LinkedList<>();queue.add(new int[] { x, y });visited[x][y] = true; // 只要加入隊列，立刻標記while (!queue.isEmpty()) {int[] cur = queue.poll();int curx = cur[0];// 取出當前節點(curx,cury)int cury = cur[1];// 遍歷四個方向，如果相鄰節點(nextx,nexty)在網格內切未被訪問過，并且其是陸地（1），則將其加入到隊列，并將其標記為已訪問for (int[] d : dir) {int nextx = curx + d[0];int nexty = cury + d[1];if (nextx < 0 || nextx >= grid.length || nexty < 0 || nexty >= grid[0].length)continue; // 越界了，直接跳過if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {queue.add(new int[] { nextx, nexty });visited[nextx][nexty] = true; // 只要加入隊列立刻標記}}} // 循環直到隊列為空，即所有與起始點連通的陸地都被標記為已訪問}public int numIslands(char[][] grid) {int n = grid.length;int m = grid[0].length;boolean[][] visited = new boolean[n][m];// 二維布爾數組visited，用于標記網格中每個位置是否已被訪問過int result = 0;for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (!visited[i][j] && grid[i][j] == '1') {// 當前位置 未訪問過的且是陸地，島嶼數量+1result++; // 遇到沒訪問過的陸地，+1bfs(grid, visited, i, j); // 將與其鏈接的陸地都標記上 true}}}return result;}
}

深度優先搜索 DFS—模板

//DFS
class Solution {private int[][] dir = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}}; // 四個方向private void dfs(char[][] grid, boolean[][] visited, int x, int y) {for (int[] d : dir) {int nextx = x + d[0];int nexty = y + d[1];if (nextx < 0 || nextx >= grid.length || nexty < 0 || nexty >= grid[0].length) continue;  // 越界了，直接跳過if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') { // 沒有訪問過的同時是陸地的visited[nextx][nexty] = true; dfs(grid, visited, nextx, nexty);} }}public int numIslands(char[][] grid) {int n = grid.length;int m = grid[0].length;boolean[][] visited = new boolean[n][m];int result = 0;for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (!visited[i][j] && grid[i][j] == '1') { visited[i][j] = true;result++; // 遇到沒訪問過的陸地，+1dfs(grid, visited, i, j); // 將與其鏈接的陸地都標記上 true}}}return result;}
}

下面的代碼使用的是深度優先搜索 DFS 的做法。為了統計島嶼數量同時不重復記錄，每當我們搜索到一個島后，就將這個島 “淹沒” —— 將這個島所占的地方從 “1” 改為 “0”，這樣就不用擔心后續會重復記錄這個島嶼了。而 DFS 的過程就體現在 “淹沒” 這一步中。詳見代碼：

public int numIslands(char[][] grid) {int res = 0; //記錄找到的島嶼數量for(int i = 0;i < grid.length;i++){for(int j = 0;j < grid[0].length;j++){//找到“1”，res加一，同時淹沒這個島if(grid[i][j] == '1'){res++;dfs(grid,i,j);}}}return res;
}
//使用DFS“淹沒”島嶼
public void dfs(char[][] grid, int i, int j){//搜索邊界：索引越界或遍歷到了"0"if(i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] == '0') return;//將這塊土地標記為"0"grid[i][j] = '0';//根據"每座島嶼只能由水平方向或豎直方向上相鄰的陸地連接形成"，對上下左右的相鄰頂點進行dfsdfs(grid,i - 1,j);dfs(grid,i + 1,j);dfs(grid,i,j + 1);dfs(grid,i,j - 1);
}

島嶼的最大面積

題目描述

力扣695-島嶼的最大面積

給你一個大小為 m x n 的二進制矩陣 grid 。

島嶼是由一些相鄰的 1 (代表土地) 構成的組合，這里的「相鄰」要求兩個 1 必須在 水平或者豎直的四個方向上 相鄰（斜角度的不算）。你可以假設 grid 的四個邊緣都被 0（代表水）包圍著。

島嶼的面積是島上值為 1 的單元格的數目。

計算并返回 grid 中最大的島嶼面積。如果沒有島嶼，則返回面積為 0 。

示例 1：

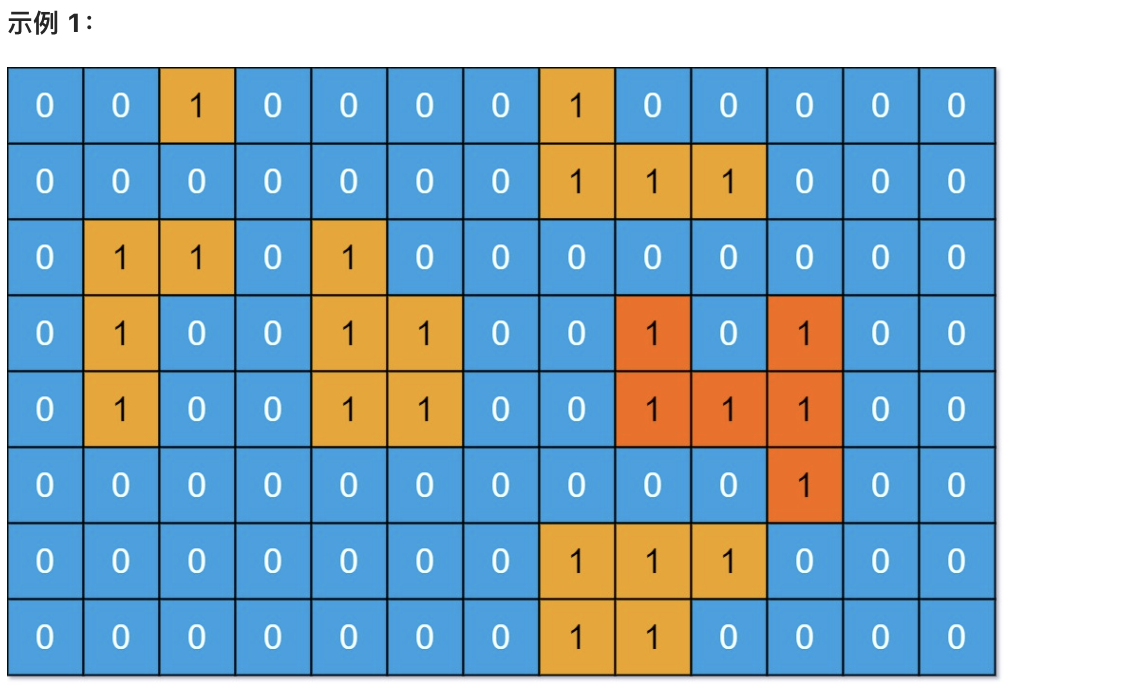
輸入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
輸出：6
解釋：答案不應該是 11 ，因為島嶼只能包含水平或垂直這四個方向上的 1 。

示例 2：

輸入：grid = [[0,0,0,0,0,0,0,0]]
輸出：0

解題思路

這道題目也是 dfs bfs基礎類題目，就是搜索每個島嶼上“1”的數量，然后取一個最大的。

本題思路上比較簡單，難點其實都是 dfs 和 bfs的理論基礎，關于理論基礎我在這里都有詳細講解：

DFS理論基礎(opens new window)

BFS理論基礎

根據BFS模板

//BFS
class Solution {private int[][] dir = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}}; // 表示四個方向void bfs(char[][] grid, boolean[][] visited, int x, int y) {Queue<int[]> queue = new LinkedList<>(); // 定義隊列queue.offer(new int[]{x, y}); // 起始節點加入隊列visited[x][y] = true; // 只要加入隊列，立刻標記為訪問過的節點while (!queue.isEmpty()) { // 開始遍歷隊列里的元素int[] cur = queue.poll(); // 從隊列取元素int curx = cur[0];int cury = cur[1]; // 當前節點坐標for (int i = 0; i < 4; i++) { // 開始向當前節點的四個方向左右上下去遍歷int nextx = curx + dir[i][0];int nexty = cury + dir[i][1]; // 獲取周圍四個方向的坐標if (nextx < 0 || nextx >= grid.length || nexty < 0 || nexty >= grid[0].length) continue;  // 坐標越界了，直接跳過if (!visited[nextx][nexty]) { // 如果節點沒被訪問過queue.offer(new int[]{nextx, nexty}); // 隊列添加該節點為下一輪要遍歷的節點visited[nextx][nexty] = true; // 只要加入隊列立刻標記，避免重復訪問}}}}
}

BFS

//BFS
class Solution {int[][] dir = {{ 0, 1 }, { 1, 0 }, { 0, -1 }, { -1, 0 }};int count;boolean visited[][];public int maxAreaOfIsland(int[][] grid) {int res = 0;visited = new boolean[grid.length][grid[0].length];for (int i = 0; i < grid.length; i++) {for (int j = 0; j < grid[0].length; j++) {if (visited[i][j] == false && grid[i][j] == 1) {count = 0;bfs(grid, i, j);res = Math.max(res, count);}}}return res;}private void bfs(int[][] grid, int x, int y) {Queue<int[]> queue = new LinkedList<>(); // 定義隊列queue.offer(new int[] { x, y }); // 起始節點加入隊列visited[x][y] = true; // 只要加入隊列，立刻標記為訪問過的節點count++; // 將起始節點也算入島嶼面積中while (!queue.isEmpty()) { // 開始遍歷隊列里的元素int[] cur = queue.poll(); // 從隊列取元素int curx = cur[0];int cury = cur[1]; // 當前節點坐標for (int i = 0; i < 4; i++) { // 開始向當前節點的四個方向左右上下去遍歷int nextx = curx + dir[i][0];int nexty = cury + dir[i][1]; // 獲取周圍四個方向的坐標if (nextx < 0 || nextx >= grid.length || nexty < 0 || nexty >= grid[0].length)continue;if (visited[nextx][nexty] == false && grid[nextx][nexty] == 1) {queue.offer(new int[] { nextx, nexty }); // 隊列添加該節點為下一輪要遍歷的節點visited[nextx][nexty] = true;count++;}}}}}

根據DFS模板

//DFS
class Solution {private int[][] dir = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}}; // 四個方向private void dfs(char[][] grid, boolean[][] visited, int x, int y) {for (int[] d : dir) {int nextx = x + d[0];int nexty = y + d[1];if (nextx < 0 || nextx >= grid.length || nexty < 0 || nexty >= grid[0].length) continue;  // 越界了，直接跳過if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') { // 沒有訪問過的同時是陸地的visited[nextx][nexty] = true; dfs(grid, visited, nextx, nexty);} }}public int numIslands(char[][] grid) {int n = grid.length;int m = grid[0].length;boolean[][] visited = new boolean[n][m];int result = 0;for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (!visited[i][j] && grid[i][j] == '1') { visited[i][j] = true;result++; // 遇到沒訪問過的陸地，+1dfs(grid, visited, i, j); // 將與其鏈接的陸地都標記上 true}}}return result;}
}

DFS

//DFS
class Solution {private int count;private int[][] dir = { { 0, 1 }, { 1, 0 }, { -1, 0 }, { 0, -1 } }; // 四個方向private void dfs(int[][] grid, boolean[][] visited, int x, int y) {for (int[] d : dir) {int nextx = x + d[0];int nexty = y + d[1];if (nextx < 0 || nextx >= grid.length || nexty < 0 || nexty >= grid[0].length)continue; // 越界了，直接跳過if (!visited[nextx][nexty] && grid[nextx][nexty] == 1) { // 沒有訪問過的 同時 是陸地的visited[nextx][nexty] = true;count++;dfs(grid, visited, nextx, nexty);}}}public int maxAreaOfIsland(int[][] grid) {int n = grid.length;int m = grid[0].length;boolean[][] visited = new boolean[n][m];int result = 0;for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (!visited[i][j] && grid[i][j] == 1) {count = 1; // 因為dfs處理下一個節點，所以這里遇到陸地了就先計數，dfs處理接下來的相鄰陸地visited[i][j] = true;dfs(grid, visited, i, j); // 將與其鏈接的陸地都標記上 trueresult = Math.max(result, count);}}}return result;}
}