Leetcode題目鏈接

原理

重畫鏈表如下所示，線上有若干個節點。記藍色慢指針為 slow，紅色快指針為 fast。初始時 slow 和 fast 均在頭節點處。

使 slow 和 fast 同時前進，fast 的速度是 slow 的兩倍。當 slow 抵達環的入口處時，如下所示。

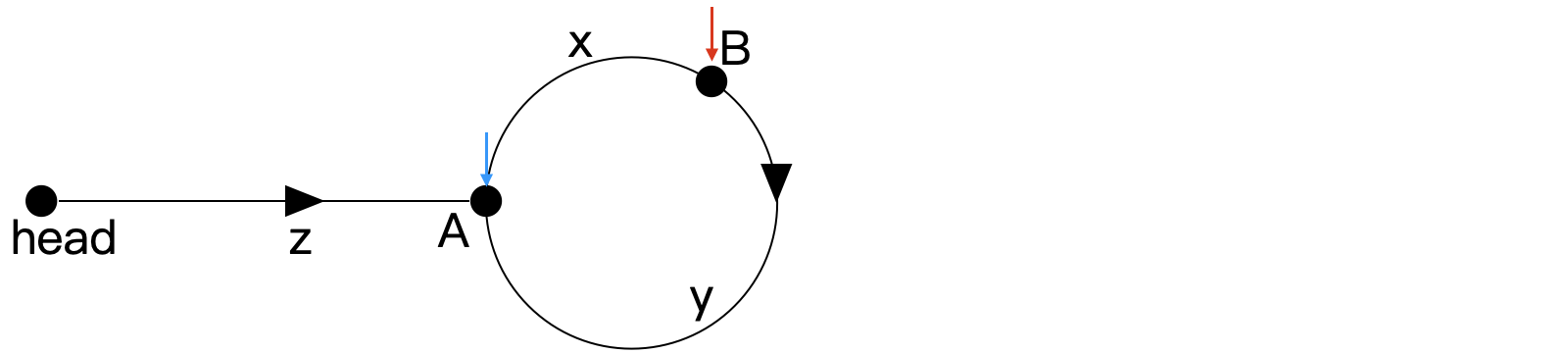
其中：

• head 和 A 的距離為 $z$
• 弧 AB (沿箭頭方向) 的長度為 $x$
• 同理，弧 BA 的長度為 $y$

可得：

• slow 走過的步數為 $z$
• 設 fast 已經走過了 $k$ 個環，$k\ge 0$，對應的步數為 $z+k(x+y)+x$

以上兩個步數中，后者為前者的兩倍，整理可得 $z=x+k(x+y)$，替換如下所示。

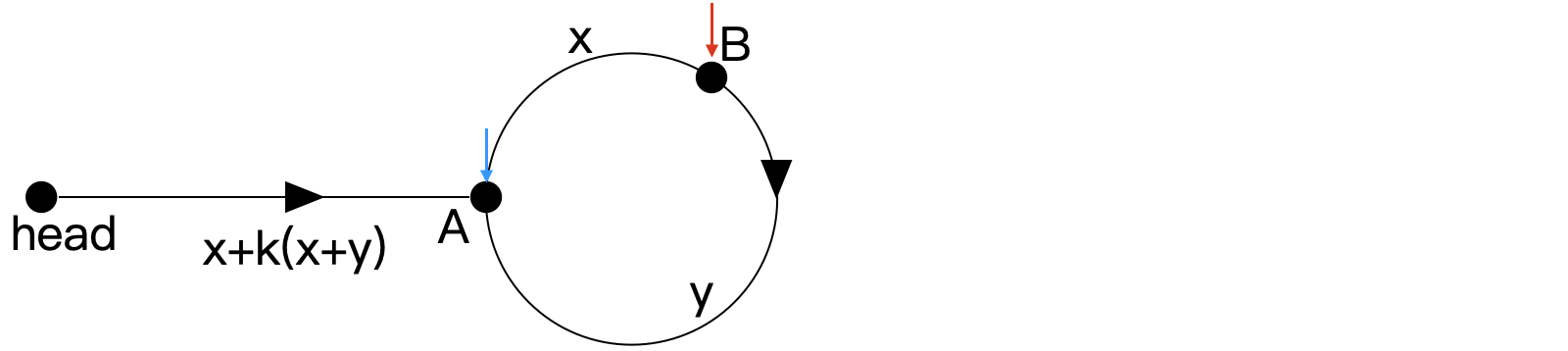
此時因為 fast 比 slow 快 1 個單位的速度，且弧 BA 的長度為整數，所以再經過 y 個單位的時間即可追上 slow。

即 slow 再走 $y$ 步，fast 再走 $2y$ 步。設相遇在 C 點，位置如下所示，可得弧 AC 長度為 y。

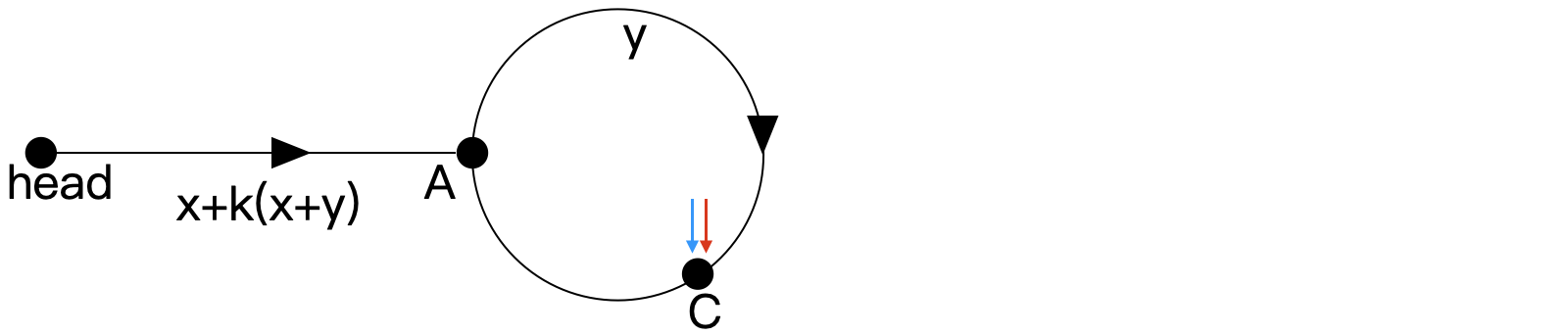
因為此前 $x+y$ 為環長，所以弧 CA 的長度為 $x$。
此時我們另用一橙色指針 ptr (pointer) 指向 head，如下所示。并使 ptr 和 slow 保持 1 個單位的速度前進，在經過 $z=x+k(x+y)$ 步后，可在 A 處相遇。

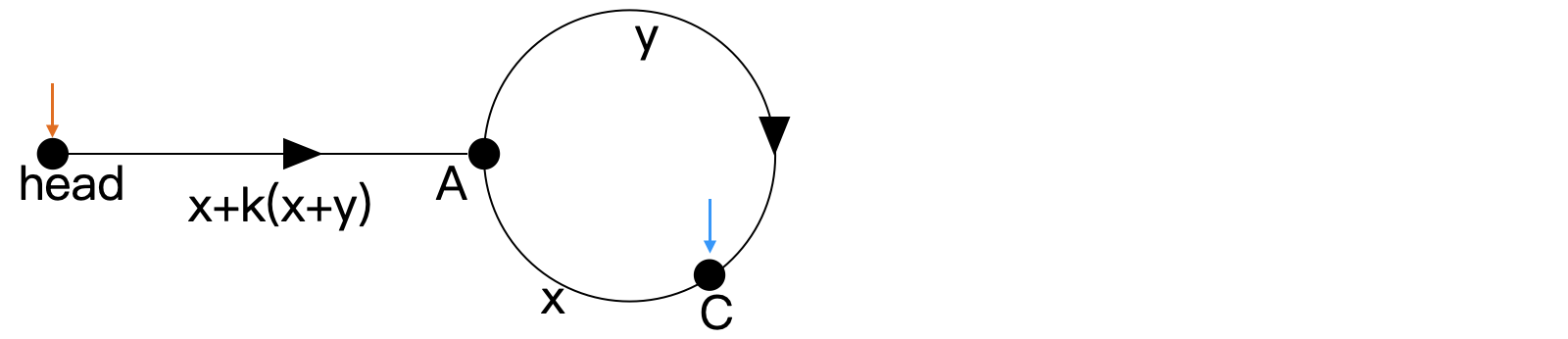
再考慮鏈表無環的情況，fast 在追到 slow 之前就會指向空節點，退出循環即可。

算法實現

復雜度

時間：$\Theta (n)$

• 如果相交
  • fast 和 slow 相遇時 slow 走過的距離 $\le n$，所以 fast 走過的距離 $\le 2n$
  • ptr 走過的距離 $<n$
  • slow 走過的距離 $\ge n$ 但 $<$ fast 和 ptr 走過的距離之和。
• 如果不相交，fast 走過 $n$ 步即結束

空間：$\Theta (1)$

推廣

以下皆為個人所著，兼顧了職場面試和本碩階段的學術考試。

• 附個人題解的雙指針題單
• 圖論入門
• 圖論進階

點贊關注不迷路，祝各位早日上岸，飛黃騰達！