什么是激活函數
計算機科學家借鑒生物的神經元機制發明了計算機上的模型,這個模型與生物的神經元非常類似
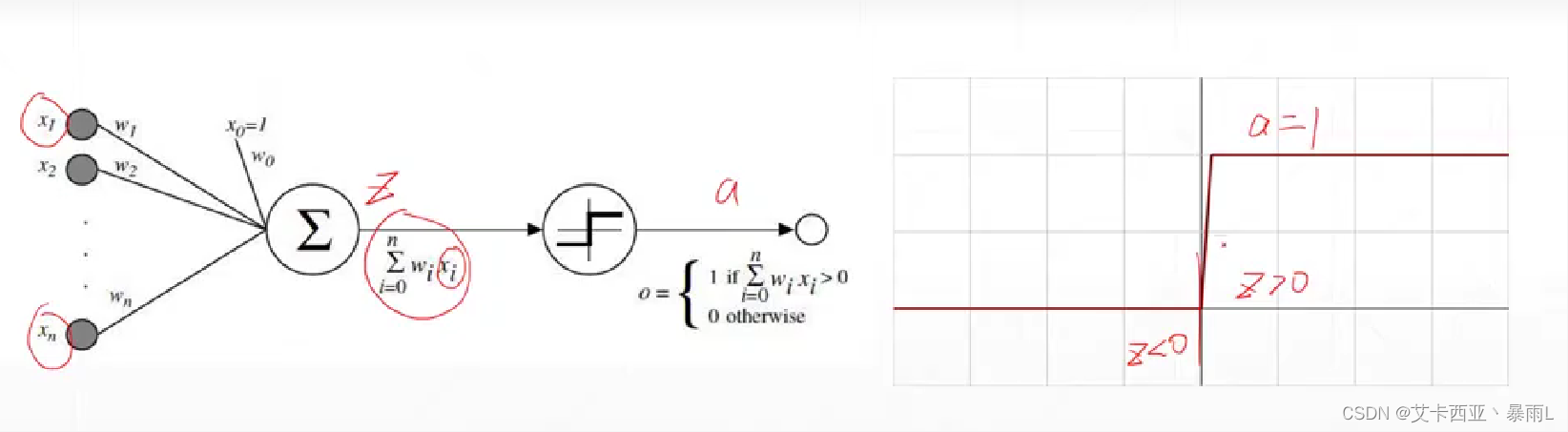
激活的意思就是z變量要大于0,這一個節點才會激活,否則就會處于睡眠狀態不會輸出電平值
該激活函數在z=0處不可導,因此不能直接使用梯度下降進行優化,使用了啟發式搜索的方法來求解單層感知機最優解的情況
sigmoid
為了解決單層感知機激活函數不可導的情況,提出了一個連續的光滑的函數即sigmoid函數或者叫logistic
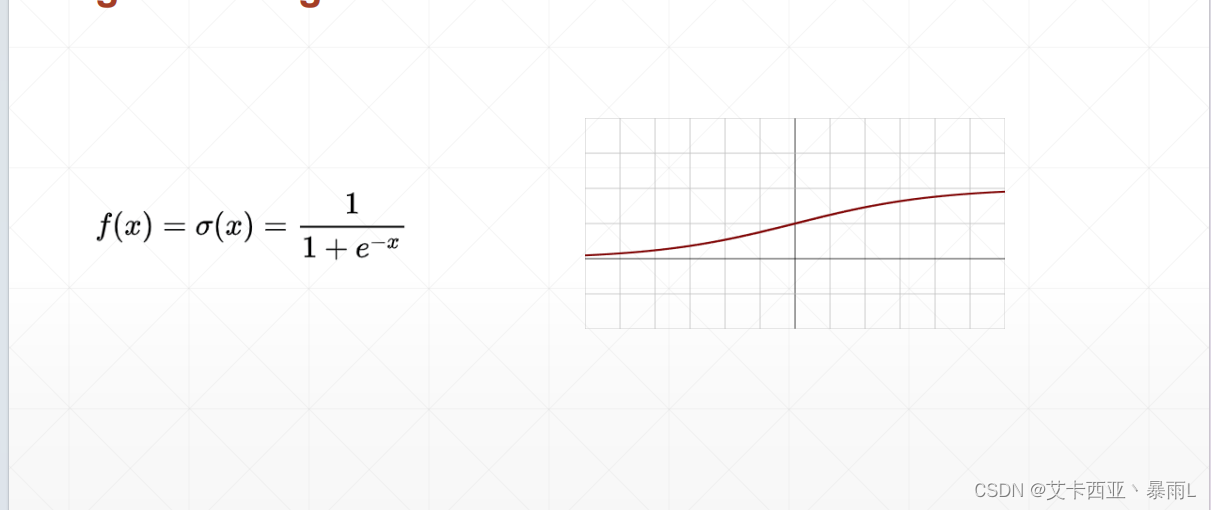
sigmoid函數z=0的時候值為0.5,最大值是接近于1,最小值是接近于0
比較適合生物學上的神經元,也就是說當z比較小的時候,接近于一個不響應的狀態,z很大的時候我這個響應也不會很大會慢慢接近于1,相當于一個壓縮的功能,把(-∞,+∞)Z的這樣的值壓縮到一個有限的范圍中間,比如(0,1)
該函數的導數在負無窮的時候接近于0,到z=0的時候會出現最大值,再慢慢導數再變成0

有一個缺陷:loss長時間保持不變,梯度彌散
torch.sigmoid和F.sigmoid是一樣的
F是一個模塊的別名,是torch.nn.functional

z的值接近于-100的時候,sigmoid的值已經接近于0了,取100的時候,sigmoid接近于1
Tanh
在RNN(循環神經網絡)中使用較多
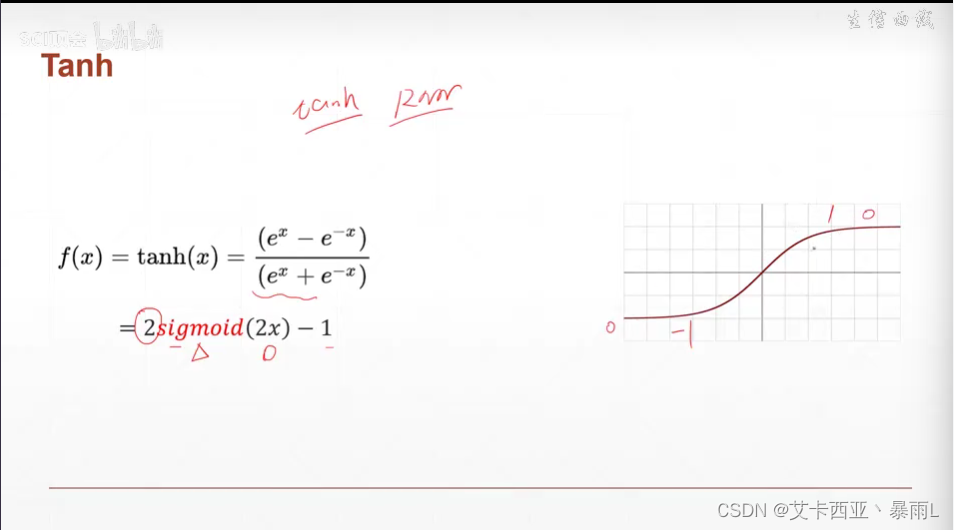
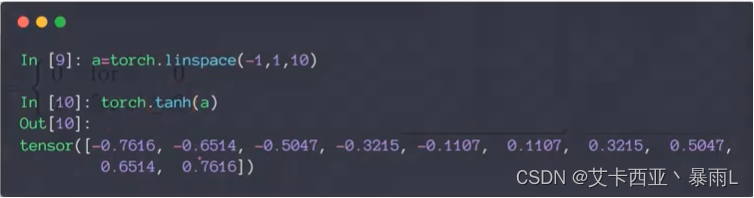
可以由sigmoid變化而來,將x壓縮二分之一,y放大兩倍,再減去1
區間從(-1,1)
ReLu
z小于0不響應,z大于0就線性響應,非常合適做深度學習
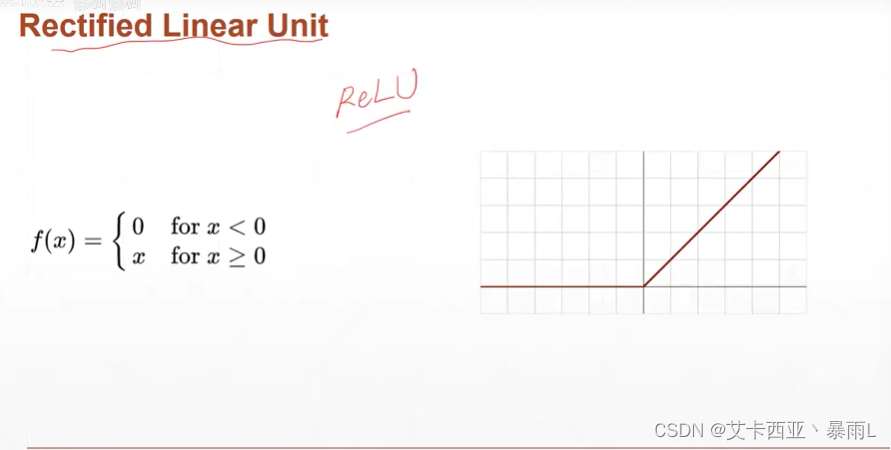
當z<0,梯度是0;z>0的時候,梯度是1,因為梯度是1,可以導致梯度計算起來非常方便,不會放大也不會縮小,因此對于搜索最優解,relu函數存在優勢,不會出現梯度彌散和梯度爆炸的情況

loss以及loss的梯度
- Mean Squared Error (均方差)
- Cross Entropy Loss(用于分類中的誤差)
- binary(二分類)
- multi-class(多分類)
- +softmax(一般跟softmax激活函數一起使用)
- leave it to logistic regression part
MSE

MSE的基本形式就是y的實際值減去模型輸出的值
MSE與L2-norm是有一定區別的,對于第一個tensor y1和第二個tensor xw+b 設其為y2,l2 norm是對應元素相減再開根號,如下
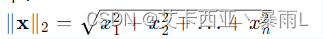
所以跟MSE還是有區別的,MSE是沒有開根號這個步驟的
如果要用norm函數來求解MSE,需求平方,比如說
torch.norm(y-pred,2).pow(2)第二個參數是給出 L幾-norm,一定要加一個pow(2)
MSE梯度求解情況

使用pytorch自動求導
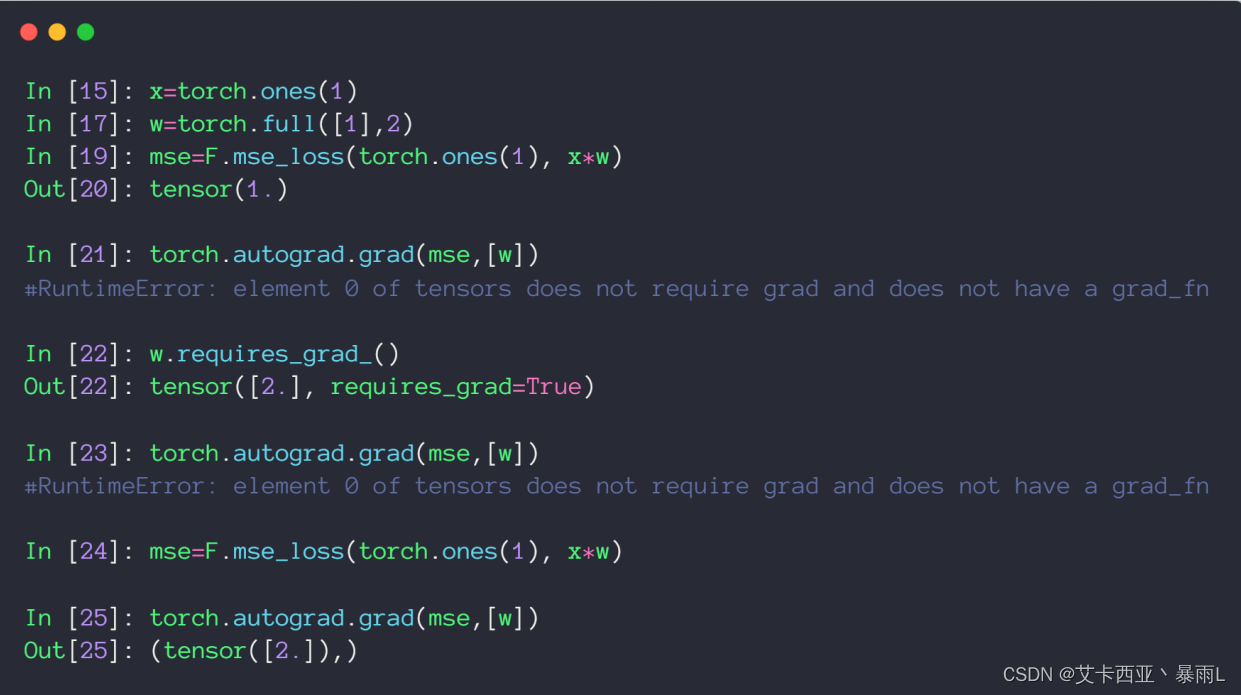
x初始化為1 w初始化為dimension為1,長度為1,值為2的tensor,b為0
求解MSE可以使用torch.norm加平方,也可以使用F.mse_loss第一個參數給的是predict的值,第二個參數給的是真實值,因為是平方所以這里順序亂了也沒有關系
使用torch.autograd.grad接收兩個參數,第一個參數是y,第二個參數是[x1,x2,…](即有多少個自變量,要對多少個自變量求導),對于深度學習來說,第一個參數就是predict,第二個參數是[w1,w2,…]這種參數
直接使用MSE也就是輸出的這個loss對W求導的時候,上圖返回該參數不需要求導的ERROR,出現該錯誤的根本原因是w初始化的時候沒有設置為需要導出信息,因此pytorch在建圖的時候對w標注了不需要求導信息,這樣對w求導就會觸發錯誤
需要使用requires_grad進行更新,但是更新完之后還是會報錯,因為pytorch是一個動態圖,這里更新了w但是圖還沒有更新,pytorch是做一步計算,一步圖,所以w更新之后,圖還是用的原來的圖,所以還是會出現原來的錯誤
使用另一種方法
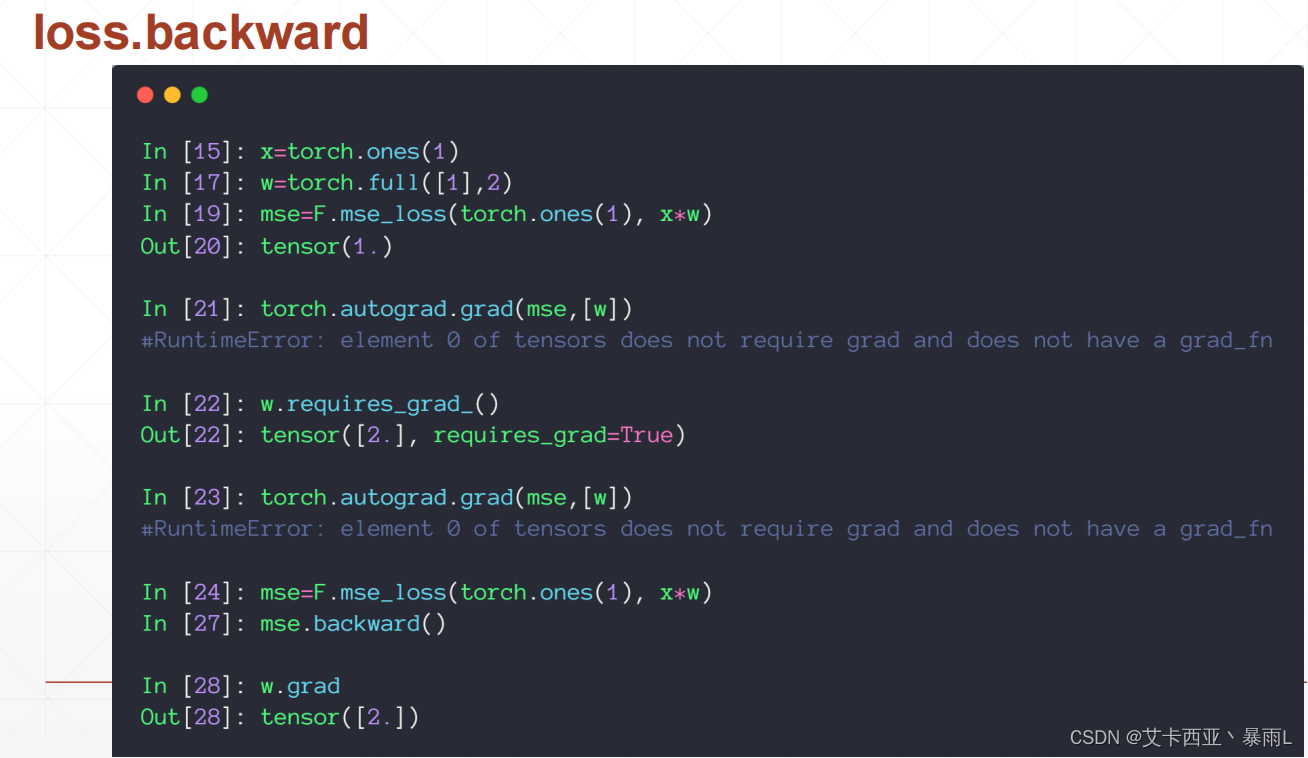
首先也是要用F.mse_loss動態圖建圖,直接在loss上使用backward(表示向后傳播),自動對這個圖(在完成前向傳播的時候建圖的過程中會記錄下來這個圖的所有路徑,因此在最后的loss節點調用backward的時候,會自動的從后往前傳播,完成路徑上所有需要梯度的tensor的gradient的計算方法,計算的gradient不會再返回出來,會自動把所有的gradient信息附加在每個tensor的成員變量上面)

softmax

首先對于三個節點的輸出,如果把這個數值轉換成一個概率的話,希望概率最大的那個值做預測的Label,比如這里輸入的索引是0,1,2,我們希望數值最大的值所在的索引作為我們預測的label,因此2.0最大,把2.0所在的索引0作為我們預測的一個label,因為probability是屬于一個區間的(0~1這樣的范圍),我們需要把這個值轉換成一個probability的話必須人為的壓縮到這樣的一個空間,可以使用sigmoid函數把值壓縮到0 ~ 1的區間,但是對于一個分類問題來說一個物體屬于哪個類是有一個概率的屬性的(即物體屬于x分類的概率,y分類的概率,z分類的概率等)總是屬于著三個分類中的一種,因此這三個分類加起來總是會等于1,即sigmoid并不能表述所有輸出節點的概率相加為1的情況,會把原來大的放大,原來小的壓縮到密集的空間

a i a_{i} ai?經過softmax得到 p i p_{i} pi?, p i p_{i} pi?對 a j a_{j} aj?求導,假設i=j時如右圖所示,softmax的梯度等于

之所以要利用 p j p_{j} pj?的輸出是因為神經網絡向前傳播的時候,這些值是已知的可以直接得到,因此向后傳播的時候不需要額外計算,只需要利用這個公式就可以一次求出
當i不等于j的時候

i不等于j的時候

總結

i=j時偏導時正數,不相等時是負數

loss必須只有一個量[1],否則就會有邏輯錯誤,這里p.shape為[3],因此在求梯度的時候不能直接傳入p,只能對中的變量進行求導,此時圖中是 p 1 p_{1} p1?對 a i a_{i} ai? i屬于[0,2],所以會返回dimension為1 長度為3 的tensor,其中第一個元素表示 p 1 p_{1} p1?對 a 0 a_{0} a0?求偏導以此類推,可以看出如果i等于j的話梯度信息就是正的,其他的都是負的






使用教程)






:堆排序)





