PDF文檔公眾號回復關鍵字:20240701

2021 CSP-J 選擇題
單項選擇題(共15題,每題2分,共計30分:每題有且僅有一個正確選項)
4.以比較作為基本運算,在N個數中找出最大數,最壞情況下所需要的最少比較次數為
A. N^2
B. N
C. N-1
D. N+1
6.對于有n個頂點、m條邊的無向連通圖(m>n),需要刪掉( )條邊才能使其成為一棵樹
A. n-1
B. m-n
C. m-n-1
D. m-n+1
12.由 1,1,2,2,3這五個數字組成不同的三位數有( )種
A. 18
B. 15
C. 12
D. 24
13.考慮如下遞歸算法
solve(n)if n<=1 return 1 else if n>=5 return n*solve(n-2)else return n*solve(n-1)
則調用solve(7)得到的返回結果為( )
A. 105
B. 840
C. 210
D. 420
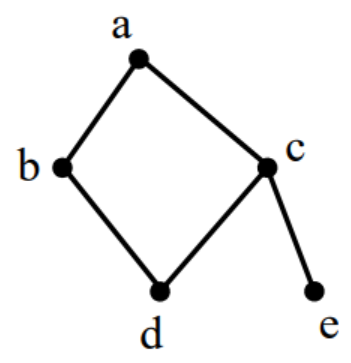
14.以a為起點,對右邊的無向圖進行深度優先遍歷,則b、c、d、e四個點中有可能作為最后一個遍歷的點的個數為( )
A. 1
B. 2
C. 3
D. 4
2 相關知識點
1) n個數取最大
3個數取最大,需比較2次
#include<bits/stdc++.h>
using namespace std;
/*3個數取最大 比較2次
*/
int main(){int a,b,c ;scanf("%d%d%d",&a,&b,&c) ;if(b > a)a = b ;if(c > a)a = c ;printf("%d",a) ;return 0;
}
/*輸入 1 2 3輸出 3輸入 9 5 10輸出 10
*/
n個數取最大,需比較n-1次
#include<bits/stdc++.h>
using namespace std;
/*n數進行比較,循環1~n-1,進行n-1次循環
*/
int n,a[10000];
int main(){scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&a[i]);}for(int i=1;i<n;i++){if(a[0]<a[i]){a[0]=a[i];}}printf("%d",a[0]);return 0;
}
/*輸入 4 5 9 10 8輸出 10輸入 3 9 5 10輸出 10
*/
2) 樹的邊數
樹的邊數是指樹中所有邊的數量。在非空樹中,邊的數量等于結點數量減1
3) 枚舉算法
枚舉算法是一種通過列舉所有可能情況來求解問題的策略。它通常適用于問題規模較小且解空間明確、有限的情況。枚舉算法的關鍵在于如何有效地遍歷解空間,并在遍歷過程中判斷每個候選解是否滿足問題的要求
枚舉算法一般需要按一定規則進行分類,避免重復枚舉或遺漏的情況
4) 遞歸、遞推
遞歸
遞歸是一種解決問題的方法,它通過將問題分解為更小的子問題來解決。
一個遞歸函數會在其定義中直接或間接地調用自身
遞歸通常包括兩個部分:基本情況(Base case)和遞歸步驟(Recursive step)。
基本情況是指當問題規模變得足夠小時,可以直接得到解決方案的情況。
遞推
遞推是一種描述序列中項與項之間關系的方法。遞推關系通常用于定義具有某種規律性的數列,如斐波那契數列
遞推關系可以用一個公式或方程來表示,該公式或方程描述了序列中的每一項如何由前一項(或前幾項)計算得出
遞歸和遞推區別
遞歸是一種解決問題的方法,通過將問題分解為更小的子問題來解決,自上而下分解,通常會出現多次重復計算問題
遞推是一種描述序列中項與項之間關系的方法,自底而上計算,避免重復計算
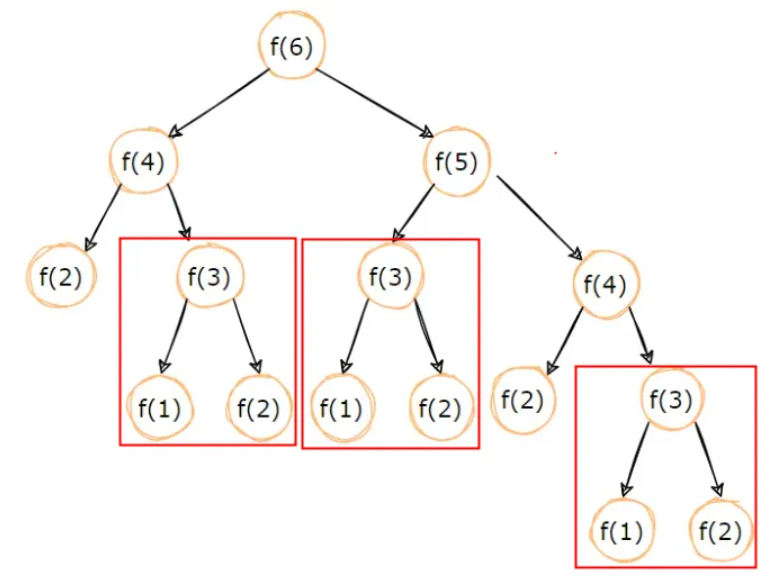
通過斐波那契數列演示區別
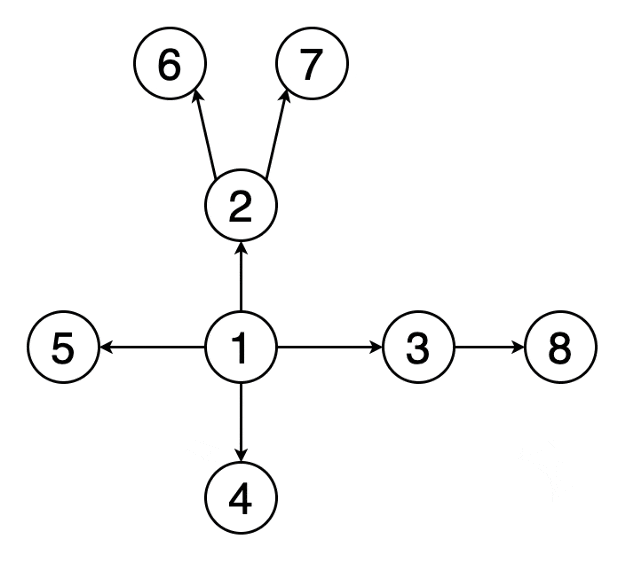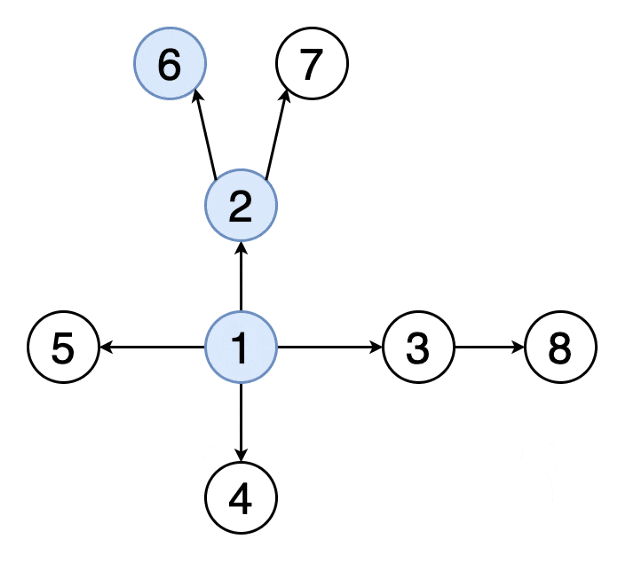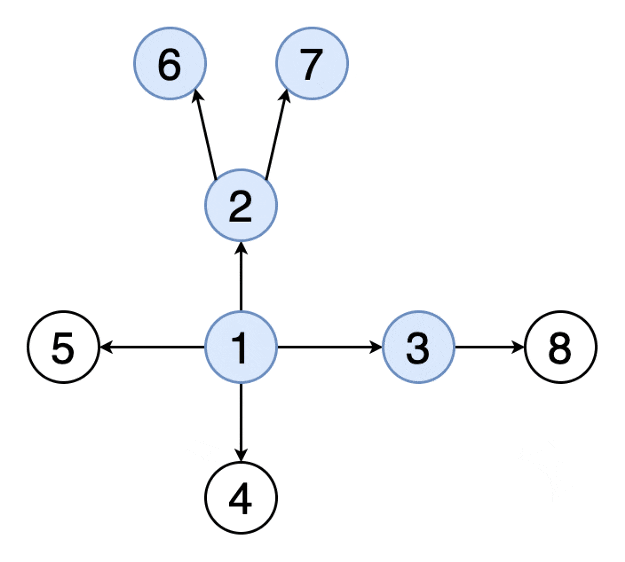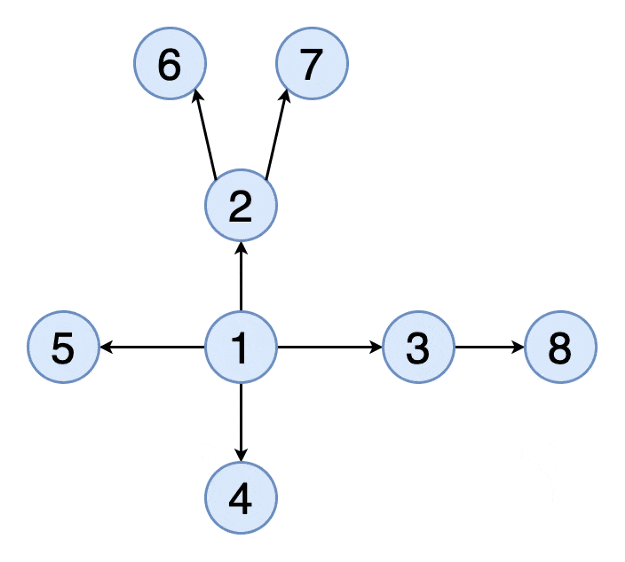
遞歸f(3)重復計算3次,如果數更大重復更多
遞推計算是從最底層計算,計算上一層時使用前面的計算結果,所以f(3)只計算1次
5) 深度優先搜索
從某個特定頂點開始,盡可能深地搜索樹的分支,直到達到葉子節點,然后回溯到前一個節點,繼續搜索下一個分支,實現DFS時,通常使用堆棧數據結構來實現
3 思路分析
4.以比較作為基本運算,在N個數中找出最大數,最壞情況下所需要的最少比較次數為( C )
A. N^2
B. N
C. N-1
D. N+1
分析
比較作為基本運算,用第1個數做基準數,和第2個比較,然后保留最大的,逐一和后面的數進行比較
1和2,2和3,3和4,… n-1和n
最多為n-1次
6.對于有n個頂點、m條邊的無向連通圖(m>n),需要刪掉( D )條邊才能使其成為一棵樹
A. n-1
B. m-n
C. m-n-1
D. m-n+1
分析
n個節點的樹,有n-1條邊
無向圖有m條邊,需要變成n-1條邊
應刪掉m-(n-1)=m-n+1
所以選D
12.由 1,1,2,2,3這五個數字組成不同的三位數有( A )種
A. 18
B. 15
C. 12
D. 24
分析
分類枚舉
1有1 2 3這3個不同數字組成的3位數個數有A(3,3)=3 * 2 *1=6種
2有1 1 2 這3個數字組成的3位數 112 121 211 這3種
3有1 2 2 這3個數字組成的3位數 122 212 221 這3種
4有1 1 3 這3個數字組成的3位數 112 131 311 這3種
5有2 2 3 這3個數字組成的3位數 223 232 322 這3種
上述分5類枚舉,根據加法原理
6+3+3+3+3=18
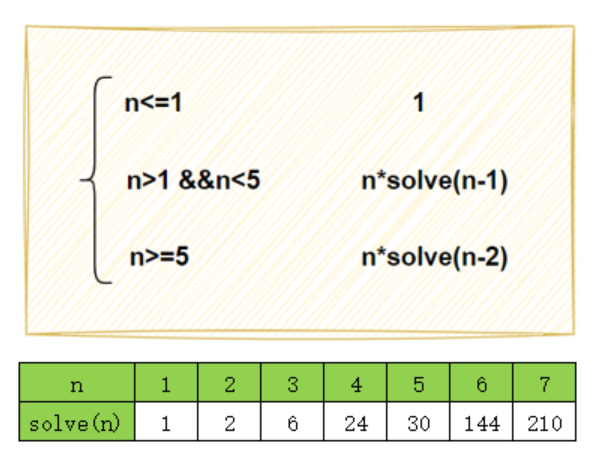
13.考慮如下遞歸算法
solve(n)if n<=1 return 1 else if n>=5 return n*solve(n-2)else return n*solve(n-1)
則調用solve(7)得到的返回結果為( C )
A. 105
B. 840
C. 210
D. 420
分析
遞歸從大到小計算會出現一些重復計算,可以從小到大遞推得到solve(7)的值
solve(1)=1
solve(2)=n * solve(n-1)=2* solve(1)=2*1=2
solve(3)=n * solve(n-1)=3* solve(2)=3*2=6
solve(4)=n * solve(n-1)=4* solve(3)=4*6=24
solve(5)=n * solve(n-2)=5* solve(3)=5*6=30
solve(6)=n * solve(n-2)=6* solve(4)=6*24=144
solve(7)=n * solve(n-2)=7* solve(5)=7*30=210
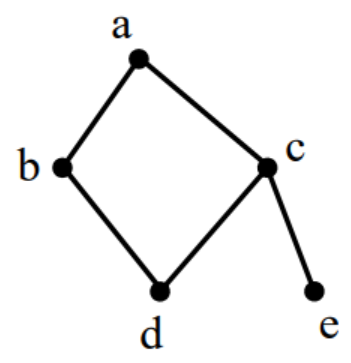
14.以a為起點,對右邊的無向圖進行深度優先遍歷,則b、c、d、e四個點中有可能作為最后一個遍歷的點的個數為( B )
A. 1
B. 2
C. 3
D. 4
分析
從a點出發沿著一個分支節點盡可能深的搜索樹的分支,直到達到葉子節點,然后回溯到前一個節點,繼續搜索下一個分支
1 從a出發沿bdce一個分支搜索完所有節點,最后節點為e
2 從a出發沿ce搜索到葉子節點,回溯到c沿db搜結束,最后節點為b
深度優先搜索只有上述2種情況,可能作為最后節點的為e和b這2個節點
具體如下圖




















