沒有上司的舞會
Ural 大學有 𝑁 名職員,編號為1~𝑁。
他們的關系就像一棵以校長為根的樹,父節點就是子節點的直接上司。
每個職員有一個快樂指數,用整數 𝐻𝑖 給出,其中1≤𝑖≤𝑁。
現在要召開一場周年慶宴會,不過,沒有職員愿意和直接上司一起參會。
在滿足這個條件的前提下,主辦方希望邀請一部分職員參會,使得所有參會職員的快樂指數總和最大,求這個最大值。
輸入格式
第一行一個整數 𝑁。
接下來 𝑁 行,第 𝑖 行表示 𝑖 號職員的快樂指數 𝐻𝑖。
接下來𝑁?1 行,每行輸入一對整數 𝐿,𝐾,表示 𝐾 是 𝐿 的直接上司。(注意一下,后一個數是前一個數的父節點,不要搞反)。
輸出格式
輸出最大的快樂指數。
數據范圍
1≤𝑁≤6000,
?128≤𝐻𝑖≤127
輸入樣例:
7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
輸出樣例:
5
題意簡化
這道題題目看上去花里胡哨的,但其實挺好理解的
前N行表示第i號職工的快樂指數
后面的N?1行輸入兩個整數L,K,表示 K是 L 的直接上司,如圖。

要求使得所有參會職員的快樂指數總和最大。
在這兒講解一下樣例
根據這個樣例,我們可以畫出一張圖(如果還不知道樣例是什么意思的看上面),如下:

那輸出樣例的 5 是怎么來的呢?
請看:
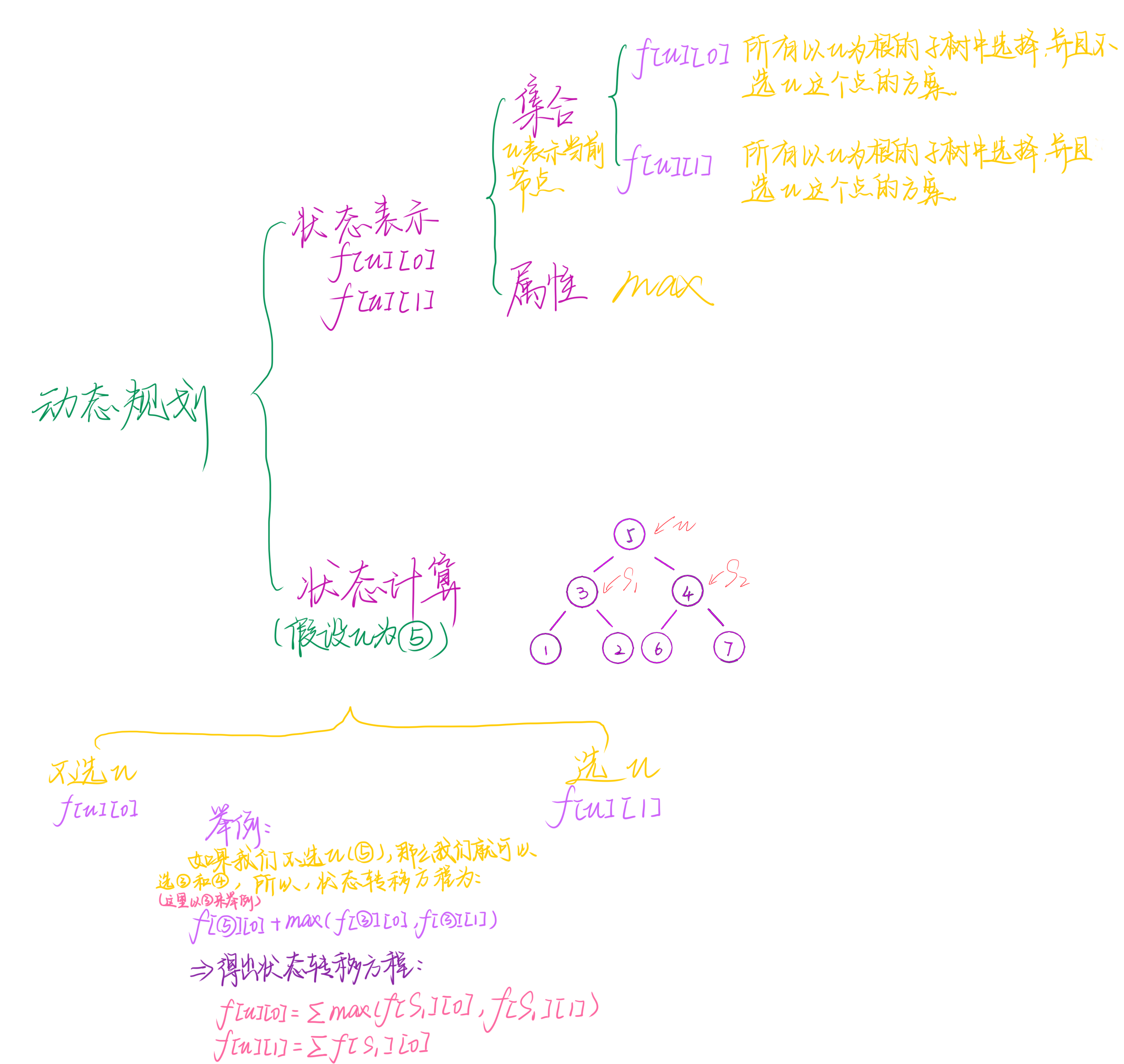
根據畫圖得出,⑤ 是根節點(校長)。
我們知道樣例中每個節點的快樂值都為 1,所以決定最大快樂值的是節點的數量在這個樣例里,我們必須選校長,為什么呢?
比如我們選了 ③,那他的下屬全部KO,或者選了 ④,也是一樣
那我們的最大快樂值就變成了 3,錯誤只有我們選了 ⑤,那剩下的 ①、 ②、 ⑥、 ⑦才能茍活被選中
我們現在選了 ⑤,那我們就可以有五個人參加,且快樂值是最大的,為 5,選中的清晰,如圖:

發現什么了嗎?
-
當不選 i 節點時,影響最大高興值的節點為i的子節點或其他節點
-
當選 i 節點時,影響最大高興值的節點只為i的子節點
由此我們可以得出狀態轉移方程:
當 f[i][1]時表示選 i號節點。
那么很明顯 i號節點的快樂值需要算上
然后我們知道,如果選了這個點,它的所有字節點都是不能選的,所以我們應該給它加上
f[j][0]
當 f[i][0]時表示不選 i
這時我們不需要加上 i號點的快樂值
如果不選這個點,它的子節點可以選也可以不選,所以我們應該給它加上maxf[j][0],f[j][1]
算法1
(樹形DP) O(n)
看圖:
時間復雜度
C++ 代碼
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 6010;
int n;
int happy[N]; //每個職工的高興度
int f[N][2]; //上面有解釋哦~
int e[N],ne[N],h[N],idx; //鏈表,用來模擬建一個樹
bool has_father[N]; //判斷當前節點是否有父節點
void add(int a,int b){ //把a插入樹中e[idx] = b,ne[idx] = h[a],h[a] = idx ++;
}
void dfs(int u){ //開始求解題目f[u][1] = happy[u]; //如果選當前節點u,就可以把f[u,1]先懟上他的高興度for(int i = h[u];~i;i = ne[i]){ //遍歷樹int j = e[i];dfs(j); //回溯//狀態轉移部分,上面有詳細講解~f[u][0] += max(f[j][1],f[j][0]);f[u][1] += f[j][0];}
}
int main(){scanf("%d",&n);for(int i = 1;i <= n;i ++) scanf("%d",&happy[i]); //輸入每個人的高興度memset(h,-1,sizeof h); //把h都賦值為-1for(int i = 1;i < n;i ++){int a,b; //對應題目中的L,K,表示b是a的上司scanf("%d%d",&a,&b); //輸入~has_father[a] = true; //說明a他有上司add(b,a); //把a加入到b的后面}int root = 1; //用來找根節點while(has_father[root]) root ++; //找根節點dfs(root); //從根節點開始搜索printf("%d\n",max(f[root][0],f[root][1])); //輸出不選根節點與選根節點的最大值return 0;
}


)



原則)
是什么?進程與線程的定義、關系與差異)











