1 概述！！
1.1 原型和模型
原型：客觀存在的研究對象稱為原型，也稱為“系統”、“過程”。
機械系統、電力系統、化學反應過程、生產銷售過程等都是原型； 研究原型的結構和原理，?從而進行優化、預測、評價和控制。
研究原型時的困難：無法直接研究，例如恐龍的生活習性、地質演變等問題； 不允許直接研究，例如克隆人、生化武器等； 研究成本高，具有破壞性，例如核爆炸實驗等。
為了解決這些問題，引入模型！
為了一定目的，對原型的一部分進行減縮、抽象、提煉，形成的替代物。
1.2 模型的分類
概念模型：以圖示、文字、符號等組成的流程圖形式對事物的結構和機理進行描述的模型；概念模型只能? “知其然”，無法“知其所以然”
物理模型：根據相似原理，把客觀事物按比例放大或縮小制成的模型，其結構和機理與原事物基本相同。通過dna結構的啟發建立出?港珠澳大橋潮流泥沙物理模型
優點：與原型機理有一定的相似性直觀形象，直觀形象； 缺點：往往需要占用巨大的場地、研究成本昂貴，試驗周期長。
數學模型：基于數學理論和方法，對客觀事物的結構和機理進行數量化和幾何化的模型。
1.3 數學建模
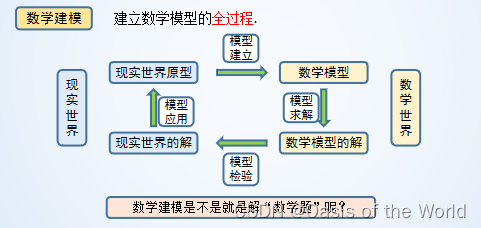
模型建立、模型求解、模型檢驗、模型應用！
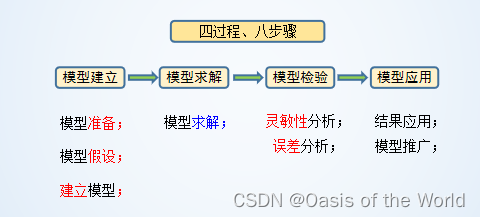
2 山崖高度的估計
2.1 不考慮空氣阻力
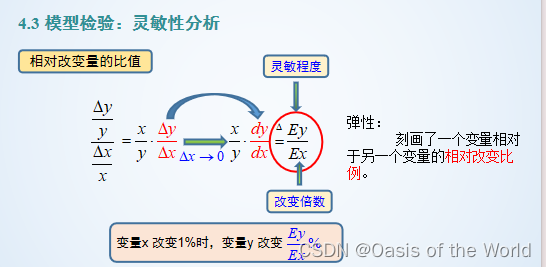
靈敏度分析
靈敏度比較好的話說明模型和結果的魯棒性比較好！！！
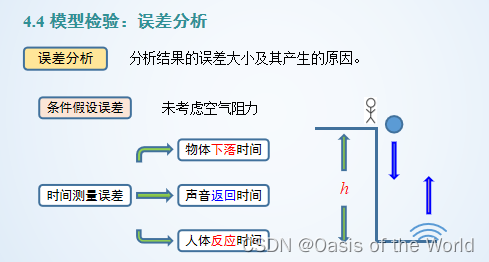
2.2 考慮空氣阻力
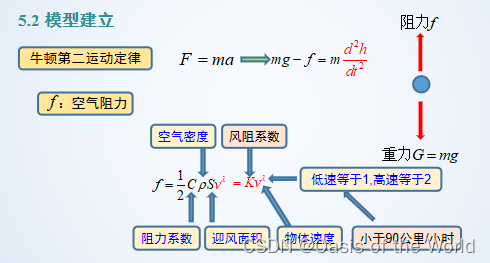
注意這個是微分方程注意微分方程的解法！！！
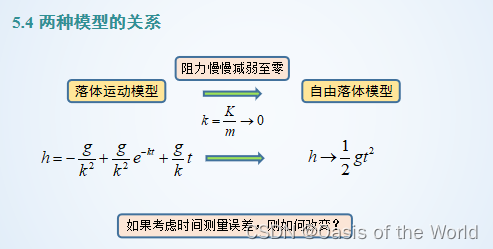
3 行車距離模型
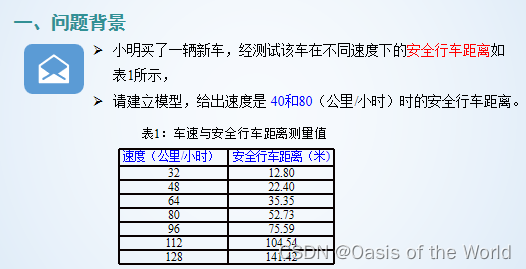
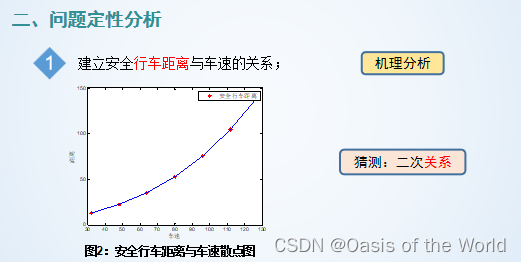
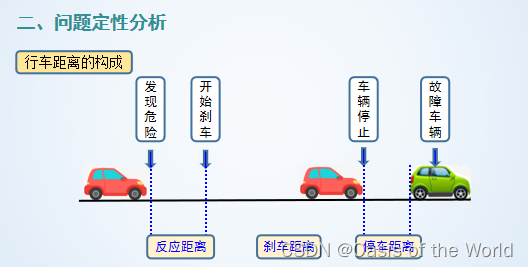
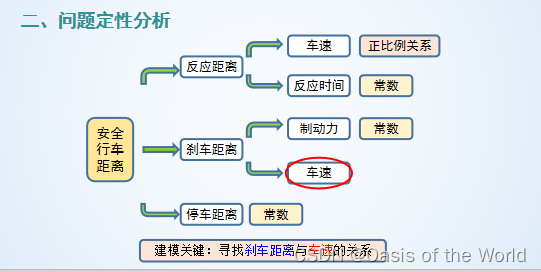
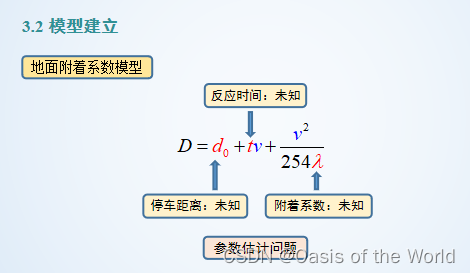
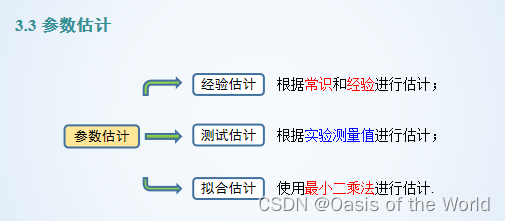
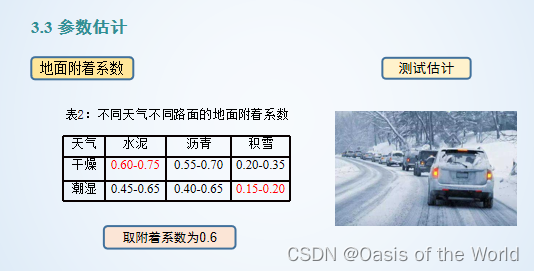
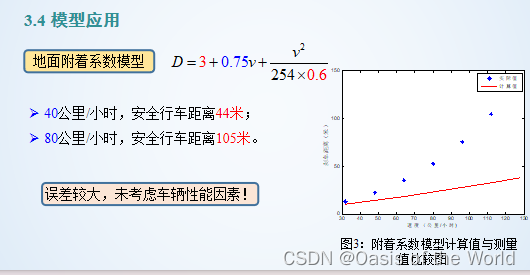
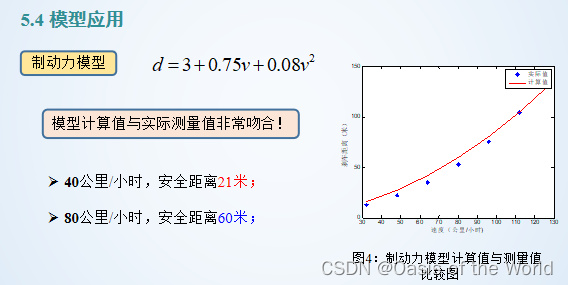
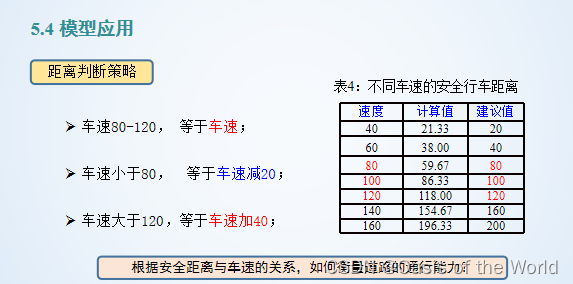
這個模型通過圖就知道誤差太大了，因為沒有考慮到車輛的性能！！！
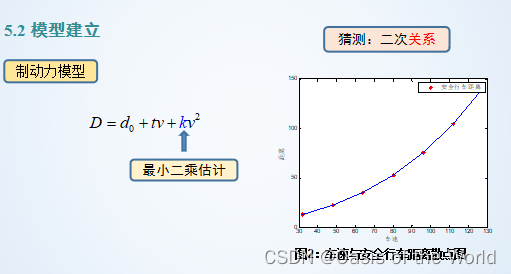
參數估計：最小二乘法【算一下】
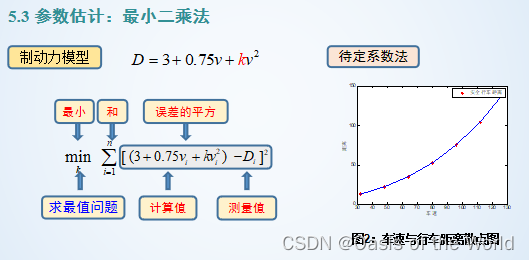
思想：讓誤差平方和達到最小！
就可以解出來了！！！！！matlab指令！！！
4 存貯模型！！！
看之前寫的那個
優化問題：在一定的約束條件下尋找最佳方案達到目的！
?不允許缺貨、允許缺貨兩種問題
不允許缺貨
多少天生產一次，一次生產多少！
生產周期變長的過程中先變小再變大！
目標是：找到目標函數！！！【每天平均下來少才是真正的少！！！】
模型假設：
模型建立：
Q=rT 一次生產就要夠這個周期所有的用量！！！
直線的斜率是r！！！！！！！【連續化】
總費用 = 貯存費＋生產費！
讓目標函數最小，求T，那就對T求導！
模型求解：
模型解釋：
敏感性分析：
自變量先變，然后T變，算出變化量！
約等那是因為：當C1趨于0的時候，就相當于求導了，然后其他的C2、r看作是常數！
負的話就是減少，正的話就是增加！
允許缺貨
模型假設：
Q = T1*r
兩個模型比較
在可以缺貨的前提下：生產周期可以長一點，每一個周期的生產量可以減少一點！
當缺貨損失特別大的時候那么 允許缺貨的模型就越來越接近不允許缺貨的了！
每個周期的生產量！！是坑！
5 森林滅火模型
總的費用一共有兩個部分！
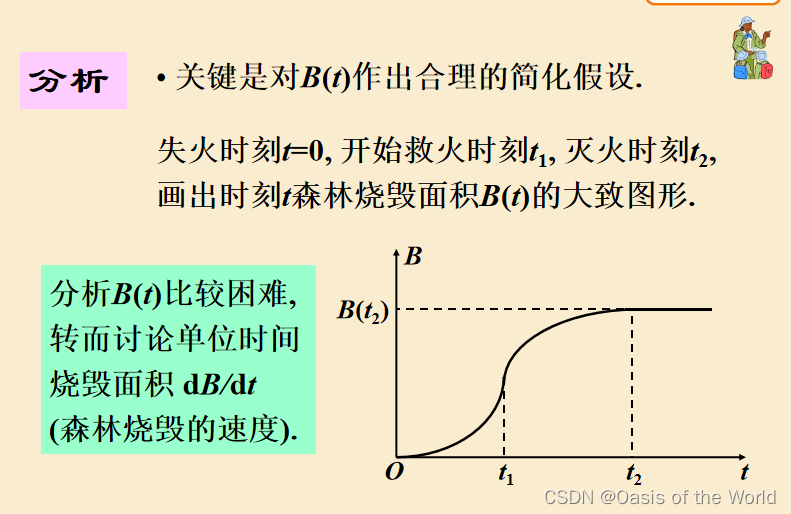
主要是目標函數的轉換：從B(t)變成了B'(t)
面積B和t方成正比 則求導之后dB/dt 與t成正比！則面積就是原目標函數咯！！！
確定出森林滅火的面積！
當x?=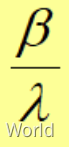
時，說明火勢蔓延的速度 = 撲滅的速度，也就是說人要再多一點！
分析變大變小的依據只有式子！！！
6 購物效用模型【不買貴的只買對的】
貴的還是好的
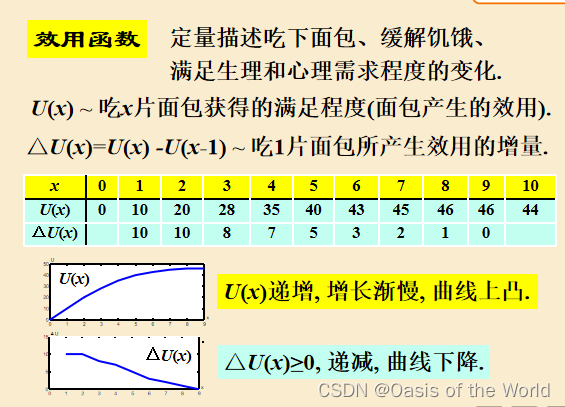
增長的越來越慢！！！
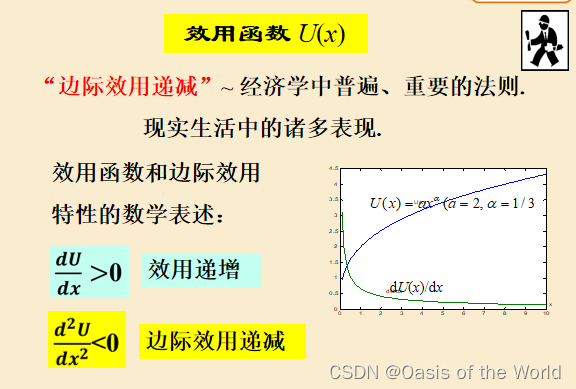
三維是不好畫圖的所以按照組合的方法！！！
無差別曲線
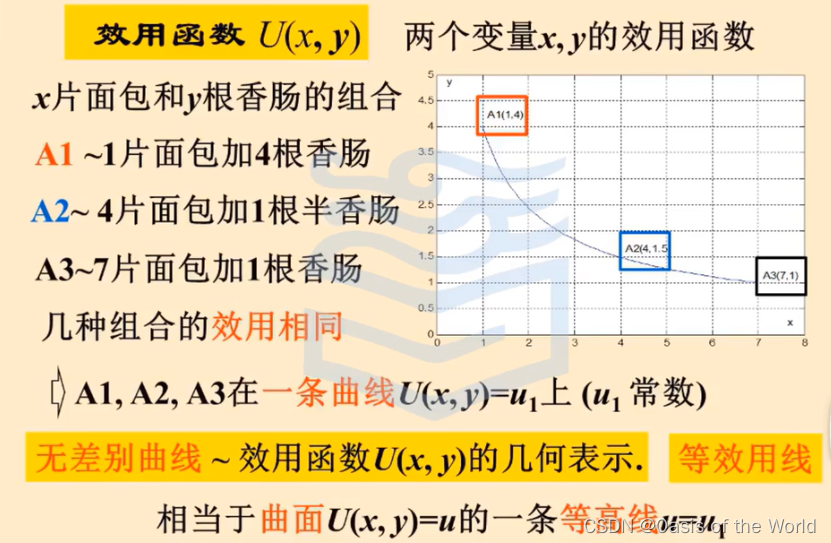
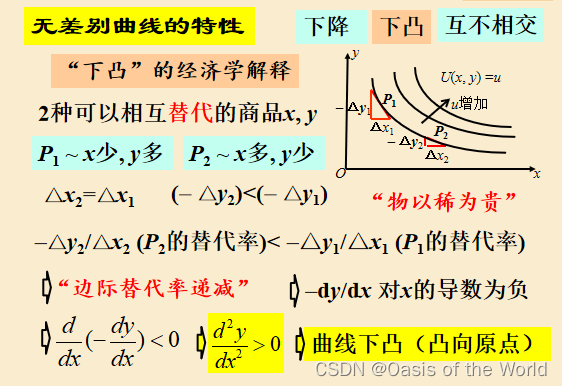
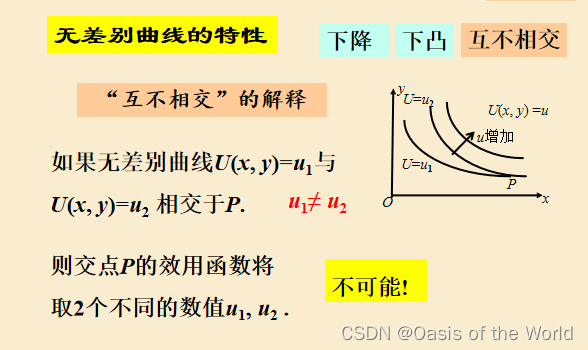
效用最大化模型：兩種商品可以相互替代！
幾何解釋相切：【無差別曲線上的效用都是一樣的！！！】
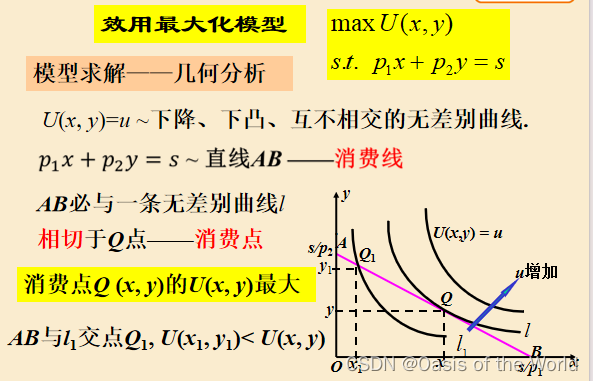
二元函數求極值！
拉格朗日乘子法！
結論
！邊際效用之比等于價格之比是 效用函數最大
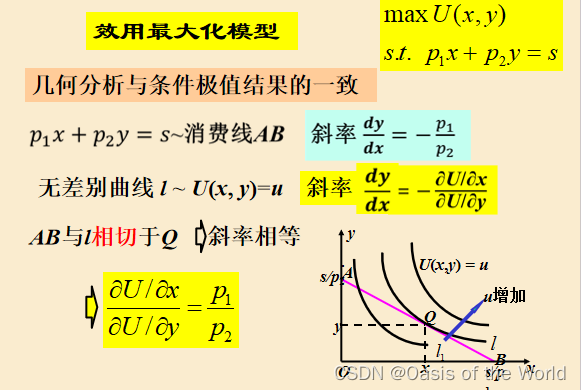
結論：
兩種商品的費用之比和商品的價格無關只和效用函數的參數有關，參數可以看作是偏愛程度
結論：
當n個商品時，單位金額邊際效用相等時效用函數最大！
重點是確定效用函數
例題
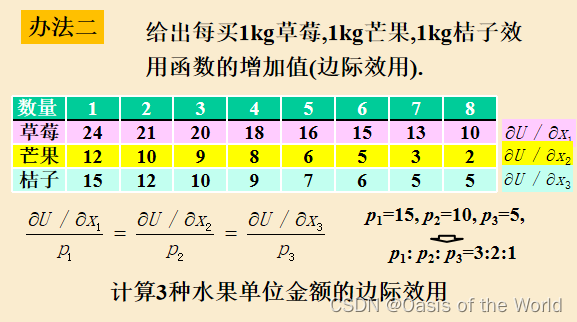
計算出單位金額的邊際效用！！！水果的價格用比值之后的就可以這樣數比較簡單好除一點！！！
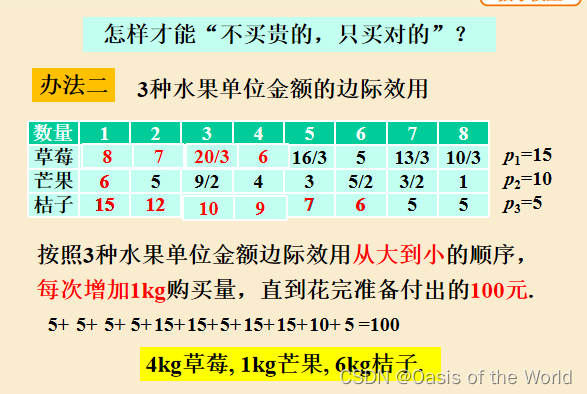
15最大 則花5塊錢買一千克桔子然后是 12? 則再花5塊錢買一千克桔子 依次類推！！！直到花夠100元
兩個方法比較：
7 牛奶加工【數學規劃模型】
難以使用多元函數極值求出最大/最小值是因為：
在這些題目里決策變量的個數n和約束條件個數m較大、最優解在可行域的邊界上取得！
因此可以通過數學規劃進行求解！！
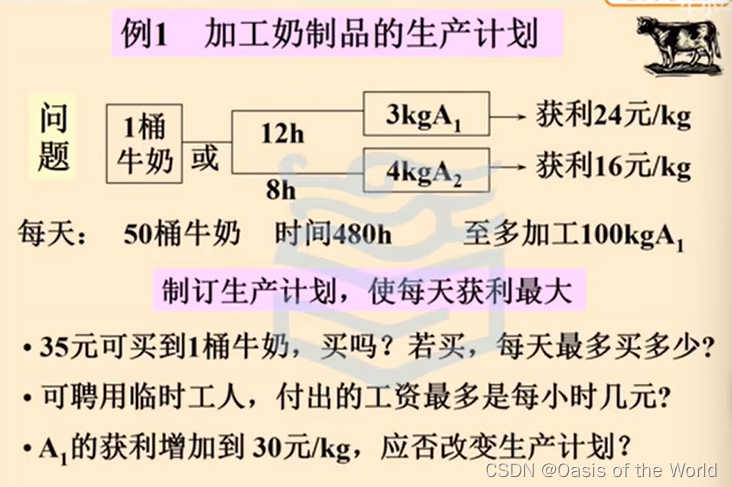
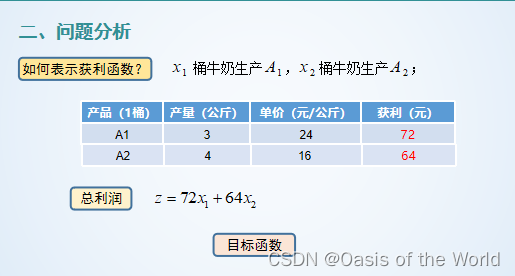
線性規劃模型
模型假設：
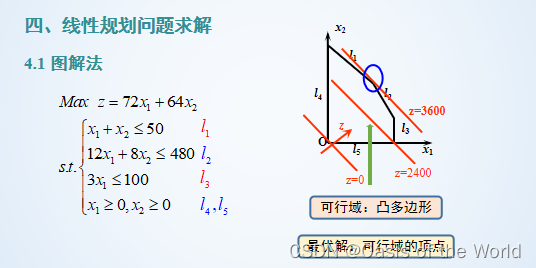
小于和小于等于是一樣的！
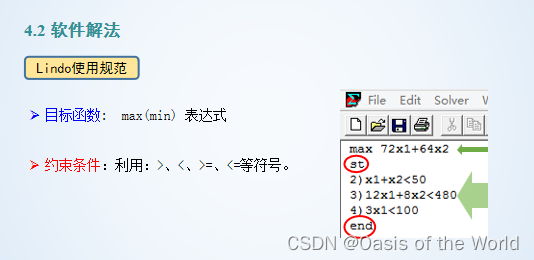
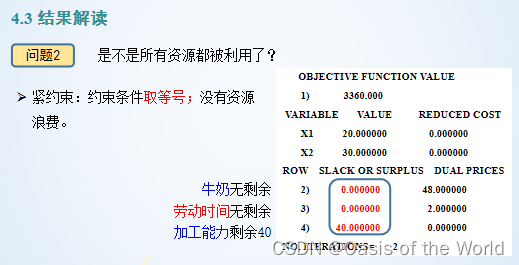
緊約束還是松約束？
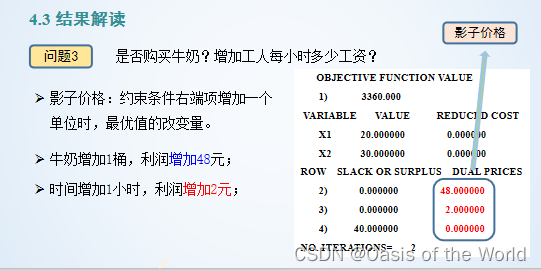
影子價格
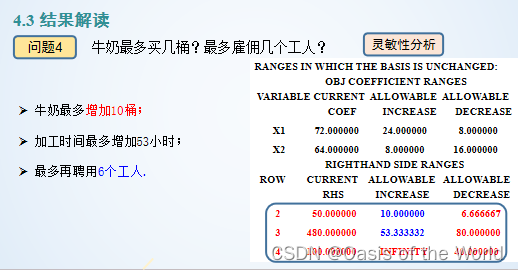
敏感性分析【"LINGO|Ranges"】
lingo-option-general solver-Dual Computation - price
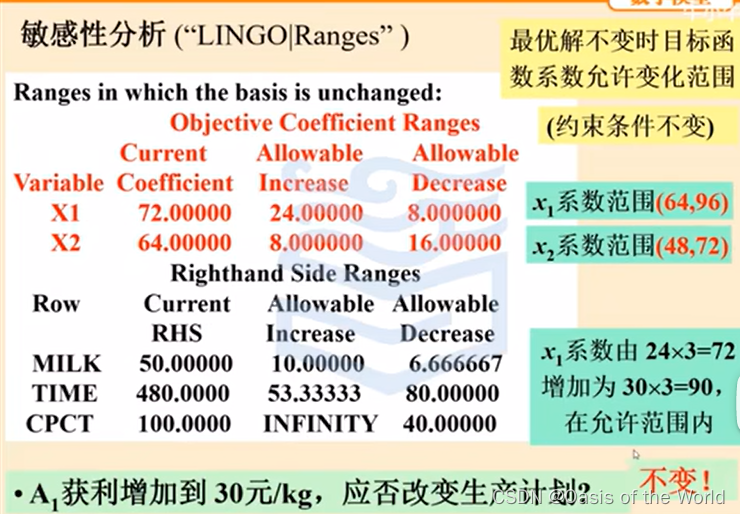
看下面
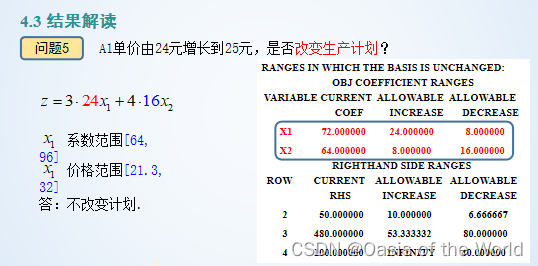
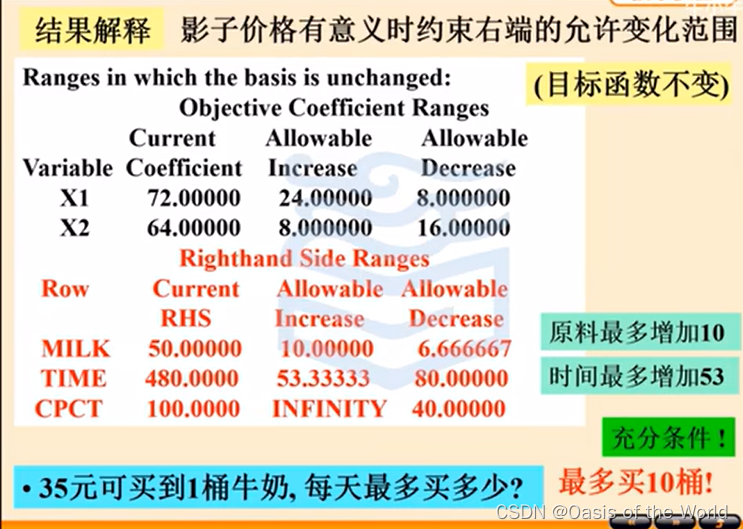
充分條件：在這個范圍里影子價格一定有意義，但不在這個范圍是可能有意義的！！！！
?
8 人口模型！！
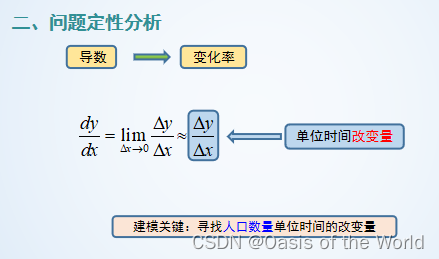
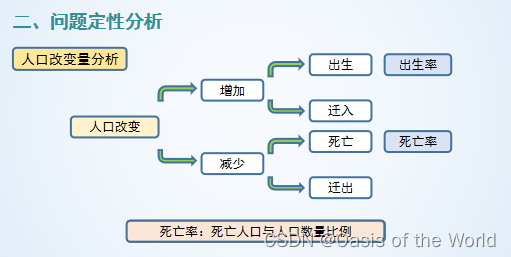
模型1假設
模型1建立：單位時間內x(t)的增量為rx(t)
與常用公式一致因為進行了泰勒展開哦
模型1求解：最小二乘法
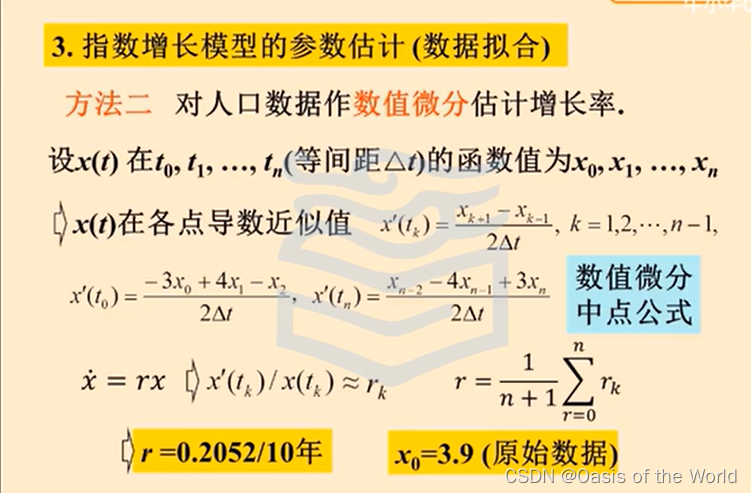
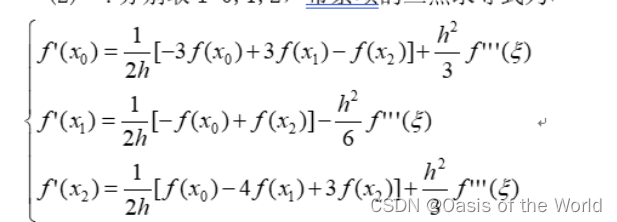
第一個公式是4x1
模型2改進
指數增長模型只適用于短期預測不適用于長期應用
logistic模型 ！！！！！
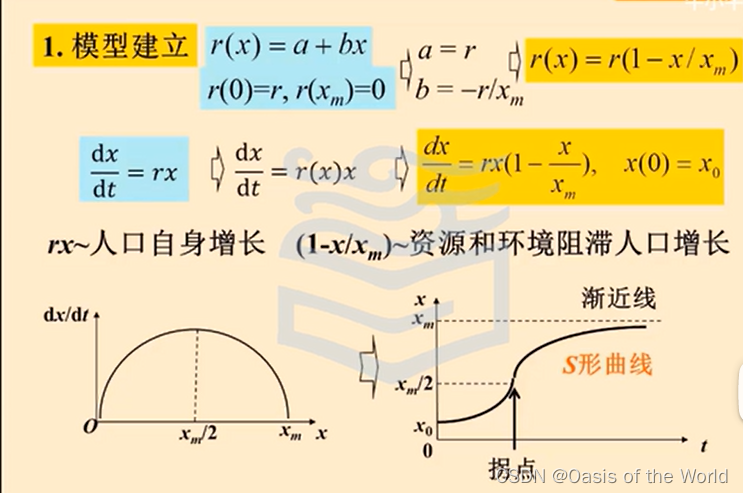
x增加的先快后慢！
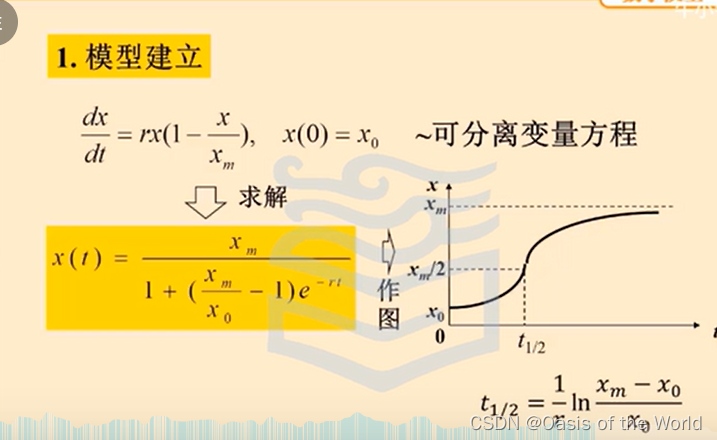
參數估計
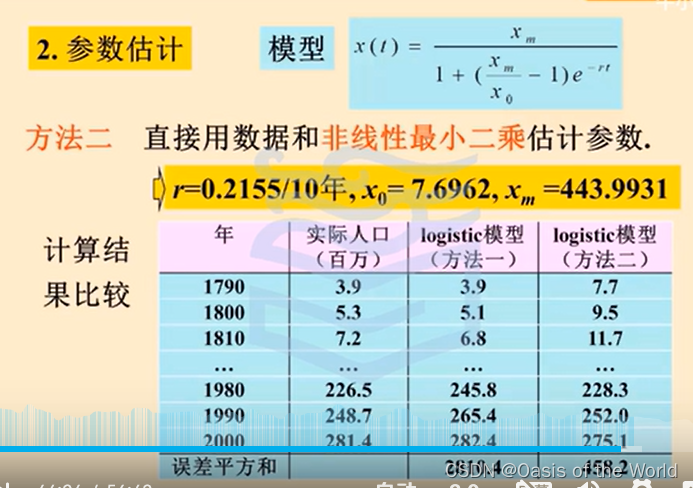
第二個估計的比較好！
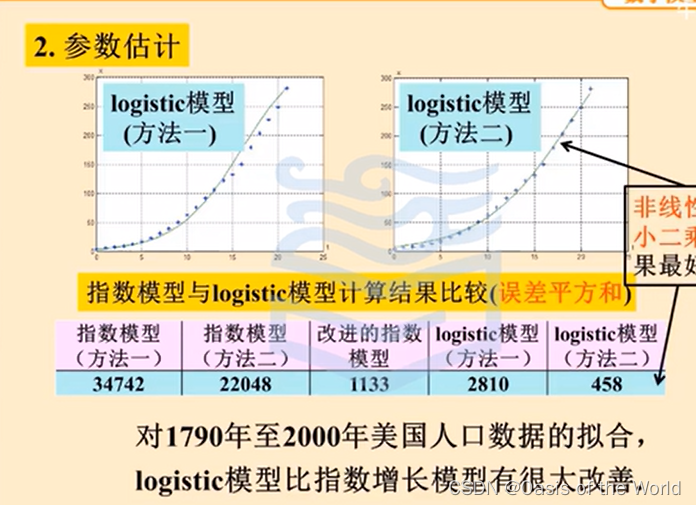
模型檢驗和預測
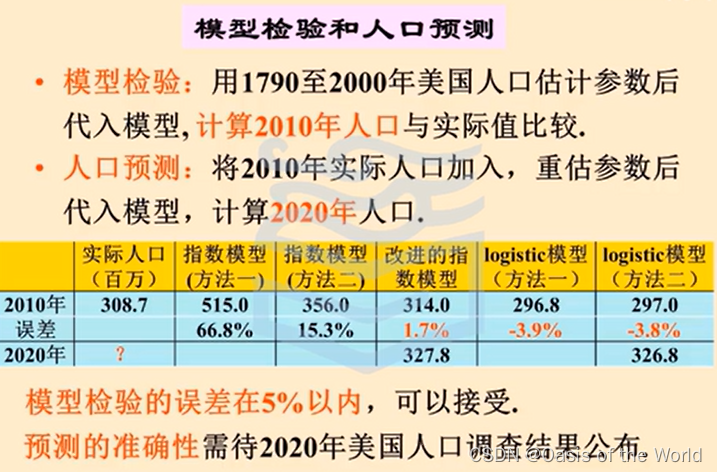
9 傳染病模型！！！
SI
左右兩邊都是患者的數量！
最大值的一半出現拐點！！！！
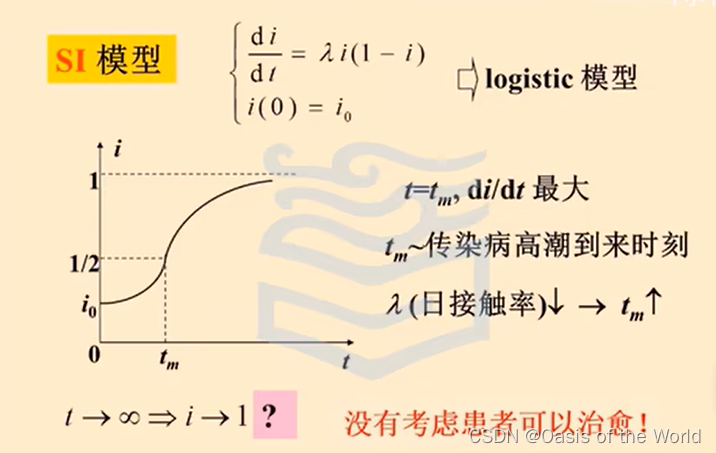
SIS
左邊還是一段時間內患者數量的增加！
記住感染期的定義！
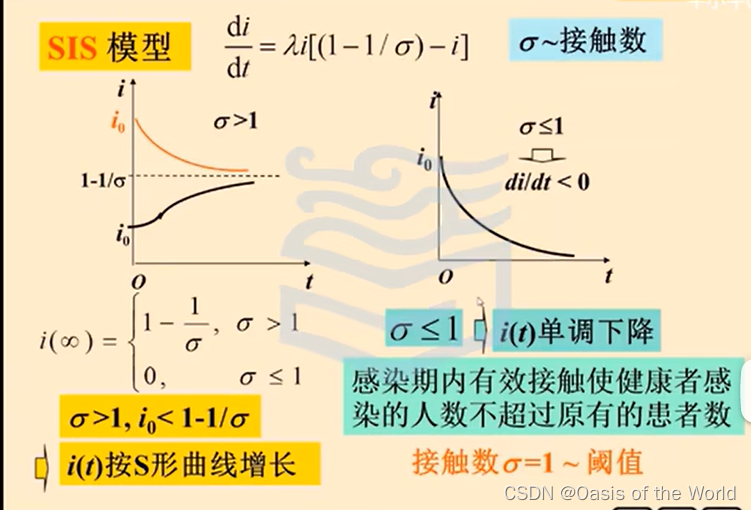
SIR
移出者不會被感染了
健康人感染之后就不是健康人了而是移除者
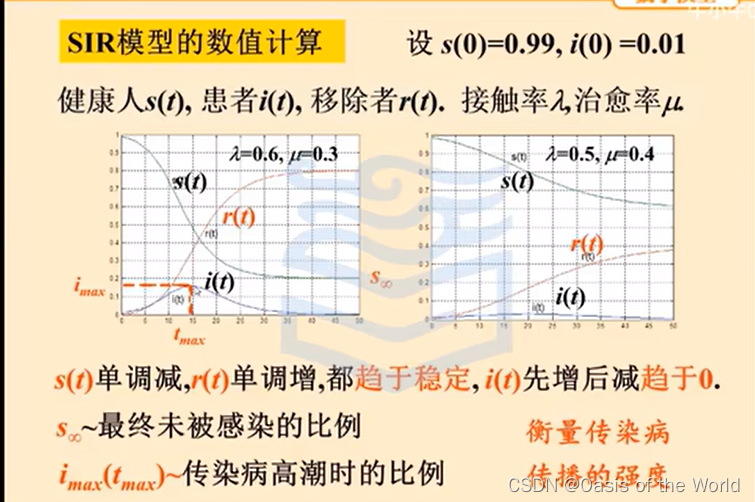
結果分析：
10 飲酒駕車模型
?
?
11 捕魚模型！！
?
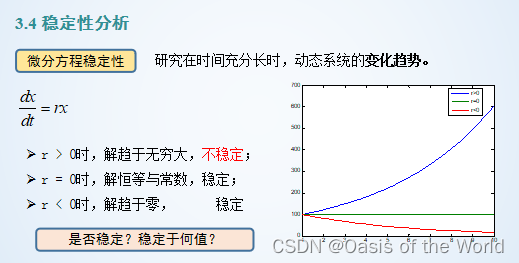
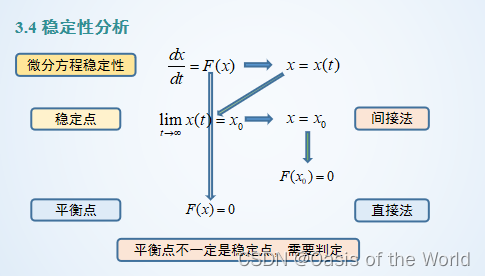
只需要知道穩定的條件！！！
一階微分方程平衡點！！！
?
你就別管：導數小于0就是穩定的，詳情可見高等數學學習筆記——第一百講——微分方程穩定性初步_線性微分方程組的穩定性判據-CSDN博客
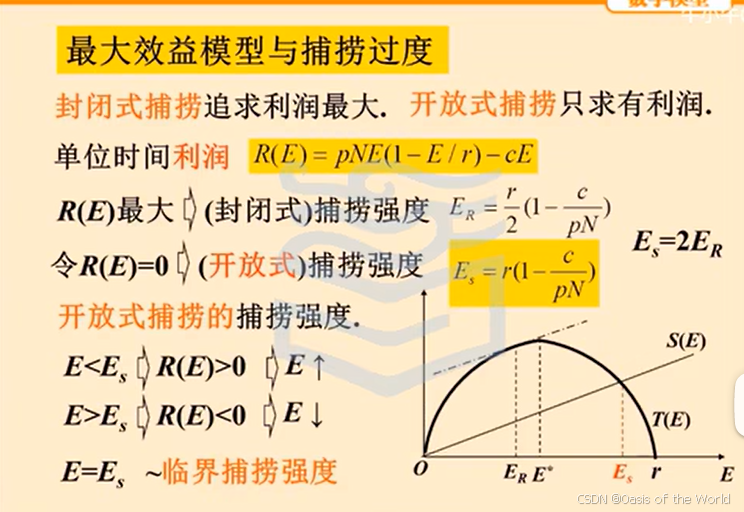
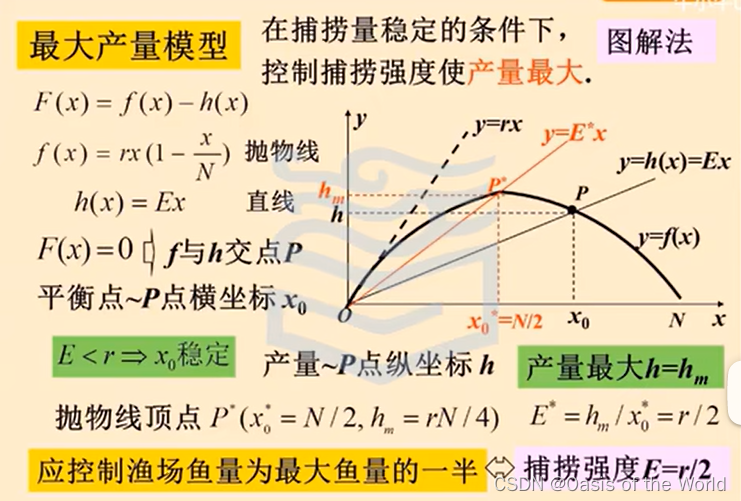最大效益模型
追求最大效益時，捕魚的強度比最大產量時小；當前魚的余量大于x0=（N/2）捕魚強度小則余量剩的多！
?
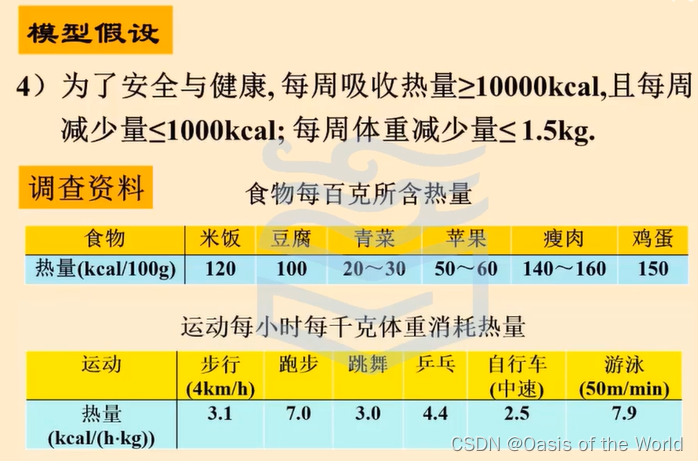
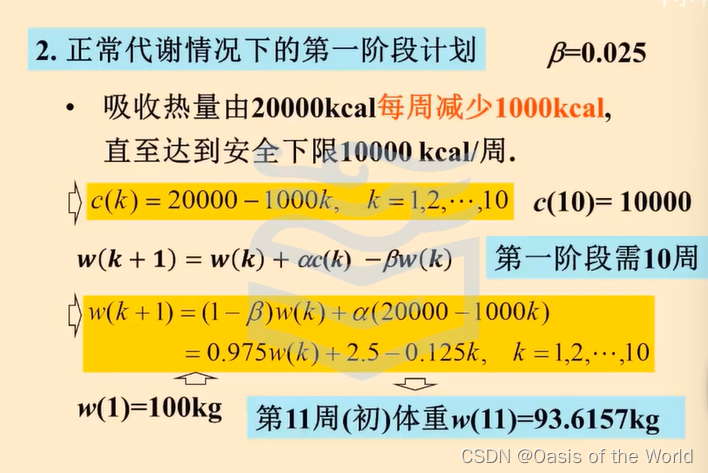
12 減肥模型【差分模型】
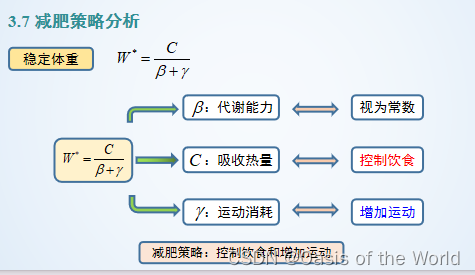
13 貸款購房【差分方程！】
等額本息貸款找的是 每個月欠款之間的遞推關系；等額本金還款找的是 每個月所還錢之間的遞推關系！
錢會越還越少，因為每個月所欠的錢都會減少x0/n，那么每個月都會減少相應的利息為（x0/n）*r
則遞推公式就寫出來了
?
?
?
?
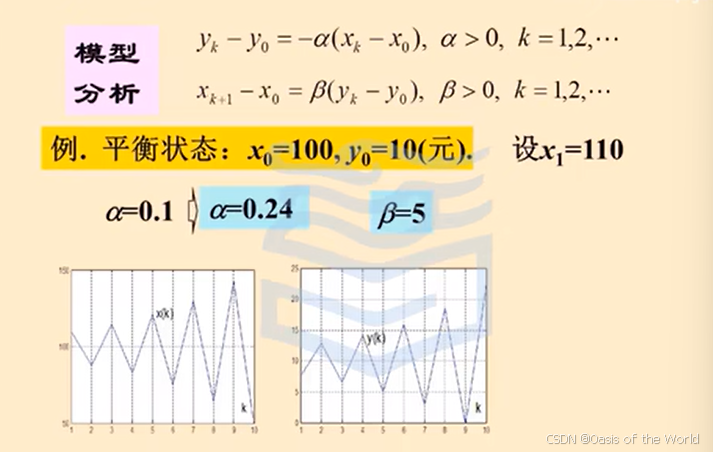
14 蛛網模型【物價的波動！】！！！
?
?
?
?
?
?
蛛網模型
?
?
?
?
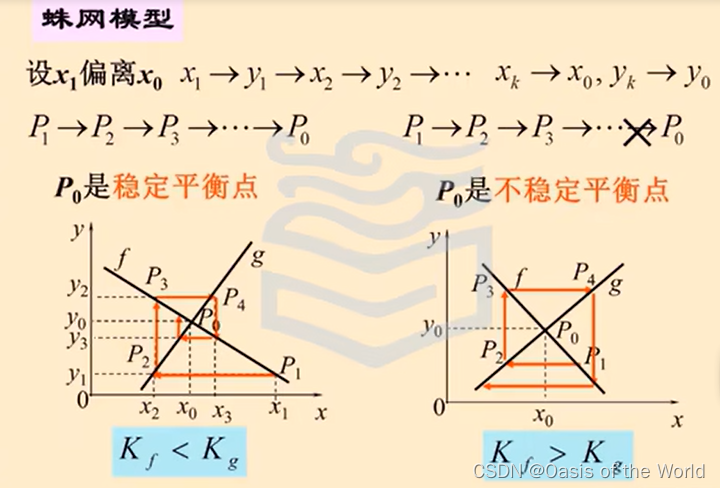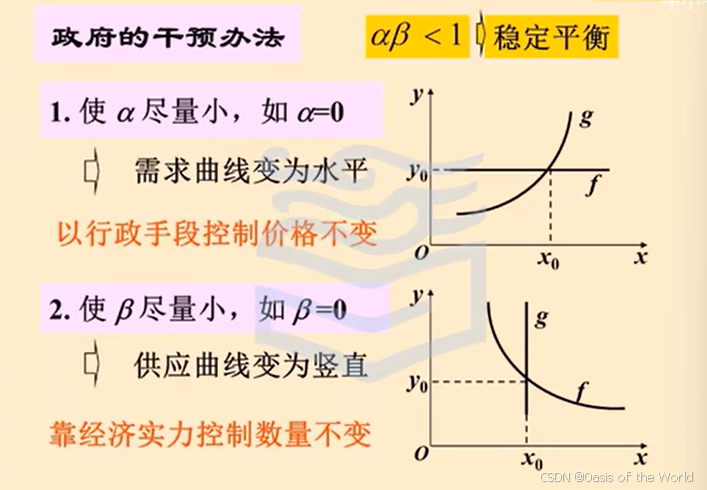
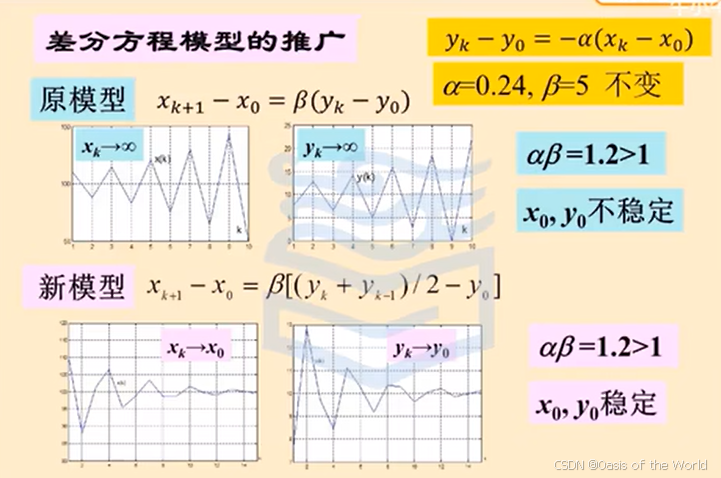
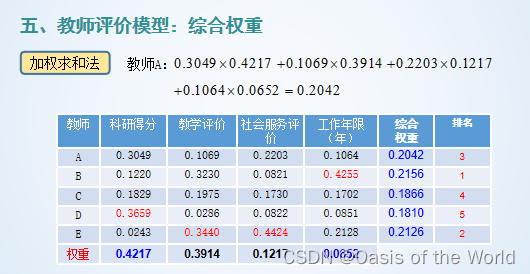
15 教師評價模型
層次分析法
?
?
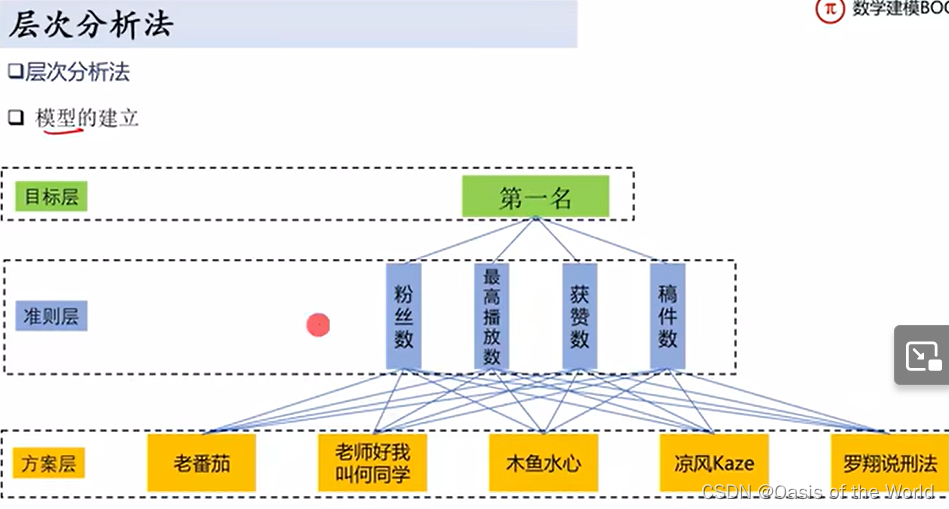
（1）歸一化處理！
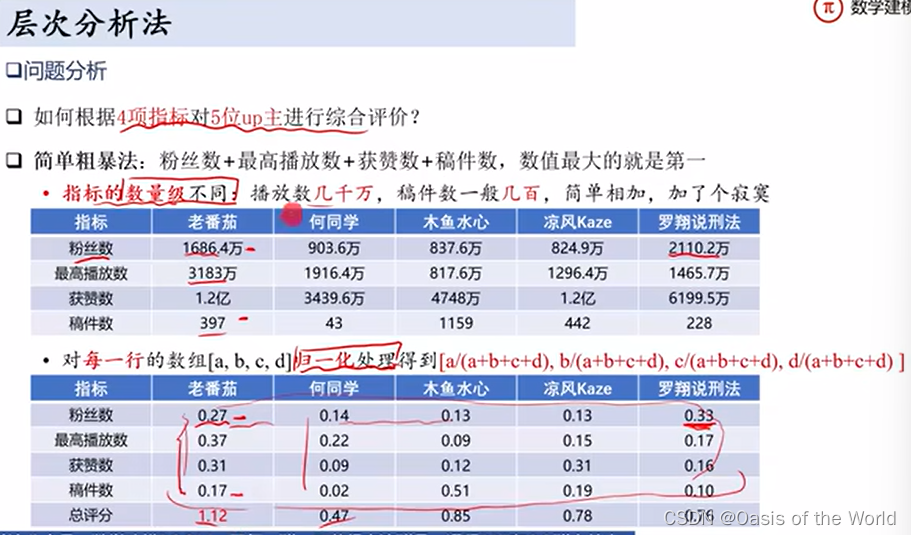
（2）給一個權重！
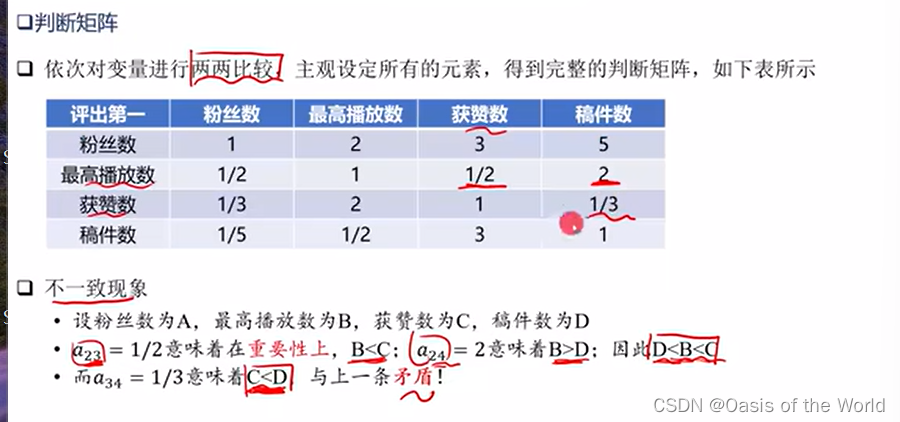
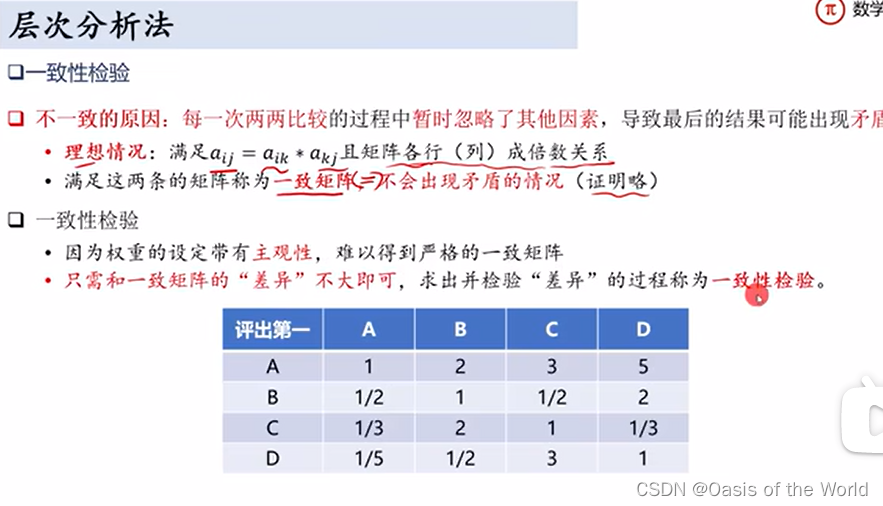
一致性檢驗：求出差異！
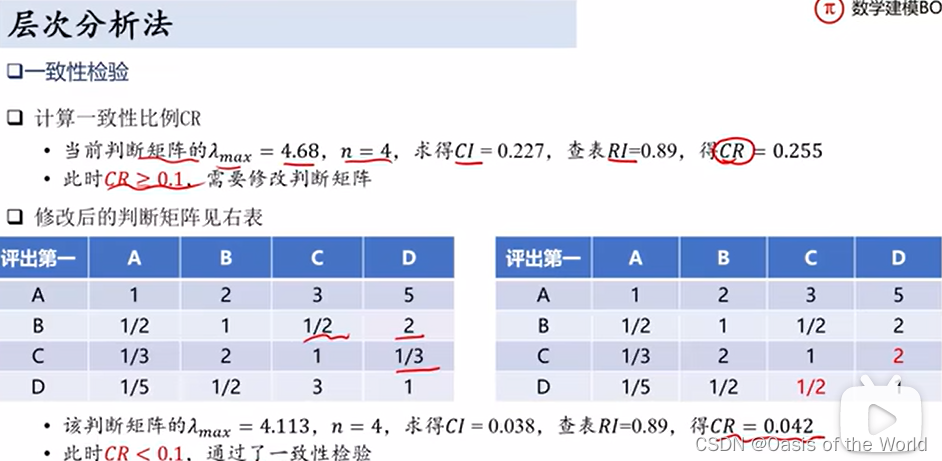
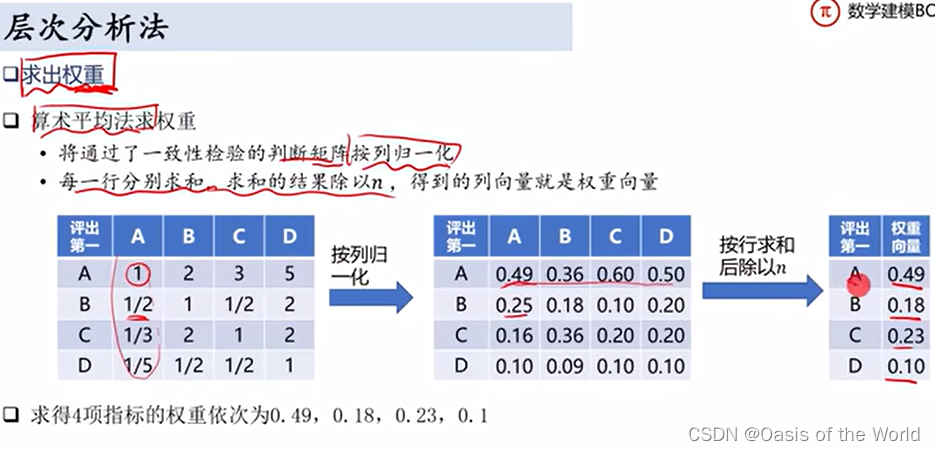
層次法的歸一化就是，除以這一列的和！
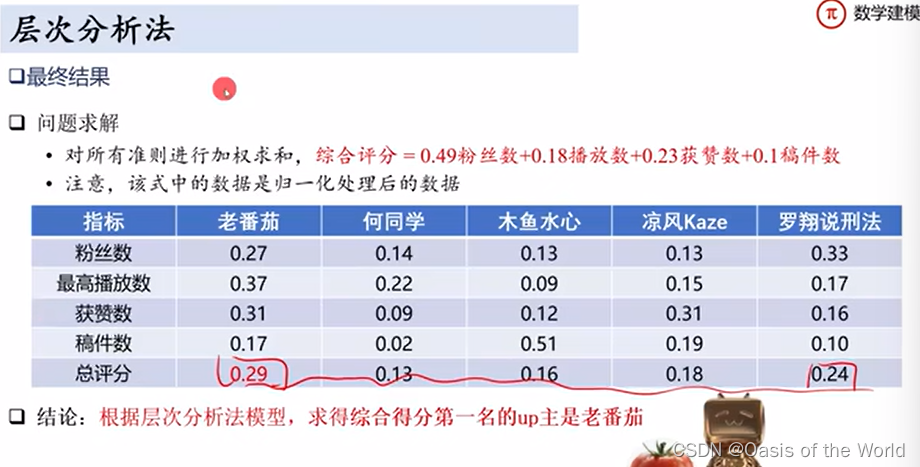
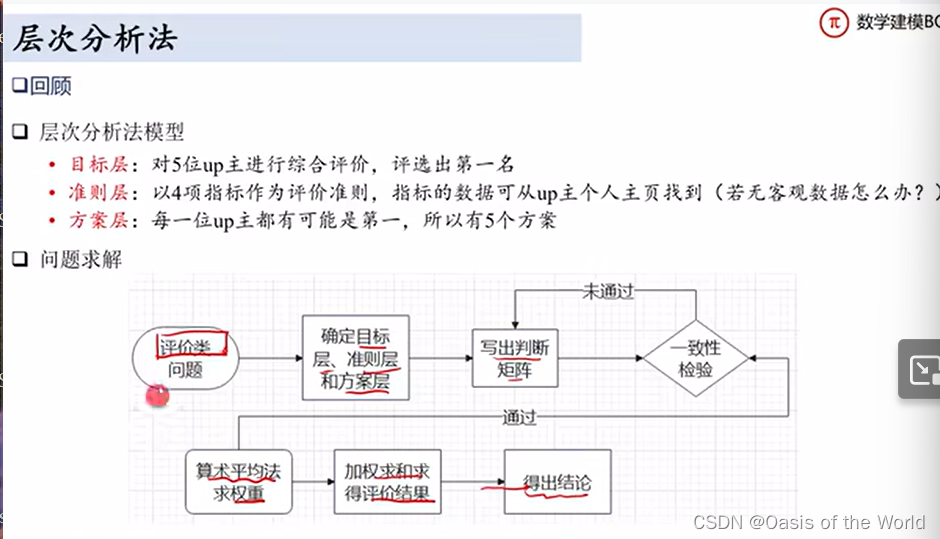
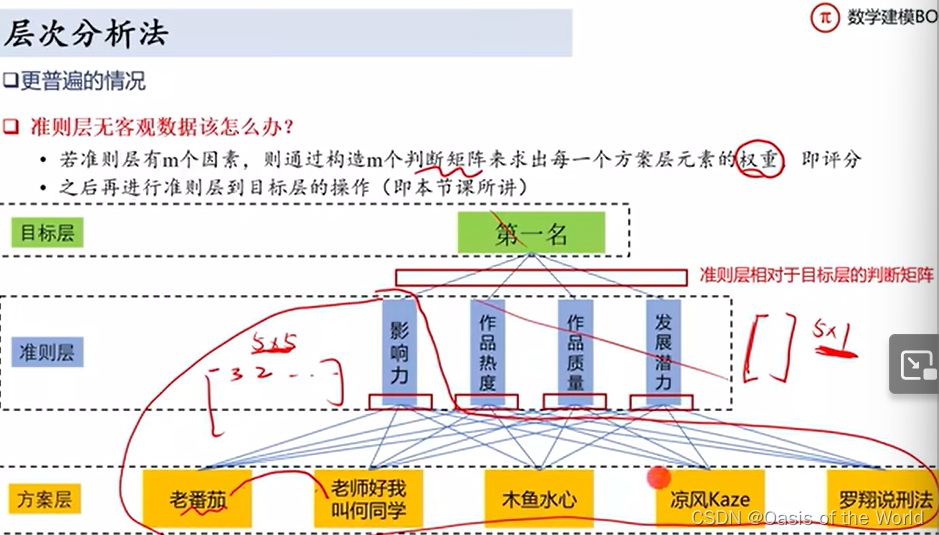
例題：
16 考研高校選擇[熵權法]
信息熵：
熵權法：
【1】歸一化
熵權法的歸一化也是除以分量和！！
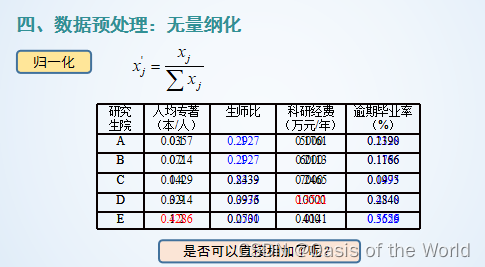
【2】計算信息熵
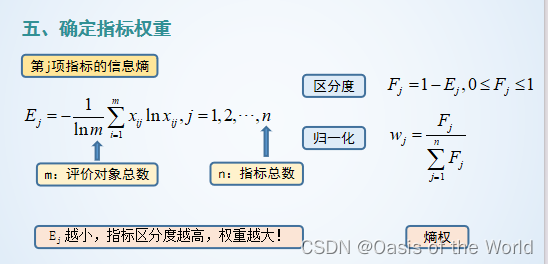
各個指標的，一個指標的算！
【3】確定權重
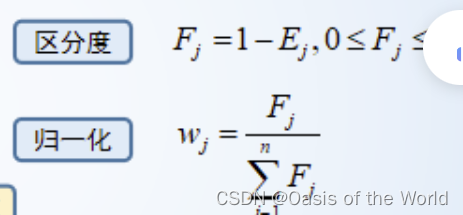
17 公平席位分配！！！
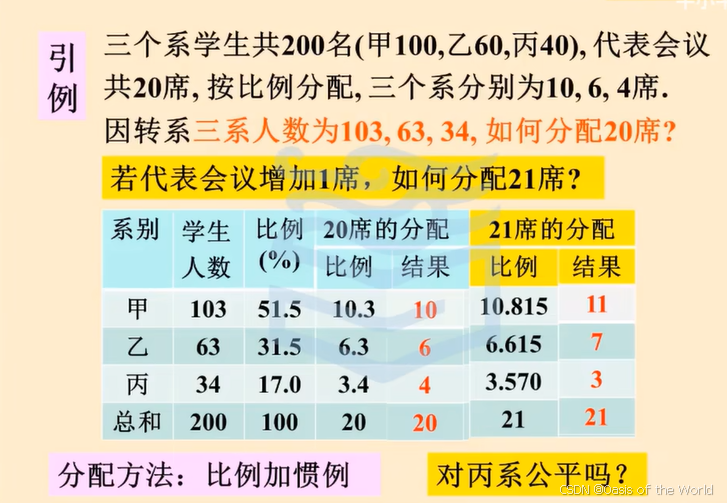
為什么席位少了
比例＋慣例的方法：
?
每個席位代表的人數多了，則對A不公平！
原則就是讓rA和rB盡量小！
1）分之前對A就不公平，分了之后還是不公平說明就該給A
Q值方法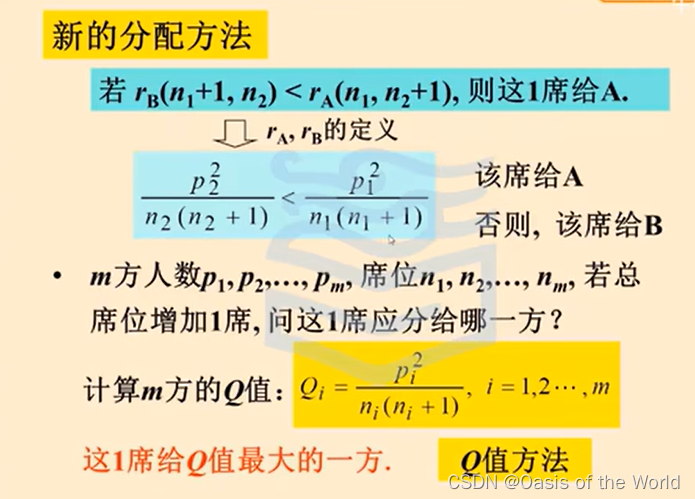
但是還不是絕對公平的哦！！！！
?
18 報童模型【隨機優化問題】
需求具有隨機性
所以平均值就有兩個部分
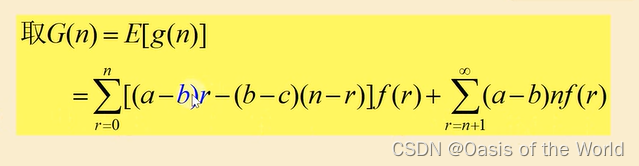
連續化求最大值！
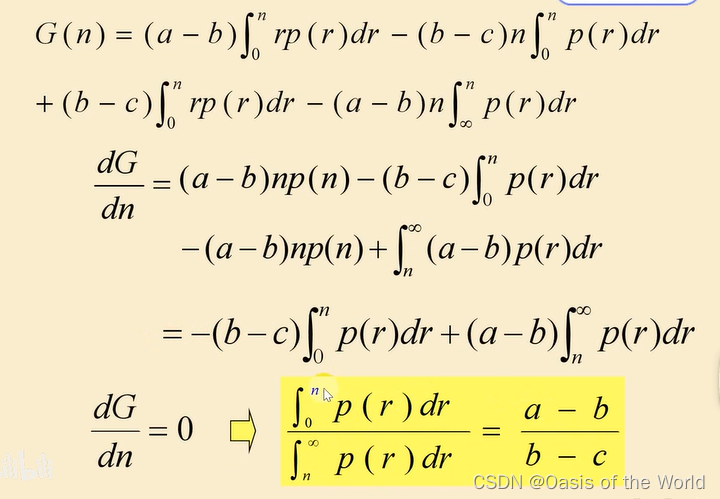
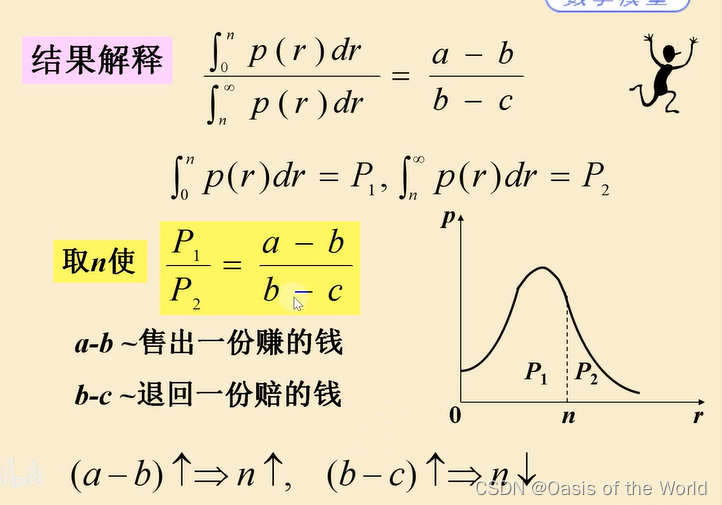
19 線性回歸
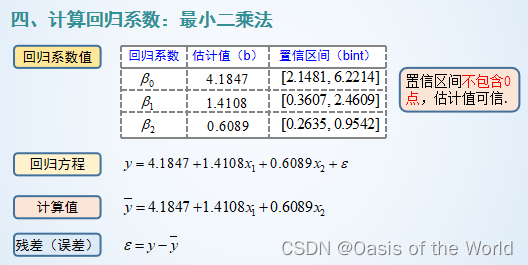
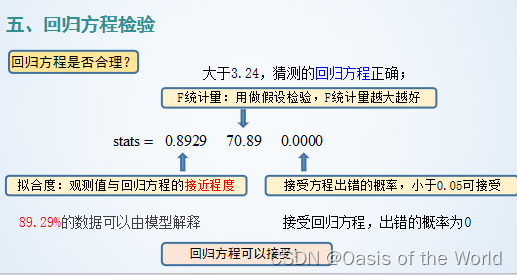
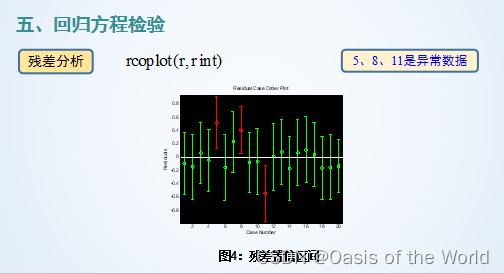
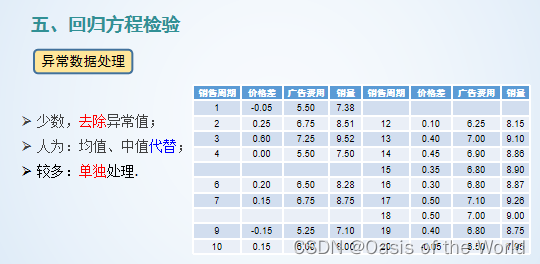
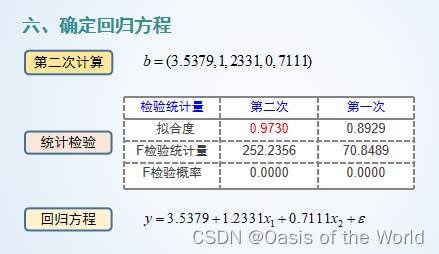
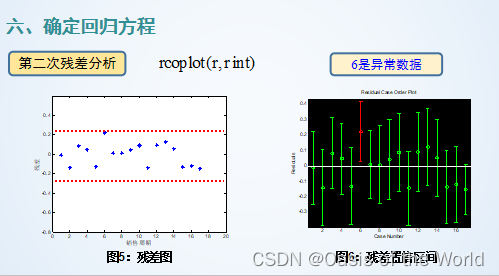
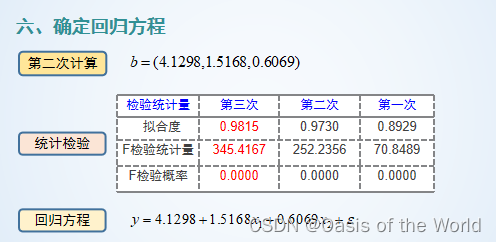
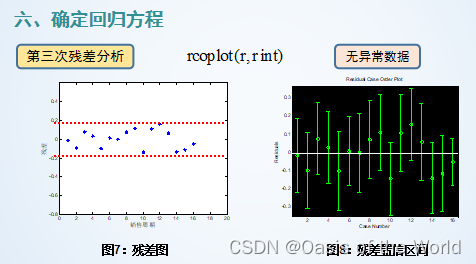
20 市場占有率
?
?
?
?
?
?
——XML文件操作sql)
