把夜熬成粥，然后喝了它。

——2024年7月1日

---

書接上回：區間動態規劃——最長回文子串（C++）-CSDN博客，大家有想到解決辦法嗎？

題目描述

????????給定一個字符串s（s僅由數字和英文大小寫字母組成，長度為1~1000），求s中最長的回文子序列長度。例如，s = “aferegga”，最長的回文子序列為“aerea”，其長度為5。

---

題解思路

? ? ? ? 區間動態規劃

下面是個人的思路：

1. 定義dp數組

????????定義 dp[i][j]表示 s[i...j] 中最長回文子序列長度。

2. 確定dp限制條件

注：len表示字符串長度

? ? ? ? ①對于任何 len == 1 的字符串，dp[i][j] = 1；

? ? ? ? ②對于任何 len == 2 的字符串，dp[i][j] = dp[i][j-1] + (s[i] == s[j])；

? ? ? ? ③對于任何 len ?≥ ?3 的字符串，有兩種情況：

????????如果 s[i] == s[j]，那么dp[i][j] = dp[i+1][j-1] + 2；

? ? ? ? 如果?s[i] != s[j]，那么dp[i][j] = max(dp[i+1][j]，dp[i][j-1])；

解釋如下：

? ? ? ? 第一種情況，如果字符串長度為1的話，那么它一定是回文子串，長度唯一；

? ? ? ? 第二種情況，如果字符串長度為2，那它就有兩種可能，要么這兩個字符相等，要么不等，不管哪一種情況，這個字符串的回文子序列至少是大于等于1的（第一種情況），如果相等，無非是把這個相等的加上即可。

? ? ? ? 第三種情況，字符串長度不小于3時，也有兩種可能：
????????如果?s[i] == s[j]，那么當前最長回文子序列長度就等于上一次的回文子序列長度加上2（兩個相同的字符），也可以表示為dp[i][j] = dp[i+1][j-1] + 2*(s[i] == s[j])；
????????如果?s[i] != s[j]，那么當前最長回文子序列長度至少是在 s[i+1....j]和s[i....j-1]中取最大值，即dp[i][j] = max(dp[i+1][j]，dp[i][j-1])。

---

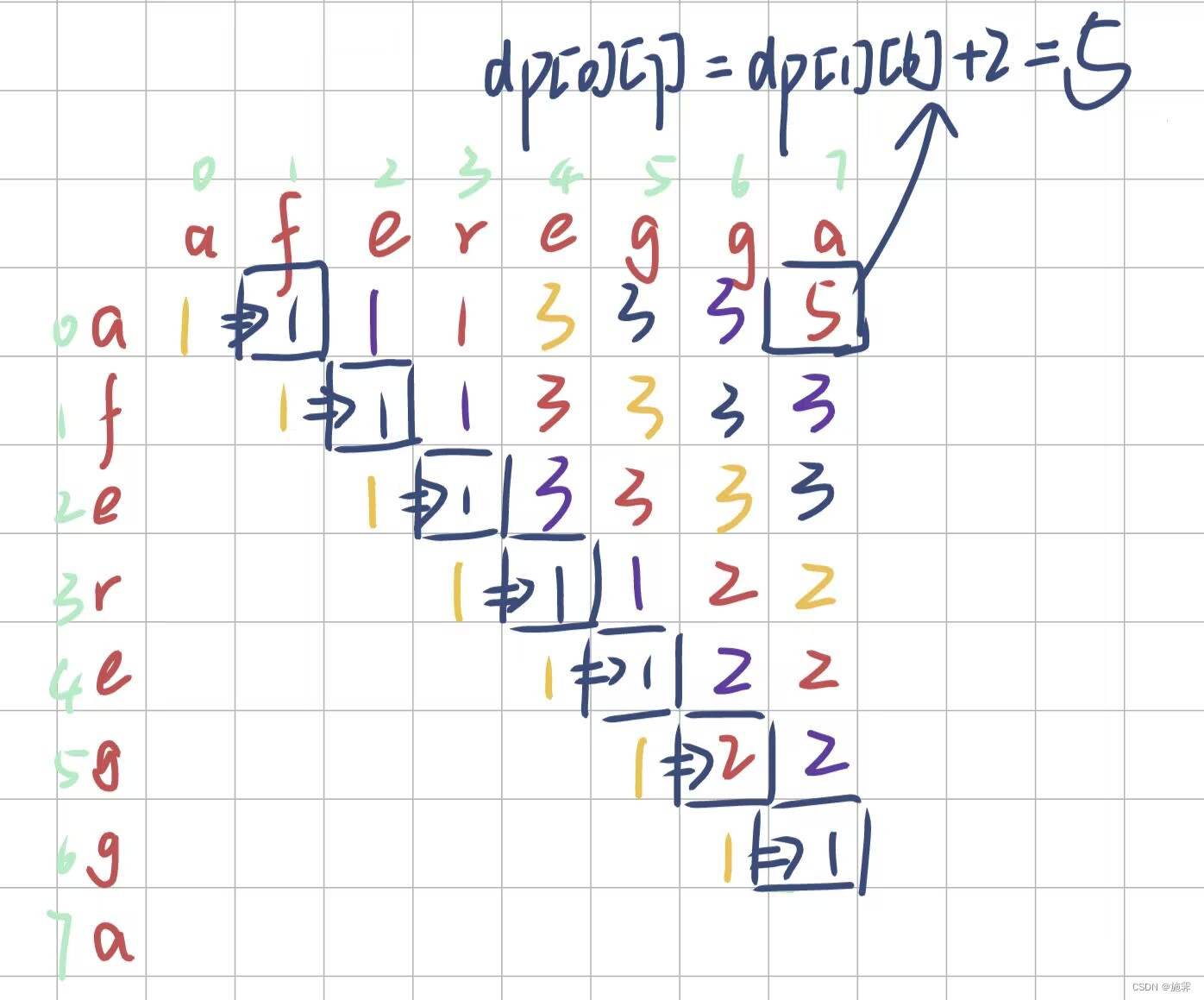
推導過程

用矩陣推導如下：

?

代碼展示

// 最長回文子序列長度
int getLongestPalind(string s){int size = s.size();vector<vector<int>> dp(size, vector<int> (size, 0));// 定義dp數組// dp[i][j]表示從i到j的最長子回文字符串長度for(int len = 1; len <= size; len++){for(int i = 0; i + len - 1 < size; i++){int j = i + len - 1;if(len == 1){dp[i][j] = 1;}else if(len == 2){dp[i][j] = dp[i][j-1] + (s[i] == s[j]);}else{if(s[i] == s[j]){dp[i][j] = dp[i+1][j-1] + 2 * (s[i] == s[j]);}else{dp[i][j] = max(dp[i+1][j], dp[i][j-1]);}}}}return dp[0][size-1];
}

運行結果

完整代碼

// 區間動態規劃
#include<iostream>
#include<vector>
#include<string>using namespace std;// 最長回文子序列長度
int getLongestPalind(string s){int size = s.size();vector<vector<int>> dp(size, vector<int> (size, 0));// 定義dp數組// dp[i][j]表示從i到j的最長子回文字符串長度for(int len = 1; len <= size; len++){for(int i = 0; i + len - 1 < size; i++){int j = i + len - 1;if(len == 1){dp[i][j] = 1;}else if(len == 2){dp[i][j] = dp[i][j-1] + (s[i] == s[j]);}else{if(s[i] == s[j]){dp[i][j] = dp[i+1][j-1] + 2 * (s[i] == s[j]);}else{dp[i][j] = max(dp[i+1][j], dp[i][j-1]);}}}}return dp[0][size-1];
}int main(){string s;cout<<"請輸入字符串s：";cin>>s;cout<<"最長回文子序列長度為"<<getLongestPalind(s)<<endl;return 0;
}