常見函數的導數
常量函數的導數
d d x ( c ) = 0 \frac{d}{dx}(c) = 0 dxd?(c)=0
常量函數的圖像是一條水平線 y = c y = c y=c,它的斜率為0,所以我們必須有 f ′ ( x ) = 0 f'(x) = 0 f′(x)=0。從導數的定義來看,證明也很簡單:
f ′ ( x ) = lim ? h → 0 f ( x + h ) ? f ( x ) h = lim ? h → 0 c ? c h = lim ? h → 0 0 h = 0 f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} = \lim_{h \to 0} \frac{c - c}{h} = \lim_{h \to 0} \frac{0}{h} = 0 f′(x)=h→0lim?hf(x+h)?f(x)?=h→0lim?hc?c?=h→0lim?h0?=0
冪函數的導數
接下來看冪函數 f ( x ) = x n f(x) = x^n f(x)=xn,其中 n n n為正整數。當 n = 1 n = 1 n=1時,函數的圖像是一條直線,斜率為 1 1 1。
d d x ( x ) = 1 \frac{d}{dx}(x) = 1 dxd?(x)=1
當 n = 2 n = 2 n=2或 n = 3 n = 3 n=3時,根據上一節的計算,我們得知它們的導數為
d d x ( x 2 ) = 2 x \frac{d}{dx}(x^2) = 2x dxd?(x2)=2x
d d x ( x 3 ) = 3 x 2 \frac{d}{dx}(x^3) = 3x^2 dxd?(x3)=3x2
從上面的冪函數導數,我們有理由猜測 ( d / d x ) ( x n ) = n x n ? 1 (d/dx)(x^n) = nx^{n-1} (d/dx)(xn)=nxn?1。
冪函數的導數
d d x ( x n ) = n x n ? 1 \frac{d}{dx}(x^n) = nx^{n-1} dxd?(xn)=nxn?1
第一種證明
已知公式
x n ? a n = ( x ? a ) ( x n ? 1 + x n ? 2 a + ? + x a n ? 2 + a n ? 1 ) x^n - a^n = (x - a)(x^{n-1} + x^{n-2}a + \dots +xa^{n-2} + a^{n-1}) xn?an=(x?a)(xn?1+xn?2a+?+xan?2+an?1)
因此:
f ′ ( a ) = lim ? x → a f ( x ) ? f ( a ) x ? a = lim ? x → a x n ? a n x ? a = lim ? x → a ( x n ? 1 + x n ? 2 a + ? + x a n ? 2 + a n ? 1 ) = a n ? 1 + a n ? 2 a + ? + a a n ? 2 + a n ? 1 = n a n ? 1 \begin{align*} f'(a) = \lim_{x \to a} \frac{f(x) - f(a)}{x - a} &= \lim_{x \to a} \frac{x^n - a^n}{x - a} \\ &= \lim_{x \to a} (x^{n-1} + x^{n-2}a + \dots + xa^{n-2} + a^{n-1}) \\ &= a^{n-1} + a^{n-2} a+ \dots + aa^{n-2} + a^{n-1} \\ &= n a^{n-1} \end{align*} f′(a)=x→alim?x?af(x)?f(a)??=x→alim?x?axn?an?=x→alim?(xn?1+xn?2a+?+xan?2+an?1)=an?1+an?2a+?+aan?2+an?1=nan?1?
第二種證明
使用二項式定理進行展開:
f ′ ( x ) = lim ? h → 0 ( x + h ) n ? x n h = lim ? h → 0 [ x n + n x n ? 1 h + n ( n ? 1 ) 2 x n ? 2 h 2 + ? + n h x n ? 1 + h n ] ? x n h = lim ? h → 0 [ n x n ? 1 h + n ( n ? 1 ) 2 x n ? 2 h 2 + ? + n h x n ? 1 + h n h ] = lim ? h → 0 [ n x n ? 1 + n ( n ? 1 ) 2 x n ? 2 h + ? + n h x n ? 1 + h n ? 1 ] = n x n ? 1 \begin{align*}f'(x) = \lim_{h \to 0} \frac{(x + h)^n - x^n}{h} &= \lim_{h \to 0} \frac{\left[ x^n + nx^{n-1}h + \frac{n(n-1)}{2}x^{n-2}h^2 + \cdots + nhx^{n-1} + h^n \right] - x^n}{h} \\ &= \lim_{h \to 0} \left[ \frac{nx^{n-1}h + \frac{n(n-1)}{2}x^{n-2}h^2 + \cdots + nhx^{n-1} + h^n}{h} \right] \\ &= \lim_{h \to 0} \left[ nx^{n-1} + \frac{n(n-1)}{2}x^{n-2}h + \cdots + nhx^{n-1} + h^{n-1} \right] \\ &= nx^{n-1}\end{align*} f′(x)=h→0lim?h(x+h)n?xn??=h→0lim?h[xn+nxn?1h+2n(n?1)?xn?2h2+?+nhxn?1+hn]?xn?=h→0lim?[hnxn?1h+2n(n?1)?xn?2h2+?+nhxn?1+hn?]=h→0lim?[nxn?1+2n(n?1)?xn?2h+?+nhxn?1+hn?1]=nxn?1?
例子 1
(a) 如果 f ( x ) = x 6 f(x) = x^6 f(x)=x6,則 f ’ ( x ) = 6 x 5 f’(x) = 6x^5 f’(x)=6x5。
(b) 如果 y = x 1000 y = x^{1000} y=x1000,則 y ’ = 1000 x 999 y’ = 1000x^{999} y’=1000x999。
(c) 如果 y = t 4 y = t^4 y=t4,則 d y d t = 4 t 3 \frac{dy}{dt} = 4t^3 dtdy?=4t3。
(d) 如果 d d r ( r 3 ) = 3 r 2 \frac{d}{dr} (r^3) = 3r^2 drd?(r3)=3r2。
組合函數的導數
常數倍法則
如果 c c c 是一個常數且 f f f 是可微函數,則
d d x [ c f ( x ) ] = c d d x [ f ( x ) ] \frac{d}{dx}[c f(x)] = c \frac{d}{dx}[f(x)] dxd?[cf(x)]=cdxd?[f(x)]
證明
令 t ( x ) = c f ( x ) t(x) = c f(x) t(x)=cf(x)。則
t ’ ( x ) = lim ? h → 0 t ( x + h ) ? t ( x ) h = lim ? h → 0 c f ( x + h ) ? c f ( x ) h = lim ? h → 0 [ c f ( x + h ) ? f ( x ) h ] = c lim ? h → 0 f ( x + h ) ? f ( x ) h = c f ’ ( x ) \begin{align*}t’(x) = \lim_{h \to 0} \frac{t(x+h) - t(x)}{h} &= \lim_{h \to 0} \frac{c f(x+h) - c f(x)}{h} \\ &= \lim_{h \to 0} \left[ c \frac{f(x+h) - f(x)}{h} \right] \\ &= c \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \\ &= c f’(x)\end{align*} t’(x)=h→0lim?ht(x+h)?t(x)??=h→0lim?hcf(x+h)?cf(x)?=h→0lim?[chf(x+h)?f(x)?]=ch→0lim?hf(x+h)?f(x)?=cf’(x)?
例子 2
(a) d d x ( 3 x 4 ) = 3 d d x ( x 4 ) = 3 ( 4 x 3 ) = 12 x 3 \frac{d}{dx}(3x^4) = 3 \frac{d}{dx}(x^4) = 3(4x^3) = 12x^3 dxd?(3x4)=3dxd?(x4)=3(4x3)=12x3
(b) d d x ( 2 x ) = d d x [ 2 ? x ] = 2 ? d d x ( x ) = 2 ? 1 = 2 \frac{d}{dx}(2x) = \frac{d}{dx}[2 \cdot x] = 2 \cdot \frac{d}{dx}(x) = 2 \cdot 1 = 2 dxd?(2x)=dxd?[2?x]=2?dxd?(x)=2?1=2
和法則
如果 f f f 和 t t t 都是可微的,則
d d x [ f ( x ) + t ( x ) ] = d d x [ f ( x ) ] + d d x [ t ( x ) ] \frac{d}{dx}[f(x) + t(x)] = \frac{d}{dx}[f(x)] + \frac{d}{dx}[t(x)] dxd?[f(x)+t(x)]=dxd?[f(x)]+dxd?[t(x)]
用導數符號表示,可以寫成:
( f + t ) ′ = f ′ + t ′ (f + t)' = f' + t' (f+t)′=f′+t′
證明
令 F ( x ) = f ( x ) + g ( x ) F(x) = f(x) + g(x) F(x)=f(x)+g(x)。則
F ′ ( x ) = lim ? h → 0 F ( x + h ) ? F ( x ) h = lim ? h → 0 [ f ( x + h ) + g ( x + h ) ] ? [ f ( x ) + g ( x ) ] h = lim ? h → 0 [ f ( x + h ) ? f ( x ) h + g ( x + h ) ? g ( x ) h ] = lim ? h → 0 f ( x + h ) ? f ( x ) h + lim ? h → 0 g ( x + h ) ? g ( x ) h = f ′ ( x ) + g ′ ( x ) \begin{align*}F'(x) &= \lim_{h \to 0} \frac{F(x+h) - F(x)}{h} \\ &= \lim_{h \to 0} \frac{[f(x+h) + g(x+h)] - [f(x) + g(x)]}{h} \\ &= \lim_{h \to 0} \left[\frac{f(x+h) - f(x)}{h} + \frac{g(x+h) - g(x)}{h}\right] \\ &= \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} + \lim_{h \to 0} \frac{g(x+h) - g(x)}{h} \\ &= f'(x) + g'(x)\end{align*} F′(x)?=h→0lim?hF(x+h)?F(x)?=h→0lim?h[f(x+h)+g(x+h)]?[f(x)+g(x)]?=h→0lim?[hf(x+h)?f(x)?+hg(x+h)?g(x)?]=h→0lim?hf(x+h)?f(x)?+h→0lim?hg(x+h)?g(x)?=f′(x)+g′(x)?
和法則可以擴展到任意數量函數的和。例如,使用這個定理兩次,我們得到
( f + t + h ) ′ = [ ( f + t ) + h ] ′ = ( f + t ) ′ + h ′ = f ′ + t ′ + h ′ (f + t + h)' = [(f + t) + h]' = (f + t)' + h' = f' + t' + h' (f+t+h)′=[(f+t)+h]′=(f+t)′+h′=f′+t′+h′
差法則
通過將 f ? g f - g f?g 寫成 f + ( ? g ) f + (-g) f+(?g) 并應用和法則和常數倍法則,我們得到如下公式。
d d x [ f ( x ) ? g ( x ) ] = d d x [ f ( x ) ] ? d d x [ g ( x ) ] \frac{d}{dx}[f(x) - g(x)] = \frac{d}{dx}[f(x)] - \frac{d}{dx}[g(x)] dxd?[f(x)?g(x)]=dxd?[f(x)]?dxd?[g(x)]
常數倍法則、和法則和差法則可以與冪法則結合,來求任何多項式的導數,如下例所示。
例子 3
d d x ( x 8 + 12 x 5 ? 24 x 4 + 10 x 3 ? 26 x + 5 ) = d d x ( x 8 ) + 12 d d x ( x 5 ) ? 24 d d x ( x 4 ) + 10 d d x ( x 3 ) ? 26 d d x ( x ) + d d x ( 5 ) = 8 x 7 + 12 ( 5 x 4 ) ? 24 ( 4 x 3 ) + 10 ( 3 x 2 ) ? 26 ( 1 ) + 0 = 8 x 7 + 60 x 4 ? 96 x 3 + 30 x 2 ? 26 \begin{align*} & \frac{d}{dx}(x^8 + 12x^5 - 24x^4 + 10x^3 - 26x + 5) \\ &= \frac{d}{dx}(x^8) + 12 \frac{d}{dx}(x^5) - 24 \frac{d}{dx}(x^4) + 10 \frac{d}{dx}(x^3) - 26 \frac{d}{dx}(x) + \frac{d}{dx}(5)\\ &= 8x^7 + 12(5x^4) - 24(4x^3) + 10(3x^2) - 26(1) + 0 \\ &= 8x^7 + 60x^4 - 96x^3 + 30x^2 - 26\end{align*} ?dxd?(x8+12x5?24x4+10x3?26x+5)=dxd?(x8)+12dxd?(x5)?24dxd?(x4)+10dxd?(x3)?26dxd?(x)+dxd?(5)=8x7+12(5x4)?24(4x3)+10(3x2)?26(1)+0=8x7+60x4?96x3+30x2?26?
例子 4
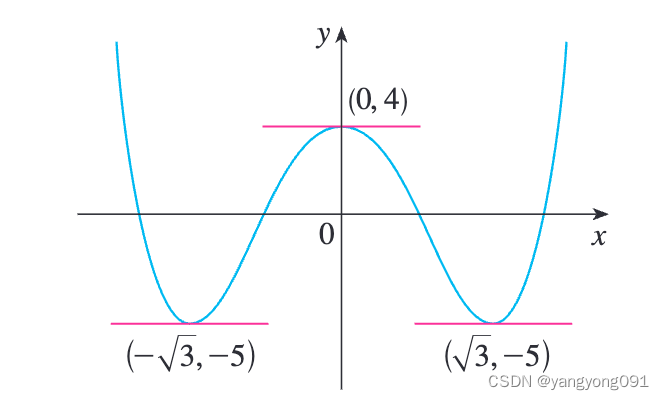
求曲線 y = x 4 ? 6 x 2 + 4 y = x^4 - 6x^2 + 4 y=x4?6x2+4 上切線為水平線的點。
解
水平切線出現在導數為零的地方。我們有
d y d x = d d x ( x 4 ) ? 6 d d x ( x 2 ) + d d x ( 4 ) = 4 x 3 ? 12 x = 4 x ( x 2 ? 3 ) \frac{dy}{dx} = \frac{d}{dx}(x^4) - 6 \frac{d}{dx}(x^2) + \frac{d}{dx}(4) = 4x^3 - 12x = 4x(x^2 - 3) dxdy?=dxd?(x4)?6dxd?(x2)+dxd?(4)=4x3?12x=4x(x2?3)
因此,當 x = 0 x = 0 x=0 或 x 2 ? 3 = 0 x^2 - 3 = 0 x2?3=0 時,即 x = ± 3 x = \pm\sqrt{3} x=±3?,導數為零。因此,給定曲線在 x = 0 , 3 , ? 3 x = 0, \sqrt{3}, -\sqrt{3} x=0,3?,?3? 時有水平切線。相應的點是 ( 0 , 4 ) (0, 4) (0,4), ( 3 , ? 5 ) (\sqrt{3}, -5) (3?,?5) 和 ( ? 3 , ? 5 ) (-\sqrt{3}, -5) (?3?,?5)。
例子 5
粒子的運動方程是 s = 2 t 3 ? 5 t 2 + 13 t + 4 s = 2t^3 - 5t^2 + 13t + 4 s=2t3?5t2+13t+4,其中 s s s 的單位是厘米, t t t 的單位是秒。求加速度作為時間的函數。2秒后的加速度是多少?
解
速度和加速度是
v ( t ) = d s d t = 6 t 2 ? 10 t + 13 v(t) = \frac{ds}{dt} = 6t^2 - 10t + 13 v(t)=dtds?=6t2?10t+13
a ( t ) = d v d t = 12 t ? 10 a(t) = \frac{dv}{dt} = 12t - 10 a(t)=dtdv?=12t?10
2秒后的加速度是 a ( 2 ) = 12 ( 2 ) ? 10 = 24 ? 10 = 14 cm/s 2 a(2) = 12(2) - 10 = 24 - 10 = 14 \text{ cm/s}^2 a(2)=12(2)?10=24?10=14?cm/s2
乘積法則
如果 f f f 和 t t t 都是可微的,則
d d x [ f ( x ) g ( x ) ] = f ( x ) d d x [ g ( x ) ] + t ( x ) d d x [ f ( x ) ] \frac{d}{dx}[f(x) g(x)] = f(x) \frac{d}{dx}[g(x)] + t(x) \frac{d}{dx}[f(x)] dxd?[f(x)g(x)]=f(x)dxd?[g(x)]+t(x)dxd?[f(x)]
證明
令 F ( x ) = f ( x ) t ( x ) F(x) = f(x)t(x) F(x)=f(x)t(x)。則
F ′ ( x ) = lim ? h → 0 F ( x + h ) ? F ( x ) h = lim ? h → 0 f ( x + h ) t ( x + h ) ? f ( x ) t ( x ) h F'(x) = \lim_{h \to 0} \frac{F(x+h) - F(x)}{h} = \lim_{h \to 0} \frac{f(x+h)t(x+h) - f(x)t(x)}{h} F′(x)=h→0lim?hF(x+h)?F(x)?=h→0lim?hf(x+h)t(x+h)?f(x)t(x)?
為了求解這個極限,我們希望像在和法則的證明中那樣,將函數 f f f 和 g g g 分開。我們可以通過在分子中加上和減去 f ( x + h ) g ( x ) f(x+h)g(x) f(x+h)g(x) 來實現這種分離:
F ′ ( x ) = lim ? h → 0 f ( x + h ) t ( x + h ) ? f ( x + h ) g ( x ) + f ( x + h ) g ( x ) ? f ( x ) g ( x ) h = lim ? h → 0 [ f ( x + h ) g ( x + h ) ? f ( x + h ) g ( x ) h + f ( x + h ) g ( x ) ? f ( x ) g ( x ) h ] = lim ? h → 0 [ f ( x + h ) g ( x + h ) ? g ( x ) h + g ( x ) f ( x + h ) ? f ( x ) h ] = f ( x ) lim ? h → 0 t ( x + h ) ? g ( x ) h + g ( x ) lim ? h → 0 f ( x + h ) ? f ( x ) h = f ( x ) g ′ ( x ) + g ( x ) f ′ ( x ) \begin{align*}F'(x) &= \lim_{h \to 0} \frac{f(x+h)t(x+h) - f(x+h)g(x) + f(x+h)g(x) - f(x)g(x)}{h} \\ &= \lim_{h \to 0} \left[\frac{f(x+h)g(x+h) - f(x+h)g(x)}{h} + \frac{f(x+h)g(x) - f(x)g(x)}{h}\right] \\ &= \lim_{h \to 0} \left[f(x+h) \frac{g(x+h) - g(x)}{h} + g(x) \frac{f(x+h) - f(x)}{h}\right] \\ &= f(x) \lim_{h \to 0} \frac{t(x+h) - g(x)}{h} + g(x) \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \\ &= f(x) g'(x) + g(x) f'(x)\end{align*} F′(x)?=h→0lim?hf(x+h)t(x+h)?f(x+h)g(x)+f(x+h)g(x)?f(x)g(x)?=h→0lim?[hf(x+h)g(x+h)?f(x+h)g(x)?+hf(x+h)g(x)?f(x)g(x)?]=h→0lim?[f(x+h)hg(x+h)?g(x)?+g(x)hf(x+h)?f(x)?]=f(x)h→0lim?ht(x+h)?g(x)?+g(x)h→0lim?hf(x+h)?f(x)?=f(x)g′(x)+g(x)f′(x)?
簡而言之,乘積法則表明,兩個函數的乘積的導數是第一個函數乘以第二個函數的導數加上第二個函數乘以第一個函數的導數。
例子 6
如果 h ( x ) = x g ( x ) h(x) = x g(x) h(x)=xg(x) 并且已知 g ( 3 ) = 5 g(3) = 5 g(3)=5 和 g ′ ( 3 ) = ? 2 g'(3) = -2 g′(3)=?2,求 h ′ ( 3 ) h'(3) h′(3)。
解
應用乘積法則,我們得到
h ′ ( x ) = d d x [ x g ( x ) ] = x d d x [ g ( x ) ] + g ( x ) d d x [ x ] = x g ′ ( x ) + g ( x ) ? 1 h'(x) = \frac{d}{dx}[x g(x)] = x \frac{d}{dx}[g(x)] + g(x) \frac{d}{dx}[x] = x g'(x) + g(x) \cdot 1 h′(x)=dxd?[xg(x)]=xdxd?[g(x)]+g(x)dxd?[x]=xg′(x)+g(x)?1
因此,
h ′ ( 3 ) = 3 t ′ ( 3 ) + t ( 3 ) = 3 ? ( ? 2 ) + 5 = ? 6 + 5 = ? 1 h'(3) = 3 t'(3) + t(3) = 3 \cdot (-2) + 5 = -6 + 5 = -1 h′(3)=3t′(3)+t(3)=3?(?2)+5=?6+5=?1
商法則
如果 f f f 和 g g g 可微,則
d d x ( f ( x ) g ( x ) ) = g ( x ) d d x [ f ( x ) ] ? f ( x ) d d x [ g ( x ) ] [ g ( x ) ] 2 \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \frac{g(x) \frac{d}{dx}[f(x)] - f(x) \frac{d}{dx}[g(x)]}{[g(x)]^2} dxd?(g(x)f(x)?)=[g(x)]2g(x)dxd?[f(x)]?f(x)dxd?[g(x)]?
用導數符號表示:
( f g ) ′ = g f ′ ? f g ′ g 2 \left(\frac{f}{g}\right)' = \frac{g f' - f g'}{g^2} (gf?)′=g2gf′?fg′?
證明
令 F ( x ) = f ( x ) g ( x ) F(x) = \frac{f(x)}{g(x)} F(x)=g(x)f(x)?。則
F ′ ( x ) = lim ? h → 0 F ( x + h ) ? F ( x ) h = lim ? h → 0 f ( x + h ) g ( x + h ) ? f ( x ) g ( x ) h = lim ? h → 0 f ( x + h ) g ( x ) ? f ( x ) g ( x + h ) h g ( x ) g ( x + h ) \begin{align*}F'(x) &= \lim_{h \to 0} \frac{F(x+h) - F(x)}{h} = \lim_{h \to 0} \frac{\frac{f(x+h)}{g(x+h)} - \frac{f(x)}{g(x)}}{h} \\ &= \lim_{h \to 0} \frac{f(x+h) g(x) - f(x) g(x+h)}{h g(x) g(x+h)}\end{align*} F′(x)?=h→0lim?hF(x+h)?F(x)?=h→0lim?hg(x+h)f(x+h)??g(x)f(x)??=h→0lim?hg(x)g(x+h)f(x+h)g(x)?f(x)g(x+h)??
我們可以通過在分子中加上和減去 f ( x ) g ( x ) f(x) g(x) f(x)g(x) 來將 f f f 和 g g g 分開:
F ′ ( x ) = lim ? h → 0 f ( x + h ) g ( x ) ? f ( x ) g ( x ) + f ( x ) g ( x ) ? f ( x ) g ( x + h ) h g ( x ) g ( x + h ) = lim ? h → 0 [ f ( x + h ) g ( x ) ? f ( x ) g ( x ) h g ( x ) g ( x + h ) + f ( x ) g ( x ) ? f ( x ) g ( x + h ) h g ( x ) g ( x + h ) ] = lim ? h → 0 [ g ( x ) f ( x + h ) ? f ( x ) h g ( x ) g ( x + h ) ? f ( x ) g ( x + h ) ? g ( x ) h g ( x ) g ( x + h ) ] = g ( x ) f ′ ( x ) ? f ( x ) g ′ ( x ) [ g ( x ) ] 2 \begin{align*}F'(x) &= \lim_{h \to 0} \frac{f(x+h) g(x) - f(x) g(x) + f(x) g(x) - f(x) g(x+h)}{h g(x) g(x+h)} \\ &= \lim_{h \to 0} \left[ \frac{f(x+h) g(x) - f(x) g(x)}{h g(x) g(x+h)} + \frac{f(x) g(x) - f(x) g(x+h)}{h g(x) g(x+h)} \right] \\ &= \lim_{h \to 0} \left[ \frac{g(x) \frac{f(x+h) - f(x)}{h}}{g(x) g(x+h)} - \frac{f(x) \frac{g(x+h) - g(x)}{h}}{g(x) g(x+h)} \right] \\ &= \frac{g(x) f'(x) - f(x) g'(x)}{\left[g(x)\right]^2}\end{align*} F′(x)?=h→0lim?hg(x)g(x+h)f(x+h)g(x)?f(x)g(x)+f(x)g(x)?f(x)g(x+h)?=h→0lim?[hg(x)g(x+h)f(x+h)g(x)?f(x)g(x)?+hg(x)g(x+h)f(x)g(x)?f(x)g(x+h)?]=h→0lim?[g(x)g(x+h)g(x)hf(x+h)?f(x)???g(x)g(x+h)f(x)hg(x+h)?g(x)??]=[g(x)]2g(x)f′(x)?f(x)g′(x)??
因為 g g g 在 x x x 處是連續的,所以 lim ? h → 0 g ( x + h ) = g ( x ) \lim_{h \to 0} g(x+h) = g(x) limh→0?g(x+h)=g(x)。
用語言描述,商法則表示一個商的導數是分母乘以分子導數減去分子乘以分母導數,然后除以分母的平方。
例子 7
令 y = x 3 + 1 x 2 + 2 x + 1 y = \frac{x^3 + 1}{x^2 + 2x + 1} y=x2+2x+1x3+1?。則
y ′ = ( x 2 + 2 x + 1 ) d d x ( x 3 + 1 ) ? ( x 3 + 1 ) d d x ( x 2 + 2 x + 1 ) ( x 2 + 2 x + 1 ) 2 = ( x 2 + 2 x + 1 ) ( 3 x 2 ) ? ( x 3 + 1 ) ( 2 x + 2 ) ( x 2 + 2 x + 1 ) 2 = ( 3 x 4 + 6 x 3 + 3 x 2 ) ? ( 2 x 4 + 2 x 3 + 2 x + 2 x 3 + 2 ) ( x 2 + 2 x + 1 ) 2 = 3 x 4 + 6 x 3 + 3 x 2 ? 2 x 4 ? 4 x 3 ? 2 x 3 ? 2 x ? 2 ( x 2 + 2 x + 1 ) 2 = x 4 + 2 x 3 + 3 x 2 ? 2 x ? 2 ( x 2 + 2 x + 1 ) 2 \begin{align*}y' &= \frac{(x^2 + 2x + 1) \frac{d}{dx}(x^3 + 1) - (x^3 + 1) \frac{d}{dx}(x^2 + 2x + 1)}{(x^2 + 2x + 1)^2} \\ &= \frac{(x^2 + 2x + 1)(3x^2) - (x^3 + 1)(2x + 2)}{(x^2 + 2x + 1)^2} \\ &= \frac{(3x^4 + 6x^3 + 3x^2) - (2x^4 + 2x^3 + 2x + 2x^3 + 2)}{(x^2 + 2x + 1)^2} \\ &= \frac{3x^4 + 6x^3 + 3x^2 - 2x^4 - 4x^3 - 2x^3 - 2x - 2}{(x^2 + 2x + 1)^2} \\ &= \frac{x^4 + 2x^3 + 3x^2 - 2x - 2}{(x^2 + 2x + 1)^2}\end{align*} y′?=(x2+2x+1)2(x2+2x+1)dxd?(x3+1)?(x3+1)dxd?(x2+2x+1)?=(x2+2x+1)2(x2+2x+1)(3x2)?(x3+1)(2x+2)?=(x2+2x+1)2(3x4+6x3+3x2)?(2x4+2x3+2x+2x3+2)?=(x2+2x+1)23x4+6x3+3x2?2x4?4x3?2x3?2x?2?=(x2+2x+1)2x4+2x3+3x2?2x?2??
注意
不要每次看到商都使用商法則。有時候,先重寫商使其形式更簡化以便求導會更容易。例如,盡管可以使用商法則來求導函數 F ( x ) = 3 x 2 + 1 2 x F(x) = \frac{3x^2 + 1}{2x} F(x)=2x3x2+1?,但更簡單的方法是先進行除法,寫成
F ( x ) = 3 x 2 2 x + 1 2 x = 3 x 2 + 1 2 x F(x) = \frac{3x^2}{2x} + \frac{1}{2x} = \frac{3x}{2} + \frac{1}{2x} F(x)=2x3x2?+2x1?=23x?+2x1?
然后再求導。
一般冪函數
商法則可以用來將冪法則擴展到指數為負整數的情況。
如果 n n n 是正整數,則
d d x ( x ? n ) = ? n x ? n ? 1 \frac{d}{dx}(x^{-n}) = -nx^{-n-1} dxd?(x?n)=?nx?n?1
證明
d d x ( x ? n ) = d d x ( 1 x n ) = x n ? d d x ( 1 ) ? 1 ? d d x ( x n ) ( x n ) 2 = 0 ? n x n ? 1 x 2 n = ? n x n ? 1 x 2 n = ? n x ? n ? 1 \begin{align*}\frac{d}{dx}(x^{-n}) &= \frac{d}{dx}\left(\frac{1}{x^n}\right) \\ &= \frac{x^n \cdot \frac{d}{dx}(1) - 1 \cdot \frac{d}{dx}(x^n)}{(x^n)^2} = \frac{0 - nx^{n-1}}{x^{2n}} \\ &= -n \frac{x^{n-1}}{x^{2n}} = -n x^{-n-1}\end{align*} dxd?(x?n)?=dxd?(xn1?)=(xn)2xn?dxd?(1)?1?dxd?(xn)?=x2n0?nxn?1?=?nx2nxn?1?=?nx?n?1?
例子 8
(a) 如果 y = 1 x y = \frac{1}{x} y=x1?,則 d y d x = d d x ( x ? 1 ) = ? x ? 2 = ? 1 x 2 \frac{dy}{dx} = \frac{d}{dx}(x^{-1}) = -x^{-2} = -\frac{1}{x^2} dxdy?=dxd?(x?1)=?x?2=?x21?
(b) d d t ( 6 t 3 ) = 6 d d t ( t ? 3 ) = 6 ? ( ? 3 t ? 4 ) = ? 18 t ? 4 \frac{d}{dt}\left(\frac{6}{t^3}\right) = 6 \frac{d}{dt}(t^{-3}) = 6 \cdot (-3t^{-4}) = -18t^{-4} dtd?(t36?)=6dtd?(t?3)=6?(?3t?4)=?18t?4
到目前為止,我們知道當指數 n n n 是正整數或負整數時,冪法則成立。如果 n = 0 n = 0 n=0,則 x 0 = 1 x^0 = 1 x0=1,其導數為 0 0 0。因此,冪法則對任何整數 n n n 都成立。那么如果指數是分數呢?在前面章節得例子中,我們發現
d d x ( x 1 / 2 ) = 1 2 x ? 1 / 2 \frac{d}{dx}(x^{1/2}) = \frac{1}{2}x^{-1/2} dxd?(x1/2)=21?x?1/2
這表明冪法則在 n = 1 / 2 n = 1/2 n=1/2 時也成立。事實上,它對任何實數 n n n 都成立,我們將在后面的章節中證明這一點。
冪法則(一般版本)
如果 n n n 是任意實數,則
d d x ( x n ) = n x n ? 1 \frac{d}{dx}(x^n) = nx^{n-1} dxd?(xn)=nxn?1
例子 9
(a) 如果 f ( x ) = x π f(x) = x^{\pi} f(x)=xπ,則
f ′ ( x ) = π x π ? 1 f'(x) = \pi x^{\pi - 1} f′(x)=πxπ?1
(b) 如果 y = 1 3 x 2 y = \frac{1}{3x^2} y=3x21?,則
d y d x = d d x ( 3 ? 1 x ? 2 ) = 3 ? 1 ? ? 2 x ? 3 = ? 2 3 x 3 \frac{dy}{dx} = \frac{d}{dx}(3^{-1}x^{-2}) = 3^{-1} \cdot -2x^{-3} = -\frac{2}{3x^3} dxdy?=dxd?(3?1x?2)=3?1??2x?3=?3x32?
例子 10
求函數 f ( t ) = t a + b t f(t) = t \sqrt{a + bt} f(t)=ta+bt? 的導數。
解
使用乘積法則,我們有
f ′ ( t ) = t d d t ( a + b t ) + a + b t d d t ( t ) f'(t) = t \frac{d}{dt}(\sqrt{a + bt}) + \sqrt{a + bt} \frac{d}{dt}(t) f′(t)=tdtd?(a+bt?)+a+bt?dtd?(t)
= t ? b 2 a + b t + a + b t ? 1 = t \cdot \frac{b}{2\sqrt{a + bt}} + \sqrt{a + bt} \cdot 1 =t?2a+bt?b?+a+bt??1
= b t 2 a + b t + a + b t = \frac{bt}{2\sqrt{a + bt}} + \sqrt{a + bt} =2a+bt?bt?+a+bt?
微分法則使我們能夠找到切線,而無需求助于導數的定義。它還使我們能夠找到法線。曲線 C C C 在點 P P P 處的法線是通過 P P P 的與 P P P 處的切線垂直的線。(在光學研究中,需要考慮光線與透鏡法線之間的角度。)
例子 11
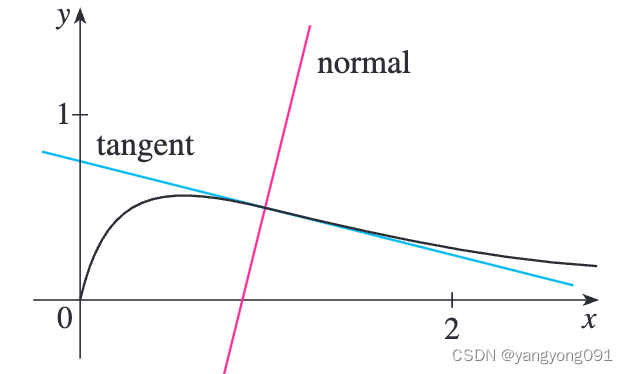
求曲線 y = x 1 + x 2 y = \frac{\sqrt{x}}{1 + x^2} y=1+x2x?? 在點 ( 1 , 1 2 ) (1, \frac{1}{2}) (1,21?) 處的切線和法線的方程。
解
根據商法則,我們有
d y d x = ( 1 + x 2 ) ? d d x ( x ) ? x ? d d x ( 1 + x 2 ) ( 1 + x 2 ) 2 = ( 1 + x 2 ) ? 1 2 x ? x ? 2 x ( 1 + x 2 ) 2 \frac{dy}{dx} = \frac{(1 + x^2) \cdot \frac{d}{dx}(\sqrt{x}) - \sqrt{x} \cdot \frac{d}{dx}(1 + x^2)}{(1 + x^2)^2} = \frac{(1 + x^2) \cdot \frac{1}{2\sqrt{x}} - \sqrt{x} \cdot 2x}{(1 + x^2)^2} dxdy?=(1+x2)2(1+x2)?dxd?(x?)?x??dxd?(1+x2)?=(1+x2)2(1+x2)?2x?1??x??2x?
簡化得
d y d x = 1 + x 2 2 x ? 2 x x ( 1 + x 2 ) 2 = 1 + x 2 ? 4 x 2 2 x ( 1 + x 2 ) 2 = 1 ? 3 x 2 2 x ( 1 + x 2 ) 2 = 1 ? 3 x 2 2 x ( 1 + x 2 ) 2 \frac{dy}{dx} = \frac{\frac{1 + x^2}{2\sqrt{x}} - 2x\sqrt{x}}{(1 + x^2)^2} = \frac{\frac{1 + x^2 - 4x^2}{2\sqrt{x}}}{(1 + x^2)^2} = \frac{\frac{1 - 3x^2}{2\sqrt{x}}}{(1 + x^2)^2} = \frac{1 - 3x^2}{2\sqrt{x}(1 + x^2)^2} dxdy?=(1+x2)22x?1+x2??2xx??=(1+x2)22x?1+x2?4x2??=(1+x2)22x?1?3x2??=2x?(1+x2)21?3x2?
所以在點 ( 1 , 1 2 ) (1, \frac{1}{2}) (1,21?) 處切線的斜率是
d y d x ∣ x = 1 = 1 ? 3 ? 1 2 2 ? 1 ? ( 1 + 1 2 ) 2 = 1 ? 3 2 ? 1 ? ( 1 + 1 ) 2 = ? 2 2 ? 4 = ? 2 8 = ? 1 4 \left. \frac{dy}{dx} \right|_{x = 1} = \frac{1 - 3 \cdot 1^2}{2 \cdot \sqrt{1} \cdot (1 + 1^2)^2} = \frac{1 - 3}{2 \cdot 1 \cdot (1 + 1)^2} = \frac{-2}{2 \cdot 4} = \frac{-2}{8} = -\frac{1}{4} dxdy? ?x=1?=2?1??(1+12)21?3?12?=2?1?(1+1)21?3?=2?4?2?=8?2?=?41?
我們使用點斜式來寫在點 ( 1 , 1 2 ) (1, \frac{1}{2}) (1,21?) 處切線的方程:
y ? 1 2 = ? 1 4 ( x ? 1 ) 或 y = ? 1 4 x + 3 4 y - \frac{1}{2} = -\frac{1}{4}(x - 1) \quad \text{或} \quad y = -\frac{1}{4}x + \frac{3}{4} y?21?=?41?(x?1)或y=?41?x+43?
在點 ( 1 , 1 2 ) (1, \frac{1}{2}) (1,21?) 處法線的斜率是 ? 1 4 -\frac{1}{4} ?41? 的負倒數,即 4,因此法線的方程是
y ? 1 2 = 4 ( x ? 1 ) 或 y = 4 x ? 7 2 y - \frac{1}{2} = 4(x - 1) \quad \text{或} \quad y = 4x - \frac{7}{2} y?21?=4(x?1)或y=4x?27?
曲線及其切線和法線如圖所示。
例子 12
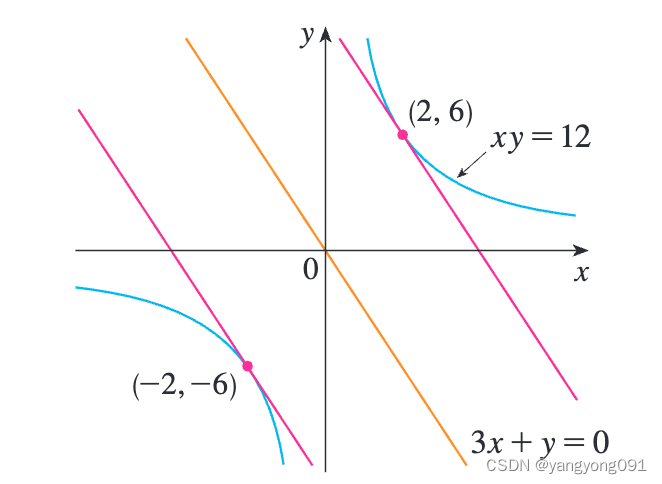
雙曲線 x y = 12 xy = 12 xy=12 上的哪些點處的切線與直線 3 x + y = 0 3x + y = 0 3x+y=0 平行?
解
由于 x y = 12 xy = 12 xy=12 可以寫成 y = 12 x y = \frac{12}{x} y=x12?,我們有
d y d x = d d x ( 12 x ) = 12 ? d d x ( x ? 1 ) = 12 ? ( ? x ? 2 ) = ? 12 x 2 \frac{dy}{dx} = \frac{d}{dx} \left( \frac{12}{x} \right) = 12 \cdot \frac{d}{dx} \left( x^{-1} \right) = 12 \cdot (-x^{-2}) = -\frac{12}{x^2} dxdy?=dxd?(x12?)=12?dxd?(x?1)=12?(?x?2)=?x212?
令所求點的 x x x 坐標為 a a a,則切線的斜率為
? 12 a 2 -\frac{12}{a^2} ?a212?
切線與直線 3 x + y = 0 3x + y = 0 3x+y=0 平行,這意味著兩條直線的斜率相同。直線 3 x + y = 0 3x + y = 0 3x+y=0 的斜率為 ? 3 -3 ?3。因此,
? 12 a 2 = ? 3 -\frac{12}{a^2} = -3 ?a212?=?3
解這個方程,我們得到
12 a 2 = 3 \frac{12}{a^2} = 3 a212?=3
a 2 = 12 3 a^2 = \frac{12}{3} a2=312?
a 2 = 4 a^2 = 4 a2=4
a = 2 或 a = ? 2 a = 2 \quad \text{或} \quad a = -2 a=2或a=?2
因此, x x x 坐標為 2 2 2 或 ? 2 -2 ?2 的點上,切線與直線 3 x + y = 0 3x + y = 0 3x+y=0 平行。
對應的 y y y 坐標為:
當 a = 2 a = 2 a=2 時, y = 12 2 = 6 y = \frac{12}{2} = 6 y=212?=6,
當 a = ? 2 a = -2 a=?2 時, y = 12 ? 2 = ? 6 y = \frac{12}{-2} = -6 y=?212?=?6。
所以切線與直線 3 x + y = 0 3x + y = 0 3x+y=0 平行的點是 ( 2 , 6 ) (2, 6) (2,6) 和 ( ? 2 , ? 6 ) (-2, -6) (?2,?6)。
我們總結一下迄今為止學到的微分公式如下:
微分公式表
d d x ( c ) = 0 d d x ( x n ) = n x n ? 1 d d x ( c f ) = c f ′ ( f + g ) ′ = f ′ + g ′ ( f ? g ) ′ = f ′ ? g ′ ( f g ) ′ = f g ′ + g f ′ ( f g ) ′ = g f ′ ? f g ′ g 2 \begin{aligned} &\frac{d}{dx}(c) = 0 \\ &\frac{d}{dx}(x^n) = nx^{n-1} \\ &\frac{d}{dx}(cf) = c f' \\ &(f + g)' = f' + g' \\ &(f - g)' = f' - g' \\ &(f g)' = f g' + g f' \\ &\left(\frac{f}{g}\right)' = \frac{g f' - f g'}{g^2} \\ \end{aligned} ?dxd?(c)=0dxd?(xn)=nxn?1dxd?(cf)=cf′(f+g)′=f′+g′(f?g)′=f′?g′(fg)′=fg′+gf′(gf?)′=g2gf′?fg′??



考試題庫,高效備考!!!)



)









)

pem, der, crt, cer, key等各類證書與密鑰文件后綴解析)