1. 實驗目的

①掌握圖像分割的含義與目的；
②掌握迭代法、最大類間方差法、直方圖法等閾值分割方法；
③掌握霍夫變換、區域生長法、區域分裂與合并法的原理，并能編程實現。

2. 實驗內容

①調用Matlab / Python+OpenCV中的相關函數，分別通過實驗法、直方圖法、大津算法確定閾值，實現圖像的全局閾值分割。
②調用Matlab / Python+OpenCV中的霍夫變換函數，檢測圖像中的直線和圓。
③自行編寫代碼，實現區域生長法及區域分裂與合并算法。

3. 實驗過程

3.1 全局閾值分割

3.1.1迭代法

初始化一個閾值，通過迭代法求出最佳閾值，使用最佳閾值對圖像進行分割，并顯示原圖和分割結果(參考圖1)。
(1) 主要調用的函數、功能及參數說明

函數名	函數功能	參數說明
imread(A)	讀取圖片	A：圖片在文件夾的位置
rgb2gray(A)	灰度轉化	A：圖片
mean(A)	求列或行的平均數	A：矩陣
mean2(image)	對整一個矩陣求像素平均值	image：圖片
find(A)	查找非零元素的索引和值	A：查找條件
abs(A)	返回數組A中每個元素的絕對值和復數的模	A：矩陣

(2) 源代碼及實驗結果(添加必要注釋)

A= imread('lena.png');
image=rgb2gray(A);%灰度轉化
T=mean2(image);%取均值作為初始閾值
done=false;%定義跳出循環的量i=0;
%while循環進行迭代
while ~doner1=find(image<=T);%小于閾值的部分r2=find(image>T);%大于閾值的部分Tnew=(mean(image(r1))+mean(image(r2)))/2;%計算分割后兩部分的閾值均值的均值done=abs(Tnew-T)<1;%判斷迭代是否收斂T=Tnew;%如不收斂,則將分割后的均值的均值作為新的閾值進行循環計算i=i+1;
end
%這兩步是將圖像轉換成二值圖像
image(r1)=0;%將小于閾值的部分賦值為0
image(r2)=1;%將大于閾值的部分賦值為1   subplot(121);imshow(A);title('原圖')
subplot(122);imshow(image,[]);title('迭代處理后')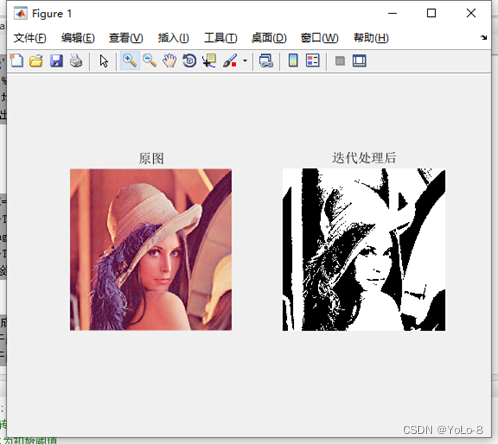

(3) 總結(總結實驗法步驟，對實驗結果進行分析)
當目標與背景的面積相差較大時，更好地選擇是將初始閾值T設置為最大灰度值和最小灰度值的中間值。

3.1.2最大類間方差法

使用最大類間方差法求出最佳閾值后，使用最佳閾值對圖像進行分割，并顯示原圖和分割結果(參考圖2)
(1) 主要調用的函數、功能及參數說明

函數名	函數功能	參數說明
graythresh	采用OTSU算法來獲取全局閾值，自動選取閾	...

(2) 源代碼及實驗結果(添加必要注釋)

I = imread('lena.png');
T = graythresh(I); %采用OTSU算法來獲取全局閾值，自動選取閾值
K = im2bw(I, T);%二值化
figure;
subplot(121), imshow(I);title('原圖')
subplot(122), imshow(K);title('最大類間方差法')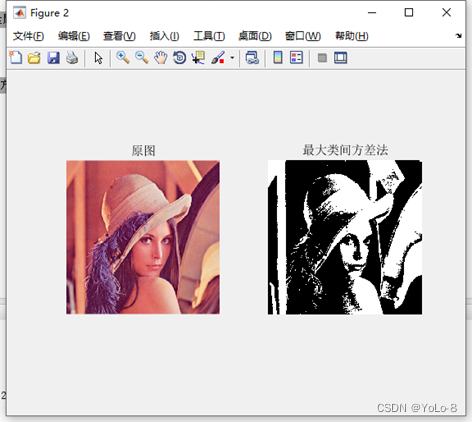

(3) 總結(總結最大類間差分算法步驟，對實驗結果進行分析)
最大類間差分算法是根據圖像的灰度特性,將圖像分為前景和背景兩個部分。當取最佳閾值時，兩部分之間的差別應該是最大的，前景和背景之間的類間方差如果越大，就說明構成圖像的兩個部分之間的差別越大。

3.1.3直方圖法

首先得到圖像的直方圖，選出最佳閾值后，使用最佳閾值對圖像進行分割，并顯示原圖和分割結果(參考下圖)。

(1) 主要調用的函數、功能及參數說明

函數名	函數功能	參數說明
imread(A)	讀取圖片	A：圖片在文件夾的位置
rgb2gray(A)	灰度轉化	A：圖片

(2) 源代碼及實驗結果(添加必要注釋)

A = imread('lena.png');
image=rgb2gray(A);%灰度轉化[m,n]=size(image);%測量圖像尺寸參數
GK=zeros(1,256); %預創建存放灰度出現概率的向量
for k=0:255GK(k+1)=length(find(image==k))/(m*n);%計算每級灰度出現的概率，將其存入GK中相應位置
endsubplot(2,2,1);imshow(image);title('灰度圖像')
grid on;%顯示網格線
axis on;%顯示坐標系subplot(2,2,2),bar(0:255,GK,'g')%繪制直方圖
title('灰度直方圖')
xlabel('灰度值')
ylabel(' 出現概率')image2=im2bw(A,150/255);
subplot(2,2,3),imshow(image2);title('閾值150的分割圖像')
grid on;
axis on;image3=im2bw(A,200/255);
subplot(2,2,4),imshow(image3);title('閾值200的分割圖像')
grid on;
axis on;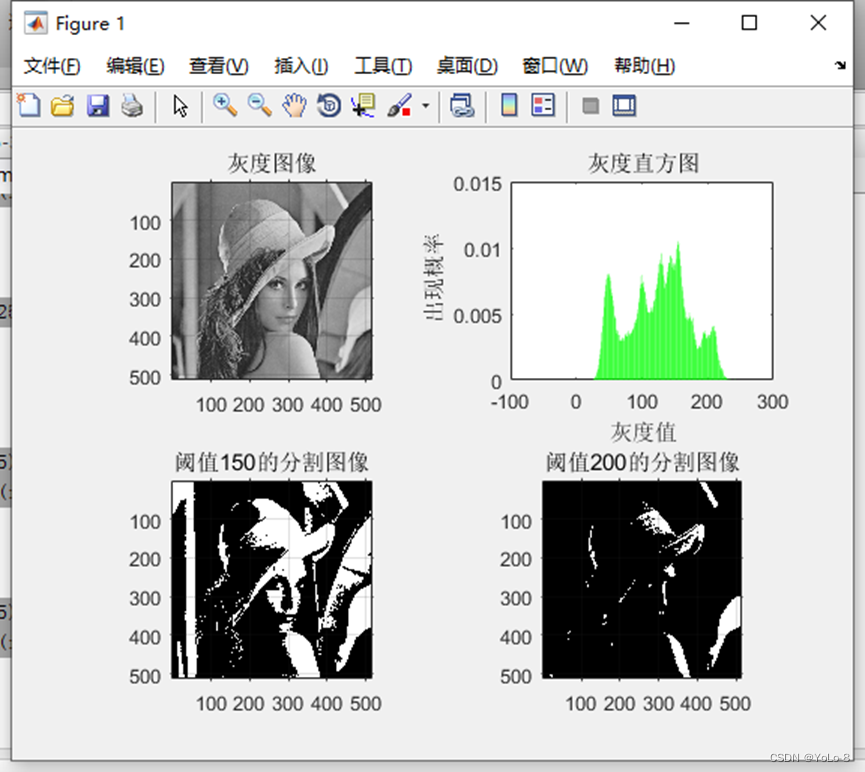

(3) 總結(總結直方圖法步驟，對實驗結果進行分析)
圖像分割是圖像識別的基礎，對圖像進行圖像分割，將目標從背景區域中分離出，可以避免圖像識別時在圖像上進行盲目的搜索，大大提高圖像識別的效率以及識別準確率。基于灰度直方圖的閾值分割計算簡單，適用于目標與背景分布于不同灰度范圍的灰度圖像，特別是遙感圖像。

3.2 霍夫變換

3.2.1 調用霍夫變換函數檢測直線和圓

如下圖所示，調用 Matlab/Python+OpenCV中的霍夫變換函數，檢測圖像中的直線和圓。

(1) 主要調用的函數、功能及參數說明

函數名	函數功能	參數說明
imread(A)	讀取圖片	A：圖片在文件夾的位置

(2) 源代碼及實驗結果(添加必要注釋)

①直線檢測代碼及實驗結果：

A= imread('lena.png');I=rgb2gray(A);%灰度轉化BW = edge(I,'canny');%Canny方法提取圖像邊界，返回二值圖像(邊界1,否則0)
[H,T,R] = hough(BW);%計算二值圖像的標準霍夫變換，H為霍夫變換矩陣，I,R為計算霍夫變換的角度和半徑值
P = houghpeaks(H,3);%提取3個極值點
x = T(P(:,2)); 
y = R(P(:,1));
lines=houghlines(BW,T,R,P);%提取線段subplot(1,2,1);imshow(A);title('原圖')
subplot(1,2,2);imshow(I);title('直線檢測')
hold on;for k = 1:length(lines)
xy = [lines(k).point1; lines(k).point2];
plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','green');%畫出線段
plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow');%起點
plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red');%終點
end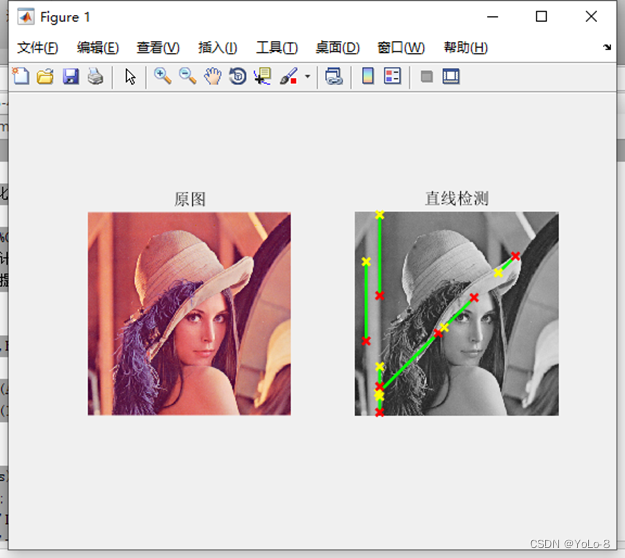

②圓形檢測代碼及實驗結果：

rgb= imread('lena.png');
image = rgb2gray(rgb);
imshow(image)d = imdistline(gca);
delete(d)
[centersBright,radiiBright,metricBright] = imfindcircles(rgb,[55 90],'ObjectPolarity','dark','Method','TwoStage','Sensitivity',0.94,'EdgeThreshold',0.1);
hBright = viscircles(centersBright, radiiBright,'Color','b');
b=length(radiiBright);
total_number=b;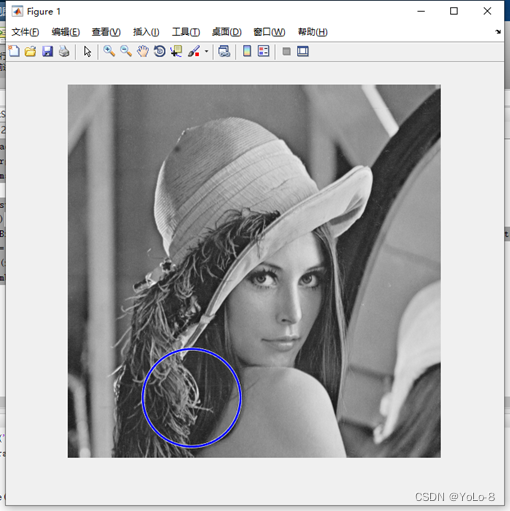

③總結(總結霍夫變換檢測步驟，并對實驗結果進行分析)
霍夫變換的過程是在一個參數空間中通過計算累計結果的局部最大值得到一個符合該特定形狀的集合作為霍夫變換結果，該方法可以進行圓，直線，橢圓等形狀的檢測。

3.2.2 實現極坐標系下的霍夫變換(參考圖5，6)

⑴ 源代碼及實驗結果(添加必要注釋)

A= imread('lena.png');
I=rgb2gray(A);%灰度轉化BW = edge(I,'canny');%Canny方法提取圖像邊界，返回二值圖像(邊界1,否則0)
[H,T,R] = hough(BW);%計算二值圖像的標準霍夫變換，H為霍夫變換矩陣，I,R為計算霍夫變換的角度和半徑值subplot(1,2,1);imshow(A);title('原圖')
subplot(1,2,2);imshow(H,[],'XData',T,'YData',R,'InitialMagnification','fit');%hough變換的圖像
title('霍夫變換結果')
xlabel('\theta'), ylabel('\rho');
axis on,axis square,hold on;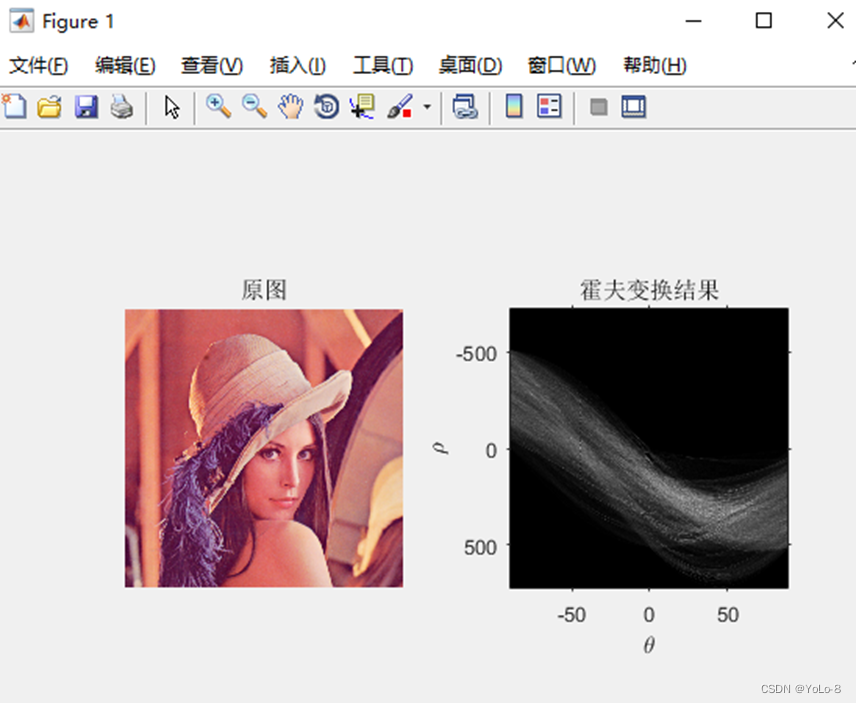

⑵ 總結(總結極坐標下霍夫變換步驟，對實驗結果進行分析)
圖像x?yx?y坐標空間中，經過點(xi,yi)(xi,yi)的直線表示為：yi=axi+b(1)，yi=axi+b(1)。其中，參數a為斜率，b為截矩。其中，參數a為斜率，b為截矩。通過點(xi,yi)點(xi,yi)的直線有無數條。變換到了參數平面a?ba?b。這個變換就是直角坐標中對于(xi,yi)(xi,yi)點的Hough變換。

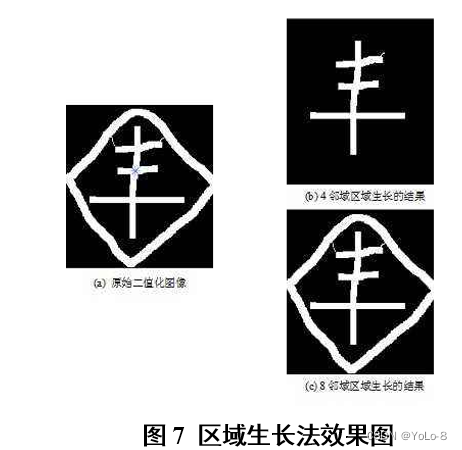
3.3 區域生長法

分別使用不同生長準則實現區域生長算法(參考圖7)

⑴ 源代碼及實驗結果(添加必要注釋及結果圖)

I=imread('lena.png');if isinteger(I)I=im2double(I);
end
I = rgb2gray(I);figure 
imshow(I)
[M,N]=size(I);
[y,x]=getpts; %單擊取點后，按enter結束
x1=round(x);
y1=round(y);
seed=I(x1,y1); %獲取中心像素灰度值J=zeros(M,N);
J(x1,y1)=1;count=1; %待處理點個數
threshold=0.15;
while count>0count=0;for i=1:M %遍歷整幅圖像for j=1:Nif J(i,j)==1 %點在“棧”內if (i-1)>1&(i+1)<M&(j-1)>1&(j+1)<N %3*3鄰域在圖像范圍內for u=-1:1 %8-鄰域生長for v=-1:1if J(i+u,j+v)==0&abs(I(i+u,j+v)-seed)<=thresholdJ(i+u,j+v)=1;count=count+1;  %記錄此次新生長的點個數endendendendendendend
endsubplot(1,2,1),imshow(I);title('原圖')
subplot(1,2,2),imshow(J);title('區域生長實現')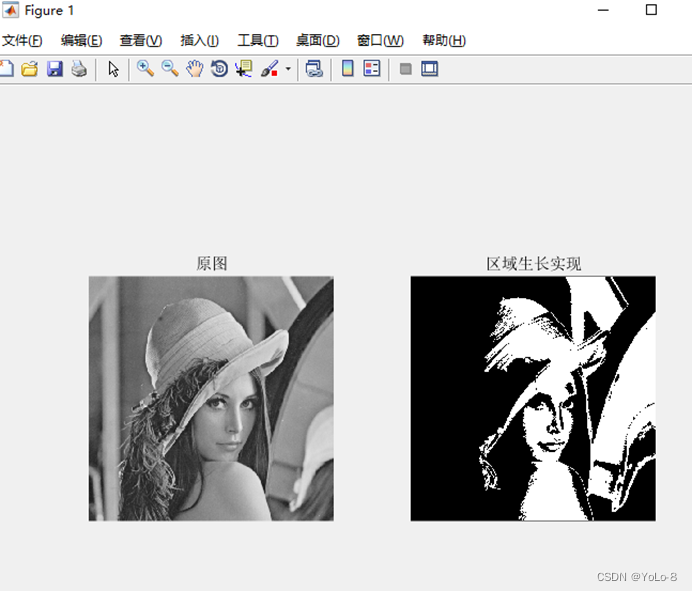

4. 實驗小結

①分析和總結全局閾值分割的幾種實驗結果，能夠得到哪些啟發或結論？
答：在上面的圖像分割中，通過不同的閾值處理方法，得到良好的圖像分割結果。不難發現， 對于不同的噪聲環境和光照影響等等，一種單一的閾值分割方法往往無法出色的完成任務。
在今后的實驗中，要合理的根據自己的圖像樣本來選擇合理的算法。例如是否需要對圖像進行平滑去噪，是否需要圖像分區來使光照近似均勻。不僅要掌握上面的處理方法，也明白了為什么對上面的圖像進行這樣的處理和分析。
②當圖片過曝或者過暗造成霍夫變換檢測效果不理想時，可以采用哪些圖像處理方法提升效果？
答：依賴直方圖來調整圖像強度值
③查閱相關資料，了解更多的圖像分割方法，并從原理和結果等方面對比它們之間的異同。
答：
(1)基于闞值的分割方法是按照原圖像的灰度特征劃分出一個或者幾個灰度閾值將原圖像的每個像素的灰度值與灰度閾值進行比較，繼而確定每個像素應該位于哪個區域。
(2)基于邊緣的圖像分割
邊緣是指一個區域的結束與另一個區域的開始，也就是說圖像邊緣代表的是兩個不同的區域邊界線上的一些像素的集合，它一般代表著圖像的灰度、紋路、顏色發生了一些突變，是圖像局部特征不連續的體現。基于邊緣的圖像分割方法一般是基于圖像灰度值檢測的分割方法，即圖像邊緣是圖像灰度值發生突變的一個轉折，圖像邊緣有兩個要素:幅度與方向。沿著邊緣的方向，灰度值的變化比較小，垂直于邊緣的方向，灰度值的變化比較大。因此我們可以對像素的灰度值進行求導來判斷圖像的邊緣。
(3)基于區域的分割方法
區域生長指的是根據同一區域內像素具有一些相似的性質(灰度值、紋路、顏色)來聚集像素點的一種方法。我們可以從一個像素或者是一塊很小的區域開始，將周圍具有相同性質的像素或者區域劃入到目前的區域當中，直到沒有其他的像素或者是區域能夠劃入到當前區域為止，以此來實現區域不斷增長的過程。