每日一題——Python實現PAT乙級1073 多選題常見計分法（舉一反三+思想解讀+逐步優化）9千字好文

一個認為一切根源都是“自己不夠強”的INTJ

個人主頁：用哲學編程-CSDN博客
專欄：每日一題——舉一反三
Python編程學習
Python內置函數

Python-3.12.0文檔解讀

初次嘗試

再次嘗試

有何不同

版本一（原始版本）：

版本二（優化版本）：

總結：

代碼結構和邏輯

時間復雜度分析

空間復雜度分析

總結

我要更強

優化方法

優化后的代碼

優化說明

時間復雜度和空間復雜度分析

哲學和編程思想

1. 抽象和封裝

2. 效率和優化

3. 簡潔和清晰

4. 模塊化和可擴展性

5. 防御性編程

6. 函數式編程思想

7. 面向對象編程思想

8. 敏捷開發思想

舉一反三

1. 抽象和封裝

2. 效率和優化

3. 簡潔和清晰

4. 模塊化和可擴展性

5. 防御性編程

6. 函數式編程思想

7. 面向對象編程思想

8. 敏捷開發思想

通用技巧

題目鏈接：https://pintia.cn/problem-sets/994805260223102976/exam/problems/type/7?problemSetProblemId=994805263624683520&page=0

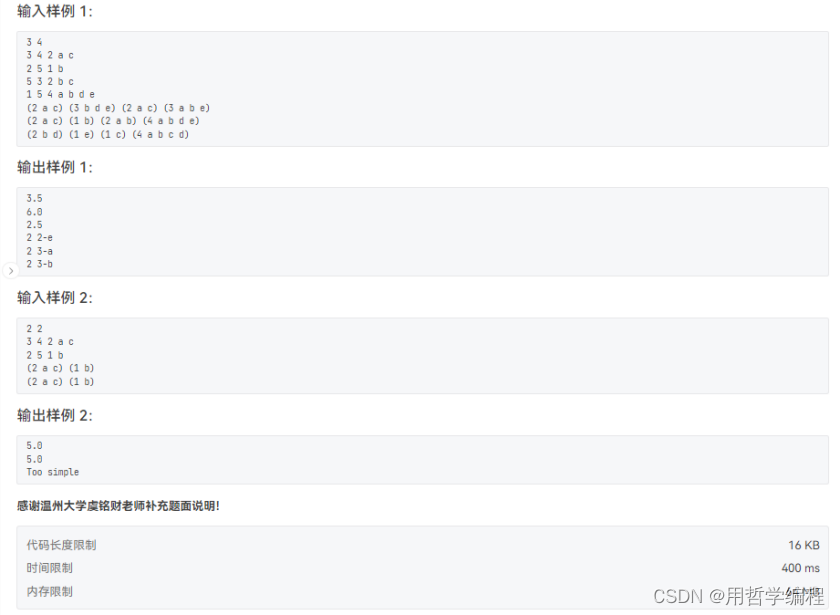
初次嘗試

N_students_num, M_ques_num = map(int, input().split())  # 讀取學生人數和題目數量
answers = {}  # 初始化答案字典
for i in range(M_ques_num):full_score, option_num, right_option_num, *right_options = input().split()full_score = int(full_score)option_num = int(option_num)right_option_num = int(right_option_num)#print(full_score, option_num, right_option_num, *right_options)#3 4 2 a canswers[i+1] = [right_option_num, ''.join(right_options), full_score, option_num]  # 將題目的正確選項和分數等信息存入字典#print(answers)
#{1: [2, 'ac', 3, 4], 2: [1, 'b', 2, 5], 3: [2, 'bc', 5, 3], 4: [4, 'abde', 1, 5]}options_wrong_times = {}  # 初始化錯誤選項次數字典for i in range(N_students_num):student_options = input()student_options = student_options.replace(' ', '')student_options = student_options.replace(')', '')student_options = student_options[1:].split('(')#print(student_options)#['2ac', '2bd', '2ac', '3abe']for j in range(M_ques_num):student_options[j] = int(student_options[j][0]), student_options[j][1:]  # 將學生答案轉換為元組列表，每個元組包含選項數量和選項字符串#print(student_options)#[(2, 'ac'), (2, 'bd'), (2, 'ac'), (3, 'abe')]this_student_score = 0for j in range(M_ques_num):if answers[j+1][0] == student_options[j][0] and answers[j+1][1] == student_options[j][1]:this_student_score += answers[j+1][2]  # 完全正確，加上全部分數continueelif set(student_options[j][1]) < set(answers[j+1][1]):this_student_score += 0.5 * answers[j+1][2]  # 部分正確，加上一半分數wrong_options = list(set(student_options[j][1]) ^ set(answers[j+1][1]))  # 計算錯誤選項wrong_options.sort()for option in wrong_options:if str(j+1) + '-' + option not in options_wrong_times:options_wrong_times[str(j+1) + '-' + option] = 1  # 記錄錯誤選項次數else:options_wrong_times[str(j+1) + '-' + option] += 1print(f"{this_student_score:.1f}")  # 輸出每個學生的得分if len(options_wrong_times) == 0:print("Too simple")  # 如果沒有錯誤選項，輸出"Too simple"
else:tmp = max(options_wrong_times.values())output = [option for option in options_wrong_times if options_wrong_times[option] == tmp]for i in range(len(output)):print(tmp, output[i])  # 輸出錯誤次數最多的選項及其錯誤次數

再次嘗試

N_students_num, M_ques_num = map(int, input().split())  # 讀取學生人數和題目數量
answers = {}  # 初始化答案字典
for i in range(M_ques_num):full_score, option_num, right_option_num, *right_options = input().split()full_score = int(full_score)option_num = int(option_num)right_option_num = int(right_option_num)answers[i+1] = [right_option_num, set(right_options), full_score]  # 將題目的正確選項和分數等信息存入字典options_wrong_times = {}  # 初始化錯誤選項次數字典for i in range(N_students_num):student_options = input().replace(' ', '').replace(')', '')[1:].split('(')student_options = [set(opt[1:]) for opt in student_options]  # 將學生答案轉換為集合列表this_student_score = 0for j in range(M_ques_num):student_option_set = student_options[j]correct_option_set = answers[j+1][1]if student_option_set == correct_option_set:this_student_score += answers[j+1][2]  # 完全正確，加上全部分數elif student_option_set.issubset(correct_option_set):this_student_score += 0.5 * answers[j+1][2]  # 部分正確，加上一半分數wrong_options = student_option_set.symmetric_difference(correct_option_set)  # 計算錯誤選項for option in wrong_options:key = f"{j+1}-{option}"options_wrong_times[key] = options_wrong_times.get(key, 0) + 1  # 記錄錯誤選項次數print(f"{this_student_score:.1f}")  # 輸出每個學生的得分if not options_wrong_times:print("Too simple")  # 如果沒有錯誤選項，輸出"Too simple"
else:max_wrong_times = max(options_wrong_times.values())for option, times in sorted(options_wrong_times.items(), key=lambda x: (int(x[0].split('-')[0]), x[0].split('-')[1])):if times == max_wrong_times:print(max_wrong_times, option)  # 輸出錯誤次數最多的選項及其錯誤次數

有何不同

這兩個版本的代碼在功能上是相同的，都是為了計算每個學生的得分并找出錯得最多的題目選項。然而，它們在實現上有一些差異，主要體現在代碼的簡潔性、效率和可讀性上。以下是兩個版本的主要差異分析：

版本一（原始版本）：

字符串操作較多：
- 使用多次字符串替換和分割操作，例如?student_options = student_options.replace(' ', '').replace(')', '')?和?student_options = student_options[1:].split('(')。
- 將學生答案轉換為元組列表，例如?student_options[j] = int(student_options[j][0]), student_options[j][1:]。
使用列表和集合操作：
- 使用列表操作來處理學生答案和正確答案，例如?wrong_options = list(set(student_options[j][1]) ^ set(answers[j+1][1]))。
- 使用集合操作來判斷部分正確的情況，例如?set(student_options[j][1]) < set(answers[j+1][1])。
錯誤選項次數的記錄：
- 使用字典來記錄錯誤選項次數，例如?options_wrong_times[str(j+1) + '-' + option] = 1。
輸出錯誤次數最多的選項：

使用列表推導式來找出錯誤次數最多的選項，例如?output = [option for option in options_wrong_times if options_wrong_times[option] == tmp]。

版本二（優化版本）：

減少字符串操作：
- 通過一次性的字符串替換和分割操作，減少了多次的字符串操作，例如?student_options = input().replace(' ', '').replace(')', '')[1:].split('(')。
使用集合操作：
- 將學生答案和正確答案都轉換為集合，利用集合的快速操作，例如?student_options = [set(opt[1:]) for opt in student_options]?和?correct_option_set = answers[j+1][1]。
錯誤選項次數的記錄：
- 使用字典的?get?方法來簡?編輯文章化錯誤選項次數的更新，例如?options_wrong_times[key] = options_wrong_times.get(key, 0) + 1。
輸出錯誤次數最多的選項：

使用排序來確保輸出順序正確，例如?for option, times in sorted(options_wrong_times.items(), key=lambda x: (int(x[0].split('-')[0]), x[0].split('-')[1]))。

總結：

優化版本在代碼簡潔性、效率和可讀性上都有所提升。
優化版本減少了不必要的字符串操作，利用集合操作提高了處理速度。
優化版本使用字典的?get?方法簡化了錯誤選項次數的更新，并使用排序確保輸出順序正確。

總體來說，優化版本在性能和代碼質量上都有顯著提升。

這段代碼的主要功能是計算每個學生的得分，并找出錯得最多的題目選項。下面是對這段代碼的專業點評，包括時間復雜度和空間復雜度的分析。

代碼結構和邏輯

輸入處理：
- 首先讀取學生人數?N_students_num?和題目數量?M_ques_num。
- 然后讀取每個題目的詳細信息（包括滿分、選項數量、正確選項數量和正確選項）并存儲在字典?answers?中。
學生得分計算：
- 對于每個學生，讀取其答案并轉換為集合列表。
- 計算每個學生的得分，并記錄每個錯誤選項的出現次數。
輸出結果：

輸出每個學生的得分。
如果沒有錯誤選項，輸出 "Too simple"。
否則，輸出錯誤次數最多的選項及其錯誤次數。

時間復雜度分析

初始化答案字典：
- 這部分的時間復雜度是 O(M)，其中 M 是題目數量。
學生得分計算：
- 對于每個學生，需要處理其答案并計算得分。這部分的時間復雜度是 O(N * M)，其中 N 是學生人數，M 是題目數量。
- 在計算得分時，需要比較學生答案和正確答案，這部分的時間復雜度是 O(M * K)，其中 K 是每個題目的選項數量。
- 記錄錯誤選項的出現次數，這部分的時間復雜度是 O(M * K)。
輸出結果：

輸出每個學生的得分，這部分的時間復雜度是 O(N)。
輸出錯誤次數最多的選項，這部分的時間復雜度是 O(M * K log(M * K))，因為需要對錯誤選項進行排序。

綜合來看，整個代碼的時間復雜度是 O(N * M * K + M * K log(M * K))。

空間復雜度分析

答案字典：
- 存儲每個題目的詳細信息，空間復雜度是 O(M * K)。
錯誤選項次數字典：
- 存儲每個錯誤選項的出現次數，空間復雜度是 O(M * K)。
學生答案：

存儲每個學生的答案，空間復雜度是 O(N * M * K)。

綜合來看，整個代碼的空間復雜度是 O(N * M * K)。

總結

時間復雜度：O(N * M * K + M * K log(M * K))
空間復雜度：O(N * M * K)

這段代碼在邏輯上是清晰的，但在處理大量數據時可能會面臨性能問題。特別是當 N、M 和 K 都很大時，時間復雜度和空間復雜度都會顯著增加。優化方向可以考慮減少不必要的字符串操作和集合操作，以及優化數據結構的使用。

我要更強

優化時間復雜度和空間復雜度的方法通常涉及減少不必要的計算和數據結構的使用。以下是一些可能的優化方法，并附上相應的代碼和注釋。

優化方法

減少字符串操作：減少不必要的字符串替換和分割操作。
使用高效的集合操作：利用集合的快速操作來減少比較時間。
避免重復計算：緩存一些計算結果以避免重復計算。
優化數據結構：選擇合適的數據結構來存儲和處理數據。

優化后的代碼

from collections import defaultdict# 讀取學生人數和題目數量
N_students_num, M_ques_num = map(int, input().split())# 初始化答案字典
answers = {}
for i in range(M_ques_num):full_score, option_num, right_option_num, *right_options = input().split()answers[i+1] = [int(right_option_num), set(right_options), int(full_score)]# 初始化錯誤選項次數字典
options_wrong_times = defaultdict(int)# 計算每個學生的得分并記錄錯誤選項次數
for _ in range(N_students_num):student_options = input().replace(' ', '').replace(')', '')[1:].split('(')student_options = [set(opt[1:]) for opt in student_options]this_student_score = 0for j in range(M_ques_num):student_option_set = student_options[j]correct_option_set = answers[j+1][1]if student_option_set == correct_option_set:this_student_score += answers[j+1][2]elif student_option_set.issubset(correct_option_set):this_student_score += 0.5 * answers[j+1][2]wrong_options = student_option_set.symmetric_difference(correct_option_set)for option in wrong_options:key = f"{j+1}-{option}"options_wrong_times[key] += 1print(f"{this_student_score:.1f}")# 輸出錯誤次數最多的選項
if not options_wrong_times:print("Too simple")
else:max_wrong_times = max(options_wrong_times.values())for option, times in sorted(options_wrong_times.items(), key=lambda x: (int(x[0].split('-')[0]), x[0].split('-')[1])):if times == max_wrong_times:print(max_wrong_times, option)

優化說明

減少字符串操作：
- 使用?input().replace(' ', '').replace(')', '')[1:].split('(')?一次性完成字符串替換和分割操作。
使用高效的集合操作：
- 使用集合的?symmetric_difference?方法來計算錯誤選項，這比手動比較更高效。
避免重復計算：
- 使用?defaultdict?來簡化錯誤選項次數的更新，避免重復的?get?操作。
優化數據結構：