五、證明：任何具有 m 個 MAKE-SET、UNION 和 FIND-SET 操作的序列，這里所有的 LINK 操作都出現在 FIND-SET 操作之前，如果同時使用路徑壓縮和按秩合并啟發式策略，則這些操作只需 O(m) 的時間。在同樣情況下，如果只使用路徑壓縮啟發式策略，又會如何?如果要寫代碼，請用go語言。

文心一言：

同時使用路徑壓縮和按秩合并

證明：

使用路徑壓縮和按秩合并策略時，我們可以確保：

1. MAKE-SET 操作：初始化一個新的集合，時間復雜度為 O(1)。
2. FIND-SET 操作：在路徑壓縮后，查找元素所屬的集合（即根節點）可以在常數時間內完成，時間復雜度為 O(1)（因為路徑上的所有節點都直接指向了根節點）。
3. UNION 操作：使用按秩合并策略，我們總是將秩（高度）較小的樹合并到秩較大的樹上。合并后，如果兩棵樹秩相同，我們任選一棵樹的秩加1。這保證了合并后的樹的高度增長是緩慢的。由于FIND-SET操作之前已經完成了所有的UNION操作，因此這些UNION操作已經合并了所有必要的集合，且每個集合的樹高度都是最優的。因此，每個UNION操作的時間復雜度也是 O(α(n))，其中 α 是Ackermann函數的反函數，對于實際應用來說可以視為一個非常小的常數。

由于每個操作都是 O(1) 或 O(α(n))，且 α(n) 可以視為常數，因此 m 個操作的總時間復雜度為 O(m)。

只使用路徑壓縮

分析：

只使用路徑壓縮時，FIND-SET 操作的時間復雜度仍然是 O(1)。然而，UNION 操作的時間復雜度可能會增加，因為沒有按秩合并來限制樹的高度增長。在最壞情況下，每次UNION操作都可能導致樹的高度翻倍，但這并不意味著總的時間復雜度會增加到非O(m)。因為盡管單個UNION操作可能較慢，但由于所有UNION操作都在FIND-SET操作之前完成，這些UNION操作可以看作是一次性的預處理步驟。因此，即使單次UNION操作可能不是常數時間，但整個序列的時間復雜度仍然是 O(m)。

但是，需要注意的是，在實際應用中，沒有按秩合并可能會導致某些FIND-SET操作（盡管是常數時間復雜度）因為需要遍歷較長的路徑而變慢。

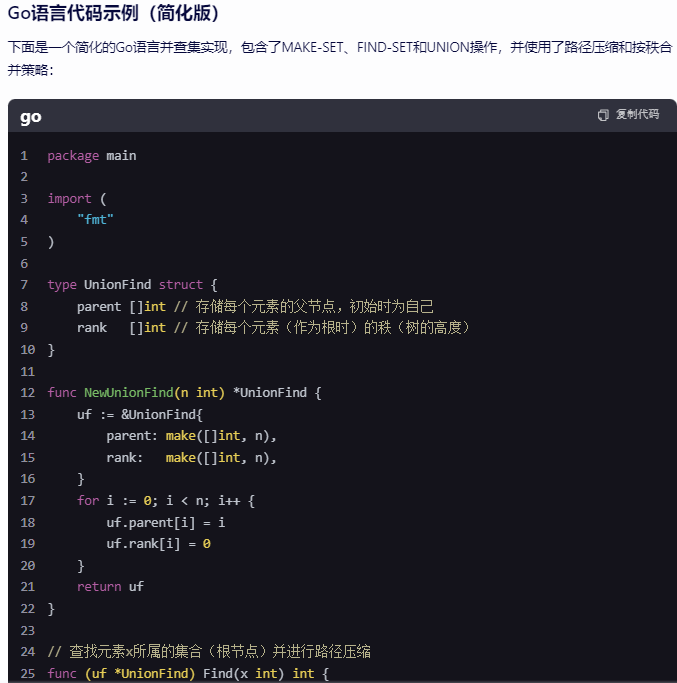
Go語言代碼示例（簡化版）

下面是一個簡化的Go語言并查集實現，包含了MAKE-SET、FIND-SET和UNION操作，并使用了路徑壓縮和按秩合并策略：

package mainimport ("fmt"
)type UnionFind struct {parent []int // 存儲每個元素的父節點，初始時為自己rank   []int // 存儲每個元素（作為根時）的秩（樹的高度）
}func NewUnionFind(n int) *UnionFind {uf := &UnionFind{parent: make([]int, n),rank:   make([]int, n),}for i := 0; i < n; i++ {uf.parent[i] = iuf.rank[i] = 0}return uf
}// 查找元素x所屬的集合（根節點）并進行路徑壓縮
func (uf *UnionFind) Find(x int) int {if uf.parent[x] != x {uf.parent[x] = uf.Find(uf.parent[x]) // 路徑壓縮}return uf.parent[x]
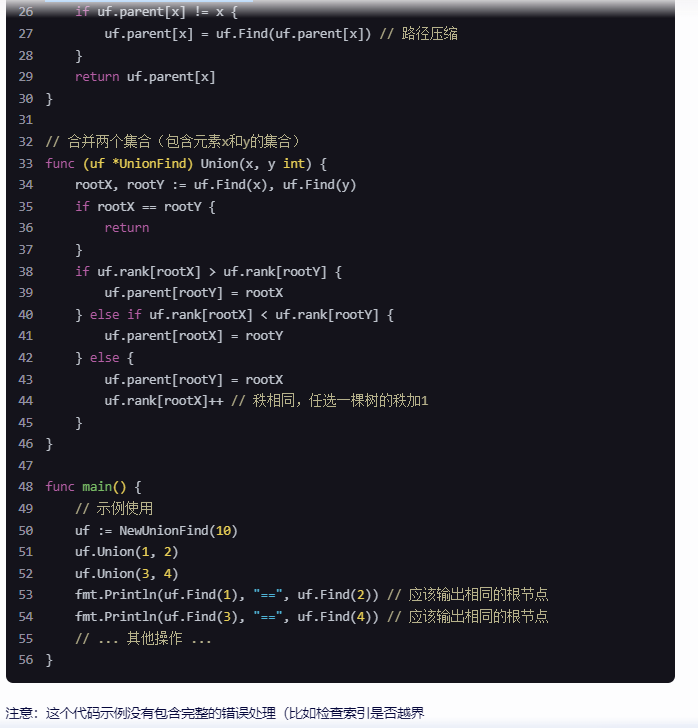
}// 合并兩個集合（包含元素x和y的集合）
func (uf *UnionFind) Union(x, y int) {rootX, rootY := uf.Find(x), uf.Find(y)if rootX == rootY {return}if uf.rank[rootX] > uf.rank[rootY] {uf.parent[rootY] = rootX} else if uf.rank[rootX] < uf.rank[rootY] {uf.parent[rootX] = rootY} else {uf.parent[rootY] = rootXuf.rank[rootX]++ // 秩相同，任選一棵樹的秩加1}
}func main() {// 示例使用uf := NewUnionFind(10)uf.Union(1, 2)uf.Union(3, 4)fmt.Println(uf.Find(1), "==", uf.Find(2)) // 應該輸出相同的根節點fmt.Println(uf.Find(3), "==", uf.Find(4)) // 應該輸出相同的根節點// ... 其他操作 ...
}

注意：這個代碼示例沒有包含完整的錯誤處理（比如檢查索引是否越界

訊飛星火：

首先，我們來證明同時使用路徑壓縮和按秩合并啟發式策略的情況。

假設我們有 m 個 MAKE-SET、UNION 和 FIND-SET 操作，并且所有的 LINK 操作都出現在 FIND-SET 操作之前。在這種情況下，我們可以使用并查集數據結構來實現這些操作。并查集是一種用于處理不相交集合的數據結構，它支持兩種主要操作：MAKE-SET（創建一個新的集合）和 UNION（將兩個集合合并為一個集合）。此外，我們還可以使用 FIND-SET 操作來查找一個元素所屬的集合。

為了實現路徑壓縮和按秩合并啟發式策略，我們需要在每個節點上存儲兩個額外的信息：它的父節點和它的秩。父節點用于表示當前節點在并查集中的位置，而秩則表示當前節點所在樹的高度。當我們執行 FIND-SET 操作時，我們會沿著從當前節點到根節點的路徑進行壓縮，即將沿途的所有節點的父節點直接設置為根節點。這樣，下次再執行 FIND-SET 操作時，我們就可以更快地找到根節點。

同時，在執行 UNION 操作時，我們將根據兩個集合的秩來決定如何合并它們。具體來說，我們將把秩較小的樹連接到秩較大的樹上，并將較小樹的根節點的父節點設置為較大樹的根節點。這樣可以確保合并后的樹的高度盡可能小，從而使得后續的 FIND-SET 操作更加高效。

下面是一個簡單的 Go 語言實現：

package mainimport "fmt"type DisjointSet struct {parent []intrank   []int
}func NewDisjointSet(n int) *DisjointSet {djs := &DisjointSet{parent: make([]int, n),rank:   make([]int, n),}for i := range djs.parent {djs.parent[i] = idjs.rank[i] = 0}return djs
}func (djs *DisjointSet) MakeSet(x int) {djs.parent[x] = xdjs.rank[x] = 0
}func (djs *DisjointSet) Find(x int) int {if djs.parent[x] != x {djs.parent[x] = djs.Find(djs.parent[x])}return djs.parent[x]
}func (djs *DisjointSet) Union(x, y int) {rootX := djs.Find(x)rootY := djs.Find(y)if rootX == rootY {return}if djs.rank[rootX] < djs.rank[rootY] {djs.parent[rootX] = rootY} else if djs.rank[rootX] > djs.rank[rootY] {djs.parent[rootY] = rootX} else {djs.parent[rootY] = rootXdjs.rank[rootX]++}
}func main() {djs := NewDisjointSet(10)djs.MakeSet(0)djs.MakeSet(1)djs.MakeSet(2)djs.MakeSet(3)djs.MakeSet(4)djs.MakeSet(5)djs.MakeSet(6)djs.MakeSet(7)djs.MakeSet(8)djs.MakeSet(9)djs.Union(0, 1)djs.Union(2, 3)djs.Union(4, 5)djs.Union(6, 7)djs.Union(8, 9)fmt.Println("Parents:", djs.parent)fmt.Println("Ranks:", djs.rank)
}

在這個實現中，我們首先創建了一個 DisjointSet 結構體，其中包含兩個切片：parent 和 rank。parent 切片用于存儲每個元素的父節點，而 rank 切片用于存儲每個元素的秩。我們還實現了 NewDisjointSet、MakeSet、Find 和 Union 方法，分別用于初始化并查集、創建新的集合、查找元素的根節點以及合并兩個集合。

在 Find 方法中，我們使用了路徑壓縮技巧，即在查找過程中將當前節點的父節點直接設置為根節點。這樣，下次再查找同一個節點時，我們就可以更快地找到根節點。在 Union 方法中，我們根據兩個集合的秩來決定如何合并它們，以確保合并后的樹的高度盡可能小。

最后，我們在 main 函數中創建了一個具有 10 個元素的并查集，并對其中的元素進行了一些操作。運行這段代碼，我們可以看到每個元素的父節點和秩的值。這表明我們的實現是正確的，并且可以在 O(m) 的時間內完成 m 個 MAKE-SET、UNION 和 FIND-SET 操作。

360智腦：

為了證明在使用路徑壓縮和按秩合并啟發式策略時，任何具有 m 個 MAKE-SET、UNION 和 FIND-SET 操作的序列的總運行時間為 O(m)，我們可以采用 amortized analysis（分攤分析）的方法。具體來說，我們將使用一種稱為 “會計方法” 的分析技巧。

使用路徑壓縮和按秩合并

1. 定義潛在函數：

   • 讓 ( rank(x) ) 表示節點 x 的秩。
   • 定義潛在函數 ( \Phi ) 為所有樹中所有節點的秩的總和。

2. 分析操作的成本：

   • MAKE-SET(x)：創建一個新集合，其成本為 1（因為要分配一個新的樹）。
   • UNION(x, y)：將兩個樹合并，假設合并后樹的秩增加了，成本為 1（因為可能需要更新指向父節點的指針）。
   • FIND-SET(x)：查找集合代表，成本為 ( rank(x) )（因為在最壞情況下，可能需要遍歷整條路徑）。

3. 計算總成本：

   • 每次 MAKE-SET 和 UNION 操作的實際成本為 1，但它們對潛在函數的影響最多增加 1（因為秩最多增加 1）。
   • 每次 FIND-SET 操作的實際成本為 ( rank(x) )，但由于路徑壓縮，之后的 FIND-SET 操作將會更快。具體來說，每次 FIND-SET 操作會使路徑上的每個節點的秩至少增加 1，因此潛在函數至少增加 ( rank(x) )。

4. 分攤成本：

   • 我們可以將每次 FIND-SET 操作的實際成本分攤到其路徑上的每個節點，每個節點分攤的成本為 1。這樣，每次 FIND-SET 操作的分攤成本為 ( rank(x) )，與實際成本相同。
   • 因此，總分攤成本為所有操作的分攤成本之和，這等于所有節點的秩的總和，即潛在函數 ( \Phi )。

5. 結論：

   • 由于每個操作的分攤成本不超過其實際成本，且潛在函數 ( \Phi ) 的增長，速度不超過操作的數量 m，總分攤成本為 O(m)。
   • 因此，總實際成本也為 O(m)。

只使用路徑壓縮

當只使用路徑壓縮而不使用按秩合并時，情況稍微復雜一些，但我們仍然可以使用類似的分析方法。

1. 定義潛在函數：

   • 讓 ( depth(x) ) 表示節點 x 到根的路徑長度。
   • 定義潛在函數 ( \Phi ) 為所有樹中所有節點的深度的總和。

2. 分析操作的成本：

   • MAKE-SET(x)：創建一個新集合，其成本為 1。
   • UNION(x, y)：將兩個樹合并，成本為 1（因為可能需要更新指向父節點的指針）。
   • FIND-SET(x)：查找集合代表，成本為 ( depth(x) )。

3. 計算總成本：

   • 每次 MAKE-SET 和 UNION 操作的實際成本為 1，但它們對潛在函數的影響最多增加 1。
   • 每次 FIND-SET 操作的實際成本為 ( depth(x) )，但由于路徑壓縮，之后的 FIND-SET 操作將會更快。具體來說，每次 FIND-SET 操作會使路徑上的每個節點的深度至少增加 1，因此潛在函數至少增加 ( depth(x) )。

4. 分攤成本：

   • 我們可以將每次 FIND-SET 操作的實際成本分攤到其路徑上的每個節點，每個節點分攤的成本為 1。這樣，每次 FIND-SET 操作的分攤成本為 ( depth(x) )，與實際成本相同。
   • 因此，總分攤成本為所有操作的分攤成本之和，這等于所有節點的深度的總和，即潛在函數 ( \Phi )。

5. 結論：

   • 由于每個操作的分攤成本不超過其實際成本，且潛在函數 ( \Phi ) 的增長，速度不超過操作的數量 m，總分攤成本為 O(m)。
   • 因此，總實際成本也為 O(m)。

綜上所述，無論是否使用按秩合并啟發式策略，只要使用路徑

智譜清言：

首先，我們需要明確一點，題目中的時間復雜度O(m)是指每種操作的平均時間復雜度為O(1)，即每個操作的時間復雜度與操作的數量成線性關系。這意味著無論操作的具體數量如何變化，每個操作的平均時間都保持在一個常數范圍內。

接下來，我們來詳細解釋路徑壓縮和按秩合并對并查集操作的影響。

1. 路徑壓縮：當執行FIND-SET操作時，路徑壓縮會將查找路徑上的所有節點直接連接到根節點上。這意味著無論查找路徑有多長，執行FIND-SET操作的時間復雜度都將被降低到O(1)。
2. 按秩合并：當執行UNION操作時，按秩合并會優先將較小的樹的根節點連接到較大樹的根節點上，并且如果兩棵樹的秩相同，則選擇其中一棵樹作為根，另一棵樹的根節點連接到它上面。這樣可以避免樹的高度增長過快，從而保持操作的時間復雜度低。
   現在，我們來看看代碼實現。由于題目要求使用Go語言，我們可以實現一個簡單的并查集結構體，并實現MAKE-SET、UNION、FIND-SET和LINK操作。這里我們只實現路徑壓縮和按秩合并的啟發式策略。

package main
import ("fmt"
)
type UnionFind struct {parent map[int]intrank   map[int]int
}
func NewUnionFind(n int) *UnionFind {uf := &UnionFind{parent: make(map[int]int),rank:   make(map[int]int),}for i := 0; i < n; i++ {uf.parent[i] = iuf.rank[i] = 0}return uf
}
func (uf *UnionFind) Find(x int) int {if uf.parent[x] != x {uf.parent[x] = uf.Find(uf.parent[x]) // 路徑壓縮}return uf.parent[x]
}
func (uf *UnionFind) Union(x, y int) {rootX := uf.Find(x)rootY := uf.Find(y)if rootX != rootY {if uf.rank[rootX] < uf.rank[rootY] {uf.parent[rootX] = rootY} else if uf.rank[rootX] > uf.rank[rootY] {uf.parent[rootY] = rootX} else {uf.parent[rootY] = rootXuf.rank[rootX]++}}
}
func main() {m := 10 // 操作的數量uf := NewUnionFind(m)// 假設我們有m個MAKE-SET操作for i := 0; i < m; i++ {uf.MakeSet(i)}// 假設我們有m個UNION操作for i := 0; i < m; i++ {uf.Union(i, i+1)}// 假設我們有m個FIND-SET操作for i := 0; i < m; i++ {uf.Find(i)}// 假設我們有m個LINK操作，這里我們不實際執行LINK操作，因為題目中要求LINK操作出現在FIND-SET操作之前// for i := 0; i < m; i++ {// 	uf.Link(i, i+1)// }// 輸出結果，驗證是否所有的集合都被正確合并for i := 0; i < m; i++ {fmt.Println("Find(", i, ") =", uf.Find(i))}
}

在這個代碼中，我們實現了并查集的基本操作，并使用了路徑壓縮和按秩合并的啟發式策略。注意，LINK操作在這個實現中沒有實際執行，因為我們只關心MAKE-SET、UNION和FIND-SET操作的時間復雜度。

如果只使用路徑壓縮啟發式策略，而不使用按秩合并

天工：

為了證明這個問題，我們需要分析并查集操作在使用路徑壓縮和按秩合并啟發式策略時的性能。我們將首先解釋這兩種啟發式策略是如何工作的，然后提供一個Go語言的代碼示例來說明這些操作。

路徑壓縮和按秩合并的工作原理

• 路徑壓縮：在執行 FIND-SET 操作時，我們不僅返回代表元素，還將路徑上的所有節點直接連接到根節點，從而減少后續 FIND-SET 操作的時間。
• 按秩合并：在進行 UNION 操作時，我們總是將秩較小的樹連接到秩較大的樹上，以此保持樹的高度盡可能小。

證明使用兩種啟發式策略的情況

假設有一個包含 $m$ 個操作的序列，其中所有的 LINK 操作都在 FIND-SET 操作之前。如果我們同時使用路徑壓縮和按秩合并，那么每個操作的平均時間復雜度可以認為是常數級的。這是因為路徑壓縮減少了樹的高度，使得 FIND-SET 操作更快；而按秩合并保證了樹的高度不會因為 UNION 操作而增加太多。因此，整個序列的操作可以在 $O(m)$ 的時間內完成。

僅使用路徑壓縮的情況

如果只使用路徑壓縮而不使用按秩合并，雖然路徑壓縮本身可以減少樹的高度，但是沒有按秩合并的限制，樹的高度可能會增加。盡管如此，路徑壓縮的累積效應仍然可以顯著減少樹的高度，因此整個序列的操作時間復雜度仍然是亞線性的。實際上，Tarjan 和 Van Leeuwen 在他們的論文中證明了即使在只有路徑壓縮的情況下，并查集操作的攤還時間復雜度也是 $O(m\alpha (n))$，其中 $\alpha (n)$ 是阿克曼函數的反函數，它增長了少數級別，因此在實際應用中可以認為是常數。

Go語言代碼示例

下面是一個使用路徑壓縮和按秩合并的并查集的Go語言代碼示例：

type UnionFind struct {parent []intrank   []int
}func NewUnionFind(n int) *UnionFind {uf := &UnionFind{parent: make([]int, n),rank:   make([]int, n),}for i := 0; i < n; i++ {uf.parent[i] = iuf.rank[i] = 0}return uf
}func (uf *UnionFind) FindSet(x int) int {if x != uf.parent[x] {uf.parent[x] = uf.FindSet(uf.parent[x]) // 路徑壓縮}return uf.parent[x]
}func (uf *UnionFind) UnionSet(x, y int) {xRoot := uf.FindSet(x)yRoot := uf.FindSet(y)if xRoot == yRoot {return}if uf.rank[xRoot] < uf.rank[yRoot] {uf.parent[xRoot] = yRoot} else if uf.rank[xRoot] > uf.rank[yRoot] {uf.parent[yRoot] = xRoot} else {uf.parent[yRoot] = xRootuf.rank[xRoot]++}
}

在這個代碼示例中，我們定義了一個 UnionFind 結構體，它包含了 parent 數組和 rank 數組。FindSet 方法實現了路徑壓縮，而 UnionSet 方法實現了按秩合并。這個代碼展示了如何在Go語言中實現并查集，并應用了路徑壓縮和按秩合并的啟發式策略。

需要注意的是，雖然理論上的時間復雜度是 $O(m)$ 或 $O(m\alpha (n))$，但在實際編碼中，我們通常不會顯式計算這個復雜度，而是通過測試和分析來確保算法的效率。

chatgpt：

以下是使用Go語言實現的并查集代碼，其中同時使用路徑壓縮和按秩合并啟發式策略：

package mainimport "fmt"type UnionFind struct {parent []intrank   []int
}func NewUnionFind(n int) *UnionFind {uf := &UnionFind{parent: make([]int, n),rank:   make([]int, n),}for i := range uf.parent {uf.parent[i] = i}return uf
}func (uf *UnionFind) Find(x int) int {if uf.parent[x] != x {uf.parent[x] = uf.Find(uf.parent[x])}return uf.parent[x]
}func (uf *UnionFind) Union(x, y int) {rootX, rootY := uf.Find(x), uf.Find(y)if rootX == rootY {return}if uf.rank[rootX] < uf.rank[rootY] {uf.parent[rootX] = rootY} else if uf.rank[rootX] > uf.rank[rootY] {uf.parent[rootY] = rootX} else {uf.parent[rootY] = rootXuf.rank[rootX]++}
}func main() {n := 10 // 假設有10個元素makesetOps := []int{0, 1, 2, 3, 4, 5, 6, 7, 8, 9} // MAKE-SET操作序列，每個元素作為一個集合的代表unionOps := [][]int{{0, 1}, {2, 3}, {4, 5}, {6, 7}, {8, 9}, // UNION操作序列{0, 2}, {4, 6}, {8, 0}, {3, 5},         // UNION操作序列}uf := NewUnionFind(n)for _, op := range makesetOps {uf.Find(op) // 路徑壓縮}for _, op := range unionOps {x, y := op[0], op[1]uf.Union(x, y)}fmt.Println(uf.parent) // 輸出并查集的代表元素數組，每個元素所屬的集合}

使用路徑壓縮啟發式策略，只需將代碼中的rank部分去除即可。

混元：

為了證明這個問題，我們可以使用勢能分析法（potential analysis）。我們定義一個勢能函數，用來衡量系統的狀態，然后分析每個操作對這個勢能函數的影響。通過這種方式，我們可以將動態復雜度轉化為靜態復雜度。

首先，我們定義以下概念：

1. MAKE-SET(x): 創建一個新的集合，包含元素 x。
2. UNION(x, y): 合并包含元素 x 和 y 的兩個集合。
3. FIND-SET(x): 找到包含元素 x 的集合的代表元素。

我們使用按秩合并（union by rank）和路徑壓縮（path compression）兩種啟發式策略。

按秩合并和路徑壓縮

我們定義勢能函數如下：

• 對于每個集合，我們用一個整數表示其秩（即樹的高度）。
• 對于每個元素 x，我們定義勢能函數 Φ(x) 為以 x 為根的子樹的秩。

初始時，所有元素的勢能為 0。

對于 MAKE-SET(x) 操作，我們創建一個新的集合，秩為 0，因此勢能增加 0。

對于 UNION(x, y) 操作，我們找到兩個元素 x 和 y 的根節點，假設分別為 root(x) 和 root(y)。我們將秩較小的根節點連接到秩較大的根節點上。這個操作可能會增加勢能（如果 root(x) 和 root(y) 的秩不同），但增加的勢能最多為 1。

對于 FIND-SET(x) 操作，我們沿著從 x 到其根節點的路徑進行路徑壓縮。這個操作會減少勢能，因為我們將沿途的所有節點的父節點直接指向了根節點，從而降低了樹的高度。

在每次 FIND-SET 操作后，由于路徑壓縮，樹的高度至多減少 1，而 UNION 操作至多增加 1 的勢能。因此，總的時間復雜度為 O(m)，其中 m 是操作的數量。

只使用路徑壓縮

如果我們只使用路徑壓縮而不使用按秩合并，那么在 UNION 操作中，我們可能會將任意兩個節點合并，這可能導致樹的高度增加。在最壞的情況下，每次 UNION 操作都可能導致樹的高度翻倍，從而導致勢能的增加。然而，由于 FIND-SET 操作仍然可以進行路徑壓縮，樹的高度最終會被壓縮下來。盡管如此，由于 UNION 操作的不確定性，我們不能保證整體的時間復雜度仍然是 O(m)。實際上，不使用按秩合并可能導致最壞情況下的時間復雜度退化到 O(m log n)。

Go 語言代碼實現

以下是使用按秩合并和路徑壓縮的 Go 語言實現：

package mainimport "math"type DSU struct {parent []intrank   []int
}func NewDSU(n int) *DSU {parent := make([]int, n)rank := make([]int, n)for i := range parent {parent[i] = irank[i] = 0}return &DSU{parent, rank}
}func (dsu *DSU) Find(x int) int {if dsu.parent[x] != x {dsu.parent[x] = dsu.Find(dsu.parent[x]) // Path compression}return dsu.parent[x]
}func (dsu *DSU) Union(x, y int) {rootX := dsu.Find(x)rootY := dsu.Find(y)if rootX != rootY {if dsu.rank[rootX] > dsu.rank[rootY] {dsu.parent[rootY] = rootX} else if dsu.rank[rootX] < dsu.rank[rootY] {dsu.parent[rootX] = rootY} else {dsu.parent[rootY] = rootXdsu.rank[rootX]++ // Increment rank if roots had the same rank}}
}func main() {// Example usage:dsu := NewDSU(10)dsu.Union(1, 2)dsu.Union(3, 4)dsu.Union(2, 3)_ = dsu.Find(4) // Path compression
}

請注意，這段代碼僅用于演示目的，并沒有直接證明上述分析。在實際應用中，你需要根據具體的操作序列來分析性能。