摘要

本周閱讀了一篇利用圖神經網絡結合Transformer的長時間序列預測論文，提出了一種新的模型Graphformer。Graphformer通過改進稀疏自注意力機制，結合圖卷積網絡（GCN）考慮不同尺度下變量之間的空間相關性，實現了Transformer架構與GCN的緊密集成。此外，論文還開發了自注意力降采樣模塊、多尺度特征融合操作以及時間慣性融合操作。實驗分析表明，Graphformer在預測精度上顯著優于之前的最新方法。研究還指出，未來可以通過使用各種分解方法預處理時間序列，并結合自動機器學習（AutoML）技術進一步提高模型精度?。

ABSTRACT

This week, We read a paper on long-term time series forecasting that combines Graph Neural Networks (GNN) with Transformer models and proposes a new model called Graphformer. Graphformer improves the sparse self-attention mechanism and incorporates Graph Convolutional Networks (GCN) to consider spatial correlations between variables at different scales, achieving a close integration of the Transformer architecture with GCN. Additionally, the paper develops a self-attention down-sampling module, a multi-scale feature fusion operation, and a time inertia fusion operation. Experimental analysis shows that Graphformer significantly outperforms previous state-of-the-art methods in prediction accuracy. The study also suggests that future improvements in model accuracy can be achieved by using various decomposition methods to preprocess time series and combining them with Automated Machine Learning (AutoML) techniques.

1 論文信息

SCI：1區
IF：7.2
發表單位：重慶大學計算機學院

1.1 論文標題

Graphformer: Adaptive graph correlation transformer for multivariate long sequence time series forecasting

1.2 論文摘要

準確的長序列時間序列預測（LSTF）由于其復雜的時間依賴性，仍然是一項關鍵挑戰。多變量時間序列預測方法本質上假設變量是相互關聯的，每個變量的未來狀態不僅依賴于其歷史，還依賴于其他變量。然而，大多數現有方法（如Transformer）無法有效利用變量之間的潛在空間相關性。為了解決上述問題，我們提出了一種基于Transformer的LSTF模型，稱為Graphformer，該模型能夠高效地學習多個變量之間復雜的時間模式和依賴關系。首先，在編碼器的自注意下采樣層中，Graphformer用膨脹卷積層取代了標準卷積層，以高效捕捉不同粒度水平下的長時間依賴關系。同時，Graphformer用圖自注意機制取代了自注意機制，該機制可以從數據中自動推斷隱含的稀疏圖結構，對于沒有顯式圖結構的時間序列表現出更好的泛化能力，并學習序列間的隱含空間依賴關系。此外，Graphformer使用時間慣性模塊增強未來時間步對最近輸入的敏感性，并通過切片和融合特征圖的多尺度特征融合操作，在不同粒度水平上提取時間相關性，以提高模型的準確性和效率。與現有的SOTA Transformer模型相比，我們提出的Graphformer可以顯著提高長序列時間序列預測的準確性。

1.3 論文引言

時間序列是一組按時間順序排列的隨機變量，通常是以固定采樣率觀察潛在過程的結果。基于歷史時間序列觀測，時間序列預測旨在估計和預測未來時間步長的變量狀態，廣泛應用于統計學、運籌學和交通事故預防等領域。通常需要基于歷史觀測獲得多個連續未來時間步的預測，即多步預測。與經典的多步預測相比，長序列時間序列預測鼓勵盡可能長的預測范圍。預測范圍的增長帶來了額外的復雜性，例如誤差積累、準確性降低和不確定性增加。因此，準確的長序列時間序列預測對時間序列預測研究領域來說仍然是一個挑戰性問題。

類似于其他領域的預測任務，時間序列預測受益于近年來深度神經網絡研究的發展，并已廣泛應用于決策系統中，如交通事故預防、云計算資源重編程和最優投資策略。特別是，由于Transformer模型在自然語言處理中的成功，基于注意力機制的模型在時間序列預測中也取得了很大進展。然而，現有方法未能有效利用變量之間的潛在依賴關系。最近提出的基于Transformer的模型，包括Reformer、LogTrans和Informer，側重于建模時間特征，而未顯式建模不同序列之間的成對依賴關系，這削弱了模型的可解釋性和預測能力。

在現實生活中，傳感器可能跟蹤交通流量、能源使用、溫度等各種數據的變化。多個傳感器收集的時間序列可以結合成多變量時間序列。多變量時間序列預測技術隱含地假定變量是相互關聯的，每個變量的未來狀態不僅依賴于其過去的值，還依賴于其他變量，而且研究人員可能還需要預測任意或所有變量的時間序列。在交通系統中，了解交通流量的未來趨勢有助于減少交通事故和擁堵的發生。然而，交通流量的未來值不僅與其過去的值有關，還與其他變量（例如車輛的平均速度、空間占用率）有關。不論上述場景如何，挖掘不同變量之間的隱含相關性可以提高時間序列預測的整體準確性。

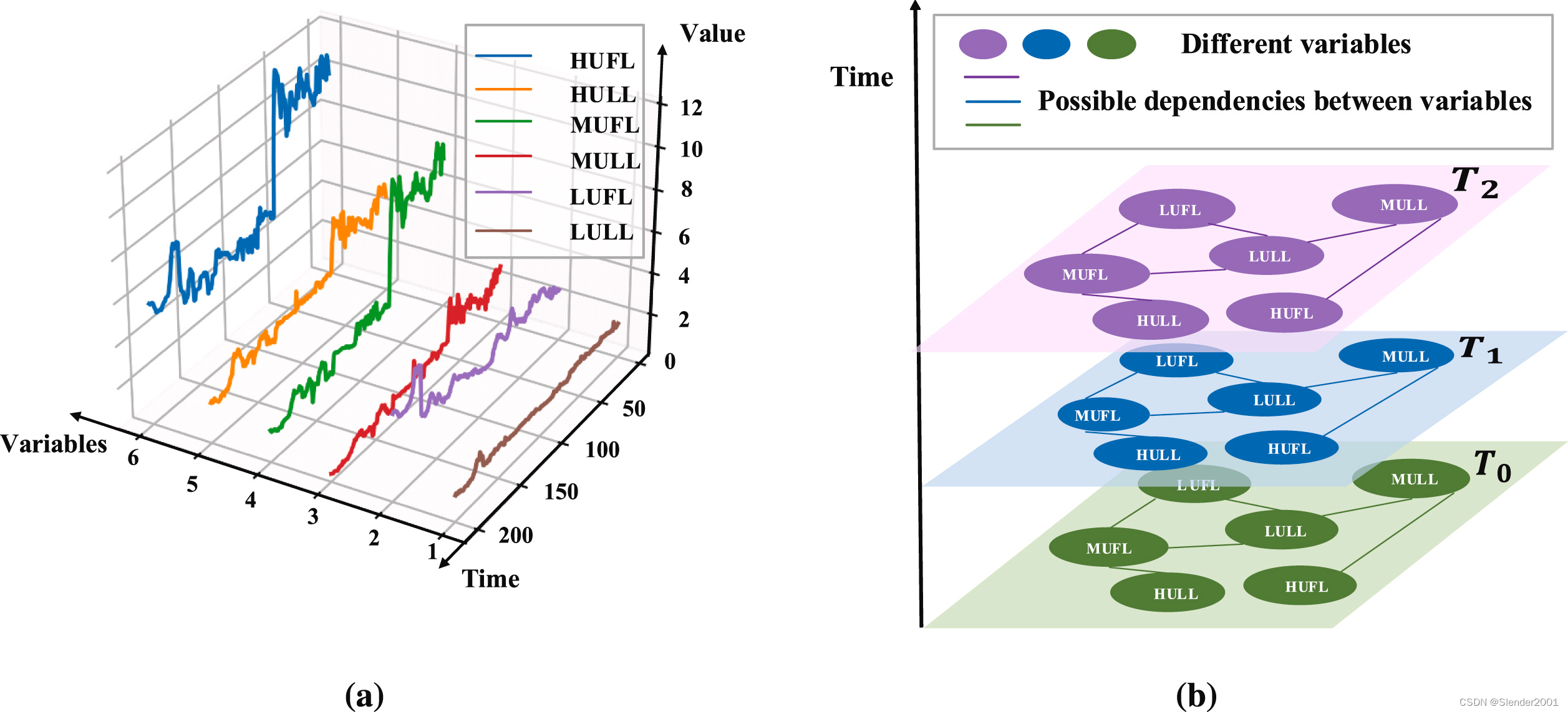
如何提取不同變量之間的交互特征是一個非常具有挑戰性的問題。圖是一種描述網絡中不同實體之間關系的數據類型，將不同變量視為圖的節點，將變量之間的依賴關系視為邊，例如，電力資源數據集ETT的多變量時間序列可以建模為如 Fig.1 所示的結構，其中HUFL、HULL等都是描述電力資源的變量。最近，GCN在處理圖結構數據方面取得了巨大成功。使用GCN進行多變量時間序列預測是一種很有前景的方法，通過聚合鄰居節點的信息并探索時間序列之間的隱含依賴關系，同時保持序列的時間軌跡。

然而，基于GCN的時間序列預測方法需要通過距離或相似性度量預定義圖結構。在大多數情況下，多變量時間序列沒有顯式圖結構。這些變量之間的關系不是先驗知識，而需要從數據中挖掘出來。即使對于存在顯式圖結構的時間序列，這些圖也嚴重依賴于相應的領域知識。同時考慮人為定義的因素，也可能導致某些隱含信息的遺漏或偏差。

Fig.1 ETT數據集的多變量時間序列圖結構建模

1.4 論文貢獻

① 提出了一種基于Transformer的模型，名為Graphformer，該模型遵循編碼器-解碼器結構，結合了稀疏圖自注意機制、多尺度特征融合和時間慣性機制，可以實現相等或更高的預測準確性。

② 將稀疏自注意機制改為稀疏圖自注意機制，考慮了不同尺度下變量之間的空間相關性，實現了Transformer架構與GCN的緊密結合。其內部的自適應圖卷積模塊不依賴于任何先驗知識，對于沒有顯式圖結構的多變量時間序列具有更好的通用性。

2 論文模型

2.1 問題定義

將時間序列視為具有長度$L$、維度$d_x$且時間間隔相同的一系列連續觀測值，可以表示為$X_t=\left\{x_1^t,x_2^t,\dots ,x_L^t|x_i^t\in R^{d_x}\right\}$。如果$d_x>1$，則該時間序列稱為多變量時間序列，其中$X$可以表示為$L\times D$二維矩陣：
$$X=\left[\begin{array}{cccc}{X}_{1,1}^t& X_{1,2}^t& \dots & X_{1,d_x}^t\\ X_{2,1}^t& X_{2,2}^t& \dots & X_{2,d_x}^t\\ ?& ?& ?& ?\\ X_{L,1}^t& X_{L,2}^t& \dots & X_{L,d_x}^t\end{array}\right](1)$$
其中，$X_i^t=\left[X_{i,1}^t,X_{i,2}^t,\dots ,X_{i,d_x}^t\right]$表示在時間$i$觀察到的$X_t$的值，$X_{i,k}^t$表示在時間$i$觀察到的$X_i^t$的第$k$個變量值。特別是，當變量維度為$d_x=1$時，時間序列稱為單變量時間序列。顯然，多變量時間序列可以看作是多個單變量時間序列的組合，這些變量可能相互影響，這里主要研究在多變量條件下的長時間序列預測。

圖$G$是一種描述網絡中實體關系的結構。本文參考了Graph WaveNet，引入了一種自適應圖學習方法，以反映稀疏query矩陣的圖結構。圖$G=(V,E)$由一組頂點集$V$和一組邊集$E$組成，可以用鄰接矩陣$A$表示。如果頂點$v_i$和$v_j$之間存在一條邊$e_{ij}$，則為$A_{ij}>0$，否則，如果不存在邊，則為$A_{ij}=0$。

2.2 模型架構

Fig.2 展示了所提出的Graphformer模型的架構，該模型遵循編碼器-解碼器架構來提取輸入序列中的長期時間相關性。編碼器堆疊了三個多頭稀疏圖自注意模塊、兩個自注意下采樣模塊和一個多尺度特征融合層。解碼器由一個掩碼稀疏圖自注意模塊和一個稀疏圖自注意模塊組成。

Fig.2 Graphformer總體架構

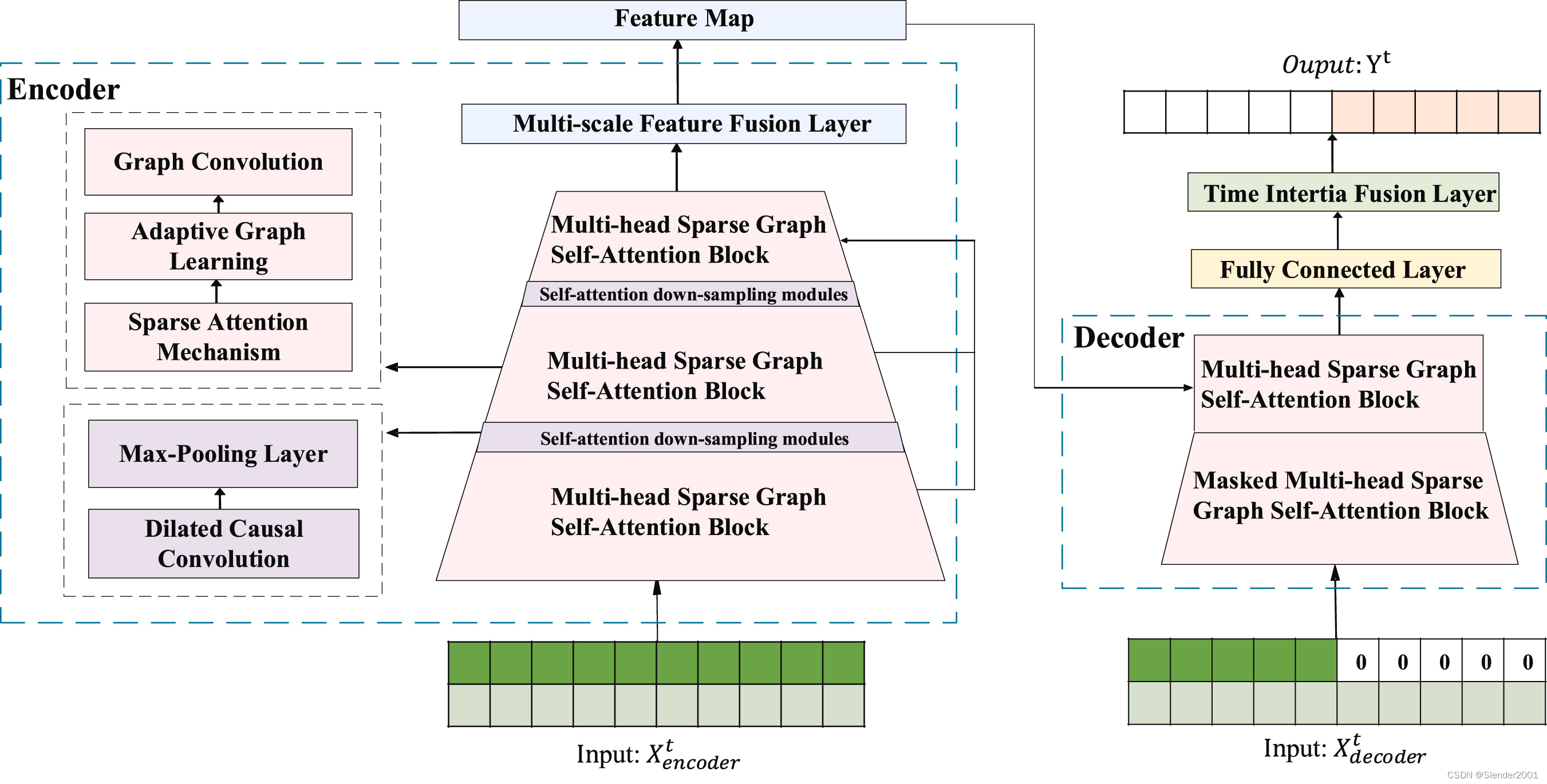
在編碼器中，每個圖稀疏自注意模塊包括一個稀疏自注意機制、自適應圖學習機制和圖卷積網絡。稀疏自注意機制計算query-key的縮放點積注意力。隨后，自適應圖學習機制捕捉稀疏query矩陣的圖結構，并自適應地推斷出稀疏query矩陣中的隱藏空間依賴關系。圖卷積網絡通過聚合和轉換節點的領域信息來學習節點特征，基于學習權重和預定義的圖結構。對于沒有顯式圖結構的多變量時間序列，稀疏圖自注意模塊也能夠自適應地學習序列之間的潛在空間相關性。每兩個多頭稀疏圖自注意塊由一個自注意下采樣模塊連接。Graphformer在Informer的自注意下采樣模塊基礎上，通過用膨脹因果卷積層替換標準卷積層，以高效地捕捉不同粒度水平下時間序列的長期依賴關系。后面跟隨一個最大池化層，極大地減少了網絡大小。

在基于CNN的計算機視覺領域，通常使用特征金字塔網絡提取更細粒度的特征。應用于目標檢測的CNN網絡Yolov5使用一個聚焦層，將早期網絡的特征圖與最終特征圖合并，以獲得更細粒度的信息。Graphformer將這一結構遷移到基于Transformer的模型領域，以合并不同尺度的特征圖。在不增加額外編碼器的情況下，多尺度特征融合層融合了三個稀疏自注意塊輸出的特征圖，然后將其轉換為適當維度的最終輸出。

在解碼器中，輸入序列中要預測的元素用零填充。從掩碼多頭自注意塊中學習到的特征與來自編碼器的特征圖融合。然后，解碼器的輸出被輸入到一個全連接層，最終通過時間慣性融合層發現基于時間周期的時間模式，并與模型輸出聚合。

2.2.1 自注意下采樣模塊（Self-attention down-sampling module）

為了提取更深層次的特征圖，需要堆疊多個自注意塊，這帶來了更高的時間和空間復雜度。為了解決這一問題，Graphformer利用了Informer的自注意下采樣模塊，通過用膨脹因果卷積層替換標準卷積層，以高效地捕捉不同粒度水平下時間序列的長期依賴關系。膨脹因果卷積以固定步長對特征元素進行采樣，在時間維度上在元素前填充零以確保濾波器大小相等，并對采樣的特征元素進行卷積操作。對于每個自注意塊之后的膨脹因果卷積，卷積操作$DConv(?)$的公式如下所示：
$$DConv\left(x_n\right)=\left[\begin{array}{c}{x}_n\\ x_{n?i}\\ .\\ .\\ .\\ x_{n?(s?1)\times i}\end{array}\right]W(2)$$
其中，$x_n\in R^d$是序列$X\in R^{L\times d}$的特征元素， n ∈ { 0 , 1 , 2 , … , L } n\in\{0,1,2,\ldots,L\} n∈{0,1,2,…,L}，$s$是濾波器的大小，$W\in R^{d\times d}$是可學習的權重，$i$是膨脹因子。隨著層數的增加，第$i$個膨脹因果卷積層的卷積核在兩個相鄰特征點之間跳過$2^{i?1}?1$個元素，并在輸入上滑動。此外，根據因果關系的性質，時間$t$的每個元素$x$只與$t$時刻或之前的元素進行卷積，以確保不會泄露未來信息。特別是，當$i=1(2^0)$時，膨脹因果卷積將退化為普通因果卷積。

從膨脹因果卷積層得到的特征圖通過最大池化層進行下采樣，其公式如下所示：
$$X_{i+1}^t=MaxPool\left(\begin{array}{c}Dconv\left({\left[\begin{array}{c}{X}_i^t\end{array}\right]}_{MSA}\right)\end{array}\right)(3)$$
其中，${\left[\begin{array}{c}?\end{array}\right]}_{MSA}$表示多頭稀疏自注意塊，$MaxPool(?)$表示最大池化操作。

Fig.3 顯示了Graphformer編碼器中具有核大小為3的兩個膨脹因果卷積層。與標準卷積相比，即使僅使用兩個膨脹因果卷積層，它也能捕捉更大的感受野，并減少計算成本和內存開銷。此外，膨脹因果卷積層和最大池化層的組合不僅消除了稀疏自注意機制塊（由value均值引起）的冗余并賦予了主導特征特權，而且將輸入長度從$X_{i+1}$剪切到$X_i$的一半，因此內存開銷也減少到$\mathcal{O}(L\ln L)$。

Fig.3 使用自注意下采樣模塊的編碼器結構

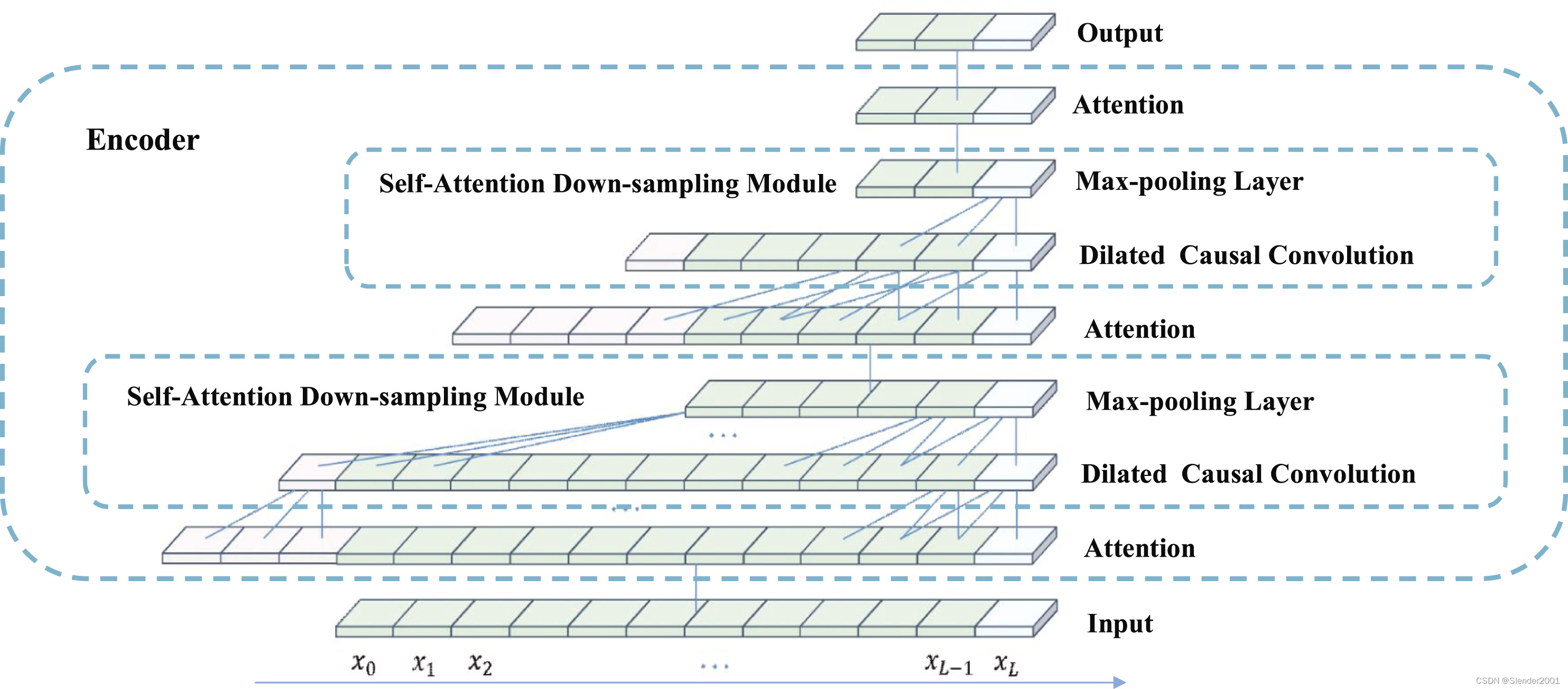
2.2.2 稀疏圖自注意力機制（Sparse graph self-attention mechanism）

稀疏圖自注意塊包括三個部分：稀疏自注意機制、自適應圖學習和圖卷積網絡，旨在提取主導注意力和潛在的空間依賴關系。

稀疏自注意機制： Informer中的稀疏自注意機制基于Transformer，接收元組輸入（query, key, value），執行縮放點積操作，如下所示：
$\mathcal{A}(Q,K,V)=softmax\left(\frac{Q{K}^T}{\sqrt{d}}\right)V$，其中$Q\in {\mathbb{R}}^{L_Q\times d}$，$K\in {\mathbb{R}}^{L_K\times d}$，$V\in {\mathbb{R}}^{L_k\times d}$，同時$d$表示輸入維度。根據上述公式，第$i$個query的注意權重可以轉換為概率卷積核平滑器：
$$\begin{array}{rl}& Attention\left(q_i,K,V\right)=\sum _{j}p(k_j|q_i)v_j\\ & =\sum _j\frac{k(q_i,k_j)}{{\sum }_{l}k(q_i,k_j)}{v}_j\end{array}(4)$$
基于Informer，Graphformer使用KL（Kullback-Leibler）散度來衡量第$i$個query $KL\left(q_i,K\right)$的概率分布$p\left(k_j|q_i\right)$與均勻分布$q\left(k_j|q_i\right)$之間的相似性。通過計算所有query的KL散度，并按降序排列，選擇前$u$個queries $\bar{Q}\in {\mathbb{R}}^{u\times d_{sq}}$作為稀疏query矩陣，其中$u=cln{L}_Q$，然后對所有key計算稀疏自注意分數。

自適應圖學習： 進一步討論稀疏自注意機制時，參考Graph WaveNet模型，Graphformer引入一種自適應圖學習方法來反映稀疏query矩陣$\bar{Q}$的圖結構$G_{sq}$，并自適應推斷出$\bar{Q}$中的隱藏空間依賴關系。對于$G_{sq}$，這個過程如下：
$$G_{sq}=Softmax\left(Elu\right(E_{\bar{q}}?E_{\bar{q}}^T\left)\right)(5)$$

其中每行$E_{\bar{q}}\in {\mathbb{R}}^{d_e\times d_{sq}}$表示一個query的嵌入，$d_e$表示嵌入的維度。在訓練過程中，可訓練query的嵌入$E_{\bar{q}}$被隨機初始化并分配給所有節點，每對query之間的隱藏空間依賴關系通過矩陣乘法推斷，并在訓練過程中自動更新$E_{\bar{q}}$的梯度。

與Graph WaveNet不同，Graphformer選擇ELU激活函數來消除弱連接：
$$f\left(x\right)=\{\begin{array}{l}\alpha \times \left(e^x?1\right),x\le 0\\ x,x>0\end{array}(6)$$

其中$\alpha$是設置的參數，$(e^x?1)$函數部分使$ELU(?)$對輸入噪聲更加穩健，線性部分使$ELU(?)$避免梯度消失問題。$ELU(?)$輸出的平均值接近于零，因此其收斂速度更快。最后，softmax用于歸一化和生成$\bar{Q}$的自適應鄰接矩陣$G_{sq}$，$G_{sq}$的節點數$d_{sq}$。通過這種方式，可以在沒有任何先驗知識的情況下學習稀疏query矩陣$\bar{Q}$的自適應鄰接矩陣，并將主導query映射到低維密集圖結構，這對于各種時間序列數據建模任務非常有效。

Graph Convolution Network： 對于時間序列輸入$X\in {\mathbb{R}}^{L\times d}$，GCN可以通過一階切比雪夫多項式擴展很好地近似，并擴展到高維GCN。基于譜圖的圖卷積操作GC可以定義為：
$$X_g=GC\times X=\tilde{A}X\Theta (7)$$

其中$X_g\in {\mathbb{R}}^{P\times d}$表示GCN的輸出，$\tilde{A}\in {\mathbb{R}}^{d\times d}$表示圖的自循環歸一化鄰接矩陣，$\Theta \in {\mathbb{R}}^{L\times P}$表示參數矩陣。擴展GC后，可以得到：
$$X_g=GC\times X=\left(I_N+D^{?\frac{1}{2}}A{D}^{?\frac{1}{2}}\right)X\Theta +b(8)$$

其中，$I_N$表示單位矩陣，$D\in {\mathbb{R}}^{d\times d}$表示圖的度矩陣，$A\in {\mathbb{R}}^{d\times d}$表示圖的鄰接矩陣，且$D_{ii}={\sum }_j{A}_{ij}$，$\Theta \in {\mathbb{R}}^{L\times P}$和$b\in {\mathbb{R}}^P$表示可訓練的權重和偏置，$D^{?\frac{1}{2}}A{D}^{?\frac{1}{2}}$表示歸一化拉普拉斯矩陣。Graphformer使用上述自適應生成的圖結構$G_{sq}$來替換Eq.8中的$D^{?\frac{1}{2}}A{D}^{?\frac{1}{2}}$，以提取主導query的依賴關系，并引入AGCRN提出的節點自適應參數學習模塊，來挖掘每個節點的獨特空間特征。計算過程如下所示：
$$X_g=GC\times X=(I_{sq}+G_{sq})X{E}_{\bar{q}}{W}_g+E_{\bar{q}}{b}_g(9)$$

其中，$T_{sq}$表示單位矩陣，$W_g$和$b_g$表示可訓練的超參數。節點自適應參數學習模塊解決了由于$\Theta$過大而導致的過擬合現象，因為難以優化每個節點的參數分配。具體來說，借鑒矩陣分解的思想，GCN學習兩個相對較小的矩陣$W_g$和$b_g$來替換權重$\Theta \in {\mathbb{R}}^{(k\times u)\times (k\times u)\times d_{sq}}$和偏差$b\in {\mathbb{R}}^{(k\times u)\times d_{sq}}$。在這里，$\Theta =E_{\bar{q}}?W_g$、$b=E_{\bar{q}}?b_g$，其中$W_g\in {\mathbb{R}}^{(k\times u)\times (k\times u)\times d_e}$表示權重池，$b_g\in {\mathbb{R}}^{(k\times u)\times d_e}$表示偏差池，$E_{\bar{q}}\in {\mathbb{R}}^{d_e\times d_{sq}}$表示可訓練的query嵌入，$d_e$表示嵌入維度，$d_{sq}$表示圖中節點的數量，即序列特征維度，$k$表示多頭稀疏注意力頭的數量。通過這種分解方法，每個節點根據$E_{\bar{q}}$從共享的權重池$W_g和偏差池$b_{g}$中提取自己的參數，減少參數大小和訓練負擔，同時幫助模型學習時間序列的隱藏和獨特空間依賴關系。

綜上所述，為了找到稀疏query矩陣$\bar{Q}$上節點之間的隱藏關聯，自適應圖學習層計算圖的鄰接矩陣，然后將該矩陣作為GCN的輸入，擴展到具有潛在空間相關性的稀疏query矩陣${\bar{Q}}_g$：
$$\begin{array}{rl}& {\bar{Q}}_g=GC\times \bar{Q}\\ & =\left(I_{sq}+Softmax\left(Elu\left(E_{\bar{q}}?E_{\bar{q}}^T\right)\right)\right)\bar{Q}\Theta \end{array}(10)$$

其中${\bar{Q}}_g\in {\mathbb{R}}^{d_{sq}\times P}$，$\Theta$表示所有可訓練參數的集合。根據Graphformer中衡量稀疏性的近似方法，第$i$個query在稀疏query空間矩陣${\bar{Q}}_g$中的概率分布$p(k_j|q_{ig})$與均勻分布$q(k_j|q_{ig})$之間的相似性，即第$i$個query的稀疏性最大均值$(q_{ig},K)$，可以重寫為如下形式：
$$\begin{array}{rl}& MaxMean\left(q_{ig},K\right)=ma{x}_j\left\{\frac{q_{ig}{k_j}^T}{\sqrt{d}}\right\}\\ & ?\frac{1}{L_K}\sum _{j=1}^{L_K}\frac{q_{ig}{k_j}^T}{\sqrt{d}}\end{array}(11)$$

在實踐中，Graphformer只需隨機抽樣$U=L_Q\ln L_K$個點積對（其余點積賦值為0），計算最大均值$MaxMean(q_i,K)$，并按大小排序，選擇前$u$個query作為稀疏query矩陣$\bar{Q}$，在自適應圖學習和GCN來提取空間依賴關系后生成${\bar{Q}}_g$，更新$MaxMean(q_{ig},K)$，然后計算所有key以獲取稀疏圖自注意力分數SparseGraphAttention：
$$\begin{array}{rl}& SparseGraphAttention\left(Q,K,V\right)\\ & =Softmax\left(\frac{{\bar{Q}}_g{K}^T}{\sqrt{d}}\right)V\end{array}(12)$$

與傳統的稀疏自注意力機制相比，稀疏圖自注意力機制在學習的高維空間中計算隱藏的空間相關性，并與多頭自注意力結合，探索不同尺度潛在關系空間中的多種空間依賴關系。

2.2.3 多尺度特征融合（Multi-scale feature fusion）

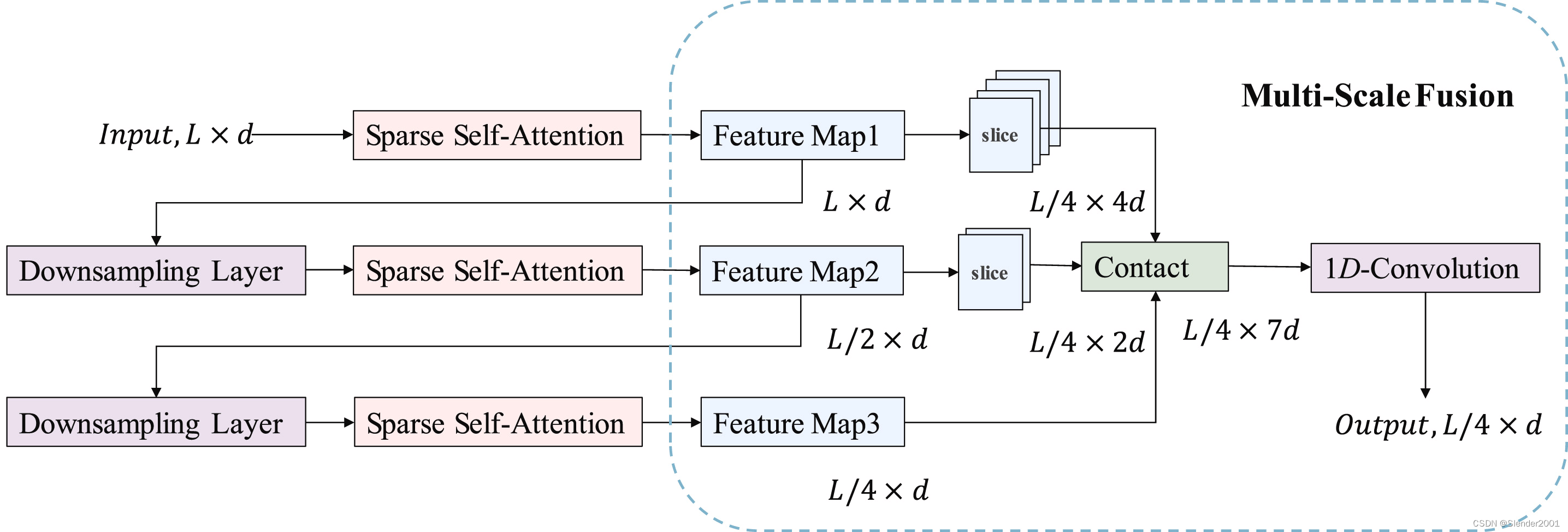
受計算機視覺中focus層設計的啟發，Graphformer模型在編碼器中引入了多尺度特征融合設計，應用于長序列時間序列預測。Fig.4 展示了多尺度特征融合層在Graphformer編碼器中的設計，其中來自每個自注意力塊的不同粒度級別的三個特征圖被融合成一個特征圖。具體來說，當編碼器堆疊n個自注意力塊時，每個自注意力塊將生成一個特征圖，其中第k個(k=1,2,…,n)特征圖的長度為$L/2^{k?1}$，維度為d。為了融合不同粒度級別的特征圖，第k個特征圖被輸入到多尺度特征融合層，切割成長度為$L/2^{n?1}$的$2^{n?k}$個特征圖。切割操作后，所有特征圖沿維度連接成一個維度為$(2^n?1)\times d$的融合特征圖。最后，添加一個1D卷積層，確保整個編碼器輸出一個具有適當維度d的特征圖，以形成隱藏狀態$H^t?{\mathbb{R}}^{\frac{L}{4}\times d}$。

需要注意的是，多尺度特征融合操作的功能類似于Informer中的蒸餾操作。然而，蒸餾操作需要構建許多額外的編碼器，其數量與自注意力塊的數量相同，導致相當大的計算開銷。而Graphformer模型只需要使用一個多尺度特征融合的編碼器，就可以降低計算成本并提取各種細粒度特征。

Fig.4 堆疊了三個自注意力塊的編碼器結構

2.2.4 時間慣性融合層（Time inertia fusion layer）

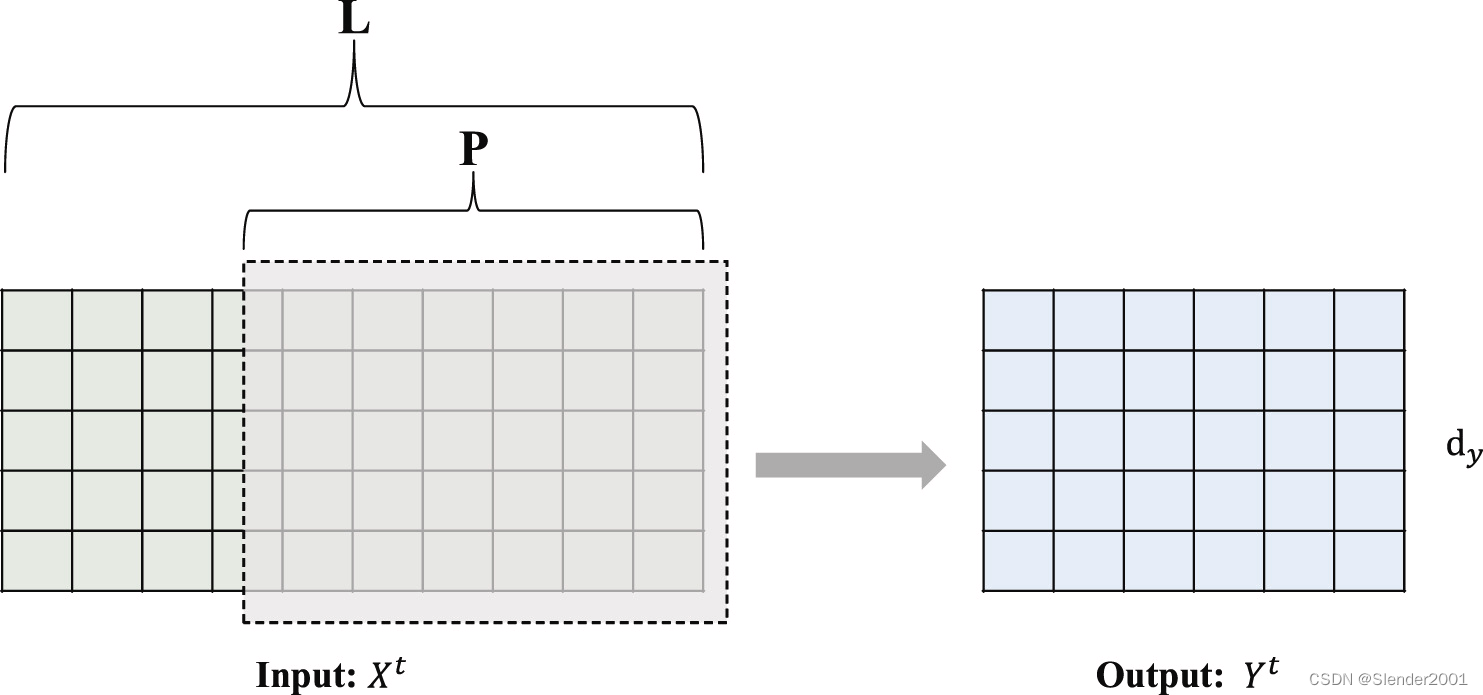
時間慣性塊直接將輸入序列$X^t$中長度最后的子序列作為預測范圍P的輸出，即$\overline{Y^t}=\left\{x_{L?P+1}^t,x_{L?P+2}^t,\dots ,x_L^t\right\}$，具體過程如 Fig.5 所示。不難看出，時間慣性要求預測序列的長度小于輸入序列的長度，即$P\le L$。在長時間序列預測的實際應用場景中，數據集通常比預測范圍P大幾個數量級，這很容易實現。獲得時間慣性輸出后，將深度學習模型的輸出進行加權和求和，得到最終的預測結果。

預測序列和輸入序列之間的相似性對于時間慣性至關重要。對于長時間序列，可預測序列的時間模式更加穩定，反映了更完整的周期性，這體現在預測序列和輸入序列的相位和振幅的相似性上。在這種情況下，應用時間慣性可能會顯著提高預測性能，尤其是當預測范圍是時間序列周期長度的整數倍時。

復雜的深度學習模型在一定程度上通過嵌入周期時間戳作為輸入序列考慮了這種慣性。然而，自注意力機制和卷積操作的非線性特性導致它們的輸出對最近范圍內的輸入不夠敏感。這意味著在某些變化相對平緩的長時間序列周期中，時間慣性將發揮重要作用。因此，直接利用時間慣性信息來改進最終的預測結果可能是有益的。

Fig.5 時間慣性機制的輸入輸出示意圖