最近在學習項目的時候經常用到隨機森林，所以對決策樹進行探索學習。

基尼系數

基尼系數用來判斷不確定性或不純度，數值范圍在0~0.5之間，數值越低，數據集越純。
基尼系數的計算：
假設數據集有K個類別，類別K在數據集中出現的概率為Pk，則基尼系數為：

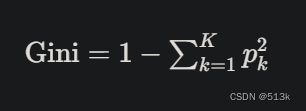
上式是用來求某個節點的基尼系數，要求某個屬性的基尼系數用下面的公式：

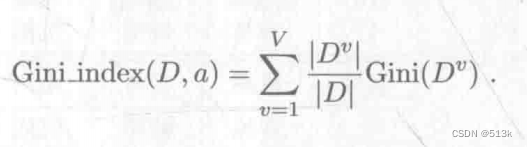
最后選擇基尼系數最小的屬性進行劃分即可。

基尼系數的應用

在決策樹中，假如某個節點的基尼系數就是0，此時被分類到這個節點的數據集是純的，意思就是按照此葉節點的父節點的分類方法來說，此葉節點都是同一個類別的，不需要再次分裂決策。

信息熵

信息熵和基尼系數作用相同，都是用來度量樣本集合純度的指標。
計算方法：

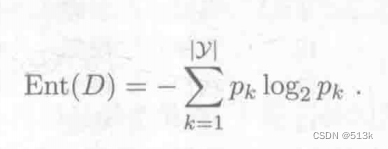
Pk是當前樣本集合中第k類樣本所占比例，Ent(D)(信息熵)越小，集合D的純度越高。

這里約定當Pk為0時Ent(D)=0；

信息增益

計算公式：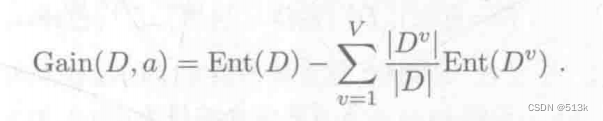
假設現在對集合D使用屬性a來進行劃分，屬性a有v個取值，也就是有v個節點，上式中Dv是第v個節點就是取值為v的樣本個數。

信息增益的使用

信息增益越大，說明使用屬性a來劃分所獲得的純度提升越大，決策樹越好。

信息增益準則的局限性

從上面的公式可以看出，信息增益偏好可取值數目較多的屬性，假如某個屬性可取值達到了n，也就是每個樣本都不一樣，比如“編號”屬性，那可以計算出這個屬性的信息增益接近1，選擇這樣的屬性來劃分很可能不具有泛化能力。
改進：
使用增益率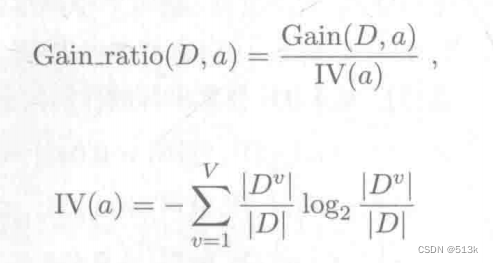
對于這個公式，當屬性a的可取值越多時，則IV(a)會越大，增益率變小，進行了平衡。同樣的，增益率準則也有局限，它對可取值較少的屬性又有所偏好。

最終：先找出信息增益高于平均水平的屬性，再從中選擇增益率最高的即可。