目錄





第一章:人工神經網絡基礎
比較人工智能和傳統機器學習
人工神經網絡(Artificial Neural Network,ANN) 是一種受人類大腦運作方式啟發而構建的監督學習算法。神經網絡與人類大腦中神經元連接和激活的方式比較類似,神經網絡接收輸入并通過一個函數傳遞,導致隨后的某些神經元被激活,從而產生輸出。
有幾種標準的 ANN 架構。通用近似定理認為,總是可以找到一個足夠大的神經網絡結構,它具有正確的權重集,可以準確地預測任何給定輸入下的任何輸出。這就意味著,對于給定的數據集 / 任務,我們可以創建一個架構,并可以不斷調整其權重,直到 ANN 預測出我們希望它預測的內容為止。調整權重直到這種情況發生的過程稱為神經網絡訓練過程。ANN 在大型數據集和自定義架構上能夠獲得成功的訓練,這正是 ANN 能夠在解決各種相關任務中獲得突出地位的主要原因。
在本章中,我們將在一個簡單的數據集上創建一個非常簡單的架構,主要關注 ANN 的各種構建模塊(前向、反向傳播、學習率)如何幫助調整神經網絡權重,以便該神經網絡學習從給定的輸入預測出預期的輸出。我們將首先從數學上學習什么是神經網絡,然后從零
開始建立一個堅實的基礎,接著將學習負責訓練神經網絡的每個組件,并對它們進行編碼。
神經網絡提供了結合特征提取(手工調整)和使用這些特征進行分類 / 回歸的獨特優勢,幾乎不需要手工特征工程。只需要標記數據(例如,哪些圖片是狗,哪些圖片不是狗)和神經網絡架構這兩個子任務。它不需要人類想出分類圖像的規則,這樣就消除了傳統技術強加給程序員的大部分負擔。
人工神經網絡的構建模塊
人工神經網絡是一系列張量(權重)和數學運算的組合,它們以一種松散的排列方式復制人腦的功能。可以將人工神經網絡看作一個數學函數,輸入一個或多個張量,輸出一個或多個張量。連接這些輸入和輸出的運算排列稱為神經網絡的架構—我們可以根據手頭
的任務對它們進行定制,也就是說,基于這個問題是否包含結構化(表格)數據或非結構化(圖像、文本、音頻)數據(即輸入張量和輸出張量的列表)。
人工神經網絡由下列模塊構成:
輸入層:該層將自變量作為輸入。
隱藏(中間)層:該層連接輸入層和輸出層,并對輸入數據進行轉換。此外,隱藏層包含節點(圖 1-6 中的單元 / 圓圈),用于將其輸入值修改為更高 / 更低維度的值。可以通過修改中間層節點的各種激活函數來實現更加復雜的表示功能。
輸出層:該層包含了輸入變量期望產生的值。
根據上述內容,神經網絡的典型結構如圖 1-6 所示。
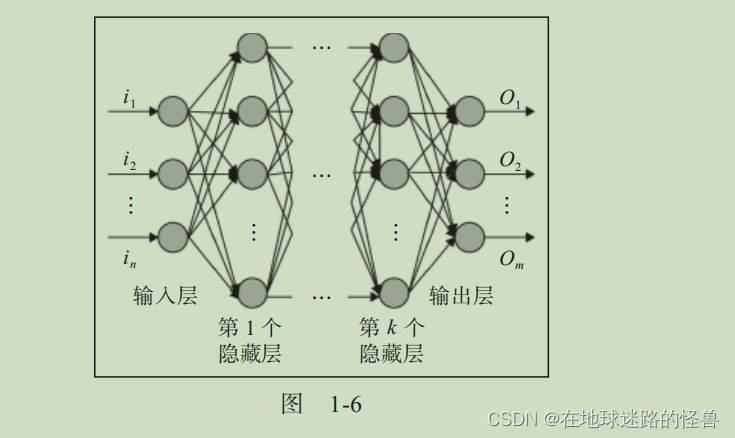
輸出層中的節點數量(圖 1-6 中的圓圈)取決于手頭的任務以及試圖預測的是連續變量還是分類變量。如果輸出是一個連續變量,則輸出層只有一個節點。如果輸出具有 m 個可能的類別,那么輸出層中將有 m 個節點。
術語深度學習指的是具有更多的隱藏層。在神經網絡必須理解一些諸如圖像識別等復雜事情的時候,通常需要更多的隱藏層。
實現前向傳播
為了對前向傳播的工作原理有一個深入的了解,我們訓練一個簡單的神經網絡,其中神經網絡的輸入是(1,1),對應的(期望)輸出是0。這里將基于這個單一的輸入 – 輸出對找到神經網絡的最優權重。然而,你應該注意到,事實上將有成千上萬的數據點用于訓練 ANN。
注意,如果不在隱藏層中應用非線性激活函數,那么無論存在多少隱藏層,神經網絡從輸入到輸出都將成為一個巨大的線性連接。
計算隱藏層的值
總結:輸入數據(通常是張量,浮點類型)乘以權重參數加上偏置項的結果通過非線性激活函數即可完成隱藏層中一個隱藏單元的值的計算。
激活函數
激活函數有助于建模輸入和輸出之間的復雜關系。
一些常用的激活函數計算公式如下(其中 x 為輸入):
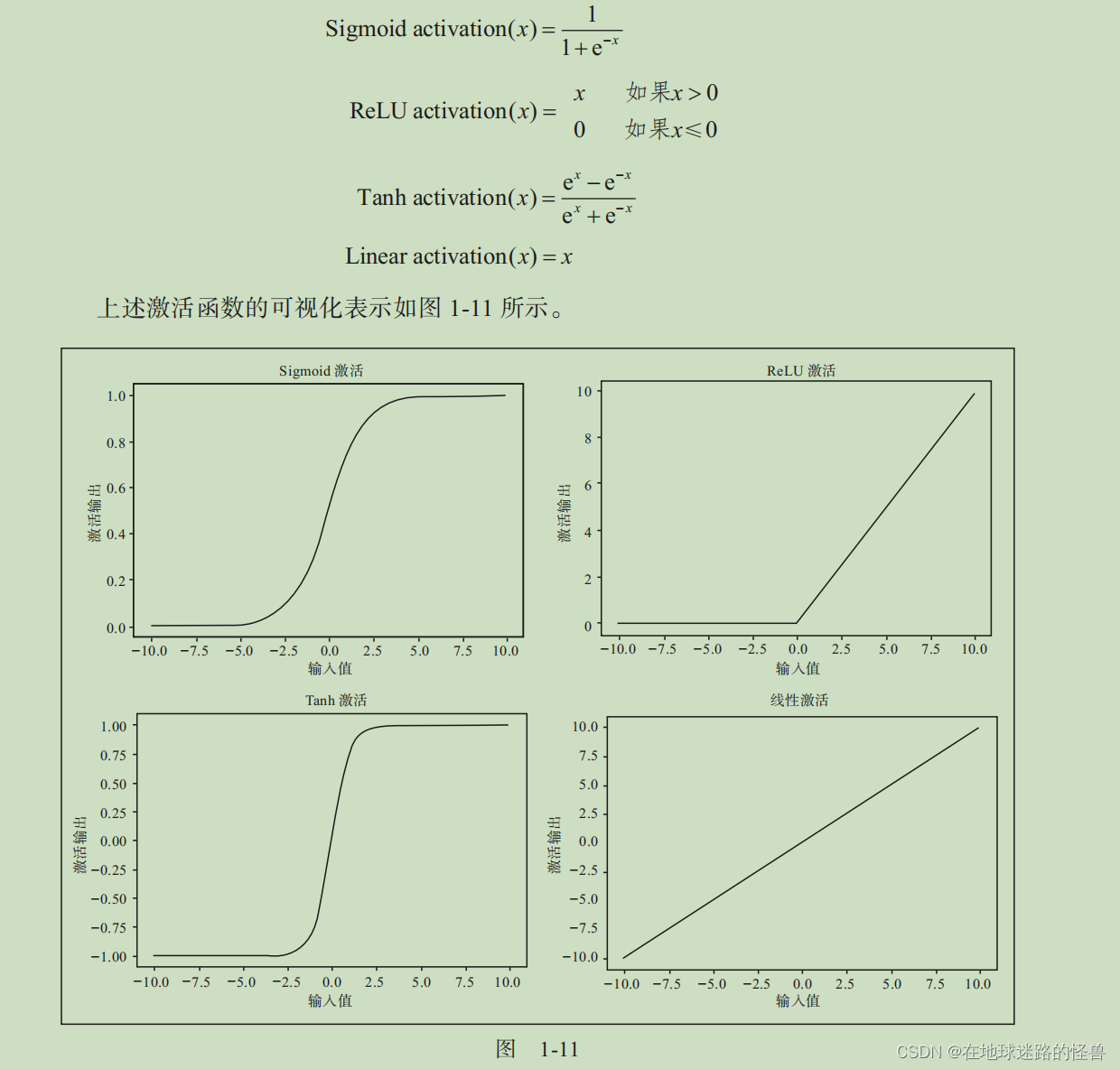
計算輸出層的值
總結:使用隱藏層值(被激活函數激活之后的值)和權重值的乘積加上偏置項后的和(因為隱藏層中的隱藏單元有多個)來計算輸出的值。
計算損失值
損失值(或者稱為損失函數)是需要在神經網絡中進行優化的值。
為了正確理解損失值是如何計算的,我們看看如下兩種情況:
分類變量預測;
連續變量預測。
計算連續變量預測的損失:
當變量連續時,損失值通常是實際值和預測值之差平方的平均值,也就是說,我們通過改變與神經網絡相關的權重值來盡量減小均方誤差。均方誤差值的計算公式如下:
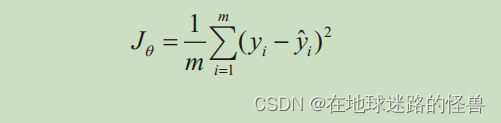

在上式中, yi 為實際輸出; y?i 是神經網絡計算出來的預測值(其權重以 θ 的形式存儲),其中輸入為 xi , m 為數據集的行數。
關鍵的結論應該是,對于每個唯一的權重集,神經網絡將會預測出相應的損失值,我們需要找到損失值為零(或者,在現實場景中,盡可能接近零)的黃金權重集。
說白了,我感覺意思就是如果最后我們的ANN輸出的只有一個值,那么損失函數就應該選擇均方誤差(因為它就只會算出一個值嘛),而分類變量預測則相反,在下面會說到。
計算分類變量預測的損失:
對于預測變量是離散值(即變量中只有幾個類別)的情形,通常使用分類交叉熵損失函數。當預測變量只有兩個不同取值的時候,損失函數是二元交叉熵。
二元交叉熵的計算公式如下:
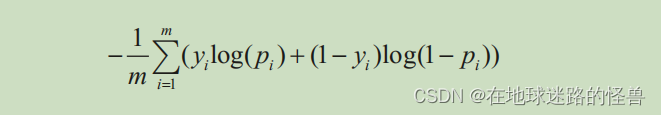
yi 為實際的輸出值,pi 為預測的輸出值,m 為數據點總數。
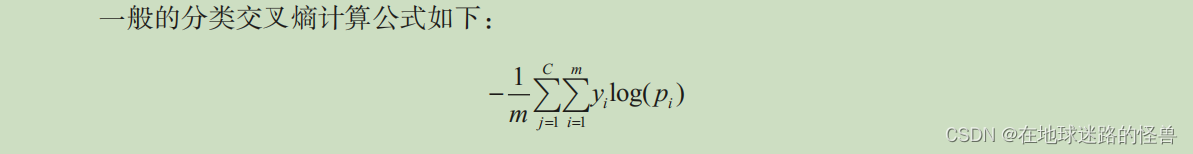
yi 為輸出的實際值,pi 為輸出的預測值, m 為數據點總數, C 為類別總數。
前向傳播的代碼
import numpy as np# 這個函數 feed_forward 實現了一個簡單的前向傳播過程,用于一個單隱藏層的神經網絡
def feed_forward(inputs, outputs, weights):""":param inputs: 輸入數據:param outputs: 實際輸出數據:param weights: 權重列表,包含了神經網絡當中的所有權重和偏置項weights[0]:連接輸入層和隱藏層的權重矩陣weights[1]:隱藏層的偏置向量weights[2]:連接隱藏層和輸出層的權重矩陣weights[3]:輸出層的偏置向量:return: 函數返回 mean_square_error,即整個批次數據的均方誤差,用于評估神經網絡的性能和用于優化訓練過程中的權重和偏置。"""# 首先,計算隱藏層的加權輸入 pre_hidden,通過矩陣乘法 np.dot(inputs, weights[0]) 加上偏置 weights[1] 得到:pre_hidden = np.dot(inputs, weights[0]) + weights[1]# 將加權輸入 pre_hidden 經過激活函數處理,這里使用了 sigmoid 函數 1/(1+np.exp(-pre_hidden)),# 得到隱藏層的輸出 hidden,形狀為 (batch_size, hidden_dim):hidden = 1/(1+np.exp(-pre_hidden))# 接著,計算輸出層的加權輸入 pred_out,# 同樣通過矩陣乘法 np.dot(hidden, weights[2]) 加上偏置 weights[3] 得到,這里需要注意修正過的索引:pred_out = np.dot(hidden, weights[2]) + weights[3]# 最后,計算預測輸出與實際輸出之間的均方誤差 mean_square_error,# 使用 np.mean(np.square(pred_out - outputs)) 計算整個批次的誤差,并返回:mean_square_error = np.mean(np.square(pred_out - outputs))return mean_square_error
此時當數據向前通過網絡時,就可以得到均方誤差值。
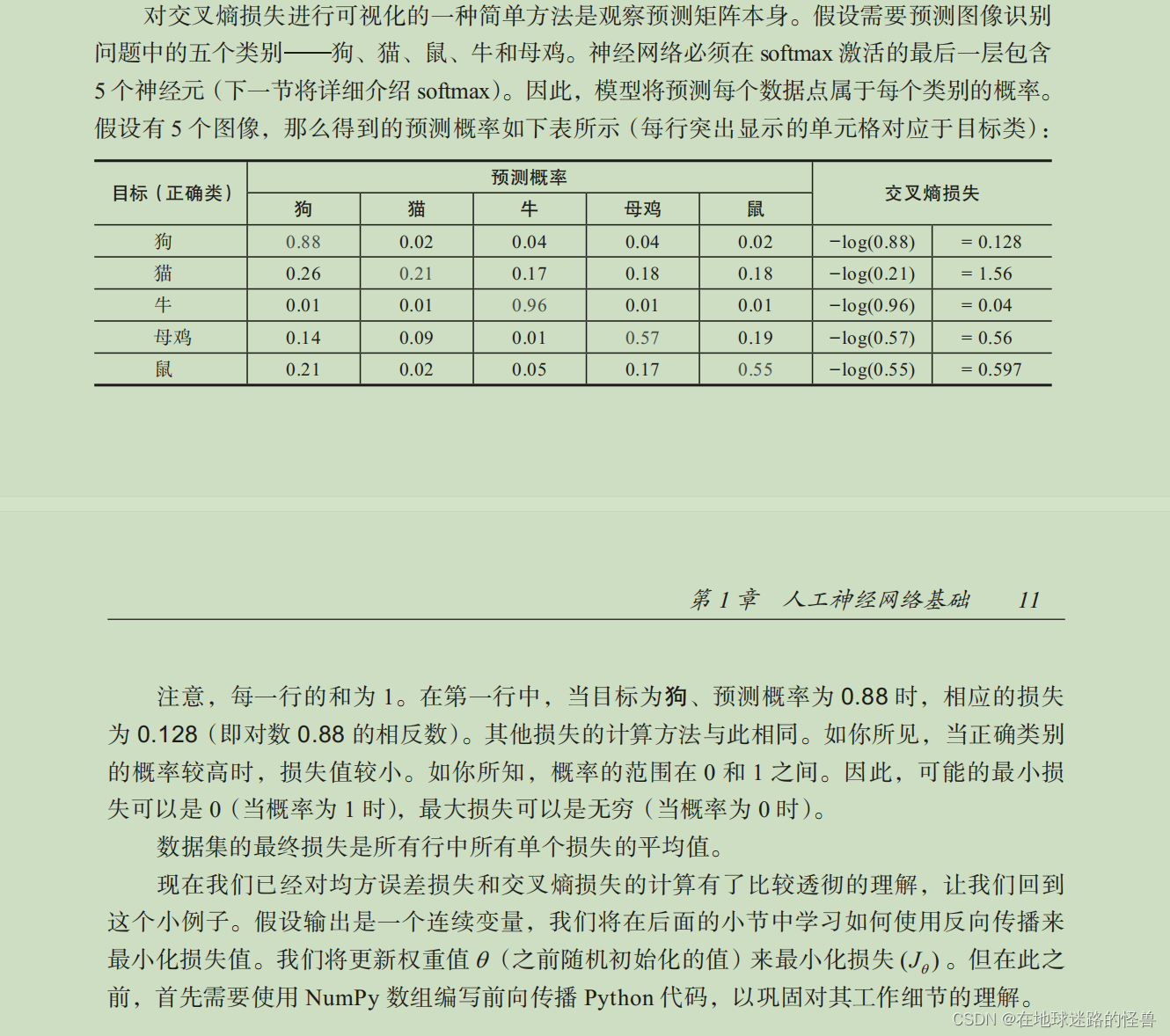
softmax
與其他激活函數不同,softmax 在一組值上執行。這樣做通常是為了確定某個輸入屬于給定場景中m個可能輸出類別中某個類別的概率。假設需要分類的圖像具有 10 個可能的類別(對應數字 0 到 9)。此時就有 10 個輸出值,每個輸出值代表輸入圖像屬于這 10 個類別中某一個類別的概率。
softmax 激活用于為輸出中的每個類提供一個概率值,計算代碼如下:
def softmax(x):return np.exp(x)/np.sum(np.exp(x))
注意輸入 x 上面的兩個操作 —np.exp 將使所有值為正,除以所有這些指數的 np.sum(np.exp(x)) 可以將所有值限制在 0 和 1 之間。這個范圍與事件發生的概率一致。這就是我們所說的返回一個概率向量。
損失函數的代碼
損失值(在神經網絡訓練過程中被最小化)通過更新權重值被最小化。確定合理的損失函數是建立可靠神經網絡模型的關鍵。構建神經網絡時,通常使用的損失函數如下:


目前已經學習了前向傳播,以及構成前向傳播的各種組件,如權重初始化、與節點相關的偏置項、激活和損失函數。在下一節中,我們將學習反向傳播(backpropagation),這是一種調整權重的技術,使損失值盡可能小。
實現反向傳播
在前向傳播中,將輸入層連接到隱藏層,隱藏層再連接到輸出層。在第一次迭代中,隨機初始化權重,然后計算這些權重造成的損失。在反向傳播中,我們采用相反的方法。從前向傳播中得到的損失值開始,更新網絡的權重,使損失值盡可能小。
我們執行以下步驟來減小損失值:

如果在整個數據集上執行n次上述步驟(完成前向傳播和反向傳播),就會實現對模型n輪(epoch)的訓練。
由于一個典型的神經網絡包含數千或數百萬(如果不是數十億)個權重,改變每個權重的值,并檢查損失是增加還是減少并不是最優的做法。上述列表中的核心步驟是權重變化時對“損失變化”的度量。正如你可能在微積分中學習過的那樣,這個度量和計算權重相關的損失梯度是一樣的。在下一節討論反向傳播鏈式法則時,將有更多關于利用微積分中的偏導數來計算與權重相關的損失梯度的內容。
在本節中,我們將通過每次對一個權重進行少量更新的方式來實現梯度下降,這在本節開始部分已經進行了詳細介紹。不過,在實現反向傳播之前,需要先了解神經網絡的另一個細節:學習率。
直觀地說,學習率有助于在算法中建立信任。例如,在決定權重更新大小的時候,可能不會一次性改變權重值,而是進行較慢的更新。
模型通過學習率獲得了穩定性,將在 1.6 節中具體討論學習率如何有助于提高穩定性。
通過更新權重來減少誤差的整個過程稱為梯度下降。
隨機梯度下降是最小化前述誤差的一種具體實現方法。如前所述,梯度表示差異(即權重值被少量更新時損失值的差異),下降表示減少。隨機表示對隨機樣本的選擇,并在此基礎上做出決定。
除了隨機梯度下降之外,還有許多其他類似的優化器可以幫助最小化損失值。下一章將討論這些不同的優化器。
在接下來的兩節中,我們將學習如何使用 Python 從頭開始編寫反向傳播算法的代碼,并簡要討論如何使用鏈式法則進行反向傳播。
梯度下降的代碼
在上一節的前饋網絡代碼的基礎上,將每個權重和偏置項增加一個非常小的量(0.0001),并對每個權重和偏置項更新一次,計算總體誤差損失的平方值。
# 這段代碼用于實現簡單的梯度下降算法來更新神經網絡的權重
# update_weights 函數的目的是通過計算每個權重的梯度來更新神經網絡的權重,以減少前向傳播過程中的損失函數值。
def update_weights(inputs, outputs, weights, lr):""":param inputs: 輸入數據:param outputs: 實際輸出數據:param weights: 當前的權重和偏置項:param lr: 學習率,用于控制每次更新的步長大小:return: updated_weights:更新后的權重矩陣和偏置向量。original_loss:使用原始權重計算的損失值,用于評估權重更新的效果。"""original_weights = deepcopy(weights)temp_weights = deepcopy(weights)updated_weights = deepcopy(weights)original_loss = feed_forward(inputs, outputs, original_weights)# 遍歷 original_weights 中的每一層和每一個權重元素,# 使用 np.ndenumerate 獲取權重矩陣中每個元素的索引。for i, layer in enumerate(original_weights):for index, weight in np.ndenumerate(layer):temp_weights = deepcopy(weights)# 對每個權重元素,將 temp_weights 中對應位置的權重增加一個小的增量 0.0001,# 這里使用一個小的數值增量來近似計算梯度。temp_weights[i][index] += 0.0001# 使用修改后的 temp_weights 計算新的損失 _loss_plus。_loss_plus = feed_forward(inputs, outputs, temp_weights)# 計算權重元素的梯度 grad,通過 (新損失 - 原始損失) / 增量 計算得到。grad = (_loss_plus - original_loss) / (0.0001)# 根據梯度和學習率 lr 更新 updated_weights 中對應權重的值。updated_weights[i][index] -= grad*lrreturn updated_weights, original_loss

神經網絡的另一個參數是在計算損失值時需要考慮的批大小(batch size)。
前面使用所有數據點來計算損失(均方誤差)值。然而在實踐中,當有成千上萬(或者在某些情況下數百萬)的數據點時,使用較多數據點計算損失值,其增量貢獻將遵循收益遞減規律,因此我們將使用比數據點總數要小得多的批大小進行模型訓練。在一輪的訓練中,每次使用一個批次數據點進行梯度下降(在前向傳播之后),直到用盡所有的數據點。
訓練模型時典型的批大小是 32 和 1024 之間的任意數。
在本節中,我們了解了當權重值發生少量變化時,如何基于損失值的變化更新權重值。在下一節中,將學習如何在不計算梯度的情況下更新權重。
使用鏈式法則實現反向傳播
很簡單:上面我們說過在前向網絡計算過程中,會通過一系列的計算公式拿到最后的損失值:
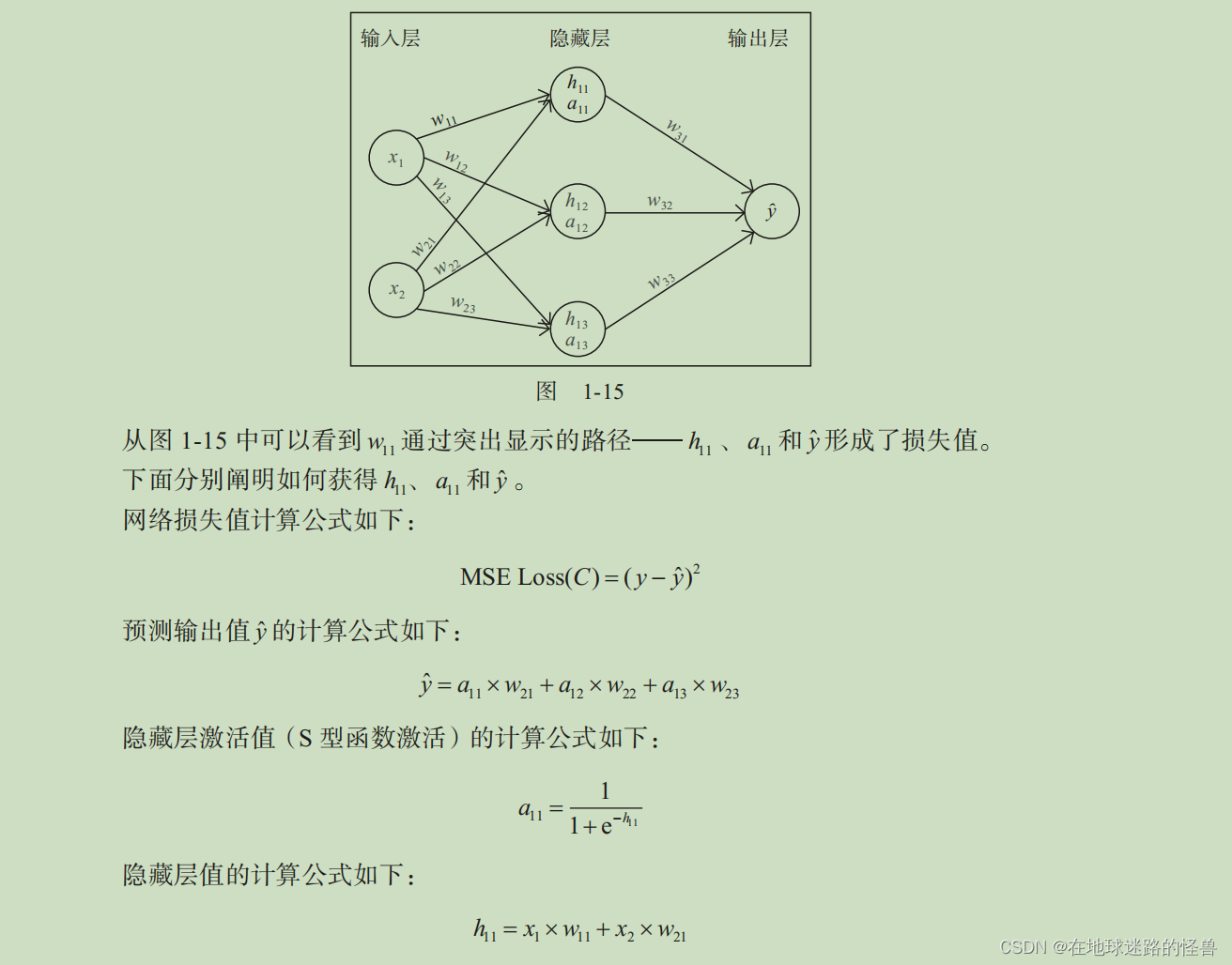
上圖已經寫出了所有的計算公式,可以計算權重變化對損失值(C)變化的影響,具體計算公式如下:
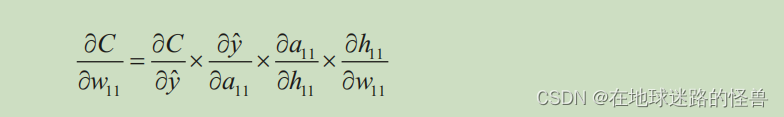
這稱為鏈式法則。它本質上是通過一系列的微分獲得需要的微分。
現在我們對權重參數 w11 進行一個值的微調,那么就會反向傳播影響到最后的 C 的值,也就是損失值(從上圖可以形象的看出這樣的反向傳播是一個鏈式的影響)。
另外從數學上說,求偏微分的本質簡單理解也就是一個函數中的某一個自變量產生的微小變化(極微小)對于該函數的函數值所產生的影響,也可以說是函數變化率的大小。
為了方便理解,可以回憶一下導數的定義:
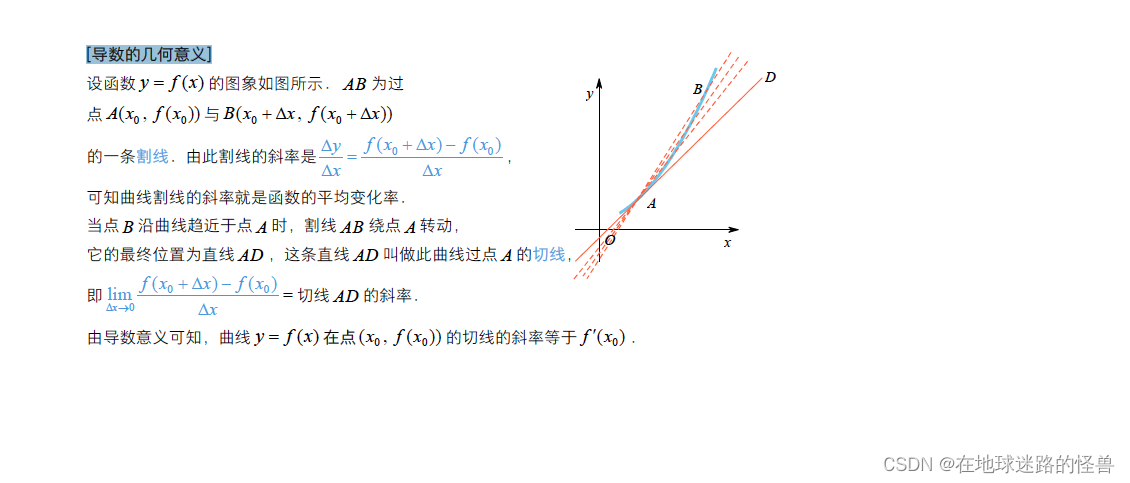
import numpy as npfrom chapter_01.Forward_Propagation import *
import matplotlib.pyplot as plt# 1、定義數據集
x = np.array([[1, 1]])
y = np.array([[0]])# 2、隨機初始化權重和偏置項
# 隱藏層中有 3 個單元,每個輸入節點與每個隱藏層單元相連。
# 因此,總共有 6 個權重值和 3 個偏置項,其中 1 個偏置和 2 個權重(2 個權重來自 2個輸入節點)對應每個隱藏單元。
# 另外,最后一層有 1 個單元連接到隱藏層的 3 個單元。因此,輸出層的值由 3 個權重和 1 個偏置項決定。
# 這段代碼是用 Python 和 NumPy 定義了一個簡單的神經網絡的權重和偏置項
# W 是一個包含四個元素的列表,每個元素分別對應神經網絡中的不同層的權重矩陣或偏置向量。
W = [# 第一個元素:輸入層到隱藏層的權重矩陣,.T 表示進行轉置操作,數組中的值是初始化的權重值,類型為 np.float32np.array([[-0.0053, 0.3793], [-0.5820, -0.5204], [-0.2723, 0.1896]], dtype=np.float32).T,# 第二個元素:隱藏層的偏置向量np.array([-0.0140, 0.5607, -0.0628], dtype=np.float32),# 第三個元素:隱藏層到輸出層的權重矩陣np.array([[0.1528, -0.1745, -0.1135]], dtype=np.float32).T,# 第四個元素:輸出層的偏置項np.array([-0.5516], dtype=np.float32)
]# 3、更新超過100輪的權重,并獲取損失值和更新的權重值:
losses = []
for epoch in range(100):W, loss = update_weights(x, y, W, 0.01)losses.append(loss)# 4、繪制損失值的圖像:
plt.plot(losses)
plt.title('Loss over increasing number of epochs')
plt.xlabel('Epochs')
plt.ylabel('Loss value')
plt.show()# 5、 一旦有了更新的權重,就可以通過將輸入傳遞給網絡進行預測,并計算輸出值
# 這里的代碼是模擬了將輸入數據傳遞給“神經網絡”進行預測概率的行為
pre_hidden = np.dot(x, W[0]) + W[1]
hidden = 1/(1+np.exp(-pre_hidden))
pred_out = np.dot(hidden, W[2]) + W[3]
# 輸出 -0.0174781
print(pred_out)
運行效果如下:
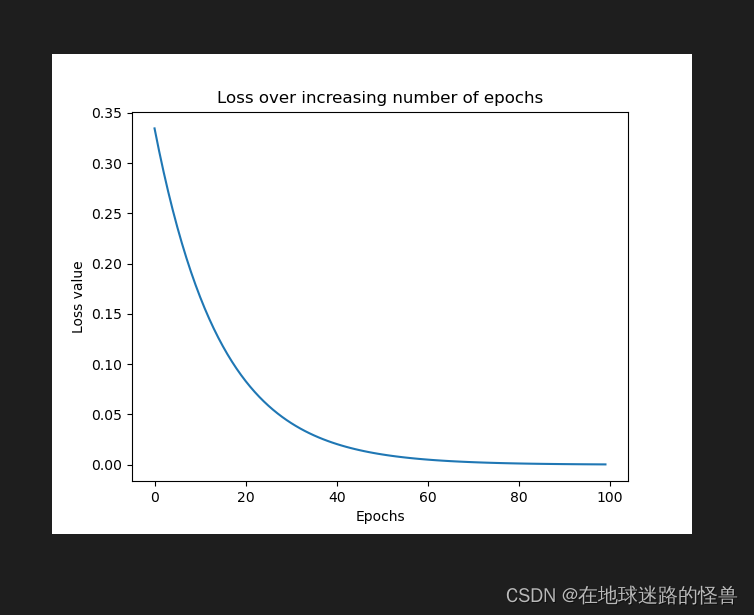
可以看出來,損失從 0.33 開始,穩步下降到 0.0001 左右。
這表明,權重是根據輸入 – 輸出數據進行調整的,當給定輸入時,就可以期望它預測出與損失函數進行比較的輸出。
理解學習率的影響
使用小學習率不會導致權重值大幅變化的原因是我們限制了權重更新的數值等于梯度 × 學習率,小的學習率本質上導致了權重的少量更新。然而,當學習率較大時,權重值的更新量也較大,之后損失的變化(權重值更新量較小時)非常小,使得權重值無法達到最優值。
總結:一般來說,學習率越小越好。這樣,模型可以慢慢地學習,會有利于將權重調整到最優值。典型的學習率參數值范圍是 0.0001 到 0.01。
總結神經網絡的訓練過程
訓練神經網絡是一個為神經網絡架構構造最優權重的過程,通過重復在給定學習率下的前向傳播和反向傳播這兩個關鍵步驟來實現。
在前向傳播中,對輸入數據施加一組權重,把它傳遞給隱藏層,并執行非線性激活函數實現隱藏層的輸出,隱藏層到輸出層則是使用隱藏層節點的值與另一組權重值相乘來估計輸出值,最后計算出給定權重集對應的總體損失。對于第一次前向傳播,權重值被隨機初始化。
在反向傳播中,通過在一個方向上調整權重來減小損失值(誤差),以減少總體損失。此外,權重更新的大小是梯度乘以學習率。
前向傳播和反向傳播的過程不斷重復,直到達到盡可能少的損失。這就意味著,在訓練結束時,神經網絡調整了它的權重θ,以便預測出希望的預測輸出值。在上述例子中,網絡模型經過訓練后,當 {1, 1} 作為輸入時,更新后的網絡預測輸出值為 0。
第二章:PyTorch基礎
PyTorch 提供了多個輔助構建神經網絡的功能:使用高級方法對各種組件進行抽象化處理,并提供了張量對象,利用 GPU 更快地訓練神經網絡。
PyTorch 張量
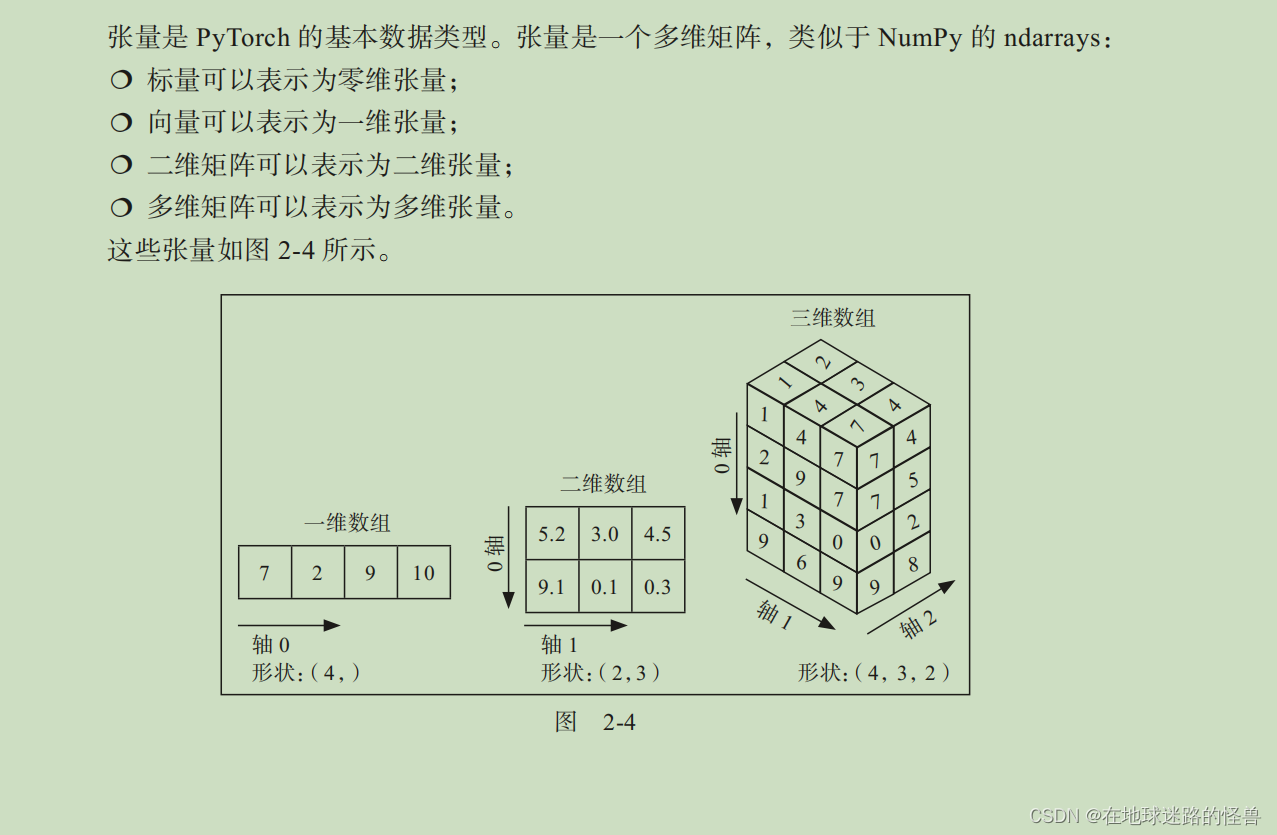
例如,可以將一幅彩色圖像看作像素值的三維張量,因為一幅彩色圖像由 height×width×3 像素組成—其中這三個通道對應于 RGB 通道。類似地,可以將灰度圖像看成二維張量,因為它由 height×width 像素組成。
初始化張量
張量在很多方面都很有用,除了可以作為圖像的基本數據結構之外,還有一個更加突出的用途,就是可以利用張量來初始化連接神經網絡不同層的權重。
import numpy as np
import torch# 導入 PyTorch 并通過調用 torch.tensor 在列表中初始化一個張量:
x = torch.tensor([[1, 2]])
y = torch.tensor([[1], [2]])# 接下來,訪問張量對象的形狀和數據類型:
# torch.Size([1, 2])
print(x.shape)
# torch.Size([2, 1])
print(y.shape)
# torch.int64
print(x.dtype)# 張量內所有元素的數據類型是相同的。
# 這就意味著如果一個張量包含不同數據類型的數據(比如布爾、整數和浮點數),
# 那么整個張量被強制轉換為一種最為通用的數據類型:
x = torch.tensor([False, 1, 2.0])
# tensor([0., 1., 2.])
print(x)# 類似于 NumPy,可以使用內置函數初始化張量對象
# 注意,這里畫出的張量和神經網絡權重之間的相似之處現在開始顯現了:
# 這里初始化張量,使它們能夠表示神經網絡的權重初始化。# 生成一個張量對象,其有三行四列,填充0
torch.zeros((3, 4))# 生成一個張量對象,它有三行四列,填充1
torch.ones((3, 4))# 生成值介于0和10之間(包括小值不包括大值)的三行四列
torch.randint(low=0, high=10, size=(3, 4))# 生成具有 0 和 1 之間隨機數的三行四列
torch.rand(3, 4)# 生成數值服從正態分布的三行四列
torch.randn(3, 4)# 直接使用torch.tensor(<Numpy-array>) 將Numpy數組轉換位 Torch 張量
x = np.array([[10, 20, 30], [2, 3, 4]])
y = torch.tensor(x)
# 輸出:<class 'numpy.ndarray'> <class 'torch.Tensor'>
print(type(x), type(y))
張量運算
與 NumPy 類似,你可以在張量對象上執行各種基本運算。與神經網絡運算類似的是輸入數據與權重之間的矩陣乘法,添加偏置項,并在需要的時候重塑輸入數據或權重值。
import torch# 可以使用下列代碼將 x 中所有元素乘以 10:
x = torch.tensor([[1, 2, 3, 4], [5, 6, 7, 8]])
# tensor([[10, 20, 30, 40],
# [50, 60, 70, 80]])
print(x * 10)# 可以使用下列代碼將 10 加到 x 中的元素,并將得到的張量存儲到 y 中
x = torch.tensor([[1, 2, 3, 4], [5, 6, 7, 8]])
y = x.add(10)
# tensor([[11, 12, 13, 14],
# [15, 16, 17, 18]])
print(y)# 可以使用下列代碼重塑一個張量:
y = torch.tensor([2, 3, 1, 0])
print(y.shape)
print(y)
# y.shape == (4)
y = y.view(4, 1)
print(y)
print(y.shape)
# y.shape == (4, 1)# 重塑張量的另一種方法是使用 squeeze 方法,提供我們想要移除的指標軸。
# (squeeze() 方法,這個方法用于從張量中擠壓(去除)維度為 1 的軸。)
# 注意,這只適用于要刪除的軸在該維度中只有一個項的場合:
# 創建一個形狀為 (10, 1, 10) 的張量 x,即三維張量
x = torch.randn(10, 1, 10)
# 使用 squeeze() 方法擠壓掉維度為 1 的軸,注意該方法傳遞的是元組x的下標索引號
z1 = torch.squeeze(x, 1)
# 也可以直接調用 x.squeeze(1) 來實現相同的效果,1表示元組x的下標
z2 = x.squeeze(1)
# 使用 assert 語句檢查兩個張量 z1 和 z2 中的所有元素是否相等
assert torch.all(z1 == z2)
# 打印輸出張量的形狀信息
print('Squeeze: \n', x.shape, z1.shape)# 在 PyTorch 中,unsqueeze() 方法和使用 [None] 索引是用來增加張量維度的兩種方法。
# 它們的作用是在指定的位置增加一個新的維度# 與 squeeze 相反的是 unsqueeze,
# 這意味著給矩陣增加一個維度,可以使用下列代碼實現:
x = torch.randn(10, 10)
print(x.shape)
# torch.size(10,10)
# 使用 unsqueeze(0) 方法在第 0 維度(最外層維度)增加一個維度, unsqueeze方法內傳遞的同樣是元組的下標索引
z1 = x.unsqueeze(0)
# 輸出 torch.size(1,10,10)
print(z1.shape)
# 使用 [None] 索引方式增加維度,效果與 unsqueeze(0) 相同
# x[None] 等效于 unsqueeze(0),在第 0 維度增加一個維度,形狀變為 (1, 10, 10)。
# x[:, None] 在第 1 維度增加一個維度,形狀變為 (10, 1, 10)。
# x[:, :, None] 在第 2 維度增加一個維度,形狀變為 (10, 10, 1)。
z2, z3, z4 = x[None], x[:, None], x[:, :, None]
print(z2.shape, z3.shape, z4.shape)# 可以使用下列代碼實現兩個不同張量的矩陣乘法:
x = torch.tensor([[1, 2, 3, 4],[5, 6, 7, 8]])
# 輸出 tensor([[11],
# [35]])
print(torch.matmul(x, y))
# 或者,也可以使用 @ 運算符實現矩陣乘法:
print(x@y)# 在 PyTorch 中,使用 torch.cat() 函數可以實現張量的拼接(連接)操作,
# 類似于 NumPy 中的 np.concatenate() 函數。這個函數可以在指定的軸上將多個張量拼接成一個更大的張量。
x = torch.randn(10, 10, 10)
z = torch.cat([x, x], axis=0)
# Cat axis 0: torch.Size([10, 10, 10]) torch.Size([20, 10, 10])
print(' Cat axis 0: ', x.shape, z.shape)
z = torch.cat([x, x], axis=1)
# Cat axis 1: torch.Size([10, 10, 10]) torch.Size([10, 20, 10])
print('Cat axis 1:', x.shape, z.shape)# 可以使用下列代碼提取張量中的最大值:
# torch.arange(25) 創建了一個包含 0 到 24 的整數序列的一維張量
# reshape(5, 5) 將這個一維張量重新形狀為一個 5x5 的二維張量 x
x = torch.arange(25).reshape(5, 5)
# x.max() 是張量 x 的方法,用于計算張量中所有元素的最大值。
# 在這個例子中,由于張量 x 包含了從 0 到 24 的整數,因此最大值為 24。
print('Max:', x.shape, x.max())# max 和 min 不是很明白是什么意思...# 可以從存在最大值的行索引中提取最大值:
# 在 PyTorch 中,當您調用 max() 方法并傳遞 dim 參數時,可以沿著指定的維度計算張量的最大值。
# 這種操作可以幫助您在多維張量中沿著指定維度找到每列(或者其他維度)的最大值及其對應的索引。
x.max(dim=0)
# torch.return types.max(values=tensor([20, 21, 22, 23, 24]),
# indices=tensor([4, 4, 4, 4, 4]))
# 注意,在前面的輸出中,獲取的是第 0 號維度上的最大值,即張量在行上的最大值。
# 因此,所有行上的最大值都是第 4 個索引中出現的值,所以 indices 的輸出也都是 4。
# 此外,.max 返回最大值和最大值的位置(argmax)。
m, argm = x.max(dim=1)
print('Max in axis 1:\n', m, argm)
# Max in axis 1: tensor([ 4, 9, 14, 19, 24])
# tensor([4, 4, 4, 4, 4])
# min 運算與 max 運算完全相同,但在適合的情況下返回最小值和最小值的位置(arg minimum)。# 置換一個張量對象的維數:
x = torch.randn(10, 20, 30)
z = x.permute(2, 0, 1)
print('Permute dimensions:', x.shape, z.shape)
# Permute dimensions: torch.Size([10, 20, 30])
# torch.Size([30, 10, 20])
# 注意當對原始張量進行排列時,張量的形狀就會發生改變。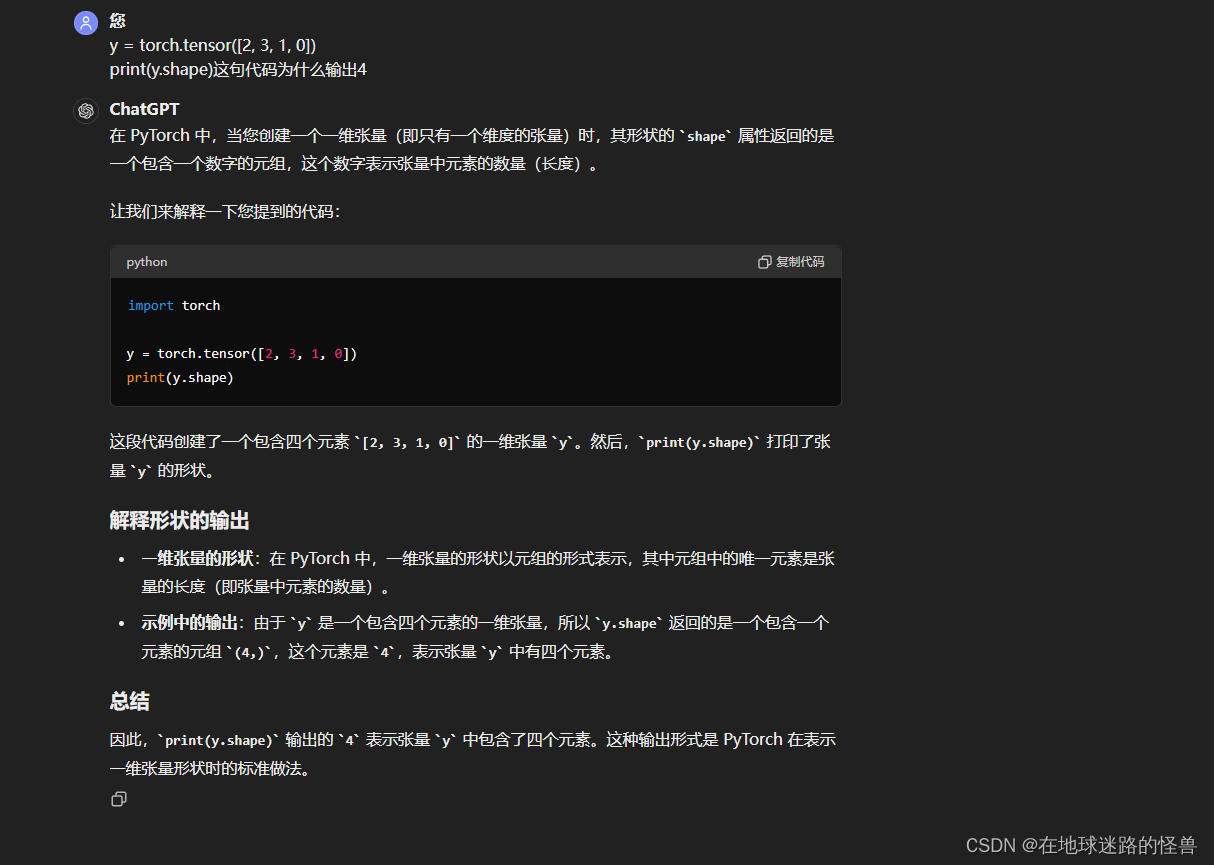
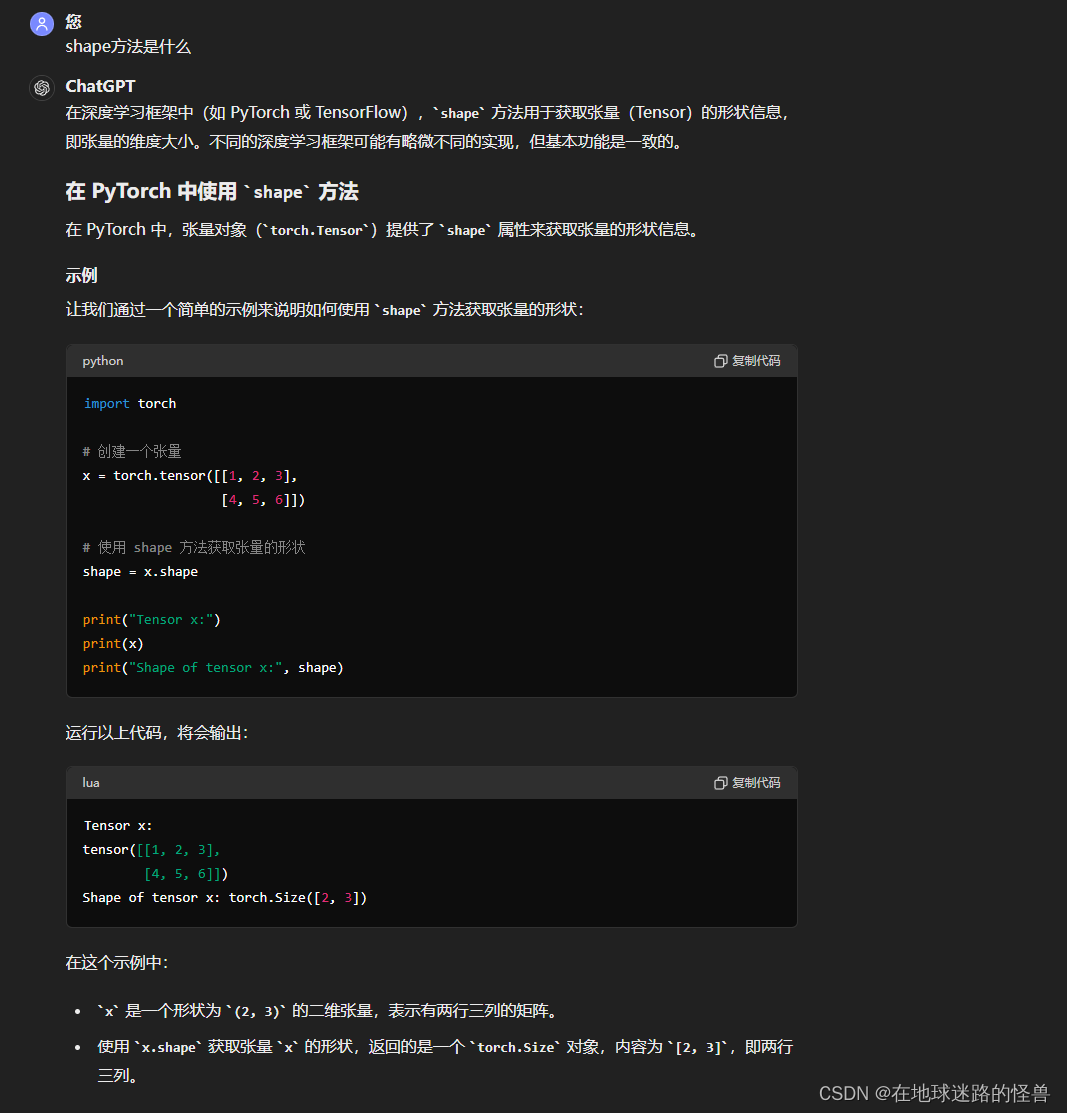



因為本書很難涵蓋所有可用的運算,所以重要的是要知道,你可以使用幾乎與 NumPy 相同的語法在 PyTorch 中執行幾乎所有的 NumPy 運算。標準的數學運算,如 abs、add、argsort、ceil、floo、sin、cos、tan、sum、cumprod、diag、eig、exp、log、
log2、log10、mean、median、mode、resize、round、sigmoid、softmax、square、sqrt、svd 和 transpose 等,均可以直接在任何有軸或沒有軸的張量上被調用。你總是可以運行 dir(torch.Tensor) 來查看所有可能的 Torch 張量方法,并通過 help(torch.tensor.<method>) 來查看關于該方法的官方幫助和相關文檔。
接下來,我們將學習如何利用張量在數據上執行梯度計算,這是神經網絡執行反向傳播的一個關鍵點。
張量對象的自動梯度
PyTorch 的張量對象自帶了計算梯度的內置功能。
import torch# 定義一個張量對象,并指定要為張量對象計算梯度:
x = torch.tensor([[2., -1.], [1, 1.]], requires_grad=True)
# 在上述代碼中,requires_grad 參數指定要為張量對象計算梯度。
# 這意味著后續可以通過自動求導功能計算相對于這個張量的梯度。
print(x)# 接下來,定義計算輸出的方式,在這個特定的例子中,輸出是所有輸入的平方和:
# x.pow(2) 對張量 x 中的每個元素進行平方運算。
# .sum() 對平方后的張量元素進行求和操作,得到標量值,即所有元素的平方和
# 輸出 out 為 7
out = x.pow(2).sum()# 可以通過對某個值調用 backward() 方法來計算該值的梯度
# out.backward() 調用了自動求導的 backward() 方法,
# 用來計算 out 相對于所有 requires_grad=True 的張量的梯度。
out.backward()# 現在可以得到 out 關于 x 的梯度
# 由于 out 是通過對 x 的平方和操作得到的,梯度 x.grad 將會是 out 相對于 x 的梯度。
print(x.grad)
運行結果如下:
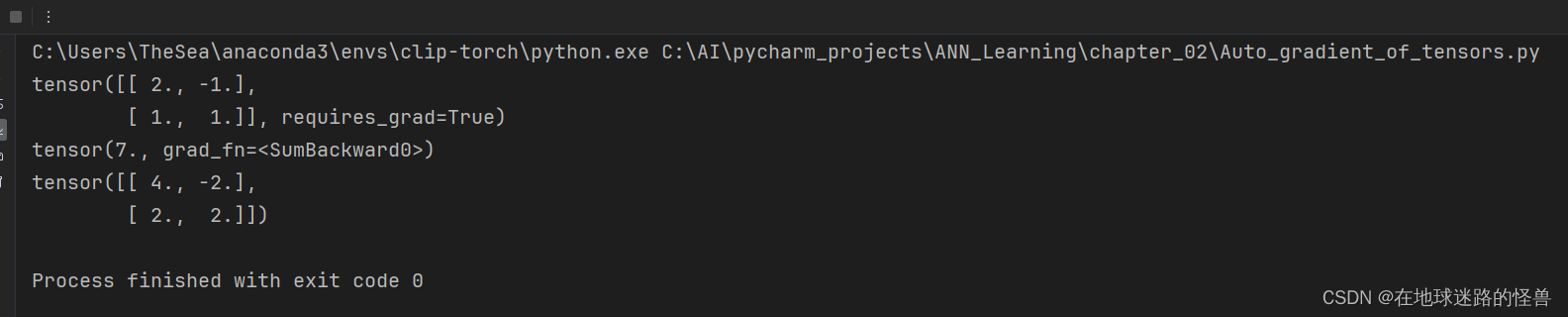
具體原因解釋如下:
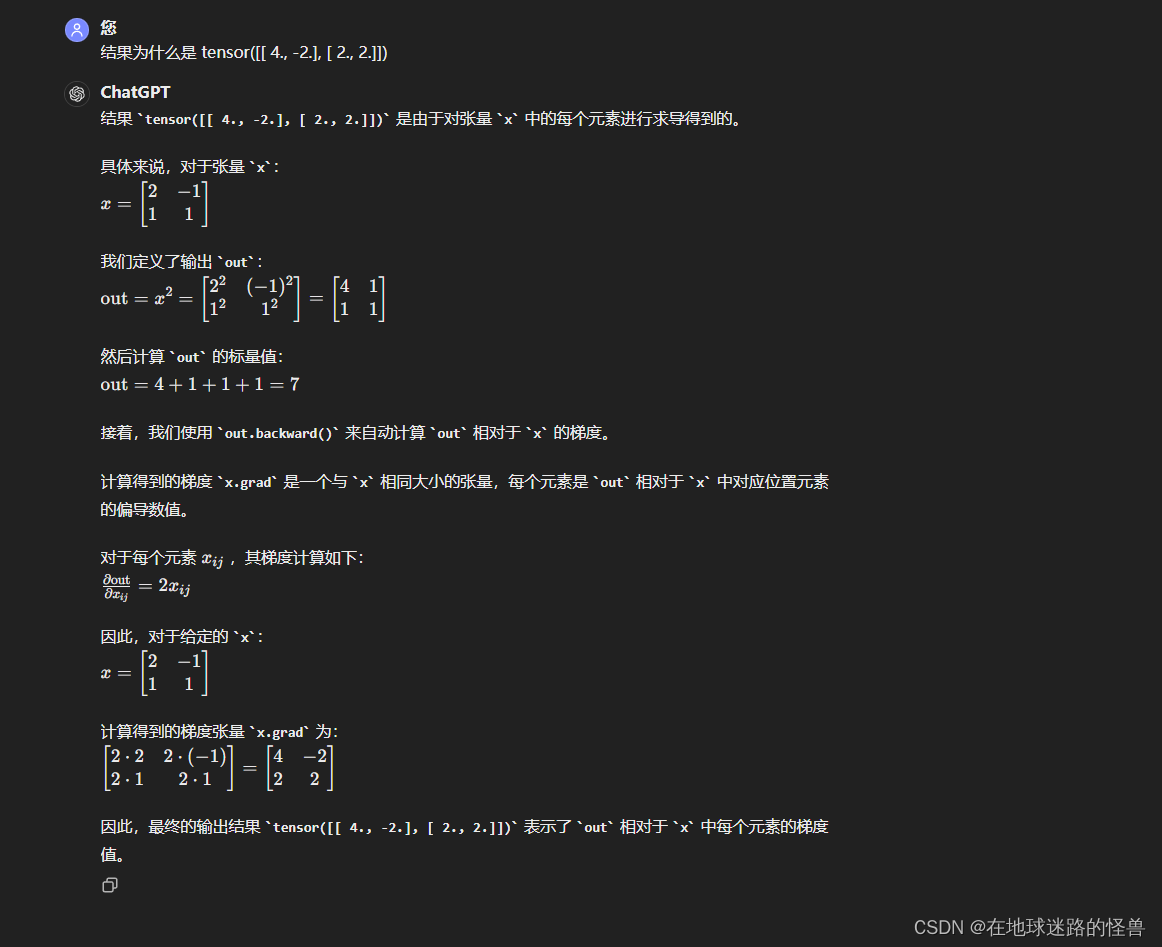
PyTorch 的張量較 Numpy 的 ndarrays 的優勢
在前文計算權重值的時候,對每個權重都進行了少量的改變,并考察其對減少總損失值的影響。注意到,在同一次迭代中,基于某個權重更新的損失計算并不影響其他權重更新的損失計算。因此,如果每個權重更新分別由不同的內核并行完成,而不是按順序更新權重,則可以優化這個計算過程。在這種情況下,GPU 非常有用,因為與 CPU(通常情況下,CPU 可能有≤ 64 個內核)相比,GPU 由數千個內核組成。
與 NumPy 相比,Torch 張量對象被優化為與 GPU 一起工作。
使用 PyTorch 構建神經網絡
前一章中學習了從零開始構建神經網絡,其中神經網絡的組件如下:

為了能夠理解使用 PyTorch 實現神經網絡,這里將解決一個簡單的問題—兩個數字相加。
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from torch.optim import SGD# 定義輸入值(x)和輸出值(y):
# 注意:輸入和輸出是一個列表的列表,其中輸入列表中的值之和就是輸出列表中的值
x = [[1, 2], [3, 4], [5, 6], [7, 8]]
y = [[3], [7], [11], [15]]# 將輸入列表轉換成張量對象:
# 將張量對象轉換為浮點對象。
# 將張量對象作為浮點數或長整數是一個良好的實踐,因為它們將與十進制值(權重)相乘。
X = torch.tensor(x).float()
Y = torch.tensor(y).float()device = 'cuda' if torch.cuda.is_available() else 'cpu'X = X.to(device)
Y = Y.to(device)# 定義神經網絡架構:
# 創建一個類(MyNeuralNet),可以使用它構建神經網絡架構。
# 在使用模塊創建模型架構的時候,從 nn.Module 繼承是強制性的,因為它是所有神經網絡模塊的基類:
class MyNeuralNet(nn.Module):# 在該類中,使用 __init__ 方法初始化神經網絡的所有組件。# 必須調用 super().__init__() 來確保類繼承 nn.Module:def __init__(self):super().__init__()# 使用上述代碼,通過適當指定 super().__init__(),就可以利用 nn.Module 中所有事先編寫好的預制功能。# 這些組件將在 init 方法中進行初始化,并將用于 MyNeuralNet 類中的多種不同方法。# 定義神經網絡的層:self.input_to_hidden_layer = nn.Linear(2, 8)self.hidden_layer_activation = nn.ReLU()self.hidden_to_output_layer = nn.Linear(8, 1)# 前述代碼指定了神經網絡的所有層—線性層(self.input_to_hidden_layer),# 然后是 ReLU 激活(self.hidden_layer_activation),# 最后是線性層(self.hidden_to_output_layer)。# 注意,層數和激活的選擇目前是任意的。我們將在下一章中更詳細地了解層中單元的數量和層激活的影響。# 在定義了神經網絡組件之后,定義網絡前向傳播時就可以將這些組件連接起來:# 注意:必須使用 forward 作為函數名,因為 PyTorch 保留了這個函數作為執行前向傳播的方法。# 使用任何其他名稱都會引發錯誤。def forward(self, x):x = self.input_to_hidden_layer(x)x = self.hidden_layer_activation(x)x = self.hidden_to_output_layer(x)return x# 到目前為止,我們已經構建了神經網絡模型架構,下一步將檢查權重值的隨機初始化。
# 你可以通過下列步驟獲取每個組件的初始權重:
# 首先定義 MyNeuralNet 類對象的一個實例,并將其注冊到 device:
mynet = MyNeuralNet().to(device)# 定義用于最優化的損失函數。鑒于預測的是連續輸出,這里將優化均方誤差
# 其他重要的損失函數如下:
# CrossEntropyLoss(多項分類);
# BCELoss(二元分類的二元交叉熵損失)
loss_func = nn.MSELoss()# 通過將輸入值傳遞給 neuralnet 對象,然后計算給定輸入的 MSELoss,
# 就可以計算出神經網絡的損失值:
_Y = mynet(X)
loss_value = loss_func(_Y, Y)
print(loss_value)
# 在上述代碼中,mynet(X) 在神經網絡獲得輸入值時計算輸出值。
# 此外,loss_func函數用于計算神經網絡預測(_Y)和實際值(Y)對應的 MSELoss 值。
# 需要注意的是,在計算損失時,總是先發送預測,然后發送真實數據。這是一個PyTorch 約定。# 定義了損失函數之后,下面將定義試圖減少損失值的優化器。
# 優化器的輸入是神經網絡對應的參數(權重與偏置項)和更新權重時的學習率
# 對于這個實例,將考慮隨機梯度下降
# 從 torch.optim 模塊導入 SGD 方法,然后將神經網絡對象(mynet)和學習率
# (lr)作為參數傳遞給 SGD 方法:
opt = SGD(mynet.parameters(), lr=0.001)# 在下面的例子中,將在總共 50 輪執行權重更新過程。
# 此外,在列表 loss_history 中的每輪中存儲損失值:
loss_history = []
for _ in range(50):opt.zero_grad()loss_value = loss_func(mynet(X), Y)loss_value.backward()opt.step()loss_history.append(loss_value)# 遍歷損失值列表,看是不是越來越小:
for loss in loss_history:print(loss)# 正如預期的那樣,損失值隨著輪數的增加而減少。#------------------- 下面的內容都是演示使用,和神經網絡的搭建沒有關系 -------------------------# 可以通過下列方式獲取每一層的權重和偏置項:
# 注意:權重的輸出值每一次都與前面的不同,因為神經網絡每次都使用隨機值進行初始化。
# print(mynet.input_to_hidden_layer.weight)
#
# 可以使用下列代碼獲得神經網絡的所有參數:
# parameters方法返回一個生成器對象。
print(mynet.parameters())
# 通過循環遍歷生成器,可以得到如下參數
for par in mynet.parameters():print(par)
# 該模型將這些張量注冊為特殊的對象,以保持對前向傳播和反向傳播的跟蹤。
# 當在 __init__ 方法中定義任何 nn 層時,它將自動創建相應的張量并進行注冊。# 可以通過輸出來理解上述代碼中函數 nn.Linear 方法完成的功能:
print(nn.Linear(2, 7))
# 在上述代碼中,線性方法有 2 個輸入值,7 個輸出值,還有一個與之相關的偏置項參數# 在一輪中一起執行所有要做的步驟:
# ? 計算給定輸入和輸出所對應的損失值。
# ? 計算每個參數對應的梯度。
# ? 根據每個參數的學習率和梯度更新權重。
# ? 一旦權重被更新,就要確保在下輪計算梯度之前刷新上一步計算的梯度:
opt.zero_grad() # flush the previous epoch's gradients
loss_value = loss_func(mynet(X), Y) # compute loss
loss_value.backward() # perform back-propagation
opt.step() # update the weights according to the gradients數據集、數據加載器和批大小
目前,神經網絡還沒有考慮到的一個超參數是批大小。批大小是指用于計算損失值或更新權重的數據點的數量。
這個超參數在有數百萬個數據點的情況下特別有用,而將所有數據點用于一個權重的更新不是最佳的情形,因為內存不能存儲這么多信息。另外,一個樣本可以代表足夠多的數據。批大小有助于獲取具有足夠代表性的多個數據樣本,但不一定能 100% 代表全部數據。
在本節中,我們將提出一種方法來指定在計算權重梯度時要考慮的批大小,用于更新權重,進而用于計算更新的損失值:
from torch.utils.data import Dataset, DataLoader
import torch
import torch.nn as nn
from torch.optim import SGDx = [[1, 2], [3, 4], [5, 6], [7, 8]]
y = [[3], [7], [11], [15]]X = torch.tensor(x).float()
Y = torch.tensor(y).float()device = 'cuda' if torch.cuda.is_available() else 'cpu'
X = X.to(device)
Y = Y.to(device)# 實例化一個數據集類 MyDataset:
# 在 MyDataset 類中,存儲信息每次獲取一個數據點,
# 以便可以將一批數據點捆綁在一起(使用 DataLoader),并通過一個前向和一個反向傳播發送,以更新權重:
class MyDataset(Dataset):# 定義一個 __init__ 方法,用于接收輸入和輸出對,并將它們轉換為 Torch 浮點對象:def __init__(self, x, y):self.x = torch.tensor(x).float()self.y = torch.tensor(y).float()# 指定輸入數據集的長度(__len__):def __len__(self):return len(self.x)# 最后,用 __getitem__ 方法獲取特定的行:def __getitem__(self, ix):return self.x[ix], self.y[ix]# 在上述代碼中,ix 指的是需要從數據集中獲取的行的索引# 創建已定義類的實例:
ds = MyDataset(X, Y)# 通過 DataLoader 傳遞之前定義的數據集實例,
# 獲取原始輸入和輸出張量對象中數據點的 batch_size:
dl = DataLoader(ds, batch_size=2, shuffle=True)
# 在上述代碼中,還指定從原始輸入數據集(ds)中獲取兩個數據點(通過batch_size=2)的一個隨機樣本(通過 shuffle=True)。# 為了從 dl 中獲取批數據,需要進行如下循環(每次從x和y中取兩個數據,然后是隨機抽取的):
for x, y in dl:print(x, y)# 現在,按照前文的定義來定義神經網絡類:
class MyNeuralNet(nn.Module):def __init__(self):super().__init__()self.input_to_hidden_layer = nn.Linear(2, 8)self.hidden_layer_activation = nn.ReLU()self.hidden_to_output_layer = nn.Linear(8, 1)def forward(self, x):x = self.input_to_hidden_layer(x)x = self.hidden_layer_activation(x)x = self.hidden_to_output_layer(x)return x# 接下來,定義模型對象(mynet)、損失函數(loss_func)和優化器(opt),
# 這與前文所定義的一樣:
mynet = MyNeuralNet().to(device)
loss_func = nn.MSELoss(mynet(X), Y)
opt = SGD(mynet.parameters(), lr=0.001)# 最后,循環遍歷各批數據點以最小化損失值,正如前一節第 6 步中所做的那樣
loss_history = []
for _ in range(50):for data in dl:x, y = dataopt.zero_grad()loss_value = loss_func(mynet(X), Y)loss_value.backward()opt.step()loss_history.append(loss_value)# 雖然上述代碼看起來與我們在前一部分中學習的代碼非常相似,但與前一部分中權重更新的次數相比,
# 我們在每輪中執行的權重更新次數是 2X,因為本節的批大小是2,而前一部分的批大小是 4(數據點的總數)。
預測新的數據點
我們在前文中學習了如何在已知數據點上擬合模型。這一節將學習如何使用前文已訓練模型 mynet 中定義的前向傳播方法來預測新的數據點。下面將從上一節構建的代碼繼續:
from torch.utils.data import Dataset, DataLoader
import torch
import torch.nn as nn
from torch.optim import SGDx = [[1, 2], [3, 4], [5, 6], [7, 8]]
y = [[3], [7], [11], [15]]X = torch.tensor(x).float()
Y = torch.tensor(y).float()device = 'cuda' if torch.cuda.is_available() else 'cpu'
X = X.to(device)
Y = Y.to(device)# 實例化一個數據集類 MyDataset:
# 在 MyDataset 類中,存儲信息每次獲取一個數據點,
# 以便可以將一批數據點捆綁在一起(使用 DataLoader),并通過一個前向和一個反向傳播發送,以更新權重:
class MyDataset(Dataset):# 定義一個 __init__ 方法,用于接收輸入和輸出對,并將它們轉換為 Torch 浮點對象:def __init__(self, x, y):self.x = torch.tensor(x).float()self.y = torch.tensor(y).float()# 指定輸入數據集的長度(__len__):def __len__(self):return len(self.x)# 最后,用 __getitem__ 方法獲取特定的行:def __getitem__(self, ix):return self.x[ix], self.y[ix]# 在上述代碼中,ix 指的是需要從數據集中獲取的行的索引# 創建已定義類的實例:
ds = MyDataset(X, Y)# 通過 DataLoader 傳遞之前定義的數據集實例,
# 獲取原始輸入和輸出張量對象中數據點的 batch_size:
dl = DataLoader(ds, batch_size=2, shuffle=True)
# 在上述代碼中,還指定從原始輸入數據集(ds)中獲取兩個數據點(通過batch_size=2)的一個隨機樣本(通過 shuffle=True)。# 為了從 dl 中獲取批數據,需要進行如下循環(每次從x和y中取兩個數據,然后是隨機抽取的):
for x, y in dl:print(x, y)# 現在,按照前文的定義來定義神經網絡類:
class MyNeuralNet(nn.Module):def __init__(self):super().__init__()self.input_to_hidden_layer = nn.Linear(2, 8)self.hidden_layer_activation = nn.ReLU()self.hidden_to_output_layer = nn.Linear(8, 1)def forward(self, x):x = self.input_to_hidden_layer(x)x = self.hidden_layer_activation(x)x = self.hidden_to_output_layer(x)return x# 接下來,定義模型對象(mynet)、損失函數(loss_func)和優化器(opt),
# 這與前文所定義的一樣:
mynet = MyNeuralNet().to(device)
loss_func = nn.MSELoss()
opt = SGD(mynet.parameters(), lr=0.001)# 最后,循環遍歷各批數據點以最小化損失值,正如前一節第 6 步中所做的那樣
loss_history = []
for _ in range(1000):for data in dl:x, y = dataopt.zero_grad()loss_value = loss_func(mynet(X), Y)loss_value.backward()opt.step()loss_history.append(loss_value)# 雖然上述代碼看起來與我們在前一部分中學習的代碼非常相似,但與前一部分中權重更新的次數相比,
# 我們在每輪中執行的權重更新次數是 2X,因為本節的批大小是2,而前一部分的批大小是 4(數據點的總數)。# ----------- 下面將學習如何使用前文已訓練模型 mynet 中定義的前向傳播方法來預測新的數據點 -----------
# 1、創建用于測試模型的數據點:
val_x = [[10, 11]]# 2. 將新數據點轉換為一個張量浮點對象并注冊到設備:
val_x = torch.tensor(val_x).float().to(device)# 3、把張量對象當作 Python 函數傳遞通過訓練好的神經網絡 mynet
print(mynet(val_x))# 上述代碼返回與輸入數據點相關聯的預測輸出值。運行結果如下:
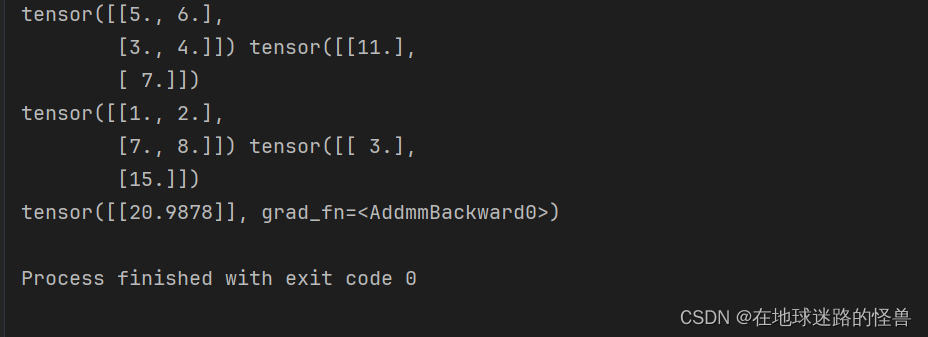
到目前為止,我們已經能夠訓練用于映射輸入和輸出的神經網絡模型,訓練過程中通過執行反向傳播的方式來更新權重值,以最小化損失值(使用預先定義的損失函數進行計算)。
獲取中間層的值
在某些情況下,獲取神經網絡中間層的值是有幫助的。
PyTorch 提供了以下兩種方式獲取神經網絡中間值。
一種方法是直接調用層,就像它們是函數一樣。可以按如下方式完成:
input_to_hidden = mynet.input_to_hidden_layer(X)
print(input_to_hidden)
hidden_activation = mynet.hidden_layer_activation(input_to_hidden)
print(hidden_activation)
輸出:
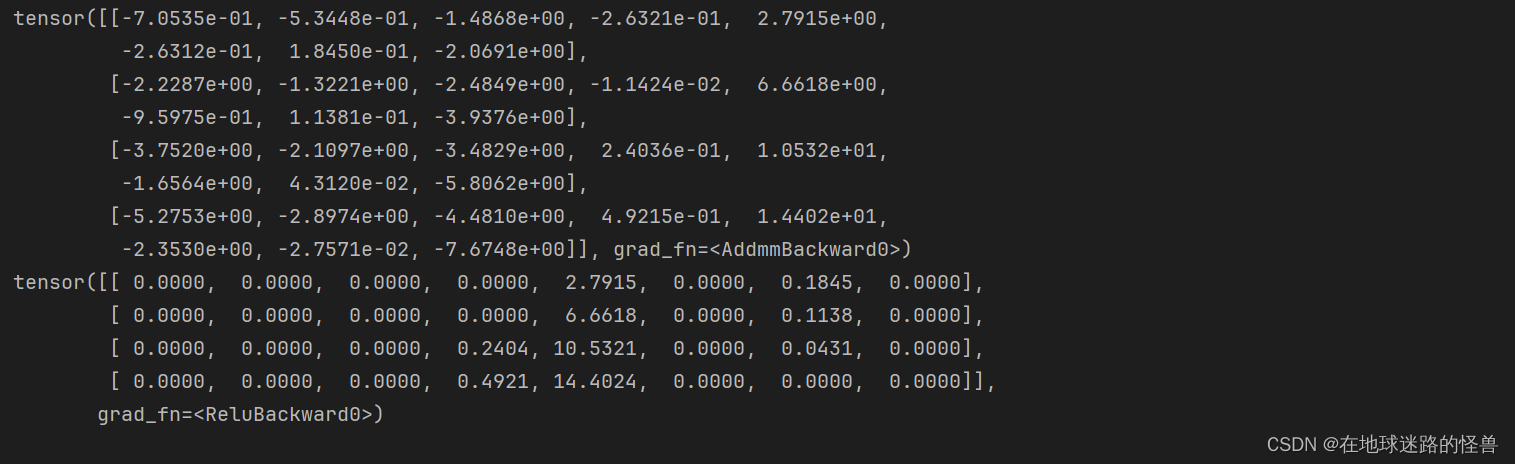
另一種方法是指定需要在 forward 方法中查看的層。

保存并加載 PyTorch 模型

訓練網絡模型的含義很簡單,就是訓練這個網絡中的各個權重參數。
而訓練好的模型的含義很簡單,其實就是一個權重參數已經被分配的很合適(即訓練過程)的一個神經網絡,可以直接拿這個網絡來進行任務的實現,如預測啊、分類等。
state dict
model.state_dict() 命令是理解保存和加載 PyTorch 模型如何工作的基礎。在model.state_dict() 中的字典對應于模型相應的參數名(鍵)和值(權重和偏置項)。state 指的是模型的當前快照(快照是每個張量處的值集)。
它返回一個包含鍵和值的字典(OrderedDict)。
鍵是模型層的名稱,值對應于這些層的權重。
保存

加載






![Leetcode[反轉鏈表]](http://pic.xiahunao.cn/Leetcode[反轉鏈表])












-- Search業務組件封裝實現全局搜索)
