240629_昇思學習打卡-Day11-Vision Transformer中的self-Attention

240629_昇思學習打卡-Day11-Transformer中的self-Attention

根據昇思課程順序來看呢，今兒應該看Vision Transformer圖像分類這里了，但是大概看了一下官方api，發現我還是太笨了，看不太明白。正巧昨天學SSD的時候不是參考了太陽花的小綠豆-CSDN博客大佬嘛，今兒看不懂就在想，欸，這個網絡大佬講沒講，就去翻了下，結果還真給我找到了，還真講過，還有b站視頻，講的賊好，簡直就是茅廁頓開，這里附大佬的b站首頁霹靂吧啦Wz的個人空間-霹靂吧啦Wz個人主頁-嗶哩嗶哩視頻 (bilibili.com)，強烈建議去看，附本期鏈接Transformer中Self-Attention以及Multi-Head Attention詳解_嗶哩嗶哩_bilibili，記得給大佬三連，有能力的給大佬充充電（本人已充）。

本文就大佬所講內容、查閱資料、昇思api及結合自己理解進行記錄。

前言

在了解Vision Transformer之前，我們需要先了解一下Transformer，Transformer最開始是應用在NLP領域的，拿過來用到Vision中就叫Vision Transformer。而這里要提到的，就是Transformer中的self-Attention（自注意力）和Multiple-Head Attention（多頭注意力）。

用在NLP領域中用到的注意力機制舉例，一般為Encoder-Decoder框架，比如中英翻譯，輸入的英文是Source，我們要獲取到的是Target（中文翻譯），Attention機制就發生在Target的元素Query和Source中的所有元素之間，其同時關注自身和目標值。

而這里說的自注意力機制只關注自身，比如Source中會有一個注意力機制，Target中會有一個注意力機制，他兩是沒有關系的。

還是用中英翻譯舉例，注意力機制的查詢和鍵分別來自于英文和中文，通過查詢（Query）英文單詞，去匹配中文漢字的鍵（Key），自注意力機制只關注自己一個語言，可以理解為：”我喜歡“后面可以跟”你“，也可以跟”吃飯“。

1）如果查詢和鍵是同一組內的特征，并且相互做注意力機制，則稱為自注意力機制或內部注意力機制。
2）多頭注意力機制的多頭表示對每個Query和所有的Key-Value做多次注意力機制。做兩次，就是兩頭，做三次，就是三頭。這樣做的意義在于獲取每個Query和所有的Key-Value的不同的依賴關系。
3）自注意力機制的優缺點簡記為【優點：感受野大。缺點：需要大數據。】

以下是關于這兩個自注意力機制的官方公式，很復雜也很難理解，但現在別盯著他不放，先慢慢往下看，這篇就是說明這個公式及其過程：

Self-Attention

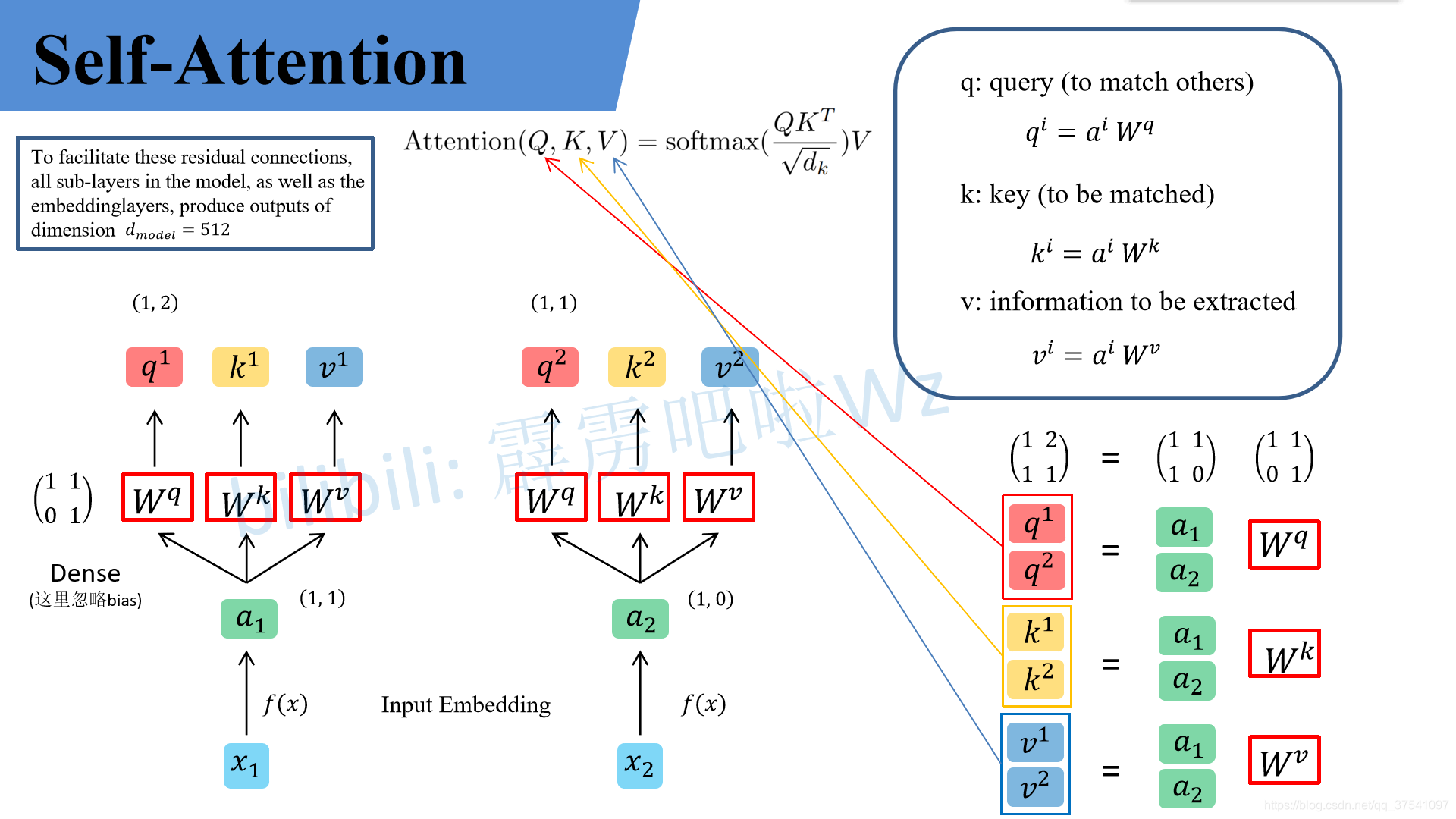
self-attention

我們先說明白這里面這些符號都是干啥的，或者求出來用來干啥的，避免看半天還一頭霧水：

q代表query，后續會去和每一個k進行匹配

k 代表key，后續會被每個q匹配

v 代表從a中提取得到的信息，后續會和q和k的乘積進行運算

d是k的維度

后續q 和k匹配的過程可以理解成計算兩者的相關性，相關性越大對應v的權重也就越大

簡單來說，最初的輸入向量首先會經過Embedding層映射成Q（Query），K（Key），V（Value）三個向量，由于是并行操作，所以代碼中是映射成為dim x 3的向量然后進行分割，換言之，如果你的輸入向量為一個向量序列（𝑥1，𝑥2，𝑥3），其中的𝑥1，𝑥2，𝑥3都是一維向量，那么每一個一維向量都會經過Embedding層映射出Q，K，V三個向量，只是Embedding矩陣不同，矩陣參數也是通過學習得到的。這里大家可以認為，Q，K，V三個矩陣是發現向量之間關聯信息的一種手段，需要經過學習得到，至于為什么是Q，K，V三個，主要是因為需要兩個向量點乘以獲得權重，又需要另一個向量來承載權重向加的結果，所以，最少需要3個矩陣。

后續我們要用q*k得到v的權重，然后進行一定縮放（除以根號d），再乘上v，就是第一個公式。

從數值上理解

wk我悟了，用引用的話行內公式不會亂

假設 $a_1=(1,1)$ ， $a_2=(1,0)$ ， $W^q=\binom{1 \ \ \ 1}{0 \ \ \ 1}$ ，那么根據以上的說法，我們可以計算出 $q^1$ 、 $q^2$ 。
$q^1=(1,2)\binom{1 \ \ \ 1}{0 \ \ \ 1}=(1,2)，q^2=(1,0)\binom{1 \ \ \ 1}{0 \ \ \ 1}=(1,1)$
此時可以并行化，就是把 $q^1$ 和 $q^2$ 在拼接起來，拼成 $\binom{1 \ \ \ 1}{1 \ \ \ 0}$ ，在與 $W^q$ 進行運算，結果不會發生改變
$\binom{q^1}{q^2}=\binom{1 \ \ \ 1}{1 \ \ \ 0}\binom{1 \ \ \ 1}{0 \ \ \ 1}=\binom{1 \ \ \ 2}{1 \ \ \ 1}$
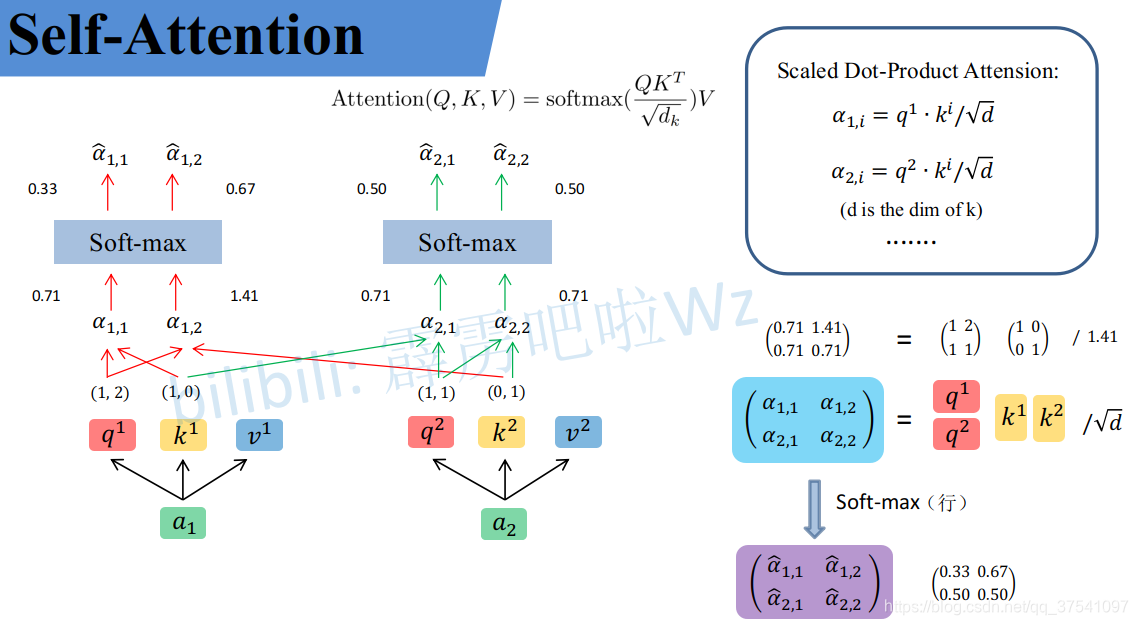
同理可以得到 $\binom{k^1}{k^2}$ 和 $\binom{v^1}{v^2}$ ，求得的這些數值依次是q（Query），k（Key），v（Value）。接著先拿 $q^1$ 和每個k進行match，點乘操作，接著除以 $\sqrt{d}$ ，得到對應的 $\alpha$ ,，其中 $d$ 代表向量 $k^i$ 的長度，此時等于2，除以 $\sqrt{d}$ 的原因在論文中的解釋是“進行點乘后的數值很大，導致通過softmax后梯度變的很小，所以通過除以 $\sqrt{d}$ 來進行縮放，比如計算 $\alpha_{1,i}$ ：
$\alpha_{1,1}=\frac{{q^1} \cdot {k^1}}{\sqrt{d}}=\frac{1*1+2*0}{\sqrt2}=0.71$

$\alpha_{1,2}=\frac{{q^1} \cdot {k^2}}{\sqrt{d}}=\frac{1*0+2*1}{\sqrt2}=1.41$

同理用 $q^2$ 去匹配所有的k能得到 $\alpha_{2,i}$ ，統一寫成矩陣乘法形式：
$\binom{\alpha_{1,1} \ \ \ \alpha_{1,2}}{\alpha_{2,1} \ \ \ \alpha_{2,2}}=\frac{\binom{q^1}{q^2}{\binom{k^1}{k^2}}^T}{\sqrt{d}}$
然后對每一行即 $(\alpha_{1,1},\alpha_{1,2})$ 分別進行softmax處理得到 $KaTeX parse error: Expected 'EOF', got '?' at position 9: (\alpha ?? _{1,1},\alpha …$ ，這里的$\alpha ? $相當于計算得到針對每個$ v $的權重，到這我們就完成了第一個公式（$ Attention(Q,K,V) $）中的$ softmax(\frac{QK^T}{\sqrt{d}})$部分

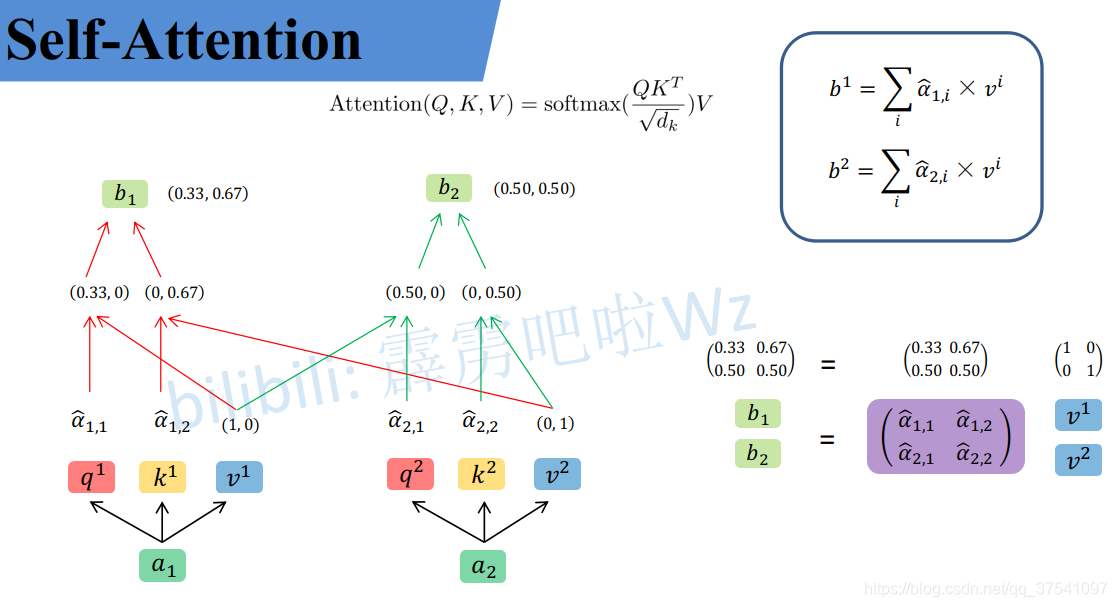
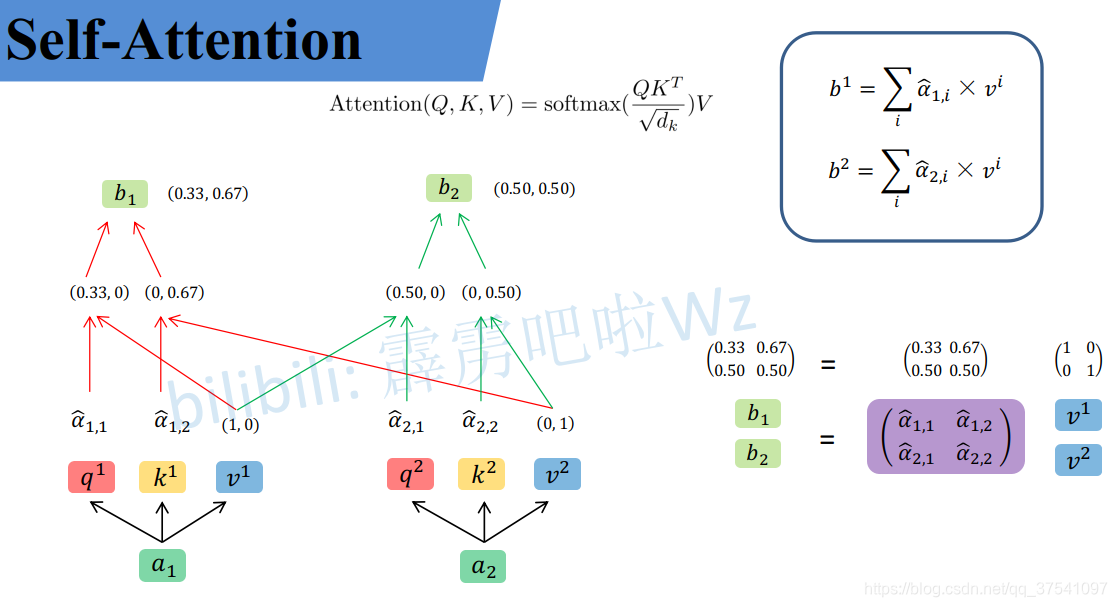
self-attention
為啥這里又亂了。。
在這里插入圖片描述

self-attention

從維度上進行理解

我們假設載入的 $x_1$ 經過Embedding后變為 $a_1$ 維度為1X4， $W^q$ 的維度為4X3，兩者進行叉乘運算后就得到了維度為1X3的Query，k和v同理

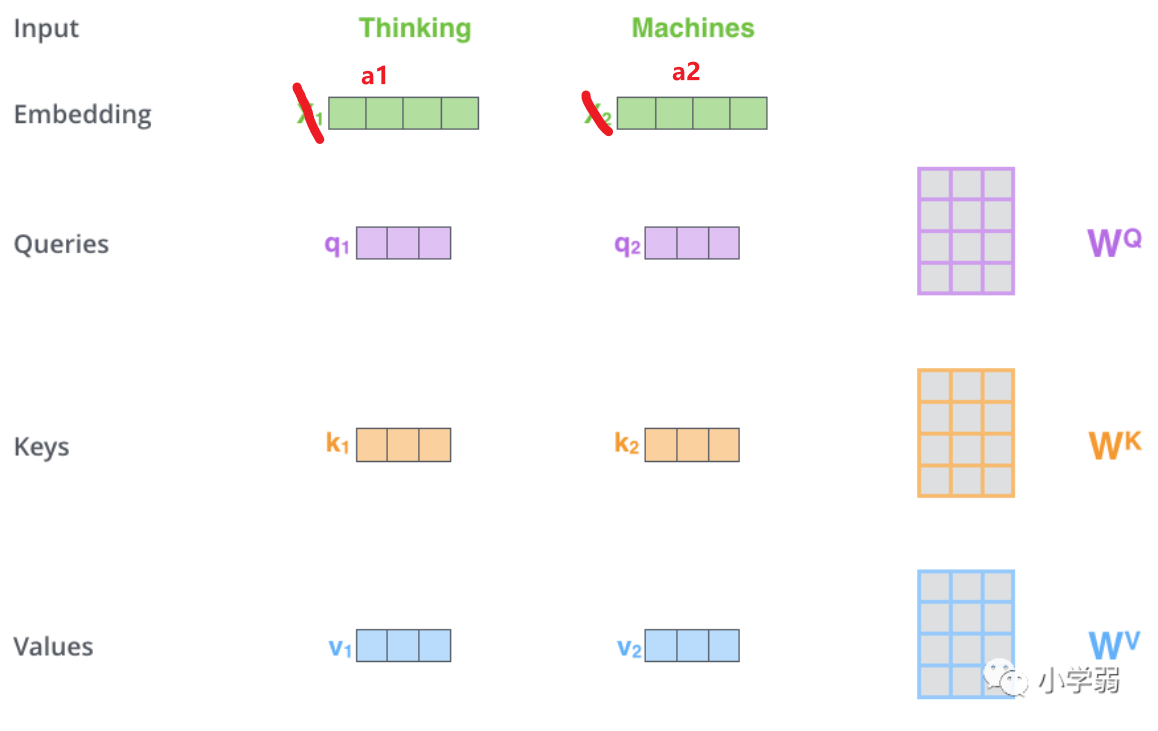
然后我們吧a1和a2并行起來

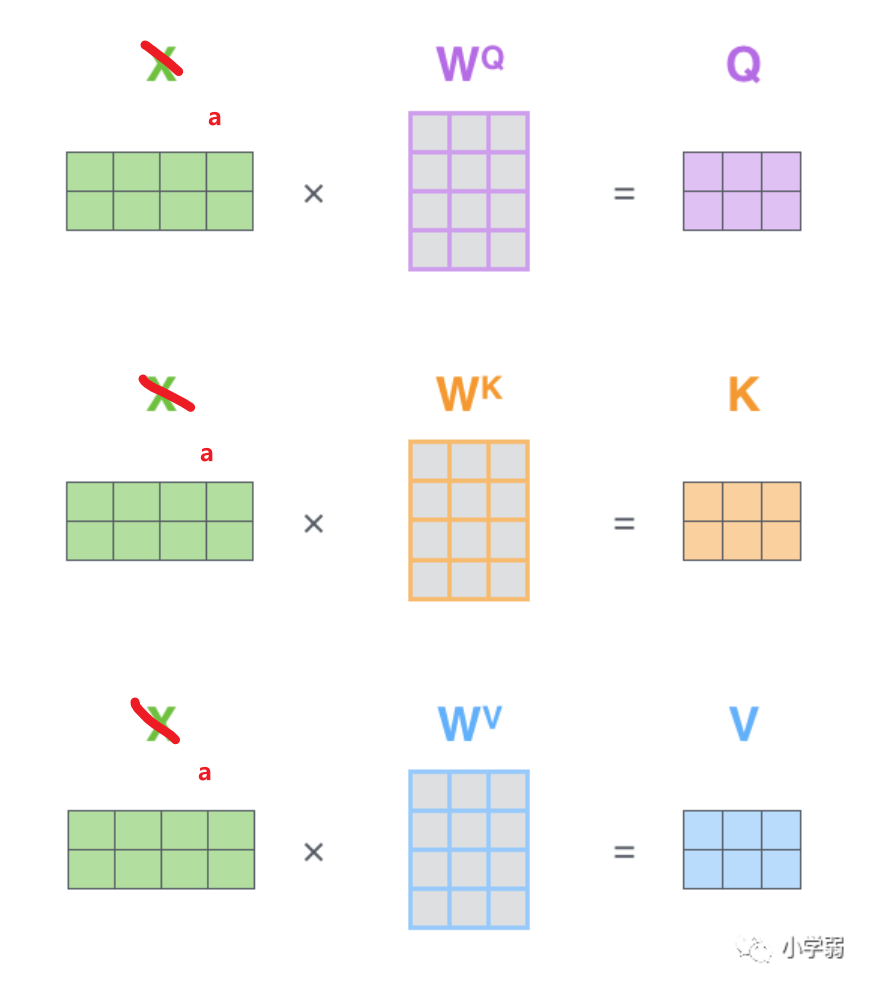
然后把公式中的式子也換成維度：

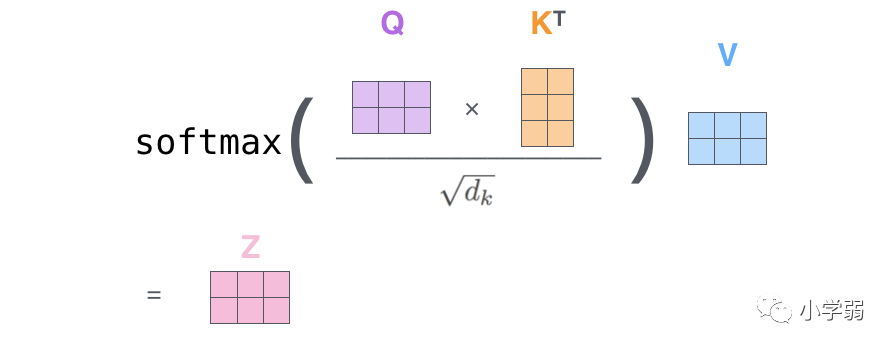
整個過程放在一張圖上可以這么看：

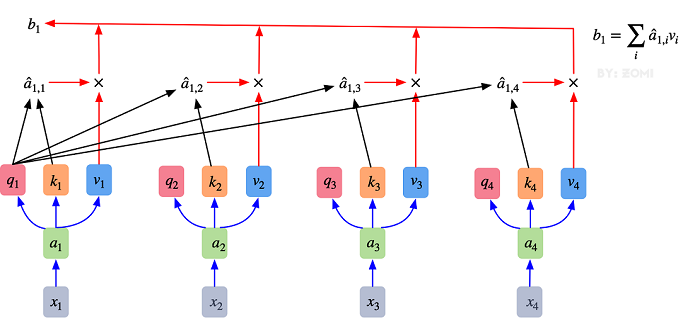
self-attention

這里暫時不附代碼，Multiple-Head Attention下篇記錄。

打卡圖片：

參考博客：

11.1 Vision Transformer(vit)網絡詳解_嗶哩嗶哩_bilibili

詳解Transformer中Self-Attention以及Multi-Head Attention_transformer multi head-CSDN博客

Vision Transformer詳解-CSDN博客

一文搞定自注意力機制（Self-Attention）-CSDN博客

以上圖片均引用自以上大佬博客，如有侵權，請聯系刪除

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/diannao/37783.shtml
繁體地址，請注明出處：http://hk.pswp.cn/diannao/37783.shtml
英文地址，請注明出處：http://en.pswp.cn/diannao/37783.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！