筆者近期上了國科大周曉飛老師《強化學習及其應用》課程，計劃整理一個強化學習系列筆記。筆記中所引用的內容部分出自周老師的課程PPT。筆記中如有不到之處，敬請批評指正。

---

1.1 概述

強化學習：通過與環境互動，獲取環境反饋的樣本；回報（作為監督），進行最優決策的機器學習。
強化學習的過程可以用下圖進行描述：在狀態S1下選擇動作a1，獲取回報R1的同時跳轉到狀態S2；在狀態S2下選擇動作a2，獲取回報R2的同時跳轉到狀態S3……如此循環下去。
強化學習的目標就是：對于給定的狀態S，我們能選一個比較好的動作a，使得回報最大。

1.2 Markov決策過程

1.2.1 Markov Process (MP) 馬爾科夫過程

一個馬爾科夫過程是一個元組<S,P>，其中S表示一個有限的狀態集合，P表示一個狀態轉移矩陣。
比如：下圖矩陣P中的P1n表示，t時刻狀態為n的情況下，t+1時刻轉移到狀態1的概率。矩陣P中的第一行表示從狀態1轉移出去的概率，最后一行表示從狀態n轉移出去的概率，所以矩陣中每一行的和都是1。

這是Markov過程的一個例子：

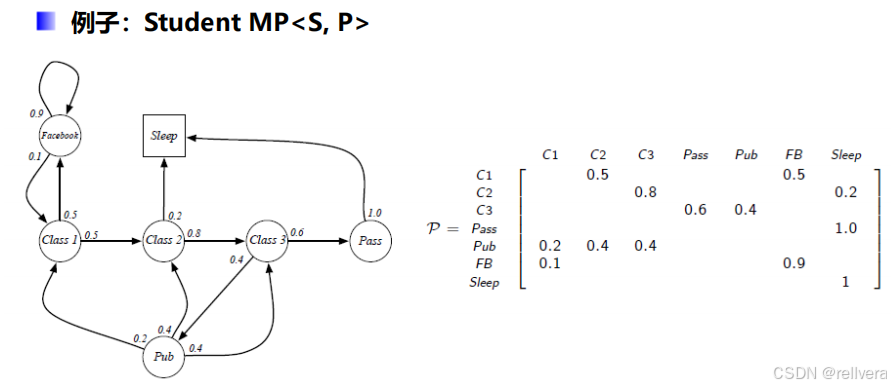
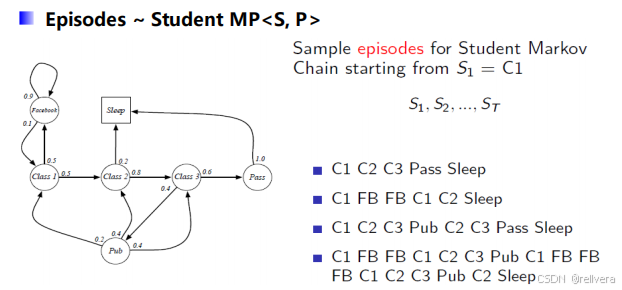
在這個例子中，假設初始狀態為C1（即class1），進行4次采樣，可以得到4個采樣結果：

1.2.2 Markov Reward Process (MRP) 馬爾科夫回報過程

馬爾科夫回報過程也是一個元組$<S,P,R,\gamma >$，相比于馬爾科夫過程MP，MRP多了$R$和$\gamma$。其中，$R$表示在給定狀態$s$的情況下，未來回報的期望。$\gamma$則是折扣因子。

那么，該怎么計算回報呢？假設當前時間為$t$，要計算從時間$t$開始獲得的獎勵$G_t$。最直接的方法是計算$G_t=R_{t+1}+R_{t+2}+R_{t+3}......$，但是這樣計算是不好的。
第一，如果這么算，就認為未來的獎勵和當前的獎勵同等重要，這在許多現實問題中并不合理。例如，在金融和經濟領域，時間越長的不確定性越高，因此更傾向于重視當前的收益。
第二，在無限時間步長的過程中，累積獎勵的和可能是發散的，這會導致價值函數無法計算和優化。
所以，引入了折扣因子$\gamma$。獎勵計算方法如下圖公式所示。$\gamma$趨向于0時，表示更注重當前獎勵，$\gamma$趨向于1時，表示更具有遠見。

下面是一個MRP的計算實例。首先進行采樣得到幾個觀測序列。然后套上面的公式得到觀測序列的回報，初始狀態為$C1$，$\gamma$取值為1/2（每一個動作對應的回報值在下一張圖片上有）。

在MRP中還有一個要提的概念是估值函數（value function），它表示以狀態s為起始，所有回報的平均。就像下圖中所畫的一樣，假設從狀態c1起始進行采樣，得到多個觀測序列，每一個觀測序列都有對應被采樣到的概率$P_t$，以及獲得的回報$G_t$。將$P_t?G_t$再求和就是估值函數v(s)。
所以，當MRP確定的時候，v(s)就是確定的值。

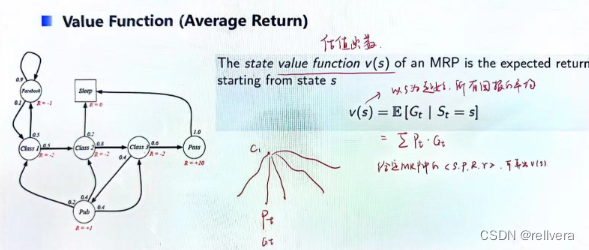
那么v(s)該如何計算呢？
Bellman方程將這個估值函數表示為即時獎勵和后續狀態價值的和，其公式如下圖所示。

然后可以通過解方程解求出v(s)，如下圖所示。下圖中的$R$、$gamma$、$P$都是MRP中的已知量，只有v(1)~v(n)是未知量。也就是說，當 MRP（環境參數）已知時，理論上通過求解 Bellman 方程式可以計算 v(s)。

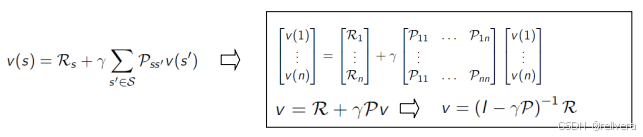
1.2.3 Markov Decision Process (MDP) 馬爾科夫決策過程

MDP的定義：相比于MRP，MDP多了一個有限的動作集A。可以理解為：MDP 是一個多層的 MRP，每一層對應一個行動 a。

那么給定一個狀態s，我們該選擇怎樣的行動a呢？這就要提到策略$\pi$（policy $\pi$）了，策略$\pi$表示在狀態s情況下，跳轉到動作a的概率。

這是一個MDP示意圖。圖中每一層代表了一個MRP，也隱含了一個動作a。選擇a的過程其實就是在不同層之間跳轉。

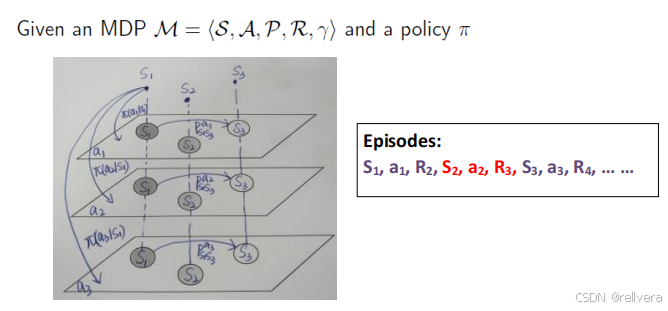
通過推導可以得出下面兩個結論：
（1）MDP by a policy is a MP
這意味著，一旦我們固定了策略 𝜋，在任意狀態 𝑠下采取動作 𝑎 的概率就確定了，這樣原來的MDP就變成了一個不再依賴動作選擇的過程，即一個Markov Process (MP)。

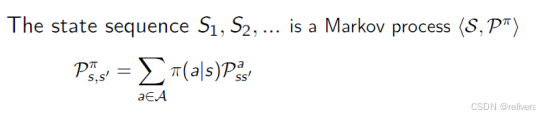
（2）MDP by a policy is also a MRP
這意味著，在有了策略 𝜋 后，MDP中的獎勵也可以固定下來，即從狀態 𝑠 到狀態 𝑠′ 的轉移的期望獎勵。

再補充幾個概念：
（1）state-value function $v_{\pi }(s)$：從狀態s開始，按照策略$\pi$進行決策得到的期望回報
（2）action-value function $q_{\pi }(s,a)$：從狀態s開始，采取動作a，按照策略$\pi$進行決策得到的期望回報
（3）$v_{\pi }(s)$和$q_{\pi }(s,a)$的關系如下圖中紅色方框中的公式所示。

此時，有了MDP by a policy is a MP、MDP by a policy is also a MRP這兩個結論后，我們可以進一步推導出：

從而得到貝爾曼期望方程：

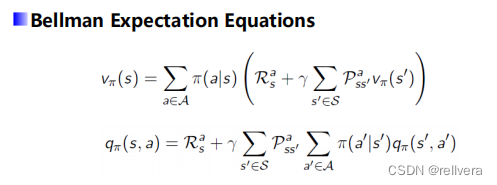
Bellman期望方程有啥用呢？
（1）策略評估。用于評估一個給定策略 𝜋 的價值函數$V^{\pi }(s)$和 $Q^{\pi }(s,a)$。通過迭代的方法，可以逐步逼近真實的值函數。
（2）策略改進。在策略迭代和值迭代算法中，Bellman期望方程用于評估當前策略，并根據評估結果改進策略，從而逐步找到最優策略。

1.3 強化學習

再回想一下強化學習的目標，在強化學習中，我們的目標是對于給定的狀態S，我們能選一個比較好的動作a，使得回報最大。即：學習一個策略$\pi$，讓$v_{\pi }(s)$和$q_{\pi }(s,a)$最大。為了達到這個目標，引入了optimal state-value function $v_{\pi }(s)$和optimal action-value function $q_{\pi }(s,a)$：

在此基礎上推導出了貝爾曼最優方程：

推導過程詳見這篇博文：貝爾曼最優方程推導，這篇文章寫得挺好的，所以筆者在此就不多贅述啦，大家直接看這篇文章就好！

貝爾曼最優方程定義了最優值函數和最優動作值函數。最優值函數表示從狀態 𝑠 出發，按照最優策略所能獲得的最大期望回報。最優動作值函數表示在狀態 𝑠 采取動作 𝑎 后，按照最優策略所能獲得的最大期望回報。
貝爾曼最優方程在強化學習中可以用來定義和求解最優策略，使得在每個狀態下的累積回報最大化。它為我們提供了一種系統的方法，通過動態規劃和迭代更新來逼近最優解，是解決強化學習問題的核心工具。