目錄

1.相關概念

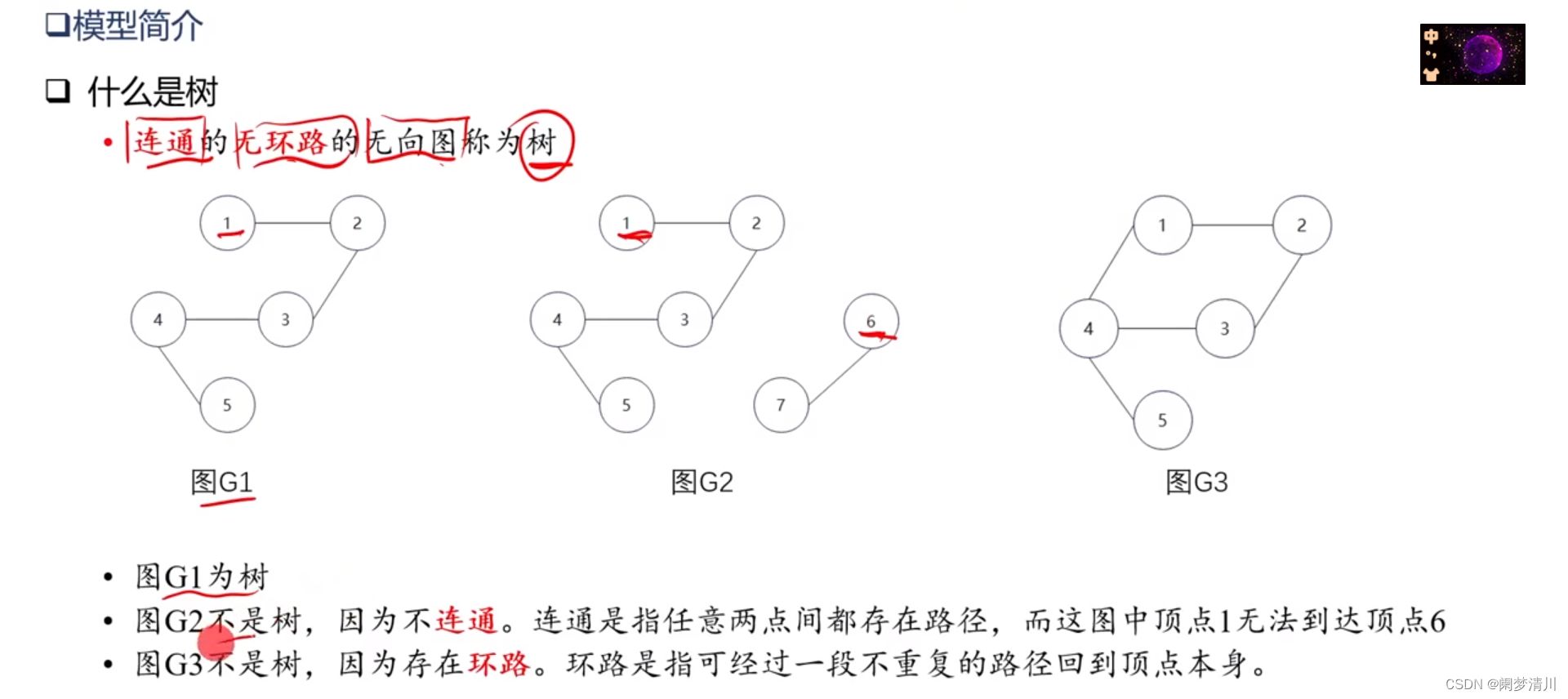
（1）什么是樹

（2）生成樹和最小生成樹：

2.適用賽題

（1）賽題分類

（2）不同之處

3.兩種算法

（1）prim算法

（2）Kruskal算法

4.典型賽題

（1）架設通信線路

（2）Matlab代碼分析

（3）運行結果

（4）代碼分享

---

1.相關概念

（1）什么是樹

連通，無環路，無向圖就是樹；

（2）生成樹和最小生成樹：

生成樹就是一個圖的子圖，而且是一個樹，包括原來的圖的所有的頂點，一個圖可能會有多個生成樹，可能會有多個最小生成樹，但是最小生成樹的長度是唯一的；

2.適用賽題

（1）賽題分類

通信建設問題，以及這個管道的鋪設問題，都是這類最小生成樹問題，求解的就是這個通信線路的最短情況和這個鋪設管道最節省的情況；

（2）不同之處

這個不同之處指的就是這個最小生成樹和最短路徑的不同之處，這個最小生成樹里面沒有指定這個起點和終點，只要求能夠把所有的頂點走一遍就可以了；

而最短路徑是指明了起點和終點，在這個限制條件下要求這個路徑最短，這個是否指定起點和終點是這兩個問題的本質區別；

3.兩種算法

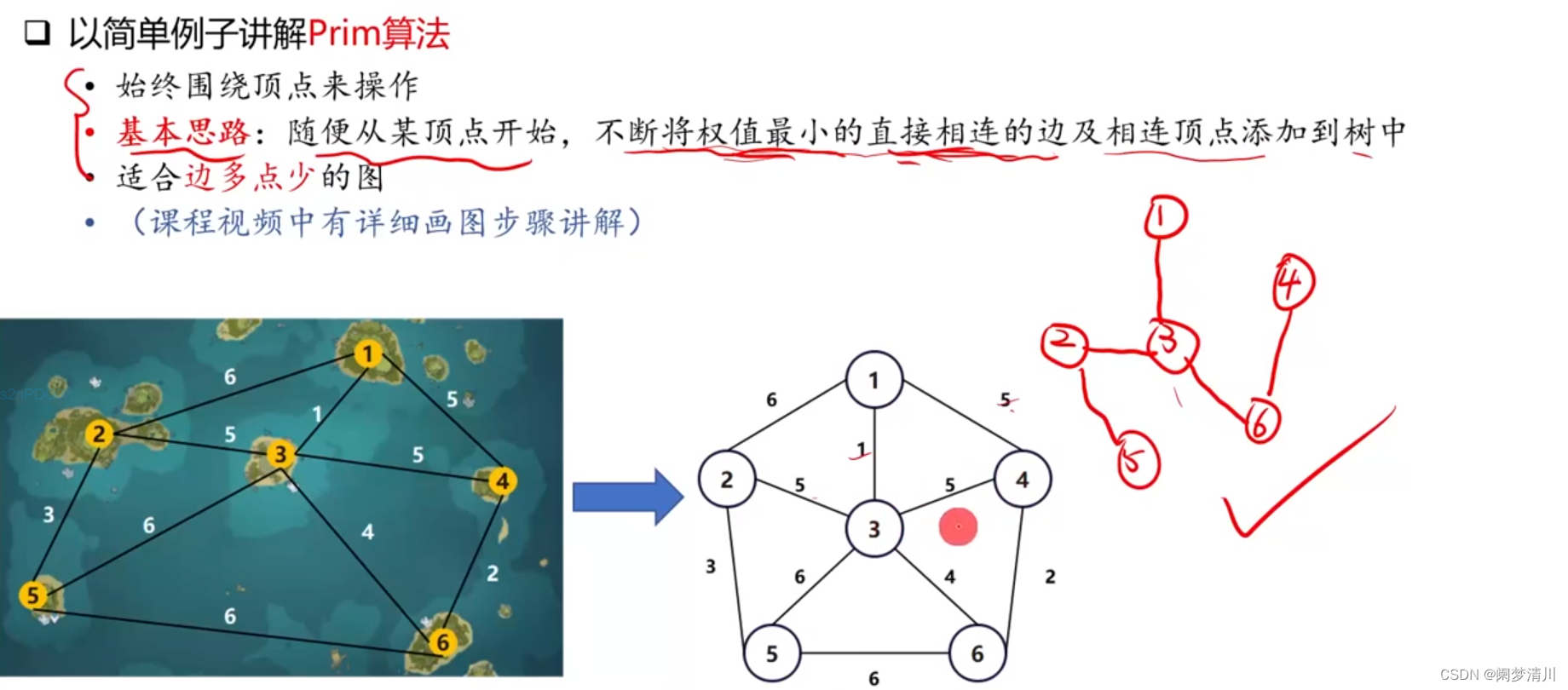
因為這個無論是在數據結構里面，還是在離散數學里面，這個算法我們都已經學習了解過了，因此下面我不會進行詳細的贅述；

（1）prim算法

（2）Kruskal算法

4.典型賽題

（1）架設通信線路

（2）Matlab代碼分析

我們首先要生成一個鄰接矩陣，然后再根據這個不同的頂點之間的長度去初始化這個不同位置的元素的數值；

我們現實生成了一個9*9的全是0的矩陣，然后就是根據不同頂點之間的權重去對于這個矩陣的相應的位置進行初始化；這個地方需要注意的是這個生成樹是沒有方向的，我們對于兩個頂點之間的邊，只需要初始化一次；

例如1,2這兩個頂點之間，權重是2，我們在對于和1相關聯的節點初始化之后，就已經把和1節點相關聯的2節點給初始化了；當我們對于這個2節點及其相關聯的邊進行初始化的時候，這個就不需要重復的進行初始化操作；

upper是指使用的是這個矩陣的上三角，因為如果全部使用就會把每兩個頂點之間出現兩條邊，這個最小生成樹是無向圖，我們只需要使用上三角即可；

這個里面使用到的相關函數的簡單介紹我放到下面了：?

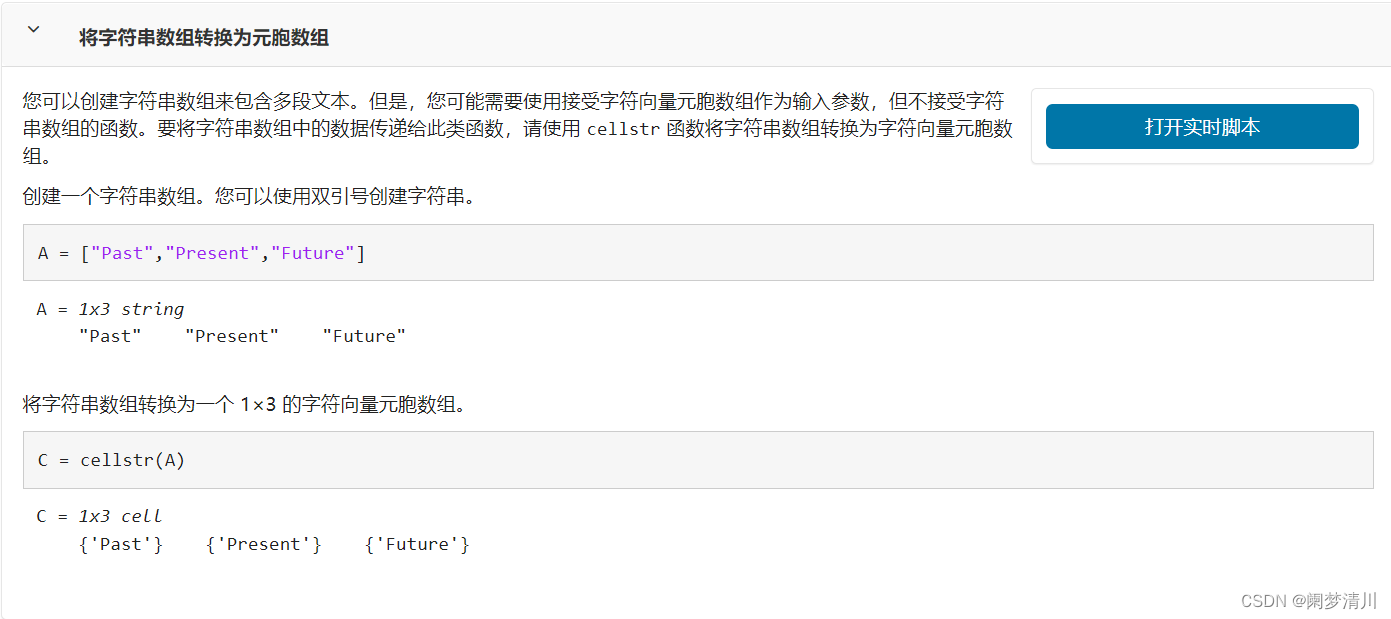
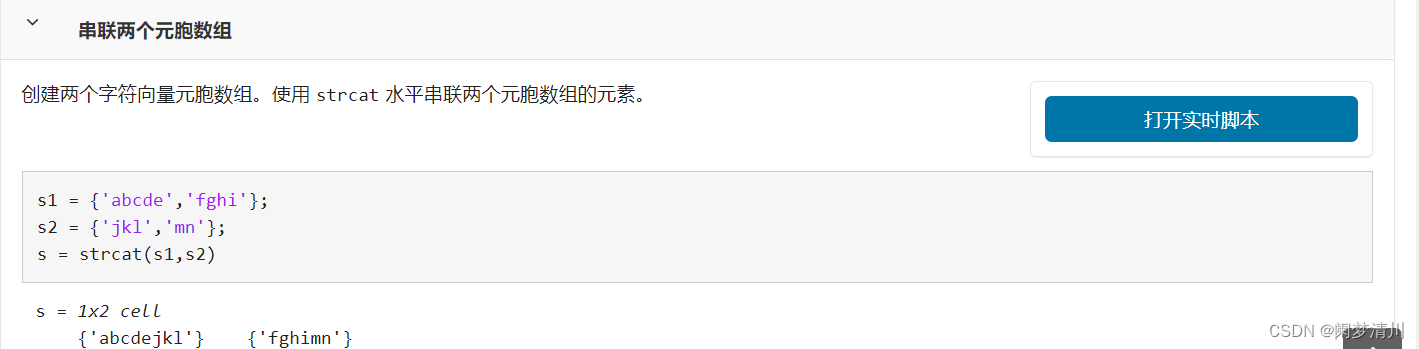
?接下來就是求解最小生成樹，sparse表示使用的是地杰斯特算法，這個是我們自己設置的，不進行設置的話就會使用默認的prim算法，這兩個都是可以進行求解的，只是這個效率上面可能會有區別，讀者可以下去進行嘗試；

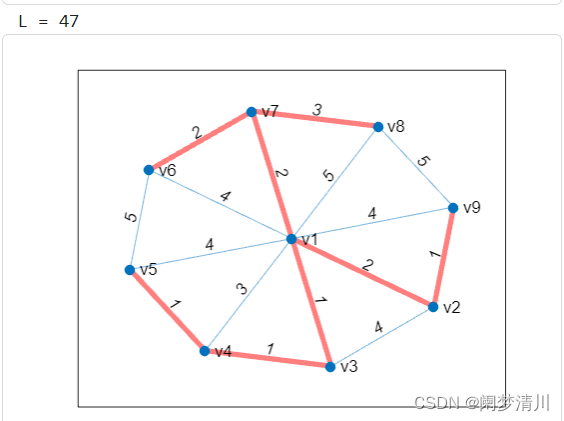
L=sum就是對于這個權重求和，求解得到這個最小權重和，highlight是對于這個圖形的優化；

（3）運行結果

最小權重和是47，這個最小生成樹如圖所示：

（4）代碼分享

clear,clc;a=zeros(9);
a(1,[2:9])=[2 1 3 4 4 2 5 4];
a(2,[3 9])=[4 1];
a(3,4)=1;
a(4,5)=1;
a(5,6)=5;
a(6,7)=2;
a(7,8)=3;
a(8,9)=5;s=cellstr(strcat('v',int2str([1:9]')));G=graph(a,s,'upper');%使用上三角矩陣畫出圖形p=plot(G,'EdgeLabel',G.Edges.Weight);T=minspantree(G,'Method','sparse');%使用迪杰斯特算法L=sum(G.Edges.Weight)highlight(p,T,'EdgeColor','Red','LineWidth',2.5)