經典排序算法詳解

創作不易，如對您有幫助，還望一鍵三連，謝謝！

前言

學習目標：

直接插入排序

基本思想：

代碼

希爾排序：

gap取值

代碼

特性總結

選擇排序

基本思想

代碼

堆排序

思想

代碼

冒泡排序：

快速排序：

思想

遞歸

非遞歸

歸并排序

基本思想：

遞歸實現

非遞歸實現

時間復雜度與空間復雜度以及穩定性

創作不易，如對您有幫助，還望一鍵三連，謝謝！

前言

排序在我們日常生活中十分常見，比如：成績按高低排序，購物網頁按價格排序......今天我們就來學習常見的幾個排序算法。

學習目標：

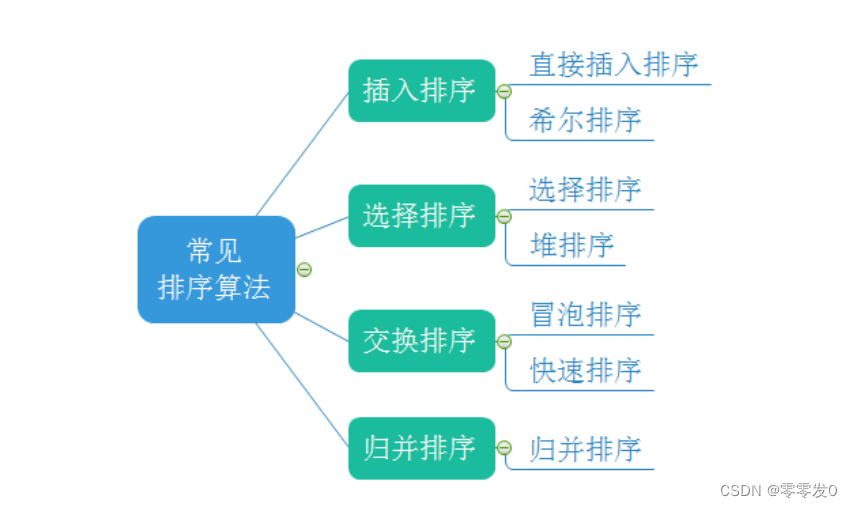
接下來我們一個一個講解。

直接插入排序

首先，我們先來看動圖：

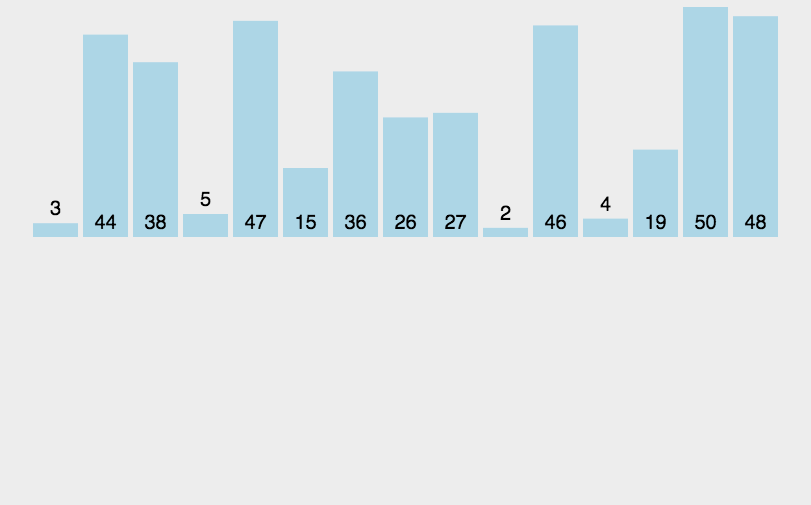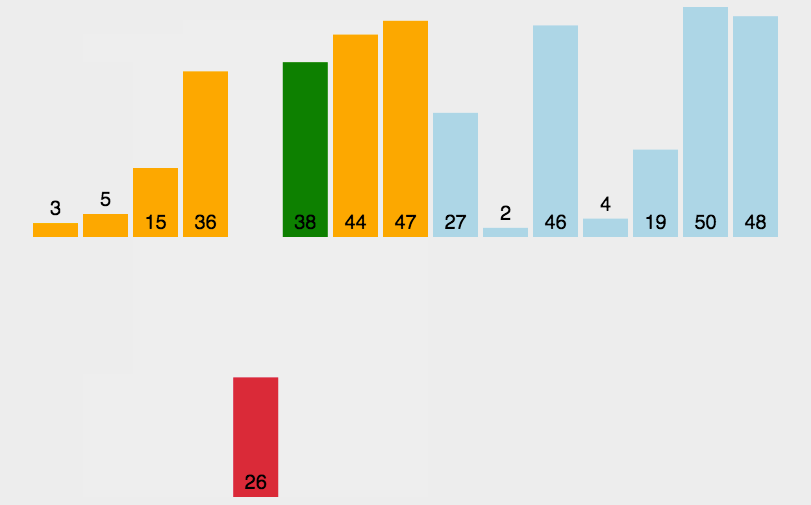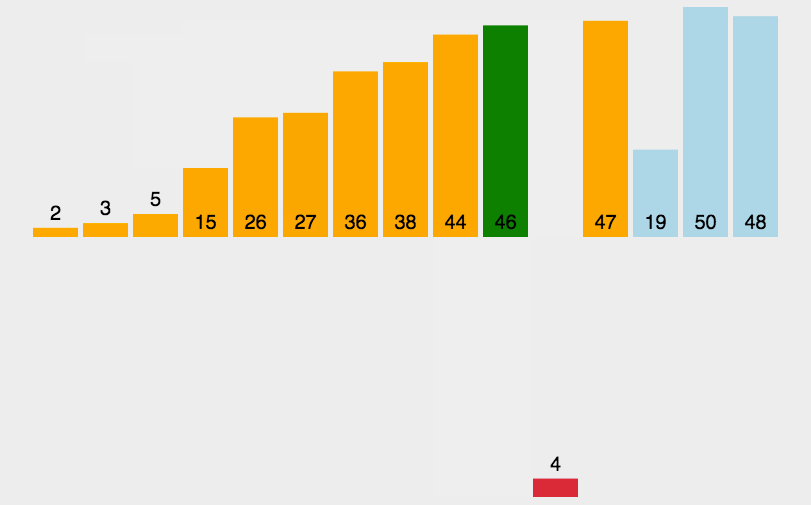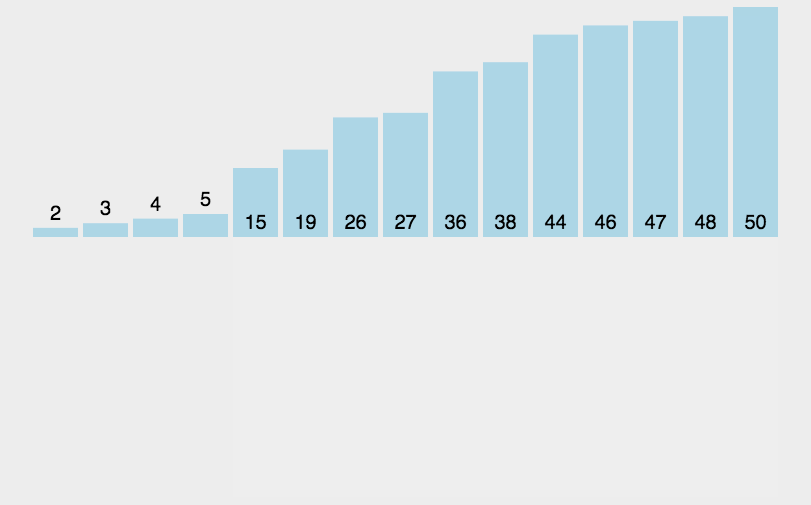
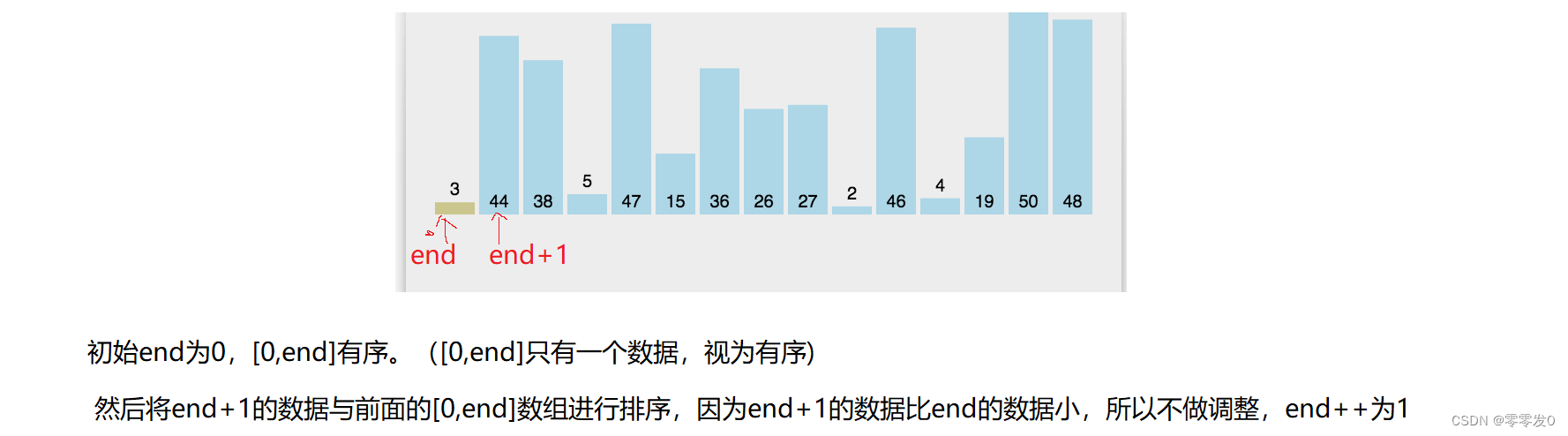
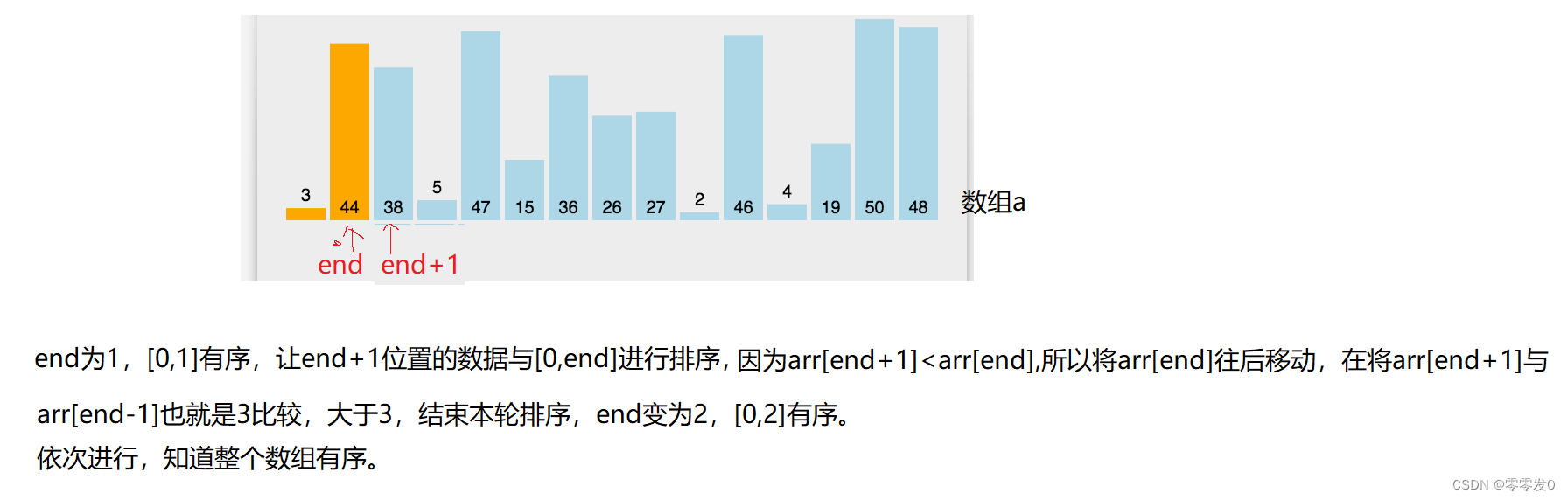
基本思想：

end從0開始，[0,end]視為一個有序的數組，然后每次都讓end+1的數據與前面有序數組[0,end]進行對比排序，然后end++，直至遍歷完整個數組，此時原數組就有序了。

代碼

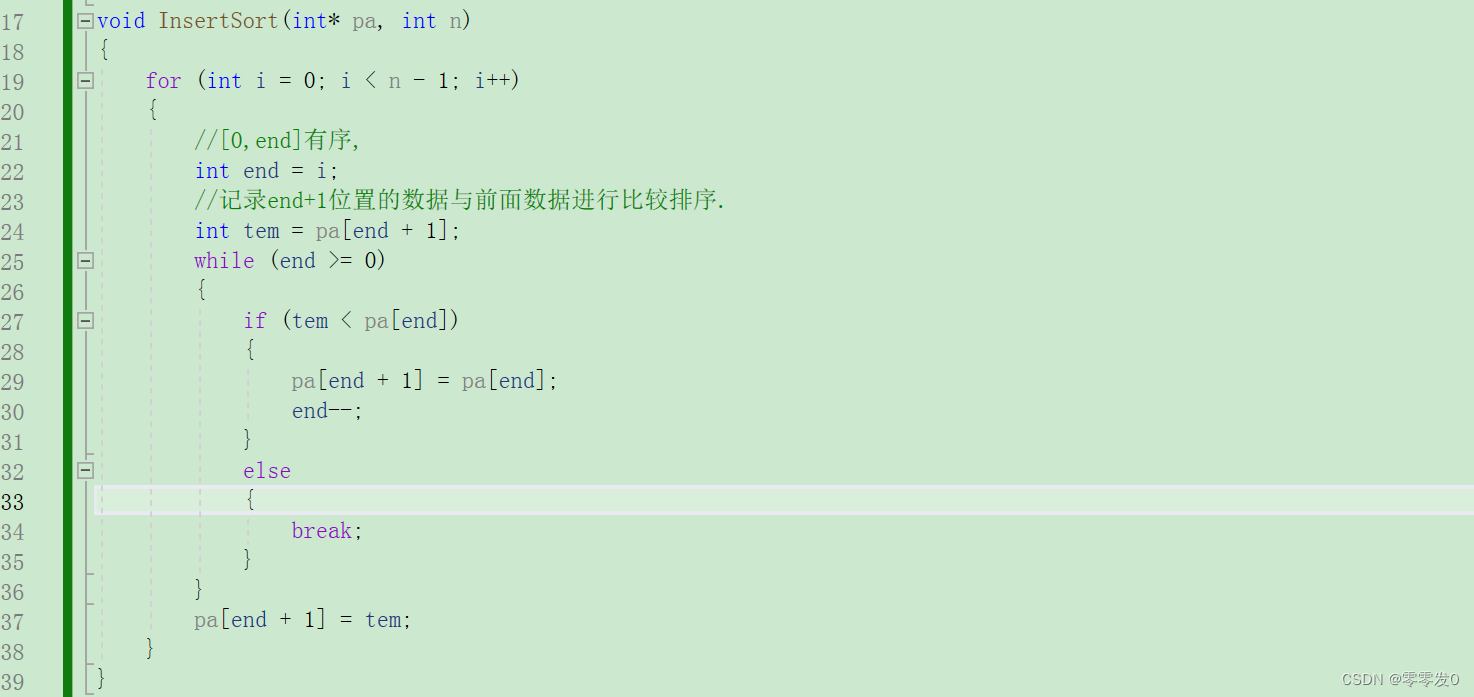
有小伙伴可能會問，為什么最后要pa[end+1]=tem ？且看此圖：

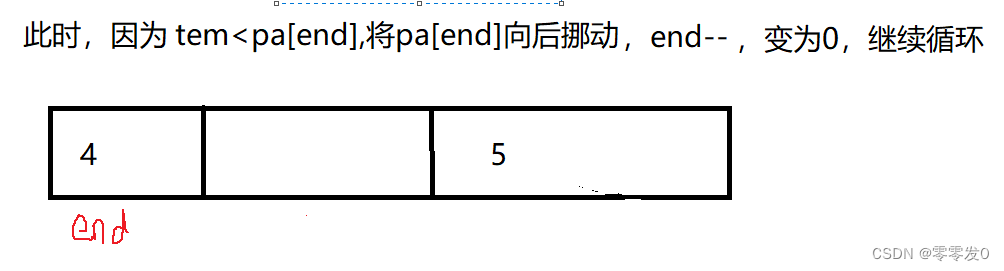
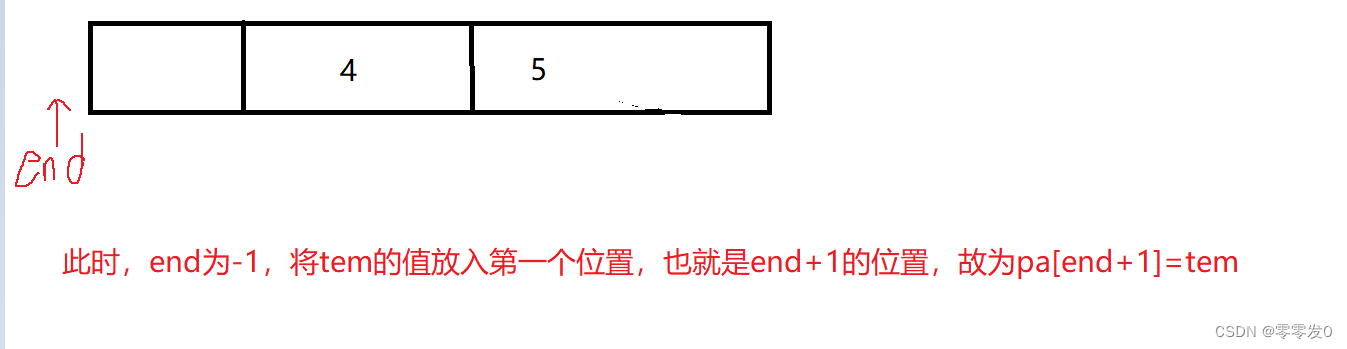
這就是上面問題的原因，其實學習數據結構時，有這種問題究其原因還是因為沒有畫圖，筆者認為學習數據結構一定要多畫圖，這樣才不容易出錯，有點跑題了哈哈，我們繼續學習下一個排序。

希爾排序：

首先，希爾排序其實就是直接插入排序的變形，所以要理解希爾排序，我們得熟練掌握直接插入排序。我們先來看一下動圖：

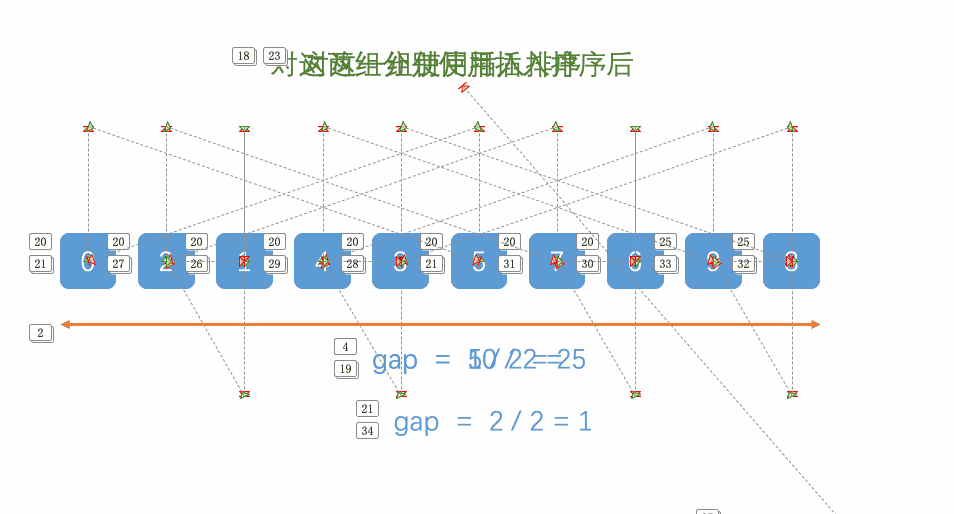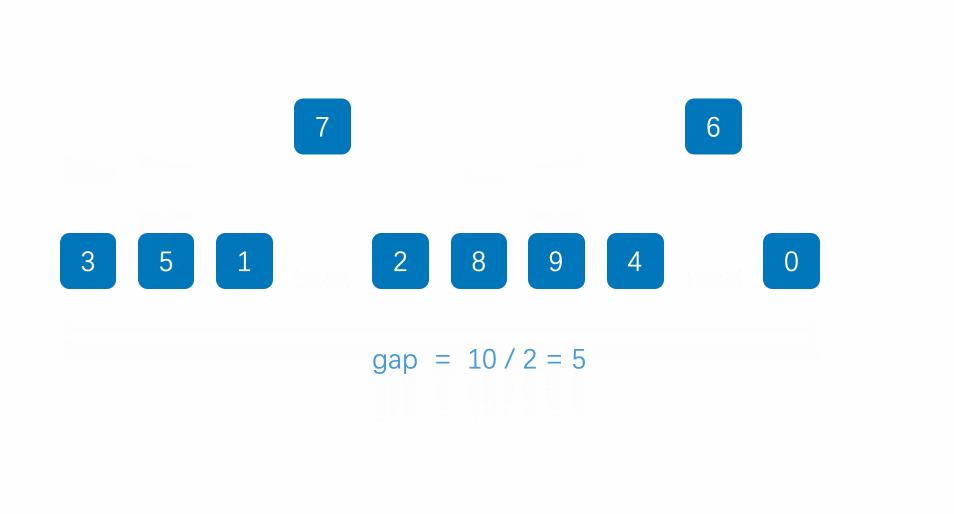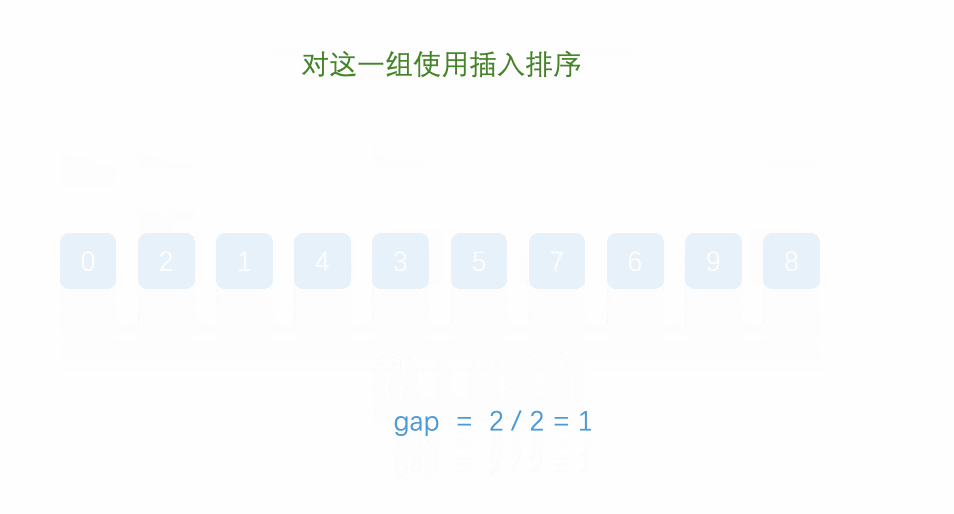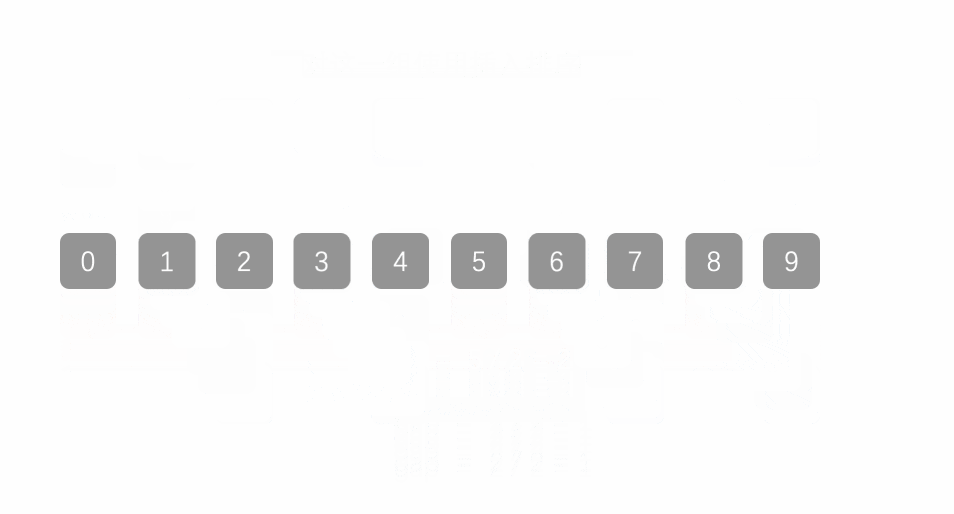
是不是看的一臉懵？這就對了，這個思路還是有點抽象的，容筆者慢慢講解：

首先，我們要知道希爾排序其實就是直接插入排序的優化，它選取了一個值gap，并把數組分成gap個組，每個組兩個元素相隔gap個位置，如下圖所示：

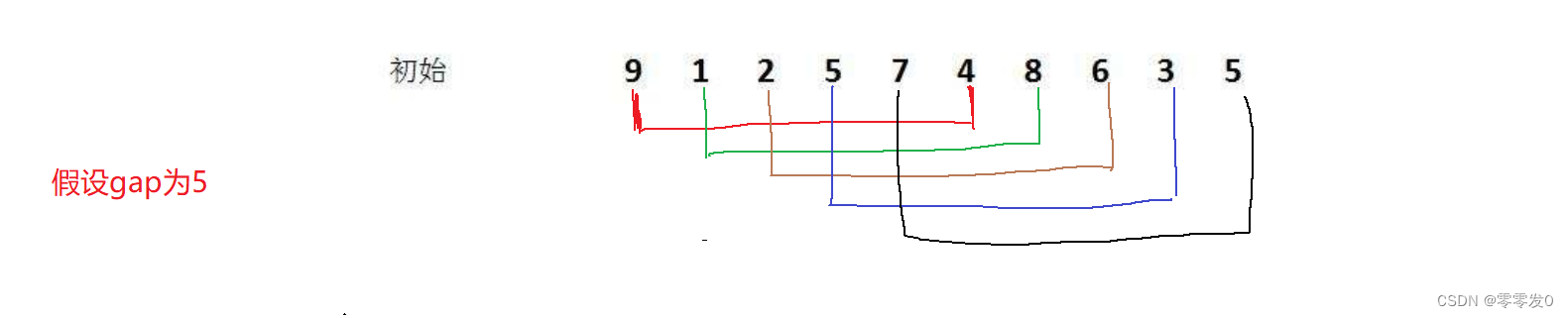
至于gap如何取值，我們一會兒再講，如上圖，我們講數組分成了gap組（5組），每組兩兩元素之間相隔gap個位置。

然后，我們對每一組進行直接插入排序，結果如下：

然后gap=gap/2，此時gap為2，在把數組分成gap（2）組，每組相鄰元素相差gap位置，如下：

在對每組進行直接插入排序，排好后如下：

然后gap為1，將數組分成了1組，有10個元素，對改組進行直接插入排序：

自此，數組有序。

有小伙伴可能發現了，當gap為1時不就是直接插入排序嗎？沒錯所以會說希爾排序就是插入排序的變形，實際上希爾排序就是插入排序的優化，希爾排序可比插入排序快多了。關于各排序的時間復雜度，我們下篇文章在講解。

gap取值

gap取值的話

一般取法有多種，其中兩種常見的是：

取 n/2：
- 最初的增量（gap）設定為數組長度的一半，即?gap = n / 2。
- 然后每次將 gap 減半，直到 gap = 1。
取 n/3+1：
- 初始增量（gap）設定為?gap = n / 3 + 1。
- 然后每次將 gap 按一定規則縮小，直到 gap = 1。

上面我們就是用了第一種方法。

當gap>1時，被稱作為預排序；當ga1p=1為插入排序。

代碼

代碼如下：

果然，當我們了解思路后寫代碼，發現還是一樣難寫，哈哈哈。

第一個for循環，是控制所有組，確保每一組都能進行排序，一共有gap組，故為i<gap.

而這段代碼，就是控制一組的排序，這個過程其實就是插入排序的變形，當gap=1時，與插入排序一模一樣，我們可以畫圖來進行理解。

需要注意的是j<n-gap:

因為我們進行排序時，有pa[end+gap]=pa[end]，所以我們要讓j<n-gap，防止越界。

希爾排序還有另外一種寫法：

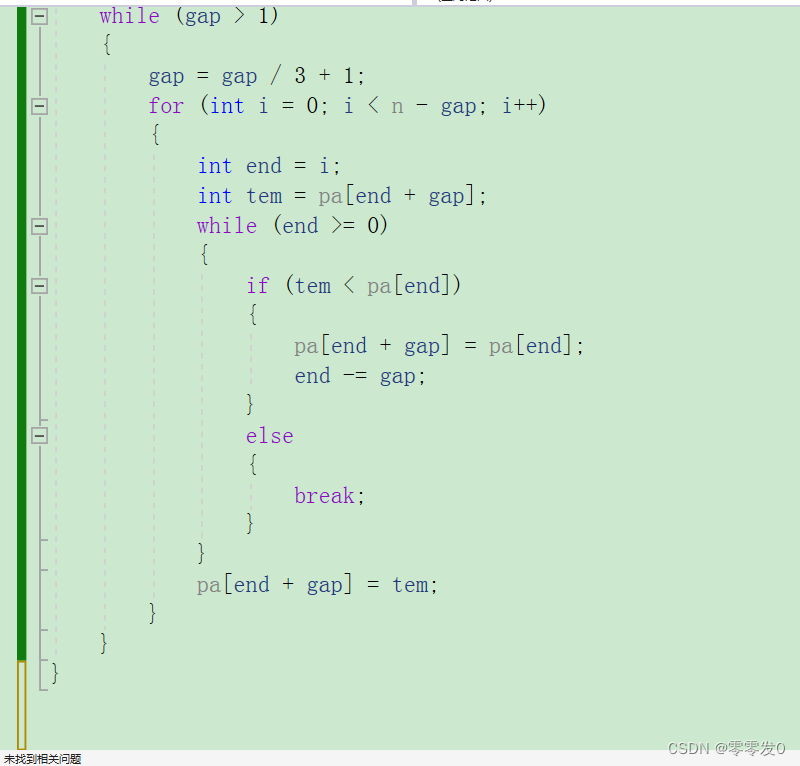
這個寫法與第一個不同的是沒有按照先排好一個組，然后再排另一個組，它直接是混著排序，小伙伴們可以畫圖理解一下。兩種方法掌握一種即可。

特性總結

選擇排序

基本思想

每一次從待排序的數據元素中選出最小（或最大）的一個元素，存放在序列的起始位置，直到全部待排序的數據元素排完。

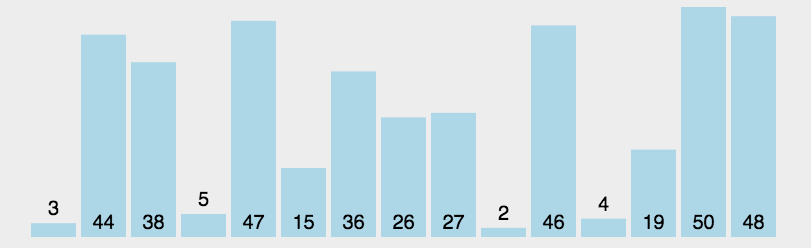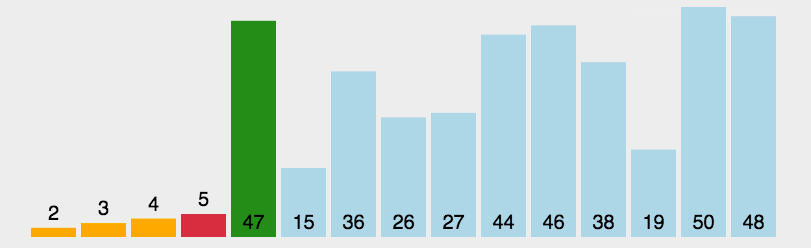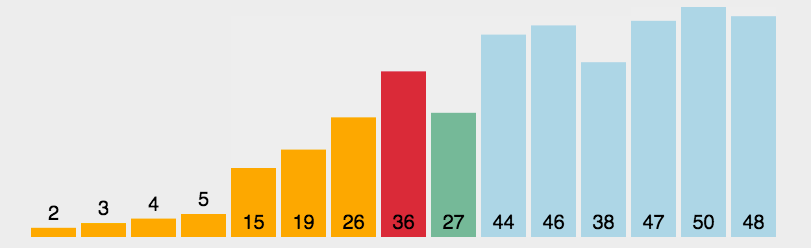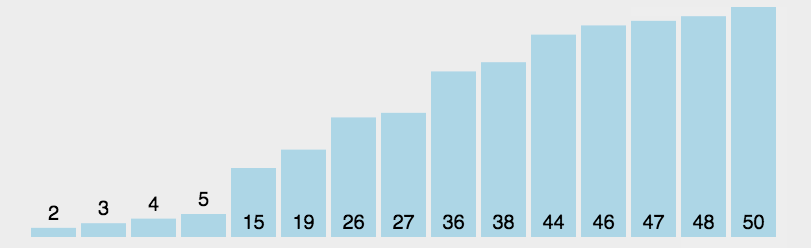
這個排序思路還是比較簡單的，

代碼

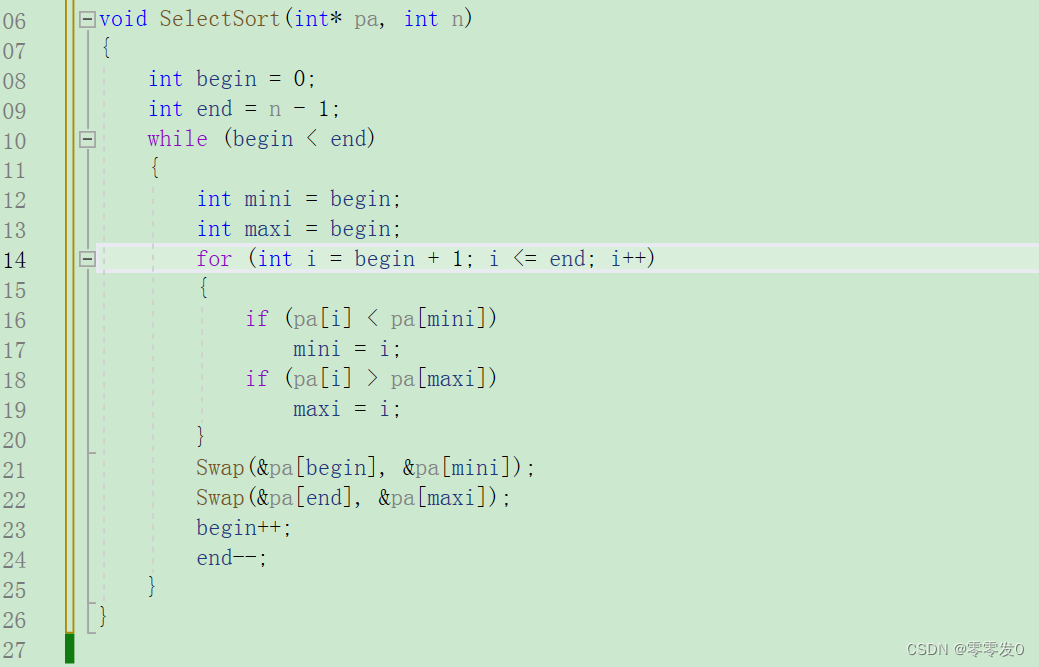
好，我們給個樣例運行一下：

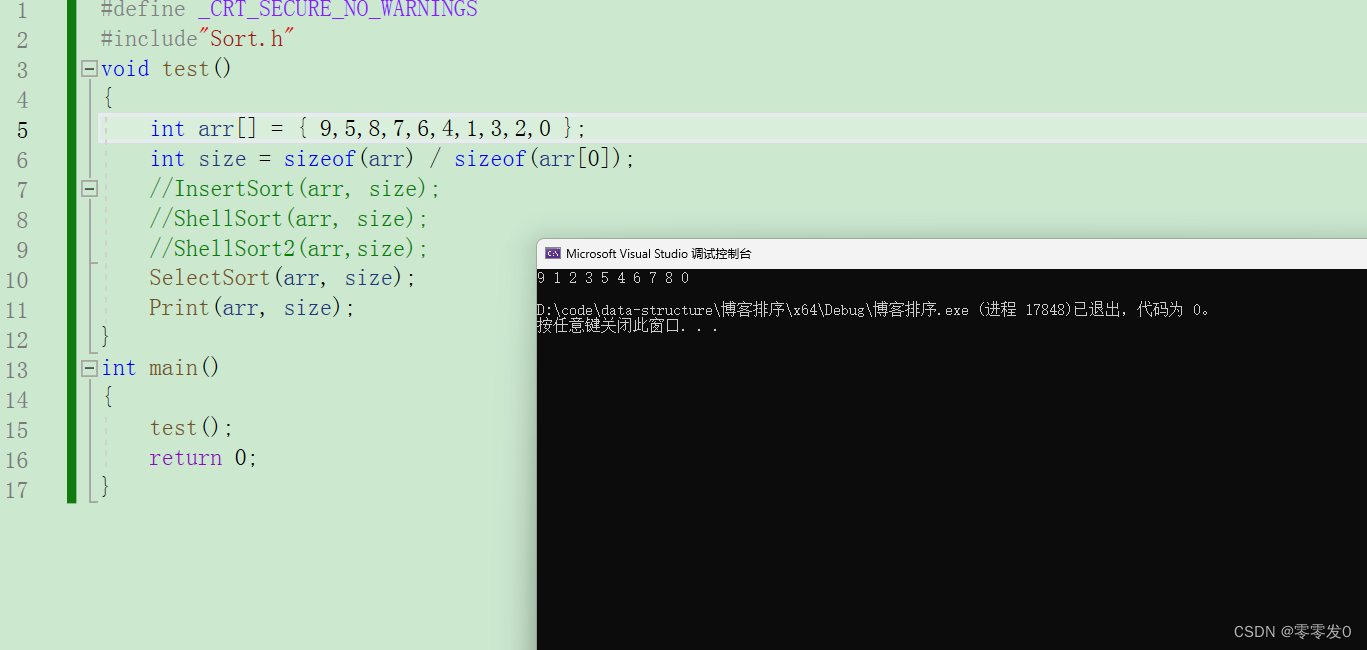
不出意外，錯了！

為啥呢？我們來調試一下：

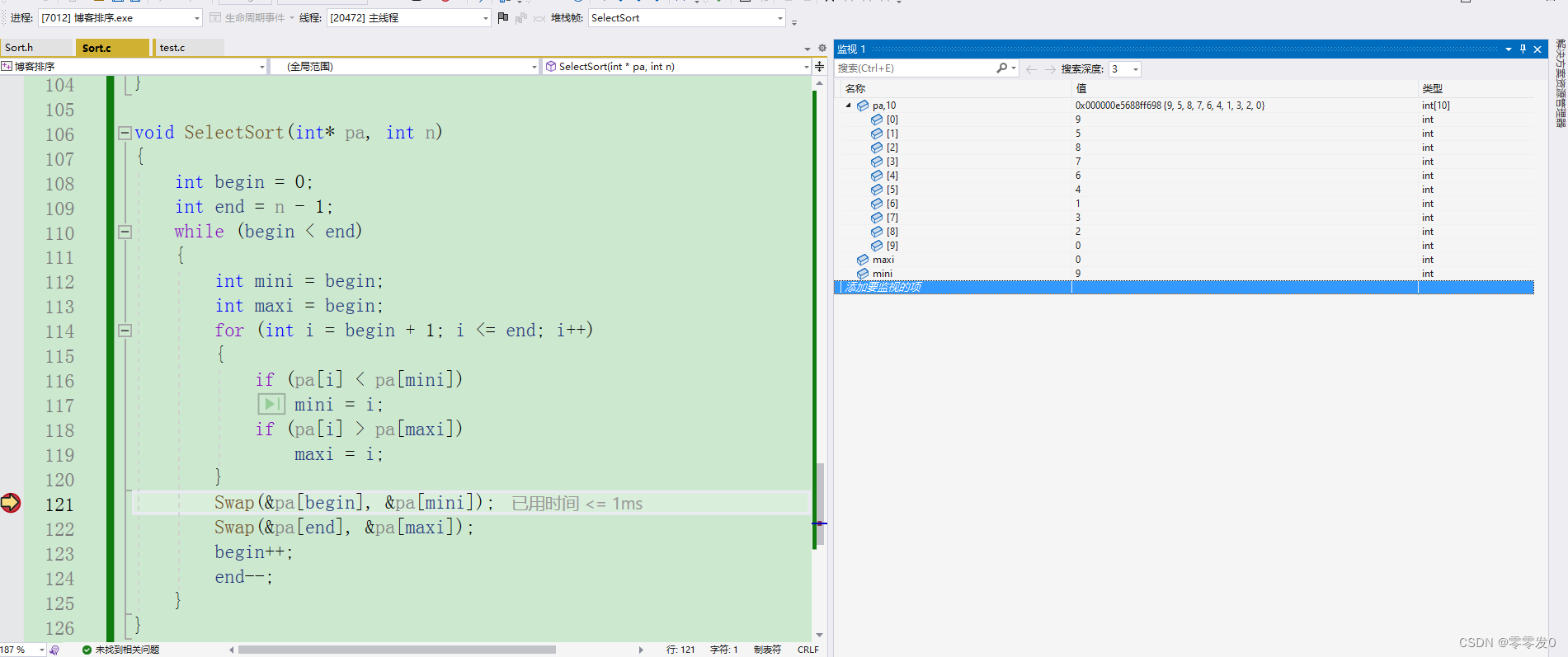
第一輪，maxi為0，mini為9，沒有錯，我們在進行下面的交換代碼。

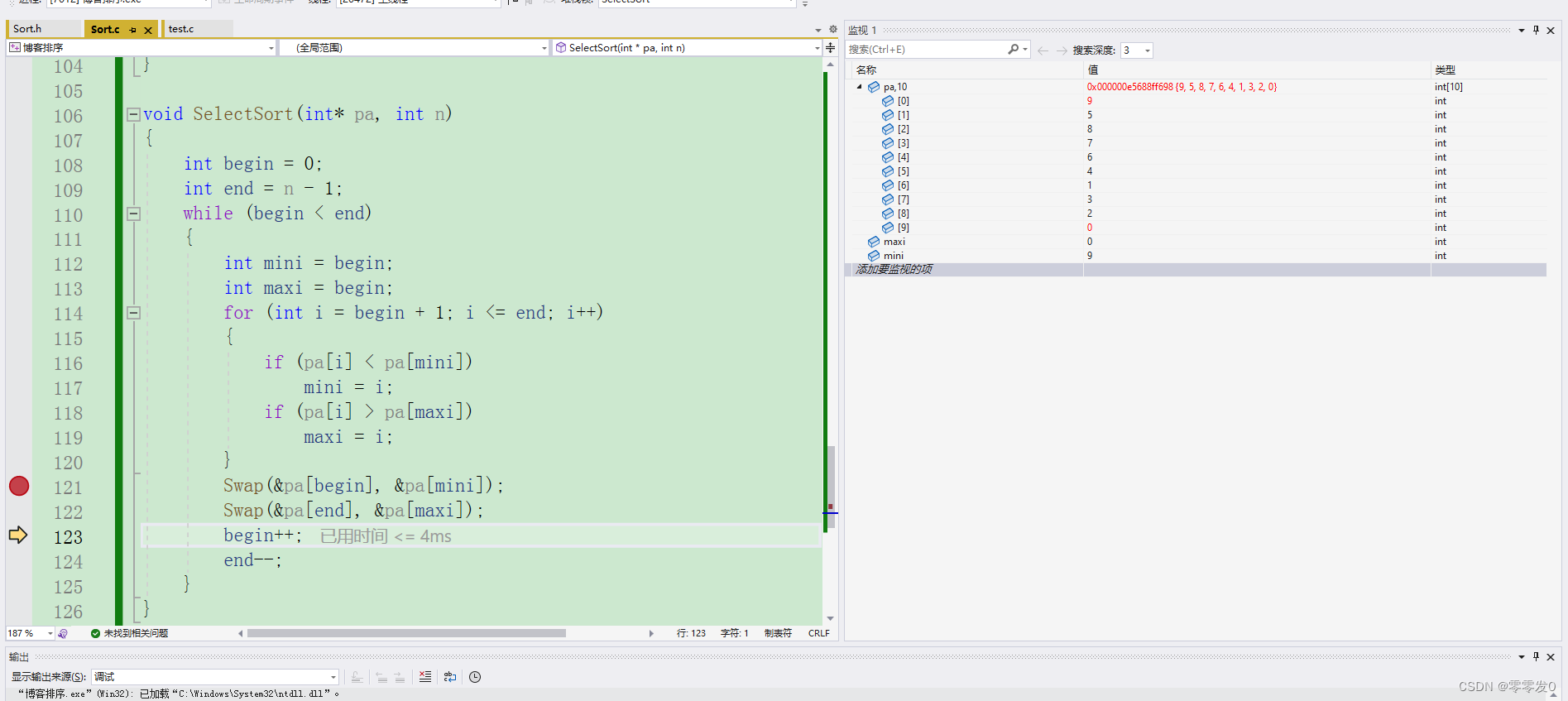
出問題了，當我們把pa[begin]和pa[mini]進行交換時，由于maxi的值與begin相等，所以當交換pa[begin]和pa[mini]后，maxi指向的值就變了，不是最大值了，所以我們要加一個if條件語句：

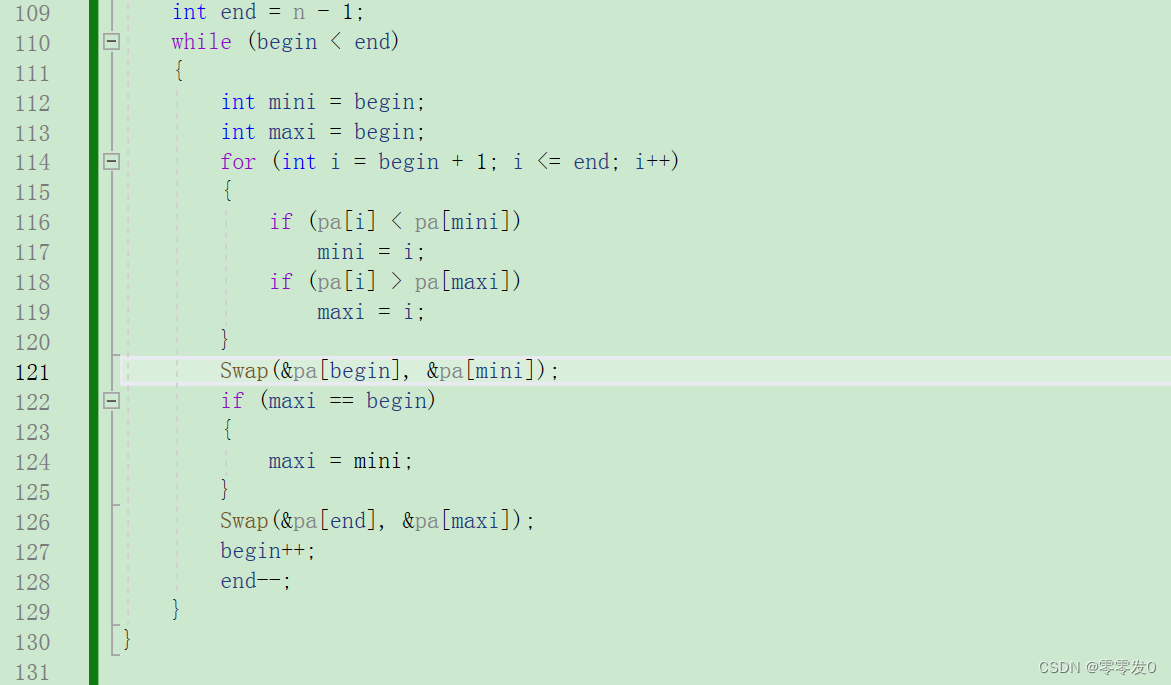
這下就對了。

堆排序

思想

首先建堆，升序建大堆，降序建小堆，建好堆之后另end等于數組長度-1，交換0位置和end位置的數據，向下調整建堆end--，直至end小于0。

、

代碼

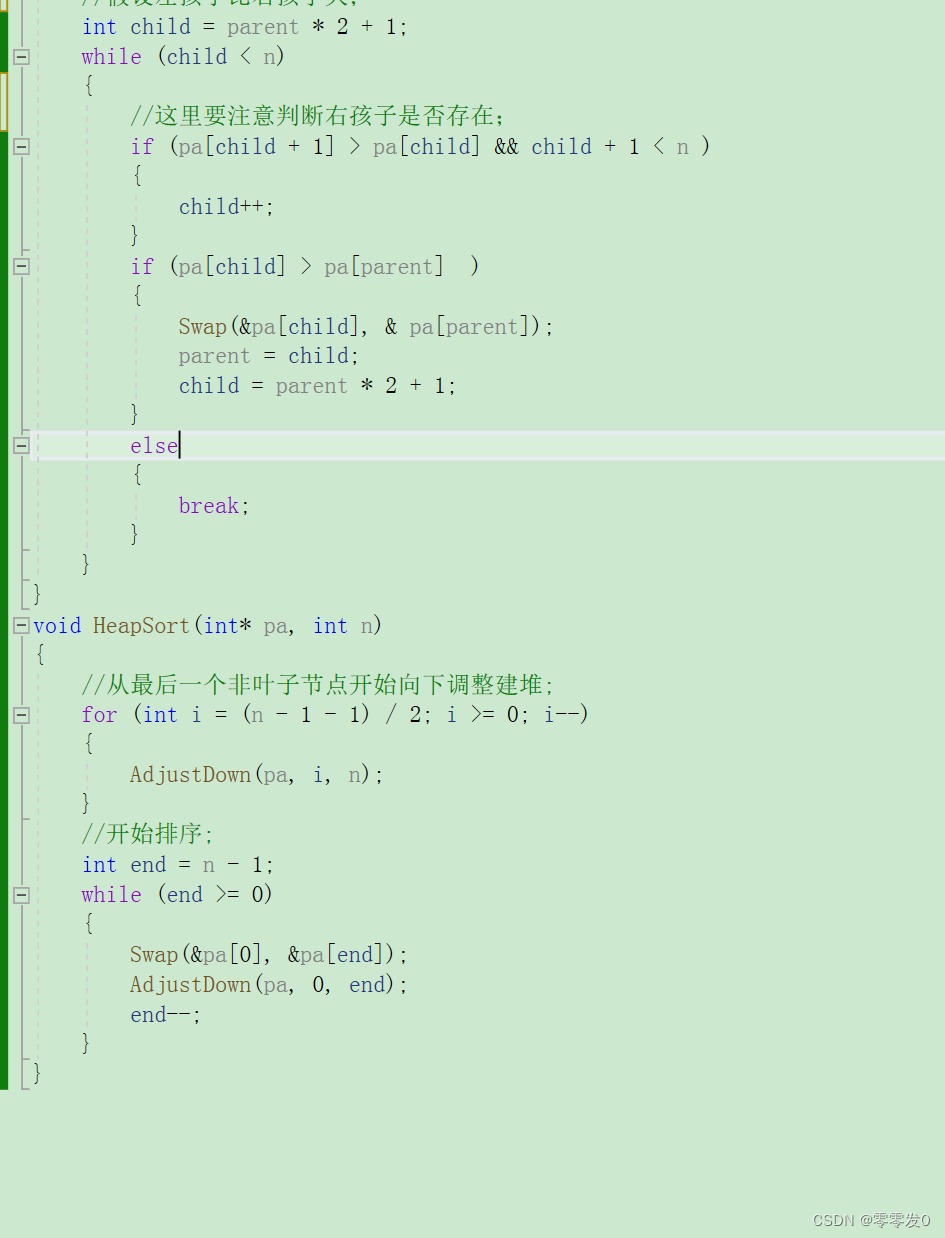
這個堆排序寫起來還是有難度的，這里看不懂也沒關系，筆者之后專門寫一篇堆排序的文章，可以暫時跳過繼續往下看。

冒泡排序：

這個就比較簡單了，冒泡排序沒有什么實踐價值，但有一定的教學意義，我們來看一下動圖：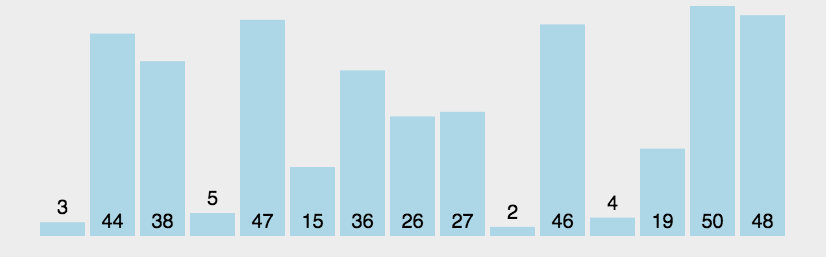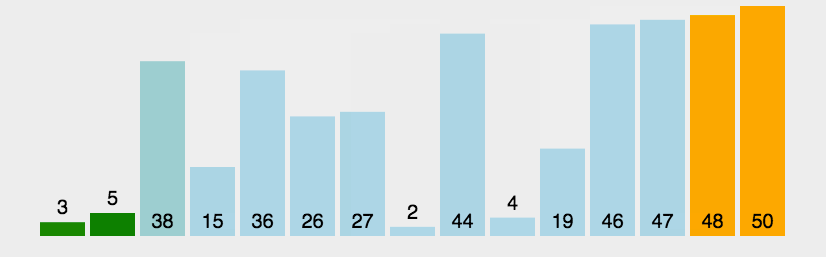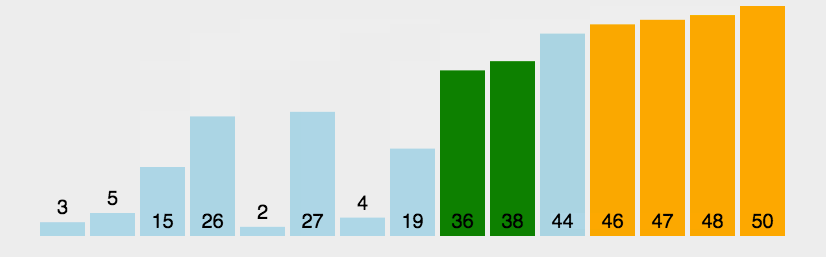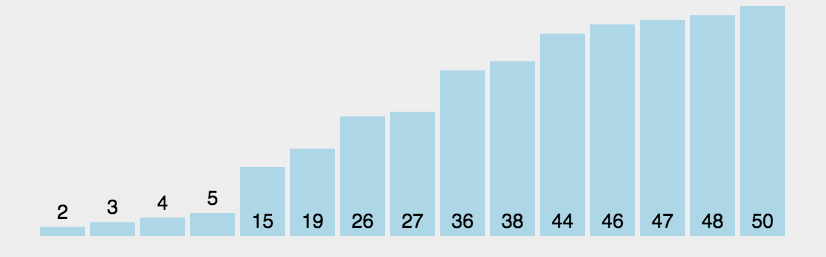

代碼如下：

快速排序：

思想

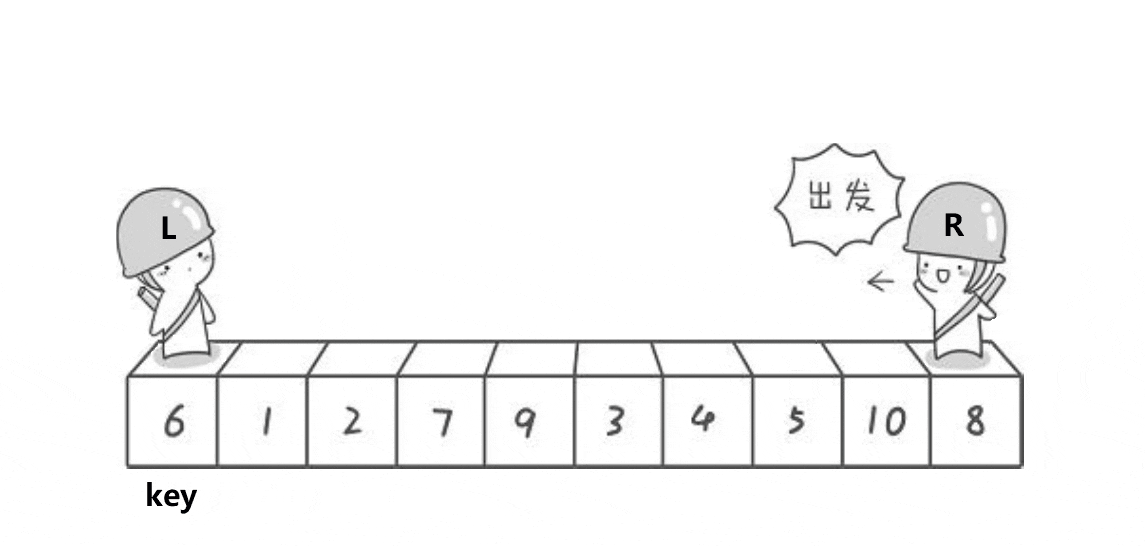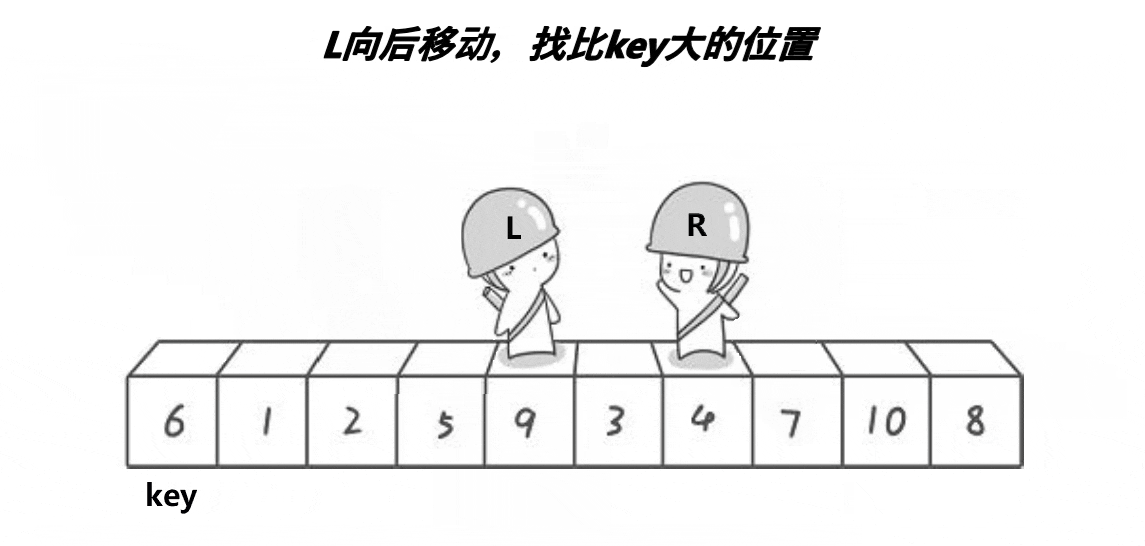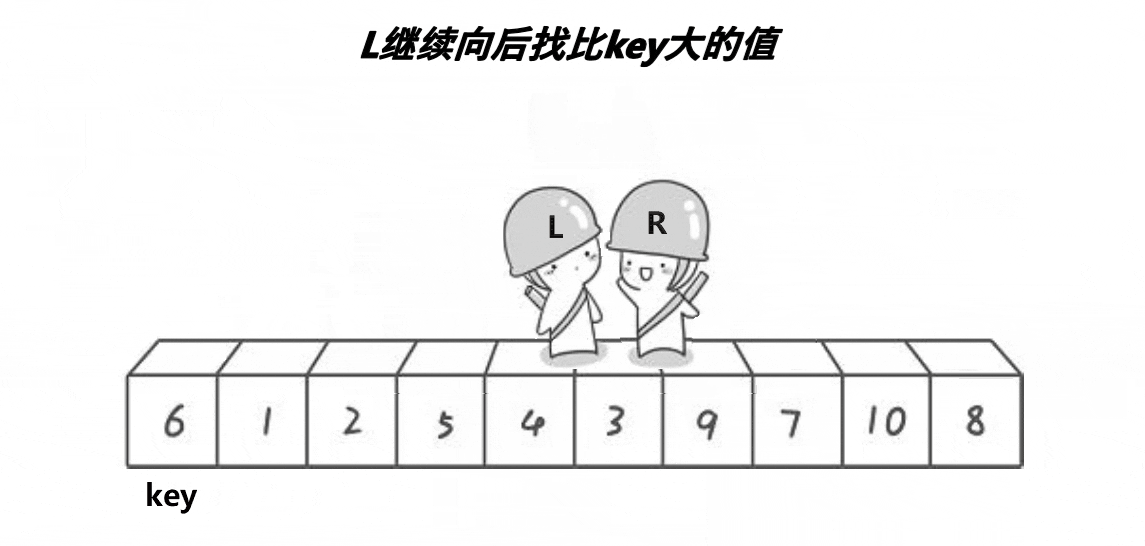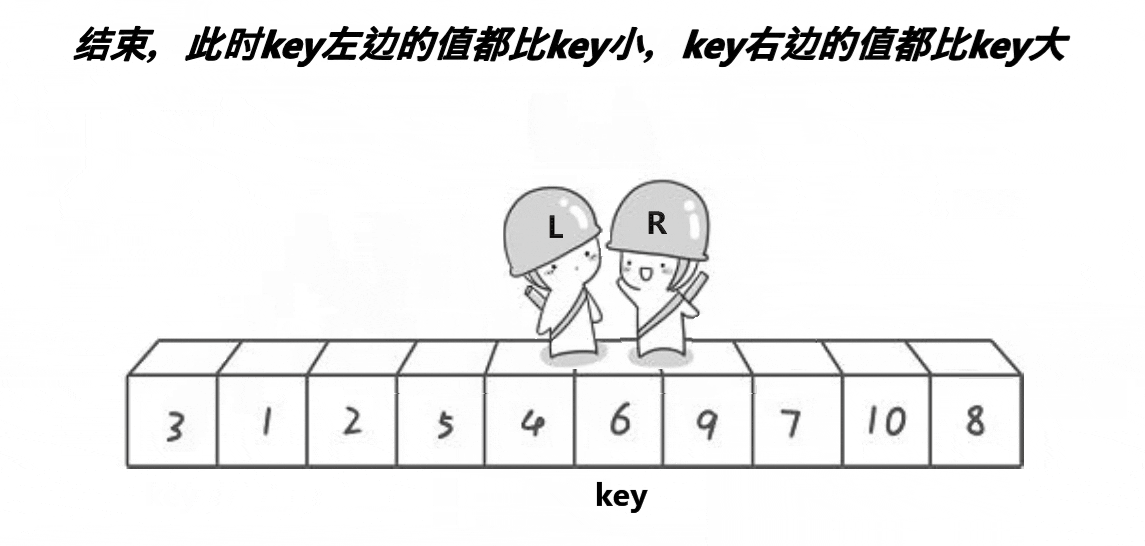
我們找一個參考值，end指向數組尾部，begin指向數組起始位置。

end先走，如果arr[end]大于key，end--直至找到小于key的位置；

同理，當end找到小于key的位置后，begin開始找大于key的位置，然后交換begin和end兩位置的值，直至begin=end。

當begin和end相遇時的位置的值一定小于key。（原因我們一會兒講），然后交換key和兩者相遇位置的值，完成第一趟排序。

快排是比較重要的，還是有很大的概率在面試時讓你手撕，所以我們一定要熟練掌握，快排實現有遞歸和非遞歸兩種方法，我們一一講解。

遞歸

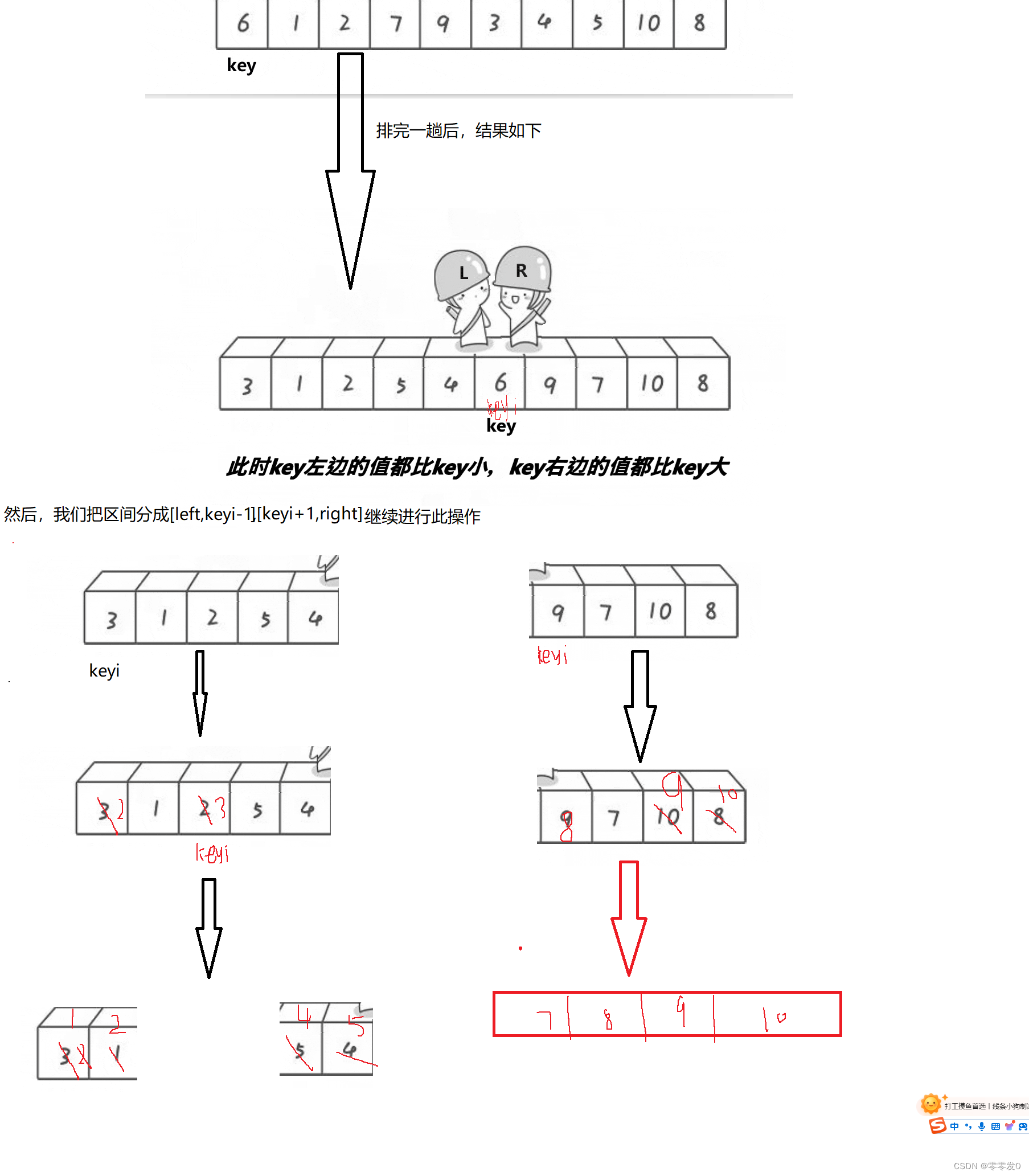
排完一次序后，以keyi為基準分割區間，繼續排序.

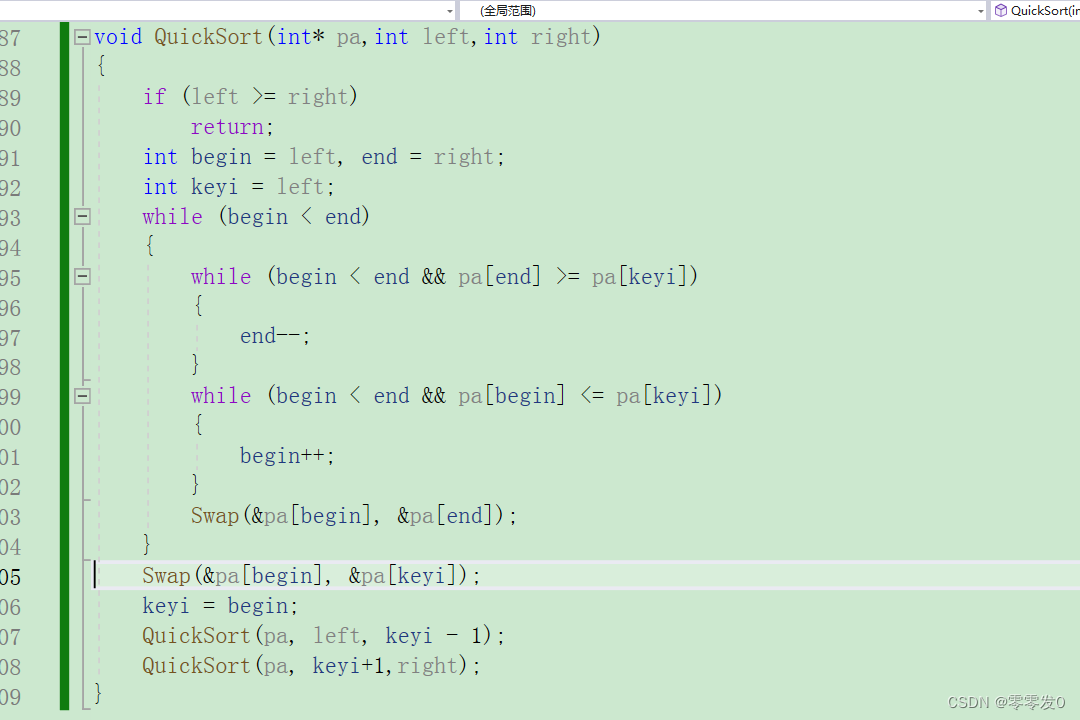
代碼如下：

非遞歸

有小伙伴可能會說：我們都已經會遞歸版本的快排了，還有必要學這個嗎？往年一個面試官是這樣問的：同學，你學過數據結構，那你了解快排嗎？這位同學非常熟練的講出來了遞歸實現的大致思路。面試官聽后笑著說：“很好，那你能用非遞歸實現嗎？”哈哈哈，所以還是有必要的。

非遞歸和遞歸思路一樣，我們也是采用分割區間，不能用遞歸，我們可以用循環來解決，那么問題來了，我們怎么來存儲分割好的區間呢？

想想我們之前講過一道括號匹配的問題，那個時候我們怎么存儲括號的？

答案是：棧。

我們用棧來存儲分割后的區間，只要區間滿足左邊界大于右邊界就入棧，然后套一個while循環，當戰不為空就繼續。

需要注意的是棧是后進先出，千萬不要把區間搞反了

代碼如下：

歸并排序

基本思想：

歸并排序（MERGE-SORT）是建立在歸并操作上的一種有效的排序算法,該算法是采用分治法（Divide and Conquer）的一個非常典型的應用。將已有序的子序列合并，得到完全有序的序列；即先使每個子序列有序，再使子序列段間有序。若將兩個有序表合并成一個有序表，稱為二路歸并。

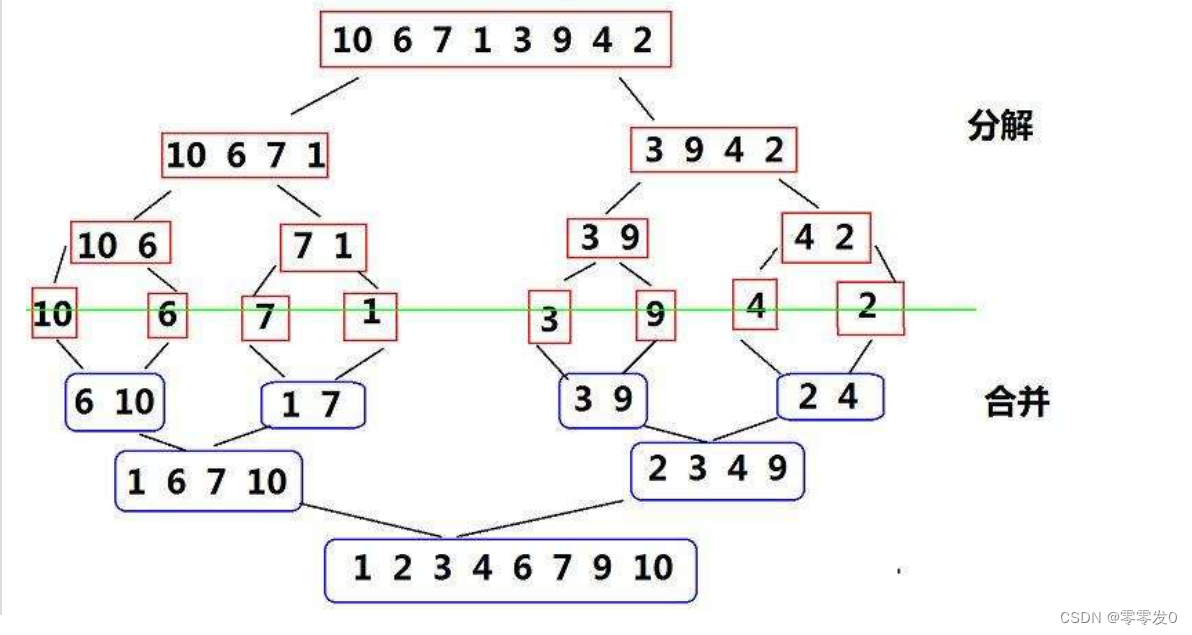
說的通俗易懂點就是把一個數組分解成兩個數組pa1,pa2,直到每個數組只有一個元素，然后在依次合并pa1和pa2,從而使原數組有序。

歸并排序的思想很像我們之前講過的合并兩個有序數組，不知道小伙伴還記不記得，只能說是一模一樣，同樣，實現歸并排序也有遞歸和非遞歸兩種方式。

遞歸實現

需要講的一點是_MergeSort是MergeSort的子函數，也可以稍作修改，寫在一起.還有就是記得釋放動態開辟的內存，養成良好的代碼風格。

下面是遞歸大致展開圖，可以幫助大家理解一下：

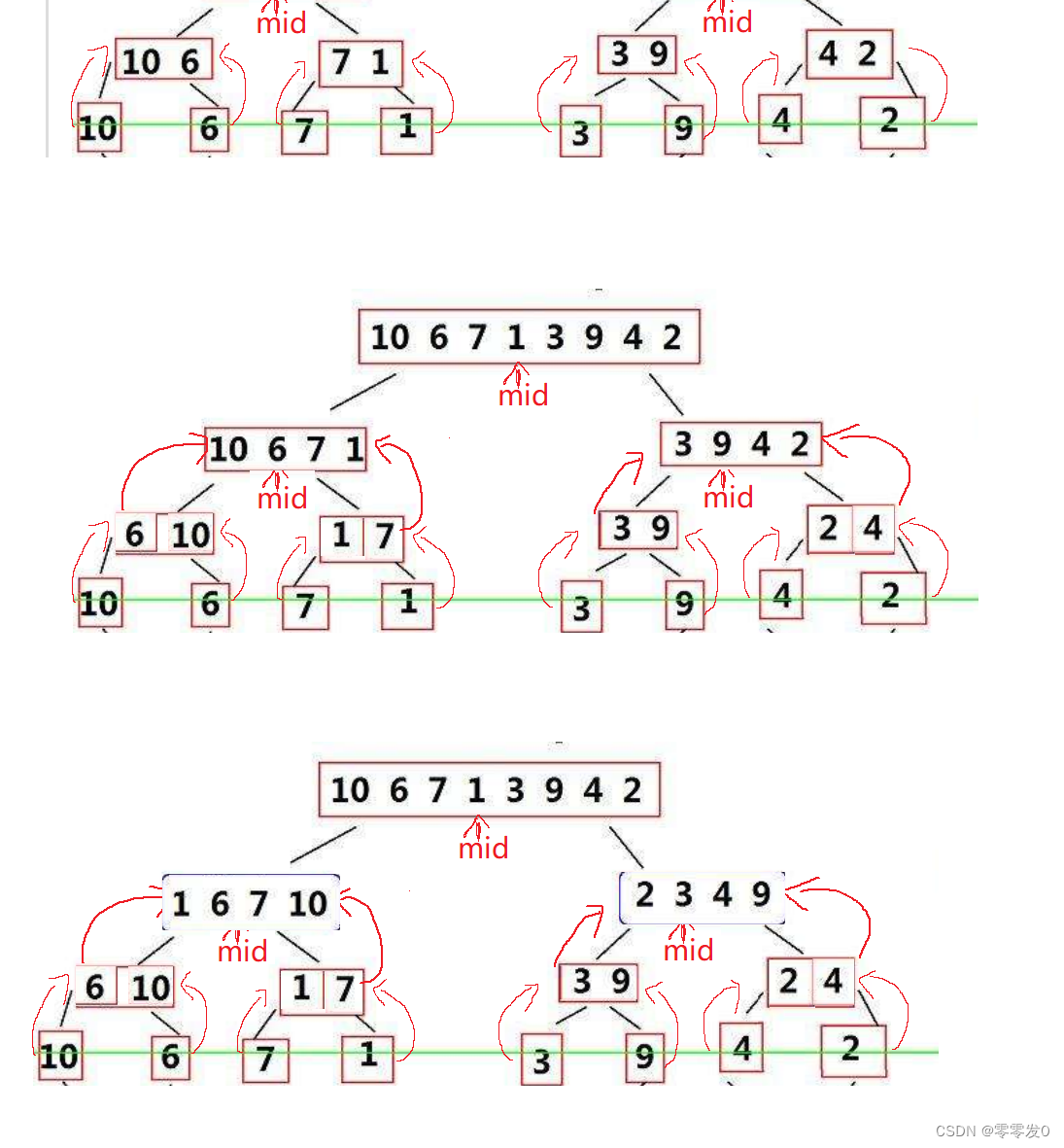
非遞歸實現

非遞歸實現，怎么實現呢?我們上面快排的非遞歸實現運用了棧來解決，那么這里能用棧來解決問題嗎?可以，但是這里就比較麻煩，如果我們用棧來解決的話，那么循環的結束條件難以判斷，同時此處棧管理起來也比較麻煩。我們這里可以用迭代來實現。

需要注意的是，我們每次要歸并的兩組數據，end1,begin2,end2有可能會越界，因為for循環的判斷條件是i<n-1,此時除了begin1其余三個都可能會越界，所以我們要判斷修正。

當begin2越界時，代表第二組越界，也就是不存在，所以不需要歸并；當只有end2越界時，只需把end2修正為最后一個元素繼續歸并即可。其余也就沒什么好說的了。

時間復雜度與空間復雜度以及穩定性

首先，我們先來了解一下穩定性的概念：

穩定性：假定在待排序的記錄序列中，存在多個具有相同的關鍵字的記錄，若經過排序，這些記錄的相對次序保持不變，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，則稱這種排序算法是穩定的；否則稱為不穩定的。

如上圖所示，即排完序后，黑6與紅6的相對位置不變（黑6還在紅6前面），那么這個排序就是穩定的。

知道了這個，我們接下來一個一個分析上面各個排序算法的時間復雜度、空間復雜度以及穩定性

1.直接插入排序

穩定性：穩定

時間復雜度：O(N^2);

空間復雜度：O(1)。

直接插入排序[0,end]有序，讓arr[end+1]與[0,end]進行比較交換，當兩數相等時，我們可以讓其不交換，那么最后拍完序相等元素的相對順序是不變的，所以說直接插入排序是穩定的。

通過上面的代碼，不難分析出直接插入排序的時間復雜度為O(n^2),由于沒開辟新的空間，所以說空間復雜度為O(1)。

2.希爾排序

穩定性：不穩定

時間復雜度：O(N*logN)

空間復雜度：O(1)

我們上面講，希爾排序是插入排序的變形，那么希爾排序穩定嗎？答案是不穩定。

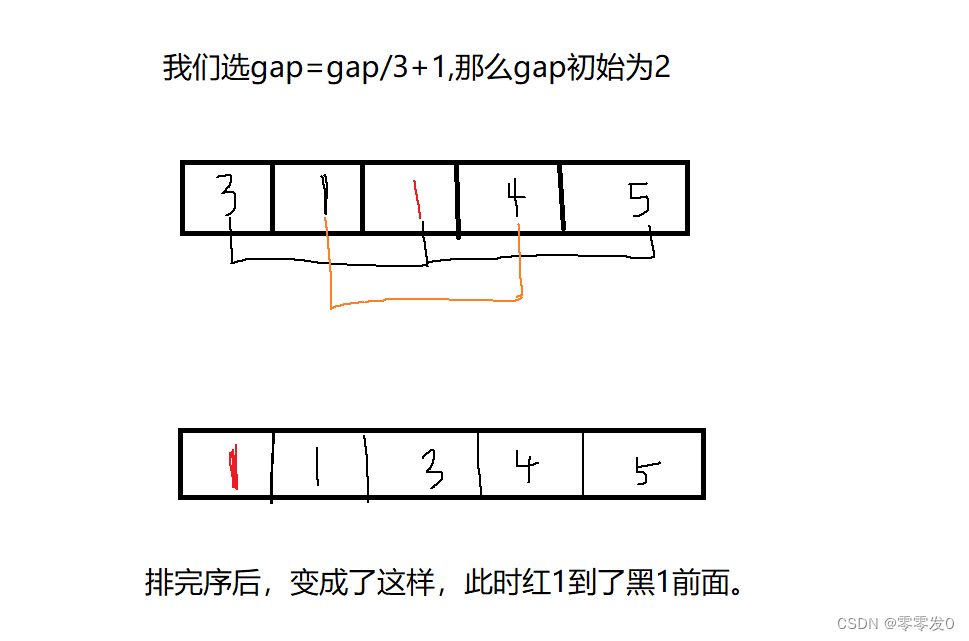
故希爾排序不穩定。那么希爾排序的時間復雜度又為多少呢？

這個就很復雜了，因為希爾排序循環次數與gap的取值有關，而gap又有很多種不同的取值方法，

同時，while循環比較次數和元素移動的次數也難以計算，所以說這需要很強的數學專業知識，筆者不會，但有大佬給出希爾排序的時間復雜度大概為O(N^1.3),記住就行。

那么希爾排序的空間復雜度為多少呢？很顯然是O(1)。

3.選擇排序

穩定性：不穩定。

時間復雜度：O(N^2);

空間復雜度：O(1)。

選擇排序為什么不穩定的，這是個易錯點，我們看下圖的分析：

這種情況就是不穩定的情況。時間復雜度空間復雜度比較簡單，不再贅述.

4.堆排序

穩定性：不穩定。

時間復雜度：O(n*logN)

空間復雜度：O(1)

由于堆我們之前沒有講解，講起來有一點麻煩，我們先放一下，之后專門講解堆的相關知識。

5.冒泡排序

穩定性：穩定

時間復雜度：O(N^2);

空間復雜度：O(1)；

6.快速排序

穩定性：不穩定。

時間復雜度：O(N*logN);

空間復雜度：O(? logn)~O(n)。

快排也無法保證相等元素的相對位置，這個很好想例子，比如下圖?：

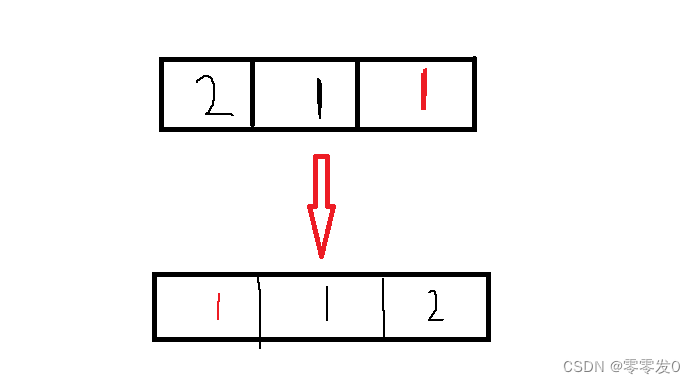
這里的易錯點就是空間復雜度不是O(1)!!!

函數遞歸需要額外開辟空間，我們上面也講了，快排通常是遞歸實現的，N個數組成的數組每次被分成兩個區間，依次分割，直到left>=right，它一共分了logN次，故需要開辟logN個新的空間

有小伙伴會問，遞歸遞歸，它往回歸的時候，不是又應該開辟一塊新空間嗎？好問題，函數遞歸，回歸時用的是已經開辟好了的空間。這涉及到函數棧幀的問題，有興趣的小伙伴可以去學習學習，增強內力。

7.歸并排序

穩定性：穩定

時間復雜度：O(N*logN).

空間復雜度：O(N).

也沒什么好說的，比較簡單。

總結圖：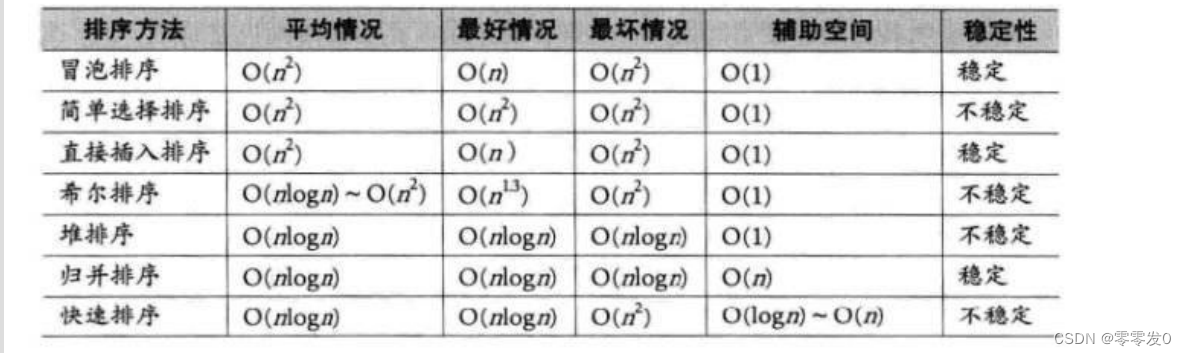

筆者希望大家能夠理解性的去記憶這些東西，理解它們的原理，這樣記憶起來就事半功倍了。