一個簡單的問題：

如果此時你正站在迷路繚繞的山坡上，能見度不高，但是你又想去往最低的山谷的位置，怎么走？

很簡單，哪里陡那就往那里走唄——而這就是梯度下降算法的思想。

古話說：“先發制于人，后發而制于人。”

想要做到有效先發呢，就得做到對事務的準確預測，要預測就得先掌握其規律。規律從哪里來？當然是從數據上來，所以關鍵就是要找到數據與數據之間的關聯。

比如氣溫越高，雪糕的銷售額也就越高，這個就是數據與數據之間的關聯：

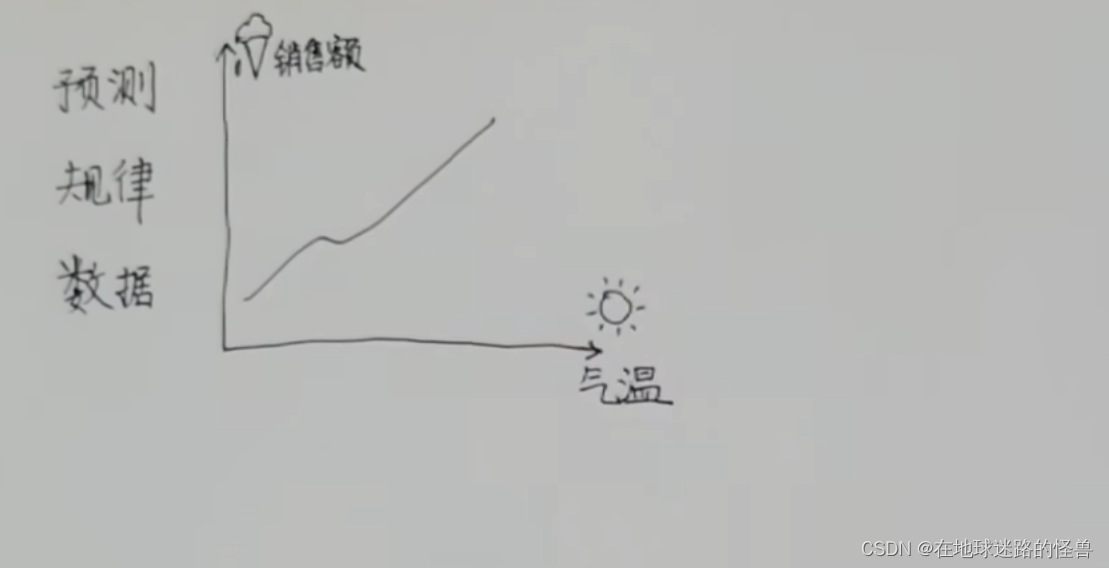
還有一個經典的例子，就是房子價格與面積的關系：

從所給數據不難看出二者是有正相關關系的。

但是要做到準確的預測的話必須要得到它們之間的函數關系式，這樣我們只需要給出一個面積值那么立馬就能直接得到價格是多少了。

要求函數關系式的話，那么需不需要做一條曲線將坐標系中的所有的點都穿過去呢？明顯是不可以的，因為當有新數據再加進來的時候，往往新數據根本就不在這條曲線上：

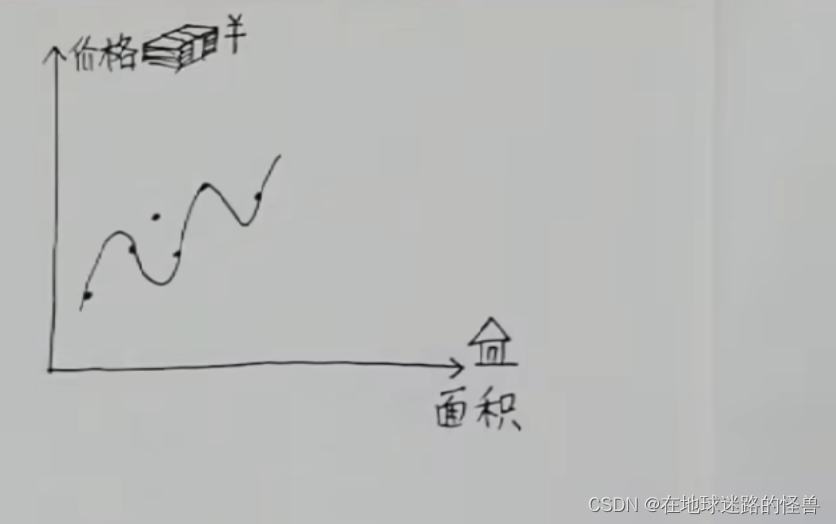
這樣吃力不討好的行為（勾畫曲線），通常叫做過擬合。

對于這種明顯有相關關系的數據往往最樸素的方法反而效果更好，直接用一條直線去擬合這些數據：

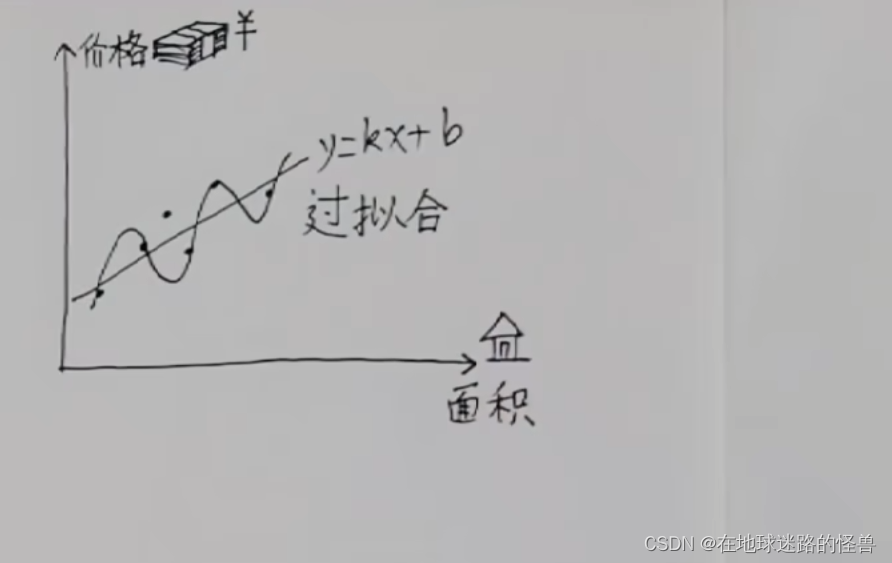
直線的話就好搞了，就是一次函數 y=kx+b 嘛，只要把這條直線的斜率和截距都找到的時候，那么這條直線就自然被找出來了。

而我們找到最合適的這條直線的這些動作，我們就稱作線性回歸。

那么哪條直線更合適呢？畢竟有那么多：

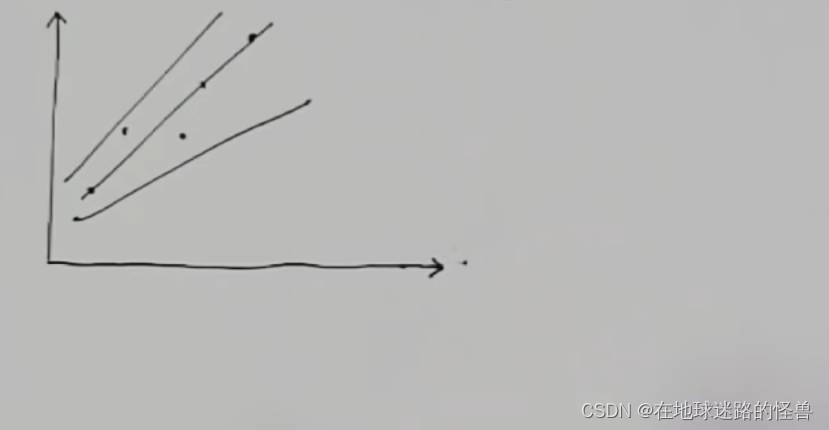
這很難說，那么既然很難決定，那就全部一起考慮，跟選秀一樣，到時候留下最合適的那個就可以了。

既然是選秀，那么就會有標準，標準是什么呢？

以下圖中的一條黑線和紅線為例，這兩條都是擬合真實數據出來的直線（二者都是理想化的估算數據）：

不難看出二者與真實數據之間都是有差距的，但我們可以把每個點的真實數據和估算數據的誤差給算出來，在圖上可以表現為真實數據豎直到這條線的距離是多長：

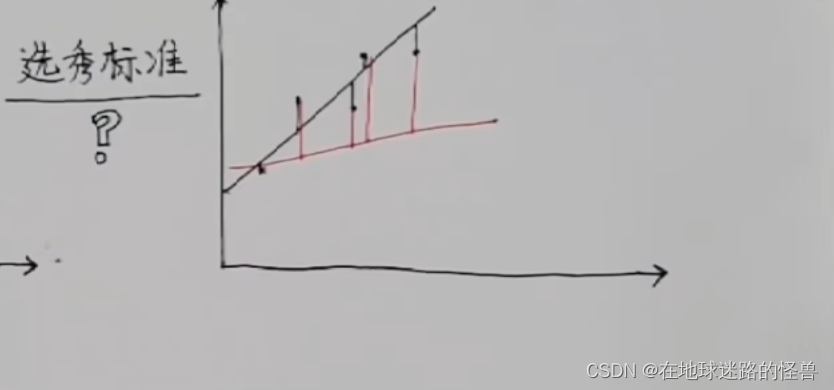
可以明顯看到，黑線的距離之和是要比紅線的距離之和要短的，那么我們就可以認為黑線更優秀，和原數據更加符合。

接下來使用數學語言來描述一下這個事情：

假如真實數據是 y1， y2， y3， y4， y5，而估算數據是 y^ = kx+b：

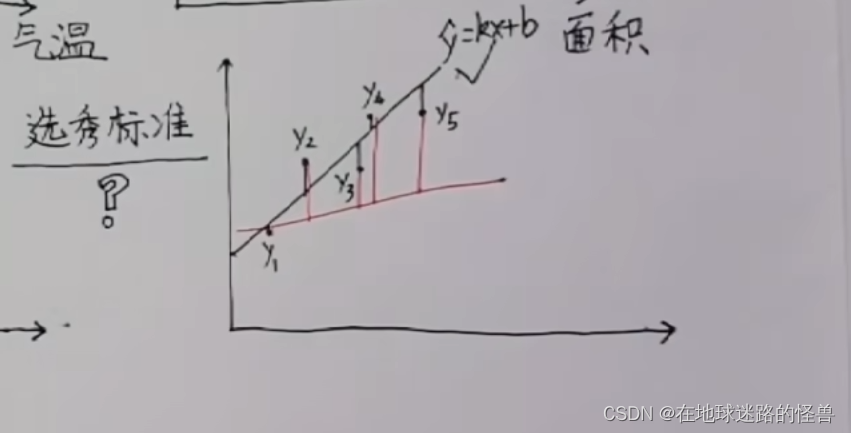
那么其距離之和可以表示為：

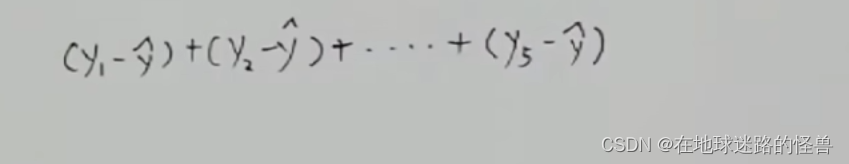
但是此時有一個問題，點在線上方的距離算出來是正的，而點在線下方算出來的距離呢則是負值：

一正一負相加是會抵消掉一些距離的，那么算出來的結果肯定就會出問題，為了消除正負距離帶過來的影響，我們可以對每一項進行取平方的操作：

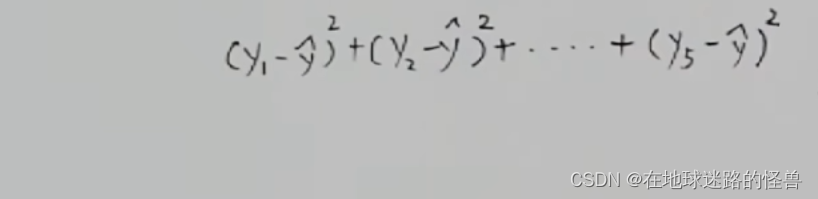
這樣再加起來就正確了，這同樣可以反映出距離之和的大小。

但還有一個新的問題，假如紅線不取五個點，而是取十個點怎么辦？因為取的點越多那么累加的距離的平方和肯定就越大，所以在取樣點的數量不一樣的時候是根本沒辦法比較的，這怎么辦？答案就是對他們取平均，主打一個眾生平等：

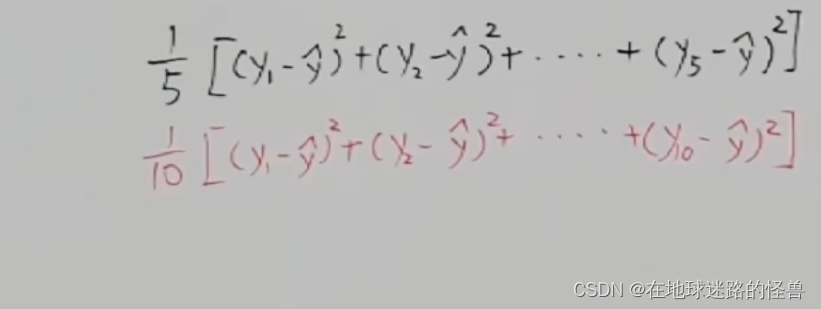
這樣取平均之后就可以進行比較了，那么這樣的話選秀的標準也就自然出來了：

上面這個值誰求出來的小，那么誰的線就和原數據符合的越好。其還有另外一個名稱：平均平方誤差MSE。

想要解決一負一正相加抵消的問題，那在這里不取平方取絕對值可以嗎？

當然可以，取絕對值的方式叫做平均絕對誤差MAE：

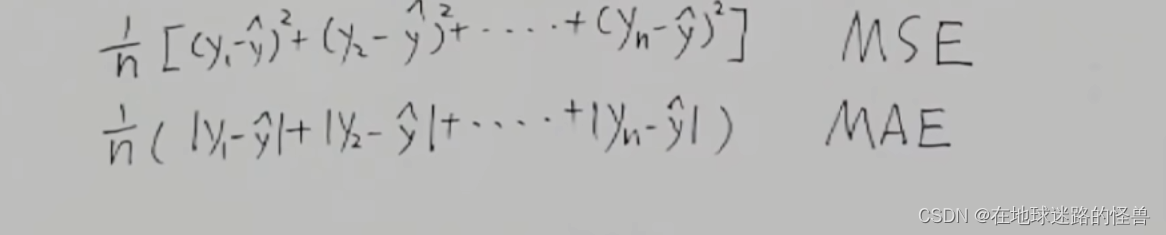
二者在不同的場景之下有不同的優缺點，但是對于梯度下降呢我們一般使用MSE，因為MSE的數學性質更好一些（肯定比求絕對值好算啊）。

在上面的情況中，在少數幾條直線的情況下，可以一眼就看出來或者說是稍微的計算一下就可以得出來擬合的較好的直線，但是如果候選者有無數多個，怎么辦呢？

簡單列個表可能更清晰一些：

我們的任務就是把所有的這個MSE的值全算出來然后挑出來最小的那一個 Zmin，而最小的那一個它所對應的 k 值和 b 值就是你要找的直線了。

上面的過程簡單說就是通過一個 k 一個 b 值來計算 MSE 值 z，而這不就是一個以 k 和 b 為自變量，z 為函數值的二元函數嗎？

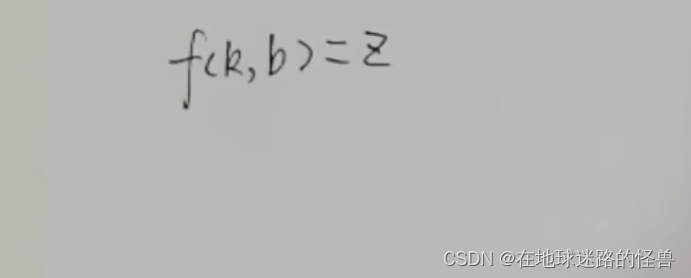
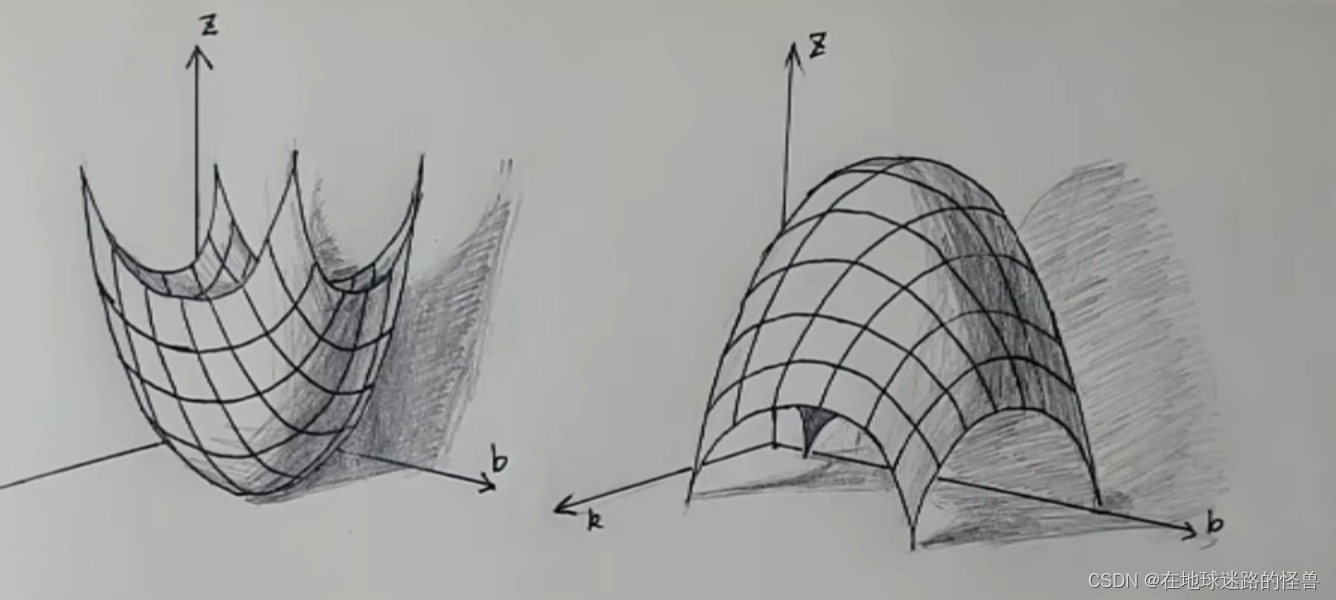
而二元函數長什么樣？可以簡單的看一下其幾何圖像：

而這個 f(k , b) = z 這個函數也被稱為損失函數，剛剛不是說任務就是要把這些 z 當中的最小值 Zmin 給找出來嗎？對應到這個損失函數其實也就是要把這個損失函數的最低的位置找出來。

那么現在我們的任務就變成了找到這個山谷的最低的位置了，要講明白下山，我們就得從上山講起：

其實就像地圖一樣，方便我們定位和指路，如果能有一個像導航一樣的上山神器就好了。

還真有！其實就是以前學習過的導數。

我們先看二維坐標系下的導數的相關概念，下圖是一個一元函數 f(x)，假如現在我們是在 x0 的位置，我們可以對這個點求導數，也就是這個點的切線的斜率，可以看到在 x0 這一點上的導數值是大于 0 的：

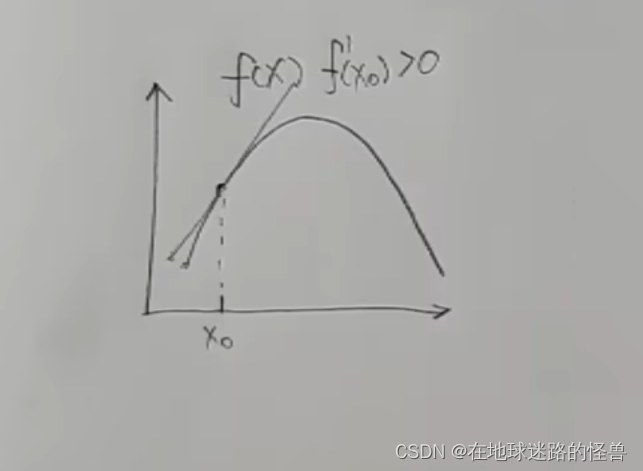
而導數值大于 0 實際上就是在告訴我們這個 x0 要往增大的方向走函數值才能變大才能上坡。

再看一個點 x1，該點上切線斜率實際上是小于零的，這就意味著這個 x1 要往減小的方向去走函數值才能變大才能上坡：

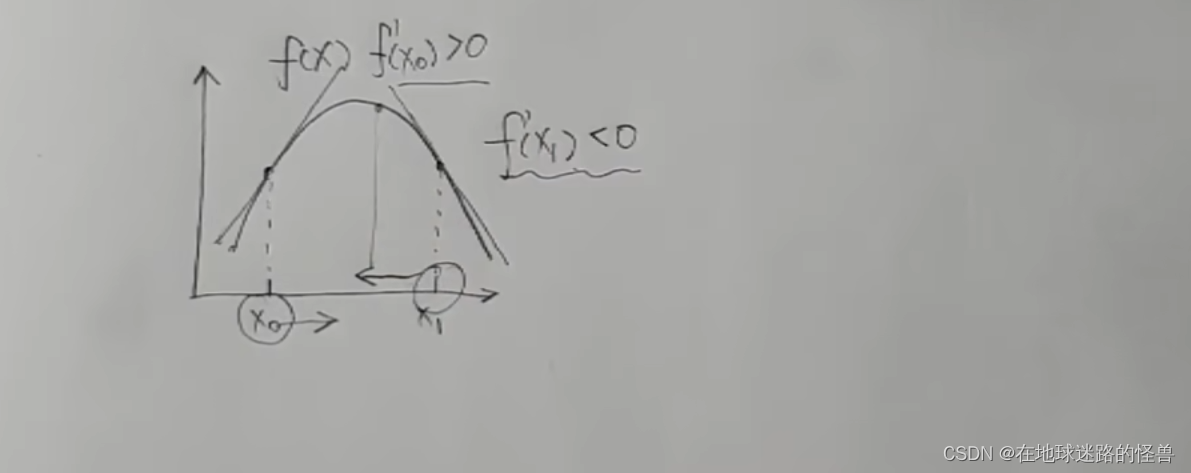
這樣一看使用導數值來指明方向還挺好用的，但是只告訴了方向還不太夠啊，最好是還能告訴我一步要走多遠，然后走到頂了最好還可以叫我停下來這樣是最好的。

恰好導數也能夠做這個事情。

我們直接拿導數的大小作為步子的長短，假如我們還是在 x0 的這個位置，然后求出這一點的導數是等于二的，那么我們直接拿這個二作為步子的長短，x0 呢就應該要往增大的方向加二來到這個位置對應的函數值。重復這個步驟，隨著越來越靠近山頂的位置，坡度就越來越小，那么步子呢也會越來越小，來到山頂的時候導數為零那么直接就是不走了，而這就是我們想要的：

找新落腳點的這個動作我們還可以使用數學語言描述出來，假設現在所在的點是 Xn，對該點求導數將其作為前進的步長就把它直接加上去，得到的結果呢作為下一個點的落腳點：

當然這是一個最理想的狀態，萬一 X0 這個位置的切線斜率太大了導致跨的步子大了一些，直接一步跨過了山頂的位置來到了對面的位置，不過這也不用慌，因為此時求導數值小于0，它還是會回來的，往復循環最終也能到達山頂：

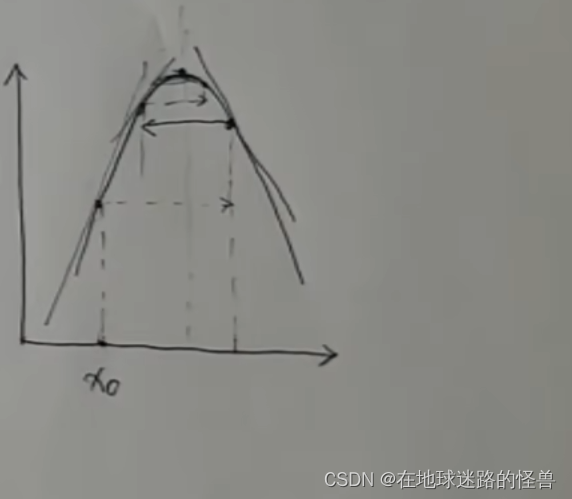
真正麻煩的其實是下面這幾種情況，一步剛好跳到了對稱的位置，因為是對稱的所以求導數再往回跳就又跳回了原來的位置，然后就會一直反復橫跳根本停不下來：

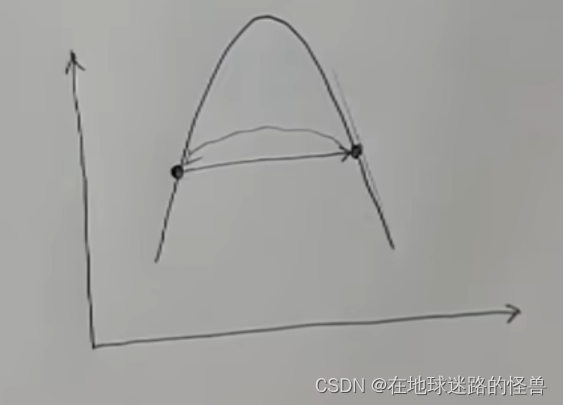
還有一種是從一個位置直接跳到了斜率更大的地方，然后它又會往回跳跳到更遠的地方去了，隨著循環它就會越跳越遠越跳越遠然后直接爆炸。

還有這種不止一個山頂的，前面的坡太小導致每一步的步伐也很小，當來到第一個小山頂的時候邁不過去了，你就會以為你已經來到了最高的位置就不走了，陷入了局部最優解：

因此我們在更新位置的時候一般會對這個每一步的長短呢做一個控制，也就是直接在這個導數面前乘以一個系數α，來改變其步長大小。而這個系數，我們又稱之為學習率。學習率也不一定是個定值，主要是看你的策略。

那么上面講的這些個東西是怎么應用到二元函數上面去的呢？

首先不難得知，二元函數的方向有兩個，一個是 k 方向，一個是 b 方向，而上山的方向則可以看作是這兩個方向的合成。這和地圖上是一樣的：往東走再往北走，其實等價于往東北方向走嘛：

既然我們要走的方向是上坡，那方向分解到 k 方向和 b 方向呢也應該都是上坡的，如何分解？

假如現在所在的位置是 K0 、B0，它所在的這條經緯線，我們沿著 K 軸的方向看過去，實際上它就是 BOZ 平面上的一條曲線：

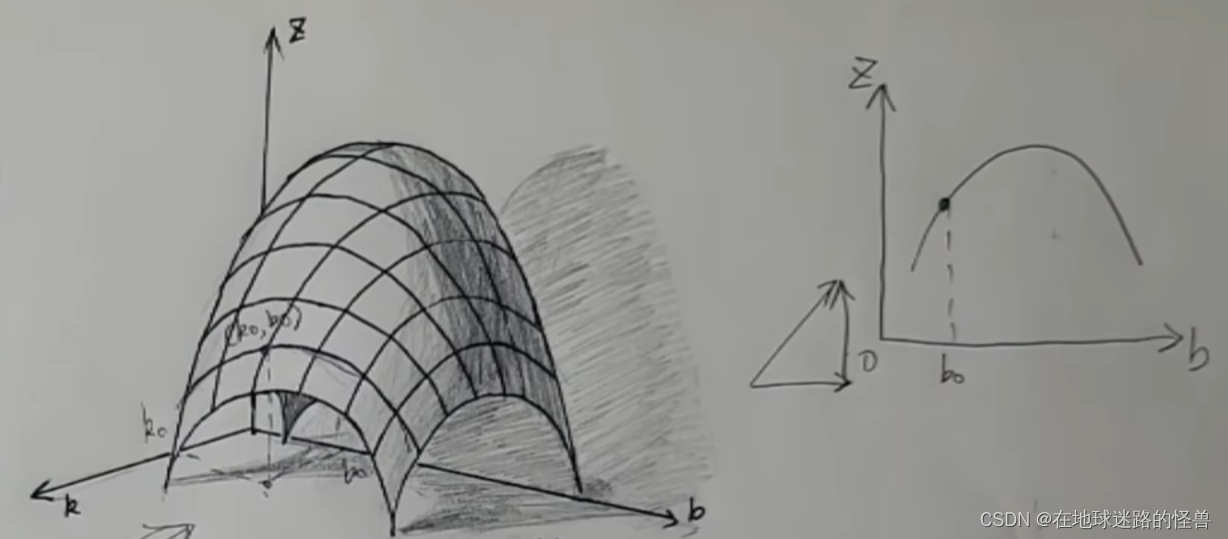
而在 B 的方向上要上坡，那么直接對 B0 這個點求導不就可以了嗎？

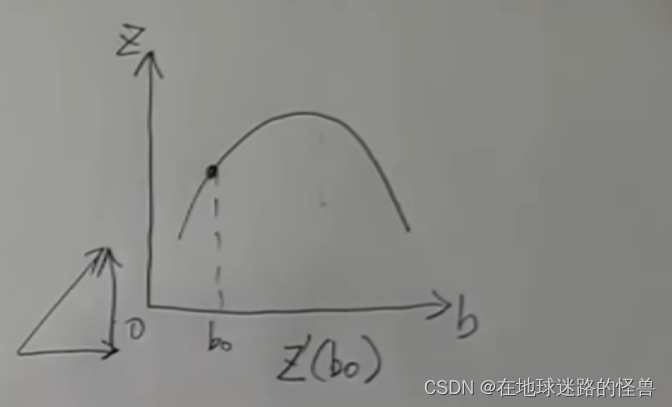
而因為上圖中這條線是垂直于這個 K 的方向截出來的，這條線上所有的 K 值都是 K0 不變的，把 K 的值當常數然后再對 B 求導，這不就是對于二元函數來求 B 的偏導嗎？然后再把 B = B0 這個點帶進去所得的值就是 B 的值的變化量啦：

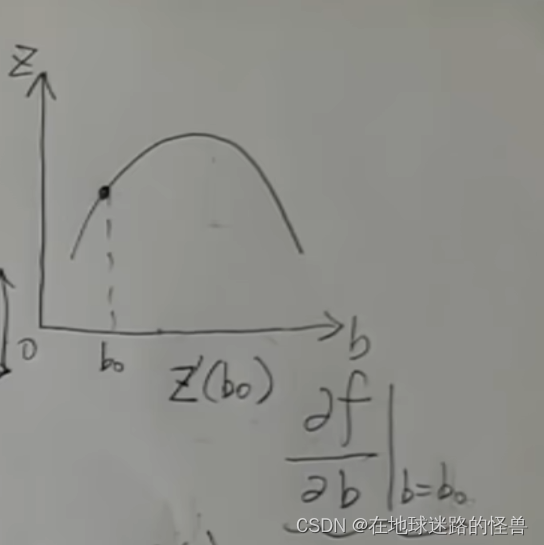
同理對于 K 值的變化量我們只需要換一個方向也就很好求解出來了，也是一個求偏導的操作，然后我們就得到了：

得到的這兩個偏導值既告訴了 K 和 B 的方向怎么走，然后呢變化量是多大，所以這個東西不就是一個向量嗎？

而這個向量的名字呢，就叫做梯度。

要注意一下，這個梯度指明了 K 方向和 B 方向的變化量，所以梯度應該是這個 KOB 平面上的一個二維向量，怎么理解？用一些具體的數字來看一下吧。

假如現在所在的點是 （1，2），然后求出來梯度的向量呢是（2，3），那么我們的下一個落腳點就應該是 1+2 = 3，2+3 = 5，也就是落腳點在點（3，5）的位置。

梯度是上山的方向，那么下山咋辦？注意一點，這里的山是連續可微的，那直接沿著上山的方向反著走不就下山了嗎？

從數學上看就是直接求出這個梯度向量，然后在它前面乘以 -1 ，然后再沿著這一個方向走，就可以下山去了呀（也就是梯度下降的形象化表示）。

因此再看回來這一幅圖：

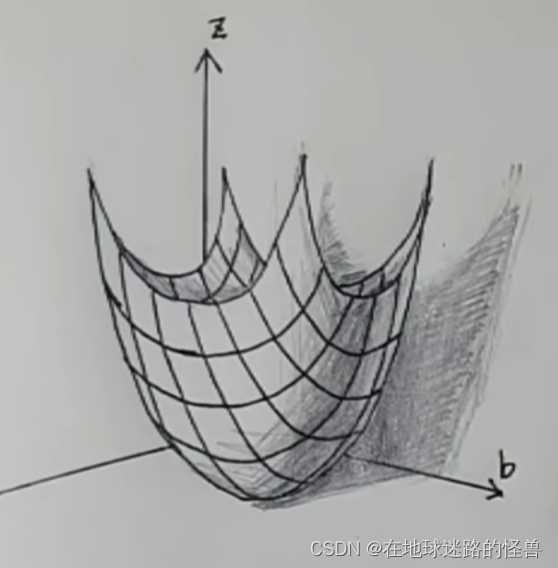
假設當前所在位置在 (Kn，Bn)，那么下一個落腳點表示為 (Kn+1，Bn+1)，按照我們上面說的，那么 Kn+1 就應該等于 Kn 加上 沿著反梯度的方向也就是減去它的導數，同理 Bn+1 也是一樣。那么就可以得到如下式子：

當然別忘記了要在偏導前面乘上一個學習率α控制步長嗷：

最后當這個偏導逐漸為 0 的時候，也就意味著你走不動了，也就來到了最低的位置了。

而此時所得到的 K 值和 B 值呢，就是我們之前線性回歸時心心念念的直線的斜率和截距了。

這便是梯度下降算法的第一印象了。